Abstract
In this paper, new approximation methods for solving systems of ordinary differential equations (SODEs) by fuzzy transform (FzT) are introduced and discussed. In particular, we propose two modified numerical schemes to solve SODEs where the technique of FzT is combined with one-stage and two-stage numerical methods. Moreover, the error analysis of the new approximation methods is discussed. Finally, numerical examples of the proposed approach are confirmed, and applications are presented.
1. Introduction
Differential equations have great potential to model and understand real-world problems in science and engineering. In many cases, differential equations cannot be solved analytically, so that numerical methods are required. Therefore, numerical methods have been elaborated frequently in scientific research for solving differential equations, for example [1,2,3,4]. In this connection, fuzzy approaches successfully cope with solving differential equations. One of fuzzy approaches that has been proposed in the literature is fuzzy transform (FzT).
FzT is a general mathematical technique coined and developed by Perfilieva [5]. The study of FzT is rapidly expanding as a new branch of approximation method based on fuzzy sets. The main idea of FzT is usually forming a fuzzy partition of a universe into fuzzy subsets. Two shapes for the basic functions of fuzzy partition, triangular- and sinusoidal-shaped membership functions, were considered by [6]. Applications of the FzT can be used in the construction of approximate models, the approximation of functions and the solution of differential equations. FzT has been generalized from the case of constant components to the case of polynomial components [7]. Later, FzT was successfully used by [8] for a second order initial value problem. From this idea, FzT was proposed for numerical solutions of two point boundary value problems by the more efficient way in comparison with the similar ones obtained by the finite difference method [9].
Recently, in [10], a new numerical method based on FzT to solve a class of delay differential equations by means of the Picard-like numerical scheme was presented. The author demonstrated the stability of the method, and the obtained results have good agreement with existing methods. Furthermore, in some cases, a better approximation was achieved through sinusoidal-shaped basic functions, while the Bernstein basis polynomials allow better results in the other examples. On the other hand, a new approach to the fuzzy boundary value problem in the form of the fuzzy relation was investigated by [11]. Another approach for the second order linear differential equation with constant coefficients and Dirichlet boundary conditions was introduced by [12], where the ability of FzT was demonstrated to deal with boundary value problems affected by noise, and the results were compared with the finite difference method. To confirm again the ability of FzT with respect to noisy and non-noisy source functions, FzT based on the shooting method was introduced by [13] for solving a nonlinear second-order ODE, and the obtained results were better than the classical method, namely the second order Runge–Kutta. Further, in [14], FzT to approximate the solution of boundary value problems by minimizing the integral squared error in the two-norm was considered. The trigonometric function based on higher degree FzT and the accuracy of the resulting approximation increase with the increase in the degree of FzT were presented by [15], while the weighted transform method was discussed by [16]. The conditions for quasi-consensus in a multi-agent system with sampled data based on FzT were proposed by [17]. In [18], the dynamical properties of a two-neuron system with respect to FzT and a single delay have been investigated. Multi-step FzT was first studied by [19] for solving ODEs. From this perspective, FzT was considered for solving a class of ODEs.
In this regard, many approximation methods have been studied for solving ODEs, for example using neural networks [20], embedded three and two pairs of nonlinear methods [21], electrical analogy [22], multi-general purpose graphical processing units [23], the differential transform method [24] and a Galerkin finite element method [25]. A numerical method based on the trapezoidal rule for the Cauchy–Smoluchowski problem was discussed by [26]. In [27,28], the authors studied ODEs with the initial value as the triangular fuzzy number. A new fuzzification of the classical Euler method and then incorporating an unconstrained optimization technique were proposed by [1]. Furthermore, most real-life problems involve systems of ODEs, for example the Lotka–Volterra prey predator model based on an autonomous model [29], a non-autonomous model [30,31] and fuzzy initial populations [4].
In this study, our aim is to extend the applicability of the FzT to general coupled Systems of ODEs (SODEs) where this method works better than its classical counterpart. The motivation of the present research stems from the fuzzy approach as follows. The first application of the FzT for solving ODEs had been proposed by [6] where a generalization of the Euler method for an ordinary Cauchy problem was developed and its potential in comparison with classical methods (Euler method) was demonstrated. The same approach has been successfully used by [32] to solve the Cauchy problem for a more accurate comparison with the classical method (the second-order Runge–Kutta method) and with the generalization of Euler method based on FzT, as proposed by [6]. Further, in [19], new fuzzy methods based on FzT for solving the Cauchy problem were presented, and the authors compared the results with existing numerical results in [6,32] and with classical methods, including one, two and three steps. All these fuzzy approximation methods performed better than the classical trapezoidal rule (one step) and the classical Adam–Moulton method (two and three steps) and outperformed the previous fuzzy methods in [6,32].
In this contribution, two new approximation methods are presented in detail to solve SODEs where the technique of FzT is combined with one-stage and two-stage numerical methods. The first approximation method improves the Euler method (one-stage), and the other approximation method improves trapezoidal rule (two-stage). The primary focus of this contribution is to demonstrate the applicability of the FzT for functions of two variables based on the uniform fuzzy partition. The error analysis is discussed in the context of the uniform fuzzy partition. Algorithms inspired by the FzT are shown for solving SODEs. Two new approximation methods are applied to the Lotka–Volterra prey-predator model. This contribution is an important modification relative to classical methods, the Euler method and the trapezoidal rule. Thus, these methods are compared with the Euler method and trapezoidal rule. Both approximation methods with the help of FzT provide better numerical solutions than the classical Euler method and the classical trapezoidal rule.
The paper is organized as follows. In Section 2, several related concepts and results associated with the FzT are reviewed. In Section 3, we construct procedures to obtain an approximate solution for SODEs by using the FzT method. Applications are discussed in Section 4. Finally, conclusions are given in Section 5.
2. Basic Concepts
Throughout this section, we deal with an interval of real numbers. Let be an interval on the real line . Fuzzy sets on will be identified with their membership functions mapping from into . We will assume an interval as a real domain. In this section, we remind about the definitions and claims that were introduced and proven by [5].
Definition 1.
(Fuzzy partition) Let be fixed nodes within such that and . The fuzzy sets are often called basic functions. We say that fuzzy sets establish a fuzzy partition of if they fulfill the following conditions for (for the uniformity of notation, we set and ):
- 1.
- is continuous with , if and if ;
- 2.
- strictly increases on , and strictly decreases on ;
- 3.
- For all , This is called the Ruspini condition.
We say that a fuzzy partition of is h-uniform if its nodes , where are equidistant. This means that where and the two additional properties are fulfilled:
- , for all and:
- for all .
Two uniform fuzzy partitions with triangular- and sinusoidal-shaped basic functions can be found in [5,6]. Throughout this paper, we will write uniform fuzzy partition instead of h-uniform fuzzy partition.
Definition 2.
Let f be a continuous function on and , , be a uniform fuzzy partition of , . A vector of real numbers given by (to complete this notation, we set and ):
is called the direct FzT of f with respect to .
Remark 1.
The elements are called components of the FzT. If forms a uniform fuzzy partition, then the expression (1) can be simplified as follows:
Definition 3.
Let be the direct FzT of with respect to , . Then, the inverse FzT of f, , given by:
Lemma 1.
[6] Let be continuous on and twice continuously differentiable in , and let basic functions form a uniform fuzzy partition of . Then, for each :
Remark 2.
An important property of the direct FzT, as well as inverse FzT is their linearity, namely, given and , if , then and .
3. FzT for Solving SODEs
In this section, we present methodological remarks and numerical schemes for solving SODEs.
3.1. Methodological Remarks to Applications of the FzT
Consider the Initial Value Problem (IVP) for the SODEs:
where , f and g are continuous functions on and satisfy the Lipschitz condition. Unfortunately, the analytical solution of Problem (5) is often difficult and sometimes impossible to obtain. Thus, approximate solutions by means of FzT are extremely important for solving (5). A numerical method for (5) is an algorithm that computes FzT components and , for each (to complete this notation, we set and ).
Below, we extend the main principles of FzT detailed in Formulas (6) that are needed later.
Definition 4.
Let f be a continuous function on and be the fuzzy partition of . A vector of real numbers given by:
is called the direct FzT of f that is extended with independent variable t and two dependent variables x and y.
Remark 3.
We need a way to approximate the direct FzT components 6. This is discussed in Corollary 1.
In the following, the necessary steps of the FzT are given.
- Construction of the fuzzy partition:
- (a)
- Specify the number n of components, and compute the step .
- (b)
- Construct the nodes , where .
- (c)
- Select the shape of basic functions. We mostly use triangular- or sinusoidal-shaped basic functions. Recall that the shape of the basic functions determines the course of , that is whether it is piecewise linear or nonlinear.
- (d)
- Construct a uniform fuzzy partition of by triangular- or sinusoidal-shaped basic functions [5].
- Computation of FzT: We replace by their approximations based on the Taylor expansion as new functions with respect to the fuzzy partition by Step 1. In this way, similarly to [6], we transfer the original SODEs to the space of fuzzy units, solve them in the new space and then transfer them back by the inverse FzT. Compute the approximation for x and y by the inverse FzT applied to and . In the next subsections, the schemes provide formulas for the computation of components of FzT.
3.2. Numerical Scheme I for SODEs
In this subsection, we present a modified scheme to solve SODEs using the FzT. Suppose that the functions f and g on are sufficiently smooth in (5). For solving SODEs (5) on , the interval is divided into subintervals. Let us choose some uniform fuzzy partition of interval with parameter , , and basic functions . In view of the methodological remarks in Subsection 3.1, we describe the complete sequence of steps, which leads to the approximation solution of SODEs (5) (see [6] for technical details). Before we apply the direct FzT to both parts of the differential equation, we will use the Taylor expansion and replace the first derivatives of the left-hand sides in (5) by their approximations, i.e.,
Denote as new functions and then apply the direct FzT components to both parts of Equation (7).
where and
Now, prove that:
For the values and by Lemma 1, we have , and for , we have:
Then, we get:
Therefore, we can introduce the matrix:
Now, let us return to the problem (5) and apply the FzT to both sides of the differential equation. Based on the linearity of FzT and Formula (9), we obtain the following system with respect to the unknown :
where are the FzT of () as a function of t w.r.t. the chosen basic functions . Note that the last components and are not presented in and , respectively, due to the dimensionality limitation, and (10) does not include two initial conditions of (5). Thus, we complete the matrix D by adding the first row as the initial value as follows:
so that is an nonsingular matrix. Based on the initial conditions and the matrix , we also expand and by adding the first element, as follows:
Then, the problem (5) can be completely represented by the following expression with respect to the unknown and :
The solution of (11) can be obtained by the following formula:
In fact, to obtain the solution of (12), we should compute the inverse matrix of . Therefore, we have:
and by (12), we get:
where is given by Formula (6). Formula (13) can be applied to the computation of and . However, it cannot be applied directly by using the function or , because it uses unknown functions x and y. Therefore, we will use the same trick as in [6] and replace functions by their FzT components:
Thus, the components of FzT of x and y can be approximated from the following Scheme I:
Finally, the approximate solution of (5) can be obtained using the inverse FzT as follows:
where are given basic functions. The proposed method is similar to the well-known Euler method and under similar assumptions. It has the same degree of accuracy. In the next theorem, we obtain an error estimate in the context of a fuzzy partition and error analysis of numerical Scheme I.
Theorem 1.
Let be twice continuously differentiable on . Let, moreover, be Lipschitz continuous with respect to x and y, i.e. there exists a constant , such that for all and ,
Proof.
Let us choose and fix some k, where , and assume that () is the k-th FzT component of x (y). We consider the SODEs (5) and their FzT representation by the system of equations (11). We start with the following easy consequences from the Taylor expansions:
By the assumption that f and g have continuous second order derivatives on and are Lipschitz continuous with respect to x and y, therefore, using the trapezoid rule and Remark 1, we get:
Similarly,
Therefore,
Denoting and using the obvious equality , we obtain from the above:
and finally,
By iteration, we come to:
where . For , we have:
where we made use of the following fact: , and the following asymptotic equalities: , .
Remark 4.
Theorem 1 extends Theorem of [6] to the SODEs.
Corollary 1.
Proof.
By Lemma 1, and (20), we get:
and using the trapezoid rule and Remark 1, we obtain:
which together with the previous estimation proves that:
Similarly,
☐
Corollary 2.
Theorem 2.
Let and bounded on . Let, moreover, basic functions form a uniform fuzzy partition of I. Assume that and , are the FzT components of and with respect to , respectively. Then, for :
where and .
Proof.
Let us write the following result from Taylor’s theorem:
where . Using the linearity of the FzT by Remark 2 and the properties of the uniform fuzzy partition by Definition 1, we get:
and:
which easily leads to (23). ☐
Lemma 2.
Proof.
Lemma 3.
Proof.
Let us choose a value of k in the range . By using Lemma 2, we get:
Similarly, ☐
Throughout the assumptions of Theorem 3, we consider instead .
Theorem 3.
Suppose that . Let and . Consider Scheme I (14)–(15) for some positive integer k, and , is a uniform fuzzy partition of , then the following hold true:
- 1.
- for a value of k in the range :where .
- 2.
- for all :where and .
Proof.
- Using (6), we can get for each and :Based on Remark 1 and Definition 1, the properties of the uniform fuzzy partition, we replace t by and then by . Thus,In a similar way, .
- We first prove the estimate for . Then, we show that for all , by using Lemma 2, for ,where . By (15), we get:By using (25), we get:where , and . In particular,where we have used inequality . Analogously, . which concludes the proof.
☐
Remark 5.
The following estimations are used in Theorem 4 for . Let satisfy the Lipschitz condition in the second and third arguments; we get:
From (20), we get:
Thus,
where , and .
Now, we show that the proposed Scheme I is convergent.
Theorem 4.
Let the assumptions of Theorem (3) be fulfilled, and further assume that satisfies a Lipschitz condition in the second and third arguments. Consider Scheme I (14)–(15) for some positive integer k, and , is a uniform fuzzy partition of . Thus, if a sequence of , and with each h, we compute the component, then , converges to zero for each .
Proof.
Let us drop the h subscript in the errors, writing and . Now, when , the result is clearly true, since , . By Taylor’s theorem, we have:
where . Denote . Then, by (15), we get:
By virtue of Remark 5, we get:
where and . Therefore,
- Case 1.
- If , , we get:where . Indeed, we have used inequality , , and the quantity is a finite geometric series; these can be calculated by:In particular, when , this implies that:
- Case 2.
- In view of Remark 5, let ,Thus,where and . Consequently,where . In particular, when , this implies that:and if a sequence of , we get , , which concludes the proof. ☐
3.3. Numerical Scheme II for SODEs
In this subsection, we will construct numerical Scheme II, a more advanced method than that of Scheme I. The components of FzT of x and y can be approximated by the average of the two methods, Scheme I (14)–(15) and the backward Scheme I (or implicit Scheme I), then the FzT is given by:
for
The problem with the previous scheme (28) is that the unknown quantities and appear on both sides (an implicit method). Therefore, one solution to this problem would be to use an explicit method such as another fuzzy approach. The following Scheme II for , :
where:
This method computes the approximate coordinates and of the direct FzT of the functions and , respectively. In the sequel, the inverse FzT (16) approximates the solution of the SODEs (5).
In the next theorem, we obtain an error estimate in the context of a fuzzy partition and error analysis of approximation Scheme II.
Theorem 5.
Suppose that . Let and . Consider Scheme II (29)–(30) for some positive integer k and , to be a uniform fuzzy partition of , then the following hold true:
- 1.
- for a value of k in the range :where .
- 2.
- for allwhere and .
Proof.
The proof is similar to the proof of Theorem 3, so we just write out the procedure. The proofs of Part 1 is as follows.
Lemma 4.
Proof.
We consider the SODEs (5). We start with the Taylor expansion and the forward divided difference approximation of the second derivative (please see Appendix A for more details), i.e.,
where . The first derivative can be replaced by the right-hand side of the differential Equation (5). The Taylor expansion becomes:
where and . We can write this as:
where:
Now, let satisfy a Lipschitz condition in the second and third arguments. By Lemma 1 and Remark 5, we have:
where is a positive constant. Once again, using Remark 5 and according to (29)–(30), we obtain for fixed :
By the trapezium formula, we have:
Note that:
Next,
This leads to:
Similarly, , where and are appropriate constants that depend on f and g, respectively. Therefore, the error of this method is . ☐
To see that Scheme II is globally a second-order method, we need to establish its convergence.
Theorem 6.
Proof.
The proof is similar to the proof of Theorem 4, so we just write out the procedure. According to Remark 5 and (31), we get:
Once again, using Remark 5 gives:
where
- ,
- , , ,
- , , ,
- is the upper bound of , , and .
Simplifying, then:
Similarly,
Therefore,
4. Applications
One of the main problems of mathematics appears with variable coefficients when are analytic functions and added to the model. The new differential equations are represented by non-autonomous SODEs. In this model, time varying values for the growth rate of the prey, the efficiency of the predator, being the ability to capture prey, the death rate of the predator and the growth rate of the predator are considered. It is important to remark that since in this problem, the coefficients are time varying, careful attention must be paid in order to obtain the correct recurrence equation system of the model. The model, incorporating the above functions, is as follows [30,33,34]:
Three examples are discussed in order to prove the results obtained by Scheme I (14)–(15) and Scheme II (29)–(30), two examples for the numerical solution of the model (35) and one example for the linear case.
Example 1.
Consider the problem of the Lotka–Volterra prey-predator model (35). We take
.
The exact solution for these coefficients is , as proposed by [30,33,34].
Example 2.
Consider the problem of the Lotka–Volterra prey-predator model (35) with
.
The exact solution for these coefficients is , as proposed by [30,33].
Example 3.
Consider the following non-autonomous SODEs with initial values (5):
The exact solution of (36) is given by .
The results are listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 by the proposed fuzzy approximation methods with respect to the raised cosine generating function and Table 8 by the proposed fuzzy approximation methods with respect to the triangular generating function and raised cosine generating function. The proposed fuzzy approximation methods are generated by Algorithms A1 and A2 (please see Appendix B). The mean square error (MSE) is defined as . This is an easily computable quantity for a particular sample. From the numerical tests, the results are summarized as follows:

Table 1.
The values of MSE for Example 1–3.

Table 2.
Comparison of numerical results of for Example 3.

Table 3.
Comparison of numerical results of for Example 3.

Table 4.
Comparison of numerical results of for Example 1.

Table 5.
Comparison of numerical results of for Example 1.

Table 6.
Comparison of numerical results of for Example 2.

Table 7.
Comparison of numerical results of for Example 2.

Table 8.
The values of MSE for Examples 1–3 by the different types of fuzzy partitions.
- Moreover, a comparison of MSE for Examples 1–3 is shown in Table 1. It is observed that the new fuzzy approximation methods yield more accurate results in comparison with the classical Euler and classical trapezoidal rule (one-step). The best result (in comparison with the Schemes I and II) is obtained by Scheme II.
- In Table 8, a comparison is given between the errors for two proposed schemes based on the FzT with respect to fuzzy partitions determined by [6,19].
The better results (in comparison with the non-linear case) are obtained by the linear case and non-autonomous SODEs in Example 3. Further, the results obtained using proposed fuzzy approximation methods for Examples 1–3 are shown in Figure 1 by using the raised cosine generating function. In view of Figure 1, the graphical results of Examples 1–3 show a comparison between numerical schemes (I and II) and the exact solution. Furthermore, in view of Figure 1, a comparison is given between the numerical results of Examples 1 and 2 and exact solutions for , while a comparison is given between the numerical results of Example 3 and exact solutions for . All the graphs are plotted using MATLAB software. This constitutes an important improvement to the previous fuzzy approach, which did not provide such information for SODEs. Thus, this study will be particularly important.
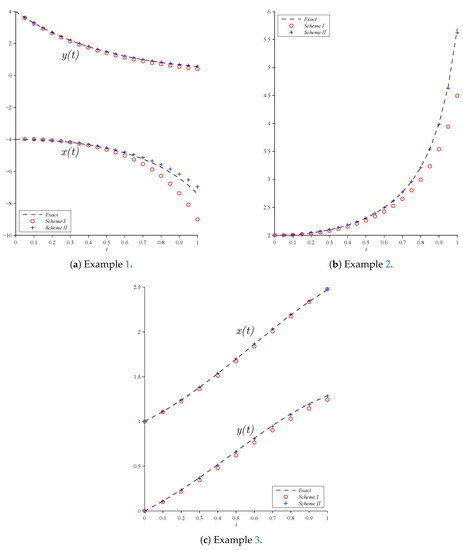
Figure 1.
A comparison between three fuzzy numerical methods and the exact solution for three examples.
Remark 6.
We compare new results based on FzT with the conventional numerical methods. For a discussion of the conventional numerical methods, the Euler method and trapezoidal rule to solve SODEs, see for example [35,36].
5. Conclusions
We extended the applicability of fuzzy-based numerical methods to the problems of conventional mathematics. In particular, we contributed to approximation methods of the SODEs. Two approximation methods based on the FzT were proposed and their error estimate analyzed. Moreover, we proved that two approximation methods, namely Schemes I and II, determine an approximate solution, which converges to the exact solution, and the local truncation error of the Scheme I (Scheme II) is . As an application, a system of nonlinear differential equations is solved by using Schemes I and II. From the numerical results, it is observed that the new fuzzy approximation methods yield more accurate results in comparison with the classical Euler method (one-stage) and classical trapezoidal rule (two-stage). Hence, the new fuzzy approximation methods provided alternative techniques for solving differential equations with better results, and the objective of this research was achieved and tested.
As a consequence, it should be noted that the numerical solutions depend on the types of uniform fuzzy partitions. For cases and , the shape of the basic functions determines the form of representation (linear or non-linear) of the numerical solution. This agrees with the results proposed by [5,6] using uniform fuzzy partitions. It is also worth pointing out that the results in this research are better in comparison with the classical numerical methods using uniform fuzzy partitions for linear and nonlinear cases. Thus, the proposed method is very much suitable for solving SODEs (5) in a linear or nonlinear case under the assumption of f and g satisfying the Lipschitz condition. If we want to obtain the best approximation of f and g as possible, then the number n of components should be large. It should be stressed that the application of the FzT can be used for removing noise from the given data. This is especially important for various practical applications of FzT. The proposed methods can also be applied to the n-dimensional system of first-order coupled differential equations in the case of a non-noisy or noisy right-hand side. The discussion will continue in [37] to give more details about the fuzzy partition and the modification of multiple steps.
Author Contributions
Conceptualization and performed the numerical experiments, H.A. ALKasasbeh; Evaluated the results and supported this work, I. Perfilieva; Project administration and designed the numerical methods, M. Z. Ahmad; Software and data curation, Z. R. Yahyaa.
Funding
The work of Irina Perfilieva has been supported by the project "IT4Innovations excellence in science, LQ1602" and by the Grant Agency of the Czech Republic (Project No. 16-09541S).
Acknowledgments
The authors would like to express their thanks to the editors and the anonymous referees for their valuable comments and suggestions that contributed to the paper. Many thanks are given to Universiti Malaysia Perlis for providing all facilities until this work was completed successfully.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Taylor Series
A Taylor series is given that:
where . Calculus can be used to derive that:
where .
Substituting Equation (A1), it is given that:
It can be rewritten as:
where:
Similarly,
where:
Appendix B. Algorithms
In this Appendix, the algorithms of the approximation methods based on FzT for Section 3.2 and Section 3.3 are explained in detail. Pseudocode is used to describe the algorithms and a simplified code that is easy to read. This pseudocode specifies the form of the input to be supplied and the form of the desired output. As a consequence, a stopping technique independent of the numerical technique is incorporated into each algorithm to avoid infinite loops. Two punctuation symbols are used in the algorithms: a period (.) indicates the termination of a step, and a semicolon (;) separates tasks within a step. The integral symbol (integral(function, upper limits, lower limits)) is used to denote a definite integral. The steps in the algorithms follow the rules of structured program construction. They have been arranged so that there should be minimal difficulty translating pseudocode into any programming language suitable for scientific applications. We approximate the solution of SODEs (5) at () equally-spaced numbers in the interval as follows.

Algorithm A1.
One-stage (modified Euler) algorithm for the system of ODEs.
Algorithm A1.
One-stage (modified Euler) algorithm for the system of ODEs.
| INPUT: and in Equation (5); endpoints ; integer N; initial condition . |
| Step 1 Set ; ; ; ; ; . |
| Step 2 Define the generalized uniform fuzzy partitions as . |
| Step 3 For to N, do Steps 4–7. |
| end. |
| OUTPUT: Approximation X and Y to x and y, respectively, at the () values of t. |

Algorithm A2.
Two-stage (modified trapezoidal rule) algorithm for the system of ODEs.
Algorithm A2.
Two-stage (modified trapezoidal rule) algorithm for the system of ODEs.
| INPUT: ; ; endpoints ; integer N; initial condition . |
| Step 1 Set ; ; ; ; ; . |
| Step 2 Define the generalized uniform fuzzy partitions as . |
| Step 3 For to N, do Steps 4–11. |
| end. |
| OUTPUT: Approximation X and Y to x and y, respectively, at the () values of t. |
References
- Ahmad, M.Z.; Hasan, M.K.; Baets, B.D. Analytical and numerical solutions of fuzzy differential equations. Inf. Sci. 2013, 236, 156–167. [Google Scholar] [CrossRef]
- Shawagfeh, N.; Kaya, D. Comparing numerical methods for the solutions of systems of ordinary differential equations. Appl. Math. Lett. 2004, 17, 323–328. [Google Scholar] [CrossRef]
- Atkinson, K.; Han, W.; Stewart, D. Numerical Solution of Ordinary Differential Equations; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Ahmad, M.Z.; De Baets, B. A Predator-Prey Model with Fuzzy Initial Populations. In Proceedings of the Joint 13th IFSA World Congress and 6th EUSFLAT Conference, Lisbon, Portugal, 20–24 July 2009; pp. 1311–1314. [Google Scholar]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transform: Application to the Reef growth problem. In Fuzzy Logic in Geology; Demicco, R.V., Klir, G.J., Eds.; Academic Press: Amsterdam, The Netherlands, 2003; Chapter 9; pp. 275–300. [Google Scholar]
- Perfilieva, I.; Daňková, M.; Bede, B. Towards a higher degree F-transform. Fuzzy Sets Syst. 2011, 180, 3–19. [Google Scholar] [CrossRef]
- Chen, W.; Shen, Y. Approximate solution for a class of second-order ordinary differential equations by the fuzzy transform. J. Intell. Fuzzy Syst. 2014, 27, 73–82. [Google Scholar]
- Alireza, K.; Zahra, A.; Irina, P. Fuzzy transform to approximate solution of two-point boundary value problems. Math. Meth. Appl. Sci. 2017, 40, 6147–6154. [Google Scholar]
- Tomasiello, S. An alternative use of fuzzy transform with application to a class of delay differential equations. Int. J. Comput. Math. 2017, 94, 1719–1726. [Google Scholar] [CrossRef]
- Hodakova, P.; Perfilieva, I.; Valasek, R. A new approach to fuzzy boundary value problem. In Uncertainty Modelling in Knowledge Engineering and Decision Making; World Scientific Proceedings Series on Computer Engineering and Information Science; World Scientific Publishing Company: Singapore, 2016; Volume 10, pp. 276–281. ISBN 978-981-3146-96-9. [Google Scholar]
- Perfilieva, I.; Števuliáková, P.; Valášek, R. F-transform for numerical solution of two-point boundary value problem. Iran. J. Fuzzy Syst. 2017, 14, 1–13. [Google Scholar]
- Perfilieva, I.; Števuliáková, P.; Valášek, R. F-transform-based shooting method for nonlinear boundary value problems. Soft Comput. 2017, 21, 3493–3502. [Google Scholar] [CrossRef]
- Alijani, Z.; Khastan, A.; Khattri, S.K.; Tomasiello, S. Fuzzy Transform to Approximate Solution of Boundary Value Problems via Optimal Coefficients. In Proceedings of the 2017 International Conference on High Performance Computing Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 466–471. [Google Scholar]
- Alikhani, R.; Zeinali, M.; Bahrami, F.; Shahmorad, S.; Perfilieva, I. Trigonometric Fm-transform and its approximative properties. Soft Comput. 2017, 21, 3567–3577. [Google Scholar] [CrossRef]
- Jahedi, S.; Javadi, F.; Mehdipour, M.J. Weighted transform and approximation of some functions on unbounded sets. Soft Comput. 2017, 21, 3579–3585. [Google Scholar] [CrossRef]
- Tomasiello, S.; Gaeta, M.; Loia, V. Quasi–consensus in Second–Order Multi–agent Systems with Sampled Data Through Fuzzy Transform. J. Uncertain Syst. 2016, 10, 243–250. [Google Scholar]
- Tomasiello, S. A First Investigation on the Dynamics of Two Delayed Neurons through Fuzzy Transform Approximation. In Proceedings of the 2017 International Conference on High Performance Computing Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 460–465. [Google Scholar]
- Alkasasbeh, H.A.; Perfilieva, I.; Ahmad, M.Z.; Yahya, Z.R. New fuzzy numerical methods for solving Cauchy problems. Appl. Syst. Innov. 2018, 1, 15. [Google Scholar] [CrossRef]
- Parapari, H.F.; Menhaj, M.B. Solving nonlinear ordinary differential equations using neural networks. In Proceedings of the 2016 4th International Conference on Control, Instrumentation, and Automation (ICCIA), Qazvin, Iran, 27–28 January 2016; pp. 351–355. [Google Scholar]
- Ramos, H.; Singh, G.; Kanwar, V.; Bhatia, S. An embedded 3 (2) pair of nonlinear methods for solving first order initial-value ordinary differential systems. Numer. Algorithms 2017, 75, 509–529. [Google Scholar] [CrossRef]
- Perez, J.F.S.; Conesa, M.; Alhama, I. Solving ordinary differential equations by electrical analogy: A multidisciplinary teaching tool. Eur. J. Phys. 2016, 37, 065703. [Google Scholar] [CrossRef]
- Al-Omari, A.; Arnold, J.; Taha, T.; Schüttler, H.B. Solving Large Nonlinear Systems of First-Order Ordinary Differential Equations with Hierarchical Structure Using Multi-GPGPUs and an Adaptive Runge Kutta ODE Solver. IEEE Access 2013, 1, 770–777. [Google Scholar] [CrossRef]
- Opanuga, A.; Edeki, S.; Okagbue, H.; Akinlabi, G.; Osheku, A.; Ajayi, B. On numerical solutions of systems of ordinary differential equations by numerical-analytical method. Appl. Math. Sci. 2014, 8, 8199–8207. [Google Scholar] [CrossRef]
- Al-Omari, A.; Schuttler, H.B.; Arnold, J.; Taha, T. Solving Nonlinear Systems of First Order Ordinary Differential Equations Using a Galerkin Finite Element Method. IEEE Access 2013, 1, 408–417. [Google Scholar] [CrossRef]
- Matveev, S.A.; Smirnov, A.P.; Tyrtyshnikov, E. A fast numerical method for the Cauchy problem for the Smoluchowski equation. J. Comput. Phys. 2015, 282, 23–32. [Google Scholar] [CrossRef]
- Mondal, S.P.; Roy, T.K. First order homogeneous ordinary differential equation with initial value as triangular intuitionistic fuzzy number. J. Uncertain. Math. Sci. 2014, 2014, 1–17. [Google Scholar] [CrossRef]
- Mondal, S.P.; Roy, T.K. System of Differential Equation with Initial Value as Triangular Intuitionistic Fuzzy Number and its Application. Int. J. Appl. Comput. Math. 2015, 1, 449–474. [Google Scholar] [CrossRef]
- Paul, S.; Mondal, S.P.; Bhattacharya, P. Numerical solution of Lotka Volterra prey predator model by using Runge-Kutta-Fehlberg method and Laplace Adomian decomposition method. Alex. Eng. J. 2016, 55, 613–617. [Google Scholar] [CrossRef]
- Yusufoğlu, E.; Erbaş, B. He’s variational iteration method applied to the solution of the prey and predator problem with variable coefficients. Phys. Lett. A 2008, 372, 3829–3835. [Google Scholar] [CrossRef]
- Li, J.; Zhao, A. Stability analysis of a non-autonomous Lotka-Volterra competition model with seasonal succession. Appl. Math. Modell. 2016, 40, 763–781. [Google Scholar] [CrossRef]
- Khastan, A.; Perfilieva, I.; Alijani, Z. A new fuzzy approximation method to Cauchy problems by fuzzy transform. Fuzzy Sets Syst. 2016, 288, 75–95. [Google Scholar] [CrossRef]
- Bougoffa, L. Solvability of the predator and prey system with variable coefficients and comparison of the results with modified decomposition. Appl. Math. Comput. 2006, 182, 383–387. [Google Scholar] [CrossRef]
- González-Parra, G.C.; Arenas, A.J.; Cogollo, M.R. Numerical-analytical solutions of predator-prey models. WSEAS Trans. Biol. Biomed. 2013, 10, 79–87. [Google Scholar]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole Cengage Learning: Boston, MA, USA, 2010; ISBN 978-0-538-73351-9. [Google Scholar]
- Alkasasbeh, H.A.; Perfilieva, I.; Ahmad, M.Z.; Yahya, Z.R. New approximation methods based on fuzzy transform for solving SODEs: II. Appl. Syst. Innov. 2018, 1, 30. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).