Next Article in Journal
A Tropical Spiny Tree Rat (Rodentia, Echimyini) in the Late Quaternary of Southern South America (Argentina): Paleoenvironmental and Paleogeographic Implications
Previous Article in Journal
Evidence of Chronic Tusk Trauma and Compensatory Scoliosis in Mammuthus meridionalis from Madonna della Strada (Scoppito, L’Aquila, Italy)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Quaternary
Volume 8
Issue 3
10.3390/quat8030047
quaternary-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Geomagnetic Secular Variation Models for Latitude Scaling of Cosmic Ray Flux and Considerations for 10Be Exposure Dating of Laurentide Ice Sheet Retreat

by
Dennis V. Kent
1,2,*,
Luca Lanci
3 and
Dorothy M. Peteet
1,4
1
Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA
2
Earth & Planetary Sciences, Rutgers University, Piscataway, NJ 08854, USA
3
Department of Pure and Applied Science, University of Urbino, 61029 Urbino, Italy
4
NASA Goddard Institute for Space Studies, New York, NY 10025, USA
*
Author to whom correspondence should be addressed.
Quaternary 2025, 8(3), 47; https://doi.org/10.3390/quat8030047
Submission received: 31 May 2025 / Revised: 21 July 2025 / Accepted: 12 August 2025 / Published: 1 September 2025
Browse Figures
Versions Notes

Abstract

Published cosmogenic 10Be exposure ages from the terminal moraine of the Laurentide Ice Sheet (LIS) in northeastern North America have been interpreted to date the start of the retreat of the LIS at the Last Glacial Maximum (LGM) about 25 thousand years ago (ka). In contrast, published 14C accelerator mass spectrometry (AMS) dates for terrestrial plant macrofossils in LIS basal deglacial clay deposits range back to only ~16 calibrated (cal) ka, more consistent with the timing of glacio-eustatic rise and associated meltwater discharge to the North Atlantic and Gulf of Mexico associated with LGM deglaciation. We apply statistical models of geomagnetic secular variation, including dipole moment, to the latitudinal scaling of cosmic ray flux to see how well the age discrepancy can be addressed. A preferred new scaling, which is essentially time-invariant over the relevant LGM age range, shifts the exposure ages only a few thousand years younger. The age discrepancy may thus stem more from potential local biases toward higher 10Be concentrations (older apparent ages) at the terminal moraine sites, such as much higher 10Be production rates at the LIS front, and especially from inheritance. Such biases can be tested by obtaining primary 10Be calibration sites in the LGM time frame, and by more comprehensive sampling strategies for glaciated terrain to discern inheritance.

1. Introduction

The Last Glacial Maximum (LGM) nominally peaked at ~21 ka (kilo-annum or thousands of years ago; equivalent in our usage to cal ka for calendar or calibrated thousands of years before the present for cited radiocarbon dates), according to the well-dated marine oxygen isotope record of glacial cycles [1]. However, there is wide disparity in estimated ages for the recession of the southeastern margin of the Laurentide Ice Sheet (LIS), the largest-variable and lowest-latitude continental ice volume for the last glaciation, which is equivalent to about 80 m of the 120 m sea-level drop that characterizes it [2,3] (Figure 1). Because of the size and southerly extent of the LIS, as marked by terminal moraines as far south as ~40.5° N in New York and New Jersey (Figure 2), the beginning of its retreat should be reflected as a distinct contemporaneous rise in the global sea-level curve. The global sea-level record would suggest that the retreat of the LIS occurred no earlier than 21 ka and not rapidly until about 16 ka [4], with possible stops and starts in a complex process [5] (Figure 1). This general timing is supported by independent evidence that meltwater to the North Atlantic was minimal prior to 18.5 ka [6] and detectable in the Gulf of Mexico only by 16.1 ka [7]. Interestingly, the initiation of the European deglaciation meltwater pulse into the Black and Caspian seas is dated as nearly contemporaneous, at 16.3–15.4 ka [8].
In the continental realm, calibrated 14C accelerator mass spectrometry (AMS) dates on terrestrial plant macrofossils in the earliest deglacial lake sediments at eleven sites from New Jersey eastward to Connecticut extend back to only ~16 cal ka [9] (Figure 2), consistent with the general timing of the LIS’s retreat inferred from the marine records. In contrast, 10Be exposure dating of glacial boulders associated with terminal moraines in New England has placed the LIS’s recession considerably older, at around 25 ka and even preceding the peak LGM at 21 ka, often quoting 14C bulk sediment dates on deglacial deposits for support [10,12,13,14,15]. For example, Corbett et al. [10] reported a mean 10Be exposure age of 25.2 ± 2.1 ka on glacial boulders and bedrock associated with the LIS terminal moraine near Allamuchy Pond in northern New Jersey. The study [10] cites support from vintage 14C bulk sediment dates: for example, 27.2 cal ka at Budd Lake (unpublished thesis [16]), 22.2 and 22.4 cal ka from nearby Francis Lake (unpublished thesis [17]), 24.3 cal ka from the glacially dammed Lake Passaic (meeting abstract [18]), as well as the youngest (26.0 cal ka) of some thirty 14C dates ranging to more than 40 cal ka on a variety of materials from a contorted exposure of glacial sediments and organic beds in northern Long Island, New York [19]. However, the same litho- and biostratigraphy is recorded at Allamuchy Pond as at Francis Lake only 6 km to the west, where tundra Dryas and willow leaves screened from clays in the basal herb zone transition are 14C AMS dated at 14.4 ± 0.8 cal ka [9,20].
Quaternary 08 00047 g002
Figure 2. (A) Laurentide ice sheet at ~21.5 ka [21]. (B) Distribution of 14C AMS dates on plant macrofossils in earliest deglacial sediments (red triangles, from [9]), 14C bulk sediment (open circles with references in labels), and 10Be exposure dates (in box around Allamuchy Pond of the study region shown in Figure 2 of [10]) associated with the retreat of the southeastern margin of the LIS in northern New Jersey and southern New York. Base map adapted from [10], and whose area is shown as a red square in the top panel.
Figure 2. (A) Laurentide ice sheet at ~21.5 ka [21]. (B) Distribution of 14C AMS dates on plant macrofossils in earliest deglacial sediments (red triangles, from [9]), 14C bulk sediment (open circles with references in labels), and 10Be exposure dates (in box around Allamuchy Pond of the study region shown in Figure 2 of [10]) associated with the retreat of the southeastern margin of the LIS in northern New Jersey and southern New York. Base map adapted from [10], and whose area is shown as a red square in the top panel.
Quaternary 08 00047 g002
The requisite usage of terrestrial macrofossils for 14C AMS dating in basal clays/silts for accurate timing of deglaciation versus 14C dates on bulk sediments, which are apt to be contaminated by older carbon in the landscape, is widely acknowledged (e.g., [22,23,24,25,26,27]). A study of three lakes in Greenland [28], for example, found offsets of between 9000 and 20,000 14C years between macrofossil and invariably older bulk sediment dates, with greater offsets in the lowermost organic-poor clays and silts. Moreover, a preference for terrestrial rather than aquatic plant macrofossils, which tend to give variably older 14C dates [29], is also essential for radiocarbon dating accuracy in these environments [30,31]. For example (Table 1 in [9]), at Alpine Swamp, New York, bulk 14C sediment is dated at 15.5 cal ka at 8.3 m depth, whereas AMS 14C-dated terrestrial plant macrofossils over a meter below were dated at 14.5 cal ka. Similarly, at Tannersville Bog, Pennsylvania, bulk 14C sediment is dated to 16.2 cal ka at 12.4 m depth, whereas AMS 14C-dated terrestrial plant macrofossils are 14.4 cal ka over 1.4 m deeper. It is thus highly problematic that the reported ~25 ka 10Be exposure ages for the terminal moraine in New Jersey and elsewhere in the Northeastern United States rely on 14C bulk sediment dates in low-organic basal sediments for support [10,32,33]. Although the North American varve chronology is reported to be calibrated by 14C AMS dating of terrestrial macrofossils [34], the data entries from the oldest series of interest (in southern Connecticut) are listed as unpublished, with apparently the oldest at 17.6 cal ka; thus, the floating varve chronology is difficult to evaluate. Moreover, the oldest varves might even have formed well before ice-free conditions, as evident in the high Arctic and in Lake Vostok sediments of Antarctica today [9,35,36].
The difference between the reported 10Be exposure dates and 14C AMS terrestrial plant macrofossil dates could imply that it took about 9000 years (from ~25 ka until ~16 cal ka) before vegetation appeared on the deglaciated landscape. However, such an extended delay is not considered plausible, especially in mid-latitudes, given that primary succession by plants typically follows deglaciation in a matter of decades in arctic, subarctic, boreal, temperate, and alpine environments throughout the world [37,38,39,40], and that trees today grow in close proximity to and even on debris-covered glaciers in southern Alaska [41]. The adjacent unglaciated New Jersey–Pennsylvania landscape during the LGM was replete with plants that would have enabled rapid primary succession recorded in the lakes on the LIS terminal moraine, including areas with permafrost. Balter-Kennedy et al. [15] listed several possible explanations for the absence of AMS radiocarbon-dated plant macrofossils in deglacial sediments to fill the age gap prior to 16 cal ka, including poor preservation, landscape instability, delay in deposition until beaver colonies were established, and sampling difficulties, but potential problems with the 10Be exposure dating were not excluded. With the overall consistency of the 14C AMS maximum dates of terrestrial macrofossils in basal clays with the timing of LIS retreat inferred from the well-calibrated marine isotope and sea-level records (and having little confidence in the accuracy of the cited, mostly unpublished, vintage 14C bulk sediment dates in basal clays), we attempt to evaluate the general scaling of cosmic ray flux with altitude-, latitude-, and time-dependent geomagnetic secular variation in 10Be exposure dating.

2. Scaling 10Be Production with Dipole Moment, Latitude, and Altitude

Cosmogenic exposure dating is based on the accumulated concentration of a cosmogenic nuclide, commonly 10Be produced in quartz, just beneath newly exposed surfaces of freshly eroded bedrock or glacial boulders [42,43,44]. A radionuclide like 10Be will also undergo spontaneous radioactive decay, but because of the comparatively long half-life for 10Be (1.387 ± 0.012 Myr [45]), only ~1% will have decayed for exposures of up to ~25 ka. Surface production of 10Be by muon interactions is calculated to be a small fraction (~2%) of total production compared to spallation [46], and in practical terms the muon gain will be largely offset by the nominal loss of 10Be due to decay. More pertinent is that the highly energetic charged particles (~90% protons, ~10% helium nuclei) constituting primary cosmic rays, which have a constant flux at a galactic scale [47], are modulated by the geomagnetic field when entering Earth’s atmosphere, with the resulting secondary flux attenuated by interactions passing through the atmosphere. Hence, the necessity for scaling of cosmogenic nuclide production at ground level (by spallation) according to (geomagnetic) latitude and altitude.
Empirical observations of cosmogenic nuclide production in the atmosphere with cosmic ray detectors (e.g., [48,49]), combined with theoretical calculations (for example, that cosmogenic dependency on dipole moment becomes negligible polewards of about |60°| in geomagnetic latitude [50]), have been incorporated in a variety of scaling schemes to relate cosmogenic nuclide production at a given location to calibration sites with independently established age control. Five scaling schemes (St, Lm, De, Du, and Li) were incorporated in a widely cited online exposure age calculator [51], whose subsequent versions and subversions (e.g., v2.2, v2.3, v3) are described in blogs and referred to on the home webpage (https://hess.ess.washington.edu/; accessed on 18 January 2023) as ‘the online exposure age calculator formerly known as the CRONUS-Earth online exposure age calculator’. Two additional schemes (LSDn and LSD) were included in a CRONUS-Earth community effort that summarized modeling results for commonly measured cosmogenic nuclides and, importantly, identified four primary calibration sites for 10Be exposure dating [52] (see also [53] for further explanation of scaling schemes).
St is the original and most widely used production rate scaling scheme [43,54]. The scaling scheme St was based on cosmic ray emulsion and neutron monitor data documenting variations in spallogenic production rates with altitude (atmospheric pressure) and geomagnetic latitude. The scheme Lm is essentially St with a time-varying geomagnetic field intensity model, whose earlier access to online documentation for v3 of the exposure age calculator indicated included a full-vector spherical harmonic analysis for the past 14 ka (SHA.DIF.14k [55]). The other scaling schemes (De, Du, Li, LSDn, and LSD) are also time-dependent and have incorporated various geomagnetic field histories (e.g., SHA.DIF.14k for LSDn in v3). De, Du, and Li are neutron-monitor-based models, whereas the LSD framework (with LSDn) is based on analytical fits to physics-based modeling. Although De, Du, and Li are described as having much poorer fits to the primary calibration data than the other four scaling schemes (St, Lm, LSDn, and LSD), even the best-fitting scheme (LSDn) failed a goodness-of-fit test after what were described as ‘extremely large’ adjustments to the primary site ages, with significant site-to-site deviations of ~10% from the model [56]. With these caveats in mind, we attempted to evaluate 10Be production rate scaling for the schemes St/Lm and De, which were relatively straightforward to calculate, using different models of geomagnetic secular variation in terms of directional dispersion after first addressing temporal changes in dipole moment. We did not attempt to directly evaluate the scheme LSDn (or LSD), whose geographic scaling is implemented on the online exposure age calculator v3.

2.1. Variations with Dipole Moment

The geomagnetic field provides fundamental shielding against cosmic ray flux on the basis of its relative strength, which can be expressed in terms of the ratio of the average dipole moment from a given time (M) to its nominal present-day value (M0~80 ZA m2) to calculate the effective vertical cutoff rigidity, Rc, as a function of site latitude (using Equation (3) of [57], Equation (3.3) of [44], or Equation (2) of [58], which we use here). The shielding effect is greatest at low geomagnetic latitudes and becomes negligible at higher latitudes above Elsasser’s ‘knee’ at ~|60°| (Figure 3). A composite record of the virtual axial dipole moment (VADM) using the full-vector geomagnetic secular variation model SHA.DIF.14k [55] for 0–14 ka, combined with a relative paleointensity (RPI) stack of sedimentary records from 14 to 45 ka [59], shows that the dominant feature since ~45 ka is a distinct low VADM associated with the Laschamp geomagnetic excursion centered at around 41 ka, when the VADM decreased to less than 20% of the modern dipole moment [60] (Figure 4A). A 10Be-based VADM inferred from Greenland ice cores [61] tends to parallel the VADM curve from SHA.DIF.14k and the RPI stack [59,60], suggesting that geomagnetic rather than heliomagnetic field variations are the primary control on cosmic ray flux in Earth’s space environment (see also [62,63]). A possible exception is a mismatch in the curves between ~24 and 19 ka, when an apparent increase in 10Be production, modeled as a dip in VADM, corresponds to a rise in VADM in the RPI stack; this could simply be a record artifact or imply a millennial-scale episode of reduced heliomagnetic field diversion of cosmic ray flux, as sometimes observed over shorter durations with modern sunspot activity [64,65]. In any case, the cumulative effect of long-term changes in VADM relevant for 10Be production and exposure scaling is relatively small, generally within about 5 percent of the modern dipole moment since about 38 ka (Figure 4B), and since about 25 ka even with an alternative VADM curve [66] (Figure S1). The scaling schemes St and Lm would thus be essentially equivalent since at least 25 ka, the time frame at issue.

2.2. Variations with Altitude and Geomagnetic Latitude

Of related importance for 10Be production are dependencies on altitude and latitude, which are illustrated for representative scaling schemes in Figure 5. The altitude scaling factor for the legacy Lal/Stone St scheme at high latitude (HL) was calculated from Equation (2) and associated coefficients in Table 1 of [54]. It is compared in Figure 5A to the HL altitude scaling factor (f(x)) for spallation using Equation (7) of [67] (see also [68]) for the De scheme (R-code [69] in the Supplementary Materials), a convenient formulation for more recent neutron monitor data given in terms of effective geomagnetic cutoff rigidity (Rc) and atmospheric depth (x) relative to sea level (1033 g/cm2, equal to standard atmospheric pressure of 1013.15 hPa). There is good mutual agreement between the St and De schemes from sea level to about 750 hPa (~2500 m altitude), where the schemes progressively diverge with increasing altitude (decreasing atmospheric pressure/depth) so that, at 6000 m, the De altitude scaling is almost 30% greater (lower shielding) compared to the St altitude scaling. A similar pattern is apparent in Figure 5A of [58], where it was attributed to a better agreement of the LSD scaling framework (described as similar in this case to De) with a variety of proxy measurements of secondary cosmic ray intensities in the atmosphere.
Latitude scaling factors normalized to sea level (SL) and a constant dipole moment are plotted for schemes St and De in Figure 5B. For clarification, the St scaling factor used to model empirical cosmic ray flux data was expressed in terms of geomagnetic latitude of the present-day field at monitoring sites [43]. However, the scaling coefficients, when recast in terms of atmospheric pressure, are described simply in terms of latitude in Table 1 of [54], and then the same data as geographic latitude in the description of the widely used exposure age online calculator [51]. However, the dipole axis by which geomagnetic latitude is gauged is presently tilted ~10° with respect to Earth’s spin axis, according to which the geographic latitude of a site is defined. The north geomagnetic pole from spherical harmonic analysis is presently in the Canadian Arctic at around 80° N 73° W (https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml?useFullSite=true; accessed 21 May 2025) and is why geomagnetic latitudes currently tend to be steeper than geographic latitudes at sites in North America. For example, actual cosmogenic production was measured in water for several months in 1959 CE at Mt. Evans in Colorado [71], which is located at around 39.6° N (nominal 4350 m altitude) but described as having a geomagnetic latitude of 51°, which is relevant to gauge the modern cosmic ray flux (although not for the time-averaged geomagnetic field). However, geomagnetic and geographic latitudes are sometimes exchanged in long-term exposure studies, as apparently occurred for the case of the classic Sierra Nevada study [42,43]: the sampling area was at about 38° N, but the latitude scaling was calculated [72] for a geomagnetic latitude of about 44°, which is for today’s instantaneous geomagnetic field at the sampling locality.
Geomagnetic latitudes for a sufficiently time-averaged geomagnetic field will closely coincide with geographic latitudes according to the GAD hypothesis, a central testable tenet of paleomagnetism. The GAD model is supported, for example, by paleomagnetic data from Pleistocene deep-sea sediments in cores taken from the World Ocean [73,74] and is closely approximated by averaging even over just ~2000 years according to the SHA.DIF.14k model [55]. A latitude scaling factor for a GAD field geometry based on Rc values for the De scheme has a sigmoidal shape and varies as follows: 0.54 at the Equator, 0.68 at |30°|, and plateauing at 1.0 at around the ‘knee’ at |60°| (geomagnetic = geographic) latitudes (Figure 5B). For reasons unclear to us, the St latitudinal scaling tends to be systematically higher (implying less shielding) than the De scheme; for example, St gives 0.59 at the Equator, 0.82 at |30°|, and even seems to reach maximum relative scaling (within 2% of unity) by only |50°| in latitude. A possible explanation is that the empirical St scaling refers to present-day geomagnetic latitude and is offset by the ~10° current difference between geomagnetic and geographic latitudes in North America, where many of the analyzed cosmic ray measurements [43] may have been taken.

2.3. Latitudinal Variations with Secular Variation in Directions

A characteristic feature of the geomagnetic field is the secular variation in directions, which occurs on historic-to-millennial time scales [75,76]. Averaging of secular variation on millennial and longer time scales produces a close approximation to a GAD field geometry. However, the actual dispersion in site-mean directions will modify the latitudinal dependence of any scaling, which will tend to be biased to somewhat higher values (reduced shielding) at low latitudes, where the static GAD reference scaling curve is gently concave up but shows appreciably lower values (increased shielding) at middle-to-high latitudes, where the static GAD scaling curve is more acutely concave down (Figure 5B). These biases in latitude scaling will depend on the geomagnetic field model, being more pronounced with larger directional dispersion. For example, the SHA.DIF.14k full-vector geomagnetic secular variation model [55] is based on a rather inhomogeneous spatiotemporal distribution of available archaeomagnetic and lava paleomagnetic data, as noted in [77]: 97% of the total data used in the analysis come from the Northern Hemisphere, 83% of the total from only 3 ka to present, and only 3% from older than 8 ka (probably contributing to the noisy character of the older part of its VADM curve in Figure 4A). Nonetheless, the directional scatter is quite small. Virtual geomagnetic poles (VGPs) calculated from estimates of the dipole coefficients (g01, g11, and h11) that are provided at 50-year intervals since 14 ka [55] give an overall mean geomagnetic pole position located at 89.3° N 337.0°E (n = 279, angular standard deviation (ASD) = 7.6°, Fisher’s precision parameter (K) = 118, and radius of circle of 95% confidence (A95) = 0.8°) (see a standard text for calculation of pole positions and Fisher statistics, e.g., [78] available at https://www.geo.arizona.edu/Paleomag/; URL accessed 23 August 2025). Even with the tight grouping, the mean geomagnetic pole position is less than 1° and not significantly different from the geographic axis (|90°| latitude). This close correspondence confirms the applicability of the GAD hypothesis as a satisfactory fit to the geomagnetic field when averaged even within just a few thousand years [55].
Because of its low VGP dispersion, SHA.DIF.14k provides a De latitude scaling that closely follows the static De-GAD curve (Figure 5B; Table 1). However, paleomagnetic directions observed in widely sampled lava flows as instantaneous recorders of the geomagnetic field show that the dispersion of the calculated site VGPs ranges from an ASD of only around 12° near the Equator (K~46) to around 24° (K~11) poleward of |60°| [79,80]. A f(Rc) latitude scaling for De using a nominal average VGP dispersion of K = 27 is somewhat higher than for the static De-GAD and De-SHA.DIF.14k models at low latitudes (<~|30°|) but has progressively lower values (implying greater shielding) at mid-latitudes because of the sharper curvature in scaling approaching the ‘knee’ (Figure 5B). The latitude scaling curves eventually converge at relative unity (minimal shielding) poleward of |60°| latitude, but more gradually for De-K27 than the static De-GAD and subdued De-SHA.DIF.14k curves.
A more comprehensive statistical model for geomagnetic secular variation (TK03 [70]) can also be considered. TK03 treats the geomagnetic field as a giant Gaussian process [81] following Model G of [82], which attributes the observed latitudinal dependence in directional dispersion to independent contributions from spherical harmonic families of odd and even symmetry for geodynamo sources (Supplementary Material; Table 1). Because of the wider directional dispersion about the GAD field, the resulting De-TK03 latitude scaling systematically departs more from the static De-GAD or De-SHA.DIF.14k scaling curves than the De-K27 scaling model (Figure 5B; Table 1). For example, De-TK03 does not plateau (to within 2% of unity) until around |75°| latitude, compared to closer to the classic |60°| ‘knee’ for De-K27, De-SHA.DIF.14k, and static De-GAD. The TK03 model extends to spherical harmonic terms of degree and order eight, and thus includes non-dipole contributions, but because the dipole defined by the degree-one terms typically represents more than 90% of the overall relative strength of the geomagnetic field, much of the departure of De-TK03 from the static De-GAD latitude scaling model can also be attributed to a dipole wobble component. Parenthetically, we note that the magnitude of the axial dipole (g01) term does not affect the VGP scatter produced by the TK03 statistical model [80]. Moreover, the statistical model is implicitly held to be valid over a broad age range, longer than the few millennia necessary for averaging to a GAD field, and within the past few million years of paleosecular variation data; thus, it can be considered to be effectively time-invariant for exposure age calculations.

3. CRONUS-Earth Primary 10Be Calibration Sites

To get a sense of how the different scaling models discussed above might influence reference 10Be production rates (and, ultimately, exposure age estimates), we used summary data for the four primary 10Be calibration sites (MR, PPT, SCOT, and HU08) identified in the CRONUS-Earth community effort [52,56]. Individual sample data can be found on the ICE-D production rate online database [83] (https://version2.ice-d.org/production%20rate%20calibration%20data/cal_data_set/4; accessed 19 June 2022); where more than one analysis of a sample is listed, we simply took the first entry for this exercise to facilitate ease of reproducibility. We also did not delve into the secondary calibration sites for 10Be listed by [56]. The basic numerical results for the four CRONUS-Earth primary calibration sites are summarized in Table 2. Some of the cited 10Be concentration values may still include a muon contribution, which in any case should be less than 2% of the total [46] and even partially compensated by radioactive decay of the accumulated 10Be and the typically small local shielding corrections if also unaccounted for.
The 10Be exposure dating parameters for the four CRONUS-Earth primary calibration sites [56] used to derive 10Be production rates normalized to sea-level high-latitude (SLHL) according to various scaling schemes: MR (Macaulay Ridge, New Zealand), PPT (Promontory Point Terrace, Utah, USA), SCOT (Scotland, UK), and HU08 (Huancane, Peru). Selected scaling schemes are St, the original empirical scaling scheme [43] as modified by [54], and applications of scheme De [67] based on the effective vertical cutoff rigidity (Rc) calculated using Equation (2) of [58] and the geomagnetic (f(Rc)), altitude (f(x)), and total scaling factor (F) calculated using Equations (5)–(7), respectively, from [67]: De-GAD, geocentric axial dipole where geographic and geomagnetic latitudes are equivalent in a static field, and De-TK03, a statistical model of secular variation in directions about a geocentric axial dipole field [70] (Supplementary Materials). Geomagnetic dipole moment averages close to present-day value (~80 ZAm2) over cumulative exposure times back to at least 25 ka (Figure 4B and Figure S1). All four primary calibration sites were used to calculate mean 10Be production rates and standard deviations (σ) for different scaling schemes; means and standard deviation using only MR, SCOT, and PPT are also shown. These means were applied to published parameters for Allamuchy terminal moraine sites in New Jersey used to estimate the 10Be exposure age for retreat of the LIS [10]; ages for each scaling scheme are based on dividing the scaled 10Be concentration (CSLHL) by the mean 10Be production rate (PSLHL).
The MR site at Macaulay Ridge, New Zealand (43.6° S, 1028 m) has well-constrained data for a rockslide not linked to a known climate event [84]. The 10Be concentrations average 87,100 atoms g−1 in seven boulder samples; 14C AMS determinations of 9690 ± 50 cal yr on wood fragments immediately beneath the rockslide containing the boulders provide tight age constraints for the duration of exposure. Our implementation of the St scaling scheme delivers a sea-level high-latitude (SLHL) 10Be production rate (PSLHL) of 3.85 atoms g−1 y−1, which is in close agreement with the quoted PSLHL of 3.84 ± 0.08 atoms g−1 y−1, indicating that our simplified calculations and choice of representative sample data are reasonable. When scaled according to the De-GAD scheme, the resulting PSLHL of 4.04 atoms g−1 y−1 is within the range (3.74–4.15 atoms g−1 y−1) quoted [84] for the four other scaling methods besides St used at the time. The results for the De-TK03 scaling scheme give a PSLHL about 9% higher (4.39 atoms g−1 y−1) (Table 2).
Comparable results to MR are obtained from the PPT site at Promontory Point, Utah USA, which is at a similar absolute latitude but a somewhat higher altitude (41.3° N, 1603 m). A mean age of 18,360 cal yr for concordant 14C dates on a variety of materials, including wood and charcoal, to date an extensive wave-cut bench [85] makes PPT the oldest of the four 10Be CRONUS-Earth primary calibration sites and which, like MR, is not linked to a specific climate event. PPT data provide bracketing PSLHL of 4.26 atoms g−1 y−1 for St and 4.73 atoms g−1 y−1 for De-TK03 (Table 2).
SCOT (Scotland, UK: 57.4° N, 136 m) is constrained by calibrated 14C dates on peats resting on either till or outwash, averaging 11,700 cal yr, slightly older than MR but linked to a glacial episode. SCOT data provide bracketing PSLHL of 4.22 atoms g−1 y−1 for St and 4.58 atoms g−1 y−1 for De-TK03 (Table 2). These three primary calibration sites (from 41.3° N, 43.6°S, and 57.4° N in latitude, 136 m to 1603 m in altitude, and ranging in age from 9630 to 18,360 cal yr) provide a mean 10Be reference PSLHL of 4.11 ± 0.23 atoms g−1 y−1 for St and about 9% higher (4.57 ± 0.17 atoms g−1 y−1) for De-TK03.
HU08, the fourth primary calibration site, from Huancane, Peru (13.9° S, 4859 m), is constrained by 14C dates with a nominal mean age of 12,300 cal yr for peats plowed up by the advancing Quelccaya Ice Cap front and incorporated into the tills. The exposure age for HU08 is within the range of the other primary sites but comes from a very different (low-latitude and high-altitude) venue [86]. The HU08 data indicate a PSLHL of 3.67 atoms g−1 y−1 for St, which is ~9% lower compared to the mean PSLHL for St (4.11 ± 0.22 atoms g−1 y−1) estimated from the three other primary calibration datasets. However, the PSLHL for HU08 is only 2.98 atoms g−1 y−1 for De-TK03, about 65% of the mutually consistent PSLHL of 4.57 ± 0.17 atoms g−1 y−1 for De-TK03 determined for MR, PPT, and SCOT. This gross disparity may point to problems with neutron monitor data and scaling factors at high altitudes, as already suggested [58], combined with possibly reduced 10Be concentrations due to rapid weathering of the boulders by granular disintegration [86]. We note that the customary inclusion of the existing HU08 data with the other three primary datasets would provide a seemingly consistent mean PSLHL of around 4 atoms g−1 y−1 (4.00 ± 0.29 atoms g−1 y−1 for St and 4.17 ± 0.81 atoms g−1 y−1 for De-TK03; Table 2), which happens to be not grossly incompatible with the mean PSLHL of 3.92 ± 0.17 atoms g−1 y−1 for all seven scaling schemes (LSDn or Sa, LSD or Sf, St, Lm, Li, Du, and De) of the CRONUS-Earth primary dataset reported for 10Be [52].
It is nonetheless clear that adjustments of the 10Be reference PSLHL beyond ~10% of currently accepted values will be difficult to justify with available data and uncertainties in scaling factors. Case in point are the published 10Be exposure age data for sixteen samples (6 glacial erratic boulders and 10 glaciated pavement outcrops) on the LIS terminal moraine at Allamuchy, New Jersey (41.0° N, 328 m) [10]. These data yielded a reported 10Be exposure age of 25.2 ± 2.1 ka with the Lal/Stone St scheme (citing version 2.2 of the CRONUS-Earth online calculator and a ‘regionally calibrated northeastern North American sea-level production rate of 3.93 ± 0.19 atoms g−1 y−1 for 10Be’ [10]). For a PSLHL (4.11 ± 0.29 atoms g−1 y−1) for ST averaged for the MR, PTT, and SCOT primary calibration sites, we would obtain a somewhat younger 10Be exposure age of 23.2 ± 1.3 ka (Table 2). Interestingly, the mean PSLHL for calibration sites MR, SCOT, and PPT of 4.57 ± 0.23 atoms g−1 y−1 for De-TK03 would give a 10Be exposure age of 24.3 ± 0.9 ka, which is slightly older than the age range that we obtained with St, reflecting detailed differences in altitude and latitude scaling functions. The HU08 primary calibration dataset alone, with a calculated PSLHL of 2.98 atoms g−1 y−1 for De-TK03, would produce an implausibly old exposure age of 37.3 ka for Allamuchy.

4. Discussion

Alternative latitude scaling schemes that we experimented with using the CRONUS-Earth primary 10Be calibration sites allow only marginal changes in exposure age from the 25.2 ka reported for the LIS terminal moraine. Even a general statistical geomagnetic secular variation model (TK03) with a broad representation of changes in directions on centennial-to-millennial time scales, which are a characteristic feature of the Earth’s dynamo process, increases PSLHL by barely ~10% from static latitudinal scaling schemes, and by even less in the calculated 10Be exposure ages of Allamuchy sites on the LIS terminal moraine (Table 2). Long-term drift in 10Be production rates from the modulation of cosmic ray flux by changes in geomagnetic dipole moment or in solar activity also seems limited, given the good general agreement between the VADM determined from paleomagnetic records and a 10Be-based record of dipole moments determined from ice cores.
Further constraints on possible long-term changes in 10Be production rates would benefit from well-dated calibration sites older than presently available at ~18 ka. On a more local scale, there are potential issues associated with assessing 10Be production at sites in close proximity to an ice front, such as the former southeastern margin of the LIS, where cosmic ray flux may have been higher due to lowered atmospheric pressure from katabatic winds and colder conditions (such as described around Antarctica today [54]) and, in the case of the LIS, lower sea level and corresponding atmospheric pressure during transition from the LGM [87].
Our experiments with different latitudinal scaling schemes reduce the 10Be exposure dates of ~25 ka on the LIS terminal moraine [10] by only a few thousand years (Table 2). This would still leave a perplexingly long (~7-thousand -year) delay, with the earliest 14C AMS dates on terrestrial plant macrofossils in basal deglacial lake sediments that range back to only ~16 cal ka [9], and an acknowledged disconnect [10] with well-dated climate histories from the marine realm, with peak LGM at ~21 ka (e.g., [1,4,88]). The possibility of 10Be deglaciation dates of glacial moraines at 25 ka and AMS 14C deglaciation dates from bogs/lakes on the moraine at 14–16 cal ka would mean that ice was preserved for about 10,000 years in a warming climate. This seems unlikely for three reasons: First, various ice blocks would have different timings of melting in the moraine, which would give a variety of ages from 25 and 14 ka, yet all of the lake/bog cores retrieved along the southern LIS margin date between 14 and 16 cal ka with 14C AMS on terrestrial macrofossils in basal clays [9]. Second, stratigraphic evidence for trash layers in glacial lakes has been reported in Minnesota [89] as woody debris occurring at the base of the sediment core and overlain by clays and gyttja, but none of the LIS terminal moraine cores show this stratigraphy involving a trash layer below clay and/or gyttja. This stratigraphic difference can be attributed to the maritime nature of the Laurentide moraine here and in Western Europe (e.g., the Netherlands [90]), in contrast to the mid-continental lakes in Minnesota and Poland where these trash layers appear. Third, basal dates from lakes and bogs are widely used for the timing of deglaciation—for example, in Scandinavia, Europe, Russia, Japan, China, South America, and New Zealand, recognizing that the ice had to melt down for the lake to accumulate organic matter. We used the same reasoning for lakes at the southern LIS margin, as they would have accumulated plant matter shortly after the ice’s retreat at a maritime temperate latitude adjacent to vegetated landscapes.
A recent assessment of new and previously published 10Be exposure dating of the LIS’s retreat acknowledged the apparent wide age gap and did not exclude potential problems with 10Be exposure dating [15]. Chief amongst them is cosmogenic nuclide inheritance. An early example was the wide 10Be age distribution for 12 glacial boulders in the moraine at Martha’s Vineyard [12], which shows a mode at around 23 ka, but excluded were three boulders with widely deviant older ages (~29.4, 49.7 and 56.4 ka) and regarded as recycled; two boulders with younger ages of ~15.7 and 19.8 ka were also excluded as likely suffering late exposure due to long-term melting of buried ice. The mode at 23 ka had been linked to Heinrich H2 of similar age; however, a reappraisal of 10Be production rates motivated by older radiocarbon dates on post-glacial sediments overlying recessional moraines in the region shifted the mode of the 10Be age distribution to nearly 27 ka (Figure 16 and discussion in [91]). In the study of the LIS terminal moraine at Allamuchy, Corbett et al. [10] acknowledged that between-sample 10Be concentrations for the erratic boulders and glaciated bedrock surfaces vary several times more than expected from analytical uncertainties alone, and they discussed the possibility of inheritance bias. Recent modeling of existing data from Allamuchy indeed suggests that 10Be inherited from earlier exposure(s) may add up to 6000 years to exposure ages near the terminal moraine due to short ice occupation times [33]. Balter-Kennedy et al. [15] also noted that exposure ages for bedrock surfaces tended to be older than those of co-located boulders in Central Park, New York City (23.2 and 25.0 ka versus 20.0 ka in a nearby boulder), and especially in the lower Hudson Valley up to ~80 km north (upstream) of the terminal moraine, such as a bedrock sample from Palisades, New York dated at 29 ka, three bedrock samples at Black Rock Forest in the Hudson Highlands at 25.0 ka, and two at ~100 ka compared to nearby boulders at 22.1 and 23.7 ka. The older exposure dates for bedrock show that subglacial erosion can be inadequate to remove previously acquired cosmogenic nuclide inventories, consistent with theory [92].
Post-depositional disturbance and/or cosmogenic nuclide inheritance are suspected when the scatter of exposure ages for glacial boulders in a moraine exceeds analytical uncertainties, as found to be the case for the LIS terminal moraine at Allamuchy [10]. Various strategies have been developed to understand the source of the uncertainties and determine the true age of a moraine [91]. For example, if the degree of excess scatter in an exposure-age dataset increases with presumed moraine age, post-depositional disturbance due to weathering and erosion of moraine boulders is the likely cause, in which case the youngest samples in the dataset are excluded and the oldest samples in the dataset may best approximate the true age of the moraine. On the other hand, boulders emplaced with significant inherited nuclide concentrations will produce excess scatter that might be expected to decrease with increasing moraine age, allowing the magnitude of nuclide inheritance to be estimated in principle from comparison of the dataset to a statistical model (e.g., [33] for the LIS terminal moraine). The apparent agreement of 10Be exposure dates for the LIS terminal moraine with radiocarbon dates from overlying sediments tends to be cited as supportive evidence for mutual dating reliability [10,15,32]. However, the counterargument is that reliance on the largely unpublished vintage 14C bulk sediment dates, which have a documented tendency to be contaminated by old carbon, casts doubt on the accuracy of the 10Be exposure dates, especially with the availability of invariably younger unbiased 14C AMS dates from basal deglacial sediments that motivated this assessment.
Given the potential importance of cosmogenic nuclide inheritance to exposure dating accuracy, sampling strategies tailored to specifically constrain bias from inheritance on a boulder-by-boulder basis might be worth further consideration. Single samples are typically taken from individual boulders with the optimal shielding factor, the least obstructed exposure to cosmic ray flux compared to a horizontal surface, and a clear horizon [51]. Now, suppose that another sample was taken from each boulder in a less favorable location, for example, from a near-vertical surface on the side of the boulder, with such a low resulting shielding factor that any measurable concentration of a cosmogenic nuclide like 10Be would be strongly influenced by inheritance (and/or prolonged exposure to deeper-penetrating muons). The measured estimates of inheritance from the boulder side-samples could then be compared to statistical models based on the least obstructed topmost samples, as a cross-check to derive improved estimates for inheritance contributions. If subglacial erosion is often demonstrably inadequate to scrape off previously acquired cosmogenic nuclide inventories in glaciated bedrock pavements, consistent with theory [92], glacial erratics may not fare better being reset. So, rather than relying on inheritance being signaled by rare and easily recognizable age outliers in a boulder population, it might be worth estimating inheritance more directly in the boulders with a comprehensive sampling scheme.

5. Conclusions

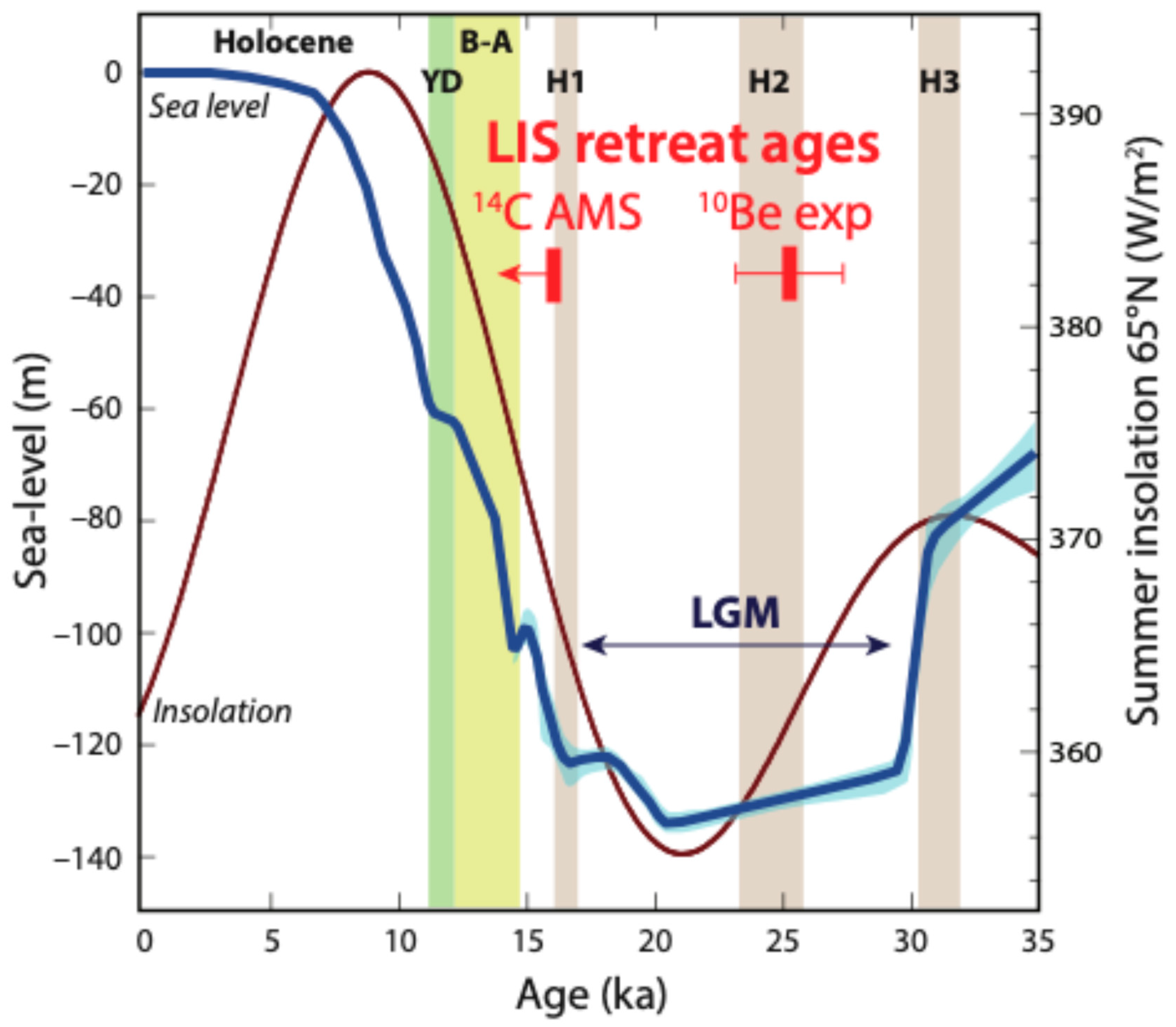
  • Reported 10Be exposure ages of ~25 ka for the retreat of the southeastern LIS margin in North America are anomalously old for the tempo of deglaciation compared to sea-level and deep-sea sediment oxygen isotope records, as well as 14C AMS dates on terrestrial plant macrofossils in LIS basal deglacial clay deposits in the same areas, which range back to only ~16 cal ka. This age discrepancy prompted our reevaluation of geomagnetic field modulation of cosmic ray flux as a potential contributing factor.
  • CRONUS-Earth identified four primary calibration sites for cosmogenic 10Be production in quartz in rock surfaces (at ~9.7, 11.7, 12.3, and 18.2 ka in age), and whose results from a variety of geographic locations require scaling to the LIS terminal moraine locale in terms of altitude and of geomagnetic latitude, including secular variation in dipole moment.
  • Over the time frame of a few ka to about 25 ka or longer, empirical and statistical models of geomagnetic secular variation suggest that a geocentric axial dipole provides a good approximation to the time-averaged field; for latitude scaling of cosmic ray flux, geomagnetic latitude can thus be assumed to be equivalent to geographic latitude, but the effect of dispersion in the geomagnetic directions (e.g., as in the statistical model TK03) needs to be taken into account.
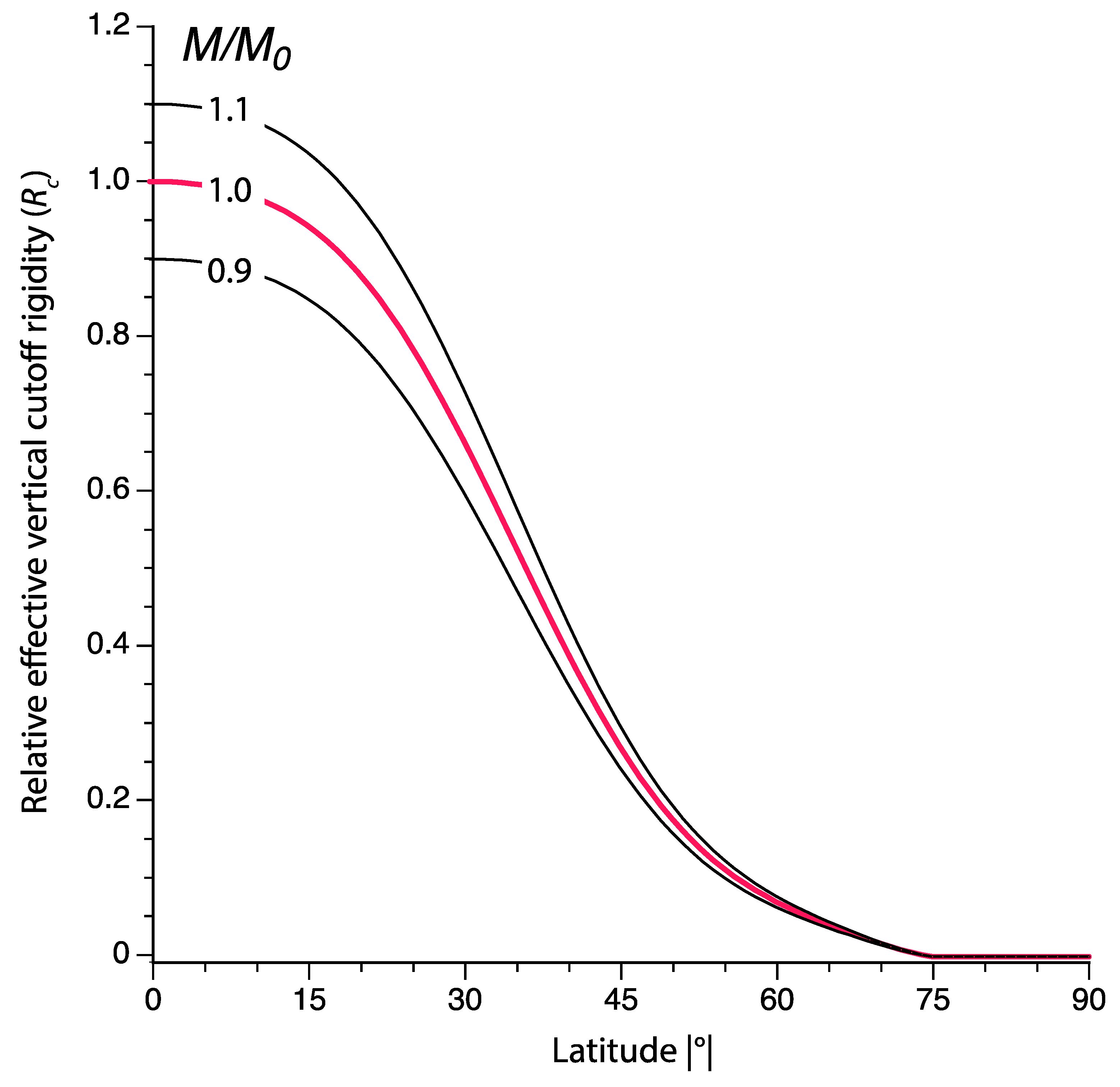
  • Over the same time frame of a few ka to about 25 ka or longer, the best available records show there are some large secular changes in axial dipole moment, but the cumulative effects relevant to 10Be exposure dating are within about ±5% of the present dipole moment.
  • Points #3 & #4 above indicate that the geomagnetic latitude and dipole moment at a given site can be considered to be time-invariant over a time frame of a few ka to at least 25 ka, but the effects of latitudinal scaling will still depend on which of the seven CRONUS-Earth schemes is employed (i.e., based on empirical neutron monitor data or analytical approximations).
  • Application of two representative scaling schemes (St and De) with the updated geomagnetic secular variation models for the four CRONUS-Earth primary calibration sites reduces the published 10Be exposure age estimate for the LIS terminal moraine by only up to ~10% and, thus, does not resolve the age discrepancy.
  • The 10Be inheritance from previous exposure that was not erased by subglacial erosion becomes a leading potential source of age bias that could be gauged by additional sampling of shielded surfaces in individual boulders and, as suggested by several reviewers, measurements of additional cosmogenic nuclides such as in situ cosmogenic 14C. The objective would be to make 10Be exposure dating less reliant on old bulk 14C dates and more on internal controls for assessing accuracy as a geochronological tool.
  • More generally, constraints on long-term changes in 10Be production rates extending into the LGM (including possible solar modulation) and that consider glacio-eustatically lowered sea level (and corresponding reduced air pressure compared to present-day site altitude) would benefit from well-dated primary calibration sites older than the oldest presently available at ~18 ka.
  • In the meantime, we maintain that 14C AMS dates that are invariably no older than 16 cal ka for terrestrial plant macrofossils in the earliest deglacial sediments provide a more coherent age estimate for the LIS’s retreat than the currently proposed 10Be exposure dates of ~25 ka.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/quat8030047/s1: File S1: Routines used for heuristic purposes relevant to 10Be production rate scaling and geomagnetic field models in the R programming language [69]. Table S1: Effective vertical cutoff rigidity (Rc) and corresponding magnetic scaling factor (f(Rc)) as a function of latitude for various geomagnetic field models. Table S2: Relative paleointensity (RPI) 14 to 45 ka [59,60]. Table S3: 10Be-based VADM since 45 ka (from [59]). Figure S1: Variations in geomagnetic axial dipole moment since 50 ka from Model GGF100k [66].

Author Contributions

Authorship in alphabetical order: D.M.P. initiated the study and assessed radiocarbon dates, L.L. wrote the R-code, and D.V.K. helped incorporate the geomagnetic field models and drafted the manuscript with input from D.M.P. and L.L. All authors have read and agreed to the published version of the manuscript.

Funding

Our research was supported by internal support from NASA (D.M.P.), the University of Urbino (L.L.), and the Lamont Paleomagnetic Research Fund (D.V.K.).

Acknowledgments

Our collaborative effort sprang from a presentation on the subject by D.M.P. at a Memorial Symposium for Wally Broecker in 2019 and eventually came to fruition after the COVID-19 shutdowns. We appreciate the many detailed critical comments by reviewers of this version and several earlier versions of the manuscript that pushed the evolution of our thinking on exposure dating. We also greatly appreciate receiving data files from Jim Channell to construct Figure 4.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 2005, 20, PA1003. [Google Scholar]
  2. Tarasov, L.; Dyke, A.S.; Neal, R.M.; Peltier, W.R. A data-calibrated distribution of deglacial chronologies for the North American ice complex from glaciological modeling. Earth Planet. Sci. Lett. 2012, 315–316, 30–40. [Google Scholar] [CrossRef]
  3. Clark, P.U.; Mix, A.C. Ice sheets and sea level of the Last Glacial Maximum. Quat. Sci. Rev. 2002, 21, 1–7. [Google Scholar] [CrossRef]
  4. Lambeck, K.; Rouby, H.; Purcell, A.; Sun, Y.; Sambridge, M. Sea level and global ice volumes from the Last Glacial Maximum to the Holocene. Proc. Natl. Acad. Sci. USA 2014, 111, 15296. [Google Scholar] [CrossRef] [PubMed]
  5. Carlson, A.E.; Clark, P.U. Ice sheet sources of sea level rise and freshwater discharge during the last deglaciation. Rev. Geophys. 2012, 50, RG4007. [Google Scholar] [CrossRef]
  6. Keigwin, L.D.; Jones, G.A.; Lehman, S.J.; Boyle, E.A. Deglacial meltwater discharge, North Atlantic Deep Circulation, and abrupt climate change. J. Geophys. Res. Ocean 1991, 96, 16811–16826. [Google Scholar] [CrossRef]
  7. Flower, B.P.; Hastings, D.W.; Hill, H.W.; Quinn, T.M. Phasing of deglacial warming and Laurentide Ice Sheet meltwater in the Gulf of Mexico. Geology 2004, 32, 597–600. [Google Scholar] [CrossRef]
  8. Yanchilina, A.G.; Ryan, W.B.F.; Kenna, T.C.; McManus, J.F. Meltwater floods into the Black and Caspian Seas during Heinrich Stadial 1. Earth-Sci. Rev. 2019, 198, 102931. [Google Scholar] [CrossRef]
  9. Peteet, D.M.; Beh, M.; Orr, C.; Kurdyla, D.; Nichols, J.; Guilderson, T. Delayed deglaciation or extreme Arctic conditions 21-16 cal. kyr at southeastern Laurentide Ice Sheet margin? Geophys. Res. Lett. 2012, 39, L11706. [Google Scholar] [CrossRef]
  10. Corbett, L.B.; Bierman, P.R.; Stone, B.D.; Caffee, M.W.; Larsen, P.L. Cosmogenic nuclide age estimate for Laurentide Ice Sheet recession from the terminal moraine, New Jersey, USA, and constraints on latest Pleistocene ice sheet history. Quat. Res. 2017, 87, 482–498. [Google Scholar] [CrossRef]
  11. Paillard, D.; Labeyrie, L.; Yiou, P. Macintosh program performs time-series analysis. Eos Trans. AGU 1996, 77, 379. [Google Scholar] [CrossRef]
  12. Balco, G.; Stone, J.O.H.; Porter, S.C.; Caffee, M.W. Cosmogenic-nuclide ages for New England coastal moraines, Martha’s Vineyard and Cape Cod, Massachusetts, USA. Quat. Sci. Rev. 2002, 21, 2127–2135. [Google Scholar] [CrossRef]
  13. Balco, G.; Schaefer, J.M. Cosmogenic-nuclide and varve chronologies for the deglaciation of southern New England. Quat. Geochronol. 2006, 1, 15–28. [Google Scholar] [CrossRef]
  14. Balco, G.; Briner, J.; Finkel, R.C.; Rayburn, J.A.; Ridge, J.C.; Schaefer, J.M. Regional beryllium-10 production rate calibration for late-glacial northeastern North America. Quat. Geochronol. 2009, 4, 93–107. [Google Scholar] [CrossRef]
  15. Balter-Kennedy, A.; Schaefer, J.M.; Balco, G.; Kelly, M.A.; Kaplan, M.R.; Schwartz, R.; Oakley, B.; Young, N.E.; Hanley, J.; Varuolo-Clarke, A.M. The Laurentide Ice Sheet in southern New England and New York during and at the end of the Last Glacial Maximum: A cosmogenic-nuclide chronology. Clim. Past 2024, 20, 2167–2190. [Google Scholar] [CrossRef]
  16. Harmon, K. Late Pleistocene Forest Succession in Northern New Jersey; Rutgers University: New Brunswick, NJ, USA, 1968; p. 203. [Google Scholar]
  17. Cotter, J.F.P. The Minimum Age of the Woodfordian Deglaciation of Northeastern Pennsylvania and Northwestern New Jersey; Lehigh University: Bethlehem, PA, USA, 1983; p. 159. [Google Scholar]
  18. Stone, B.; Reimer, G.; Pardi, R. Revised stratigraphy and history of glacial Lake Passaic, New Jersey. Geol. Soc. Am. Abstr. Programs (Northeast. Sect. Meet.) 1989, 21, 69. [Google Scholar]
  19. Sirkin, L.; Stuckenrath, R. The Port Washingtonian warm interval in the northern Atlantic coastal plain. Geol. Soc. Am. Bull. 1980, 91, 332–336. [Google Scholar] [CrossRef]
  20. Peteet, D.M.; Daniels, R.A.; Heusser, L.E.; Vogel, J.S.; Southon, J.R.; Nelson, D.E. Late-glacial pollen, macrofossils and fish remains in Northeastern, USA: The Younger Dryas oscillation. Quat. Sci. Rev. 1993, 12, 597–612. [Google Scholar] [CrossRef]
  21. Dalton, A.S.; Dulfer, H.E.; Margold, M.; Heyman, J.; Clague, J.J.; Froese, D.G.; Gauthier, M.S.; Hughes, A.L.C.; Jennings, C.E.; Norris, S.L.; et al. Deglaciation of the North American ice sheet complex in calendar years based on a comprehensive database of chronological data: NADI-1. Quat. Sci. Rev. 2023, 321, 108345. [Google Scholar] [CrossRef]
  22. Birks, H. The importance of plant macrofossils in late-glacial climatic reconstructions: An example from western Norway. Quat. Sci. Rev. 1993, 12, 719–726. [Google Scholar] [CrossRef]
  23. Zimmerman, S.; Wahl, D. Holocene paleoclimate change in the western US: The importance of chronology in discerning patterns and drivers. Quat. Sci. Rev. 2020, 246, 106487. [Google Scholar] [CrossRef]
  24. Peteet, D.M.; Vogel, J.S.; Nelson, D.E.; Southon, J.R.; Nickmann, R.J.; Heusser, L.E. Younger Dryas climatic reversal in northeastern USA? AMS ages for an old problem. Quat. Res. 1990, 33, 219–230. [Google Scholar] [CrossRef]
  25. Hajdas, I.; Ivy, S.D.; Beer, J.; Bonani, G.; Imboden, D.; Lotter, A.F.; Sturm, M.; Suter, M. AMS radiocarbon dating and varve chronology of Lake Soppensee e 6000 to 12000 14C years BP. Clim. Dyn. 1993, 9, 107e116. [Google Scholar] [CrossRef]
  26. Grimm, E.C.; Maher, L.J.; Nelson, D.M. The magnitude of error in conventional bulk-sediment radiocarbon dates from central North America. Quat. Res. 2009, 72, 301–308. [Google Scholar] [CrossRef]
  27. Gaglioti, B.V.; Mann, D.H.; Jones, B.M.; Pohlman, J.W.; Kunz, M.L.; Wooller, M.J. Radiocarbon age-offsets in an arctic lake reveal the long-term response of permafrost carbon to climate change. J. Geophys. Res. Biogeosci 2014, 119, 1630–1651. [Google Scholar] [CrossRef]
  28. Strunk, A.; Olsen, J.; Sanei, H.; Rudra, A.; Larsen, N.K. Improving the reliability of bulk sediment radiocarbon dating. Quat. Sci. Rev. 2020, 242, 106442. [Google Scholar] [CrossRef]
  29. MacDonald, G.M.; Beukens, R.P.; Kieser, W.E.; Vitt, D.H. Comparative radiocarbon dating of terrestrial plant macrofossils and aquatic moss from the “ice-free corridor” of western Canada. Geology 1987, 15, 837–840. [Google Scholar] [CrossRef]
  30. Birks, H.H. Plant macrofossils. In Tracking Environmental Change Using Lake Sediments; Smol, J.P., Birks, H.J.B., Last, W.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; Volume 3: Terrestrial, Algal, and Siliceous Indicators, pp. 49–74. [Google Scholar]
  31. Marty, J.; Myrbo, A. Radiocarbon dating suitability of aquatic plant macrofossils. J. Paleolimnol. 2014, 52, 435–443. [Google Scholar] [CrossRef]
  32. Stanford, S.D.; Stone, B.D.; Ridge, J.C.; Witte, R.W.; Pardi, R.R.; Reimer, G.E. Chronology of Laurentide glaciation in New Jersey and the New York City area, United States. Quat. Res. 2021, 99, 142–167. [Google Scholar] [CrossRef]
  33. Halsted, C.T.; Bierman, P.R.; Shakun, J.D.; Davis, P.T.; Corbett, L.B.; Drebber, J.S.; Ridge, J.C. A critical re-analysis of constraints on the timing and rate of Laurentide Ice Sheet recession in the northeastern United States. J. Quat. Sci. 2024, 39, 54–69. [Google Scholar] [CrossRef]
  34. Ridge, J.C.; Balco, G.; Bayless, R.L.; Beck, C.C.; Carter, L.B.; Dean, J.L.; Voytek, E.B.; Wei, J.H. The new North American Varve Chronology: A precise record of southeastern Laurentide Ice Sheet deglaciation and climate, 18.2–12.5 kyr BP, and correlations with Greenland ice core records. Am. J. Sci. 2012, 312, 685–722. [Google Scholar] [CrossRef]
  35. Francus, P.; Bradley, R.S.; Lewis, T.; Abbott, M.; Retelle, M.; Stoner, J.S. Limnological and sedimentary processes at Sawtooth Lake, Canadian High Arctic, and their influence on varve formation. J. Paleolimnol. 2008, 40, 963–985. [Google Scholar] [CrossRef]
  36. Bentley, M.J.; Christoffersen, P.; Hodgson, D.A.; Smith, A.M.; Tulaczyk, S.; Brocq, A.M.L. Subglacial Lake Sediments and Sedimentary Processes: Potential Archives of Ice Sheet Evolution, Past Environmental Change, and the Presence of Life. In Antarctic Subglacial Aquatic Environments; Siegert, M.J., Kennicutt, M.C., II, Bindschadler, R.A., Eds.; American Geophysical Union: Washington, DC, USA, 2011; Volume Geophysical Monograph Series 192, pp. 83–110. [Google Scholar]
  37. Kasanke, S.A.; Walker, D.A.; Chapin Iii, F.S.; Mann, D.H. Plant succession on glacial moraines in the Arctic Brooks Range along a >125,000-year glacial chronosequence/toposequence. Arct. Antarct. Alp. Res. 2023, 55, 2178151. [Google Scholar] [CrossRef]
  38. Cooper, W.S. The recent ecological history of Glacier Bay, Alaska. II. The present vegetation cycle. Ecology 1923, 4, 223–246. [Google Scholar] [CrossRef]
  39. Chapin, F.S.; Walker, L.R.; Fastie, C.L.; Sharman, L.C. Mechanisms of Primary Succession Following Deglaciation at Glacier Bay, Alaska. Ecol. Monogr. 1994, 64, 149–175. [Google Scholar] [CrossRef]
  40. Hodkinson, I.D.; Coulson, S.J.; Webb, N.R. Community Assembly along Proglacial Chronosequences in the High Arctic: Vegetation and Soil Development in North-West Svalbard. J. Ecol. 2003, 91, 651–663. [Google Scholar] [CrossRef]
  41. Fickert, T.; Friend, D.; Grüninger, F.; Molnia, B.; Richter, M. Did Debris-Covered Glaciers Serve as Pleistocene Refugia for Plants? A New Hypothesis Derived from Observations of Recent Plant Growth on Glacier Surfaces. Arct. Antarct. Alp. Res. 2007, 39, 245–257. [Google Scholar] [CrossRef]
  42. Nishiizumi, K.; Winterer, E.L.; Kohl, C.P.; Klein, J.; Middleton, R.; Lal, D.; Arnold, J.R. Cosmic ray production rates of 10Be and 26Al in quartz from glacially polished rocks. J. Geophys. Res. Solid Earth 1989, 94, 17907–17915. [Google Scholar] [CrossRef]
  43. Lal, D. Cosmic ray labeling of erosion surfaces: In situ nuclide production rates and erosion models. Earth Planet. Sci. Lett. 1991, 104, 424–439. [Google Scholar] [CrossRef]
  44. Gosse, J.C.; Phillips, F.M. Terrestrial in situ cosmogenic nuclides: Theory and application. Quat. Sci. Rev. 2001, 20, 1475–1560. [Google Scholar] [CrossRef]
  45. Korschinek, G.; Bergmaier, A.; Faestermann, T.; Gerstmann, U.C.; Knie, K.; Rugel, G.; Wallner, A.; Dillmann, I.; Dollinger, G.; von Gostomski, C.L.; et al. A new value for the half-life of 10Be by Heavy-Ion Elastic Recoil Detection and liquid scintillation counting. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 187–191. [Google Scholar] [CrossRef]
  46. Balco, G. Production rate calculations for cosmic-ray-muon-produced 10Be and 26Al benchmarked against geological calibration data. Quat. Geochronol. 2017, 39, 150–173. [Google Scholar] [CrossRef]
  47. Pierre Auger Collaboration; Aab, A.; Abreu, P.; Aglietta, M.; Al Samarai, I.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; et al. The Pierre Auger Collaboration. Science 2017, 357, 1266. [Google Scholar] [CrossRef]
  48. Lal, D.; Peters, B. Cosmic ray produced radioactivity on the Earth. In Handbuch der Physik; Sitte, K., Ed.; Springer: New York, NY, USA, 1967; pp. 551–612. [Google Scholar]
  49. Lal, D. Theoretically expected variations in the terrestrial cosmic ray production rates of isotopes. In Solar-Terrestrial Relationships and the Earth Environment in the Last Millennia, Proceedings Fermi School Physics 95th; Castagnoli, G.G., Ed.; Italian Physical Society, Varenna on Lake Como: Amsterdam, Netherlands, 1988; pp. 216–233. [Google Scholar]
  50. Elsasser, W.; Ney, E.P.; Winckler, J.R. Cosmic-ray intensity and geomagnetism. Nature 1956, 178, 1226–1227. [Google Scholar] [CrossRef]
  51. Balco, G.; Stone, J.O.; Lifton, N.A.; Dunai, T.J. A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements. Quat. Geochronol. 2008, 3, 174–195. [Google Scholar] [CrossRef]
  52. Phillips, F.M.; Argento, D.C.; Balco, G.; Caffee, M.W.; Clem, J.; Dunai, T.J.; Finkel, R.; Goehring, B.; Gosse, J.C.; Hudson, A.M.; et al. The CRONUS-Earth Project: A synthesis. Quat. Geochronol. 2016, 31, 119–154. [Google Scholar] [CrossRef]
  53. Marrero, S.M.; Phillips, F.M.; Borchers, B.; Lifton, N.; Aumer, R.; Balco, G. Cosmogenic nuclide systematics and the CRONUScalc program. Quat. Geochronol. 2016, 31, 160–187. [Google Scholar] [CrossRef]
  54. Stone, J.O. Air pressure and cosmogenic isotope production. J. Geophys. Res. Solid Earth 2000, 105, 23753–23759. [Google Scholar] [CrossRef]
  55. Pavón-Carrasco, F.J.; Osete, M.L.; Torta, J.M.; De Santis, A. A geomagnetic field model for the Holocene based on archaeomagnetic and lava flow data. Earth Planet. Sci. Lett. 2014, 388, 98–109. [Google Scholar] [CrossRef]
  56. Borchers, B.; Marrero, S.; Balco, G.; Caffee, M.; Goehring, B.; Lifton, N.; Nishiizumi, K.; Phillips, F.; Schaefer, J.; Stone, J. Geological calibration of spallation production rates in the CRONUS-Earth project. Quat. Geochronol. 2016, 31, 188–198. [Google Scholar] [CrossRef]
  57. Desilets, D.; Zreda, M. On scaling cosmogenic nuclide production rates for altitude and latitude using cosmic-ray measurements. Earth Planet. Sci. Lett. 2001, 193, 213–225. [Google Scholar] [CrossRef]
  58. Lifton, N.; Sato, T.; Dunai, T.J. Scaling in situ cosmogenic nuclide production rates using analytical approximations to atmospheric cosmic-ray fluxes. Earth Planet. Sci. Lett. 2014, 386, 149–160. [Google Scholar] [CrossRef]
  59. Channell, J.; Hodell, D.A.; Crowhurst, S.J.; Skinner, L.C.; Muscheler, R. Relative paleointensity (RPI) in the latest Pleistocene (10–45 ka) and implications for deglacial atmospheric radiocarbon. Quat. Sci. Rev. 2018, 191, 57–72. [Google Scholar] [CrossRef]
  60. Channell, J.E.T.; Vigliotti, L. The role of geomagnetic field intensity in Late Quaternary evolution of humans and large mammals. Geophys. 2019, 57, 709–738. [Google Scholar] [CrossRef]
  61. Muscheler, R.; Beer, J.; Kubik, P.W.; Synal, H.A. Geomagnetic field intensity during the last 60,000 years based on 10Be and 36Cl from the Summit ice cores and 14C. Quat. Sci. Rev. 2005, 24, 1849–1860. [Google Scholar] [CrossRef]
  62. Nilsson, A.; Nguyen, L.; Panovska, S.; Herbst, K.; Zheng, M.; Suttie, N.; Muscheler, R. Holocene solar activity inferred from global and hemispherical cosmic-ray proxy records. Nat. Geosci. 2024, 17, 654–659. [Google Scholar] [CrossRef]
  63. Panovska, S.; Poluianov, S.; Gao, J.; Korte, M.; Mishev, A.; Shprits, Y.Y.; Usoskin, I. Effects of Global Geomagnetic Field Variations Over the Past 100,000 Years on Cosmogenic Radionuclide Production Rates in the Earth’s Atmosphere. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031158. [Google Scholar] [CrossRef]
  64. Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, H.; Heikkilä, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9400 years of cosmic radiation and solar activity from ice cores and tree rings. Proc. Natl. Acad. Sci. USA 2012, 109, 5967–5971. [Google Scholar] [CrossRef]
  65. Usoskin, I.G. A history of solar activity over millennia. Living Rev. Sol. Phys. 2017, 14, 1–97. [Google Scholar] [CrossRef]
  66. Panovska, S.; Korte, M.; Constable, C.G. One hundred thousand years of geomagnetic field evolution. Rev. Geophys. 2019, 57, 1289–1337. [Google Scholar] [CrossRef]
  67. Desilets, D.; Zreda, M.; Prabu, T. Extended scaling factors for in situ cosmogenic nuclides: New measurements at low latitude. Earth Planet. Sci. Lett. 2006, 246, 265–276. [Google Scholar] [CrossRef]
  68. Desilets, D.; Zreda, M. Spatial and temporal distribution of secondary cosmic-ray nucleon intensities and applications to in situ cosmogenic dating. Earth Planet. Sci. Lett. 2003, 206, 21–42. [Google Scholar] [CrossRef]
  69. R_Core_Team. R: A Language and Environment for Statistical Computing. 2018. Available online: http://www.r-project.org (accessed on 24 August 2025).
  70. Tauxe, L.; Kent, D.V. A simplified statistical model for the geomagnetic field and the detection of shallow bias in paleomagnetic inclinations: Was the ancient magnetic field dipolar? In Timescales of the Paleomagnetic Field, Geophysical Monograph 145; Channell, J.E.T., Kent, D.V., Lowrie, W., Meert, J., Eds.; American Geophysical Union: Washington, DC, USA, 2004; pp. 101–116. [Google Scholar]
  71. Lal, D.; Arnold, J.R.; Honda, M. Cosmic-Ray Production Rates of Be7 in Oxygen, and P32, P33, S35 in Argon at Mountain Altitudes. Phys. Rev. 1960, 118, 1626–1632. [Google Scholar] [CrossRef]
  72. Clark, D.H.; Bierman, P.R.; Larsen, P. Improving in Situ Cosmogenic Chronometers. Quat. Res. 1995, 44, 367–377. [Google Scholar] [CrossRef]
  73. Opdyke, N.D.; Henry, K.W. A test of the dipole hypothesis. Earth Planet. Sci. Lett. 1969, 6, 139–151. [Google Scholar] [CrossRef]
  74. Schneider, D.A.; Kent, D.V. The time-averaged paleomagnetic field. Rev. Geophys. 1990, 28, 71–96. [Google Scholar] [CrossRef]
  75. Alexandrescu, M.; Courtillot, V.; Le Mouel, J.-L. High-resolution secular variation of the geomagnetic field in western Europe over the last 4 centuries: Comparison and integration of historical data from Paris and London. J. Geophys. Res. 1997, 102, 20245–20258. [Google Scholar] [CrossRef]
  76. Gallet, Y.; Genevey, A.; Le Goff, M. Three millennia of directional variation of the Earth’s magnetic field in western Europe as revealed by archeological artefacts. Phys. Earth Planet. Inter. 2002, 131, 81–89. [Google Scholar] [CrossRef]
  77. Lifton, N. Implications of two Holocene time-dependent geomagnetic models for cosmogenic nuclide production rate scaling. Earth Planet. Sci. Lett. 2016, 433, 257–268. [Google Scholar] [CrossRef]
  78. Butler, R.F. Paleomagnetism: Magnetic Domains to Geologic Terranes (2004 Electronic Edition); Blackwell Scientific Publications: Boston, MA, USA, 1992; p. 319. [Google Scholar]
  79. Johnson, C.L.; Constable, C.G.; Tauxe, L.; Barendregt, R.; Brown, L.L.; Coe, R.S.; Layer, P.; Mejia, V.; Opdyke, N.D.; Singer, B.S.; et al. Recent investigations of the 0–5 Ma geomagnetic field recorded by lava flows. Geochem. Geophys. Geosyst. 2008, 9, Q04032. [Google Scholar] [CrossRef]
  80. Cromwell, G.; Johnson, C.L.; Tauxe, L.; Constable, C.G.; Jarboe, N.A. PSV10: A Global Data Set for 0–10 Ma Time-Averaged Field and Paleosecular Variation Studies. Geochem. Geophys. Geosyst. 2018, 19, 1533–1558. [Google Scholar] [CrossRef]
  81. Constable, C.G.; Parker, R.L. Statistics of the geomagnetic secular variation for the past 5 m.y. J. Geophys. Res. 1988, 93, 11569–11581. [Google Scholar] [CrossRef]
  82. McElhinny, M.W.; McFadden, P.L. Paleosecular variation over the past 5 Myr based on a new generalized database. Geophys. J. Int. 1997, 131, 240–252. [Google Scholar] [CrossRef]
  83. Martin, L.C.P.; Blard, P.H.; Balco, G.; Lavé, J.; Delunel, R.; Lifton, N.; Laurent, V. The CREp program and the ICE-D production rate calibration database: A fully parameterizable and updated online tool to compute cosmic-ray exposure ages. Quat. Geochronol. 2017, 38, 25–49. [Google Scholar] [CrossRef]
  84. Putnam, A.E.; Schaefer, J.M.; Barrell, D.J.A.; Vandergoes, M.; Denton, G.H.; Kaplan, M.R.; Finkel, R.C.; Schwartz, R.; Goehring, B.M.; Kelley, S.E. In situ cosmogenic 10Be production-rate calibration from the Southern Alps, New Zealand. Quat. Geochronol. 2010, 5, 392–409. [Google Scholar] [CrossRef]
  85. Lifton, N.; Caffee, M.; Finkel, R.; Marrero, S.; Nishiizumi, K.; Phillips, F.M.; Goehring, B.; Gosse, J.; Stone, J.; Schaefer, J.; et al. In situ cosmogenic nuclide production rate calibration for the CRONUS-Earth project from Lake Bonneville, Utah, shoreline features. Quat. Geochronol. 2015, 26, 56–69. [Google Scholar] [CrossRef]
  86. Phillips, F.M.; Kelly, M.A.; Hudson, A.M.; Stone, J.O.H.; Schaefer, J.; Marrero, S.M.; Fifield, L.K.; Finkel, R.; Lowell, T. CRONUS-Earth calibration samples from the Huancané II moraines, Quelccaya Ice Cap, Peru. Quat. Geochronol. 2016, 31, 220–236. [Google Scholar] [CrossRef]
  87. Staiger, J.; Gosse, J.; Toracinta, R.; Oglesby, B.; Fastook, J.; Johnson, J. Atmospheric scaling of cosmogenic nuclide production: Climate effect. J. Geophys. Res. 2007, 112, BO2205. [Google Scholar] [CrossRef]
  88. Niu, L.; Knorr, G.; Krebs-Kanzow, U.; Gierz, P.; Lohmann, G. Rapid Laurentide Ice Sheet growth preceding the Last Glacial Maximum due to summer snowfall. Nat. Geosci. 2024, 17, 440–449. [Google Scholar] [CrossRef]
  89. Wright, H.E.; Stefanova, I. Plant trash in the basal sediments of glacial lakes. Acta Palaeobot. 2004, 44, 141–146. [Google Scholar]
  90. Słowiński, M.; Błaszkiewicz, M.; Brauer, A.; Noryśkiewicz, B.; Ott, F.; Tyszkowski, S. The role of melting dead ice on landscape transformation in the early Holocene in Tuchola Pinewoods, North Poland. Quat. Int. 2015, 388, 64–75. [Google Scholar] [CrossRef]
  91. Balco, G. Contributions and unrealized potential contributions of cosmogenic-nuclide exposure dating to glacier chronology, 1990–2010. Quat. Sci. Rev. 2011, 30, 3–27. [Google Scholar] [CrossRef]
  92. Hallet, B. A Theoretical Model of Glacial Abrasion. J. Glaciol. 1979, 23, 39–50. [Google Scholar] [CrossRef]
Quaternary 08 00047 g001
Figure 1. Contrasting age estimates for retreat of the southeastern margin of the Laurentide Ice Sheet (LIS), based on 14C AMS dating of terrestrial plant macrofossils in basal deglacial sediments [9] and on 10Be exposure dating of glacial pavement and boulders on a terminal moraine in the Allamuchy area of New Jersey [10]. Estimated ice-volume equivalent sea-level change (thick blue curve) since 35 ka is from [4], and summer insolation at 65° N (thinner maroon curve) is calculated with software from [11]. Labeled for context from [4] are the Last Glacial Maximum (LGM), Heinrich events H1, H2, and H3, Bolling–Allerod warm period (B-A), Younger Dryas cold period (YD), and the Holocene. See [9] for additional climate proxies and discussion.
Figure 1. Contrasting age estimates for retreat of the southeastern margin of the Laurentide Ice Sheet (LIS), based on 14C AMS dating of terrestrial plant macrofossils in basal deglacial sediments [9] and on 10Be exposure dating of glacial pavement and boulders on a terminal moraine in the Allamuchy area of New Jersey [10]. Estimated ice-volume equivalent sea-level change (thick blue curve) since 35 ka is from [4], and summer insolation at 65° N (thinner maroon curve) is calculated with software from [11]. Labeled for context from [4] are the Last Glacial Maximum (LGM), Heinrich events H1, H2, and H3, Bolling–Allerod warm period (B-A), Younger Dryas cold period (YD), and the Holocene. See [9] for additional climate proxies and discussion.
Quaternary 08 00047 g001
Quaternary 08 00047 g003
Figure 3. Effective vertical cutoff rigidity (Rc) relative to its maximum value as a function of geomagnetic latitude for a bracketing range of dipole moments (M) relative to the modern value (M0), using Equation (2) of [58].
Figure 3. Effective vertical cutoff rigidity (Rc) relative to its maximum value as a function of geomagnetic latitude for a bracketing range of dipole moments (M) relative to the modern value (M0), using Equation (2) of [58].
Quaternary 08 00047 g003
Quaternary 08 00047 g004
Figure 4. (A) Variations in virtual axial dipole moment (VADM) for 0–45 ka, based on SHA.DIF.14k for 0–14 ka [55] and relative paleointensity (RPI) stack for 14–45 ka [59], compared to 10Be-based VADM from ice cores [61] as assembled in [60]. (B) Cumulative 10Be-based VADM curve (from (A)) in nominal 0.5 kyr increments going back in time from the present (red curve), compared for reference to cumulative VADMs modeled for a constant dipole moment, M, relative to the present value, M0 (dotted and dashed lines).
Figure 4. (A) Variations in virtual axial dipole moment (VADM) for 0–45 ka, based on SHA.DIF.14k for 0–14 ka [55] and relative paleointensity (RPI) stack for 14–45 ka [59], compared to 10Be-based VADM from ice cores [61] as assembled in [60]. (B) Cumulative 10Be-based VADM curve (from (A)) in nominal 0.5 kyr increments going back in time from the present (red curve), compared for reference to cumulative VADMs modeled for a constant dipole moment, M, relative to the present value, M0 (dotted and dashed lines).
Quaternary 08 00047 g004
Quaternary 08 00047 g005
Figure 5. Selected altitude and latitude scaling factors for 10Be exposure dating: (A) Altitude scaling factor at high latitude (HL) versus air pressure and equivalent altitude for the Lal/Stone St scaling scheme [54] and for the De scaling scheme [67]. (B) Latitude scaling factor at sea level (SL) as a function of geomagnetic (=geographic for GAD field) latitude for the Lal/Stone St scheme (static presumed GAD field) [54] and for the De scheme [67], according to various geomagnetic field models (Table 1): GAD, geocentric axial dipole with no dispersion; SHA.DIF.14k, spherical harmonic model for 0–14 ka [55]; K27, dispersion of virtual geomagnetic poles with a Fisher’s precision parameter of K = 27 averaging to a GAD field (Table 1); TK03, statistical geomagnetic field model to spherical harmonic degree and order 8 that averages to a GAD field [70].
Figure 5. Selected altitude and latitude scaling factors for 10Be exposure dating: (A) Altitude scaling factor at high latitude (HL) versus air pressure and equivalent altitude for the Lal/Stone St scaling scheme [54] and for the De scaling scheme [67]. (B) Latitude scaling factor at sea level (SL) as a function of geomagnetic (=geographic for GAD field) latitude for the Lal/Stone St scheme (static presumed GAD field) [54] and for the De scheme [67], according to various geomagnetic field models (Table 1): GAD, geocentric axial dipole with no dispersion; SHA.DIF.14k, spherical harmonic model for 0–14 ka [55]; K27, dispersion of virtual geomagnetic poles with a Fisher’s precision parameter of K = 27 averaging to a GAD field (Table 1); TK03, statistical geomagnetic field model to spherical harmonic degree and order 8 that averages to a GAD field [70].
Quaternary 08 00047 g005
Table 1. Latitude scaling factor at sea level for the Lal/Stone St scheme and for the Desilets De scheme.
Table 1. Latitude scaling factor at sea level for the Lal/Stone St scheme and for the Desilets De scheme.
Latitude |°|St ScalingDe Scaling
GADSHA.DIF.14kK27TK03
00.58730.53830.54020.55100.5503
5 0.53980.54280.55400.5524
100.59920.54540.55070.56300.5592
15 0.55810.56660.58000.5745
200.67730.58190.59420.60500.5998
25 0.62140.63710.64100.6373
300.83000.68020.69720.68900.6921
35 0.75890.77190.74800.7502
400.93680.84990.85120.81500.8091
45 0.93280.92020.88300.8662
501.01560.98260.96700.94100.9057
55 0.99810.99050.98000.9346
601.00220.99990.99840.99600.9529
65 1.00000.99991.00000.9662
701.00001.00001.00001.00000.9745
75 1.00001.00001.00000.9815
801.00001.00001.00001.00000.9861
85 1.00001.00001.00000.9876
901.00001.00001.00001.00000.9899
Latitude scaling factor at sea level for the Lal/Stone St scheme [54] as a function of geomagnetic latitude, assuming a geocentric axial dipole (GAD) field with no dispersion, and for the De scheme [67], based on effective vertical cutoff rigidity (Rc) using Equation (2) of [58] to derive a latitude scaling factor f(Rc) at sea level as a function of geographic (=geomagnetic) latitude according to various geomagnetic field models: GAD field with no dispersion, SHA.DIF.14k spherical harmonic model for 0–14 ka [55], K27 for VGP distribution with Fisher’s precision parameter K = 27, and TK03 statistical geomagnetic field model of secular variation [70].
Table 2. 10Be primary calibration sites and Allamuchy 10Be exposure age site on LIS terminal moraine.
Table 2. 10Be primary calibration sites and Allamuchy 10Be exposure age site on LIS terminal moraine.
Primary 10Be Calibration Sites LIS Terminal Moraine
MRPPTSCOTHU08 AL
Site Parameters
Latitude, °N−43.641.357.4−13.9 41.0
Longitude, °E170.6−112.5−5.6−70.9 −74.6
Altitude, m102816031364857 328
Air pressure (ap), hPa895.70834.93997.02550.60 974.46
Atmospheric depth (x), g cm−2913.35851.381016.66561.45 993.66
Number sampling sites76810 13
C (10Be conc.), atoms g−187,100275,00057,275559,650 122,000
Age, calendar years ago963018,36011,70012,300 TBD
P (10Be prod. rate), atoms g−1 y−19.0414.984.9045.50 TBD
Scaling Parameters Mean ± 1σ 10Be ka ± 1σ
St
F = S.lambda2.353.521.1612.41 1.28
CSLHL: C/F, atoms g−137,06478,12549,43045,097 95,313
PSLHL: C/F/age, atoms g−1 y−13.854.264.223.674.00 ± 0.29 23.8 ± 1.7
Mean PSLHL w/o HU08, atoms g−1 y−1 4.11 ± 0.23 23.2 ± 1.3
De-GAD
Rc4.485.301.3614.07 5.41
f(Rc)0.910.871.000.56 0.87
f(x)2.463.881.1326.46 1.34
F = f(Rc) × f(x)2.243.391.1314.67 1.16
CSLHL: C/F, atoms g−138,88481,11950,53838,141 104,865
PSLHL: C/F/age, atoms g−1 y−14.044.424.323.103.97 ± 0.60 26.4 ± 4.0
Mean PSLHL w/o HU08, atoms g−1 y−1 4.26 ± 0.20 24.6 ± 1.1
De-TK03
Rc5.836.442.8413.49 6.62
f(Rc)0.850.820.950.57 0.81
f(x)2.433.841.1326.77 1.34
F = f(Rc) × f(x)2.063.171.0715.27 1.10
CSLHL: C/F, atoms g−142,28686,85553,55836,641 111,101
PSLHL: C/F/age, atoms g−1 y−14.394.734.582.984.17 ± 0.81 26.6 ± 5.2
Mean PSLHL w/o HU08, atoms g−1 y−1 4.57 ± 0.17 24.3 ± 0.9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kent, D.V.; Lanci, L.; Peteet, D.M. Geomagnetic Secular Variation Models for Latitude Scaling of Cosmic Ray Flux and Considerations for 10Be Exposure Dating of Laurentide Ice Sheet Retreat. Quaternary 2025, 8, 47. https://doi.org/10.3390/quat8030047

AMA Style

Kent DV, Lanci L, Peteet DM. Geomagnetic Secular Variation Models for Latitude Scaling of Cosmic Ray Flux and Considerations for 10Be Exposure Dating of Laurentide Ice Sheet Retreat. Quaternary. 2025; 8(3):47. https://doi.org/10.3390/quat8030047

Chicago/Turabian Style

Kent, Dennis V., Luca Lanci, and Dorothy M. Peteet. 2025. "Geomagnetic Secular Variation Models for Latitude Scaling of Cosmic Ray Flux and Considerations for 10Be Exposure Dating of Laurentide Ice Sheet Retreat" Quaternary 8, no. 3: 47. https://doi.org/10.3390/quat8030047

APA Style

Kent, D. V., Lanci, L., & Peteet, D. M. (2025). Geomagnetic Secular Variation Models for Latitude Scaling of Cosmic Ray Flux and Considerations for 10Be Exposure Dating of Laurentide Ice Sheet Retreat. Quaternary, 8(3), 47. https://doi.org/10.3390/quat8030047

Article Metrics

Back to TopTop