Mathematical Analysis and Treatment for a Delayed Hepatitis B Viral Infection Model with the Adaptive Immune Response and DNA-Containing Capsids
Abstract
:1. Introduction
2. Analysis of the Model
2.1. Non-Negativity and Boundedness of Solutions
2.2. Steady States
3. Mathematical Analysis of the Optimal Control
3.1. The Optimization Problem
3.2. An Optimal Control Existence Result
- (C1)
- The set of the corresponding state variables and controls is nonempty.
- (C2)
- The set is closed and convex.
- (C3)
- The right hand side of the state system is bounded by a linear function in the state and control variables.
- (C4)
- The integrand of the objective functional is concave on .
- (C5)
- There exists an and two constants , such that the integrand of the objective functional satisfieswhere
3.3. The Optimality System
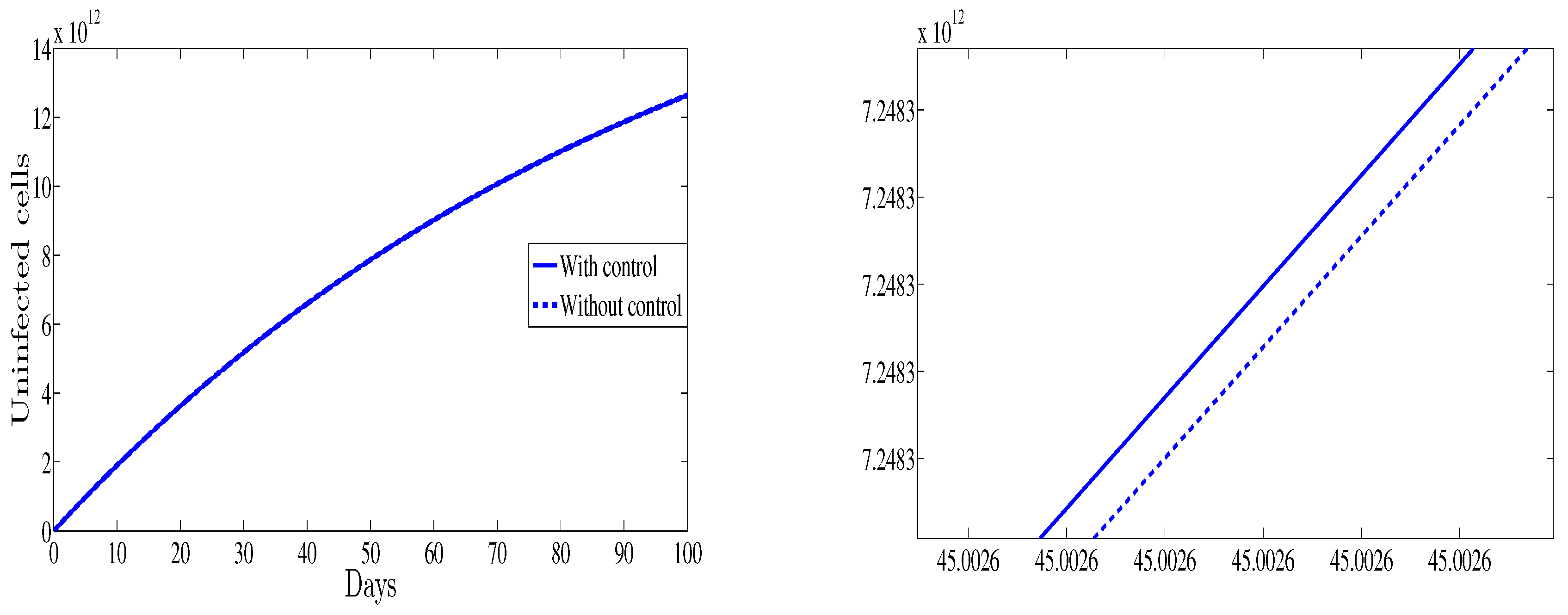
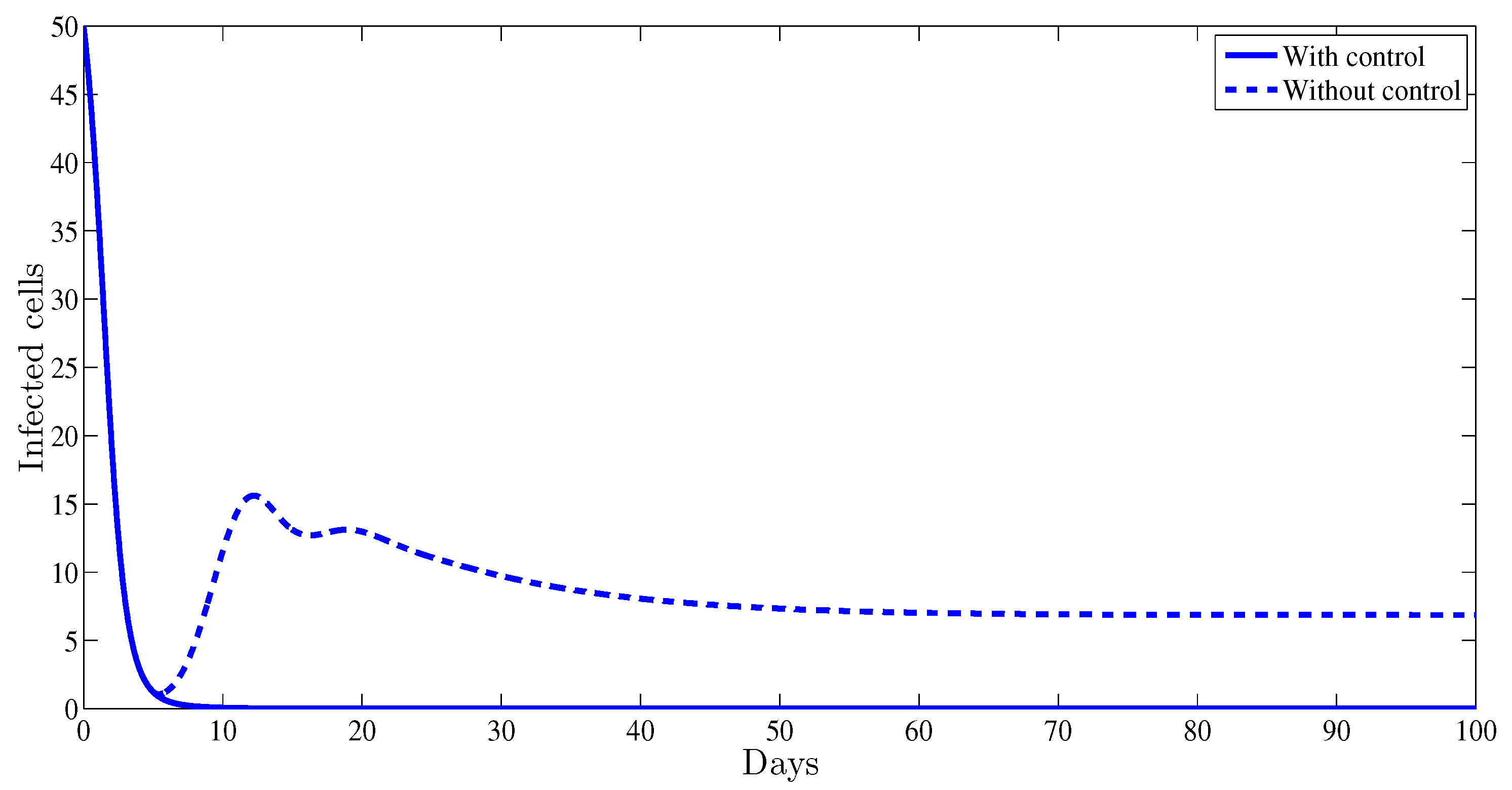
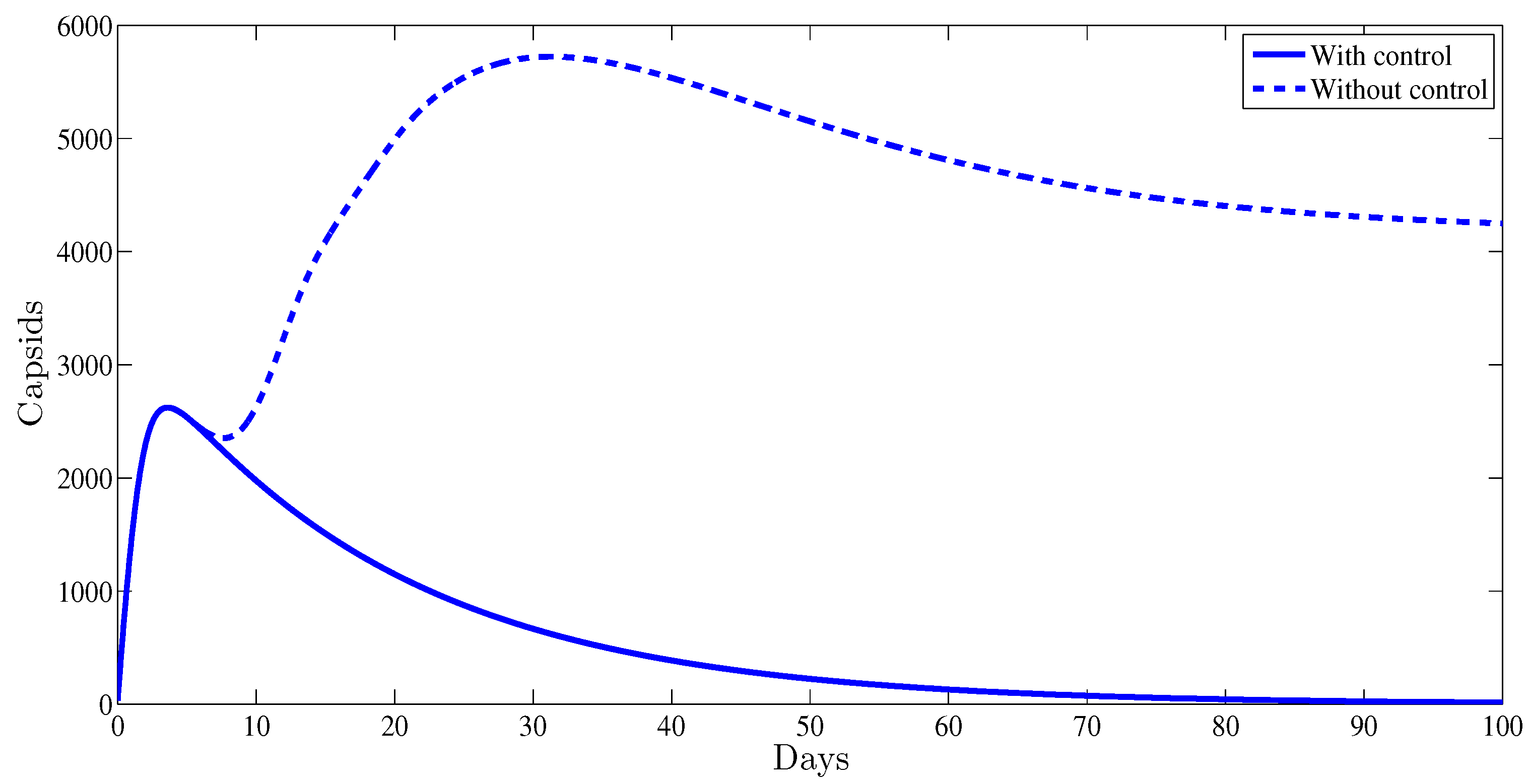
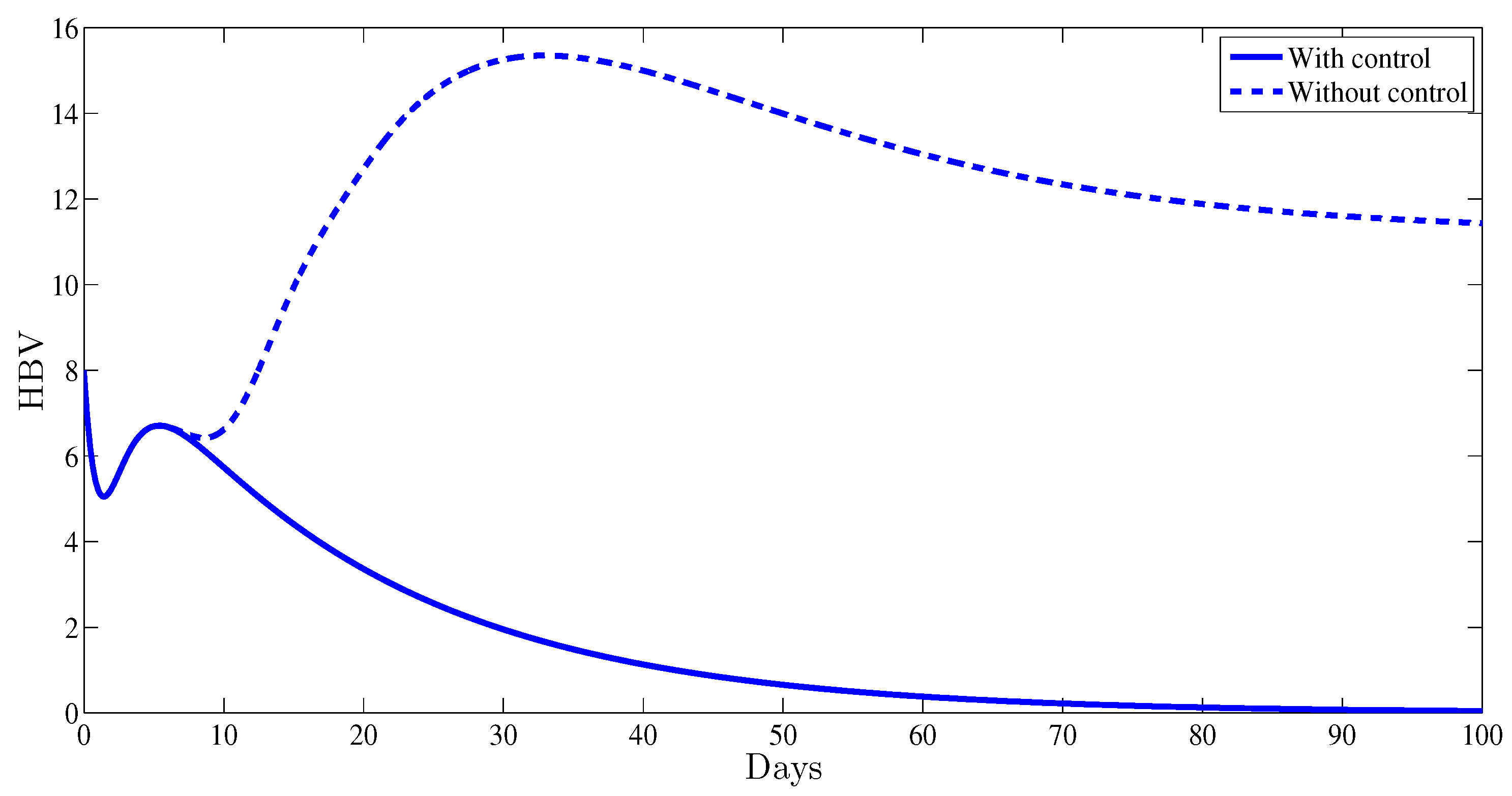
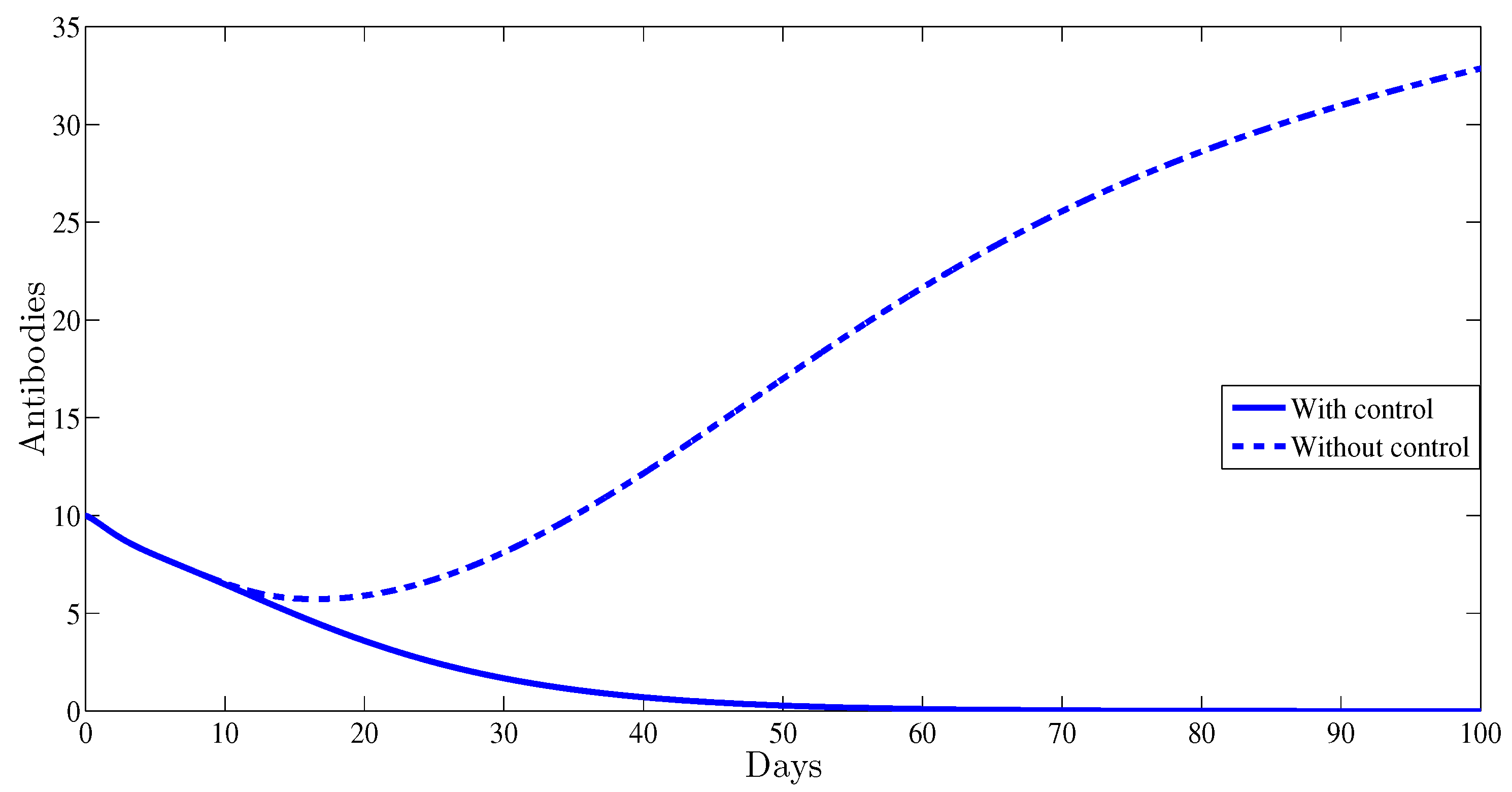
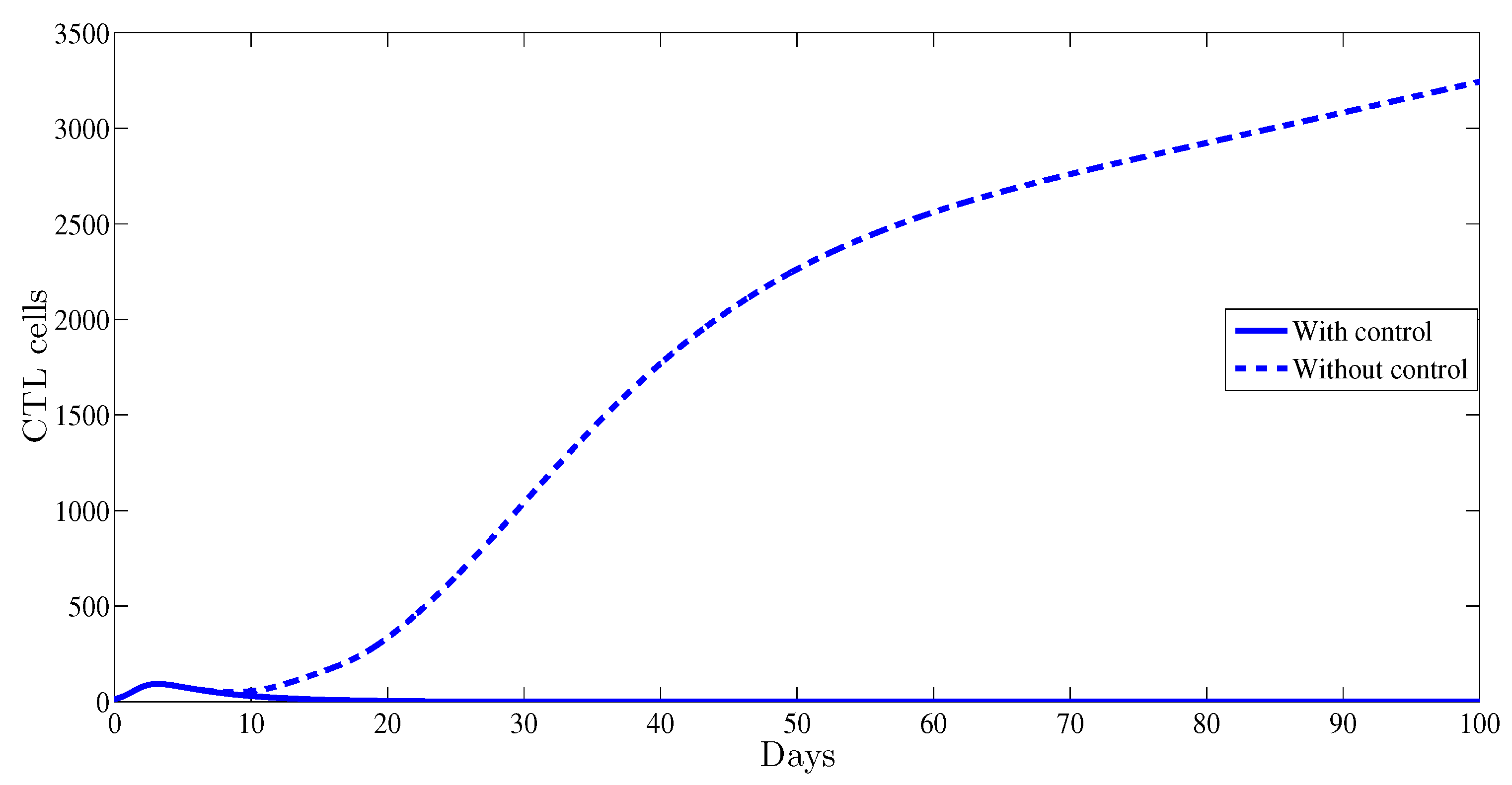
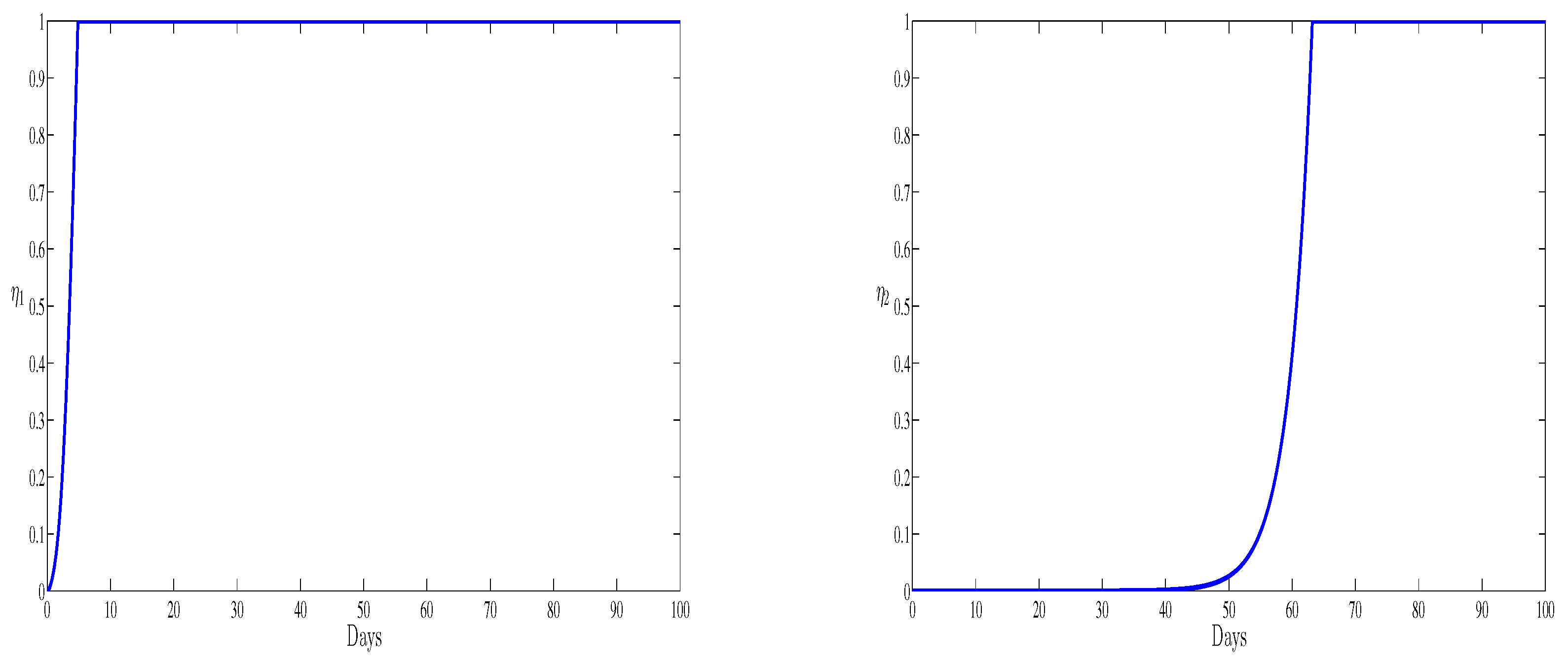
4. Numerical Results
| Algorithm 1: The forward-backward finite difference numerical scheme. |
|
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kane, M. Global programme for control of hepatitis B infection. Vaccine 1995, 13, 547–549. [Google Scholar] [CrossRef]
- World Health Organization. Progress toward Access to Hepatitis B Treatment Worldwide. WHO Web Site, 2018. Available online: http://www.who.int/hepatitis/news-events/cdc-hepatitis-b-article/en/ (accessed on 19 July 2018).
- Lavanchy, D. Hepatitis B virus epidemiology, disease burden, treatment, and current and emerging prevention and control measures. J. Viral Hepat. 2004, 11, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Perelson, A.S. Modeling the mechanisms of acute hepatitis B virus infection. J. Theor. Biol. 2007, 247, 23–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, M.A.; Bonhoeffer, S.; Hill, A.M.; Boehme, R.; Thomas, H.C.; McDade, H. Viral dynamics in hepatitis B virus infection. Proc. Natl. Acad. Sci. USA 1996, 93, 4398–4402. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wang, W. Propagation of HBV with spatial dependence. Math. Biosci. 2007, 210, 78–95. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Min, L.; Ji, Y.; Su, Y.; Kuang, Y. Global stability of endemic equilibrium point of basic virus infection model with application to HBV infection. J. Syst. Sci. Complex. 2010, 23, 1221–1230. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, K.; Yang, Y. Dynamical behaviors of an HBV infection model with logistic hepatocyte growth. Math. Comput. Model. 2011, 54, 704–711. [Google Scholar] [CrossRef]
- Yousfi, N.; Hattaf, K.; Tridane, A. Modeling the adaptive immune response in HBV infection. J. Math. Biol. 2011, 63, 933–957. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Wang, W. Complete classification of global dynamics of a virus model with immune responses. Discret. Contin. Dyn. Syst. Ser. B 2014, 19, 1087–1103. [Google Scholar] [Green Version]
- Meskaf, A.; Allali, K.; Tabit, Y. Optimal control of a delayed hepatitis B viral infection model with cytotoxic T-lymphocyte and antibody responses. Int. J. Dyn. Control 2017, 5, 893–902. [Google Scholar] [CrossRef]
- Allali, K.; Meskaf, A.; Tridane, A. Mathematical Modeling of the Adaptive Immune Responses in the Early Stage of the HBV Infection. Int. J. Differ. Equ. 2018, 2018, 6710575. [Google Scholar] [CrossRef]
- Manna, K.; Chakrabarty, S.P. Chronic hepatitis B infection and HBV DNA-containing capsids: Modeling and analysis. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 383–395. [Google Scholar] [CrossRef]
- Manna, K.; Chakrabarty, S.P. Global stability and a non-standard finite difference scheme for a diffusion driven HBV model with capsids. J. Differ. Equ. Appl. 2015, 21, 918–933. [Google Scholar] [CrossRef]
- Manna, K.; Chakrabarty, S.P. Global stability of one and two discrete delay models for chronic hepatitis B infection with HBV DNA-containing capsids. Comput. Appl. Math. 2017, 36, 525–536. [Google Scholar] [CrossRef]
- Manna, K.; Chakrabarty, S.P. Combination therapy of pegylated interferon and lamivudine and optimal controls for chronic hepatitis B infection. Int. J. Dynam. Control 2018, 6, 354–368. [Google Scholar] [CrossRef]
- Danane, J.; Meskaf, A.; Allali, K. Optimal control of a delayed hepatitis B viral infection model with HBV DNA-containing capsids and CTL immune response. Optim. Control Appl. Methods 2018, 39, 1262–1272. [Google Scholar] [CrossRef]
- Bruss, V. Envelopment of the hepatitis B virus nucleocapsid. Virus Res. 2004, 106, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Ganem, D.; Prince, A.M. Hepatitis B virus infection: Natural history and clinical consequences. N. Engl. J. Med. 2004, 350, 1118–1129. [Google Scholar] [CrossRef] [PubMed]
- Ochsenbein, A.F.; Fehr, T.; Lutz, C.; Suter, M.; Brombacher, F.; Hengartner, H.; Zinkernagel, R.M. Control of early viral and bacterial distribution and disease by natural antibodies. Science 1999, 286, 2156–2159. [Google Scholar] [CrossRef] [PubMed]
- Aasa-Chapman, M.M.; Hayman, A.; Newton, P.; Cornforth, D.; Williams, I.; Borrow, P.; Balfe, P.; McKnight, A. Development of the antibody response in acute HIV-1 infection. AIDS 2004, 18, 371–381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puoti, M.; Zonaro, A.; Ravaggi, A.; Marin, M.G.; Castelnuovo, F.; Cariani, E. Hepatitis C virus RNA and antibody response in the clinical course of acute hepatitis C virus infection. Hepatology 1992, 16, 877–881. [Google Scholar] [CrossRef] [PubMed]
- Hale, J.; Verduyn Lunel, S.M. Introduction to Functional Differential Equations; Applied Mathematical Science; Springer: New York, NY, USA, 1993; p. 99. [Google Scholar]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1975. [Google Scholar]
- Lukes, D.L. Differential Equations: Classical to Controlled, of Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1982; p. 162. [Google Scholar]
- Göllmann, L.; Kern, D.; Maurer, H. Optimal control problems with delays in state and control variables subject to mixed control-state constraints. Optim. Control Appl. Methods 2009, 30, 341–365. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Optimal control of a delayed HIV infection model with immune response using an efficient numerical method. ISRN Biomath. 2012. [Google Scholar] [CrossRef]
- Laarabi, H.; Abta, A.; Hattaf, K. Optimal control of a delayed SIRS epidemic model with vaccination and treatment. Acta Biotheor. 2015, 63, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Hattaf, K.; Sun, J. Optimal control of a delayed SLBS computer virus model. Physica A 2015, 427, 244–250. [Google Scholar] [CrossRef]
- Yan, Z.; Tan, W.; Zhao, W.; Dan, Y.; Wang, X.; Mao, Q.; Wang, Y.; Deng, G. Regulatory polymorphisms in the IL-10 gene promoter and HBV-related acute liver failure in the Chinese population. J. Viral Hepat. 2009, 16, 775–783. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danane, J.; Allali, K. Mathematical Analysis and Treatment for a Delayed Hepatitis B Viral Infection Model with the Adaptive Immune Response and DNA-Containing Capsids. High-Throughput 2018, 7, 35. https://doi.org/10.3390/ht7040035
Danane J, Allali K. Mathematical Analysis and Treatment for a Delayed Hepatitis B Viral Infection Model with the Adaptive Immune Response and DNA-Containing Capsids. High-Throughput. 2018; 7(4):35. https://doi.org/10.3390/ht7040035
Chicago/Turabian StyleDanane, Jaouad, and Karam Allali. 2018. "Mathematical Analysis and Treatment for a Delayed Hepatitis B Viral Infection Model with the Adaptive Immune Response and DNA-Containing Capsids" High-Throughput 7, no. 4: 35. https://doi.org/10.3390/ht7040035
APA StyleDanane, J., & Allali, K. (2018). Mathematical Analysis and Treatment for a Delayed Hepatitis B Viral Infection Model with the Adaptive Immune Response and DNA-Containing Capsids. High-Throughput, 7(4), 35. https://doi.org/10.3390/ht7040035




