Effect of Size Asymmetry of Latex Nanoparticles on Formation and Properties of Nanocolloidal Gels

Abstract

The study of the fundamental principles of gelation of colloidal nanoparticles (NPs) advances the understanding of the formation of colloidal systems of living organisms. In this paper, the effect of particle size for a binary system of oppositely charged latexes on the experimental parameters of the system, including the gelation region, rheological parameters and cluster size, is considered for the first time. It is shown that the gelation regions in the phase diagrams for asymmetric particles are symmetric with respect to the ratio of charge and surface area of the particles. It was found that asymmetric particles form denser gels compared with the same concentration of symmetrical particles. This work provides insight into the gelation of asymmetric NPs, which is important for numerous applications, including their utilization in colloidal gels as ink for additive manufacturing and as scaffolds for cell growth, as well as understanding the fundamental aspects of the formation of bio-colloids.

1. Introduction

Colloidal nanoparticles (NPs) are important building blocks of colloidal gels, since they give the gel special properties, including particle bioactivity, magnetic properties, optical properties, etc. [1,2,3]. Special interest in using nanocolloidal gels is associated with the appearance of thixotropic properties that allow processing of these gels by 3D extrusion printing, which significantly expands their functional application [4,5,6,7,8]. Also, an in-depth understanding of the mechanism of formation of various phases and their characterization in synthetic colloidal systems sheds light on the understanding of the processes occurring in active colloids [9,10,11], including in living systems [12,13]. For example, interactions of patchy colloidal particles are used as model systems of protein interactions [14], and the formation of clusters, gels and other aggregates based on colloidal NPs are used as biomimetic living cell models [15]. Polymer nanoparticles are a convenient, simple and functional model for producing colloidal gels, since they allow study of the effects of the same particle parameters on gels such as size [16], surface charge [17], softness [18], surface chemistry [19], geometric confinement [20] and ionic strength [21].

For the formation of colloidal gels based on nanoparticles, the most studied types of particles are SiO₂ particles [22,23,24], and latex particles of different natures [25,26,27]. Gelation for these particles is achieved in various ways, including the addition of a linear polymer to form bridging and depletion gels [26], the addition of an inorganic salt or other substance that changes the ionic strength [27], as well as a combination of oppositely charged particles of both the same and different nature [17,18,28,29,30,31]. It has been shown that the formation of colloidal gels occurs through the formation of aggregates of colloidal particles (also called clusters, blobs), which then form a colloidal gel, crystal or glass [32,33,34]. It has been shown that, by changing the gelling agents and surface chemistry, it was possible to change the porosity of the gel [35], the fractal dimension of clusters (gel building blocks) [36] and the kinetics of their formation [37], and by changing the softness of latex particles, it was possible to control the phase state of the system [18].

However, the majority of works focus on NPs with exact sizes, and only a few studies describe effect of size asymmetry in cluster and gel formation. The effect of size for a system of oppositely charged polystyrene latexes of 530 nm and alumina-coated silica particles of 12 nm was considered in the work of Ahn et al. [19]. It was shown that, with an increase in the concentration of small particles, the transition of an asymmetric system from a stabilized sol (fluid) to a short and long bridging gel, and then to dense gel occurred. The effects of charge and size asymmetry on the aggregation kinetics of oppositely charged NPs based on polymethylmethacrylate latexes were described [30]. Their simulation results show that the kinetics of both the average weight and number of aggregates exhibit power law scaling with different exponents for small and intermediate evolution times.

In this paper, for the first time, a systematic comparison of the parameters of colloidal systems based on symmetric and size-asymmetric, oppositely charged, latex nanoparticles was carried out. Colloidal systems based on particles with sizes of 60 and 400 nm in diameter with approximately the same zeta-potential in modulus were studied, namely 60⁺/60⁻, 400⁺/400⁻ systems, as well as the asymmetrical systems 60⁺/400⁻ and 400⁺/60⁻. Phase diagrams for the systems, the rheological parameters of gels with a single mass concentration, and cluster sizes were studied. The results of this work shed light on the role of particle size in the formation of colloidal clusters and gels.

2. Materials and Methods

2.1. Chemicals and Materials

Ethyl methacrylate (EtMA, 99%), sodium dodecyl sulfate (SDS, 99%), hexadecyl-trimethylammonium bromide (CTAB, 99%), fluoresceine isothiocyanate, potassium peroxodisulfate (KPS, 99%), and 2,2′-Azobis(2-methylpropionamidine) dihydrochloride (V-50, 98%) were purchased from Aldrich (St. Louis, MO, USA) and used without purification.

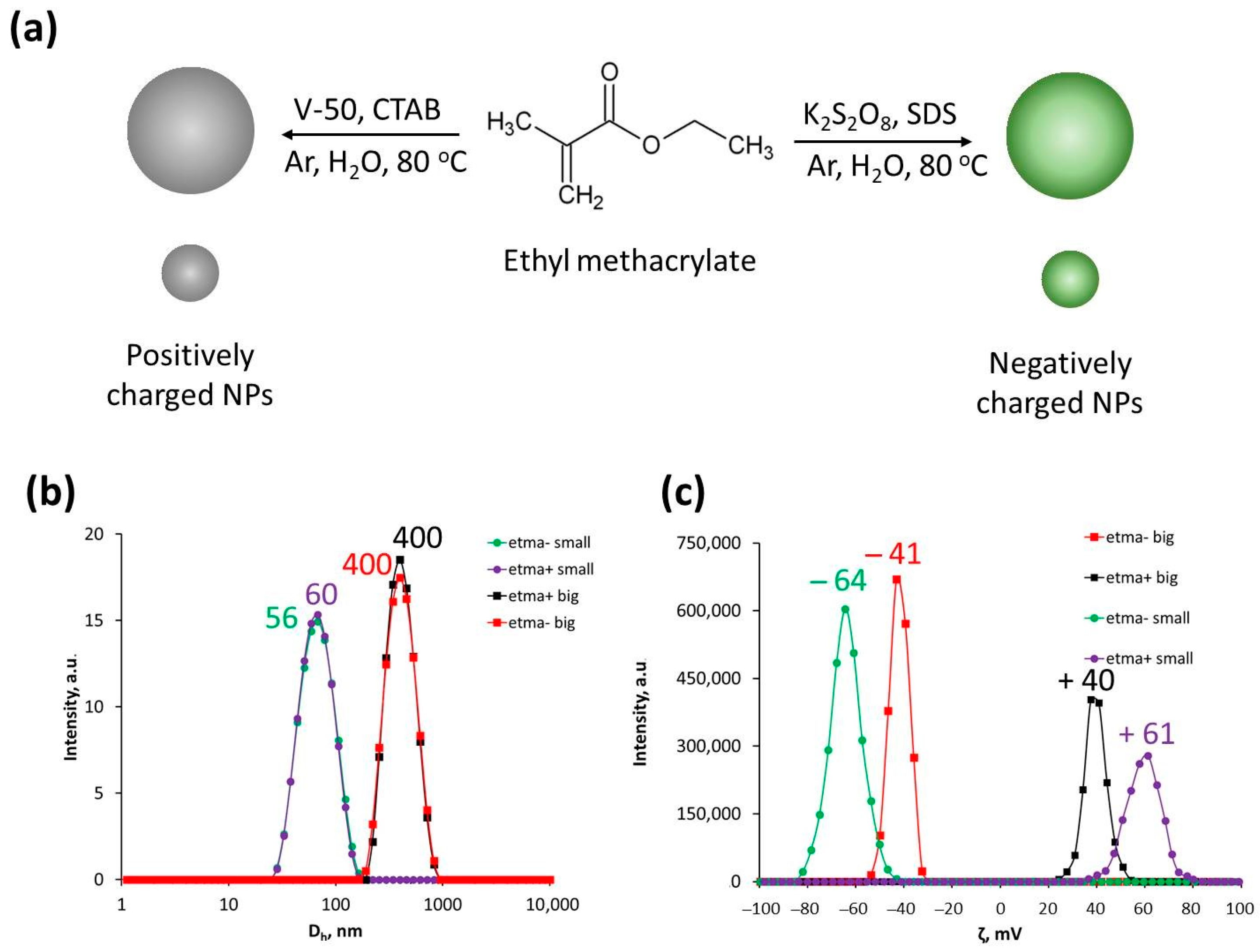
2.2. Nanoparticle Synthesis

Positively and negatively charged poly(ethyl methacrylate) nanoparticles (NPs) were synthesized as described previously [17,18,38,39]. These nanoparticles will be denoted as EtMA⁺ NPs and EtMA⁻ NPs for positively and negatively charged NPs, respectively, and as “small NPs” and “big NPs” for NPs of sizes 60 and 400 nm diameter, respectively. For the synthesis of the positively charged NPs, cetyl ammonium bromide (CTAB) served as the surfactant, while 2,2′-azo-bis(2-methylpropionamidine)dihydrochloride (V-50) was utilized as the initiator. In contrast, sodium dodecyl sulfate (SDS) and potassium persulfate (KPS) were employed as the surfactant and initiator for the negatively charged NPs. The synthesis of nanoparticles was carried out in multiple stages, tailored to the dimensions of the NPs. Specifically, NPs with diameters of 60 nm were synthesized through a two-step reaction, while a four-step process was applied for the production of 400 nm diameter p(EtMA)⁺ and p(EtMA)⁻ NPs. Following NP synthesis, the dispersion was placed in a dialysis bag (3.5 kDa) membrane and dialyzed against deionized water for 1 week with water changes every 24 h.

2.3. Characterization of Latex Nanoparticles

2.3.1. The Hydrodynamic Diameter and ζ Potential of the NPs

The electrokinetic potentials (ζ-potential) and the hydrodynamic diameter of the latex NPs were determined using DLS (Malvern Zetasizer Nano ZS instrument ZEN3600 instrument, Malvern instruments Ltd., Malvern, Worcestershire, UK). Experiments were performed at 22 °C in triplicate format, and the correlation data were analyzed by the built-in Malvern General Purpose non-negative least squares method.

2.3.2. Rheological Properties

Rheology experiments: A rheometer (Discovery Hybrid Rheometer, DHR-2, TA Instruments, New Castle, DE, USA) with a cone of 0.97° (diameter: 40 mm) and a gap of 27 µm was used to study the rheological properties of the gels. An integrated Peltier plate and solvent trap were used to provide temperature control and reduce solvent evaporation. The gel oscillation strain tests were performed at a frequency of 1 Hz for different strain levels (0.5–50%) after equilibrating the gel for 600 s at 22 °C.

2.3.3. Imaging of NPs

Scanning electron microscopy imaging of NPs was performed using SEM (Carl Zeiss CrossBeam 1540XB/Cross-beam SEM-FIB workstation Carl Zeiss CrossBeam 1540XB, Zeiss, Oberkochen, Germany) at 5.00 kV. Samples were prepared by applying a drop of gel and latex nanoparticle colloid (10 μg mL⁻¹) onto a silicon substrate and drying it at 25 °C for 180 min.

Confocal fluorescent microscopy imaging of NP clusters and gels was performed on an OLYMPUS FV4000 microscope (Evident, Waltham, MA, USA) using a 100× objective with a 60× oil immersion magnification. Positively charged NPs were labeled with Nile Red (NR), and negatively charged NPs were labeled with vinyl anthracene (VA). Ethanol was used as a solvent for NR and hexane was used for VA. A 5 µL drop of solution of fluorescent dye was added to 1 mL of NP dispersion. For the VA-labelled nanoparticles, the excitation wavelength was 405 nm and the emission wavelength was 430 nm, while for the NR-labelled nanoparticles, the excitation wavelength was 549 nm and the emission wavelength was 574 nm.

ImageJ (v1.52e) was used for SEM and fluorescent microscopy image analysis.

3. Results and Discussion

3.1. Nanoparticle Synthesis

We investigated the effect of particle size asymmetry for a binary system based on oppositely charged latex particles. Figure 1a illustrates the formation of positively and negatively charged poly(ethyl methacrylate) latex NPs (p(EtMa)⁺ and p(EtMA)⁻ NPs, which were obtained by emulsion polymerization based on a previously reported method [18]. Utilization of etyl trimethylammonium bromide (CTAB) as surfactant and 2-2-azo-bis(2-methylpropionamidine) dihydrochloride (V-50) as initiator lead to the formation of positively charged latex NPs (Figure 1a, left), and utilization of sodium dodecyl sulfate (SDS) as a surfactant and potassium persulfate (KPS) as the initiator leads to the formation of negatively charged latex NPs (Figure 1a, right).

The NP average diameter D_h was determined by dynamic light scattering and was 60 ± 5 (hereafter referred to as small NPs) and 400 ± 20 nm (hereafter referred as big NPs) (Figure 1b). The particle size distribution was monomodal and narrow (Figure 1b). The corresponding absolute values of ζ-potential were −64 and +61 mV for small NPs, and −41 and +40 mV for big NPs (Figure 1c). Thus, the ζ-potentials for oppositely charged NPs were close to equal.

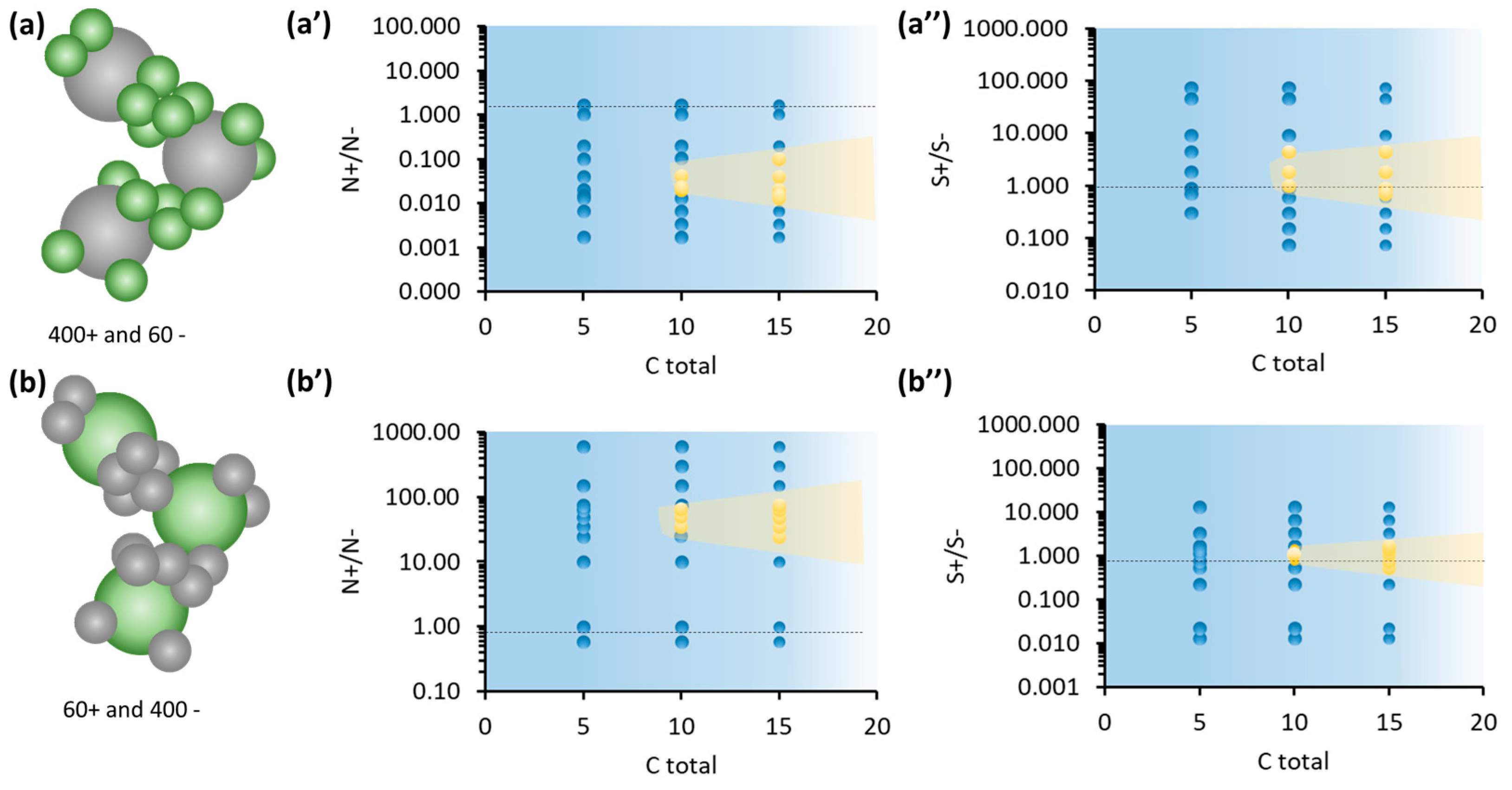
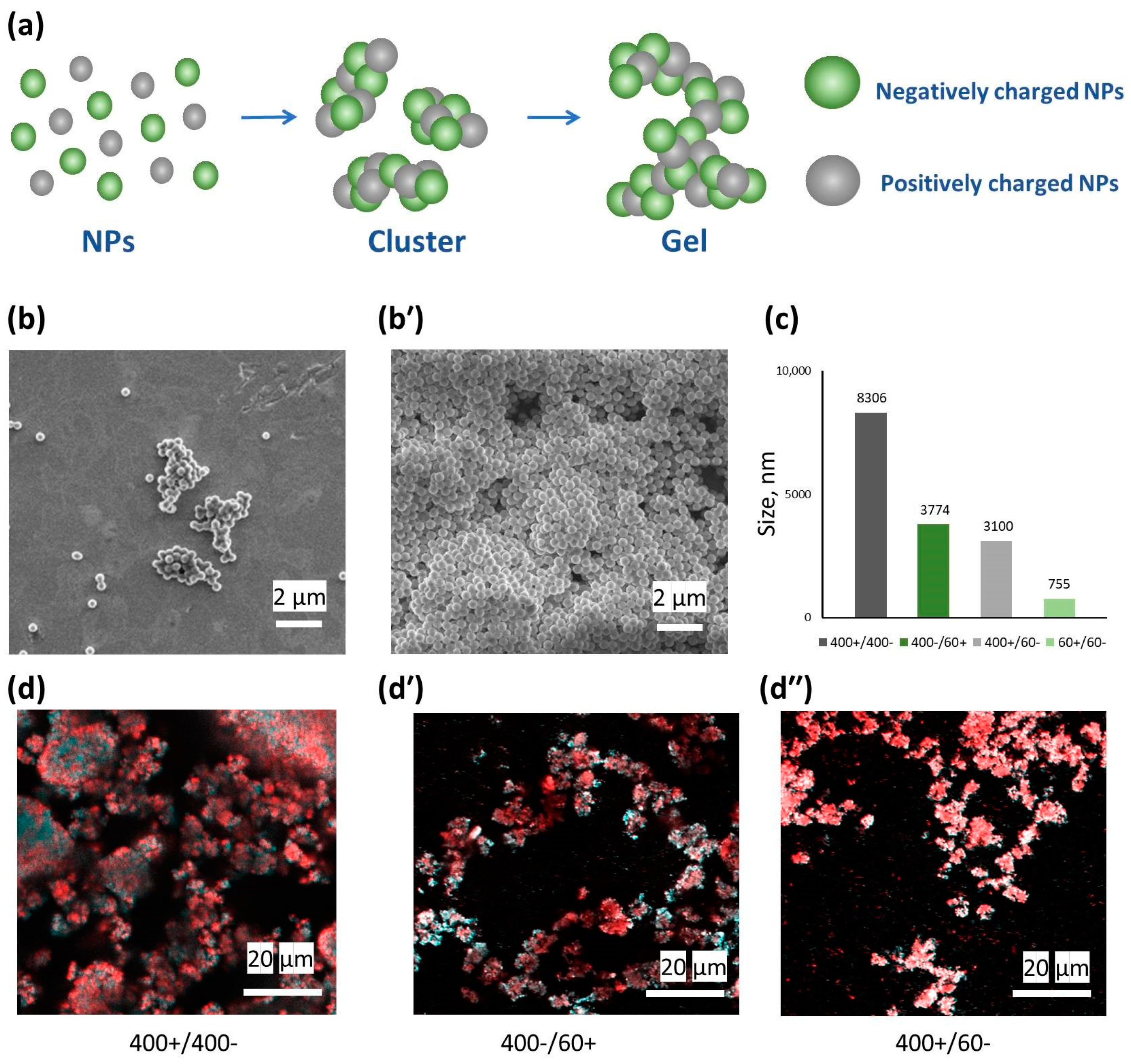
3.2. Gel Formation for Symmetric and Asymmetric Oppositely Charged Nanoparticles

To study the formation of colloidal clusters and gels we mixed oppositely charged polymer NPs (Figure 2a). As was previously shown, such mixtures form a nanocolloidal gel, which can undergo flow upon shear, i.e., sol–gel transition occurs in the system [17].

Figure 2b shows the appearance of a gel based on small particles (left) and large particles (right). Gels based on only small particles are translucent and opalescent, while gels containing large particles (both symmetrical and asymmetric) are opaque and white.

First, we investigated the state diagram of colloidal systems for symmetric NPs, i.e., 60⁺/60⁻ and 400⁺/400⁻. Mixing dispersions of oppositely charged NPs was carried out at room temperature, and subsequently, adding one dispersion to the other dropwise. The total concentration in the colloidal system, C_total, of the NPs in the mixture was in the range of 5–20 wt%. The number particle density fractions of cationic and anionic NPs are referred to as N⁺ and N⁻, respectively. Number particle density was calculated as the mass of the solid part in dispersion divided by the mass of one particle (4/3·π·(D_h³/8) ρ), where D_h is the hydrodynamic diameter by DLS and ρ is the density of poly(ethyl methacrylate). The surface number was calculated as S+ = 4·π·(D_h²/4) N⁺.

For both 60⁺/60⁻ and 400⁺/40⁻ systems, the sol (blue) and gel (yellow) regions are present in the state diagrams, which depend on the total concentration and ratio of the components (Figure 2c′,c″,d′,d″). The minimum concentration of gelation is 7.5 wt% for a system based on small particles (Figure 2c′,c″), while for a system of large particles, this concentration increases to 10 wt% (Figure 2d′,d″), which is due to the smaller number of particles in the 400⁺/400⁻ system—due to their larger size. For a size-symmetric NP system, the gel region is symmetrical with respect to an equal ratio of oppositely charged particles (marked with a dotted line in Figure 2c′,c″,d′,d″), regardless of the construction of diagrams in the coordinates of the number of particles N⁺/N⁻ or the surface area S⁺/S⁻ of the particles. Slight asymmetry in N⁺/N⁻ coordinates for small NPs is related to a less perfect match of size and zeta-potential in comparison with systems based on big NPs; however, for S⁺/S⁻ coordinates, the small NP system is symmetric. The gelation areas are narrow and S⁺/S⁻ is in the range from 0.5 to 2.

Next, we investigate state diagrams of colloidal systems for asymmetric NPs, i.e., 400⁺/60⁻ and 60⁺/400⁻. Mixing dispersions of oppositely charged NPs was carried out at room temperature, and subsequently, adding one dispersion to the other, dropwise. For both systems, the sol (blue) and gel (yellow) regions are present in the state diagrams, as for symmetric systems, which depend on the total concentrations and ratios of the components (Figure 3a′,a″,b′,b″). The minimum concentration of gelation is 10 wt% for both asymmetric systems (Figure 3a′,a″,b′,b″), which makes them more similar to systems based on big NPs (Figure 2d′,d″).

For the asymmetric systems, the gel region is non-symmetrical with respect to an equal ratio of oppositely charged particles (marked with a dotted line in Figure 2c′,d′) if the construction of diagrams is performed in the coordinates of the number of particles N⁺/N⁻. However, the gel region becomes symmetrical with respect to an equal ratio of oppositely charged particles for diagrams constructed in coordinates of the surface area S⁺/S⁻ of the particles (Figure 2c″,d″). Thus, it could be concluded that surface ratio is more important for prediction of gel region than the number of particles. The gelation areas are wider than those for symmetric systems and S⁺/S⁻ is in the range from 0.40 to 3.5.

To demonstrate the of role of surface charge, we calculate charge compensation, Ch, for the colloidal systems of oppositely charged latex NPs as Ch = (N+)·(λ+) + (N−)·(λ−), where N⁺ and N⁻ are the number particle density for positively and negatively charged NPs, respectively, and λ+ and λ− are surface charge for positively and negatively charged NPs, respectively. Calculation of λ+ (mC/m²) was performed as λ+ = 10¹²·p_water·10⁻³·(1 + D_h/2χ)/χ, where p_water is the permittivity of water, and χ is the Debay length determined as 0.304√I, where I is the ionic strength of the dispersion (mole/L) and is estimated from the NP dispersion electric conductivity. Figure 4a demonstrates the dependence of charge compensation on number particle density for the asymmetric system 400⁺/60⁻.

For small values of charge compensation (<30 mC/m²), the system is in a gel state, i.e., the surface energy of NPs is at a minimum, while with values of charge compensation reaching 30 mC/m², the colloidal system is in a sol state due to an increase in surface energy and repulsion between NPs clusters. Thus, charge compensation could be used as a prediction of sol or gel states for binary systems based on oppositely charged NPs. Interestingly, for symmetric systems we observed a narrow gel region with a number particle ratio N⁺/N⁻ up to 2, while for asymmetric systems, more NP surrounding states become possible and the ratio N⁺/N⁻ reaches 3.50.

3.3. Gel Properties for Symmetric and Asymmetric Oppositely Charged Nanoparticles

According to the generally accepted theory of gel formation based on colloidal nanoparticles, the process begins with the formation of aggregates (also called clusters and flops) [40,41] of approximately the same size, depending on the forces of interaction between the particles. Then the clusters form a colloidal gel (Figure 5a).

Figure 5a shows an example of a cluster for system 400⁺/400⁻ obtained by scanning electron microscopy (SEM). The clusters were formed by dilution of gel x20 times and have an average size of 4.7 µm diameter and a fractal-like nature. Among the clusters, individual NPs are present. However, in the SEM image of colloidal gel, clusters could not be distinguished (Figure 5b). To visualize clusters, confocal fluorescence microscopy was used and NPs were labelled by fluorescein isothiocyanate (Figure 5c). The cluster size of NPs was investigated by confocal fluorescent microscopy images. The average cluster size according to confocal fluorescence microscopy image analysis was 8.3 μm diameter for 400⁺/400⁻, 3.7 μm diameter for 400⁻/60⁺, 3.1 μm for 400⁺/60⁻, and 3.1 0.76 μm for 60⁺/60⁻ (Figure 5c). Figure 5d–d″ illustrates confocal fluorescence microscopy images of NP clusters, which were labeled with vinyl anthracene (blue) and Nile Red (red). The cluster size for the 400⁺/400⁻ system according to SEM was smaller than that estimated by confocal fluorescence analysis and was 7.2 μm in diameter. The difference in sizes is due to the fact that a gel is used for confocal microscopy, while for SEM, the sample is subjected to removal of the liquid medium, which is accompanied by partial disruption of the structure and shrinkage. The cluster size for the asymmetric system turned out to be close to the colloidal system based on the main NPs, while for the colloidal system 60⁺/60⁻, the cluster size had a diameter of less than 1 μm.

We investigated the rheological properties of symmetric and asymmetric colloidal systems with the same total concentration 10 wt%. The storage modulus, G′, and loss modulus, G″, were measured at a frequency of 1 Hz at different strain levels, γ, from 0.5 to 50% (Figure 6a).

The comparison of G′ in plateau region for symmetric and asymmetric systems reveals that the symmetric systems are denser than the asymmetric ones, i.e., G′ for 60⁺/60⁻ and 400⁺/400⁻ was 8300 Pa and 11,900 Pa, respectively, while for the asymmetric systems 400⁺/60⁻ and 60⁺/400⁻, G′ was 2650 and 2250 Pa, respectively (Figure 5b). However, the asymmetric system was more stable for shear, showing a γ value at breaking (the value at which G″ > G′) higher than that for symmetric systems (Figure 5b). This could be related to the higher number of stable surrounding states for asymmetric systems in comparison with symmetric ones (Figure 4b).

4. Conclusions

Two series of NPs differing in sizes (60 and 400 nm in diameter) and with close-to-equal absolute values of electrokinetic potentials (ζ-potentials) were obtained. Experiments for investigation of the effect of size asymmetry for colloidal systems based on oppositely charged latex NPs were carried out by mixing dispersions of oppositely charged 60 or 400 nm diameter NPs at certain ratios of components and total concentrations. The state and properties of the resulting colloidal mixtures were examined by imaging, rheology and dynamic light scattering (DLS). It was shown that surface charge plays a key role in gel formation, and gel regions could be predicted by a simple model requiring only the zeta-potential and hydrodynamic diameter of the system. The effects of asymmetry include several characteristics: (i) Asymmetric colloidal systems possess a larger gelation area than symmetric systems, i.e., there is more variability in number of neighbors for NPs; (ii) Asymmetric colloidal systems are less dense than symmetric ones, i.e., their G′ is lower. (iii) Asymmetric colloidal systems are more stable against shear than symmetric ones, i.e., the gel breaks at higher values of strain. Our results are applicable to similar colloidal systems, i.e., systems with the same softness, similar range of sizes and which are stabilized mostly by electrostatic and VdW interactions. Thus, oxide-based NPs (SiO₂, Al₂O₃, TiO₂, magnetic Fe₃O₄ and other NPs) should have similar behavior, while soft NPs such as micelles, microgels or liquids in emulsions, as well as patchy NPs, especially with DNA ligands, are not subject to our conclusions due to other types of interactions. Our results provide perspectives into the development of colloidal gels for different applications including inks for extrusion-based 3D printing for the food industry, bio-colloids formation and personal care products design. A possible extension to this work would be to study the effects of a set of parameters on the parameters of gelation, including not only particle size, but also the effects of external fields, ionic forces and geometric constraints.