Next Article in Journal
Co-Encapsulation of Paclitaxel and Doxorubicin in Liposomes Layer by Layer
Previous Article in Journal
Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Colloids and Interfaces
Volume 8
Issue 4
10.3390/colloids8040041
colloids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of Interfacial Properties of Anionic–Nonionic Surfactants Based on Succinic Acid Derivatives via Molecular Dynamics Simulations and the IGMH Method

by
Wannian Zhang
1,2,
Feng Luo
1,
Zhigang Gao
1,2,
Haizhu Chi
1,
Jinlong Wang
3,
Fang Yu
4 and
Yu-Peng He
1,2,*
1
State Key Laboratory Fine Chemicals, Ningbo Institute of Dalian University of Technology, Ningbo 315016, China
2
School of Chemical Engineering, Dalian University of Technology, No. 2 Linggong Road, Dalian 116024, China
3
SINOPEC Zhenhai Refining & Chemical Company, Ningbo 315207, China
4
School of Pharmaceutical Engineering, Zhejiang Pharmaceutical University, No 666 Siming Road, Ningbo 315207, China
*
Author to whom correspondence should be addressed.
Colloids Interfaces 2024, 8(4), 41; https://doi.org/10.3390/colloids8040041
Submission received: 29 May 2024 / Revised: 24 June 2024 / Accepted: 26 June 2024 / Published: 1 July 2024
Browse Figures
Versions Notes

Abstract

:
Surfactants are widely used in fields such as oil recovery and flotation. The properties and mechanisms of surfactants can be effectively studied using molecular dynamics (MD) simulations. Herein, the aggregation behavior of surfactants was studied at the oil–water interface by MD simulation, and the micro-morphology of surfactants was analyzed under a low concentration and saturated state at the oil–water interface, respectively. The visualization results of the MD simulation showed that DTOA was saturated at the oil–water interface at 120 surfactant molecules, whereas 160 surfactant molecules were required for BEMA. In addition, the effect of surfactant concentration on the interfacial thickness and hydrogen bond distribution was studied, with the inflection point of hydrogen bond distribution identified as a characteristic parameter for surfactant saturation at the oil–water interface. The aggregation behavior of their hydrophobic and hydrophilic chains at the oil–water interface was qualitatively assessed using order parameters. Finally, the aggregation state of surfactants in salt-containing systems was studied, and it was found that the surfactants could effectively adsorb magnesium ions and calcium ions at the oil–water interface. However, the curve of the number of hydrogen bonds varies greatly, with a possible reason being that BEMA has a different coordination manner with diverse metal ions. This study provides some original insights into both the theoretical study and practical application of anionic and nonionic surfactants.

Graphical Abstract

1. Introduction

Surfactants have been widely used in the fields of cosmetics [1], food [2,3,4], the petroleum industry [5,6], pharmaceuticals [7,8], and environmental remediation [9,10]. Currently, amphoteric surfactants and gemini surfactants, derived from traditional surfactants [11,12], have substantially improved the properties of traditional surfactants in terms of temperature resistance, salt resistance, detergence, and emulsification. Among these surfactants, anionic–nonionic surfactants have attracted wide concern because they can maintain excellent surface–interfacial properties even under high temperatures and high salt conditions [13,14,15]. As environmental pollution problems have become more prominent, some environmentally friendly and multifunctional surfactants have been studied and developed [16,17,18,19]. According to pioneer works, surfactants based on succinic acid derivatives were proven to be a class of surfactants with excellent surface–interfacial properties [20,21,22,23]. However, there are few reported studies on anionic–nonionic surfactants based on succinic acid derivatives. In addition, the aggregation behavior of these surfactants at the interface, their critical micelle concentrations, and their ability to reduce surface interfacial tension have also been poorly investigated. Moreover, the mechanism of these surfactants at the molecular level is ambiguous [24,25].
With the development of molecular dynamics (MD) simulation technology, MD simulation has been widely applied in the studies of biomedicine [26,27], assembly of amphiphilic molecules [28,29,30,31,32], catalysis [33,34], gas–liquid interfacial systems [35], liquid–liquid interfacial systems [36,37], biofilms [38], and nanomaterials [39,40]. In surfactants, MD simulations have been widely used in theoretical and applied studies to provide more detailed information at the molecular level [41,42,43], which is usually challenging to obtain from experimental methods [44]. With the help of MD simulation, the critical micelle concentration [45], surface interfacial tension [46], molecular aggregation behavior [47,48], interaction between molecules and solvents [49], structure–surface interface property relationship [50], and molecular level mechanism of salt and high-temperature resistance [51] of surfactants have been typically reported.
Herein, MD models with different surfactant concentrations were set up. The aggregation behavior of surfactants at the oil–water interface was visualized using the MD simulation method. Then, the effect of changes in surfactant concentration on the oil–water interface properties was analyzed. The densities of the various components of the different models were counted and were used to study the effect of concentration on the thickness of the oil–water interface. In addition, the distribution of hydrogen bonds and order parameters of surfactants were used to study the morphology of surfactant molecules at the interface. On this basis, different concentrations of MgCl2 and CaCl2 were added to a salt-free model, respectively, to study the salt resistance properties of surfactants using MD simulation.

2. Materials and Methods

2.1. Surfactant Molecular Conformation

Surfactants (BEMA and DTOA) were geometrically optimized using the B3LYP density functional method [52] and the 6-31G** basis set [53] to conform the structural topology for more realistic molecular dynamics simulation conditions. 3D structural models of these molecules are shown in Figure 1. The van der Waals potential was visualized for this system in Figure 1.

2.2. Simulation Details

The topology of these molecules based on the general AMBER force field (GAFF) was obtained from ACPYPE.py [54], the SPCE model was used for water molecules, and the RESP charges of the molecules were calculated using Multiwfn 3.8 (dev) [55]. All systems were initially modeled by packmol [56] in a 7.0 × 7.0 × 15.0 nm3 box with oil, surfactant (with sodium ions), water (the original thickness of the water layer was 40 angstroms), surfactant (with sodium ions), and oil in order from top to bottom, where the oil was replaced with n-decane [57]. All simulation models contained 4000 water molecules, 800 oil molecules, and several surfactant molecules, with surfactant molecules of 20, 40, 60, 80, 100, 120, 140, 160, 180, and 200. Several sodium ions were added to the simulation models to keep the system in an electrically neutral environment. For molecular dynamics simulations, the energy of the simulated system is first minimized using the steep method (steepest descent minimization). A pre-equilibrium simulation was then performed by increasing the system temperature from 198 K to 298 K in 200 ps. Finally, we performed MD simulations for 50 ns in the NPT ensemble. All simulations were performed in the Gromacs 2021.6 program [58] and the GAFF was maintained with a modified Berendsen thermostat and Parrinello–Rahman barostat, with all bonds constrained with the LINCS algorithm. Snapshots of molecular distributions were prepared by visual molecular dynamics (VMD 1.9.3) software [59].
Magnesium chloride and calcium chloride were chosen to perform salt-containing MD models as they are widely studied in surfactant applications. To set up the salt-containing surfactant system, a certain number of water molecules was replaced with the corresponding metal ions using the commands of the Gromacs2021.6 program, and chloride ions were added to keep the system in a neutral environment. A gradually increasing salt concentration was used (10~60) in the simulation models. All the simulation parameters for these systems were the same as those of the previous salt-free simulation model.

2.3. Cluster Analysis

The interactions between surfactants and different ions were graphically visualized by using an independent gradient model based on the Hirshfeld partition (IGMH) [60]. First, based on the optimized molecular conformation, the wavefunctions were obtained using DFT calculations at the original computational level, and then Multiwfn 3.8 (dev) [61] was used to process the wavefunctions and to obtain cub files for describing the weak interactions between surfactants and ions. Finally, the weak interactions were visualized using VMD 1.9.3.

3. Results and Discussion

3.1. Interfacial Membranes for MD Simulations

Molecular dynamics simulations of surfactant interfaces were studied by the Gromacs 2021.6 program. First, a series of “oil-surfactant-water-surfactant-oil” models containing different numbers of surfactant molecules were built by packmol. The numbers of all molecules are shown in Table S1, and the initial size of all boxes was 7.0 × 7.0 × 15.0 nm3. All the models were run under an NPT ensemble for 50 ns, due to the use of a semiisotropic type of pressure control, the dimensions in the x/y direction were not modified, while the z-direction was compressed to varying degrees by the pressure [47,50], and the compressed dimensions are shown in Table 1. As shown in Table 1, the measurement along the z-axis direction is consistent when there is the same number of surfactants in the system (BEMA and DTOA) during lower concentrations (entries 1~4). One possible explanation is that all the molecules have the same hydrophobic groups, and these hydrophilic groups are spread out in the aqueous layer, which did not significantly affect the volume of the boxes. However, at higher concentrations (entries 5~8), the z-axis size increase in DTOA was more significant than for the BEMA surfactant, possibly because at these concentrations, the interface of DTOA begins to bend to varying degrees, increasing in z-axis size.
To more clearly study the effect of surfactants on the oil–water interface, MD simulation snapshots of all systems were recorded in Figures S1 and S2. Snapshots of 40 surfactant molecules at an equilibrium state in the MD simulation are shown in Figure 2. In Figure 2, gray lines represent oil, blue balls represent sodium ions, red dots represent water molecules and surfactant molecules are represented using three colors (red balls for oxygen atoms, white balls for hydrogen atoms, and cyan balls for carbon atoms). All two surfactants can form a relatively smooth interface. The hydrophobic side of the surfactants points to the oil-phase side and its hydrophilic side (nonionic and ionic portions) spread out on the water layer.
With the increase in surfactant molecules, the interfaces of all the systems showed different degrees of bending, and the first one to experience interfacial bending was DTOA, which occurred when the number of surfactant molecules reached 120. At this time, aggregation occurred on both sides of the interfacial film of the DTOA system, and micelles like water-in-oil were formed. This result indicates that the surfactant reached saturation in interfaces at this concentration (Figure 3b). Similarly, the interfacial monolayers of BEMA showed bending at molecular numbers of 160 (Figure 3a). DTOA had one more –OC2H4– than the BEMA surfactant molecule, which significantly increased the hydrophilic component of the molecule, thus fewer DTOA molecules were needed to fill the entire monolayers.

3.2. Interfacial Thickness

The interfacial thickness is one of the critical parameters in the surfactant MD simulation system, which is related to the density distribution of the system. In order to study the effect of the number of surfactants on interfacial thickness, the density distributions along the -z-axis of BEMA and DTOA were counted in Figure 4. In all MD models, the densities of the water and oil phases were constant at 999 kg/m3 and 738 kg/m3, respectively, which was consistent with the experimental values for water (997 kg/m3, 298 K) and oil (decane, 735 kg/m3, 298 K). The surfactant was fully concentrated in the oil–water interfacial film, and the thickness of the interfacial film in the model was evaluated using the “90~90” interfacial thickness criterion proposed by William A. Goddard III et al. [62]. With 40 surfactant molecules, the interfacial film is thin, and when a certain amount of surfactant is added (BEMA: 160 and DTOA: 120, Table 2), the interfacial thickness of the oil–water interface increases because oil and water penetrate the alkyl tails and polar groups, respectively.

3.3. Hydrogen Bond Distributions

Hydrogen bond interaction is an effective parameter for evaluating the strength of the interaction between surfactant and water, and the hydrogen bond distributions for all models are statistically presented in Figure 5. In these models, the counted hydrogen bonds included the hydrogen bonds formed between the oxygen atoms in the surfactant and the hydrogen atoms of the water molecule, which made the surfactant exhibit certain hydrophilic properties. An apparent universal regularity was that the number of hydrogen bonds all showed a similar linear increase as the number of surfactant molecules increased because more molecules would form hydrogen bonds with more water molecules. When the number of surfactant molecules increased to a certain extent, the number of hydrogen bonds reached a relative maximum. The number of hydrogen bonds continued to grow only when the surfactant molecules further increased. At this time, a bend in the interface occurred and surfactants could form additional hydrogen bonds with water molecules, resulting in better hydrophilicity. Therefore, this inflection point (at the red dashed line in Figure 5) could effectively determine whether the surfactant reached saturation at the water–oil interface. This is consistent with the results of the previous visualization snapshots.

3.4. Order Parameter

For these structurally similar surfactant molecules, the order parameter enables a qualitative evaluation of the differences in their properties at the oil–water interface [63,64]. The order parameter is given by
S z = 3 2 cos 2 θ z − 1 2
where Sz is defined as the angle between the vector formed by the first and last carbon of the long chain and the normal axis to the interface.
The order parameters (in the z-axis direction) of the hydrophobic, long, alkyl chains and nonionic chains of BEMA and DTOA were counted, respectively, as shown in Figure 6. In Figure 6, the variation rule of the order parameter of the hydrophobic, long, alkyl chains of all models was almost the same; the carbon atoms close to the polar groups had higher-order parameters, and the order parameter gradually decreased with the extension of the carbon chains. However, the values of the order parameter for the first three carbon atoms were significantly higher than the others under a system with 40 surfactant molecules. One main reason is that the solvent effect at lower concentrations did not significantly affect the surfactant. However, the rigidity of surfactant molecules is the main reason concerning the degree of order parameter of the first three carbon atoms. At higher concentrations, the weak interactions (including hydrogen bonds and van der Waals interactions) of surfactants with water and oil reduced the order parameter of these carbon atoms.
Hydrophilic nonionic chains spread flat on a water surface and tend to interact with as many water molecules as possible, which makes the system more stabilized. Therefore, their ideal order parameter (in the z-axis direction) tends to be zero. From the red and green curves in Figure 6, it can be seen that the oxygen atom of 1′ has a larger order parameter (absolute value), which is caused by the attribution of this oxygen atom to the ester group and cannot be rotated. In addition, at lower concentrations (red lines), the order parameter of the nonionic chains was more variable, which may be because the surfactant was not spread over the entire surface of the water at this concentration, and the thermal motion of the nonionic chains on the surface of the water resulted in an unstable order parameter. However, at higher concentrations (green line), the order parameter of the nonionic chains was more stable.

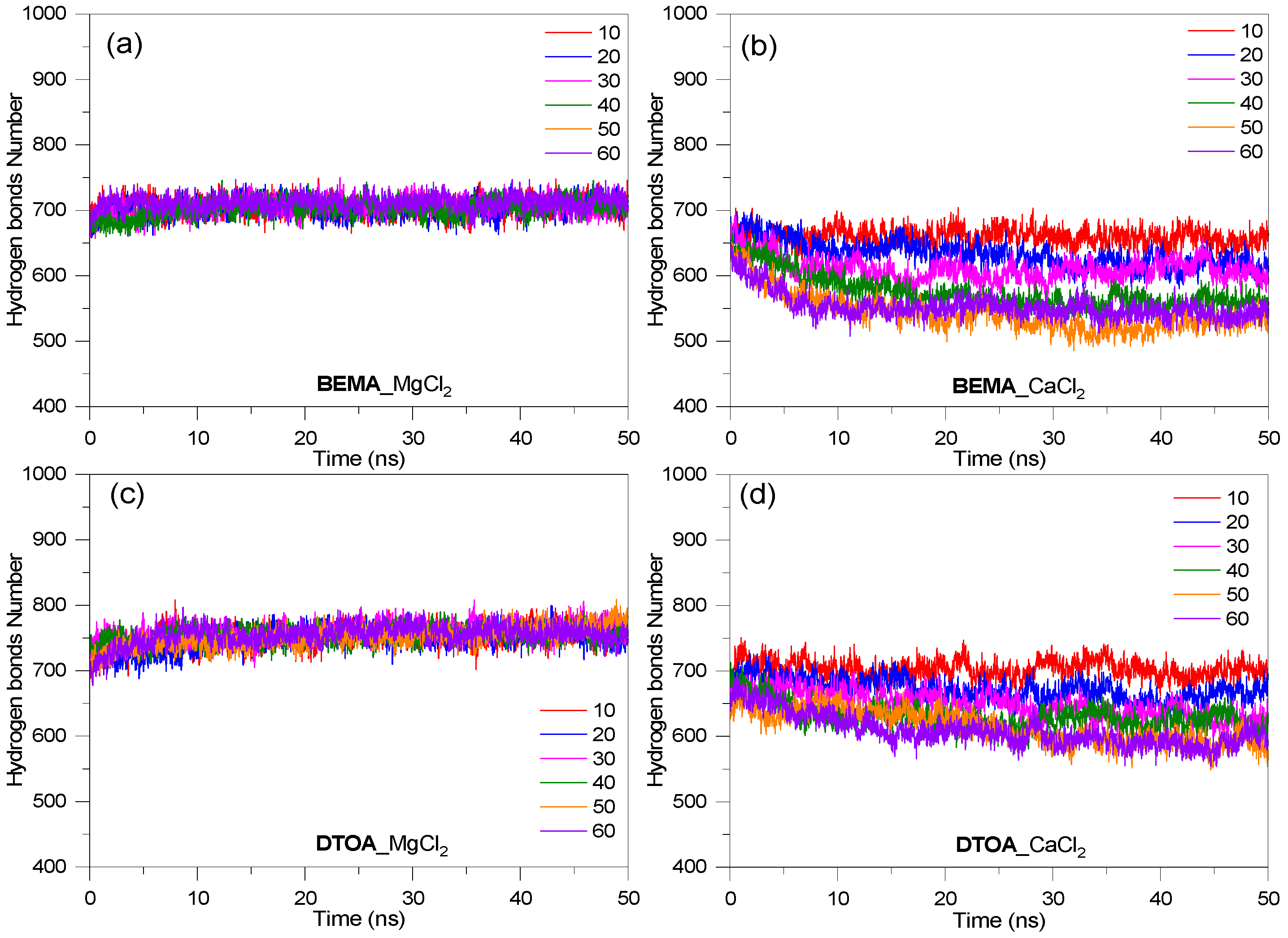
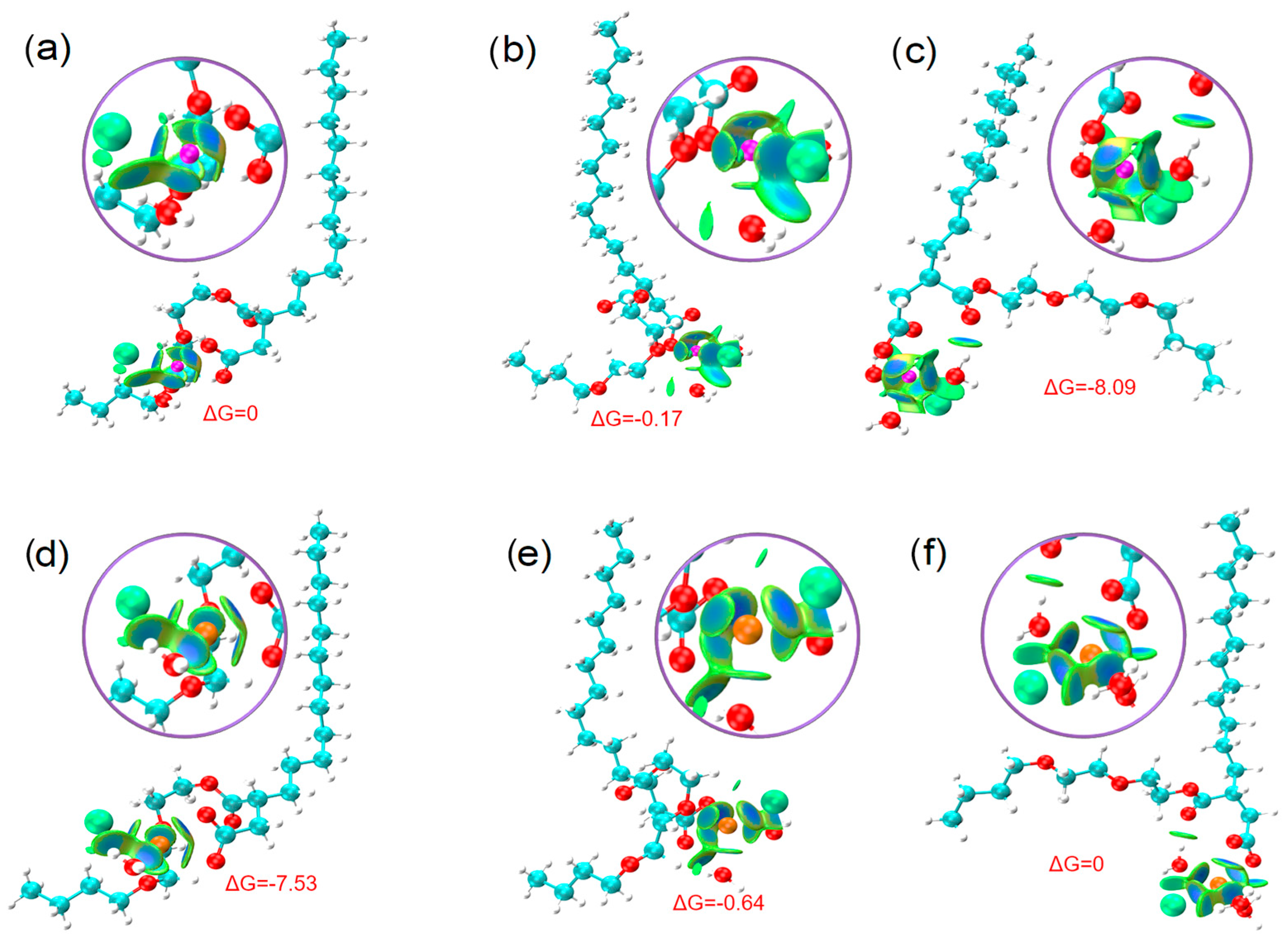
3.5. Salt Resistance of Surfactants

The salt resistance of surfactants determines their potential applications in oil recovery and flotation. For two surfactants, BEMA and DTOA, their salt-resistant properties were studied using molecular dynamics simulations and snapshots during their simulated equilibrium state with different salt concentrations (10, 20, 30, 40, 50, and 60, respectively) are shown in Figure 7. Figure 7a1–a6 show the aggregation morphology of BEMA in different concentrations of MgCl2 solution systems, respectively. As the concentration of MgCl2 increases, magnesium ions gradually replace the sodium ions (used to balance the surfactant carboxylate) and bind to the surfactants. Sodium ions were released from the interface, even as an orderly stack of sodium chloride appeared in the MgCl2 (60) system. Similarly, BEMA in the CaCl2 (Figure 7b1–b6) system and DTOA in the MgCl2 (Figure 7c1–c6) and CaCl2 (Figure 7d1–d6) systems, respectively, show a parallel rule, whereby the corresponding metal ions preferentially replace the sodium ions and bind to the surfactant molecules at a higher salt concentration. The visualization snapshots showed that the surfactant could effectively adsorb magnesium and calcium ions at the interface. As the metal ions concentration increased, the interface did not bend obviously, and the surfactants combined with calcium or magnesium ions could still keep the stability of the interface.
In order to study the effects of magnesium chloride and calcium chloride on surfactant properties, the hydrogen bonds of surfactants were counted and are shown in Figure 8. In the BEMA system, the MgCl2 solution showed an insignificant effect on the number of hydrogen bonds (Figure 8a). However, in the CaCl2 system, the number of hydrogen bonds showed a regular decrease with the increase in CaCl2 concentration (Figure 8b). A similar rule was shown for DTOA in the MgCl2 and CaCl2 systems (Figure 8c,d). The curve of the number of hydrogen bonds shows that the surfactant molecules have two different adsorption behaviors for magnesium and calcium ions.
In order to study the critical factors of hydrogen bond changes in MgCl2 and CaCl2, the weak interaction for BEMA in aqueous MgCl2 and aqueous CaCl2 solutions was analyzed by IGMH (Figure 9). Figure 9a–c shows the distribution of the weak interaction of magnesium ions binding to one water molecule, two water molecules, and three water molecules, respectively. There is a significant weak interaction of magnesium ions with water molecules, chloride ions, and BEMA molecules, where the green part is mainly dispersion, and the blue part is electrostatic interaction. Each additional one water molecule that binds to a magnesium ion reduces the coordination of one of the electronegative oxygen atoms of BEMA to the magnesium ion. The lowest energy (−8.09 kcal/mol) was found by DFT calculations when three water molecules were coordinated to the magnesium ion (Figure 9c). The identical distribution of weak interactions with calcium ions in aqueous solutions of CaCl2 is mapped in Figure 9d–f. However, only one water molecule coordinated with the calcium ion had the lowest energy (Figure 9d, −7.53 kcal/mol). This result showed that the best way for calcium ions to bind in an aqueous solution is to coordinate with the three oxygen atoms of BEMA, which affects the hydrogen bonds between BEMA and water molecules. However, the coordination of BEMA with magnesium ions is only a carboxylate group, which did not affect the formation of hydrogen bonds between BEMA and water molecules.

4. Conclusions

In this work, the aggregation behavior of surfactants at the oil–water interface was studied by MD simulation, and the micro-morphology of surfactants at the oil–water interface was analyzed at low concentration and in a saturated state, respectively. In addition, the effect of surfactant concentration on interfacial thickness and hydrogen bond distribution was studied. It was found that the inflection point of the hydrogen bond distribution was the critical data, which can be used to determine whether the surfactant molecule has reached its saturation state at the oil–water interface. Then, the aggregation behavior of their hydrophobic and hydrophilic chains at the oil–water interface was qualitatively investigated using order parameters. Finally, the aggregation state of surfactants in salt-containing systems was studied, and it was found that the surfactants could effectively adsorb magnesium ions and calcium ions. The interface could still be stabilized by BEMA and DTOA after adsorbing enough magnesium ions or calcium ions. The change in the number of hydrogen bonds revealed that surfactants exhibited different adsorption behaviors towards magnesium and calcium ions. This is because the nonionic fragments of BEMA can form stable coordination with calcium ions, but weaker coordination with magnesium ions. As a result, BEMA can still form a large number of hydrogen bonds at the oil–water interface containing magnesium chloride to function as surfactants. This study provides some original insights into both the theoretical study and practical application of anionic–nonionic surfactants.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/colloids8040041/s1, Table S1: Number of molecules for each component in the MD model; Figure S1: Snapshots of the equilibrium state of MD simulations with different concentrations of BEMA; Figure S2: Snapshots of the equilibrium state of MD simulations with different concentrations of DTOA.

Author Contributions

W.Z., methodology, software, validation, data curation, writing—original draft; F.L., compound synthesis, data curation, investigation, characterization; Z.G., visualization, validation; H.C., validation, characterization; J.W., resources, supervision; F.Y., validation, software, resources, writing—review and editing; Y.-P.H., resources, project administration, software, funding acquisition, conceptualization, supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant No. 21978124) and the Natural Science Foundation of Ningbo (Grant No. 2022J003).

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author.

Acknowledgments

We gratefully acknowledge the work of the members of our laboratory.

Conflicts of Interest

Author Jinlong Wang was employed by the company SINOPEC Zhenhai Refining & Chemical Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Su, Y.; Sun, Y.; Zhai, Y.; Gu, L.; Li, J.; Gong, L.; Chang, C.; Yang, Y. Effects of surfactants on activity and structure of egg yolk antibody. Food Bioprod. Process. 2022, 132, 167–176. [Google Scholar] [CrossRef]
  2. Nitschke, M.; e Silva, S.S. Recent food applications of microbial surfactants. Crit. Rev. Food Sci. Nutr. 2018, 58, 631–638. [Google Scholar] [CrossRef] [PubMed]
  3. Lu, X.; Ji, S.; Ren, Z.; Jiang, S.; Yu, Q.; Guo, J.; Wang, A.X.; Kong, X. Rapid, convenient, and ultrasensitive point-of-care sensing of histamine from fish: A Portable chromatographic platform based on derivatization reaction. J. Chromatogr. A 2023, 1696, 463953. [Google Scholar] [CrossRef] [PubMed]
  4. Shen, Z.; Fan, Q.; Yu, Q.; Wang, R.; Wang, H.; Kong, X. Facile detection of carbendazim in food using TLC-SERS on diatomite thin layer chromatography. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 247, 119037. [Google Scholar] [CrossRef] [PubMed]
  5. Karthick, A.; Roy, B.; Chattopadhyay, P. A review on the application of chemical surfactant and surfactant foam for remediation of petroleum oil contaminated soil. J. Environ. Manag. 2019, 243, 187–205. [Google Scholar] [CrossRef] [PubMed]
  6. Fu, L.; Gu, F.; Liao, K.; Wen, X.; Jiang, L.; Li, X.; Huang, W.; Shao, M. Molecular dynamics simulation of enhancing surfactant flooding performance by using SiO2 nanoparticles. J. Mol. Liq. 2022, 367, 120404. [Google Scholar] [CrossRef]
  7. Guagliardo, R.; Pérez-Gil, J.; De Smedt, S.; Raemdonck, K. Pulmonary surfactant and drug delivery: Focusing on the role of surfactant proteins. J. Control. Release 2018, 291, 116–126. [Google Scholar] [CrossRef] [PubMed]
  8. Jia, Y.; Li, J. Molecular Assemblies of Biomimetic Microcapsules. Langmuir 2019, 35, 8557–8564. [Google Scholar] [CrossRef] [PubMed]
  9. Pradhan, A.; Bhattacharyya, A. Quest for an eco-friendly alternative surfactant: Surface and foam characteristics of natural surfactants. J. Clean. Prod. 2017, 150, 127–134. [Google Scholar] [CrossRef]
  10. Xu, Y.; Zhang, Y.; Liu, X.; Chen, H.; Fang, Y. Retrieving Oil and Recycling Surfactant in Surfactant-Enhanced Soil Washing. ACS Sustain. Chem. Eng. 2018, 6, 4981–4986. [Google Scholar] [CrossRef]
  11. Shao, Q.; He, Y.; White, A.D.; Jiang, S. Difference in Hydration between Carboxybetaine and Sulfobetaine. J. Phys. Chem. B 2010, 114, 16625–16631. [Google Scholar] [CrossRef] [PubMed]
  12. Guo, Y.; Dong, X.; Ruan, W.; Shang, Y.; Liu, H. A thermo-sensitive OEGMA-based polymer: Synthesis, characterization and interactions with surfactants in aqueous solutions with and without salt. Colloid Polym. Sci. 2017, 295, 327–340. [Google Scholar] [CrossRef]
  13. Souayeh, M.; Al-Maamari, R.S.; Karimi, M.; Aoudia, M. Wettability alteration and oil recovery by surfactant assisted low salinity water in carbonate rock: The impact of nonionic/anionic surfactants. J. Pet. Sci. Eng. 2021, 197, 108108. [Google Scholar] [CrossRef]
  14. Zhang, D.; Kang, J.; Zhu, W. Selective flotation separation of fluorite and calcite by utilising a novel anionic/nonionic collector. Colloids Surf. A Physicochem. Eng. Asp. 2022, 642, 128687. [Google Scholar] [CrossRef]
  15. Liang, X.; Dong, J.; Zhang, W.; Mo, Y.; Li, Y.; Bai, J. Solubilization mechanism and mass-transfer model of anionic-nonionic gemini surfactants for chlorinated hydrocarbons. Sep. Purif. Technol. 2024, 330, 125534. [Google Scholar] [CrossRef]
  16. Kleinen, J. Will biosurfactants replace conventional surfactants? Curr. Opin. Colloid Interface Sci. 2023, 68, 101764. [Google Scholar] [CrossRef]
  17. Baccile, N. Are microbial biosurfactants actually only surfactants? Curr. Opin. Colloid Interface Sci. 2023, 68, 101747. [Google Scholar] [CrossRef]
  18. Johnson, P.; Trybala, A.; Starov, V.; Pinfield, V.J. Effect of synthetic surfactants on the environment and the potential for substitution by biosurfactants. Adv. Colloid Interface Sci. 2021, 288, 102340. [Google Scholar] [CrossRef] [PubMed]
  19. Muhammad, M.T.; Khan, M.N. Eco-friendly, biodegradable natural surfactant (Acacia concinna): An alternative to the synthetic surfactants. J. Clean. Prod. 2018, 188, 678–685. [Google Scholar] [CrossRef]
  20. Dix, L.R. Sodium Salts of Bis(1-dodecenylsuccinamic Acids): A Simple Route to Anionic Gemini Surfactants. J. Colloid Interface Sci. 2001, 238, 447–448. [Google Scholar] [CrossRef]
  21. Dix, L.R.; Gilblas, R. Lyotropic and interfacial behaviour of an anionic gemini surfactant. J. Colloid Interface Sci. 2006, 296, 762–765. [Google Scholar] [CrossRef] [PubMed]
  22. Zhou, Y.; Cheng, Y.; Han, C.; Lai, J.; Sui, L.; Luo, G. Synthesis and Surface Properties of Anionic Gemini Surfactants having N-acylamide and Carboxylate Groups. J. Surfactants Deterg. 2014, 17, 727–732. [Google Scholar] [CrossRef]
  23. Sun, R.; Hong, K.H.; Lv, Z.; Ding, X.; Wu, X.; Yu, F. Synthesis and Surface Properties of a Novel Anionic Gemini Surfactant using Dioxaoctane as a Linking Group. J. Surfactants Deterg. 2018, 21, 461–466. [Google Scholar] [CrossRef]
  24. Penfold, J.; Thomas, R.K. The adsorption and self-assembly of biosurfactants and biosurfactant/surfactant mixtures using neutron scattering techniques. Curr. Opin. Colloid Interface Sci. 2023, 68, 101766. [Google Scholar] [CrossRef]
  25. Fu, Z.; Shen, Z.; Fan, Q.; Hao, S.; Wang, Y.; Liu, X.; Tong, X.; Kong, X.; Yang, Z. Preparation of multi-functional magnetic–plasmonic nanocomposite for adsorption and detection of thiram using SERS. J. Hazard. Mater. 2020, 392, 122356. [Google Scholar] [CrossRef] [PubMed]
  26. Russell Lewis, B.; Uddin, M.R.; Moniruzzaman, M.; Kuo, K.M.; Higgins, A.J.; Shah, L.M.N.; Sobott, F.; Parks, J.M.; Hammerschmid, D.; Gumbart, J.C.; et al. Conformational restriction shapes the inhibition of a multidrug efflux adaptor protein. Nat. Commun. 2023, 14, 3900. [Google Scholar] [CrossRef] [PubMed]
  27. Nikolaienko, T.Y. Interaction of anticancer drug doxorubicin with sodium oleate bilayer: Insights from molecular dynamics simulations. J. Mol. Liq. 2017, 235, 31–43. [Google Scholar] [CrossRef]
  28. Sharma, A.; Bhargava, B.L. Self-Assembly of Cations in Aqueous Solutions of Multiheaded Cationic Surfactants: All Atom Molecular Dynamics Simulation Studies. J. Phys. Chem. B 2018, 122, 10943–10952. [Google Scholar] [CrossRef]
  29. Wang, K.; Zhang, W.; Liu, N.; Hu, D.; Yu, F.; He, Y.-P. Methionine-Derived Organogels as Lubricant Additives Enhance the Continuity of the Oil Film through Dynamic Self-Healing Assembly. Langmuir 2022, 38, 11492–11501. [Google Scholar] [CrossRef]
  30. Zhang, W.; Zhang, Z.; Zhao, S.; Hong, K.H.; Zhang, M.-Y.; Song, L.; Yu, F.; Luo, G.; He, Y.-P. Pyromellitic-Based Low Molecular Weight Gelators and Computational Studies of Intermolecular Interactions: A Potential Additive for Lubricant. Langmuir 2021, 37, 2954–2962. [Google Scholar] [CrossRef]
  31. Zhu, X.; Jiang, Y.; Yang, D.; Zhang, L.; Li, Y.; Liu, M. Homochiral nanotubes from heterochiral lipid mixtures: A shorter alkyl chain dominated chiral self-assembly. Chem. Sci. 2019, 10, 3873–3880. [Google Scholar] [CrossRef] [PubMed]
  32. Zhou, P.; Yuan, C.; Yan, X. Computational approaches for understanding and predicting the self-assembled peptide hydrogels. Curr. Opin. Colloid Interface Sci. 2022, 62, 101645. [Google Scholar] [CrossRef]
  33. Liu, P.-Y.; Zhao, S.-C.; Zhang, M.-Y.; Song, L.; Wang, C.; Yu, F.; Meng, Q.; Zhang, Z.; He, Y.-P. Pd-Catalyzed γ-Acetoxylation of Alkylamides: Structural Influence of Directing Groups. J. Org. Chem. 2022, 87, 6378–6386. [Google Scholar] [CrossRef] [PubMed]
  34. Liu, P.-Y.; Zhao, Y.-M.; Xu, Y.; Wang, S.; Song, L.; Meng, Q.; Zhang, Z.; Yu, F.; He, Y.-P. Experiment and Computational Study on Pd-Catalyzed Methoxyiminoacyl-Directed γ-Alkoxylation of Alkylamides. J. Org. Chem. 2023, 88, 14445–14453. [Google Scholar] [CrossRef]
  35. Yuan, M.; Nie, W.; Yu, H.; Yan, J.; Bao, Q.; Zhou, W.; Hua, Y.; Guo, L.; Niu, W. Experimental and molecular dynamics simulation study of the effect of different surfactants on the wettability of low-rank coal. J. Environ. Chem. Eng. 2021, 9, 105986. [Google Scholar] [CrossRef]
  36. Lu, C.; Liu, W.; Yuan, Z.; Wang, L.; Zhang, Z.; Gao, Q.; Ding, W. Study on the Behavior of Saturated Cardanol-Based Surfactants at the Crude Oil/Water Interface through Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 8938–8949. [Google Scholar] [CrossRef] [PubMed]
  37. Yuan, C.; Xing, R.; Cui, J.; Fan, W.; Li, J.; Yan, X. Multistep Desolvation as a Fundamental Principle Governing Peptide Self-Assembly Through Liquid–Liquid Phase Separation. CCS Chem. 2024, 6, 255–265. [Google Scholar] [CrossRef]
  38. Moosavi, S.S.; Zolghadr, A.R. Effect of quaternary ammonium surfactants on biomembranes using molecular dynamics simulation. RSC Adv. 2023, 13, 33175–33186. [Google Scholar] [CrossRef]
  39. Poorsargol, M.; Sohrabi, B.; Dehestani, M. Study of the Gemini Surfactants’ Self-Assembly on Graphene Nanosheets: Insights from Molecular Dynamic Simulation. J. Phys. Chem. A 2018, 122, 3873–3885. [Google Scholar] [CrossRef]
  40. Su, T.; Hong, K.H.; Zhang, W.; Li, F.; Li, Q.; Yu, F.; Luo, G.; Gao, H.; He, Y.-P. Scaleable two-component gelator from phthalic acid derivatives and primary alkyl amines: Acid–base interaction in the cooperative assembly. Soft Matter 2017, 13, 4066–4073. [Google Scholar] [CrossRef]
  41. Roy, S.; Skoff, D.; Perroni, D.V.; Mondal, J.; Yethiraj, A.; Mahanthappa, M.K.; Zanni, M.T.; Skinner, J.L. Water Dynamics in Gyroid Phases of Self-Assembled Gemini Surfactants. J. Am. Chem. Soc. 2016, 138, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
  42. Naullage, P.M.; Bertolazzo, A.A.; Molinero, V. How Do Surfactants Control the Agglomeration of Clathrate Hydrates? ACS Cent. Sci. 2019, 5, 428–439. [Google Scholar] [CrossRef] [PubMed]
  43. Liu, Y.; Liu, Z.; Zeng, G.; Chen, M.; Jiang, Y.; Shao, B.; Li, Z.; Liu, Y. Effect of surfactants on the interaction of phenol with laccase: Molecular docking and molecular dynamics simulation studies. J. Hazard. Mater. 2018, 357, 10–18. [Google Scholar] [CrossRef] [PubMed]
  44. Srinivas, G.; Nielsen, S.O.; Moore, P.B.; Klein, M.L. Molecular Dynamics Simulations of Surfactant Self-Organization at a Solid-Liquid Interface. J. Am. Chem. Soc. 2006, 128, 848–853. [Google Scholar] [CrossRef] [PubMed]
  45. Liu, X.; Li, Y.; Tian, S.; Yan, H. Molecular Dynamics Simulation of Emulsification/Demulsification with a Gas Switchable Surfactant. J. Phys. Chem. C 2019, 123, 25246–25254. [Google Scholar] [CrossRef]
  46. He, M.; Zheng, W.; Wang, N.; Gao, H.; Ouyang, D.; Huang, Z. Molecular Dynamics Simulation of Drug Solubilization Behavior in Surfactant and Cosolvent Injections. Pharmaceutics 2022, 14, 2366. [Google Scholar] [CrossRef] [PubMed]
  47. Zhang, W.; Zhang, M.-Y.; Wang, K.; Sun, R.; Zhao, S.; Zhang, Z.; He, Y.-P.; Yu, F. Geometry transformation of ionic surfactants and adsorption behavior on water/n-decane-interface: Calculation by molecular dynamics simulation and DFT study. RSC Adv. 2021, 11, 28286–28294. [Google Scholar] [CrossRef] [PubMed]
  48. Arbabi, S.; Deuar, P.; Denys, M.; Bennacer, R.; Che, Z.; Theodorakis, P.E. Molecular dynamics simulation of the coalescence of surfactant-laden droplets. Soft Matter 2023, 19, 8070–8080. [Google Scholar] [CrossRef] [PubMed]
  49. Chen, Y.; Liao, M.; Ma, K.; Wang, Z.; Demé, B.; Penfold, J.; Lu, J.R.; Webster, J.R.P.; Li, P. Implications of surfactant hydrophobic chain architecture on the Surfactant-Skin lipid model interaction. J. Colloid Interface Sci. 2022, 608, 405–415. [Google Scholar] [CrossRef]
  50. Zhang, W.; Wang, K.; Wang, C.; Zhao, S.; Zhang, Z.; Yu, F.; He, Y.-P. Enhanced oil recovery: QM/MM based descriptors for anionic surfactant salt-resistance. Colloids Surf. A Physicochem. Eng. Asp. 2022, 641, 128422. [Google Scholar] [CrossRef]
  51. Alonso, G.; Gamallo, P.; Mejía, A.; Sayós, R. Assessing salt-surfactant synergistic effects on interfacial tension from molecular dynamics simulations. J. Mol. Liq. 2020, 299, 112223. [Google Scholar] [CrossRef]
  52. Pereira, F.; Xiao, K.; Latino, D.A.R.S.; Wu, C.; Zhang, Q.; Aires-de-Sousa, J. Machine Learning Methods to Predict Density Functional Theory B3LYP Energies of HOMO and LUMO Orbitals. J. Chem. Inf. Model. 2017, 57, 11–21. [Google Scholar] [CrossRef] [PubMed]
  53. Zhou, A.; Schauperl, M.; Nerenberg, P.S. Benchmarking Electronic Structure Methods for Accurate Fixed-Charge Electrostatic Models. J. Chem. Inf. Model. 2020, 60, 249–258. [Google Scholar] [CrossRef]
  54. Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
  55. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  56. Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
  57. Ivanova, A.A.; Cheremisin, A.N.; Barifcani, A.; Iglauer, S.; Phan, C. Molecular insights in the temperature effect on adsorption of cationic surfactants at liquid/liquid interfaces. J. Mol. Liq. 2020, 299, 112104. [Google Scholar] [CrossRef]
  58. Páll, S.; Zhmurov, A.; Bauer, P.; Abraham, M.; Lundborg, M.; Gray, A.; Hess, B.; Lindahl, E. Heterogeneous parallelization and acceleration of molecular dynamics simulations in GROMACS. J. Chem. Phys. 2020, 153, 134110. [Google Scholar] [CrossRef] [PubMed]
  59. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  60. Lu, T.; Chen, Q. Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical systems. J. Comput. Chem. 2022, 43, 539. [Google Scholar] [CrossRef]
  61. Lu, T.; Chen, Q. Visualization Analysis of Weak Interactions in Chemical Systems. In Comprehensive Computational Chemistry, 1st ed.; Yáñez, M., Boyd, R.J., Eds.; Elsevier: Oxford, UK, 2024; pp. 240–264. [Google Scholar]
  62. Jang, S.S.; Lin, S.-T.; Maiti, P.K.; Blanco, M.; Goddard, W.A.; Shuler, P.; Tang, Y. Molecular Dynamics Study of a Surfactant-Mediated Decane-Water Interface:  Effect of Molecular Architecture of Alkyl Benzene Sulfonate. J. Phys. Chem. B 2004, 108, 12130–12140. [Google Scholar] [CrossRef]
  63. Yu, F.; Miao, Y.; Wang, M.; Liu, Q.; Yuan, L.; Geng, R.; Qiu, Q.; Ni, C.; Kay, M. Predicting nanoemulsion formulation and studying the synergism mechanism between surfactant and cosurfactant: A combined computational and experimental approach. Int. J. Pharm. 2022, 615, 121473. [Google Scholar] [CrossRef] [PubMed]
  64. Shi, P.; Luo, H.; Tan, X.; Lu, Y.; Zhang, H.; Yang, X. Molecular dynamics simulation study of adsorption of anionic–nonionic surfactants at oil/water interfaces. RSC Adv. 2022, 12, 27330–27343. [Google Scholar] [CrossRef] [PubMed]
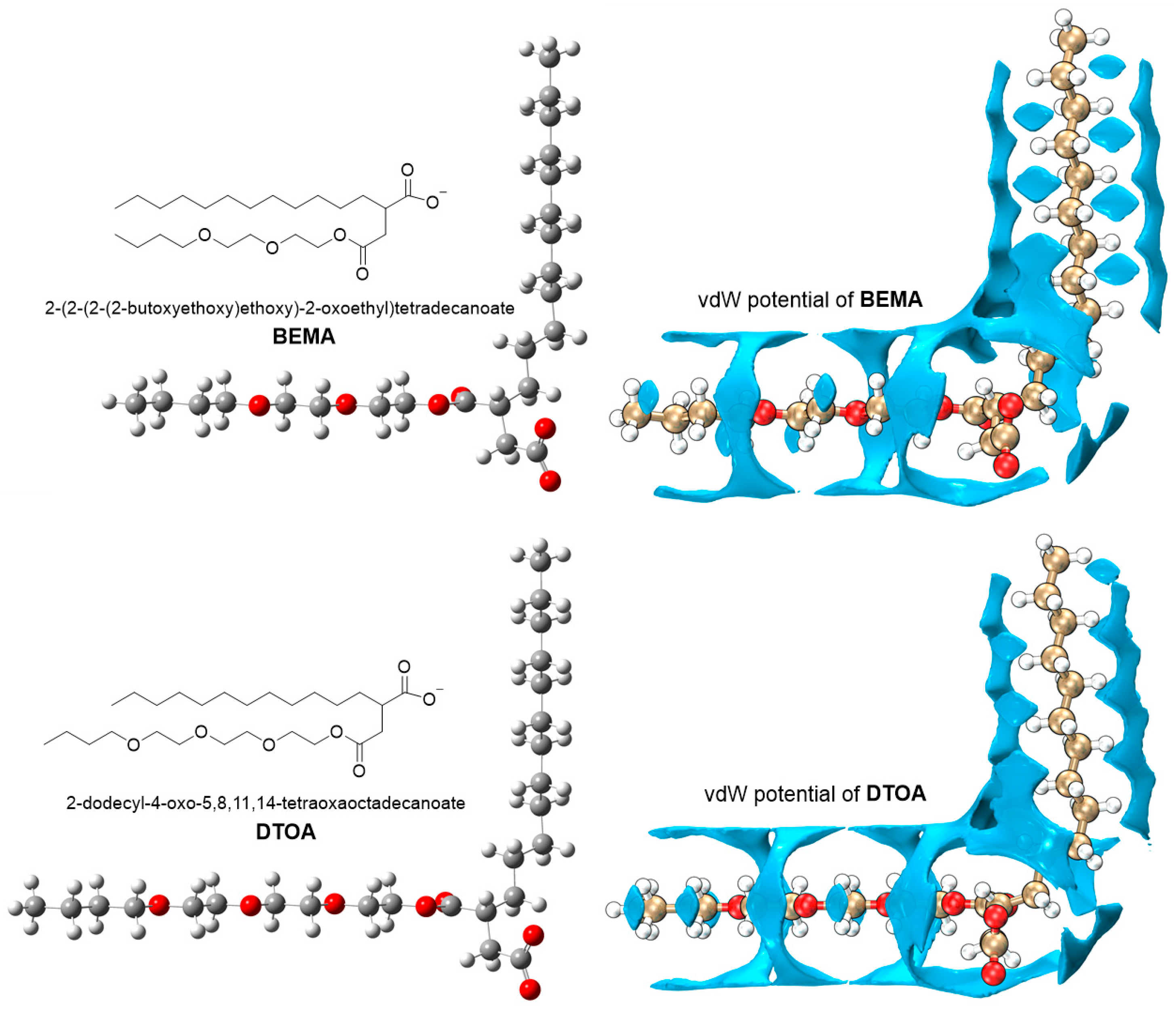
Colloids 08 00041 g001
Figure 1. Geometrically optimized surfactant structures and vdW potential. The red balls represent oxygen atoms, the gray (or yellow) balls represent carbon atoms, and the white balls represent hydrogen atoms.
Figure 1. Geometrically optimized surfactant structures and vdW potential. The red balls represent oxygen atoms, the gray (or yellow) balls represent carbon atoms, and the white balls represent hydrogen atoms.
Colloids 08 00041 g001
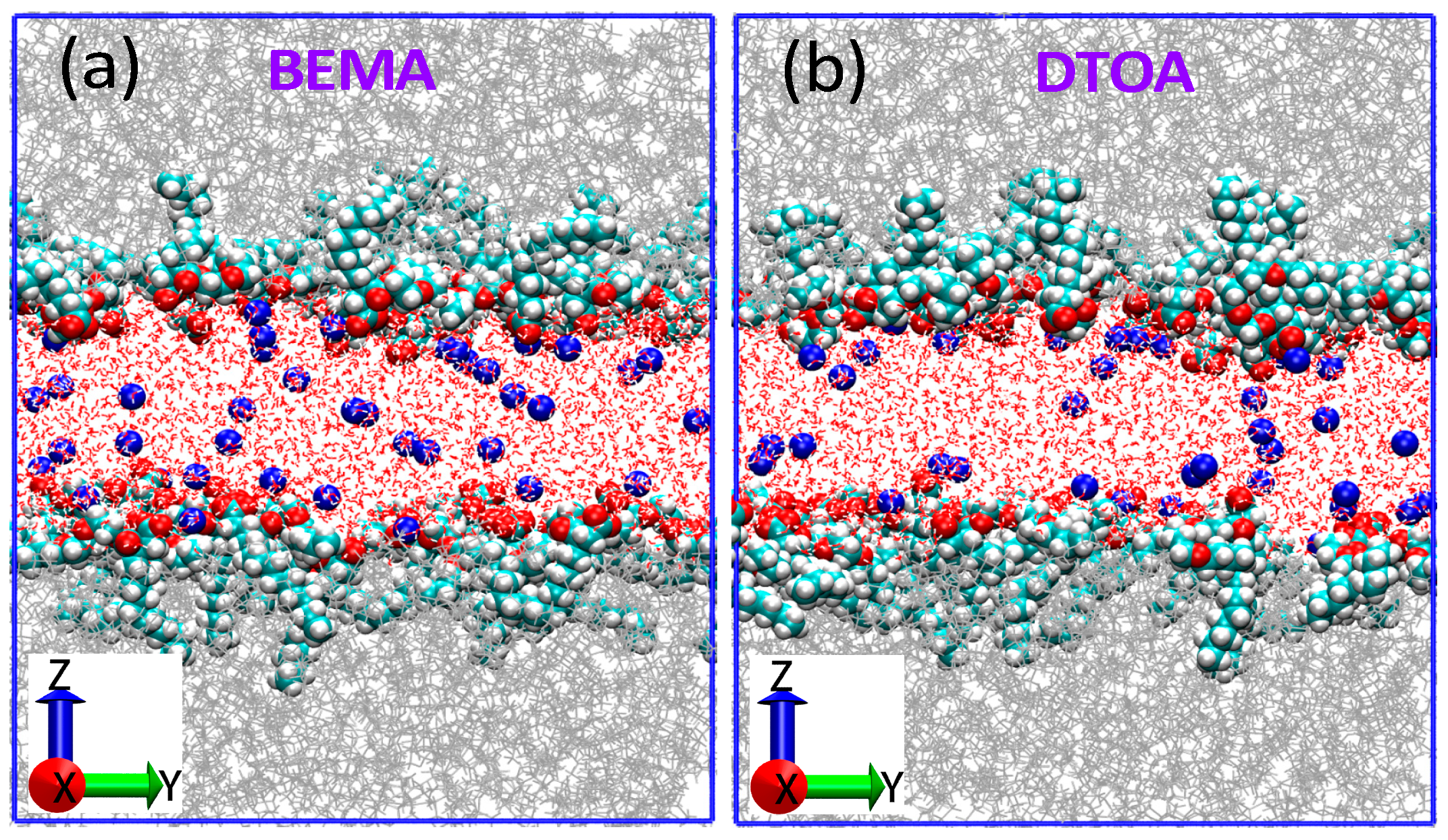
Colloids 08 00041 g002
Figure 2. Snapshots of 40 surfactant molecules at MD simulated equilibrium. (a) BEMA, (b) DTOA. Gray lines represent oil, blue balls represent sodium ions, red dots represent water molecules, and surfactant molecules are represented using three colors (red balls for oxygen atoms, white balls for hydrogen atoms, and cyan balls for carbon atoms).
Figure 2. Snapshots of 40 surfactant molecules at MD simulated equilibrium. (a) BEMA, (b) DTOA. Gray lines represent oil, blue balls represent sodium ions, red dots represent water molecules, and surfactant molecules are represented using three colors (red balls for oxygen atoms, white balls for hydrogen atoms, and cyan balls for carbon atoms).
Colloids 08 00041 g002
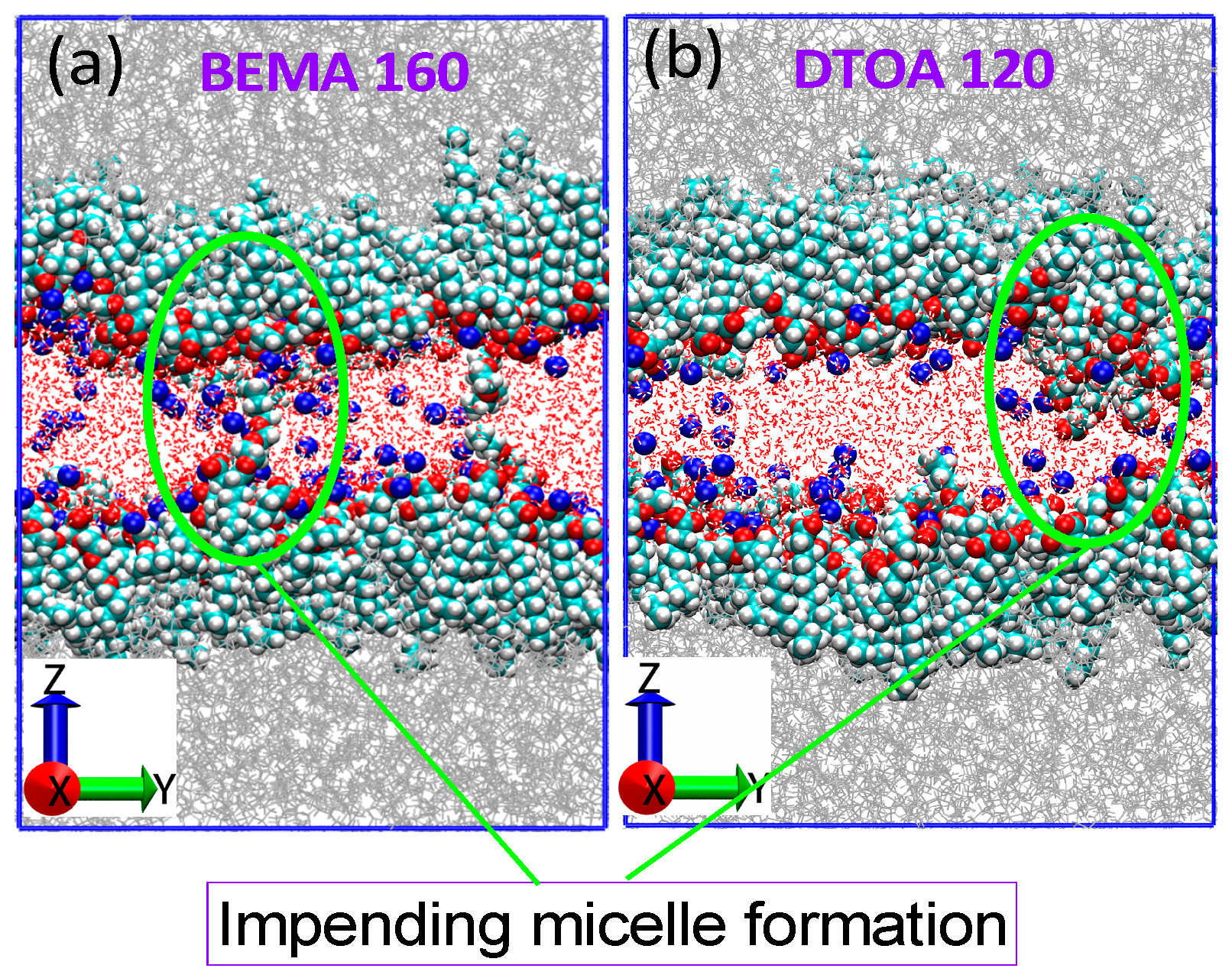
Colloids 08 00041 g003
Figure 3. Snapshots of surfactant molecules at MD simulated equilibrium. (a) BEMA (160), (b) DTOA (120). Gray lines represent oil, blue balls represent sodium ions, red dots represent water molecules, and surfactant molecules are represented using three colors (red balls for oxygen atoms, white balls for hydrogen atoms, and cyan balls for carbon atoms).
Figure 3. Snapshots of surfactant molecules at MD simulated equilibrium. (a) BEMA (160), (b) DTOA (120). Gray lines represent oil, blue balls represent sodium ions, red dots represent water molecules, and surfactant molecules are represented using three colors (red balls for oxygen atoms, white balls for hydrogen atoms, and cyan balls for carbon atoms).
Colloids 08 00041 g003
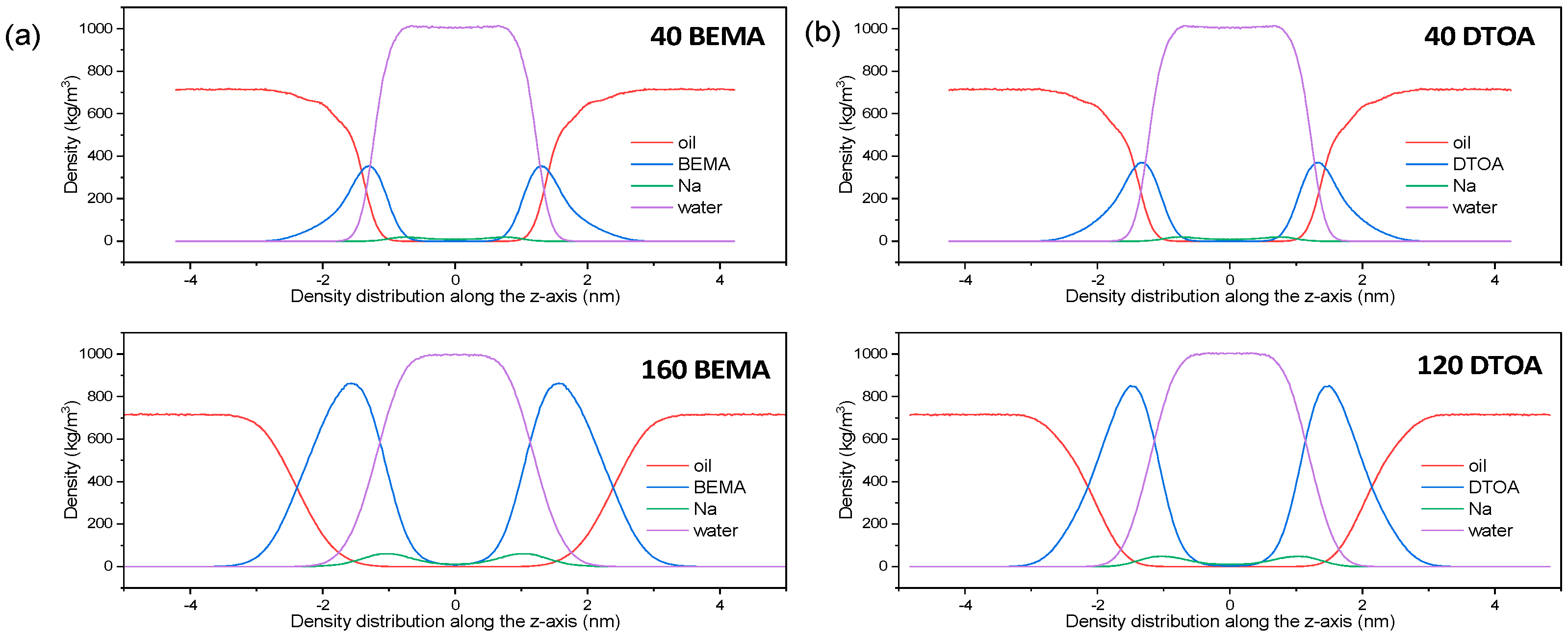
Colloids 08 00041 g004
Figure 4. Density distribution along the z-axis for models of (a) BEMA, (b) DTOA.
Figure 4. Density distribution along the z-axis for models of (a) BEMA, (b) DTOA.
Colloids 08 00041 g004
Colloids 08 00041 g005
Figure 5. Hydrogen bond distributions and their variation curves for different MD models. (a) BEMA, (b) DTOA. The x-axis is the number of surfactant molecules.
Figure 5. Hydrogen bond distributions and their variation curves for different MD models. (a) BEMA, (b) DTOA. The x-axis is the number of surfactant molecules.
Colloids 08 00041 g005
Colloids 08 00041 g006
Figure 6. Order parameters in the z-axis direction for different MD models. (a) BEMA, (b) DTOA.
Figure 6. Order parameters in the z-axis direction for different MD models. (a) BEMA, (b) DTOA.
Colloids 08 00041 g006
Colloids 08 00041 g007
Figure 7. Equilibrium snapshots of salt-containing simulation models, all of which contain 80 surfactants, with gray lines for oil molecules, red dots for water molecules, cyan for surfactant molecules, blue spheres for sodium ions, cyan spheres for chloride ions, magenta spheres for magnesium ions, and orange spheres for calcium ions. (a1) BEMA in 10 MgCl2; (a2) BEMA in 20 MgCl2; (a3) BEMA in 30 MgCl2; (a4) BEMA in 40 MgCl2; (a5) BEMA in 50 MgCl2; (a6) BEMA in 60 MgCl2; (b1) BEMA in 10 CaCl2; (b2) BEMA in 20 CaCl2; (b3) BEMA in 30 CaCl2; (b4) BEMA in 40 CaCl2; (b5) BEMA in 50 CaCl2; (b6) BEMA in 60 CaCl2; (c1) DTOA in 10 MgCl2; (c2) DTOA in 20 MgCl2; (c3) DTOA in 30 MgCl2; (c4) DTOA in 40 MgCl2; (c5) DTOA in 50 MgCl2; (c6) DTOA in 60 MgCl2; (d1) DTOA in 10 CaCl2; (d2) DTOA in 20 CaCl2; (d3) DTOA in 30 CaCl2; (d4) DTOA in 40 CaCl2; (d5) DTOA in 50 CaCl2; (d6) DTOA in 60 CaCl2.
Figure 7. Equilibrium snapshots of salt-containing simulation models, all of which contain 80 surfactants, with gray lines for oil molecules, red dots for water molecules, cyan for surfactant molecules, blue spheres for sodium ions, cyan spheres for chloride ions, magenta spheres for magnesium ions, and orange spheres for calcium ions. (a1) BEMA in 10 MgCl2; (a2) BEMA in 20 MgCl2; (a3) BEMA in 30 MgCl2; (a4) BEMA in 40 MgCl2; (a5) BEMA in 50 MgCl2; (a6) BEMA in 60 MgCl2; (b1) BEMA in 10 CaCl2; (b2) BEMA in 20 CaCl2; (b3) BEMA in 30 CaCl2; (b4) BEMA in 40 CaCl2; (b5) BEMA in 50 CaCl2; (b6) BEMA in 60 CaCl2; (c1) DTOA in 10 MgCl2; (c2) DTOA in 20 MgCl2; (c3) DTOA in 30 MgCl2; (c4) DTOA in 40 MgCl2; (c5) DTOA in 50 MgCl2; (c6) DTOA in 60 MgCl2; (d1) DTOA in 10 CaCl2; (d2) DTOA in 20 CaCl2; (d3) DTOA in 30 CaCl2; (d4) DTOA in 40 CaCl2; (d5) DTOA in 50 CaCl2; (d6) DTOA in 60 CaCl2.
Colloids 08 00041 g007
Colloids 08 00041 g008
Figure 8. Hydrogen bonding curves for BEMA and DTOA in aqueous magnesium chloride and aqueous calcium chloride at different salt concentrations. (a) BEMA in aqueous magnesium chloride; (b) BEMA in aqueous calcium chloride; (c) DTOA in aqueous magnesium chloride; (d) DTOA in aqueous calcium chloride.
Figure 8. Hydrogen bonding curves for BEMA and DTOA in aqueous magnesium chloride and aqueous calcium chloride at different salt concentrations. (a) BEMA in aqueous magnesium chloride; (b) BEMA in aqueous calcium chloride; (c) DTOA in aqueous magnesium chloride; (d) DTOA in aqueous calcium chloride.
Colloids 08 00041 g008
Colloids 08 00041 g009
Figure 9. IGMH for BEMA in aqueous magnesium chloride and aqueous calcium chloride. (a) Coordination with 1 H2O molecule in aqueous MgCl2 solution; (b) Coordination with 2 H2O molecule in aqueous MgCl2 solution; (c) Coordination with 3 H2O molecule in aqueous MgCl2 solution; (d) Coordination with 1 H2O molecule in aqueous CaCl2 solution; (e) Coordination with 2 H2O molecule in aqueous CaCl2 solution; (f) Coordination with 3 H2O molecule in aqueous CaCl2 solution.
Figure 9. IGMH for BEMA in aqueous magnesium chloride and aqueous calcium chloride. (a) Coordination with 1 H2O molecule in aqueous MgCl2 solution; (b) Coordination with 2 H2O molecule in aqueous MgCl2 solution; (c) Coordination with 3 H2O molecule in aqueous MgCl2 solution; (d) Coordination with 1 H2O molecule in aqueous CaCl2 solution; (e) Coordination with 2 H2O molecule in aqueous CaCl2 solution; (f) Coordination with 3 H2O molecule in aqueous CaCl2 solution.
Colloids 08 00041 g009
Table 1. Size of the MD model at equilibrium.
Table 1. Size of the MD model at equilibrium.
EntryNumbersBEMA (nm) 2DTOA (nm) 2
120 18.198.20
2408.468.50
3608.728.76
4808.999.03
51009.319.46
61209.579.88
71409.8510.15
816010.0910.42
918010.37–
1020010.68–
1: Number of surfactant molecules in the original MD model; 2: Length of the z-axis of the model.
Table 2. Interfacial thickness of the model.
Table 2. Interfacial thickness of the model.
ModelNumbersInterfacial Thickness
BEMA401.06
BEMA1602.14
DTOA401.09
DTOA1201.90
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, W.; Luo, F.; Gao, Z.; Chi, H.; Wang, J.; Yu, F.; He, Y.-P. Study of Interfacial Properties of Anionic–Nonionic Surfactants Based on Succinic Acid Derivatives via Molecular Dynamics Simulations and the IGMH Method. Colloids Interfaces 2024, 8, 41. https://doi.org/10.3390/colloids8040041

AMA Style

Zhang W, Luo F, Gao Z, Chi H, Wang J, Yu F, He Y-P. Study of Interfacial Properties of Anionic–Nonionic Surfactants Based on Succinic Acid Derivatives via Molecular Dynamics Simulations and the IGMH Method. Colloids and Interfaces. 2024; 8(4):41. https://doi.org/10.3390/colloids8040041

Chicago/Turabian Style

Zhang, Wannian, Feng Luo, Zhigang Gao, Haizhu Chi, Jinlong Wang, Fang Yu, and Yu-Peng He. 2024. "Study of Interfacial Properties of Anionic–Nonionic Surfactants Based on Succinic Acid Derivatives via Molecular Dynamics Simulations and the IGMH Method" Colloids and Interfaces 8, no. 4: 41. https://doi.org/10.3390/colloids8040041

APA Style

Zhang, W., Luo, F., Gao, Z., Chi, H., Wang, J., Yu, F., & He, Y. -P. (2024). Study of Interfacial Properties of Anionic–Nonionic Surfactants Based on Succinic Acid Derivatives via Molecular Dynamics Simulations and the IGMH Method. Colloids and Interfaces, 8(4), 41. https://doi.org/10.3390/colloids8040041

Article Metrics

Back to TopTop