Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis
Abstract
:1. Introduction
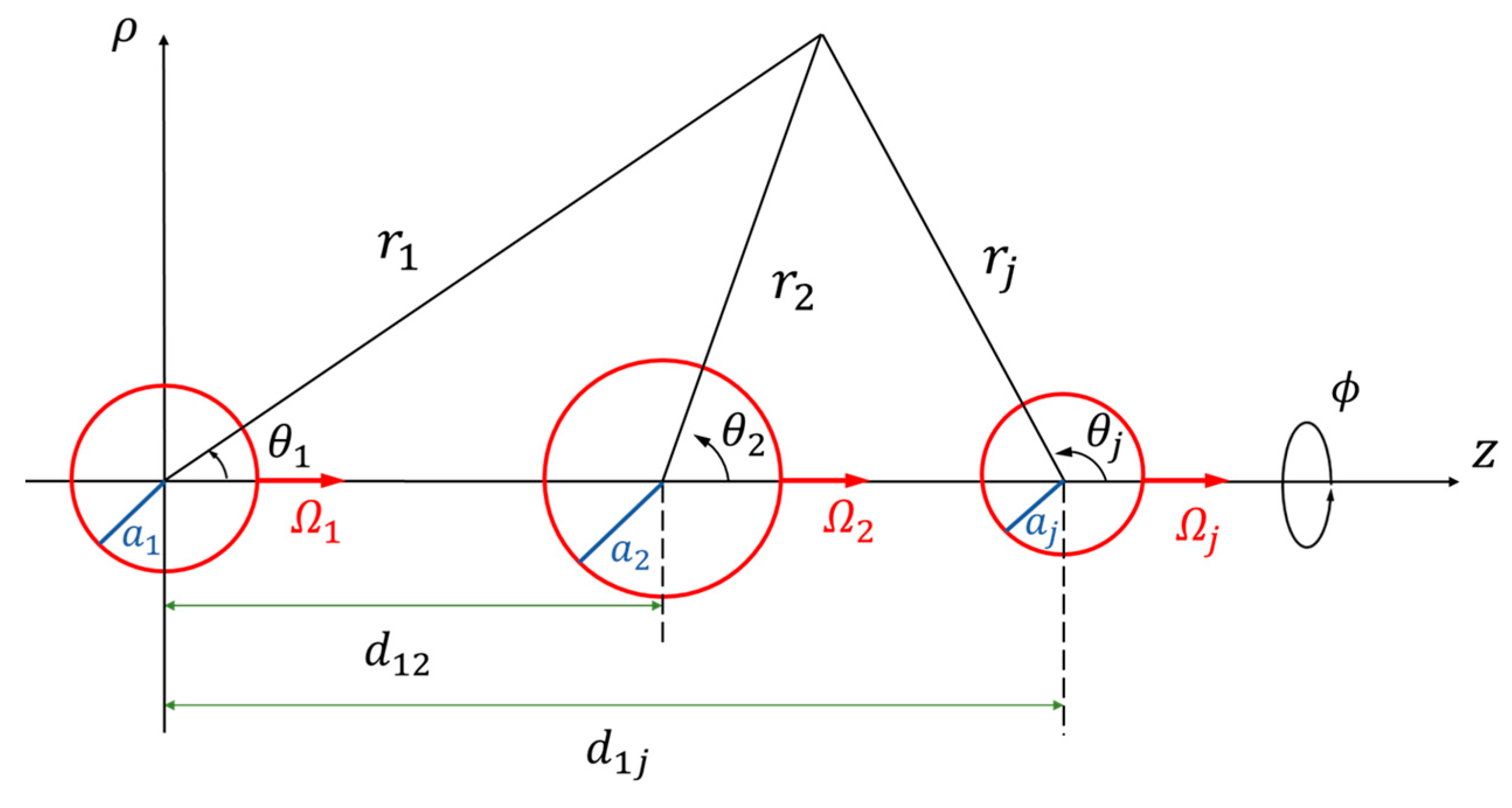
2. Analysis
3. Results for Two Particles
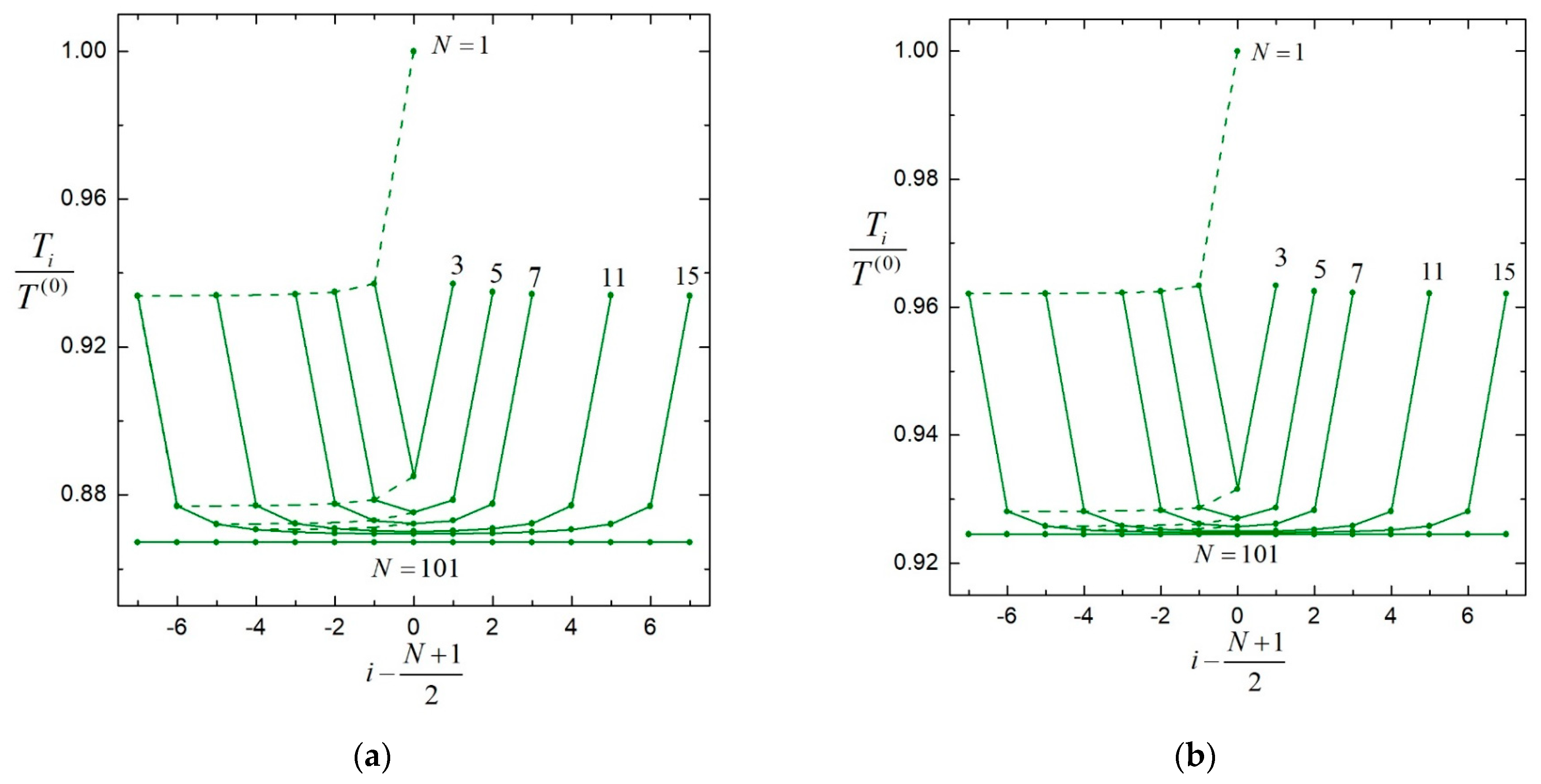
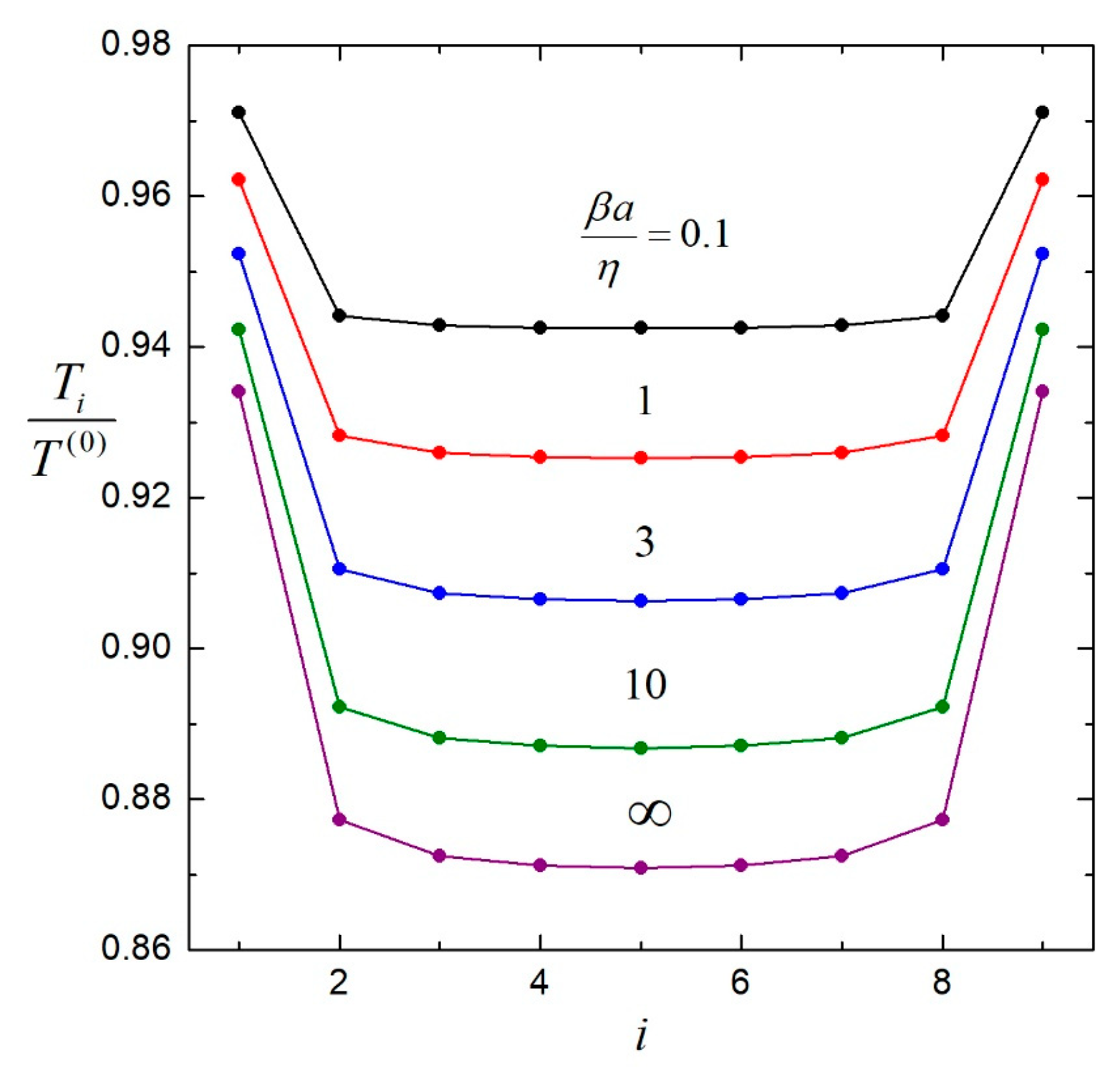
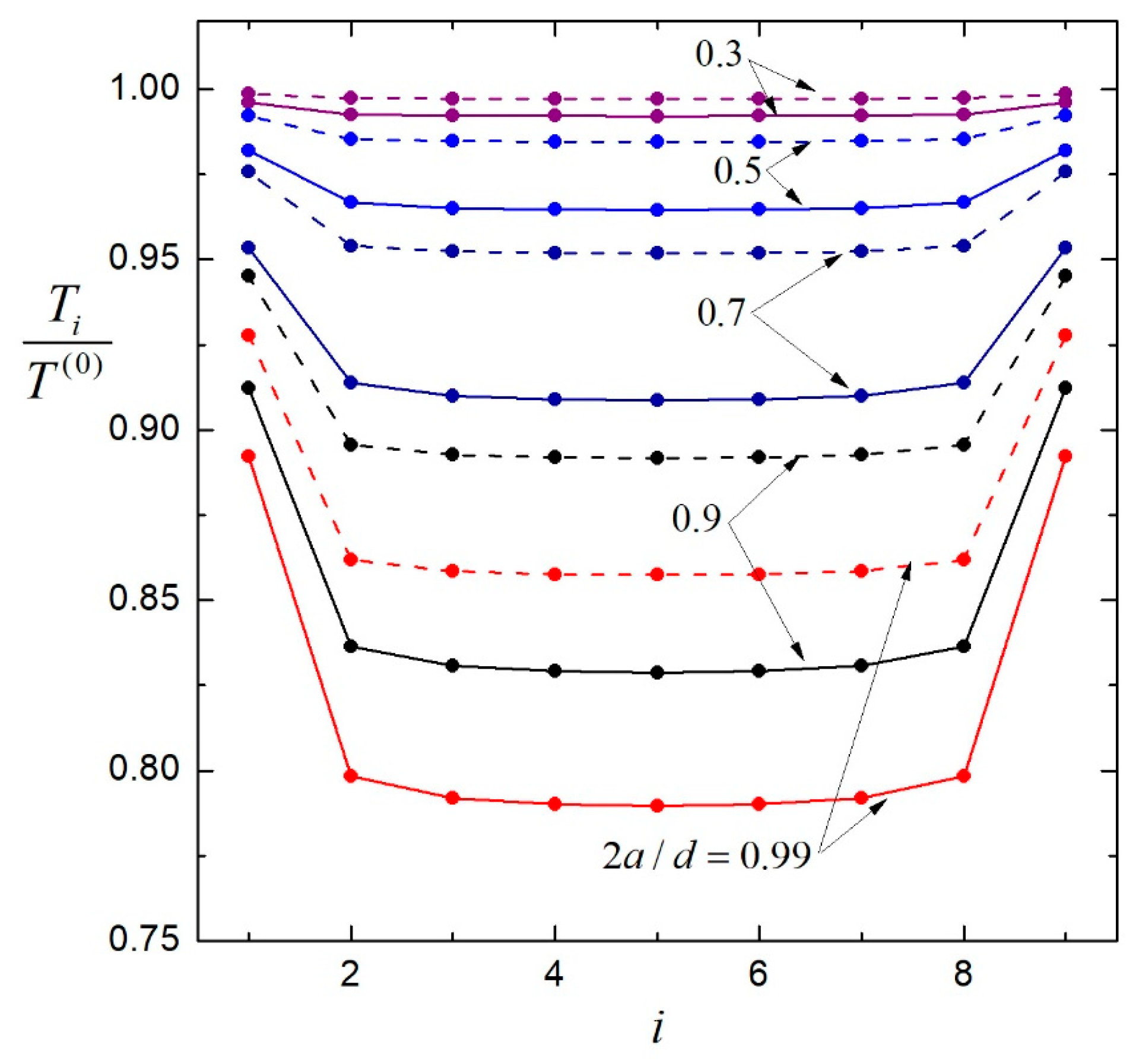
4. Results for Multiple Particles
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stokes, G.G. On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 1845, 8, 287–319. [Google Scholar]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 1851, 9, 8–106. [Google Scholar]
- Pit, R.; Hervet, H.; Leger, L. Direct experimental evidence of slip in hexadecane: Solid interfaces. Phys. Rev. Lett. 2000, 85, 980–983. [Google Scholar] [CrossRef] [PubMed]
- Tretheway, D.C.; Meinhart, C.D. Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 2002, 14, L9–L12. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.J.; Craig, V.S.J. Boundary slip in Newtonian liquids: A review of experimental studies. Rep. Prog. Phys. 2005, 68, 2859–2897. [Google Scholar] [CrossRef]
- Choi, C.H.; Ulmanella, U.; Kim, J.; Ho, C.M.; Kim, C.J. Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 2006, 18, 087105. [Google Scholar] [CrossRef]
- Cottin-Bizonne, C.; Steinberger, A.; Cross, B.; Raccurt, O.; Charlaix, E. Nanohydrodynamics: The intrinsic flow boundary condition on smooth surfaces. Langmuir 2008, 24, 1165–1172. [Google Scholar] [CrossRef] [PubMed]
- Hutchins, D.K.; Harper, M.H.; Felder, R.L. Slip correction measurements for solid spherical particles by modulated dynamic light scattering. Aerosol Sci. Technol. 1995, 22, 202–218. [Google Scholar] [CrossRef]
- Sharipov, F.; Kalempa, D. Velocity slip and temperature jump coefficients for gaseous mixtures. I. Viscous slip coefficient. Phys. Fluids 2003, 15, 1800–1806. [Google Scholar] [CrossRef]
- Myong, R.S.; Reese, J.M.; Barber, R.W.; Emerson, D.R. Velocity slip in microscale cylindrical Couette flow: The Langmuir model. Phys. Fluids 2005, 17, 087105. [Google Scholar] [CrossRef]
- Saffman, P.G. On the boundary condition at the surface of a porous medium. Studies Appl. Math. 1971, 50, 93–101. [Google Scholar] [CrossRef]
- Nir, A. Linear shear flow past a porous particle. Appl. Sci. Res. 1976, 32, 313–325. [Google Scholar] [CrossRef]
- Basset, A.B. A Treatise on Hydrodynamics; Deighton, Bell and Co.: Cambridge, UK, 1888; Volume 2. [Google Scholar]
- Felderhof, B.U. Hydrodynamic interaction between two spheres. Physica 1977, 89, 373–384. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Nijhoff: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Ramkissoon, H. Slip flow past an approximate spheroid. Acta Mech. 1997, 123, 227–233. [Google Scholar] [CrossRef]
- Chang, Y.C.; Keh, H.J. Translation and rotation of slightly deformed colloidal spheres experiencing slip. J. Colloid Interface Sci. 2009, 330, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Loyalka, S.K.; Griffin, J.L. Rotation of non-spherical axi-symmetric particles in the slip regime. J. Aerosol Sci. 1994, 25, 509–525. [Google Scholar] [CrossRef]
- Chang, Y.C.; Keh, H.J. Creeping-flow rotation of a slip spheroid about Its axis of revolution. Theor. Comput. Fluid Dyn. 2012, 26, 173–183. [Google Scholar] [CrossRef]
- Yariv, E.; Siegel, M. Rotation of a superhydrophobic cylinder in a viscous liquid. J. Fluid Mech. 2019, 880, R4. [Google Scholar] [CrossRef]
- Tekasakul, P.; Tompson, R.V.; Loyalka, S.K. A numerical study of two coaxial axisymmetric particles undergoing steady equal rotation in the slip regime. Z. Angew. Math. Phys. 1999, 50, 387–403. [Google Scholar]
- Luo, H.; Pozrikidis, C. Interception of two spheres with slip surfaces in linear Stokes flow. J. Fluid Mech. 2007, 581, 129–156. [Google Scholar] [CrossRef]
- Sherief, H.H.; Faltas, M.S.; Ashmawy, E.A. Stokes flow between two confocal rotating spheroids with slip. Arch. Appl. Mech. 2012, 82, 937–948. [Google Scholar] [CrossRef]
- Krishna Prasad, M.; Kaur, M.; Srinivasacharya, D. Slow steady rotation of an approximate sphere in an approximate spherical container with slip surfaces. Int. J. Appl. Comput. Math. 2017, 3, 987–999. [Google Scholar] [CrossRef]
- Liao, J.Q.; Keh, H.J. Slow rotation of a sphere about its diameter normal to two planes with slip surfaces. Fluid Dyn. Res. 2022, 54, 035502. [Google Scholar] [CrossRef]
- Reed, L.D.; Morrison, F.A. Particle interactions in viscous flow at small values of Knudsen number. J. Aerosol Sci. 1974, 5, 175–189. [Google Scholar] [CrossRef]
- Chen, S.H.; Keh, H.J. Axisymmetric motion of two spherical particles with slip surfaces. J. Colloid Interface Sci. 1995, 171, 63–72. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, S.H. Low Reynolds number hydrodynamic interactions in a suspension of spherical particles with slip surfaces. Chem. Eng. Sci. 1997, 52, 1789–1805. [Google Scholar] [CrossRef]
- Saad, E.I. Motion of two spheres translating and rotating through a viscous fluid with slip surfaces. Fluid Dyn. Res. 2012, 44, 055505. [Google Scholar] [CrossRef]
- Tu, H.J.; Keh, H.J. Particle interactions in diffusiophoresis and electrophoresis of colloidal spheres with thin but polarized double layers. J. Colloid Interface Sci. 2000, 231, 265–282. [Google Scholar] [CrossRef] [PubMed]
- Keh, H.J.; Hsieh, T.H. Electrophoresis of a colloidal sphere in a spherical cavity with arbitrary zeta potential distributions and arbitrary double-layer thickness. Langmuir 2008, 24, 390–398. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, S.H. Thermophoresis of an arbitrary three-dimensional array of N interacting arbitrary spheres. J. Aerosol Sci. 1996, 27, 1035–1061. [Google Scholar] [CrossRef]
- Gluckman, M.J.; Pfeffer, R.; Weinbaum, S. A new technique for treating multi-particle slow viscous flow: Axisymmetric flow past spheres and spheroids. J. Fluid Mech. 1971, 50, 705–740. [Google Scholar] [CrossRef]
- Leichtberg, S.; Pfeffer, R.; Weinbaum, S. Stokes flow past finite coaxial clusters of spheres in a circular cylinder. Int. J. Multiphase Flow 1976, 3, 147–169. [Google Scholar] [CrossRef]
- Chen, L.S.; Keh, H.J. The slow motion of coaxial droplets along their line of centers. J. Chin. Inst. Chem. Eng. 1992, 23, 53–66. [Google Scholar]
- Jeffrey, D.J.; Onishi, Y. Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 1984, 139, 261–290. [Google Scholar] [CrossRef]

| Collocation Solution | Asymptotic Solution | ||||
|---|---|---|---|---|---|
| 1 | 0.2 | 1.00000 | −0.00033 | 1.00000 | −0.00025 |
| 0.3 | 1.00000 | −0.00123 | 1.00000 | −0.00084 | |
| 0.4 | 1.00001 | −0.00322 | 1.00000 | −0.00200 | |
| 0.5 | 1.00006 | −0.00691 | 1.00002 | −0.00391 | |
| 0.6 | 1.00023 | −0.01306 | 1.00005 | −0.00675 | |
| 0.7 | 1.00079 | −0.02260 | 1.00011 | −0.01072 | |
| 0.8 | 1.00247 | −0.03676 | 1.00026 | −0.01600 | |
| 0.9 | 1.00738 | −0.05761 | 1.00052 | −0.02278 | |
| 0.99 | 1.02224 | −0.08900 | 1.00092 | −0.06064 | |
| 1.0 | 1.02693 | −0.09567 | 1.00098 | −0.06250 | |
| 10 | 0.2 | 1.00000 | −0.00079 | 1.00000 | −0.00077 |
| 0.3 | 1.00001 | −0.00271 | 1.00001 | −0.00260 | |
| 0.4 | 1.00005 | −0.00653 | 1.00004 | −0.00615 | |
| 0.5 | 1.00020 | −0.01295 | 1.00014 | −0.01202 | |
| 0.6 | 1.00068 | −0.02273 | 1.00043 | −0.02077 | |
| 0.7 | 1.00199 | −0.03674 | 1.00109 | −0.03298 | |
| 0.8 | 1.00529 | −0.05612 | 1.00242 | −0.04923 | |
| 0.9 | 1.01351 | −0.08313 | 1.00491 | −0.07010 | |
| 0.99 | 1.03508 | −0.12286 | 1.00870 | −0.01971 | |
| 1.0 | 1.04120 | −0.13103 | 1.00925 | −0.02031 | |
| ∞ | 0.2 | 1.00000 | −0.00100 | 1.00000 | −0.00100 |
| 0.3 | 1.00001 | −0.00338 | 1.00001 | −0.00338 | |
| 0.4 | 1.00007 | −0.00800 | 1.00007 | −0.00800 | |
| 0.5 | 1.00030 | −0.01563 | 1.00030 | −0.01563 | |
| 0.6 | 1.00097 | −0.02704 | 1.00096 | −0.02703 | |
| 0.7 | 1.00273 | −0.04306 | 1.00268 | −0.04301 | |
| 0.8 | 1.00702 | −0.06485 | 1.00669 | −0.06451 | |
| 0.9 | 1.01727 | −0.09494 | 1.01539 | −0.09280 | |
| 0.99 | 1.04336 | −0.13974 | 1.03082 | −0.12569 | |
| 1.0 | 1.05097 | −0.14943 | 1.03320 | −0.12988 | |
| 2 | 0.5 | 1.00024 | −0.00463 | −0.03705 | 1.00019 |
| (1.00024) | (−0.00463) | (−0.03705) | (1.00019) | ||
| 0.6 | 1.00086 | −0.00801 | −0.06406 | 1.00058 | |
| (1.00084) | (−0.00801) | (−0.06406) | (1.00058) | ||
| 0.7 | 1.00271 | −0.01275 | −0.10197 | 1.00153 | |
| (1.00250) | (−0.01273) | (−0.10187) | (1.00152) | ||
| 0.8 | 1.00795 | −0.01917 | −0.15335 | 1.00363 | |
| (1.00673) | (−0.01908) | (−0.15262) | (1.00358) | ||
| 0.9 | 1.02335 | −0.02800 | −0.22396 | 1.00809 | |
| (1.01667) | (−0.02737) | (−0.21897) | (1.00769) | ||
| 0.99 | 1.06197 | −0.04126 | −0.33012 | 1.01787 | |
| (1.03560) | (−0.03691) | (−0.29532) | (1.01444) | ||
| 1.0 | 1.09395 | −0.04449 | −0.35606 | 1.02075 | |
| (1.03861) | (−0.03812) | (−0.30497) | (1.01544) | ||
| 5 | 0.5 | 1.00007 | −0.00058 | −0.07234 | 1.00004 |
| (1.00007) | (−0.00058) | (−0.07234) | (1.00004) | ||
| 0.6 | 1.00030 | −0.00100 | −0.12504 | 1.00013 | |
| (1.00027) | (−0.00100) | (−0.12503) | (1.00013) | ||
| 0.7 | 1.00110 | −0.00159 | −0.19873 | 1.00033 | |
| (1.00086) | (−0.00159) | (−0.19862) | (1.00033) | ||
| 0.8 | 1.00412 | −0.00238 | −0.29764 | 1.00074 | |
| (1.00247) | (−0.00237) | (−0.29679) | (1.00074) | ||
| 0.9 | 1.01743 | −0.00344 | −0.43050 | 1.00156 | |
| (1.00653) | (−0.00339) | (−0.42353) | (1.00152) | ||
| 0.99 | 1.09830 | −0.00508 | −0.63487 | 1.00318 | |
| (1.01468) | (−0.00453) | (−0.56594) | (1.00274) | ||
| 1.0 | 1.14324 | −0.00556 | −0.69390 | 1.00368 | |
| (1.01601) | (−0.00467) | (−0.58361) | (1.00291) |
| , , | ||||
| 0.2 | 1.00000 | −0.00033 | −0.00100 | 1.00000 |
| 0.3 | 1.00000 | −0.00123 | −0.00338 | 1.00000 |
| 0.4 | 1.00003 | −0.00322 | −0.00800 | 1.00003 |
| 0.5 | 1.00014 | −0.00691 | −0.01563 | 1.00013 |
| 0.6 | 1.00049 | −0.01307 | −0.02702 | 1.00046 |
| 0.7 | 1.00155 | −0.02263 | −0.04298 | 1.00140 |
| 0.8 | 1.00449 | −0.03688 | −0.06453 | 1.00387 |
| 0.9 | 1.01258 | −0.05814 | −0.09382 | 1.01021 |
| 0.99 | 1.03642 | −0.09147 | −0.13622 | 1.02710 |
| 1.0 | 1.04514 | −0.09962 | −0.14624 | 1.03280 |
| , , | ||||
| 0.2 | 1.00000 | −0.00016 | −0.00169 | 1.00000 |
| 0.3 | 1.00000 | −0.00055 | −0.00588 | 1.00000 |
| 0.4 | 1.00002 | −0.00134 | −0.01438 | 1.00002 |
| 0.5 | 1.00011 | −0.00271 | −0.02901 | 1.00009 |
| 0.6 | 1.00042 | −0.00482 | −0.05184 | 1.00028 |
| 0.7 | 1.00143 | −0.00788 | −0.08532 | 1.00079 |
| 0.8 | 1.00459 | −0.01216 | −0.13272 | 1.00201 |
| 0.9 | 1.01496 | −0.01813 | −0.20015 | 1.00479 |
| 0.99 | 1.05306 | −0.02690 | −0.30147 | 1.01124 |
| 1.0 | 1.06789 | −0.02888 | −0.32475 | 1.01311 |
| 1 | 0.2 | 1.00000 | 1.00000 | −0.00033 | −0.00004 |
| 0.3 | 1.00000 | 1.00000 | −0.00123 | −0.00013 | |
| 0.4 | 1.00002 | 1.00001 | −0.00322 | −0.00032 | |
| 0.5 | 1.00012 | 1.00006 | −0.00691 | −0.00063 | |
| 0.6 | 1.00046 | 1.00023 | −0.01305 | −0.00110 | |
| 0.7 | 1.00158 | 1.00080 | −0.02256 | −0.00171 | |
| 0.8 | 1.00493 | 1.00247 | −0.03666 | −0.00244 | |
| 0.9 | 1.01473 | 1.00739 | −0.05740 | −0.00322 | |
| 0.99 | 1.04441 | 1.02225 | −0.08866 | −0.00392 | |
| 1.0 | 1.05330 | 1.02724 | −0.09501 | −0.00399 | |
| 10 | 0.2 | 1.00000 | 1.00000 | −0.00079 | −0.00010 |
| 0.3 | 1.00002 | 1.00001 | −0.00271 | −0.00032 | |
| 0.4 | 1.00010 | 1.00005 | −0.00652 | −0.00075 | |
| 0.5 | 1.00040 | 1.00020 | −0.01293 | −0.00142 | |
| 0.6 | 1.00136 | 1.00069 | −0.02267 | −0.00232 | |
| 0.7 | 1.00396 | 1.00200 | −0.03660 | −0.00341 | |
| 0.8 | 1.01054 | 1.00531 | −0.05582 | −0.00461 | |
| 0.9 | 1.02693 | 1.01355 | −0.08259 | −0.00586 | |
| 0.99 | 1.06996 | 1.03511 | −0.12204 | −0.00695 | |
| 1.0 | 1.08354 | 1.04192 | −0.13082 | −0.00707 | |
| ∞ | 0.2 | 1.00000 | 1.00000 | −0.00100 | −0.00012 |
| 0.3 | 1.00002 | 1.00001 | −0.00337 | −0.00041 | |
| 0.4 | 1.00014 | 1.00007 | −0.00799 | −0.00094 | |
| 0.5 | 1.00059 | 1.00030 | −0.01560 | −0.00175 | |
| 0.6 | 1.00193 | 1.00098 | −0.02695 | −0.00282 | |
| 0.7 | 1.00545 | 1.00275 | −0.04286 | −0.00409 | |
| 0.8 | 1.01397 | 1.00705 | −0.06445 | −0.00546 | |
| 0.9 | 1.03439 | 1.01732 | −0.09423 | −0.00687 | |
| 0.99 | 1.08644 | 1.04341 | −0.13864 | −0.00812 | |
| 1.0 | 1.10321 | 1.05182 | −0.14909 | −0.00826 |
| 1:2:1 | 0.2 | 1.00000 | 1.00000 | −0.00030 | −0.00237 | −0.00004 |
| 0.3 | 1.00002 | 1.00001 | −0.00100 | −0.00800 | −0.00012 | |
| 0.4 | 1.00009 | 1.00006 | −0.00237 | −0.01896 | −0.00026 | |
| 0.5 | 1.00037 | 1.00024 | −0.00463 | −0.03703 | −0.00045 | |
| 0.6 | 1.00116 | 1.00087 | −0.00800 | −0.06402 | −0.00067 | |
| 0.7 | 1.00306 | 1.00271 | −0.01273 | −0.10188 | −0.00088 | |
| 0.8 | 1.00726 | 1.00795 | −0.01915 | −0.15320 | −0.00103 | |
| 0.9 | 1.01616 | 1.02335 | −0.02797 | −0.22373 | −0.00110 | |
| 0.99 | 1.03572 | 1.07433 | −0.04123 | −0.32982 | −0.00110 | |
| 0.999 | 1.04058 | 1.09059 | −0.04397 | −0.35177 | −0.00110 | |
| 1.0 | 1.04136 | 1.09376 | −0.04445 | −0.35557 | −0.00110 | |
| 2:1:2 | 0.2 | 1.00000 | 1.00000 | −0.00237 | −0.00030 | −0.00030 |
| 0.3 | 1.00002 | 1.00001 | −0.00799 | −0.00100 | −0.00099 | |
| 0.4 | 1.00011 | 1.00005 | −0.01892 | −0.00236 | −0.00233 | |
| 0.5 | 1.00049 | 1.00021 | −0.03685 | −0.00461 | −0.00447 | |
| 0.6 | 1.00172 | 1.00064 | −0.06346 | −0.00793 | −0.00756 | |
| 0.7 | 1.00536 | 1.00169 | −0.10038 | −0.01255 | −0.01165 | |
| 0.8 | 1.01568 | 1.00396 | −0.14971 | −0.01871 | −0.01681 | |
| 0.9 | 1.04600 | 1.00872 | −0.21645 | −0.02706 | −0.02308 | |
| 0.99 | 1.14694 | 1.01894 | −0.31689 | −0.03961 | −0.02980 | |
| 0.999 | 1.17932 | 1.02142 | −0.33813 | −0.04227 | −0.03054 | |
| 1.0 | 1.18582 | 1.02188 | −0.34194 | −0.04274 | −0.03062 |
| 1:2:1 | 0.2 | 1.00000 | 1.00000 | −0.00006 | −0.00083 | −0.00001 |
| 0.3 | 1.00000 | 1.00000 | −0.00023 | −0.00322 | −0.00002 | |
| 0.4 | 1.00001 | 1.00001 | −0.00061 | −0.00865 | −0.00006 | |
| 0.5 | 1.00006 | 1.00004 | −0.00133 | −0.01896 | −0.00011 | |
| 0.6 | 1.00021 | 1.00017 | −0.00254 | −0.03657 | −0.00017 | |
| 0.7 | 1.00069 | 1.00067 | −0.00442 | −0.06463 | −0.00024 | |
| 0.8 | 1.00202 | 1.00254 | −0.00720 | −0.10748 | −0.00030 | |
| 0.9 | 1.00549 | 1.00977 | −0.01125 | −0.17256 | −0.00033 | |
| 0.99 | 1.01456 | 1.04047 | −0.01731 | −0.27461 | −0.00030 | |
| 0.999 | 1.01694 | 1.05118 | −0.01849 | −0.29502 | −0.00030 | |
| 1.0 | 1.01726 | 1.05328 | −0.01864 | −0.29841 | −0.00030 | |
| 2:1:2 | 0.2 | 1.00000 | 1.00000 | −0.00114 | −0.00009 | −0.00013 |
| 0.3 | 1.00000 | 1.00000 | −0.00417 | −0.00033 | −0.00046 | |
| 0.4 | 1.00002 | 1.00001 | −0.01070 | −0.00083 | −0.00113 | |
| 0.5 | 1.00011 | 1.00005 | −0.02252 | −0.00174 | −0.00228 | |
| 0.6 | 1.00047 | 1.00017 | −0.04185 | −0.00320 | −0.00406 | |
| 0.7 | 1.00175 | 1.00052 | −0.07142 | −0.00541 | −0.00658 | |
| 0.8 | 1.00619 | 1.00141 | −0.11479 | −0.00855 | −0.00995 | |
| 0.9 | 1.02229 | 1.00358 | −0.17814 | −0.01300 | −0.01428 | |
| 0.99 | 1.08748 | 1.00878 | −0.27514 | −0.01954 | −0.01910 | |
| 0.999 | 1.10984 | 1.01016 | −0.29470 | −0.02083 | −0.01964 | |
| 1.0 | 1.11423 | 1.01033 | −0.29798 | −0.02096 | −0.01970 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, M.J.; Keh, H.J. Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis. Colloids Interfaces 2023, 7, 63. https://doi.org/10.3390/colloids7040063
Tsai MJ, Keh HJ. Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis. Colloids and Interfaces. 2023; 7(4):63. https://doi.org/10.3390/colloids7040063
Chicago/Turabian StyleTsai, Min J., and Huan J. Keh. 2023. "Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis" Colloids and Interfaces 7, no. 4: 63. https://doi.org/10.3390/colloids7040063
APA StyleTsai, M. J., & Keh, H. J. (2023). Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis. Colloids and Interfaces, 7(4), 63. https://doi.org/10.3390/colloids7040063







