Formation of Myoglobin Corona at Polymer Microparticles
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
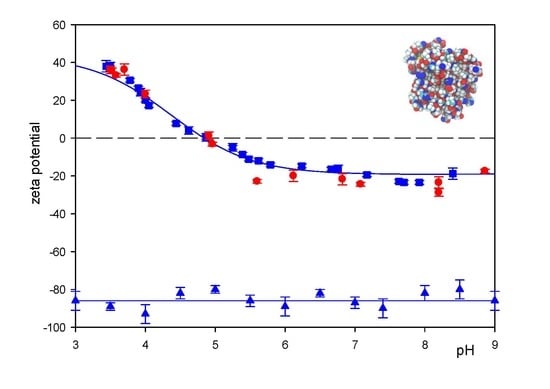
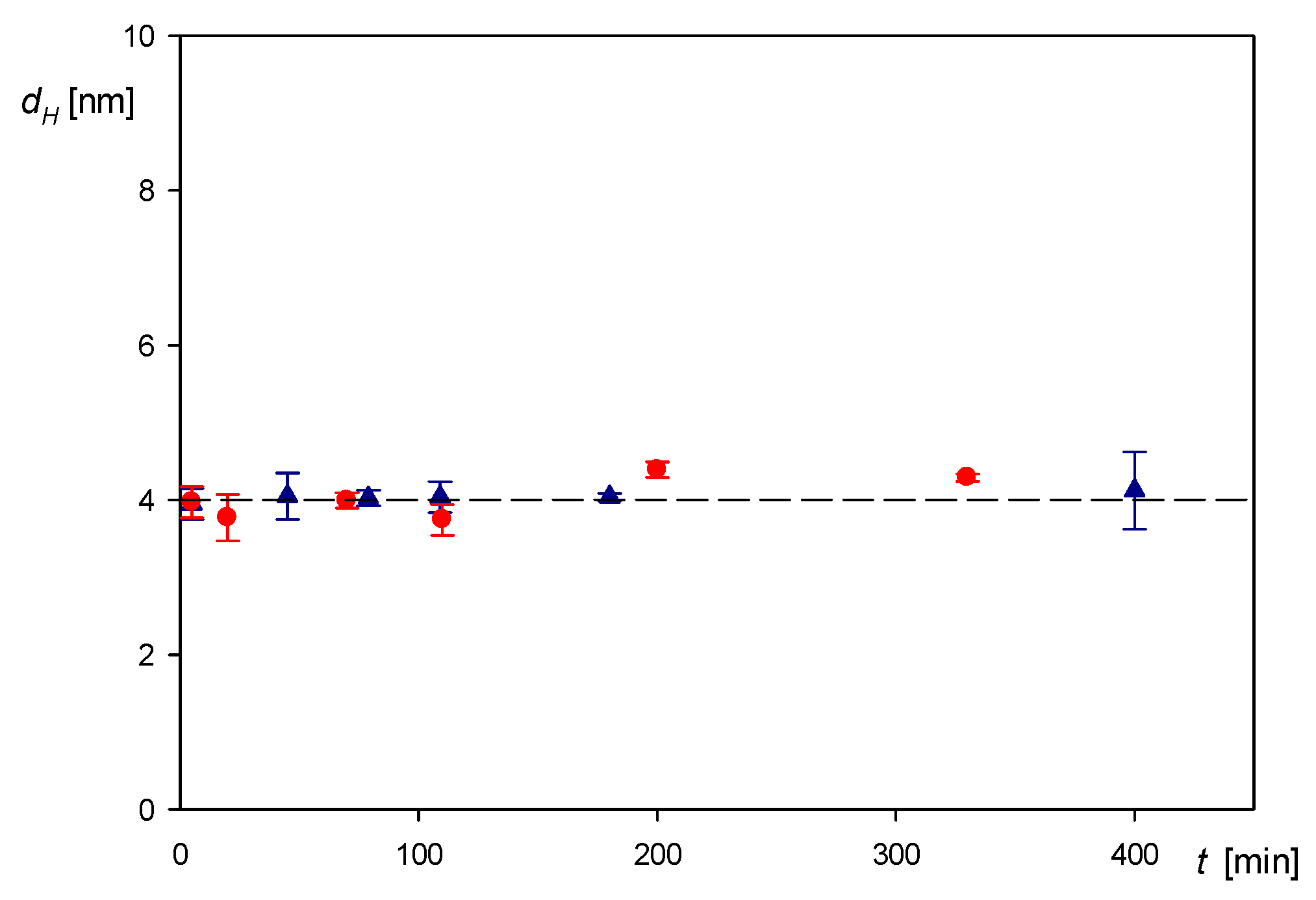
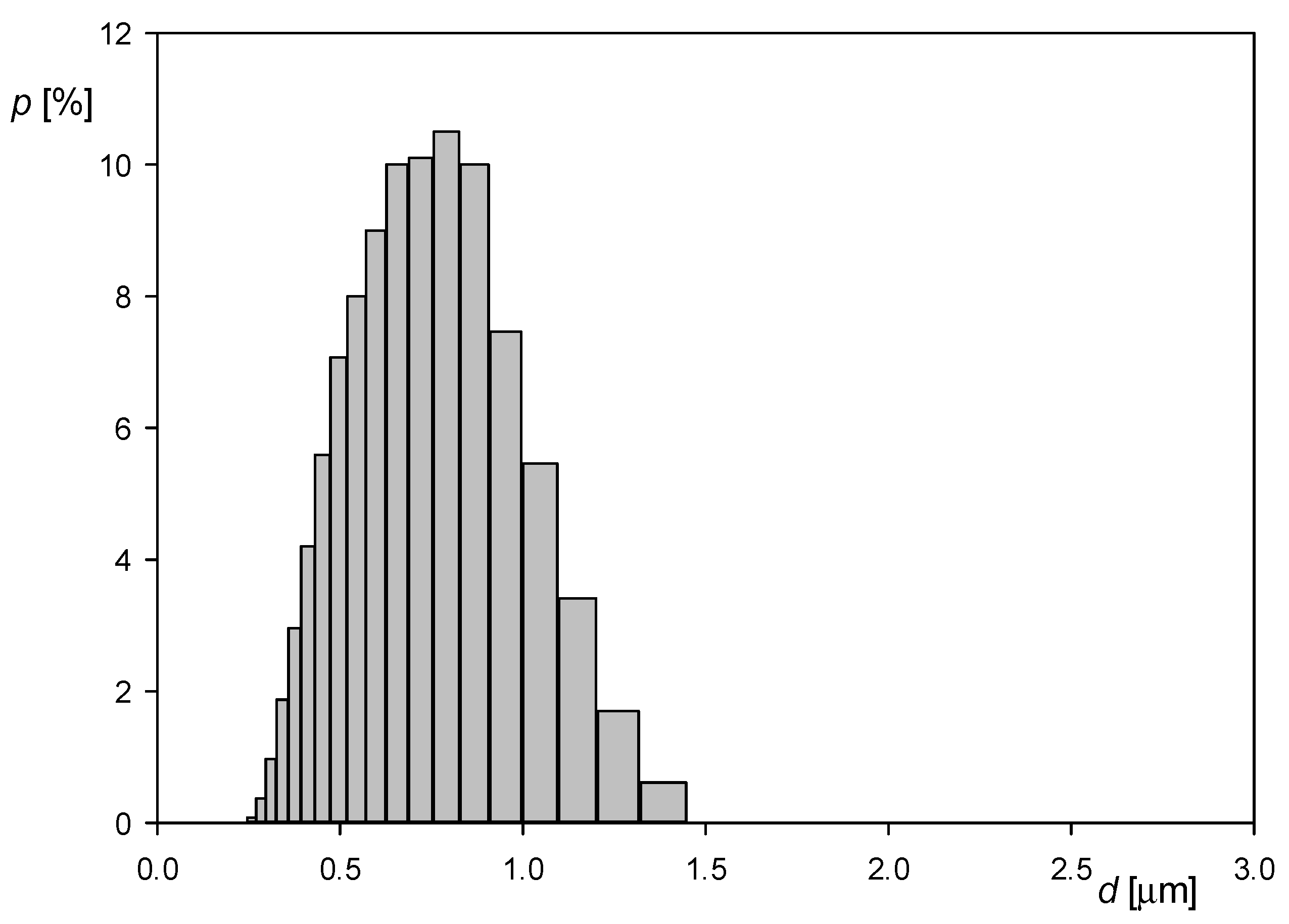
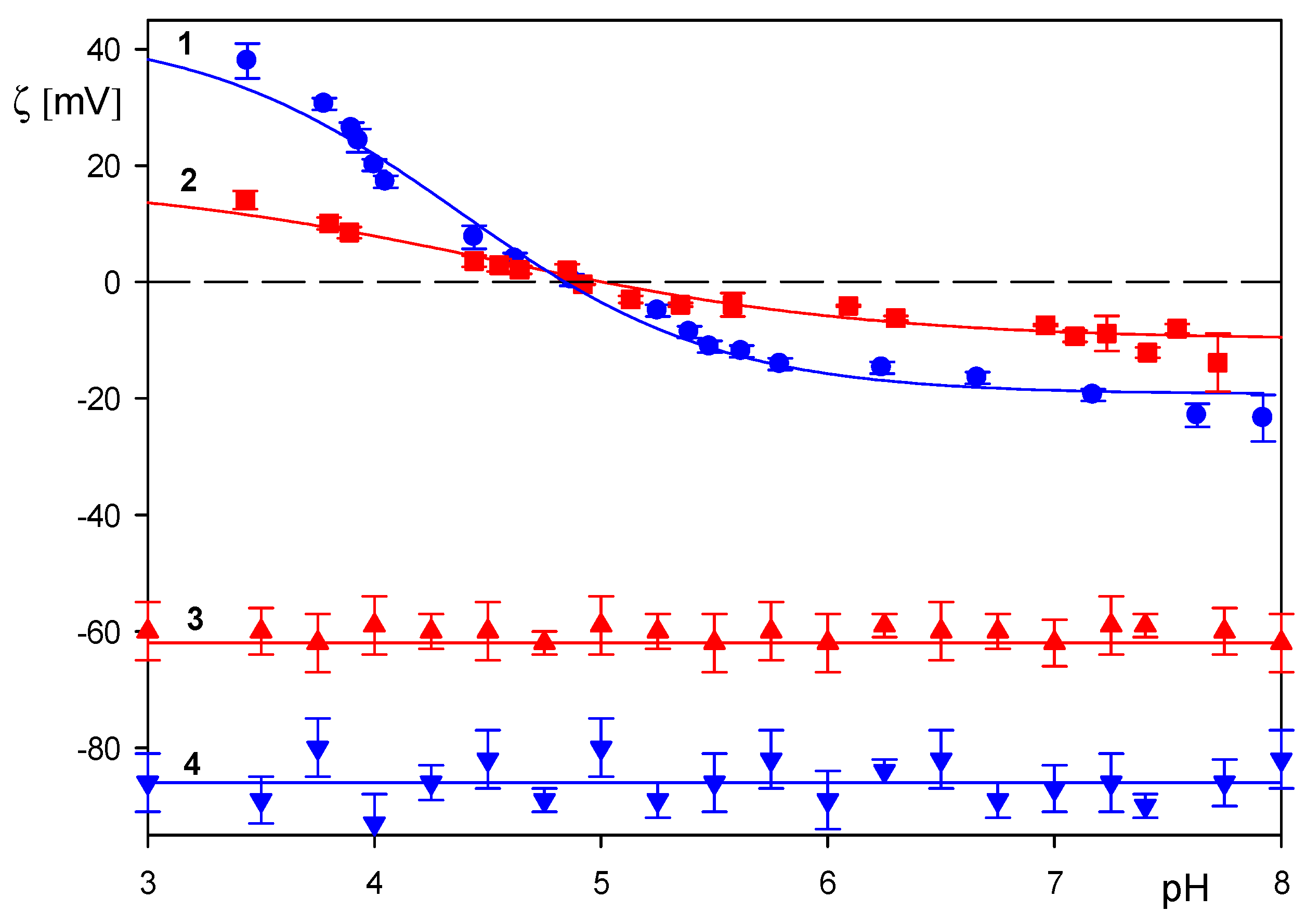
3.1. Physicochemical Characteristics of Myoglobin Molecules and Polymer Particles
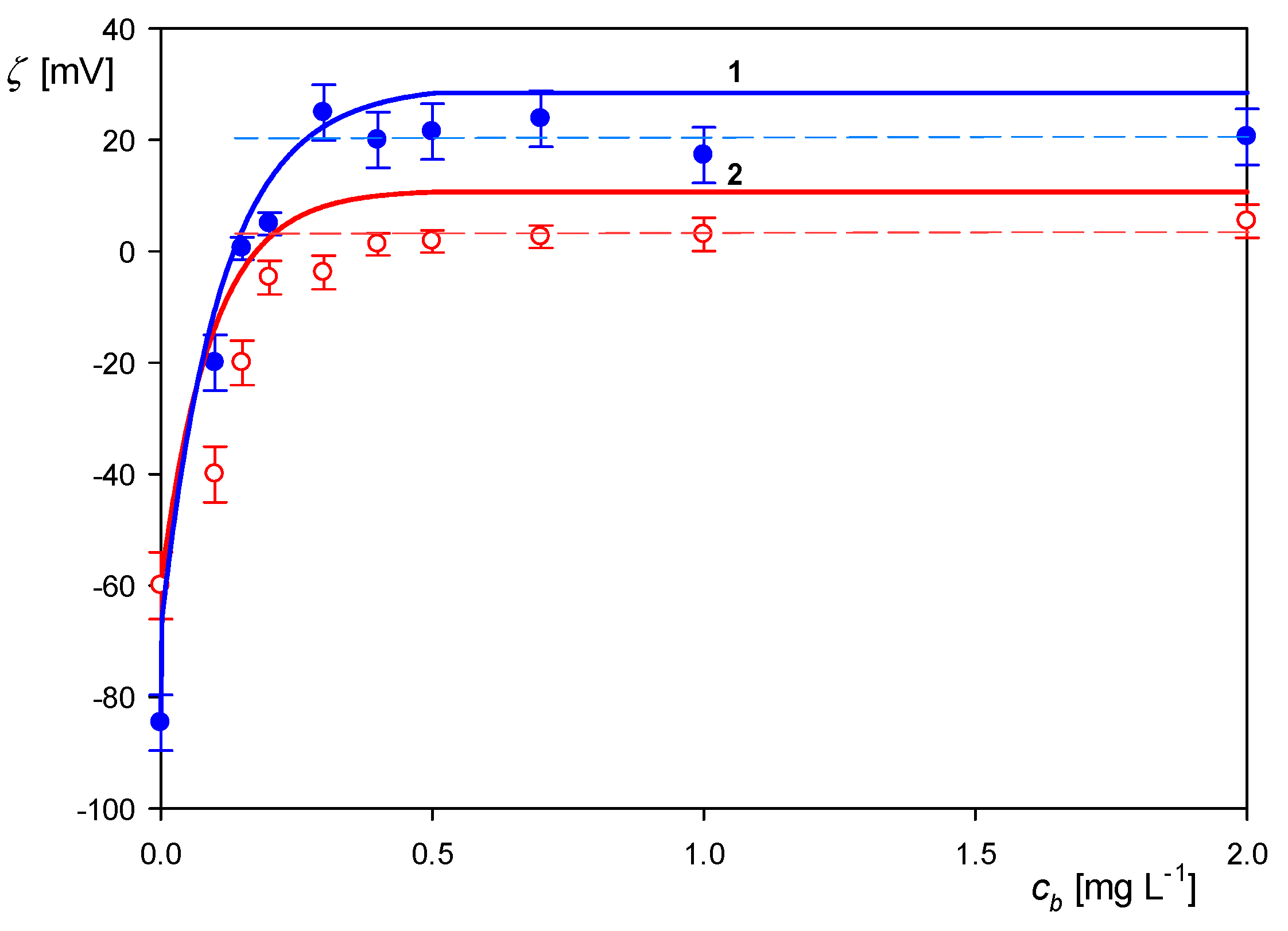
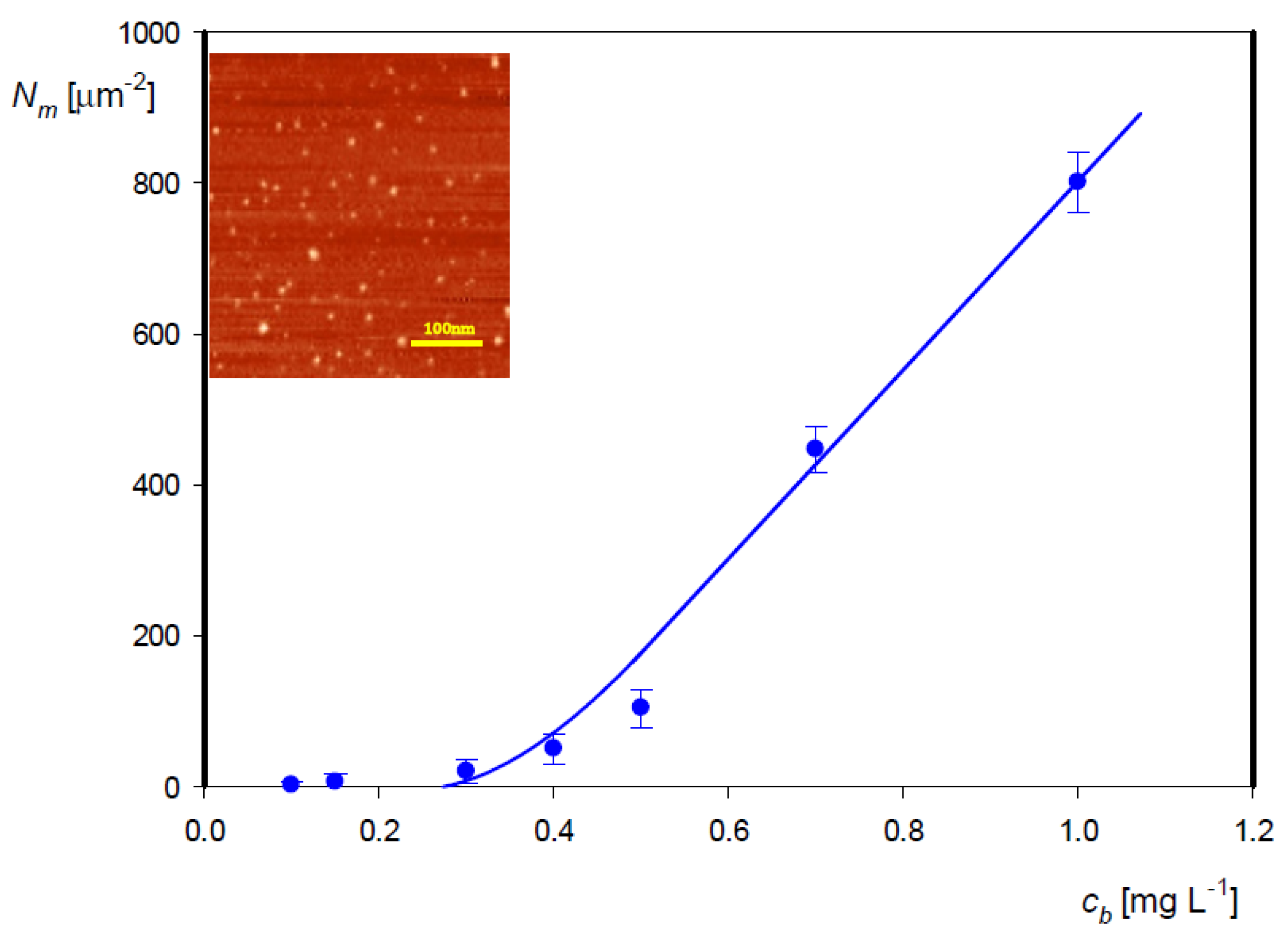
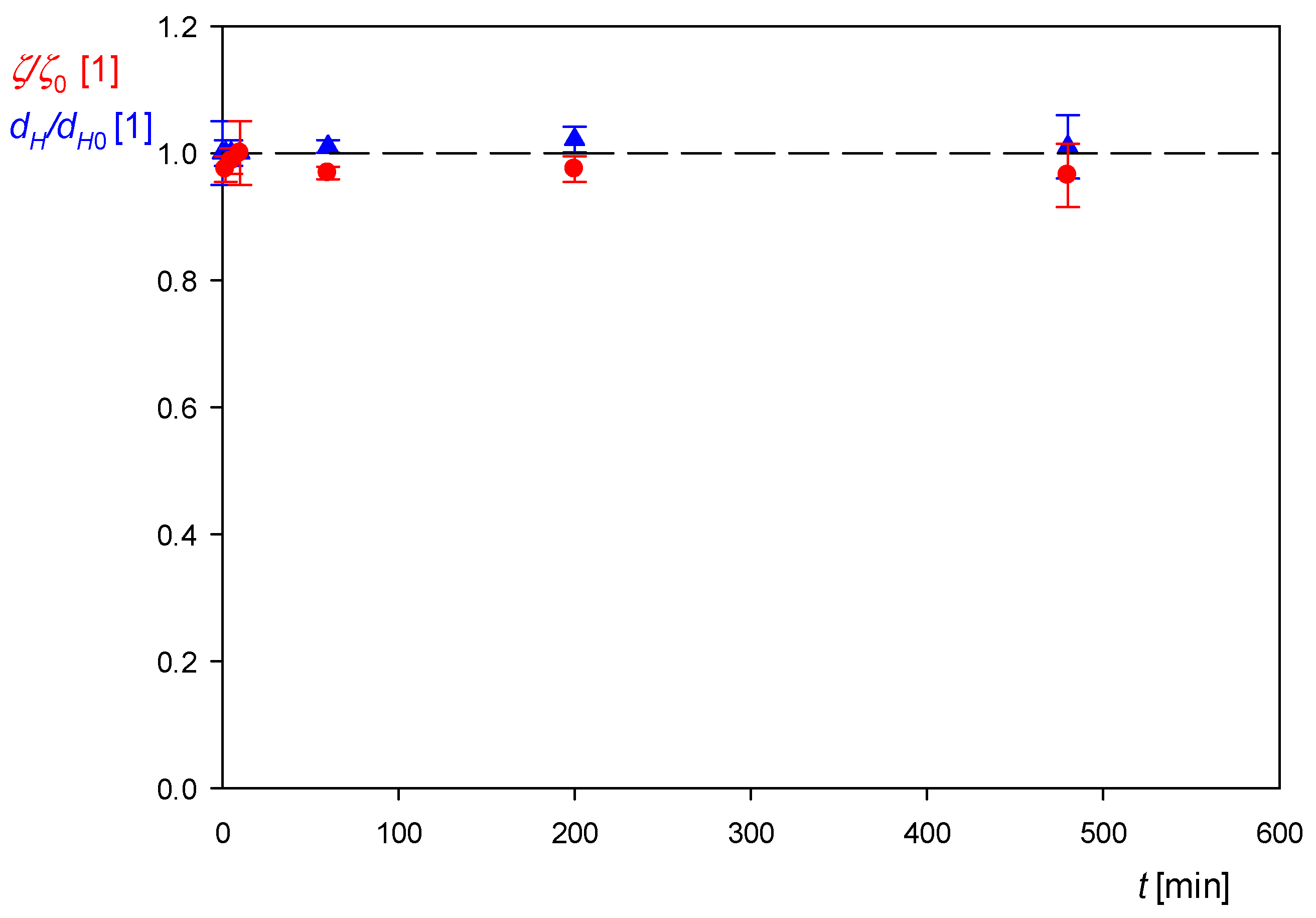
3.2. Formation of Myoglobin Corona
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cedervall, T.; Lynch, I.; Lindman, S.; Berggård, T.; Thulin, E.; Nilsson, H.; Dawson, K.A.; Linse, S. Understanding the Nanoparticle—Protein Corona Using Methods to Quantify Exchange Rates and Affinities of Proteins for Nanoparticles. Proc. Natl. Acad. Sci. USA 2007, 104, 2050–2055. [Google Scholar] [CrossRef]
- Monopoli, M.M.; Aberg, C.; Salvati, A.; Dawson, K.A. Biomolecular Coronas Provide the Biological Identity of Nanosized Materials. Nat. Nanotechnol. 2012, 7, 779–786. [Google Scholar] [CrossRef] [PubMed]
- Milani, S.; Bombelli, F.B.; Pitek, A.S.; Dawson, K.A.; Radler, J. Reversible Versus Irreversible Binding of Transferrin to Polystyrene Nanoparticles: Soft and Hard Coronas. ACS Nano 2012, 6, 2432–2541. [Google Scholar] [CrossRef] [PubMed]
- Truel, L.; Brandholt, S.; Maffre, P.; Wiegele, S.; Shang, L.; Nienhaus, G.U. Impact of Protein Modificationon the Protein Corona on Nanoparticles and Nanoparticle-Cell Interactions. ACS Nano 2014, 8, 503–513. [Google Scholar] [CrossRef]
- Winzen, S.; Schoettler, S.; Baier, G.; Rosenauer, C.; Mailaender, V.; Landfestera, K.; Mohr, K. Complementary Analysis of the Hard and Soft Protein Corona: Sample Preparation Critically Effects Corona Composition. Nanoscale 2015, 7, 2992–3001. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, G.; Daghighi, S.M.; Haririan, I.; Yousefi, I.; Raoufi, M.; Rezaee, F.; Dinarvand, R. Protein Corona Variation in Nanoparticles Revisited: A Dynamic Grouping Strategy. Colloids Surf. B Biointerfaces 2019, 179, 505–516. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Nattich-Rak, M.; Dąbkowska, M.; Kujda-Kruk, M. Albumin Adsorption at Solid Substrates: A Quest for a Unified Approach. J. Colloid Interface Sci. 2018, 514, 769–790. [Google Scholar] [CrossRef] [PubMed]
- Sofińska, K.; Adamczyk, Z.; Barbasz, J. Mechanism of Immunoglobulin G Adsorption on Polystyrene Microspheres. Colloids Surf. B Biointerfaces 2016, 137, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Dąbkowska, M.; Adamczyk, Z.; Cieśla, M.; Adamczak, M.; Bober, J. Lysozyme Monolayers at polymer Micoparticles: Electrokinetic Characteristics and Modeling. J. Phys. Chem. C 2018, 122, 17846–17855. [Google Scholar] [CrossRef]
- Evans, S.V.; Brayer, G.D. High—Resolution Study of the Three—Dimensional Structure of Horse Heart Metmyoglobin. J. Mol. Biol. 1990, 213, 885–897. [Google Scholar] [CrossRef]
- Wittenberg, B.A.; Wittenberg, J.B. Transport of Oxygen in Muscle. Annu. Rev. Physiol. 1989, 51, 857–878. [Google Scholar] [CrossRef] [PubMed]
- Brunori, M. Myoglobin Strikes Back. Protein Sci. 2010, 19, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Wahed, D.A. Clinical Chemistry, Immunology and Laboratory Quality Control: A Comprehensive Review for Board Preparation, Certification and Clinical Practice; Elsevier Inc.: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Glandières, J.M.; Calmettes, P.; Martel, P.; Zentz, C.; Massat, A.; Ramstein, J.; Alpert, B. Solvent—Induced Structural Distortions of Horse Metmyoglobin. Eur. J. Biochem. 1995, 227, 241–248. [Google Scholar] [CrossRef]
- Ibel, K.; Stuhrmann, H.B. Comparison of Neutron and X-ray Scattering of Dilute Myoglobin Solutions. J. Mol. Biol. 1975, 93, 255–265. [Google Scholar] [CrossRef]
- Nattich-Rak, M.; Pomorska, A.; Batys, P.; Adamczyk, Z. Adsorption Kinetic of Myoglobin on Mica and Silica—Role of Electrostatic Interactions. Colloids Surf. B Biointerfaces 2021, 198, 111436. [Google Scholar] [CrossRef] [PubMed]
- Bellezza, F.; Cipiciani, A.; Costantino, U.; Marmottini, F. Adsorption of Myoglobin onto Porous Zirconium Phosphate and Zirconium Benzenephosphonate Obtained with Template Synthesis. Langmuir 2006, 22, 5064–5069. [Google Scholar] [CrossRef]
- Bellezza, F.; Cipiciani, A.; Quotadamo, M.A.; Cinelli, S.; Onori, G.; Tacchi, S. Structure, Stability, and Activity of Myoglobin Adsorbed onto Phosphate—Grafted Zirconia Nanoparticles. Langmuir 2007, 23, 13007–13012. [Google Scholar] [CrossRef] [PubMed]
- Essa, H.; Magner, E.; Cooney, J.; Hodnett, B.K. Influence of pH and Ionic Strength on the Adsorption, Leaching and Activity of Myoglobin Immobilized onto Ordered Mesoporous Silicates. J. Mol. Catal. B Enzym. 2007, 49, 61–68. [Google Scholar] [CrossRef]
- Iafisco, M.; Palazzo, B.; Falini, G.; di Foggia, M.; Bonora, S.; Nicolis, S.; Casella, L.; Roveri, N. Adsorption and Conformational Change of Myoglobin on Biomimetic Hydroxyapatite Nanocrystals Functionalized with Alendronate. Langmuir 2008, 24, 4924–4930. [Google Scholar] [CrossRef] [PubMed]
- Bellezza, F.; Cipiciani, A.; Latterini, L.; Posati, T.; Sassi, P. Structure and Catalytic Behavior of Myoglobin Adsorbed onto Nanosized Hydrotalcites. Langmuir 2009, 25, 10918–10924. [Google Scholar] [CrossRef]
- Devineau, S.; Zanotti, J.M.; Loupiac, C.; Zargarian, L.; Neiers, F.; Pin, S.; Renault, J.P. Myoglobin on Silica: A Case Study of the Impact of Adsorption on Protein Structure and Dynamics. Langmuir 2013, 29, 13465–13472. [Google Scholar] [CrossRef]
- Lee, J.G.; Lanningan, K.; Shelton, W.A.; Meissner, J.; Bharti, B. Adsorption of Myoglobin and Corona Formation on Silca Nanoparticles. Langmuir 2020, 36, 14157–14165. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, Z. Protein Adsorption: A Quest for a Universal Mechanism. Curr. Opin. Colloid Interface Sci. 2019, 41, 50–65. [Google Scholar] [CrossRef]
- Ekiel-Jeżewska, M.L.; Adamczyk, Z.; Bławzdziewicz, J. Streaming Current and Effective ζ-Potential for Particle—Covered Surfaces with Random Particle Distributions. J. Phys. Chem. C 2019, 123, 3517–3531. [Google Scholar] [CrossRef]
- Nattich-Rak, M.; Sadowska, M.; Adamczyk, Z.; Cieśla, M.; Kąkol, M. Formation Mechanism of Human Serum Albumin Monolayers on Positively Charged Polymer Microparticles. Colloids Surf. B Biointerfaces 2017, 159, 929–936. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamczyk, Z.; Nattich-Rak, M. Formation of Myoglobin Corona at Polymer Microparticles. Colloids Interfaces 2021, 5, 27. https://doi.org/10.3390/colloids5020027
Adamczyk Z, Nattich-Rak M. Formation of Myoglobin Corona at Polymer Microparticles. Colloids and Interfaces. 2021; 5(2):27. https://doi.org/10.3390/colloids5020027
Chicago/Turabian StyleAdamczyk, Zbigniew, and Małgorzata Nattich-Rak. 2021. "Formation of Myoglobin Corona at Polymer Microparticles" Colloids and Interfaces 5, no. 2: 27. https://doi.org/10.3390/colloids5020027
APA StyleAdamczyk, Z., & Nattich-Rak, M. (2021). Formation of Myoglobin Corona at Polymer Microparticles. Colloids and Interfaces, 5(2), 27. https://doi.org/10.3390/colloids5020027