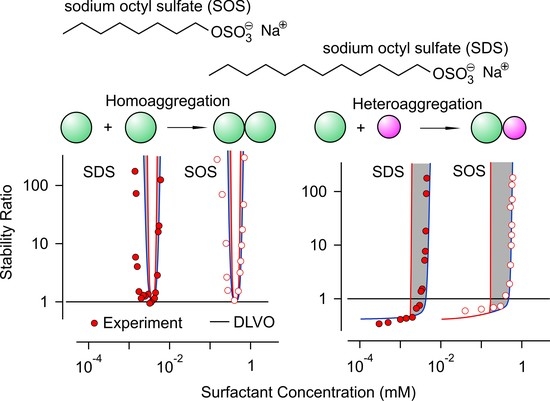
Heteroaggregation and Homoaggregation of Latex Particles in the Presence of Alkyl Sulfate Surfactants
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Electrophoresis
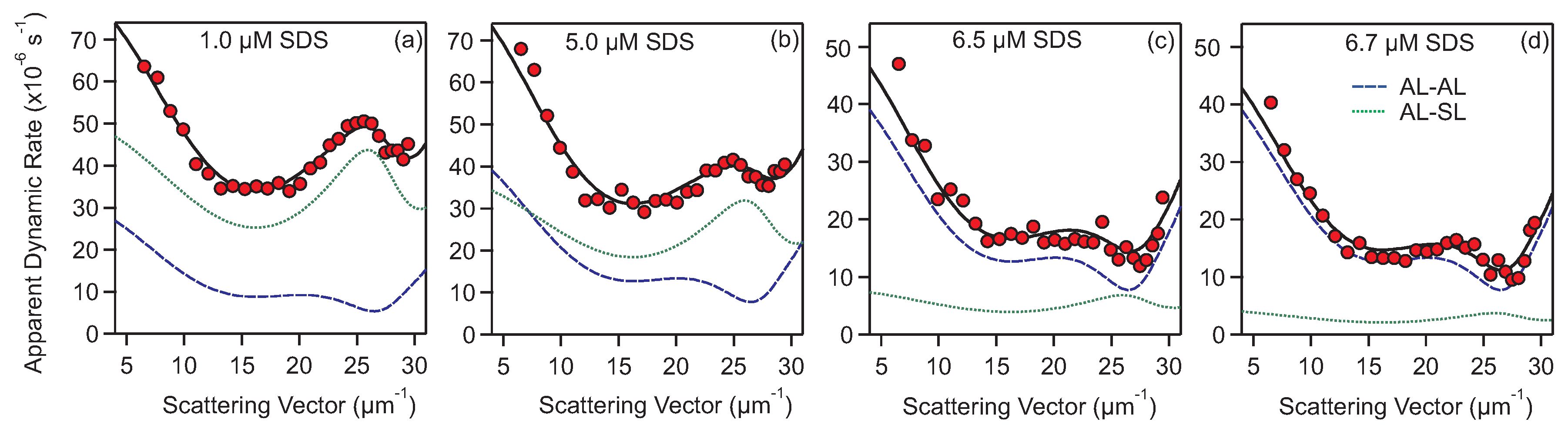
2.3. Measuring and Extracting Aggregation Rates
2.4. Calculating Aggregation Rates with DLVO Theory
3. Results and Discussion
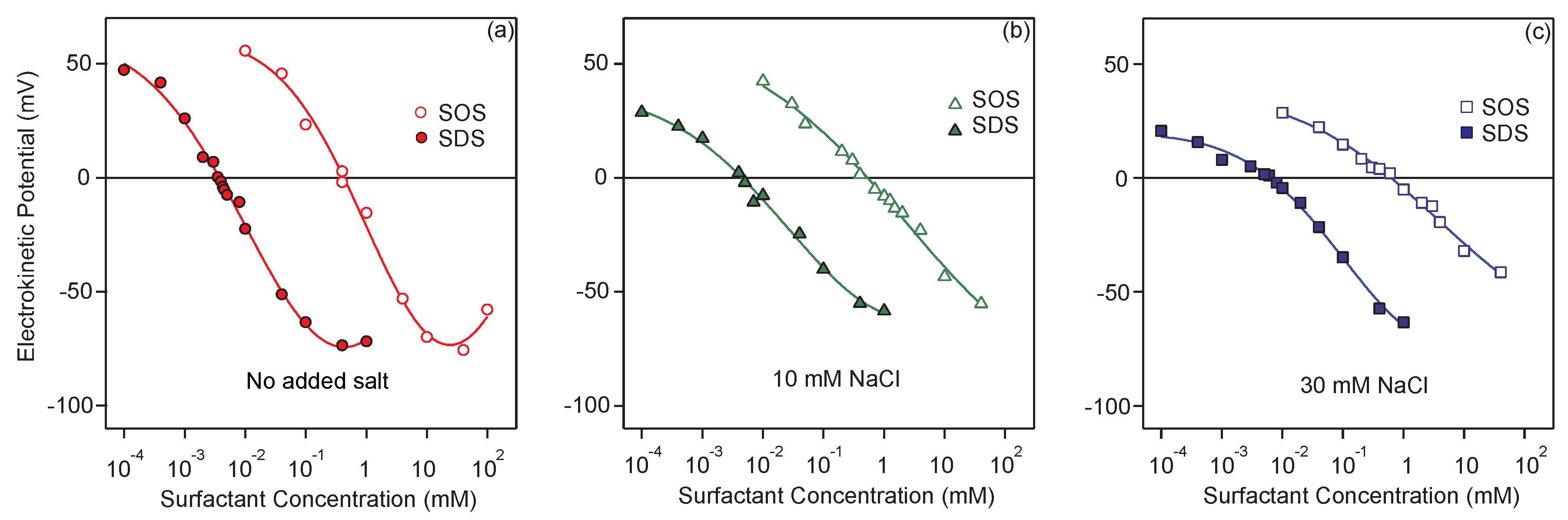
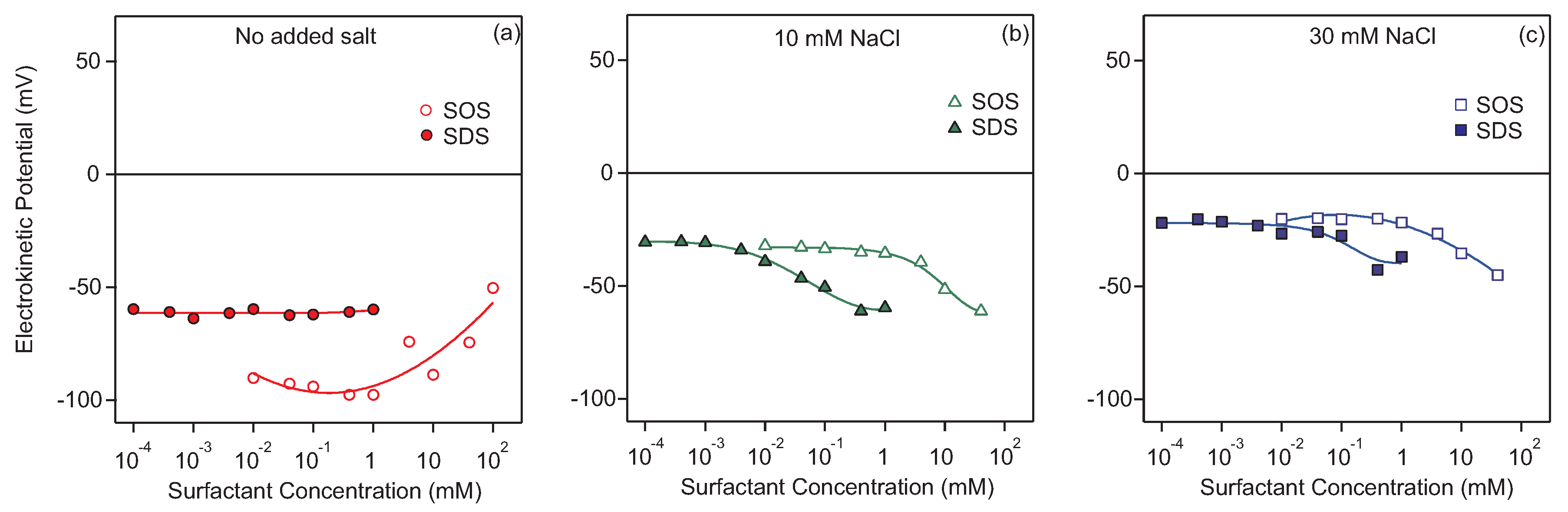
3.1. Charging of the Particles in the Presence of Surfactants
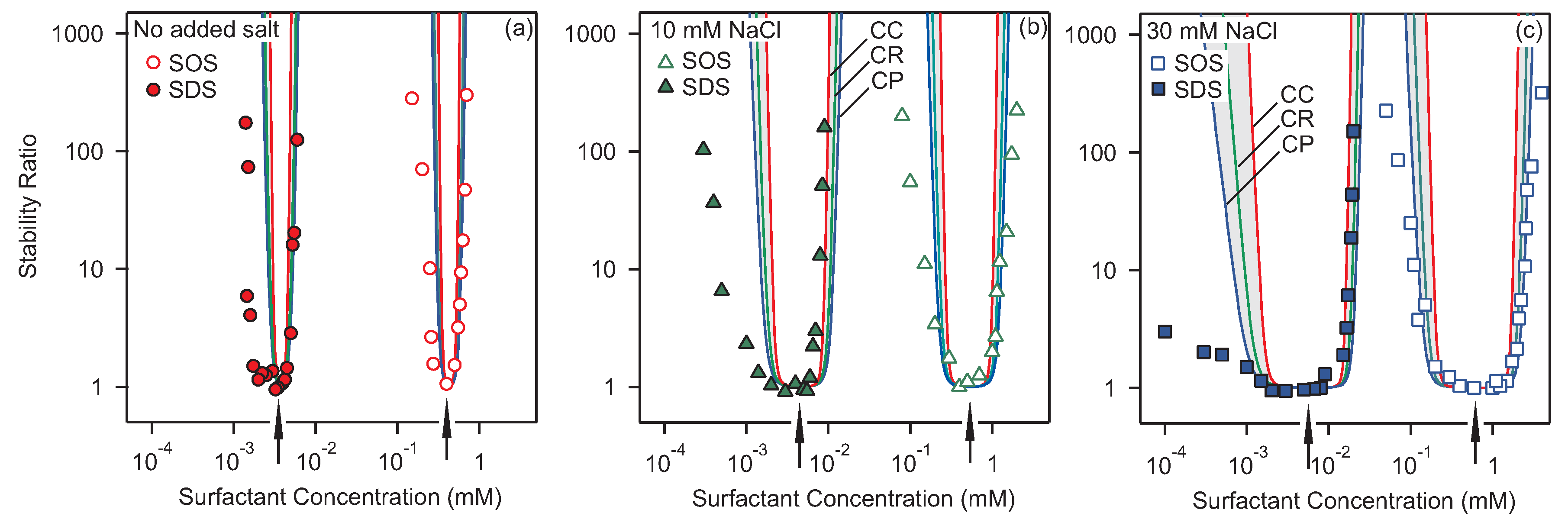
3.2. Homoaggregation
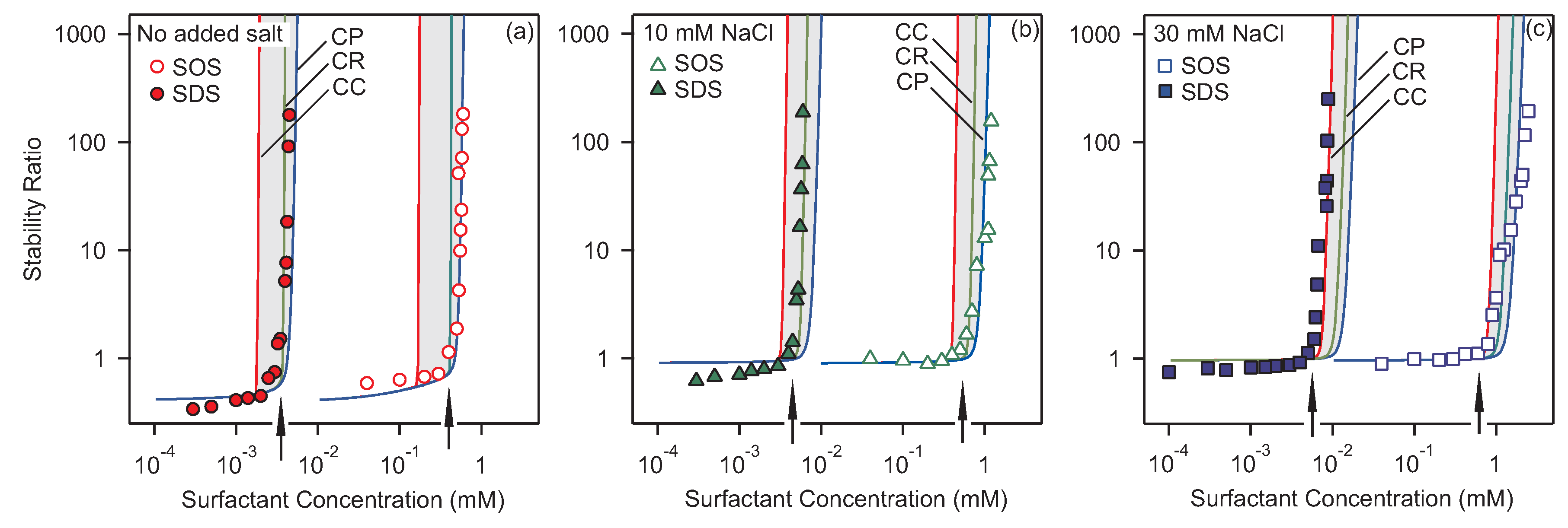
3.3. Heteroaggregation
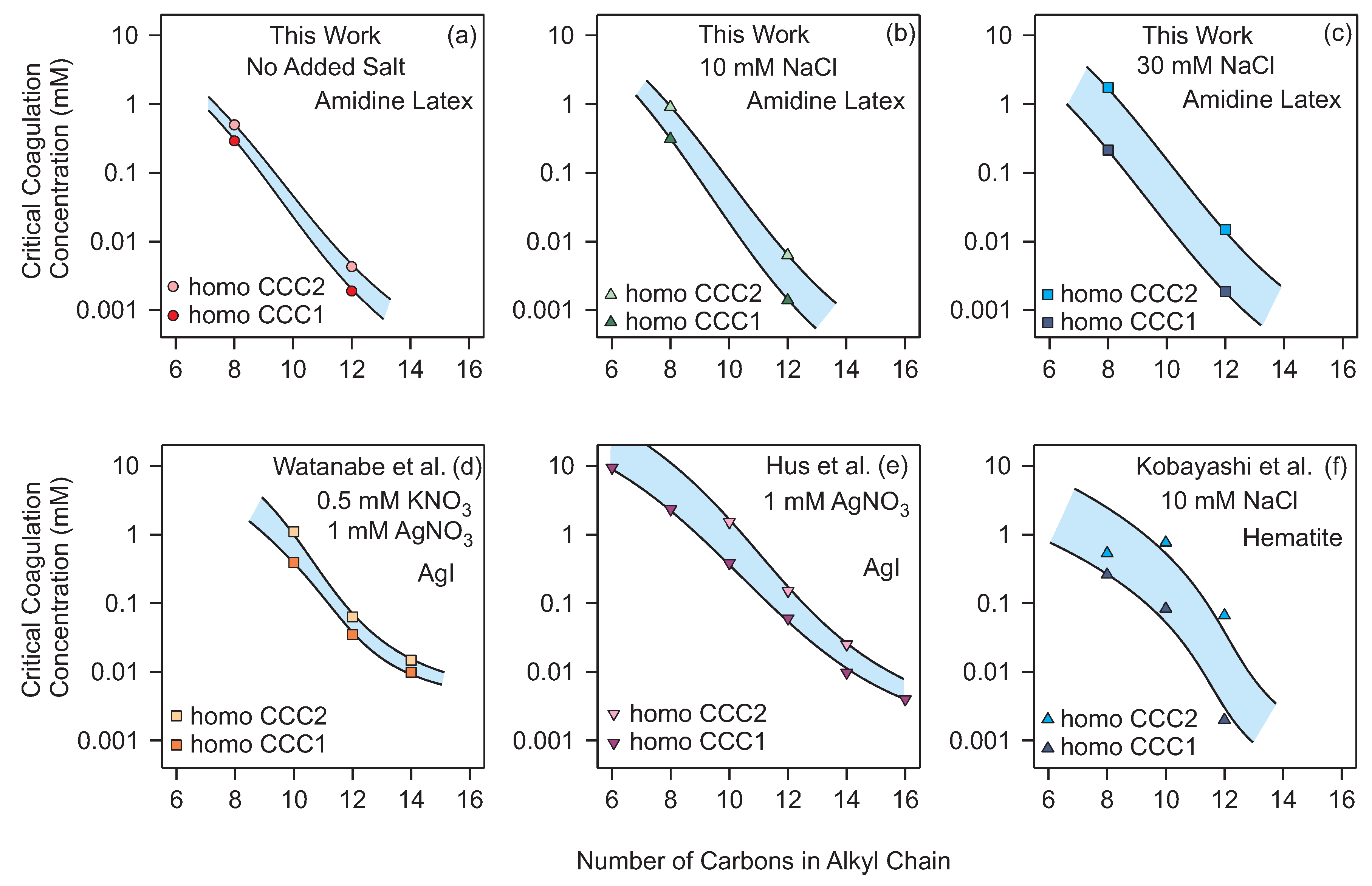
3.4. Critical Coagulation Concentration
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Balzer, B.; Hruschka, M.K.M.; Gauckler, L.J. Coagulation Kinetics and Mechanical Behavior of Wet Alumina Green Bodies Produced via DCC. J. Colloid Interface Sci. 1999, 216, 379–386. [Google Scholar] [CrossRef]
- Trefalt, G.; Tadić, B.; Kosec, M. Formation of Colloidal Assemblies in Suspensions for Pb(Mg1/3Nb2/3)O3 Synthesis: Monte Carlo Simulation Study. Soft Matter 2011, 7, 5566–5577. [Google Scholar] [CrossRef]
- Farrokhpay, S. A Review of Polymeric Dispersant Stabilisation of Titania Pigment. Adv. Colloid Interface Sci. 2009, 151, 24–32. [Google Scholar] [CrossRef]
- Volodkin, D.; Ball, V.; Schaaf, P.; Voegel, J.C.; Möhwald, H. Complexation of Phosphocholine Liposomes with Polylysine: Stabilization by Surface Coverage versus Aggregation. Biochim. Biophys. Acta 2007, 1768, 280–290. [Google Scholar] [CrossRef] [PubMed]
- Galletto, P.; Lin, W.; Borkovec, M. Measurement of Heteroaggregation Rate Constants by Simultaneous Static and Dynamic Light Scattering. Phys. Chem. Chem. Phys. 2005, 7, 1464–1471. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Kobayashi, M.; Skarba, M.; Mu, C.; Galletto, P.; Borkovec, M. Heteroaggregation in Binary Mixtures of Oppositely Charged Colloidal Particles. Langmuir 2006, 22, 1038–1047. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.; Sugimoto, T.; Szilagyi, I.; Trefalt, G.; Borkovec, M. Heteroaggregation of Oppositely Charged Particles in the Presence of Multivalent Ions. Phys. Chem. Chem. Phys. 2017, 19, 15160–15171. [Google Scholar] [CrossRef]
- Cao, T.; Trefalt, G.; Borkovec, M. Measuring Slow Heteroaggregation Rates in the Presence of Fast Homoaggregation. J. Colloid Interface Sci. 2020, 566, 143–152. [Google Scholar] [CrossRef]
- James, R.O.; Homola, A.; Healy, T.W. Heterocoagulation of Amphoteric Latex Colloids. J. Chem. Soc.-Faraday Trans. I 1977, 73, 1436–1445. [Google Scholar] [CrossRef]
- Kihira, H.; Matijevic, E. Kinetics of Heterocoagulation 3. Analysis of Effects Causing the Discrepancy between the Theory and Experiment. Langmuir 1992, 8, 2855–2862. [Google Scholar] [CrossRef]
- Imae, T.; Muto, K.; Ikeda, S. The pH Dependence of Dispersion of TiO2 Particles in Aqueous Surfactant Solutions. Colloid. Polym. Sci. 1991, 269, 43–48. [Google Scholar] [CrossRef]
- Liang, L.; Morgan, J.J. Chemical Aspects of Iron-Oxide Coagulation in Water: Laboratory Studies and Implications for Natural Systems. Aquat. Sci. 1990, 52, 32–55. [Google Scholar] [CrossRef]
- Watanabe, A. Physico-Chemical Studies on Surface Active Agents. 2. The Coagulation of Positive Silver Iodide Sols by Anionic Surface Active Agents. Bull. Inst. Chem. Res. Kyoto Univ. 1960, 38, 179–215. [Google Scholar]
- Hus, M.; Knitel, J.; Herak, M.J. The Influence of Sodium-n-Alkyl Sulphates on Positively and Negatively Charged AgI Systems. Colloid. Polym. Sci. 1978, 256, 487–489. [Google Scholar] [CrossRef]
- Kobayashi, M.; Yuki, S.; Adachi, Y. Effect of Anionic Surfactants on the Stability Ratio and Electrophoretic Mobility of Colloidal Hematite Particles. Colloids Surf. A 2016, 510, 190–197. [Google Scholar] [CrossRef]
- Koopal, L.K.; Goloub, T.; de Keizer, A.; Sidorova, M.P. The Effect of Cationic Surfactants on Wetting, Colloid Stability and Flotation of Silica. Colloids Surf. A 1999, 151, 15–25. [Google Scholar] [CrossRef]
- Hakim, A.; Kobayashi, M. Charging, Aggregation, and Aggregate Strength of Humic Substances in the Presence of Cationic Surfactants: Effects of Humic Substances Hydrophobicity and Surfactant Tail Length. Colloids Surf., A 2019, 577, 175–184. [Google Scholar] [CrossRef]
- Ottewill, R.H.; Rastogi, M.C. The Stability of Hydrophobic Sols in the Presence of Surface-Active Agents 2. The Stability of Silver Iodide Sols in the Presence of Cationic Surface-Active Agents. Trans. Faraday Soc. 1960, 56, 866–879. [Google Scholar] [CrossRef]
- Ottewill, R.H.; Rastogi, M.C. The Stability of Hydrophobic Sols in the Presence of Surface-Active Agents 3. An Examination by Microelectrophoresis of the Behaviour of Silver Iodide Sols in the Presence of Cationic Surface-Active Agents. Trans. Faraday Soc. 1960, 56, 880–892. [Google Scholar] [CrossRef]
- Oncsik, T.; Desert, A.; Trefalt, G.; Borkovec, M.; Szilagyi, I. Charging and Aggregation of Latex Particles in Aqueous Solutions of Ionic Liquids: Towards an Extended Hofmeister Series. Phys. Chem. Chem. Phys. 2016, 18, 7511–7520. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L.D. Theory of the Stability of Strongly Charged Lyophobic Sols and of the Adhesion of Strongly Charged Particles in Solutions of Electrolytes. Acta Physicochim: USSR 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Cao, T.; Trefalt, G.; Borkovec, M. Aggregation of Colloidal Particles in the Presence of Hydrophobic Anions: Importance of Attractive Non-DLVO Forces. Langmuir 2018, 34, 14368–14377. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, R.W.; White, L.R. Electrophoretic Mobility of a Spherical Colloidal Particle. J. Chem. Soc.-Faraday Trans. I 1978, 74, 1607–1626. [Google Scholar] [CrossRef]
- Holthoff, H.; Egelhaaf, S.U.; Borkovec, M.; Schurtenberger, P.; Sticher, H. Coagulation Rate Measurements of Colloidal Particles by Simultaneous Static and Dynamic Light Scattering. Langmuir 1996, 12, 5541–5549. [Google Scholar] [CrossRef]
- Elimelech, M.; Gregory, J.; Jia, X.; Williams, R.A. Particle Deposition and Aggregation: Measurement, Modeling, and Simulation; Butterworth-Heinemann Ltd.: Oxford, UK, 1995. [Google Scholar]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Trefalt, G.; Behrens, S.H.; Borkovec, M. Charge Regulation in the Electrical Double Layer: Ion Adsorption and Surface Interactions. Langmuir 2016, 32, 380–400. [Google Scholar] [CrossRef] [PubMed]
- Honig, E.P.; Roebersen, G.J.; Wiersema, P.H. Effect of Hydrodynamic Interaction on Coagulation Rate of Hydrophobic Colloids. J. Colloid Interface Sci. 1971, 36, 97–102. [Google Scholar] [CrossRef]
- Hiemstra, T.; van Riemsdijk, W.H. Effect of Different Crystal Faces on Experimental Interaction Force and Aggregation of Hematite. Langmuir 1999, 15, 8045–8051. [Google Scholar] [CrossRef]
- Schudel, M.; Behrens, S.H.; Holthoff, H.; Kretzschmar, R.; Borkovec, M. Absolute Aggregation Rate Constants of Hematite Particles in Aqueous Suspensions: A Comparison of Two Different Surface Morphologies. J. Colloid Interface Sci. 1997, 196, 241–253. [Google Scholar] [CrossRef]
- Lin, W.; Galletto, P.; Borkovec, M. Charging and Aggregation of Latex Particles by Oppositely Charged Dendrimers. Langmuir 2004, 20, 7465–7473. [Google Scholar] [CrossRef]
- Puertas, A.M.; Maroto, J.A.; Fernandez-Barbero, A.; de las Nieves, F.J. On the Kinetics of Heteroaggregation versus Electrolyte Concentration: Comparison between Simulation and Experiment. Colloids Surf. A 1999, 151, 473–481. [Google Scholar] [CrossRef]
- Trefalt, G.; Ruiz-Cabello, F.J.M.; Borkovec, M. Interaction Forces, Heteroaggregation, and Deposition Involving Charged Colloidal Particles. J. Phys. Chem. B 2014, 118, 6346–6355. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, T.; Borkovec, M.; Trefalt, G. Heteroaggregation and Homoaggregation of Latex Particles in the Presence of Alkyl Sulfate Surfactants. Colloids Interfaces 2020, 4, 52. https://doi.org/10.3390/colloids4040052
Cao T, Borkovec M, Trefalt G. Heteroaggregation and Homoaggregation of Latex Particles in the Presence of Alkyl Sulfate Surfactants. Colloids and Interfaces. 2020; 4(4):52. https://doi.org/10.3390/colloids4040052
Chicago/Turabian StyleCao, Tianchi, Michal Borkovec, and Gregor Trefalt. 2020. "Heteroaggregation and Homoaggregation of Latex Particles in the Presence of Alkyl Sulfate Surfactants" Colloids and Interfaces 4, no. 4: 52. https://doi.org/10.3390/colloids4040052
APA StyleCao, T., Borkovec, M., & Trefalt, G. (2020). Heteroaggregation and Homoaggregation of Latex Particles in the Presence of Alkyl Sulfate Surfactants. Colloids and Interfaces, 4(4), 52. https://doi.org/10.3390/colloids4040052