Abstract
The flower of Strelitzia reginae generates abundant and viscous mucilage as exudate, which is purified in periods of heating–cooling, and finally precipitated with ethanol, obtaining strelitzia gum (StrG). By means of intrinsic viscosity measurement, the viscometric molecular weight (MWv) is determined, with a value of 200,000 g/mol, as well as a hydrodynamic radius of 20 ± 1 nm and a hydration value of 445 ± 34 g/g. The size of StrG was compared against dynamic light scattering data with a value of 16 ± 2 nm and a MWDLS of 230,000 g/mol. StrG is a biopolyelectrolyte with an “a” value of 0.85, which corresponds to a flexible behavior with a great effect of volume exclusion. This statement is based on the difficulty of gum dissolution, that should be performed at 80 °C. This macromolecule is very promising and can potentially be used in several industrial applications, such as in film forming, and as a gel, thickener, and coemulsifier.
1. Introduction
The flower of the bird of paradise, Strelitzia reginae, is an herbaceous, rhizomatous angiosperm native to South Africa that grows in gardens in tropical and subtropical regions. An herbaceous plant, it has the shape of a bush, leaves with long petioles, an average height of 1.5 m, and a diameter of 1.8 m. Its leaves are alternate and distichous. Its flowers are hermaphroditic and asymmetrical, pollinated by birds, in the group zinciniform, and protected primarily by several lateral large bracts. They often have long peduncles. The perianth is formed by six tepals distributed in two groups, with three external equal and free tepals, and the other three unequal and generally welded, one of which has larger dimensions and is folded in the shape of an arrow surrounding the style. The gynoecium presents three welded carpels, and the ovary is infernal, trilocular, and with numerous seminal primordiums [1,2,3,4,5,6]. The fruit is a valvicidate capsule that opens by three valves. It needs intense light, for example, three or four hours a day of direct sunlight, and the flower does not bloom with inadequate light. During the period of active growth, it can be grown under normal conditions, requiring moderate irrigation and normal humidity. Between March and October, it requires large quantities of water, as well as a complete fertilizer solution every week. The flower generates abundant, very viscous mucilage as exudate, which is accentuated with humidity and rain. It can be collected, and the plant uses it as a defense against any disease or insect attack [7,8,9].
The flower of the bird of paradise, Strelitzia reginae, produces nectar and mucilage, harvested at different stages of development, where the production of nectar is obtained from the floret, and the production of mucilage minimizes the growth of post-harvest mold. The collected mucilage was a highly branched glucan–galactan or mannan with uronic acid residues. The glucomannan was possibly composed by mannan and galactan sidechains, and terminal arabinose and galactose residues [10].
The nature of the mucilage, precipitated with ethanol, indicates a potential (1–4) backbone of glucan and mannan branched at 3 position. Side branches of galactan (1–3) and mannan (1–2) had terminal arabinose and galactose residues [10].
In this work, we will study the mucilage obtained from the flower of Strelitzia reginae, which we purified to obtain strelitzia gum (StrG). On StrG, we will perform physicochemical studies in an aqueous solution using viscosity, density, and dynamic light scattering measurements. Also, we will obtain Mark–Houwink parameters from intrinsic viscosity measurements, from which we will determine the molecular weight and the hydrodynamic parameters of StrG.
Intrinsic Viscosity and Hydrodynamic Parameters
The viscosity of a capillary viscometer can be calculated from the following equation:
where η is viscosity (poise), A is viscometer constant, ρ is viscosity (g/cm3), and t is drainage time (s).
It should also be remembered that
where the subindex “s” indicates “solution” and “0” indicates “solvent” in viscosity and density.
The IUPAC term of “specific viscosity”, can be calculated as follows:
When dilute concentrations are used, it is better to start with the first term of the Huggins equation “ηsp/c”.
In Huggins’ method [11], intrinsic viscosity, [η], is defined as the ratio of the increase in relative viscosity (ηsp) to concentration (c, in g/cm3), when it tends to zero.
Martin’s method [12] is used:
Tanglertpaibul and Rao [13,14,15] used the following equations to obtain the intrinsic viscosity:
The intrinsic viscosity is obtained from the slope.
Mark [16] and Houwink [17], M-H, independently correlated the intrinsic viscosity with molecular weight, and this equation is applicable to many polymers and biopolymers, and is used to determine molecular weight. The k and a parameters both vary with the nature of the polymer, temperature, and solvents [18]. The calculation of M-H parameters [18,19] is carried out by the plot representation of the following equation:
The exponent a is a function of polymer geometry, and varies from 0.5 to 2.0. These constants can be determined experimentally by measuring the intrinsic viscosity of several polymer samples for which the molecular weight has been determined by an independent method (e.g., osmotic pressure or light scattering) [20].
The M-H exponent bears the signature of a polymer chain’s three-dimensional configuration in the solvent environment: a values from 0 reflect a rigid sphere in an ideal solvent; those from 0.5–0.8 a random coil in a good solvent; and from 0.8–2.0 a rigid or rod like configuration (stiff chain) [20,21].
The hydrodynamic radius (RH) is given by the Einstein relation [22],
The term f/f0 is sometimes denoted as P is called the Perrin number, where f is the friction coefficient expression.
A similar combination involves intrinsic viscosity and specific volume:
ν(a/b) is called the Einstein viscosity increment, and Vs is specific volume (cm3/g) [23].
The corresponding value of “hydration” of the molecule, δ, is defined by,
And,
where is the partial specific volume, and ρ0 is the density of the solvent (distilled water).
These mathematical approximations are used to calculate hydrodynamic properties, and calculations should be treated with great caution [24,25].
2. Materials and Methods
2.1. Strelitzia Gum
Mucilage was collected with a syringe from the flowers of Strelitzia reginae in the city of Lincoln, Buenos Aires, Argentina in January 2018 (see Figure 1). To dissolve this exudate, heating–cooling periods were conducted by agitation in periods of 2 h per day for 8 h at 80 and 20 °C, respectively. Once dissolved, the mucilage was filtered and precipitated with ethanol several times, thus obtaining StrG. Finally, the obtained product was dried at 60 °C for 24 h, and then redissolved in distilled water at a concentration of 0.5364 wt %.

Figure 1.
Strelitzia reginae flower and mucilage.
Acid hydrolysis was conducted to obtain different molecular weights. The following concentrations of 0.05, 0.01, 0.025, and 0.05 M HCl were used at 70 °C for 1 h. Each sample is then cooled and macerated for 12 h. Then, the sample is precipitated with ethanol in a ratio with the hydrolyzed solution of 70:30 (v:v). This procedure is repeated with ethanol until satisfactory purification of each of the obtained gums is achieved.
2.2. Viscosity and Density
Measurements were taken from fresh strelitzia gum in aqueous solutions of 0.01 and 0.2 wt %. with 0.1 M KCl. Solutions and dissolutions were prepared with deionized water. The different temperatures were maintained using a thermostatic bath (HAAKE C). Determinations were done using an Ubbelohde “suspended level” viscometer (IVA 1), with a water draining time of 34.91 s. The density of each solution was measured using an Anton Paar DMA35N densimeter (Graz, Austria).
2.3. Dynamic Light Scattering
A 0.1 wt % solution of StrG with 0.1 M KCl was prepared and then centrifuged at 10,000 rpm for 5 min to remove the larger aggregates. The solution was then placed in the cell of the equipment (Delsa Nano C, Beckman Coulter, Brea, CA, USA) and a monochromatic light beam of a laser diode with a wavelength of 658 nm and a dispersion angle of 165° was made [26,27,28].
The diffusion coefficient is calculated according to particle size, as per the following equation:
where D is diffusion coefficient (cm2/s), kB is Boltzmann constant, T temperature at 298 K, η is solution viscosity in poise, and RHDLS is hydrodynamic radius for DLS technique.
The MWDLS is calculated according to the following Mark–Houwink–Kuhn–Sakurada [29,30,31] (MHKS) equation:
where KD is a constant and ε is an exponent of MHKS that define the shape of the macromolecule.
3. Results & Discussion
was calculated from the studies of density vs. concentration (Figure 2) to provide a value that is consistent with other macromolecules. From the viscosity–density data as a function of the concentration, the intrinsic viscosity is determined by the Huggins method (see Figure 3), considered to be the standard against which the other methods are compared. It should be noted that the Huggins method is the one with a smaller R2. The Huggins equation is used as a standard for intrinsic viscosity calculus. It is of note that the kH measured in this work has a positive slope, since many other polysaccharides present the opposite value, especially if the ionic strength of the polyelectrolyte solution is inadequate or without the addition of salts. To substantiate this situation, it can be stated that the aqueous solvent is ideal for this macromolecule, and may indicate a special feature of this biopolyelectrolyte.
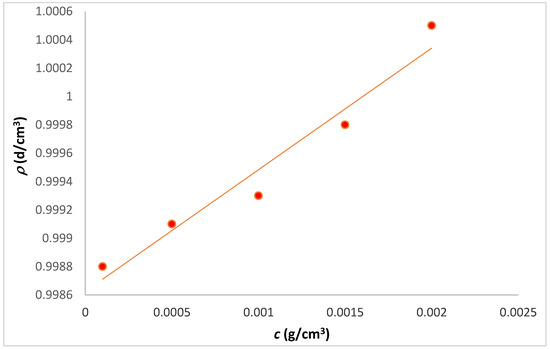
Figure 2.
Density in function of concentration (ρ vs. c).
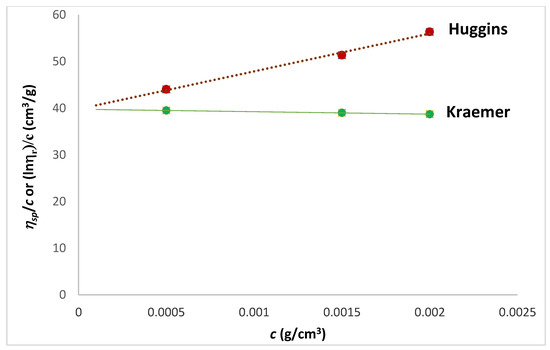
Figure 3.
Huggins and Kraemer’s plots. Huggins is ηsp/c vs. c, and Kraemer is (ln ηr)/c.
Regarding the comparative study of the data obtained from each of the methods used, the one that best fits is the Martin method (Figure 4), a little more closely than the Tanglertpeibul & Rao-a, T-R-a (Figure 5a). In some cases, the Kraemer method is more accurate. As in this case, an average of both (Huggins and Kraemer) can be calculated, which approximates the standard value, but is still far from a percentage error that is more consistent and less than 5% (see Table 1). It should be noted that the largest error in the intrinsic viscosity measurement is obtained by the T-R-a, b, and c methods (Figure 5a–c). While all methods are suitable for determining intrinsic viscosity, it should be noted that the most comparable is Martin’s and Kraemer’s with respect to Huggins.
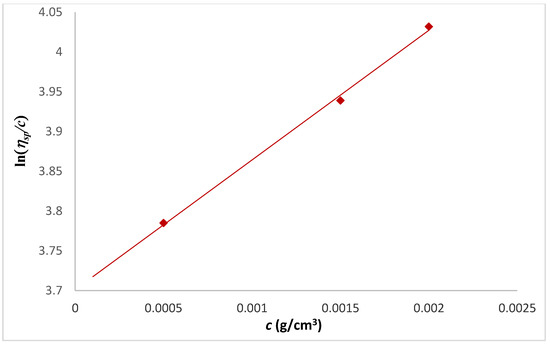
Figure 4.
Martin’s plots, ln ηsp/c vs. c.
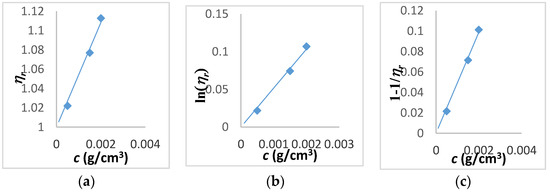
Figure 5.
Tanglertpaibul & Rao plots for (a–c) equations. Where (a) is ηr vs. c, (b) is ln ηr vs. c, and (c) is 1 − 1/ηr vs. c.

Table 1.
Intrinsic viscosity by different methods.
The hydrodynamic properties of StrG can be seen in Table 2, and are determined at 21 °C. The value of P is 1.63 and ν(a/b) with 11.47, with a RHv of 20 ± 1 nm, and RHDLS is 16 ± 2 nm; see Figure 6. The value of δ is very high, as expected; a similar phenomenon is observed in gel formation or sponge hydration.

Table 2.
Mark–Houwink and hydrodynamic parameters.
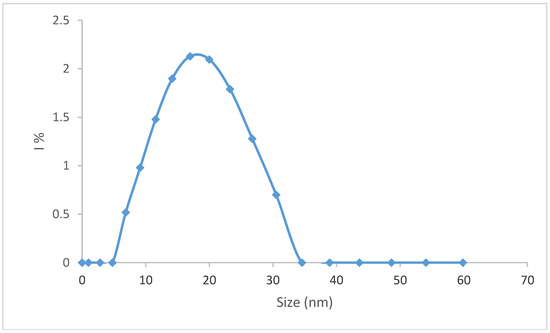
Figure 6.
Plot obtained in the DLS analysis (I% vs. Size), media is RHDLS.
In order to corroborate the data obtained from the viscosimetry, DLS measurements of StrG and its hydrolysates were conducted (see Figure 6).
The a and ε parameters, obtained from different hydrolysis of the original gum at 70 °C was satisfactorily performed, and from these data, Figure 7 and Figure 8 were made.
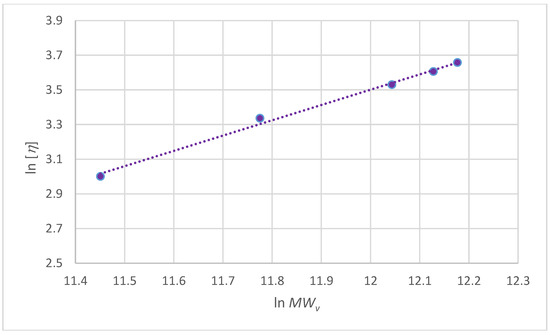
Figure 7.
Plot of ln [η] vs. ln MWv. R2 = 0.9901.
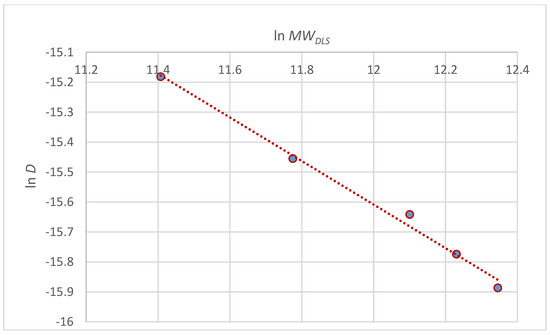
Figure 8.
Plot of ln D vs. ln MWDLS. R2 = 0.9925.
The Mark–Houwink parameters vary with the dissolvent, ionic strength, and temperature. This is because the hydrodynamic radius of the macromolecules changes with the type of solution and with temperature, through changes in chain flexibility. The viscometric molecular weight determined for this work is 200,000 g/mol, and by MWDLS is 230,000 g/mol, with an intrinsic viscosity by Huggins method of 38 ± 0.3 cm3/g, and M-H parameters with values of “a” 0.85 and “k” 0.00124 cm3/g (see Figure 7 and Table 3). In order to corroborate the viscometric values, DLS measurements were carried out to measure the MWDLS of this StrG, which for MHKS meters is for KD of 0.001323 and ε of 0.75 (see Figure 8 and Table 3). The MWDLS differs substantially with the MWV, though it is worth keeping in mind that any measurement by viscosimetry is apparent or doubtful. These types of differences in the determination of MW can be seen and justified in reference [32].

Table 3.
Data of D, molecular weight (DLS and viscometric), and intrinsic viscosity of hydrolyzed StrG.
The structure of monosaccharides and the way in which they are linked together [10] may vary, and since there are no reference physicochemical parameters or similar structural values, it is impossible to compare them with bibliographic data. What is very clear is that to a molecule which is a semirigid biopolyelectrolyte; clarifying this is only valid for the treatment carried out in the extraction and purification performed in this work. The Mark–Houwink value of “a” confirms that for these conditions. These empirical functions can be used to optimize the calculation of these hydrodynamic parameters in a suitable and acceptable way.
4. Conclusions
Regarding the procedure conducted for the extraction and purification of mucilage to obtain strelitzia gum, it is confirmed that, in aqueous solution, it is a biopolyelectrolyte with an “a” value of 0.85, which corresponds to a semirigid behavior with great effect of volume excluded. This statement is based on the difficulty of gum dissolution that should be performed at 80 °C. Regarding the intrinsic viscosity measurement, Martin’s method is the closest to Huggins, which is considered the reference method. Furthermore, it can be concluded that 0.1 M KCl solution is an ideal solvent for StrG, confirmed by the Huggins constant, which acquires a positive value and, therefore, a macromolecule with very particular characteristics, and is very much related to its biopolyelectrolyte characteristic.
Funding
This research received no external funding.
Acknowledgments
The author thanks Universidad Nacional de San Luis, Instituto de Física Aplicada (INFAP-CONICET) and Laboratorio de Investigación y Servicios de Química Física (LISeQF-UNSL). The UNSL projects 2-1712, 2-2414, 2-1916, and 2-2918: “Extraction and Characterization of natural Polysaccharides with potential use in Biotechnology” for their financial support. Rolando Curvale for their valuable contributions.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
| Symbol | Name | Units |
| η | viscosity | poise |
| t | time drainage | s |
| t0 | solvent drainage time | s |
| ts | solution drainage time | s |
| A | viscometer constant | cm2/s2 |
| ρ | density | g/cm3 |
| ρ0 | solvent density | g/cm3 |
| ρs | solution density | g/cm3 |
| ηs | solution viscosity | poise |
| T | temperature | K |
| ηr | relative viscosity | dimensionless |
| ηsp | specific viscosity | dimensionless |
| c | solution concentration | g/cm3 |
| [η] | intrinsic viscosity | cm3/g |
| kH | Huggins constant | dimensionless |
| kk | Kraemer’s constant | dimensionless |
| kM | Martin’s constant | dimensionless |
| MWv | viscometer molecular weight | g/mol |
| a | “a” Mark–Houwink parameter | dimensionless |
| k | “k” Mark–Houwink parameter | cm3/g |
| NA | Avogadro’s number | 1/mol |
| RHv | viscometer hydrodynamic radius | cm or nm |
| f | solution friction coefficient | poise |
| f0 | solvent friction coefficient | poise |
| P | Perrin number | dimensionless |
| νa/b | Einstein viscosity increment | dimensionless |
| partial specific volume | cm3/g | |
| Vs | volume specific | cm3/g |
| δ | hydration value | g/g |
| D | diffusion coefficient | cm2/g |
| RHDLS | DLS hydrodynamic radius | cm or nm |
| MWDLS | DLS molecular weight | g/mol |
References and Notes
- Odriozola Azurmendi, J.M.; García, J.A. El Cultivo de la Strelitzia; Hojas Divulgadoras del Ministerio de Agricultura: Madrid, España, 1972. [Google Scholar]
- Kronestedt, E.; Walles, B. Anatomy of the Sirelirzia reginae flower (Strelitziaceae). Nord. J. Bot. 1986, 6, 307–320. [Google Scholar] [CrossRef]
- Bayogan, E.R.; Teeranuch Jaroenkit, V.; Paull, R.E. Postharvest life of Bird-of-Paradise inflorescences. Posth. Biol. Technol. 2008, 48, 259–263. [Google Scholar] [CrossRef]
- Ribeiro da Silva Vieira, M.; Cleuma de Medeiros, D.; Nepomuceno Costa, P.; Guimarães Santos, C.M.; de Alencar Paes, R.; de Sousa Fernandez, L.M.; de Oliveira, N.G.; Flavio Silva, A.A. Effect of refrigeration on post-harvest flowers. Afr. J. Biotechnol. 2012, 11, 13065–13068. [Google Scholar] [CrossRef]
- Barbosa, J.G.; Mantovani Alvarenga, E.; Cunha Fernandes Dos Santos Dias, D.; Nunes Vieira, A. Effect of Acid Scarification and Different Temperatures on Physiological Quality of Strelitzia reginae Seeds. Parte da Dissertação de Mestrado do último autor, apresentada à Universidade Federal de Viçosa (UFV). Rev. Bras. Sementes 2005, 27, 71–77. [Google Scholar] [CrossRef]
- Mele, E.; Girardo, S.; Pisignano, D. Strelitzia reginae Leaf as a Natural Template for Anisotropic Wetting and Superhydrophobicity. Langmuir 2012, 28, 5312–5317. [Google Scholar] [CrossRef] [PubMed]
- Martin, F.W. The stigmatic exúdate of Strelitzia. Phyton. Buenos Aires 1970, 27, 47–53. [Google Scholar]
- Kronestedt-Robards, E.C.; Greger, M.; Robards, A.W. The nectar of the Strelitzia reginae flower. Physiol. Plant. 1989, 77, 341–346. [Google Scholar] [CrossRef]
- Kronestedt, E.C.; Robards, A.W. Sugar Secretion from the Nectary of Strelitzia: An Ultrastructural and Physiological Study. Protoplasma 1987, 137, 168–182. [Google Scholar] [CrossRef]
- Jaroenkit, T.; Chen, N.J.; Paull, R.E. Nectar secretion, mucilage production and mold growth on bird-of-paradise inflorescences. Posth. Biol. Technol. 2008, 49, 431–435. [Google Scholar] [CrossRef]
- Huggins, M.L. The viscosity of dilute solutions of long-chain molecules. IV. Dependence on concentration. J. Am. Chem. Soc. 1942, 64, 2716–2718. [Google Scholar] [CrossRef]
- Martin, A.F. Abstr. 103rd Am. Chem. Soc. Meeting, Memphis, TN, USA, April 20–24, 1942; p. 1-c ACS.
- Tanglertpaibul, T.; Rao, M.A. Intrinsic viscosity of tomato serum as affected by methods of determination and methods of processing concentrates. J. Food Sci. 1987, 52, 1642–1688. [Google Scholar] [CrossRef]
- Higiro, J.; Herald, T.J.; Alavi, S. Rheological study of xanthan and locust bean gum interaction in dilute solution. Food Res. Int. 2006, 39, 165–175. [Google Scholar] [CrossRef]
- Higiro, J.; Herald, T.J.; Alavi, S.; Bean, S. Rheological study of xanthan and locust bean gum interaction in dilute solution: Effect of salt. Food Res. Int. 2007, 40, 435–447. [Google Scholar] [CrossRef]
- Mark, H. Der Feste Körper; Sänger, R., Ed.; Hirzel, Switzerland; Leipzig, Germany, 1938; pp. 65–104. [Google Scholar]
- Houwink, R. Zusammenhang zwischen viscosimetrisch und osmotisch bestimm-ten polymerisationsgraden bei hochpolymeren. J. Prakt. Chem. 1940, 157, 15. [Google Scholar] [CrossRef]
- Masuelli, M.A.; Takara, A.; Acosta, A. Hydrodynamic properties of tragacanthin. Study of temperature influence. J. Argent. Chem. Soc. 2013, 100, 25–34. [Google Scholar]
- Masuelli, M.A. Mark-Houwink parameters for aqueous-soluble polymers and biopolymers at various temperatures. J. Pol. Biopol. Phys. Chem. 2014, 2, 37–43. [Google Scholar] [CrossRef]
- Masuelli, M.A. Viscometric study of pectin. Effect of temperature on the hydrodynamic properties. Int. J. Biol. Macromol. 2011, 48, 286–291. [Google Scholar] [CrossRef] [PubMed]
- Masuelli, M.A.; Sansone, M.G. Hydrodynamic properties of Gelatine. Studies from intrinsic viscosity measurements. In Products and Applications of Biopolymers; Verbeek, C.J.R., Ed.; InTech: Rijeka, Croatia, 2012; Chapter 5; ISBN 978-953-51-0226-7. [Google Scholar]
- Masuelli, M.A. Hydrodynamic Properties of Whole Arabic Gum. Am. J. Food Sci. Technol. 2013, 1, 60–66. [Google Scholar]
- Harding, S.E. The Viscosity Intrinsic of Biological Macromolecules. Progress in Measurement, Interpretation and Application to Structure in Dilute Solution. Prog. Biophys. Mol. Biol. 1997, 68, 207–262. [Google Scholar] [CrossRef]
- Curvale, R.; Masuelli, M.; Perez Padilla, A. Intrinsic viscosity of bovine serum albumin conformers. Int. J. Biol. Macromol. 2008, 42, 133–137. [Google Scholar] [CrossRef] [PubMed]
- Masuelli, M.A. Study of Bovine Serum Albumin Solubility in Aqueous Solutions by Intrinsic Viscosity Measurements. Adv. Phys. Chem. 2013, 2013, 360239. [Google Scholar] [CrossRef] [Green Version]
- Sartor, M. Dynamic Light Scattering; University of California: San Diego, CA, USA, 2003; pp. 2–21. [Google Scholar]
- Rojas, R.; Giacomelli, C. Effect of structure and bonding on the interfacial properties and the reactivity of layered double hydroxides and Zn hydroxide salts. Eng. Asp. 2013, 419, 166–173. [Google Scholar] [CrossRef]
- Zanon, M.; Masuelli, M. Purification and Characterization of Alcayota Gum. Exp. Rev. Biopolym. Res. 2018, 2, 105. [Google Scholar]
- Kuhn, W.; Kuhn, H. Die abhängigkeit der viskosität vom strömungsgefälle bei hochverdünnten suspensionen und lösungen. Helv. Chim. Acta 1945, 28, 97–127. [Google Scholar] [CrossRef]
- Sakurada, I. Kasen Koenshu 1940, 5, 33–44.
- Sakurada, I. Kasen Koenshu 1941, 6, 177–184.
- Fee, M.; Errington, N.; Jumel, K.; Illum, L.; Smith, A.; Harding, S.E. Correlation of SEC/MALLS with ultracentrifuge and viscometric data for chitosans. Eur. Biophys. J. 2003, 32, 457–464. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).