Two-Liquid Flotation for Separating Mixtures of Ultra-Fine Rare Earth Fluorescent Powders for Material Recycling—A Review
Abstract
:1. Introduction
2. Two-Liquid Flotation
2.1. Experimental Procedure for Fluorescent Powder Separation
2.2. Analysis and Evaluation of Results
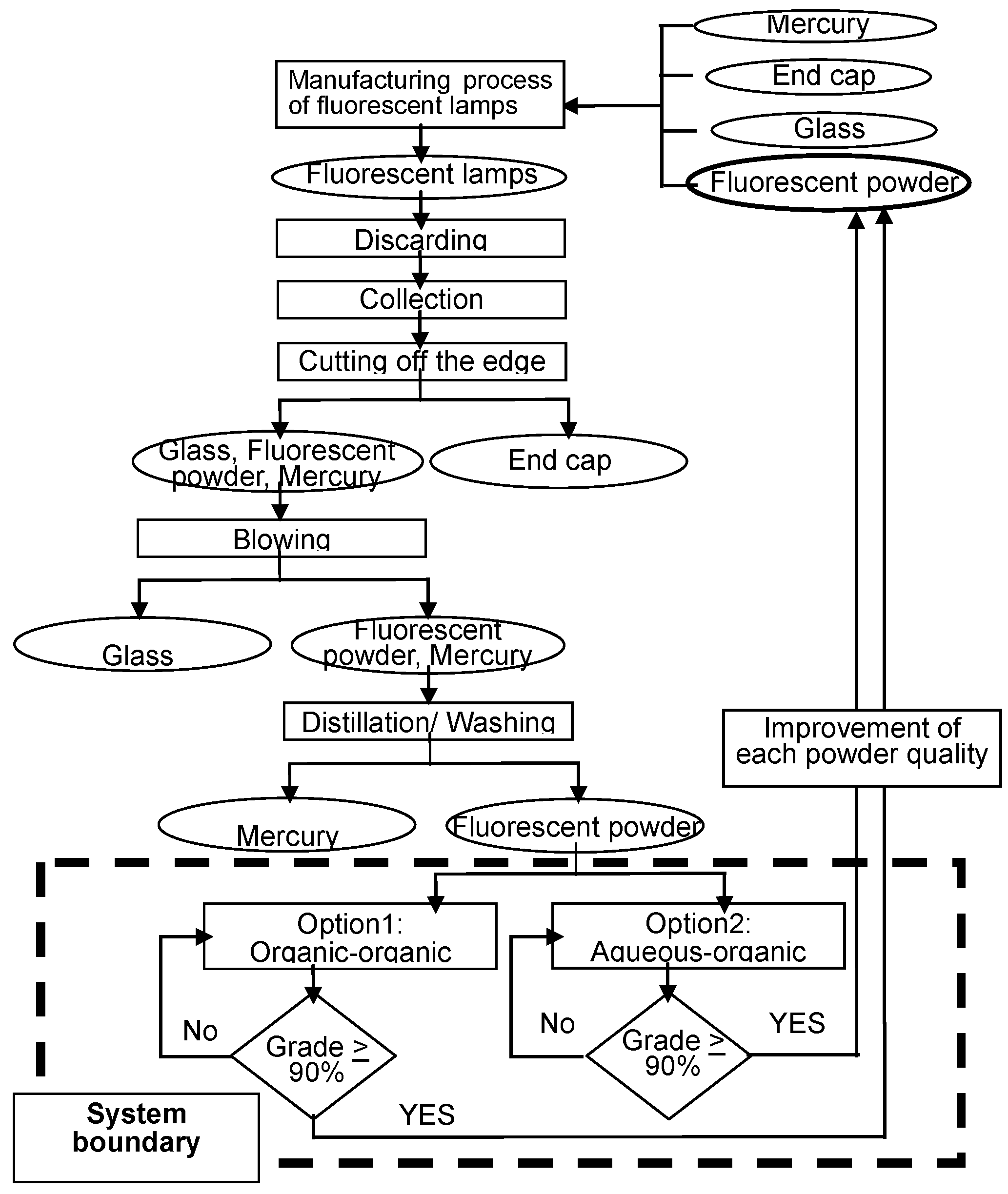
3. Flowsheet 1: Two-Liquid Flotation Using Aqueous and Organic Solvents (Aqueous-Organic System)
3.1. Materials
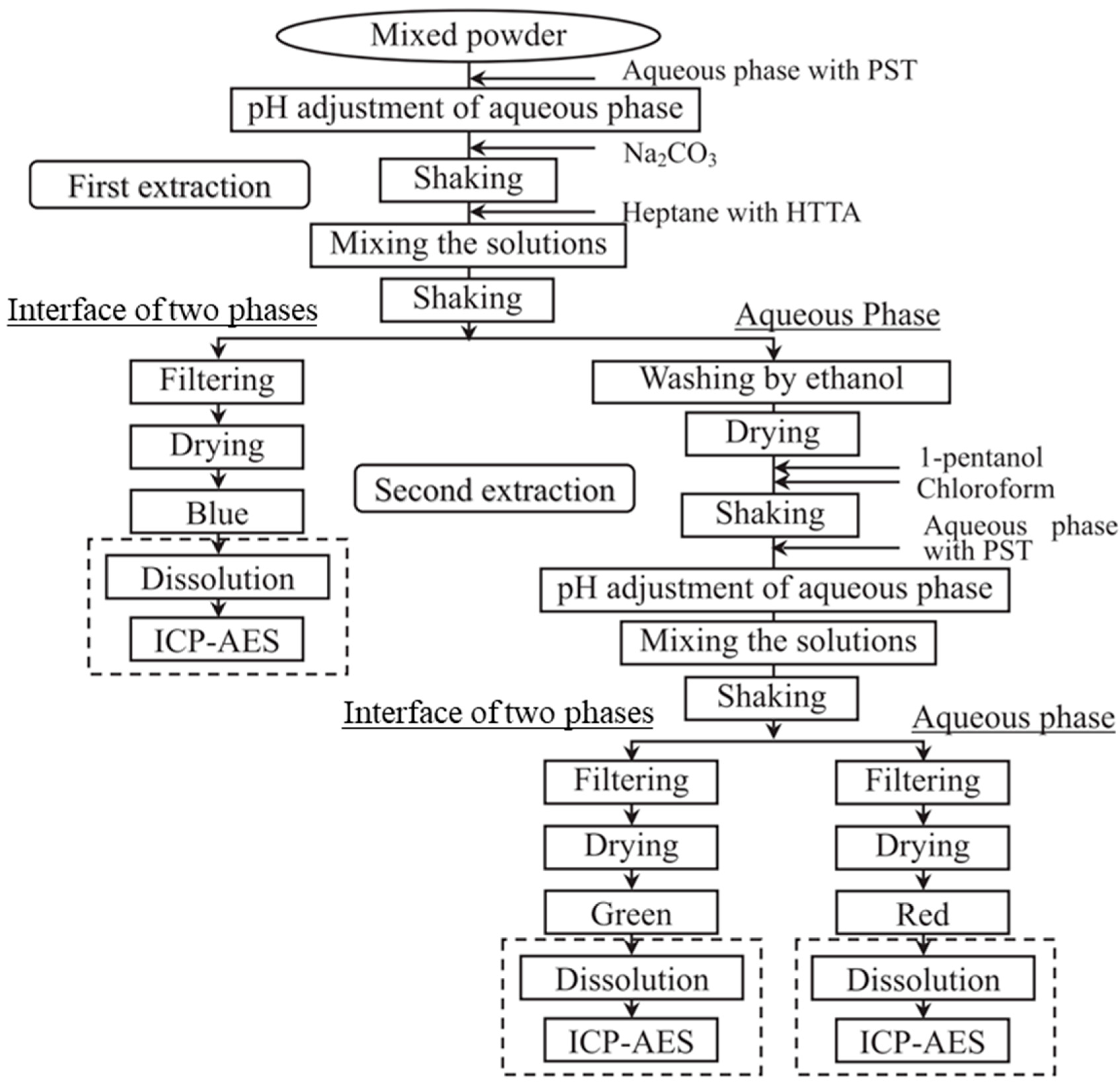
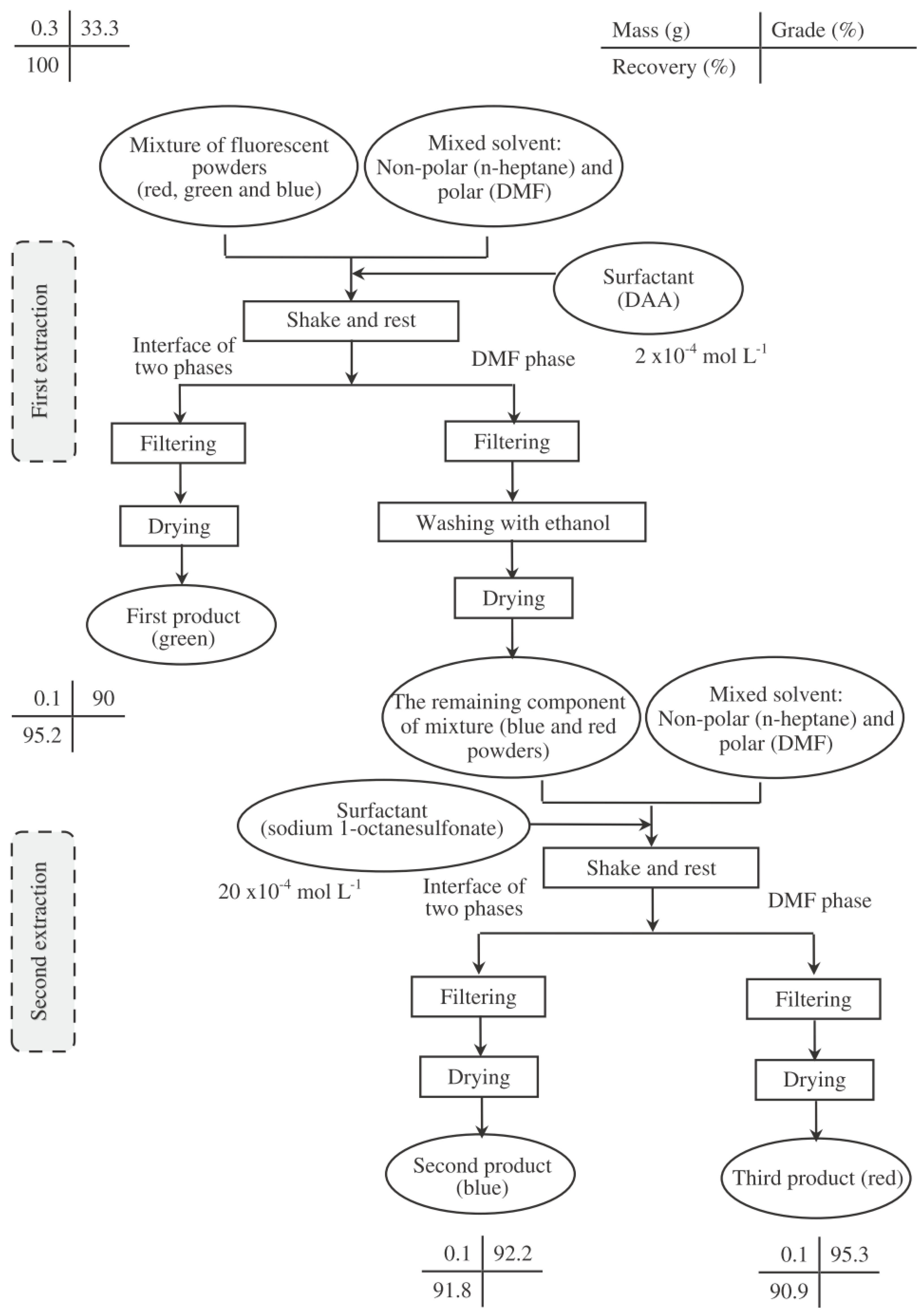
3.2. Flowsheet Design
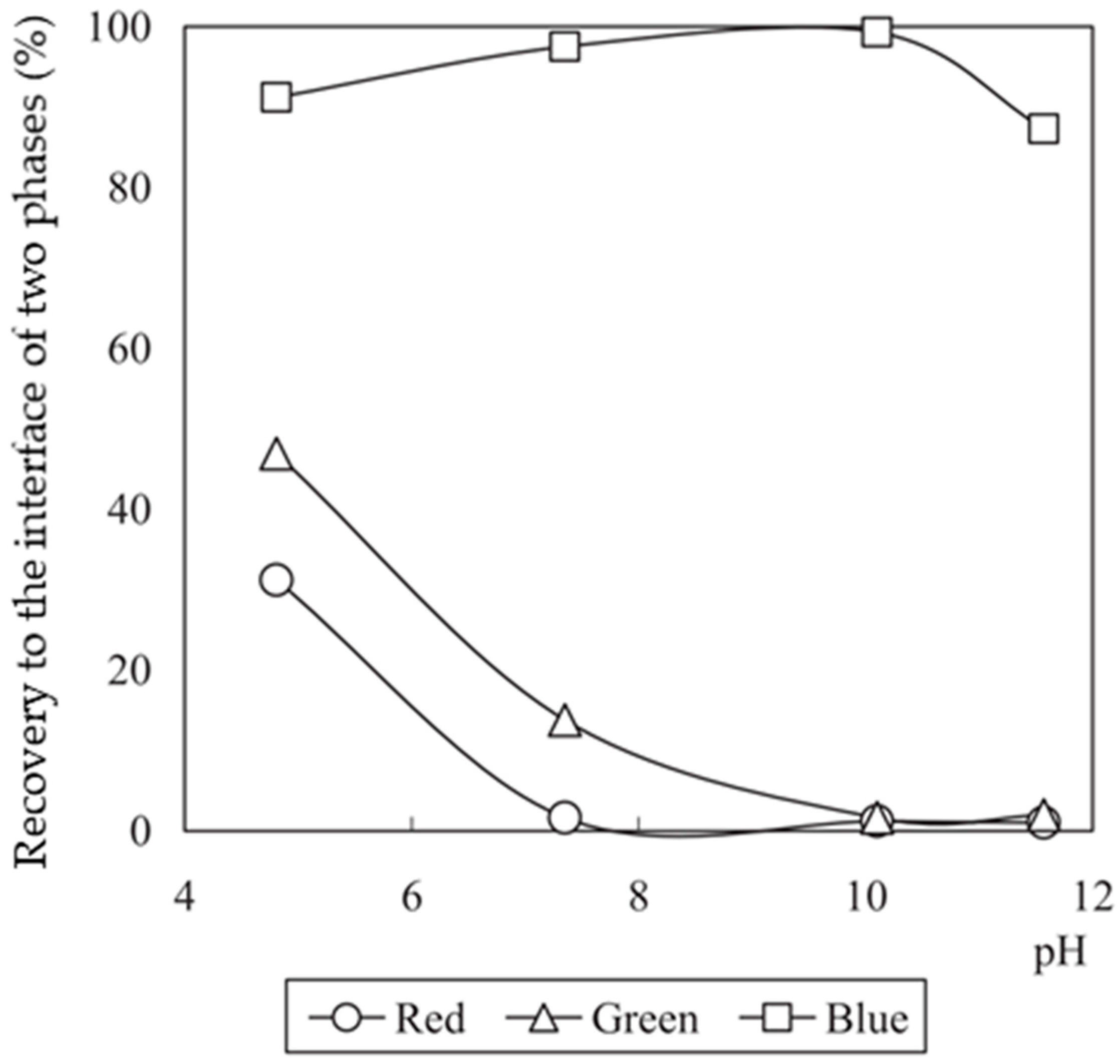
3.3. Results from the Flowsheet 1 (Aqueous-Organic System)
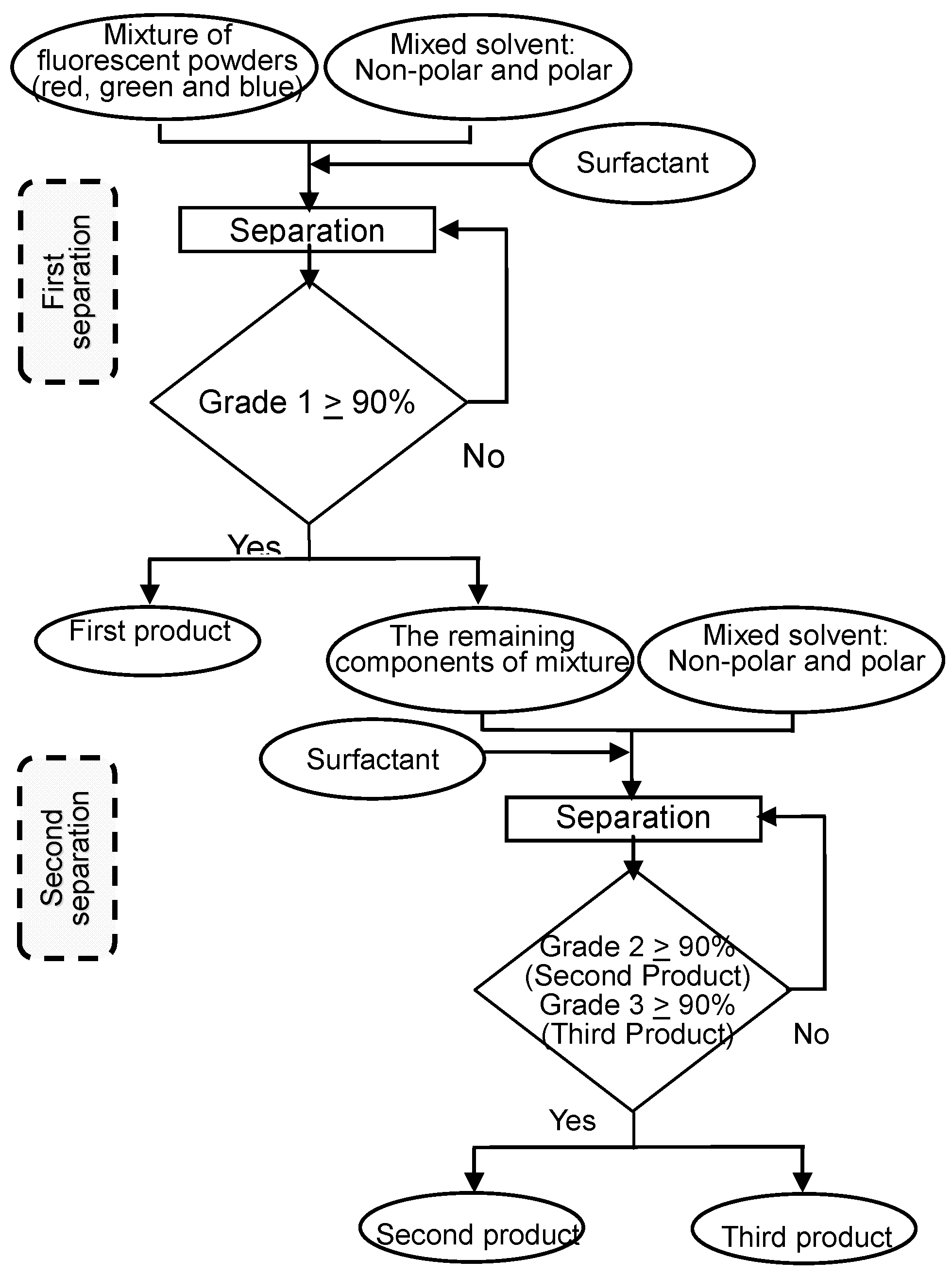
4. Flowsheet 2: Two-Liquid Flotation Using Organic Solvents (Organic-Organic System)
4.1. Materials
4.2. Flowsheet Design
4.3. Results from the Flowsheet 2
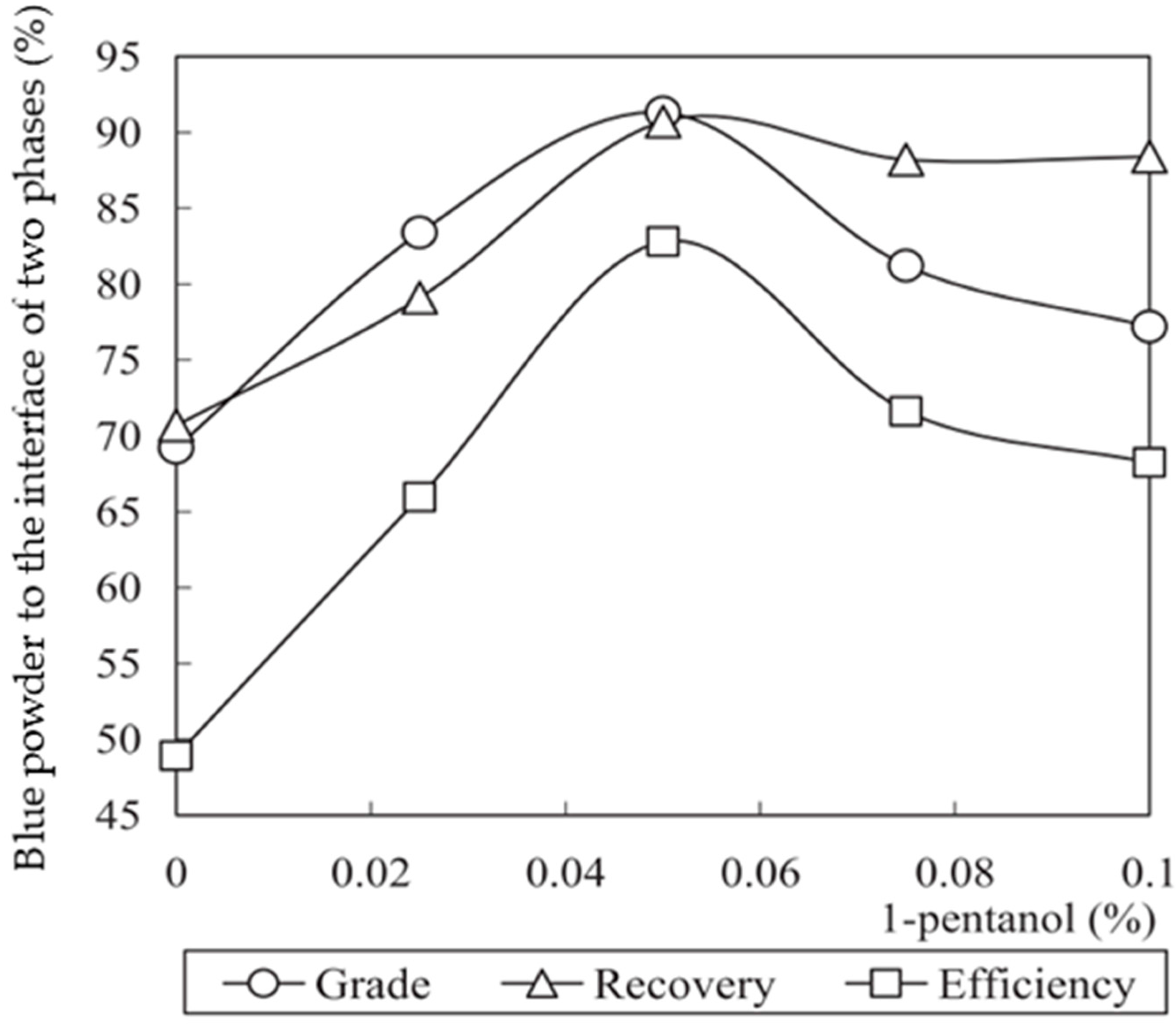
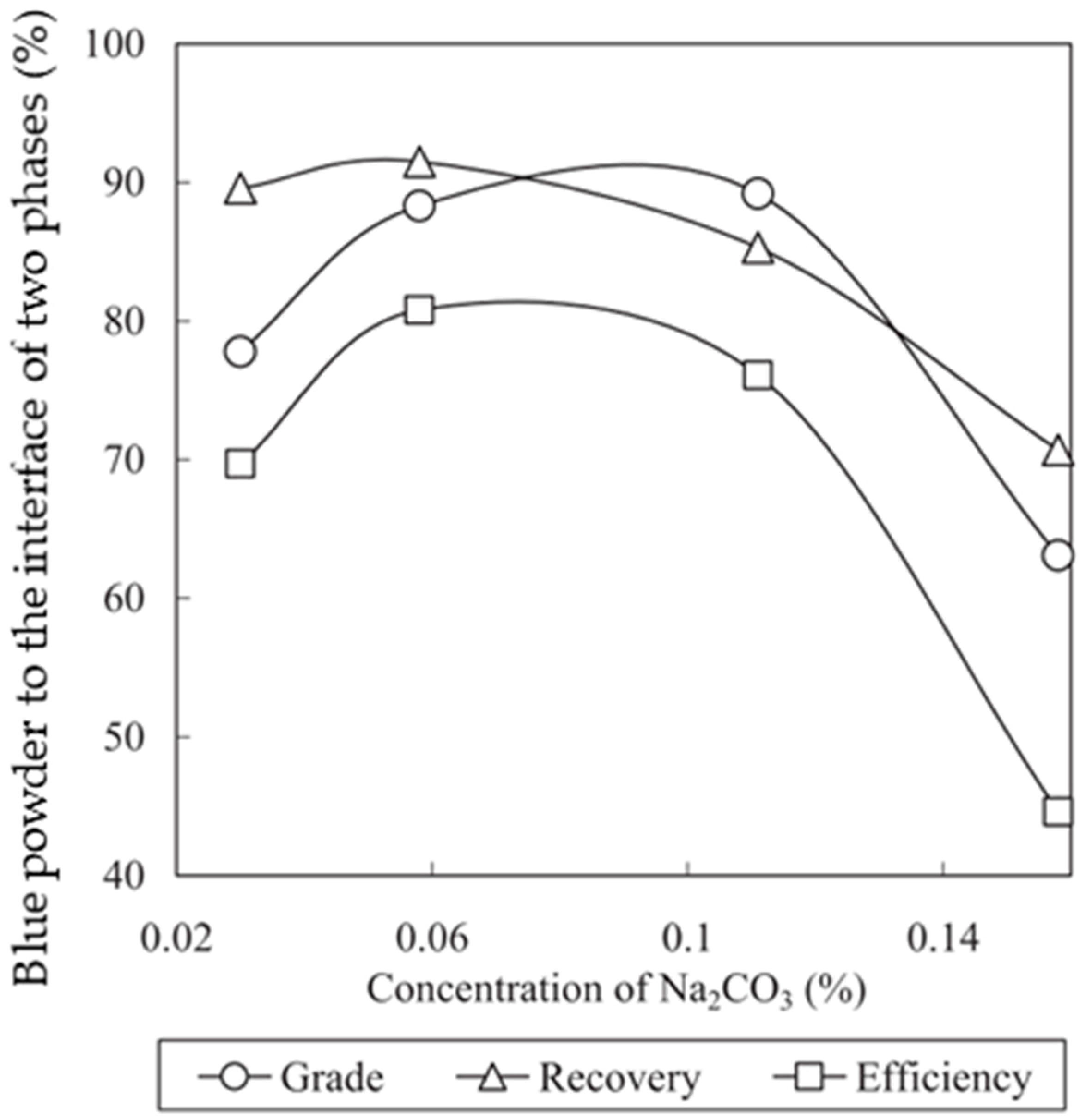
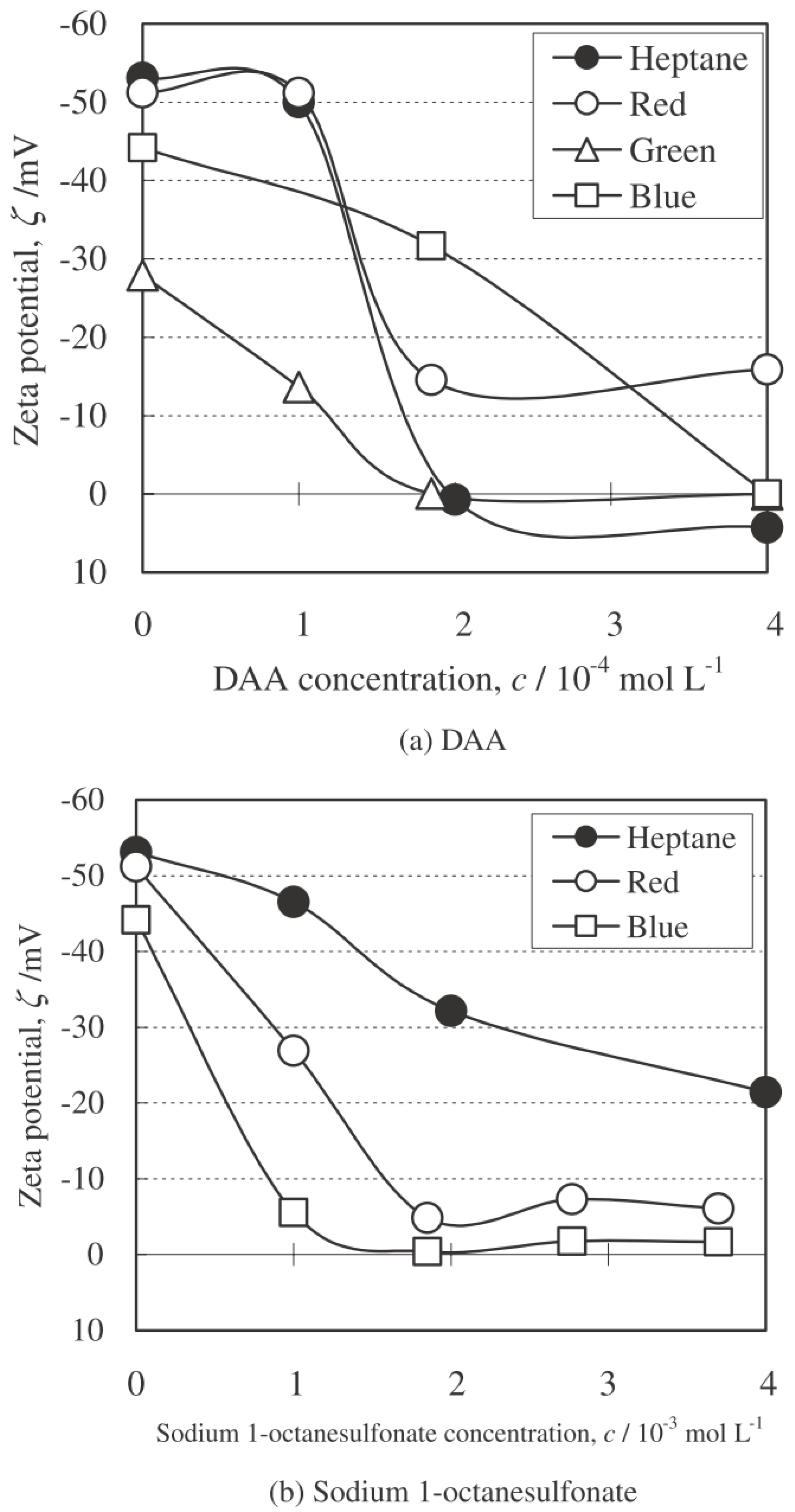
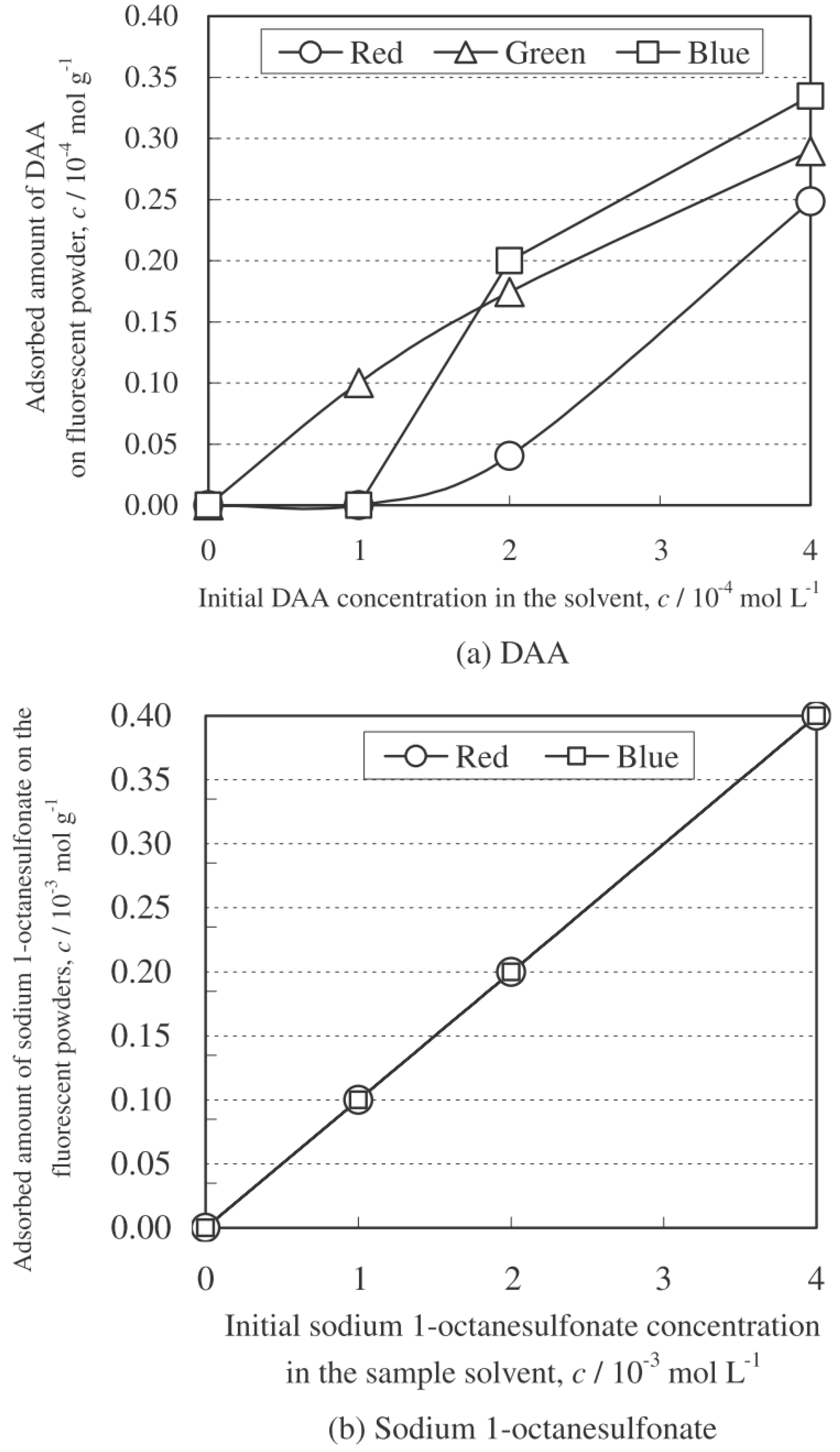
4.3.1. Effect of Surfactant
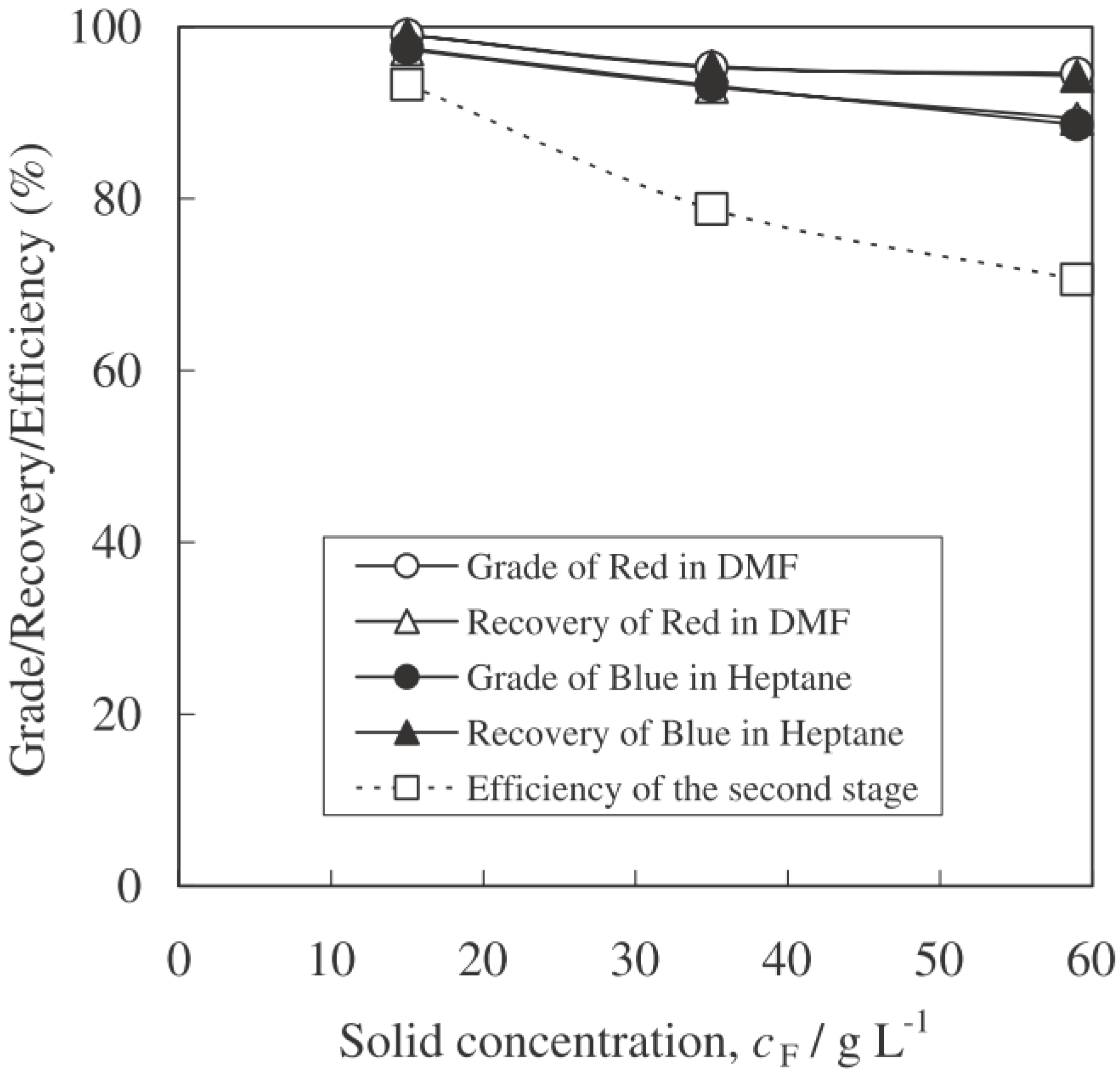
4.3.2. Effect of Solid Concentration
4.4. Heterocoagulation of Particle and Non-Polar Oil Droplet
4.4.1. DLVO Theory
4.4.2. Measuring the Physical Properties of Particle and Non-Polar Oil Droplet for Calculating the Potential Energy
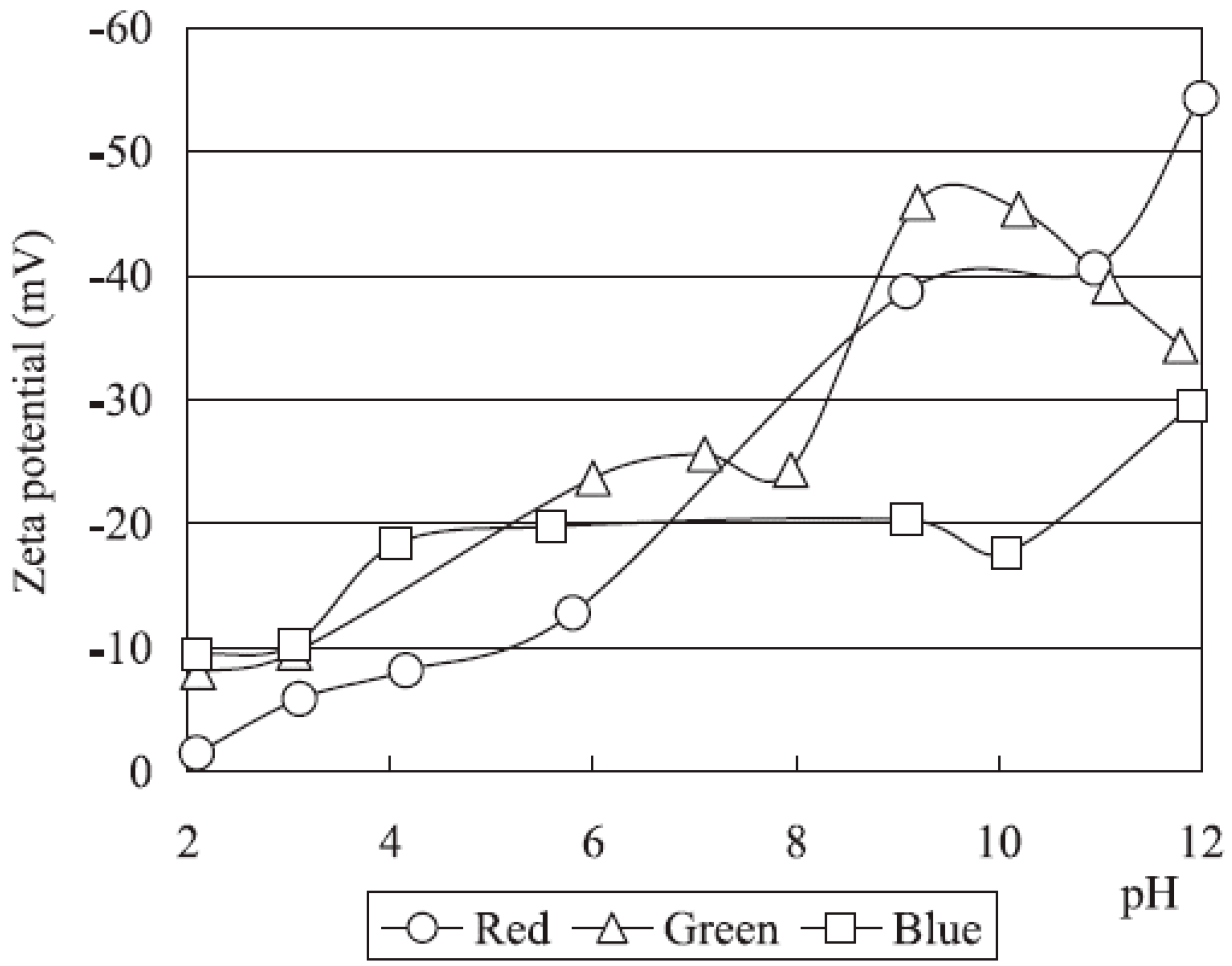
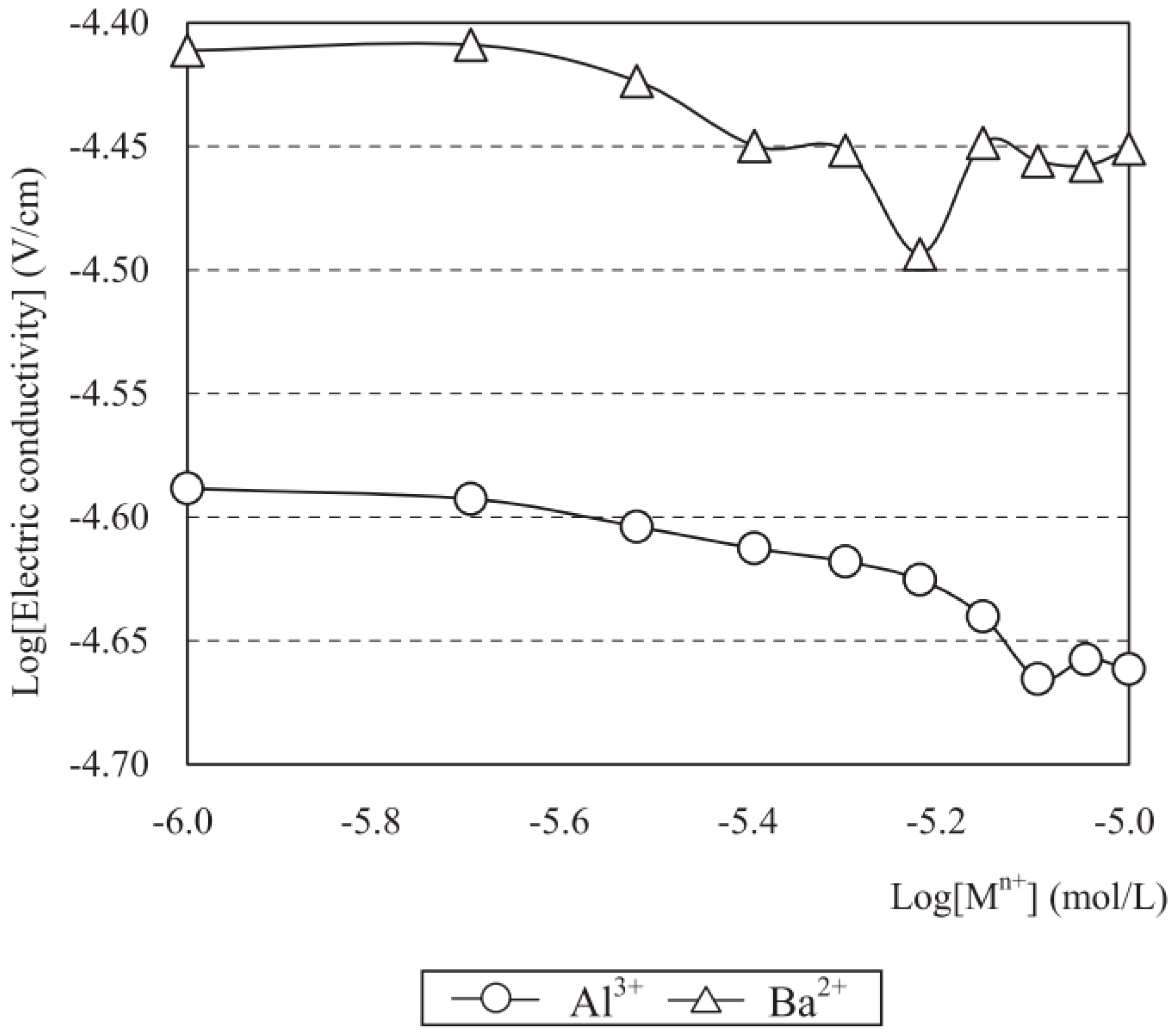
Zeta Potential
Aggregate Size
4.4.3. Calculating the Total Potential Energy
Results of Measurements
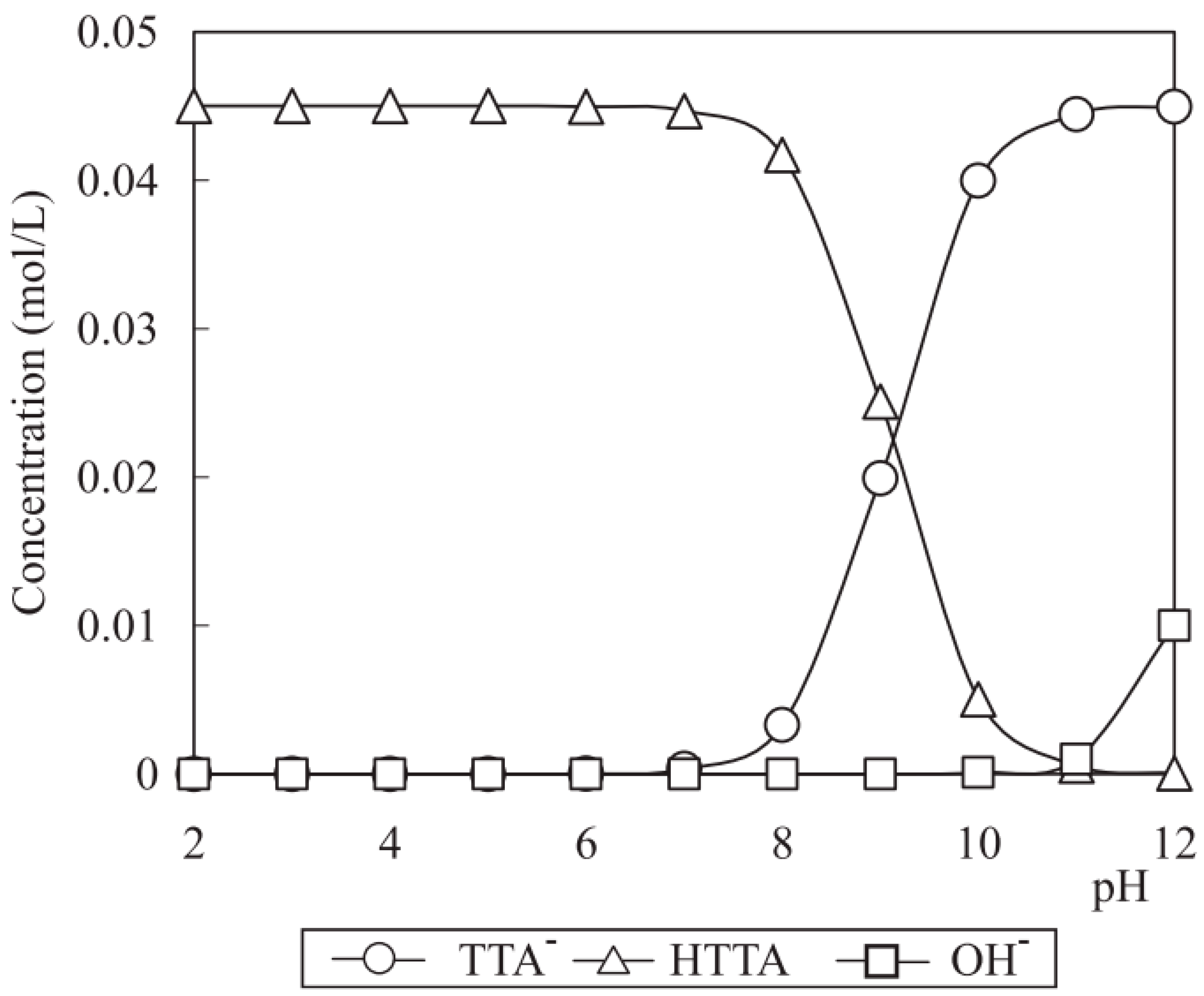
Potential Calculation
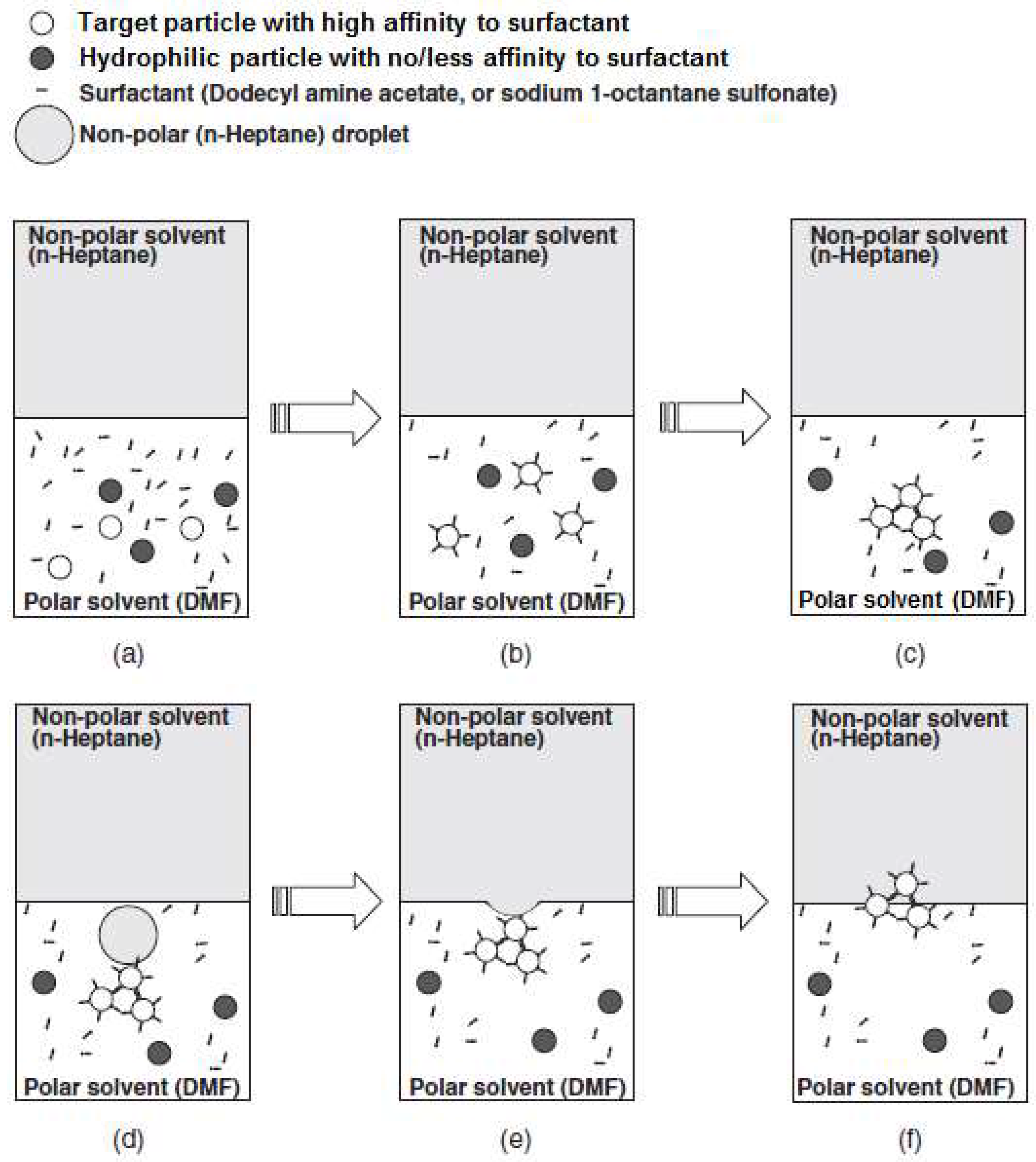
4.4.4. Separation Mechanism of Fluorescent Powders
5. Comparison between Two Different Two-Liquid Flotations
5.1. Selection of Solvents for Two-Liquid Flotation
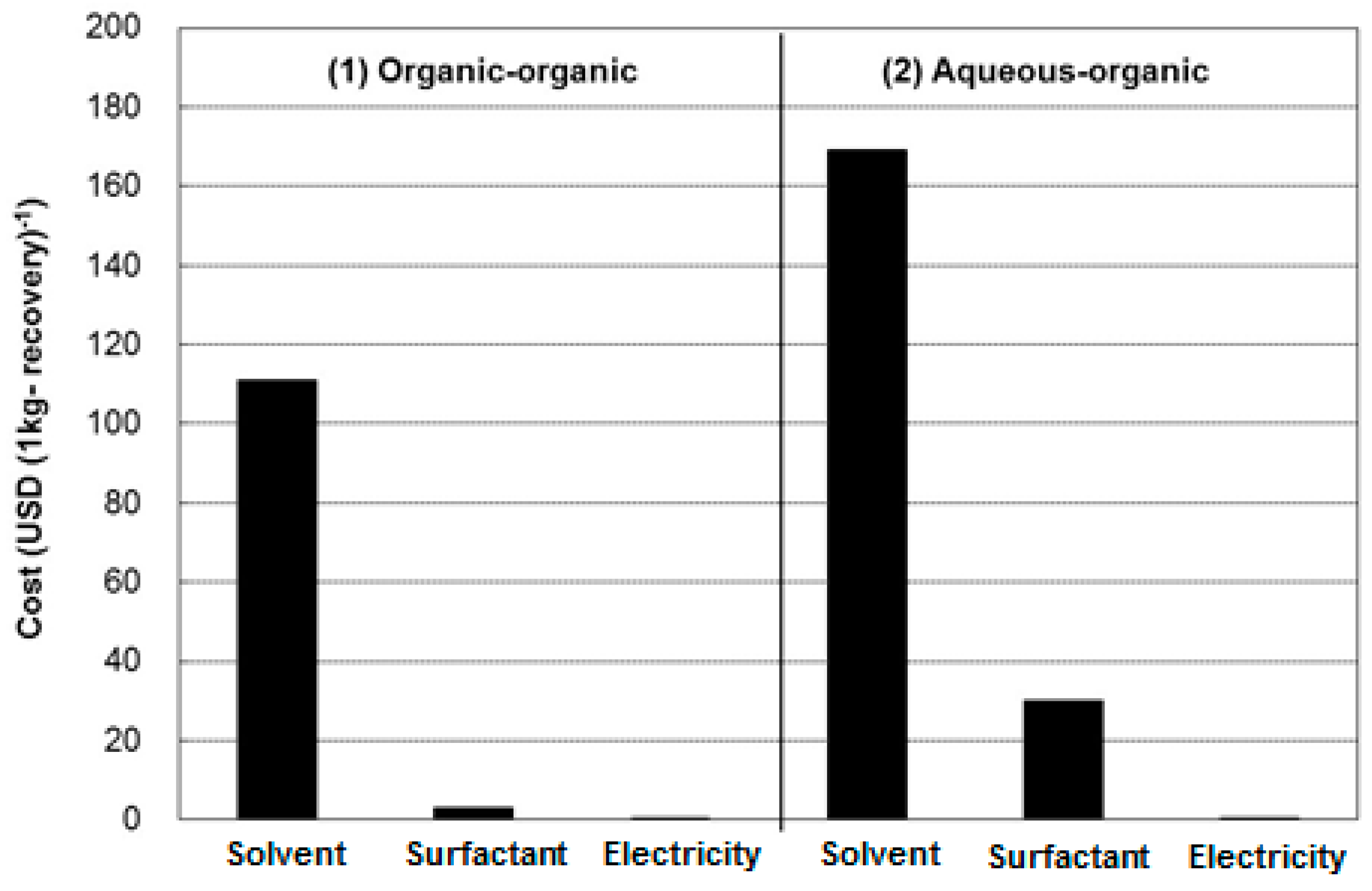
5.2. Cost Comparison
5.2.1. Methodology
5.2.2. Goal Definition
- Option 1: two-liquid flotation using the organic-organic system; and
- Option 2: two-liquid flotation using the aqueous-organic system.
5.2.3. Results and Discussion on the Cost Comparison
6. Conclusions
Conflicts of Interest
Nomenclature
| A | Hamaker constant (J) |
| a | radius of particle (m) |
| ano | radius of non-polar oil droplet (m) |
| c | concentration of surfactant (mol L−1) |
| D | average particle size (m) |
| e | elementary electrical charge (e = 1.60 × 10−19 C) (C) |
| H | distance of separation (m) |
| k | Boltzmann’s constant (k = 1.38 × 10−23 J K−1) (J K−1) |
| NA | Avogadro’s number (NA = 6.02 × 1023 mol−1) (mol−1) |
| T | absolute temperature (K) |
| VT | total potential energy (J) |
| VA | potential energy of interaction due to van der Waals forces (J) |
| VR | potential energy of interaction due to the overlap of the two electrical double layer (J) |
| z | valence of surfactant (−) |
| ɛr | dielectric coefficient of the medium (F m−1) |
| ɛ0 | dielectric constant of the free space (ɛ0 = 8.55 × 10−12 F m−1) (F m−1) |
| ψ1 | surface potential of particle (V) |
| ψ2 | surface potential of non-polar solvent (V) |
| κ | Debye-Huckel reciprocal length (m−1) |
| μ | viscosity of solvent (Pa s) |
| ρF | density of fluorescent powder (kg m−3) |
| ρS | density of solvent (kg m−3) |
| σ | electric conductivity of DMF solvent (μS cm−1) |
| ζ1 | zeta potential of particle (V) |
| ζ2 | zeta potential of non-polar oil droplet (V) |
References
- Shionoya, S.; Yen, M.W. Phosphor Handbook; CRC Press: Boca Raton, FL, USA, 1998; pp. 391–394. [Google Scholar]
- Japan Lighting Manufactures Association. Fluorescent Lamp Guidebook; Japan Lighting Manufactures Association: Tokyo, Japan, 2011; p. 14. [Google Scholar]
- Binnemans, K.; Jones, P.T.; Blanpain, B.; Gerven, T.V.; Yang, Y.; Walton, A.; Buchert, M. Recycling of rare earths: A critical review. J. Clean. Prod. 2013, 51, 1–22. [Google Scholar] [CrossRef]
- Rabah, M.A. Recovery of aluminium, nickel-copper alloys and salts from spent fluorescent lamps. Waste Manag. 2004, 24, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Takano, A.; Saito, T.; Nagano, N.; Hirai, S.; Shimakage, K. Separation and recovery of rare earth elements from phosphor sludge in processing plant of waste fluorescent lamp by pneumatic classification and sulphuric acidic leaching. J. MMIJ 2001, 117, 579–585. (In Japanese) [Google Scholar] [CrossRef]
- Takahashi, T.; Takano, A.; Saito, T.; Nagano, N.; Hirai, S.; Shimakage, K. Synthesis of red phosphor (Y2O3:Eu3+) from waste phosphor sludge by coprecipitation process. J. MMIJ 2002, 118, 413–418. (In Japanese) [Google Scholar] [CrossRef]
- Hirajima, T.; Sasaki, K.; Bissombolo, A.; Hirai, H.; Hamada, M.; Tsunekawa, M. Feasibility of an efficient recovery of rare earth-activated phosphors from waste fluorescent lamps through dense-medium centrifugation. Sep. Purif. Technol. 2005, 44, 197–204. [Google Scholar] [CrossRef]
- Hirajima, T.; Bissombolo, A.; Sasaki, K.; Nakayama, K.; Hirai, H.; Tsunekawa, M. Floatability of rare earth phosphors from waste fluorescent lamps. Int. J. Miner. Process. 2005, 77, 187–198. [Google Scholar] [CrossRef]
- Wu, Y.; Yin, X.; Zhang, Q.; Wang, W.; Mu, X. The recycling of rare earths from waste tricolor phosphors in fluorescent lamps: A review of processes and technologies. Resour. Conserv. 2014, 88, 21–31. [Google Scholar] [CrossRef]
- Tan, Q.; Li, J.; Zeng, X. Rare earth elements recovery from waste fluorescent lamps: A review. Crit. Rev. Environ. Sci. Technol. 2014, 45, 749–776. [Google Scholar] [CrossRef]
- Shergold, H.L.; Mellgren, O. Concentration of minerals at the oil/water interface. Trans. AIME 1970, 247, 149–159. [Google Scholar]
- Miettinen, T.; Ralston, J.; Fornasiero, D. The limits of fine particle flotation. Miner. Eng. 2010, 23, 420–437. [Google Scholar] [CrossRef]
- Otsuki, A.; Mei, G.; Jiang, Y.; Matsuda, M.; Shibayama, A.; Sadaki, J.; Fujita, T. Solid-Solid Separation of Fluorescent Powders By Liquid-Liquid Extraction Using Aqueous and Organic Phases. Resour. Process. 2006, 53, 121–133. [Google Scholar] [CrossRef]
- Otsuki, A.; Dodbiba, G.; Shibayama, A.; Sadaki, J.; Mei, G.; Fujita, T. Separation of rare earth fluorescent powders by two-liquid flotation using organic solvents. Jpn. J. Appl. Phys. 2008, 47, 5093–5099. [Google Scholar] [CrossRef]
- Zambrana, G.Z.; Medina, R.T.; Gutierrez, G.B.; Vargas, R.R. Recovery of minus ten micron cassiterite by liquid-liquid extraction. Int. J. Miner. Process. 1974, 1, 335–345. [Google Scholar] [CrossRef]
- Marinakis, K.I.; Kelsall, G.H. Effect of lattice cations, silicate ions and fluorosilicate ions on 2-liquid flotation of tungsten minerals. Trans. IMM Sect. C 1987, 96, 63–68. [Google Scholar]
- Laskowski, J.S.; Ralston, J. Colloid Chemistry in Mineral Processing; Elsevier: Amsterdam, The Netherlands, 1992; pp. 361–394. [Google Scholar]
- Otsuki, A.; Dodbiba, G.; Fujita, T. Two-liquid flotation: Heterocoagulation of fine particles in polar organic solvent. Mater. Trans. 2007, 48, 1095–1104. [Google Scholar] [CrossRef]
- Fuerstenau, D.W. Fine particle processing. In Proceedings of the International Symposium on Fine Particles Processing, Las Vegas, NV, USA, 24–28 February 1980; pp. 669–705. [Google Scholar]
- Kusaka, E.; Nakahiro, Y.; Wakamatsu, T. The role of zeta potentials of oil droplets and quartz particles during collectorless liquid-liquid extraction. Int. J. Miner. Process. 1994, 41, 257–269. [Google Scholar] [CrossRef]
- Otsuki, A.; Sadaki, J.; Yamaguchi, K.; Shibayama, A.; Fujita, T. Observation of Aggregate Structure of Green and Blue Fluorescent Powders Suspended in Heptane by Interactive Force Measurement. Int. J. Soc. Mater. Eng. Resour. 2006, 13, 86–91. [Google Scholar] [CrossRef]
- Kusaka, E.; Arimoto, Y.; Nakahiro, Y.; Wakamatsu, T. Collectorless liquid-liquid extraction of fine mineral particles using various organic liquids as the oil phase. Miner. Eng. 1994, 7, 39–48. [Google Scholar] [CrossRef]
- Kusaka, E.; Nakahiro, Y.; Wakamatsu, T. Collectorless liquid-liquid extraction of silica fines in trivalent metal salts solutions. Miner. Eng. 1995, 8, 817–828. [Google Scholar] [CrossRef]
- Hu, B.; Nakahiro, Y.; Wakamatsu, T. The effect of organic solvents on the recovery of fine mineral particles by liquid-liquid extraction. Miner. Eng. 1993, 6, 731–742. [Google Scholar] [CrossRef]
- Wang, L.P.; Kanemitsu, Y.; Dodbiba, G.; Fujita, T.; Oya, Y.; Yokoyama, H. Separation of ultrafine particles of alumina and zircon by liquid–liquid extraction using kerosene as the organic phase and sodium dodecylsulfate (SDS) as the surfactant collector for abrasive manufacturing waste recycling. Sep. Purif. Technol. 2013, 108, 133–138. [Google Scholar] [CrossRef]
- Kanemitsu, Y.; Wang, L.P.; Dodbiba, G.; Fujita, T. Liquid-Liquid Separation of Fine Zircon-Alumina Mixtures for Abrasives Recycling. Resour. Process. 2012, 59, 81–84. [Google Scholar] [CrossRef]
- Yoon, R.H.; Gupta, N.; Li, B.; Luttrell, G.H.; Bratton, R.C.; Reyher, J.; Suboleski, S. HHS process: A new approach for recovering fine Illinois basin coals. In Proceedings of the International Coal Preparation Conference, Louisville, KY, USA, 25–27 April 2016; pp. 99–106. [Google Scholar]
- Dodbiba, G.; Sadaki, J.; Okaya, K.; Shibayama, A.; Fujita, T. The use of air tabling and triboelectric separation for separating a mixture of three plastics. Miner. Eng. 2005, 18, 1350–1360. [Google Scholar] [CrossRef]
- Kusaka, E.; Tamai, H.; Nakahiro, Y.; Wakamatsu, T. Role of surface free energy in a solid surface during collectorless liquid-liquid extraction. Miner. Eng. 1993, 6, 455–464. [Google Scholar] [CrossRef]
- Van Uitert, L.G.; Conard, W.C.; Douglas, B.E. Studies on coordination compounds. III. The chelating tendencies of β–diketones with the chlorides of copper (II), nickel and barium in water-dioxane solutions. J. Am. Chem. Soc. 1953, 75, 457–460. [Google Scholar] [CrossRef]
- Ringbom, A. Complexation in Analytical Chemistry; Sangyo-Tosho: Tokyo, Japan, 1965; pp. 317–324. (In Japanese) [Google Scholar]
- The Chemistry Society of Japan (Ed.) Handbook of Chemistry, 5th ed.; Basic Edition Vol. II; Maruzen: Tokyo, Japan, 2004; pp. 149–152. [Google Scholar]
- Brown, T.; LeMay, H.; Bursten, B. Chemistry, 8th ed.; Prentice Hall: New York, NY, USA, 1997; pp. 616–620. [Google Scholar]
- Sawatani, T. Basic Analytical Chemistry; Nanko-do: Tokyo, Japan, 1972; pp. 210–211. (In Japanese) [Google Scholar]
- Asahara, S. Yozai Handbook (Solvent Handbook); Kodansha: Tokyo, Japan, 1976; pp. 156–158, 734–738. (In Japanese) [Google Scholar]
- Cote, A.P.; Shimizu, G.K.H. The supramolecular chemistry of the sulfonate group in extended solids. Coord. Chem. Rev. 2003, 245, 49–64. [Google Scholar] [CrossRef]
- Laskowski, J.; Iskra, J. Role of capillary effects in bubble-particle collision in flotation. Trans. Inst. Min. Metall. 1970, 79, C6–C10. [Google Scholar]
- Stratton-Crawley, R. Beneficiation of Mineral Fines-Problems and Research Needs; AIME: New York, NY, USA, 1979; pp. 317–330. [Google Scholar]
- Ralston, J.; Kent, W.; Newcombe, G. Polymer-stabilized emulsions and fine-particle recovery, i. The calcite-quartz system. Int. J. Miner. Process. 1984, 13, 167–186. [Google Scholar] [CrossRef]
- Kent, W.; Ralston, J. Polymer-stabilized emulsions and fine-particle recovery, ii. The chalcopyrite-quartz system. Int. J. Miner. Process. 1985, 14, 217–232. [Google Scholar] [CrossRef]
- Mackenzie, J.M.W. Interactions between oil drops and mineral surfaces. Trans. AIME 1970, 247, 202–208. [Google Scholar]
- Lai, R.W.M.; Fuerstenau, D.W. Liquid-liquid extraction of ultrafine particles. Trans. AIME 1968, 241, 549–556. [Google Scholar]
- Tamai, H.; Hakozaki, T.; Suzawa, T. Deposition of polymethyl methacrylate latex on fibers. Colloid Polym. Sci. 1980, 258, 870–876. [Google Scholar] [CrossRef]
- Gotoh, K.; Inoue, T.; Tagawa, M. Adhesion of nylon particles to a quartz plate in an aqueous solution and their removal by electro-osmosis. Colloid Polym. Sci. 1984, 262, 982–989. [Google Scholar] [CrossRef]
- Kallay, N.; Barouch, E.; Matijević, E. Diffusional detachment of colloidal particles from solid/solution interfaces. Adv. Colloid Interface Sci. 1987, 27, 1–42. [Google Scholar] [CrossRef]
- Furusawa, K.; Anzai, C. Heterocoagulation behaviour of polymer latices with spherical silica. Colloids Surf. 1992, 63, 103–111. [Google Scholar] [CrossRef]
- Mulvaney, P.; Perera, J.M.; Biggs, S.; Grieser, F.; Stevens, G.W. The direct measurement of the forces of interaction between a colloid particle and an oil droplet. J. Colloid Interface Sci. 1996, 183, 614–616. [Google Scholar] [CrossRef] [PubMed]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1993, 43, 30–59. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.C. Theory of the Stability of Lyophobic Colloids; Elsevier Publishing Company Inc.: New York, NY, USA, 1948. [Google Scholar]
- Israelachvili, J. Intermolecular and Surface Forces, 2nd ed.; Academic Press: London, UK, 1992; pp. 176–212. [Google Scholar]
- Otsuki, A.; Dodbiba, G.; Fujita, T. Measurements of size distribution of titanium dioxide fine particles in a highly concentrated non-aqueous suspension by using particle self-assembly under an electric field. Adv. Powder Technol. 2012, 23, 517–522. [Google Scholar] [CrossRef]
- Crowl, V.T. Floculation, flotation and flooding in phthalocyanine/titanium dioxide pigmented paints. J. Oil Colour Chem. Assoc. 1967, 50, 1023–1059. [Google Scholar]
- Nacalai Tesque Co. Ltd., Japan, Chemical Catalog. Available online: http://www.nacalai.co.jp/online/online.html (accessed on 30 November 2017).




| Powder | Formula | Elemental Content (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| O | Y | Eu | Al | Mg | Ba | Ce | Tb | ||
| Red | Y2O3: Eu3+ | 17.5 | 67.2 | 6.5 | |||||
| Green | CeMgAl10O17: Tb3+ | 42.6 | 31.3 | 5.7 | 9.5 | 5.3 | |||
| Blue | BaMgAl10O17: Eu2+ | 42.3 | 1.9 | 32.4 | 2.7 | 12.4 | |||
| Red | Green | Blue | Overall Efficiency (%) * | |||
|---|---|---|---|---|---|---|
| Grade (%) | Recovery (%) | Grade (%) | Recovery (%) | Grade (%) | Recovery (%) | |
| 96.9 | 94.1 | 94.6 | 76.0 | 74.1 | 98.7 | 47.9 |
| Powder | Formula | Components | Content (wt%) | Average Particle Size D (μm) | Density ρs (kg m−3) |
|---|---|---|---|---|---|
| Red | Y2O3: Eu3+ | Y2O3 | 91.6 | 2.6 | 5120 |
| Eu2O3 | 7.8 | ||||
| Green | LaPO4: Tb3+,Ce3+ | P2O5 | 29.8 | 1.1 | 5060 |
| La2O3 | 39.7 | ||||
| Ce2O3 | 17.9 | ||||
| Tb2O3 | 10.1 | ||||
| Blue | (Sr,Ca,Ba)10(PO4)6Cl2: Eu2+ | P2O5 | 25 | 2.1 | 4270 |
| Al2O3 | 1.3 | ||||
| Cl | 1.1 | ||||
| CaO | 1.8 | ||||
| Fe2O3 | 0.014 | ||||
| SrO | 41.2 | ||||
| BaO | 27 | ||||
| EuO | 1.0 |
| Solvent | Formula | Viscosity μ (10−4 Pa s) | Density ρs (kg m−3) | Melting Point T (K) | Boiling Point T (K) |
|---|---|---|---|---|---|
| n-Heptane | C7H16 | 4.09 | 683 | 183 | 372 |
| DMF | (CH3)2NCHO | 8.02 | 906 | 213 | 426 |
| Solvent | Powder | Zeta Potential (mV) |
|---|---|---|
| n-Heptane | Red | −53.2 |
| Green | −12.6 | |
| Blue | −28.3 | |
| DMF | Red | −51.2 |
| Green | −27.9 | |
| Blue | −44.2 |
| First Product | Second Product | Third Product | Overall Efficiency (%) * | |||
|---|---|---|---|---|---|---|
| (Green) | (Blue) | (Red) | ||||
| Grade (%) | Recovery (%) | Grade (%) | Recovery (%) | Grade (%) | Recovery (%) | |
| 90.0 | 95.2 | 92.2 | 91.8 | 95.3 | 90.9 | 62.8 |
| Material | Hamaker Constant, A/J |
|---|---|
| Fluorescent powder; A11 *1 | 2.0 × 10−19 [50] |
| n-heptane; A22 | 3.6 × 10−20 [52] |
| DMF; A33 *2 | 6.1 × 10−20 [50] |
| Separation Step | Powder | Zeta Potential, ζ1/V | Radius of Fluorescent Powder, a/m |
|---|---|---|---|
| 1st | Red | −50 × 10-3 | 1.3 × 10−6 |
| Green | −14 × 10-3 | 7.0 × 10−6 | |
| Blue | −40 × 10-3 | 1.1 × 10−6 | |
| 2nd | Red | −27 × 10-3 | 1.3 × 10−6 |
| Blue | −6 × 10-3 | 1.7 × 10−6 |
| Separation Step | Zeta Potential, ζ2/V |
|---|---|
| 1st | −53 × 10−3 |
| 2nd | −53 × 10−3 |
| Separation Step | Surfactant | Concentration, c/mol L−1 | Valency, z/- |
|---|---|---|---|
| 1st | DAA | 2 × 10−4 | 1 |
| 2nd | Sodium 1-octanesulfonate | 20 × 10−4 | −1 |
| Method | Type of Reagent | Symbols | Name | Price (USD L−1, or USD kg−1) * |
|---|---|---|---|---|
| Organic-organic | Solvent | So1 (1st/2nd) | N,N-Dimethylformamide (DMF) | 23.0 |
| So2 (1st/2nd) | n-Heptane | 81.0 | ||
| Surfactant | Su1 | Dodecylamine acetate (DAA) | 4240.0 | |
| Su2 | Sodium 1-octanesulfonate | 5800.0 | ||
| Aqueous-organic | Solvent | So3 (1st/2nd) | Water | 0.0013 |
| So4 (1st) | n-Heptane | 22.0 | ||
| So5 (2nd) | Chloroform | 81.0 | ||
| Surfactant | Su3 | 2-Thenoyltrifluoroacetone (HTTA) | 4240.0 | |
| Su4 | 1-Pentanol | 44.0 | ||
| Su5 | Potassium sodium tartrate tetrahydrate (PST) | 440.0 | ||
| Su6 | Sodium bicarbonate | 14.8 |
| 1st stage | Mass (kg) | Grade, gb1 (%) | Recovery, rb1 (%) | ||||
| Green | Others | Green | Others | Green | Others | ||
| Feed | 1.00 | 2.00 | 33.3 | 66.6 | 100.0 | 100.0 | |
| Interface | 0.95 | 0.11 | 90.0 | 10.0 | 95.2 | 5.3 | |
| In DMF phase | 0.05 | 1.89 | 2.5 | 97.5 | 4.8 | 94.7 | |
| 2nd stage | Mass (kg) | Grade, gb1 (%) | Recovery, rb1 (%) | ||||
| Blue | Red | Blue | Red | Blue | Red | ||
| Feed | 0.95 | 0.95 | 48.9 | 48.7 | 94.9 | 94.5 | |
| Interface | 0.95 | 0.08 | 92.2 | 7.8 | 95.3 | 9.1 | |
| In DMF phase | 0.07 | 0.84 | 8.2 | 91.8 | 4.7 | 90.9 | |
| 1st stage | Mass (kg) | Grade, gb2 (%) | Recovery, rb2 (%) | ||||
| Blue | Others | Blue | Others | Blue | Others | ||
| Feed | 1.00 | 2.00 | 33.3 | 66.6 | 100.0 | 100.0 | |
| Interface | 0.99 | 0.34 | 74.1 | 25.9 | 98.7 | 17.2 | |
| In aqueous phase | 0.01 | 1.66 | 0.8 | 99.2 | 1.3 | 82.8 | |
| 2nd stage | Mass (kg) | Grade, gb2 (%) | Recovery, rb2 (%) | ||||
| Green | Red | Green | Red | Green | Red | ||
| Feed | 0.82 | 0.84 | 49.0 | 50.2 | 81.8 | 83.7 | |
| Interface | 0.76 | 0.06 | 94.6 | 5.4 | 76.0 | 5.9 | |
| In aqueous phase | 0.03 | 0.82 | 3.1 | 96.9 | 24.0 | 94.1 | |
| 2nd Processing at 1st Stage | Mass (kg) | Grade, gb2 (%) | Recovery, rb2 (%) | |||
|---|---|---|---|---|---|---|
| Blue | Others | Blue | Others | Blue | Others | |
| Feed | 0.99 | 0.34 | 74.1 | 25.9 | 98.7 | 17.2 |
| Interface | 0.96 | 0.06 | 94.2 | 5.8 | 97.4 | 3.0 |
| In aqueous phase | 0.03 | 0.29 | 8.2 | 91.8 | 2.6 | 97.0 |
| Organic-organic phases | First Product (Green) | Second Product (Blue) | Third Product (Red) | Total Efficiency (%) | |||
| Grade, gb1 (%) | Recovery, rb1 (%) | Grade, gb1 (%) | Recovery, rb1 (%) | Grade, gb1 (%) | Recovery, rb1 (%) | ||
| 90.0 | 95.2 | 92.2 | 95.3 | 91.8 | 90.9 | 62.8 | |
| Aqueous-organic phases * | First Product (Blue) | Second Product (Green) | Third Product (Red) | Total Efficiency (%) | |||
| Grade, gb2 (%) | Recovery, rb2 (%) | Grade, gb2 (%) | Recovery, rb2 (%) | Grade, gb2 (%) | Recovery, rb2 (%) | ||
| 94.2 | 97.4 | 94.6 | 76.0 | 96.9 | 94.1 | 60.1 | |
| Organic-Organic (Option 1) | Aqueous-Organic (Option 2) | ||||
|---|---|---|---|---|---|
| Reagent | Cost (USD (kg-Process)−1) | Cost (USD (kg-Recovery)−1) | Reagent | Cost (USD (kg-Process)−1) | Cost (USD (kg-Recovery)−1) |
| So1 | 23.00 | 24.54 | So3 | 0.0018 | 0.0020 |
| So2 | 81.00 | 86.44 | So4 | 129.60 | 148.75 |
| So5 | 17.60 | 20.20 | |||
| Subtotal | 104.00 | 110.99 | Subtotal | 147.20 | 168.95 |
| Su1 | 0.21 | 0.22 | Su3 | 21.20 | 24.33 |
| Su2 | 2.51 | 2.68 | Su4 | 0.00022 | 0.00025 |
| Su5 | 5.05 | 5.80 | |||
| Su6 | 0.09 | 0.11 | |||
| Subtotal | 2.72 | 2.90 | Subtotal | 26.34 | 30.24 |
| Electricity | 0.13 | 0.14 | Electricity | 0.20 | 0.23 |
| Number of separation cycle required | 1 | Number of separation cycle required | 2 (for 1st stage) | ||
| Collected mass (kg) | 1 | Collected mass (kg) | 1 | ||
| Processed mass (kg) | 1.07 | Processed mass (kg) | 1.15 | ||
| Recovery(total) | 0.94 | Recovery(total) | 0.89 | ||
| Total Cost (USD (kg; process)−1) | 106.9 | Total Cost (USD (kg; process)−1) | 173.7 | ||
| Total Cost (USD (kg; recovery)−1) | 114.0 | Total Cost (USD (kg; recovery)−1) | 199.4 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otsuki, A.; Dodbiba, G.; Fujita, T. Two-Liquid Flotation for Separating Mixtures of Ultra-Fine Rare Earth Fluorescent Powders for Material Recycling—A Review. Colloids Interfaces 2018, 2, 7. https://doi.org/10.3390/colloids2010007
Otsuki A, Dodbiba G, Fujita T. Two-Liquid Flotation for Separating Mixtures of Ultra-Fine Rare Earth Fluorescent Powders for Material Recycling—A Review. Colloids and Interfaces. 2018; 2(1):7. https://doi.org/10.3390/colloids2010007
Chicago/Turabian StyleOtsuki, Akira, Gjergj Dodbiba, and Toyohisa Fujita. 2018. "Two-Liquid Flotation for Separating Mixtures of Ultra-Fine Rare Earth Fluorescent Powders for Material Recycling—A Review" Colloids and Interfaces 2, no. 1: 7. https://doi.org/10.3390/colloids2010007
APA StyleOtsuki, A., Dodbiba, G., & Fujita, T. (2018). Two-Liquid Flotation for Separating Mixtures of Ultra-Fine Rare Earth Fluorescent Powders for Material Recycling—A Review. Colloids and Interfaces, 2(1), 7. https://doi.org/10.3390/colloids2010007






