Low-SNR Northern Right Whale Upcall Detection and Classification Using Passive Acoustic Monitoring to Reduce Adverse Human–Whale Interactions
Abstract
1. Introduction
- Insight into the challenges of NARW upcall classification in real-world, low-SNR environments, specifically investigating the ideal binary mask (IBM) method as a robust detection scheme.
- A newly curated low-SNR NARW upcall dataset to simulate underwater environments where weak (or distant) NARW are masked by noise in the vicinity of the marine mammal or receivers.
- Proposed a novel classification method, IBM combined with a bidirectional long short-term memory highway network (IBM-BHN), specifically designed to be sensitive and robust to low-SNR NARW upcalls.
- Introduction of a feature fusion strategy that integrates acoustic information from the temporal, spectral, and cepstral domains, overcoming the limitations of single-domain feature methods.
- Integration of a network optimization technique—a highway network for information flow optimization—to enhance computation efficiency and enable the near-real-time classification necessary for timely conservation actions.
2. Related Work
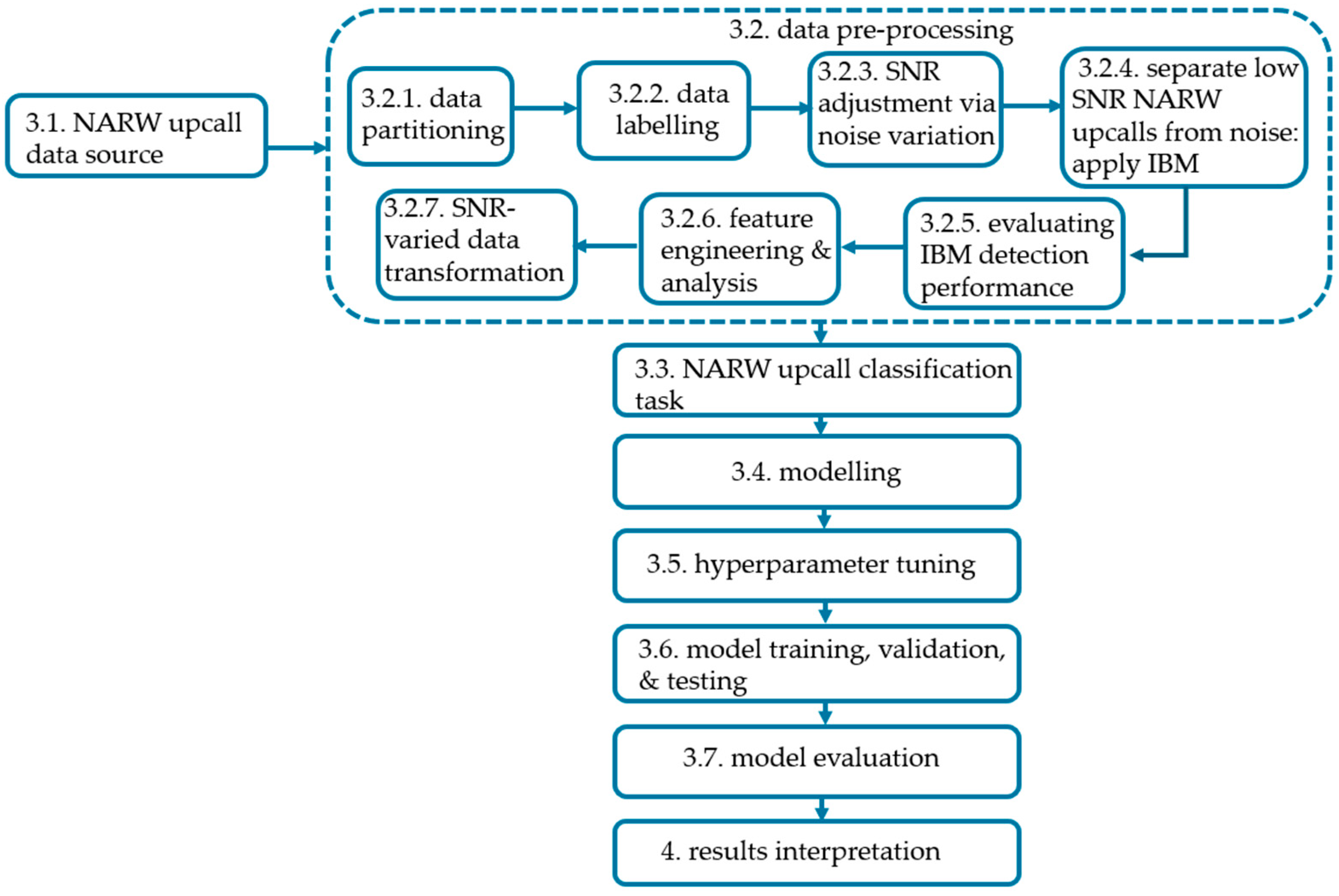
3. Methods
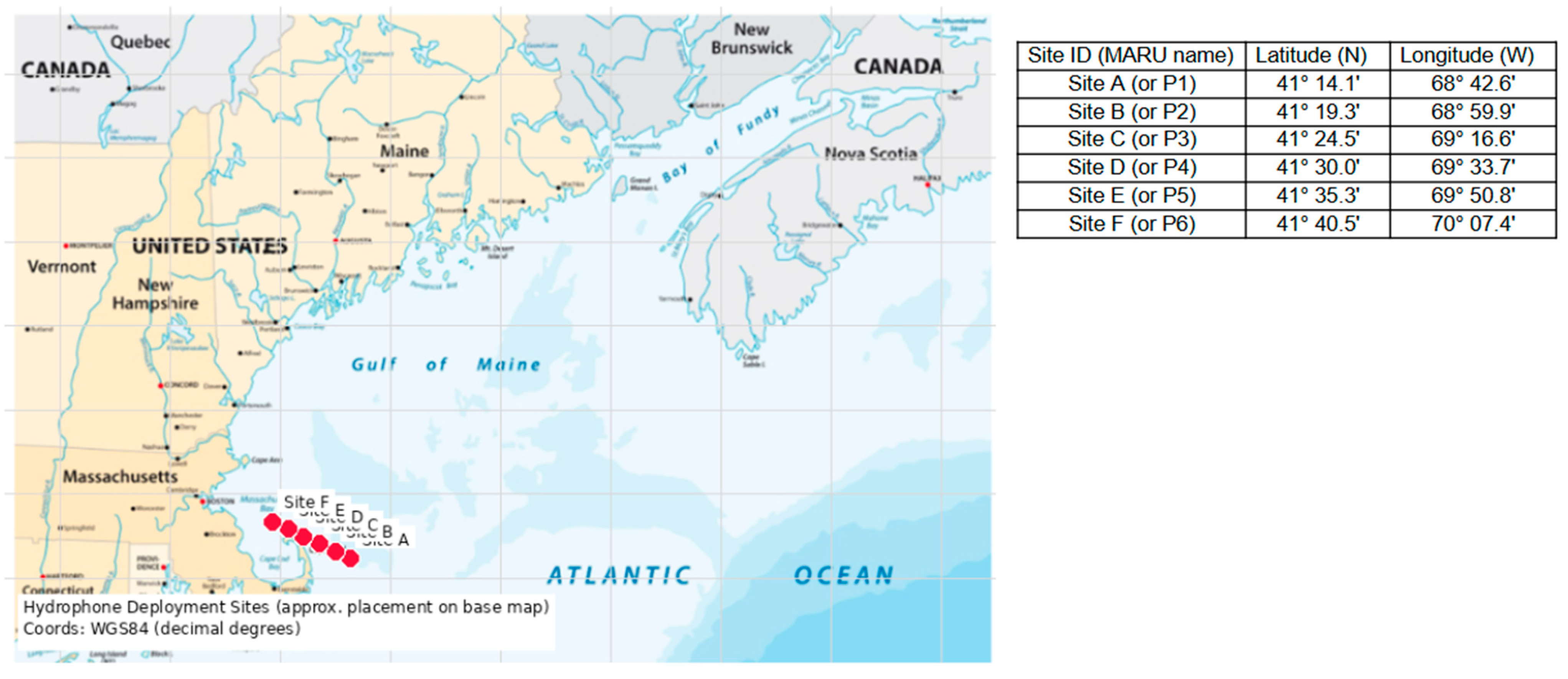
3.1. NARW Vocalization Data Source
3.2. Data Pre-Processing
3.2.1. Data Partitioning
3.2.2. Data Labeling
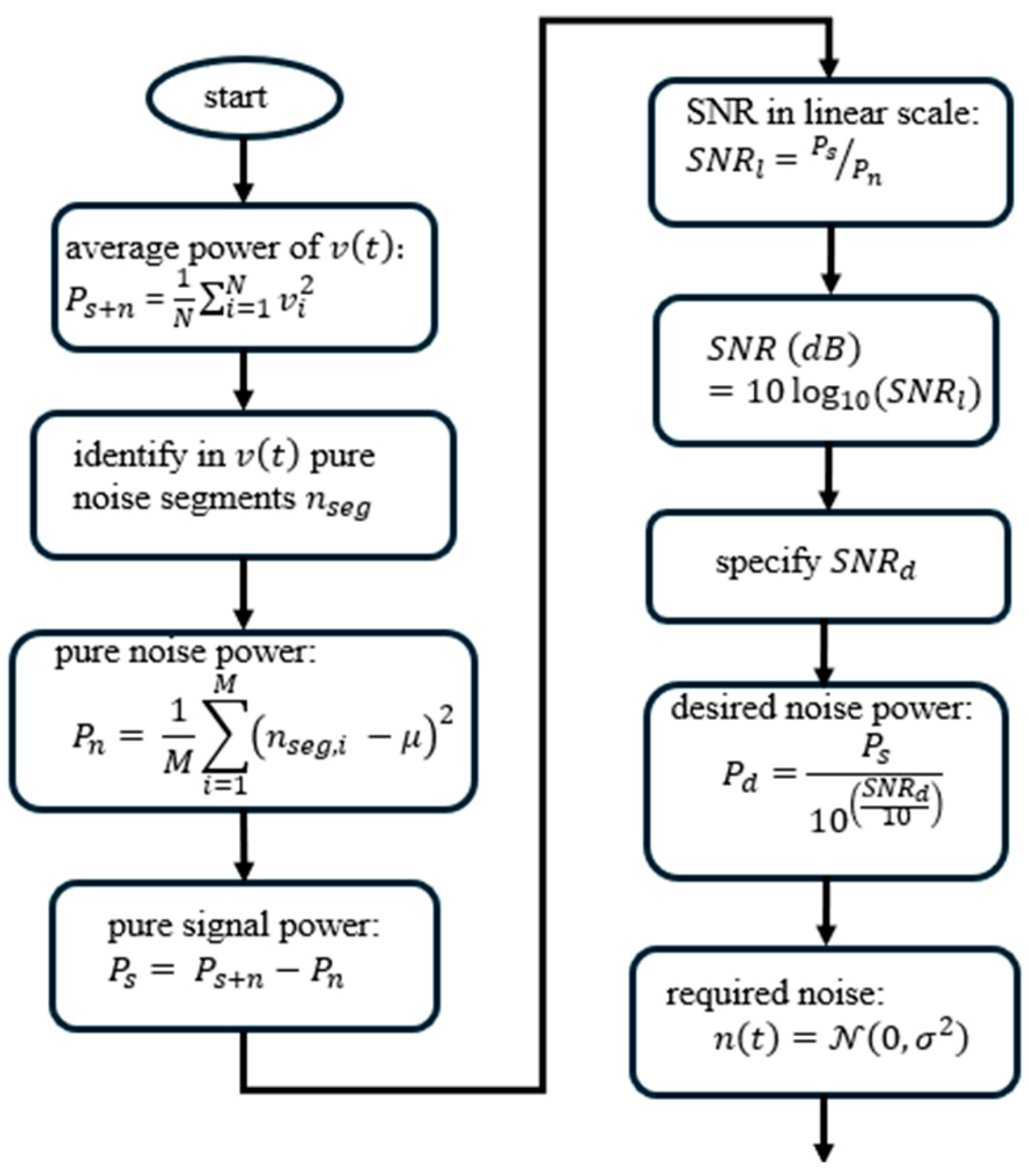
3.2.3. Upcall SNR Design via Noise Variation
- Numerical SNR verification: The SNR is mathematically defined by the ratio of signal power and noise power, which is equivalent to the ratio of their respective root mean square (RMS) amplitudes, as in Equation (2):
- Noise generation: The overall process of generating noise is detailed in Figure 3.
- Signal superposition: The mixed signal is created by superposing the upcall signal () and the scaled background noise component (), as in Equation (3):
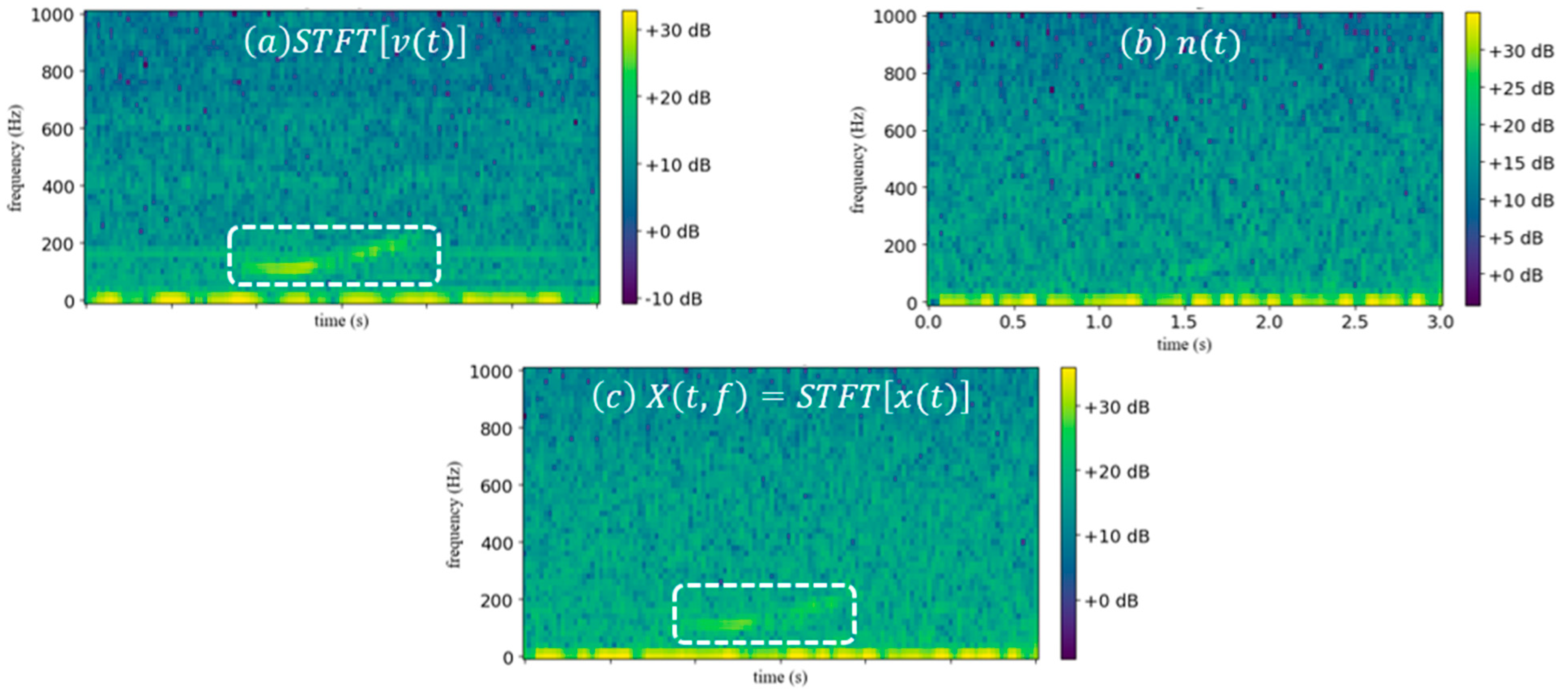
3.2.4. Separate Low-SNR NARW Upcalls from Noise: Apply Ideal Binary Mask (IBM)
3.2.5. Evaluating IBM Detection Performance
- Computation Time (CT)
- ii.
- Similarity Coefficient ( )
- iii.
- Check for Data Leakage
3.2.6. Feature Engineering and Analysis of the NARW Upcalls
- Feature Extraction
- Skew Identification
- ii.
- Identifying Outliers
- 2.
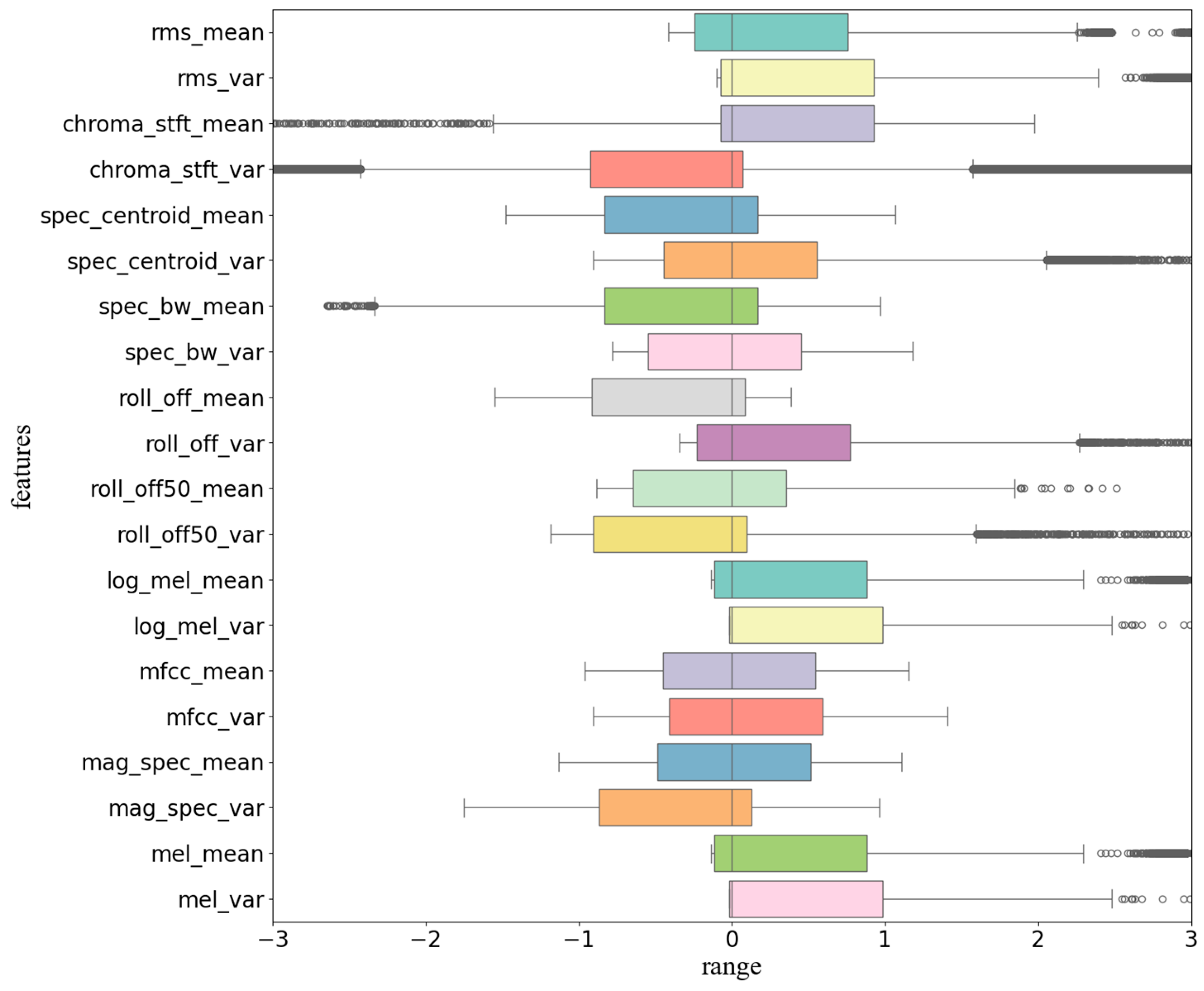
- Feature Type Correlation Analysis
3.2.7. SNR-Varied Data Transformation
3.3. NARW Upcall Classification Task
- root mean square energy (rms);
- chroma short-time Fourier transform (chroma_stft);
- spectral centroid (spec_centroid);
- spectral bandwidth (spec_bw);
- roll-off (roll_off);
- 50% roll-off (roll_off50);
- log mel-spectrogram (log_mel);
- mel-frequency cepstral coefficients (MFCCs);
- magnitude spectrogram (mag_spec); and
- mel-frequency (mel).
3.4. Modeling
3.4.1. Baseline Method
- Support Vector Machine (SVM)
- 2.
- Artificial Neural Networks (ANNs)
- 3.
- Convolutional Neural Network (CNN)
- 4.
- Long Short-Term Memory (LSTM)
- 5.
- Residual Neural Networks (ResNets)
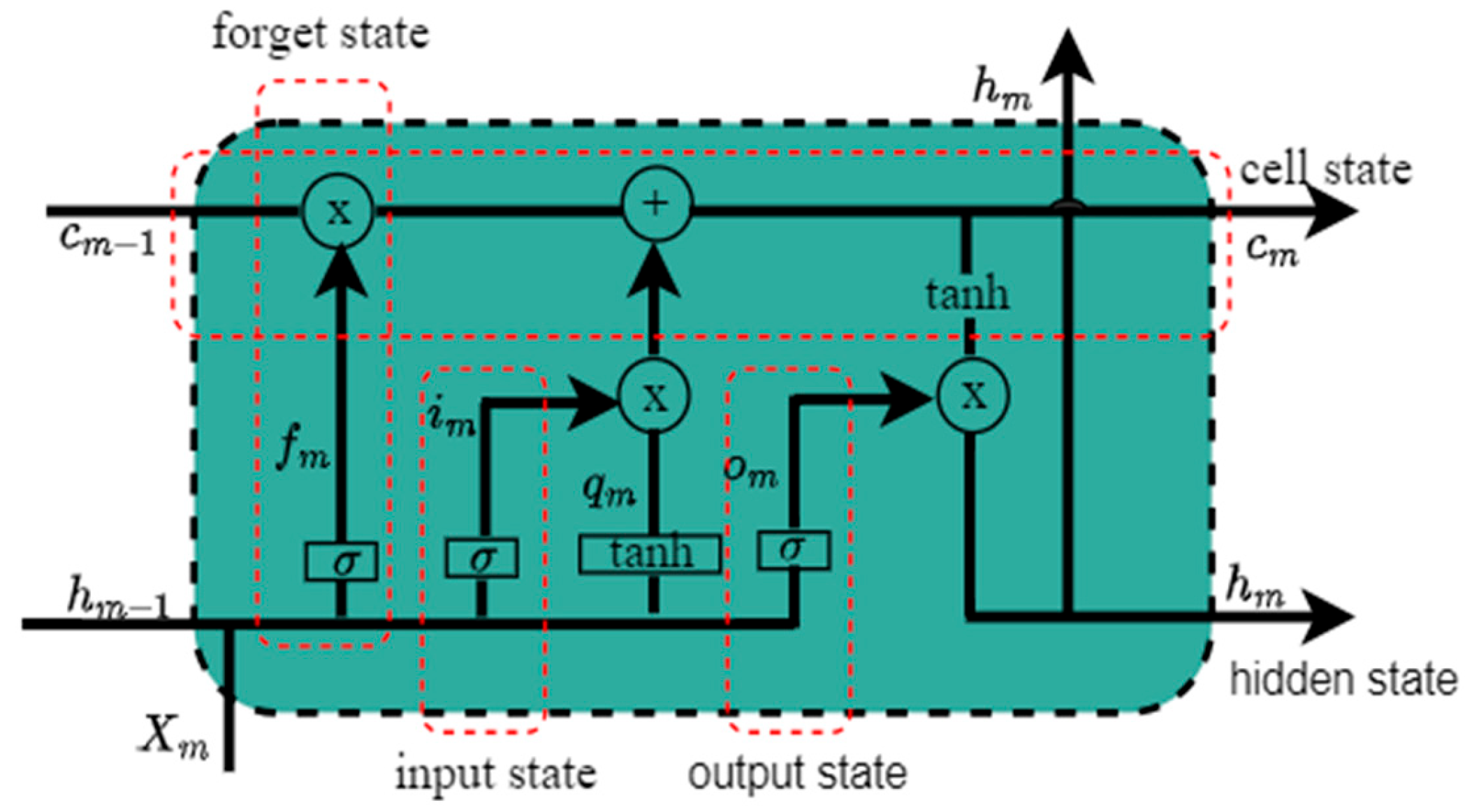
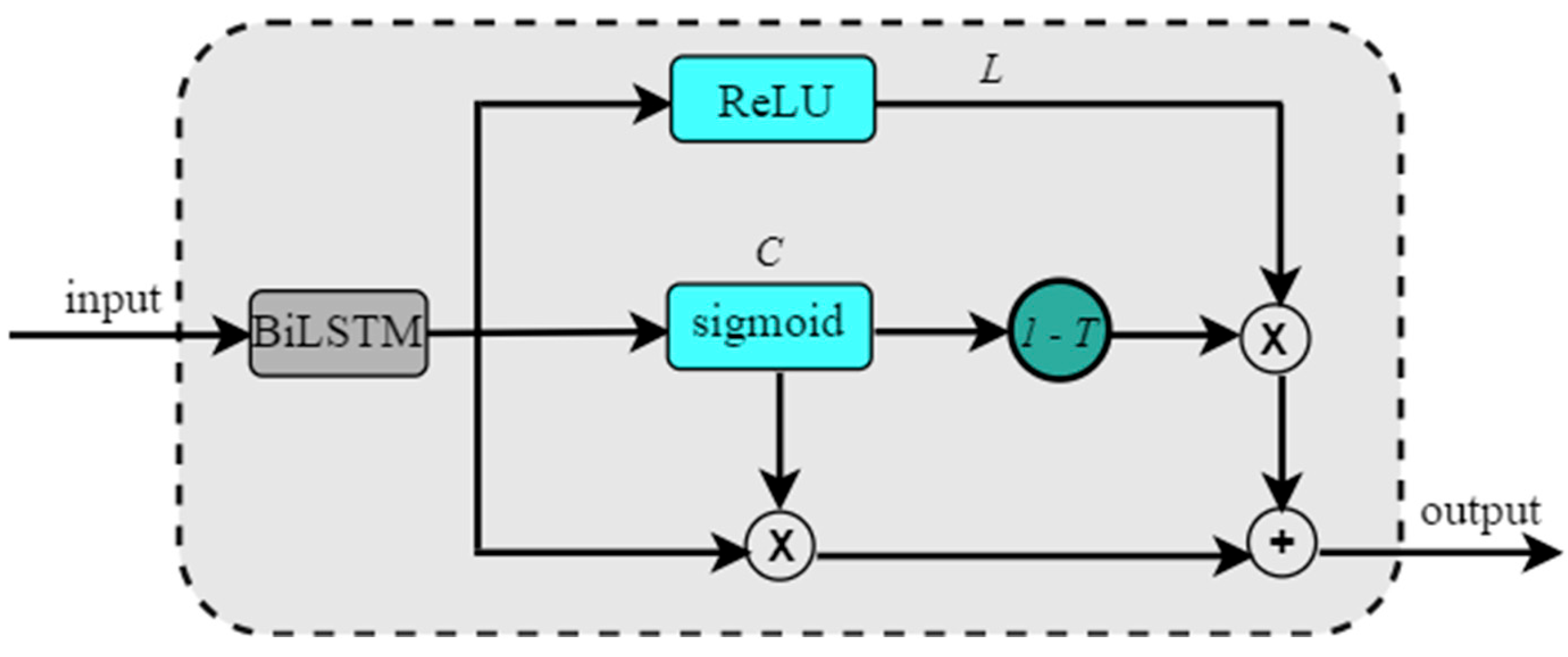
3.4.2. Proposed IBM with the BiLSTM–Highway Network (IBM-BHN) Method
- 1.
- Input Layer
- 2.
- BiLSTM Layer
- 3.
- Highway Network Layer
- 4.
- Flatten Layer
- 5.
- Dense Layer
- 6.
- Dropout Layer
- 7.
- Classification Layer
3.5. Hyperparameter Settings
3.6. Model Training, Validation, and Testing
3.6.1. Model Training
3.6.2. Model Validation
3.6.3. Model Testing
3.7. Model Evaluation
3.7.1. Metrics
3.7.2. Statistical Significance Testing
4. Results
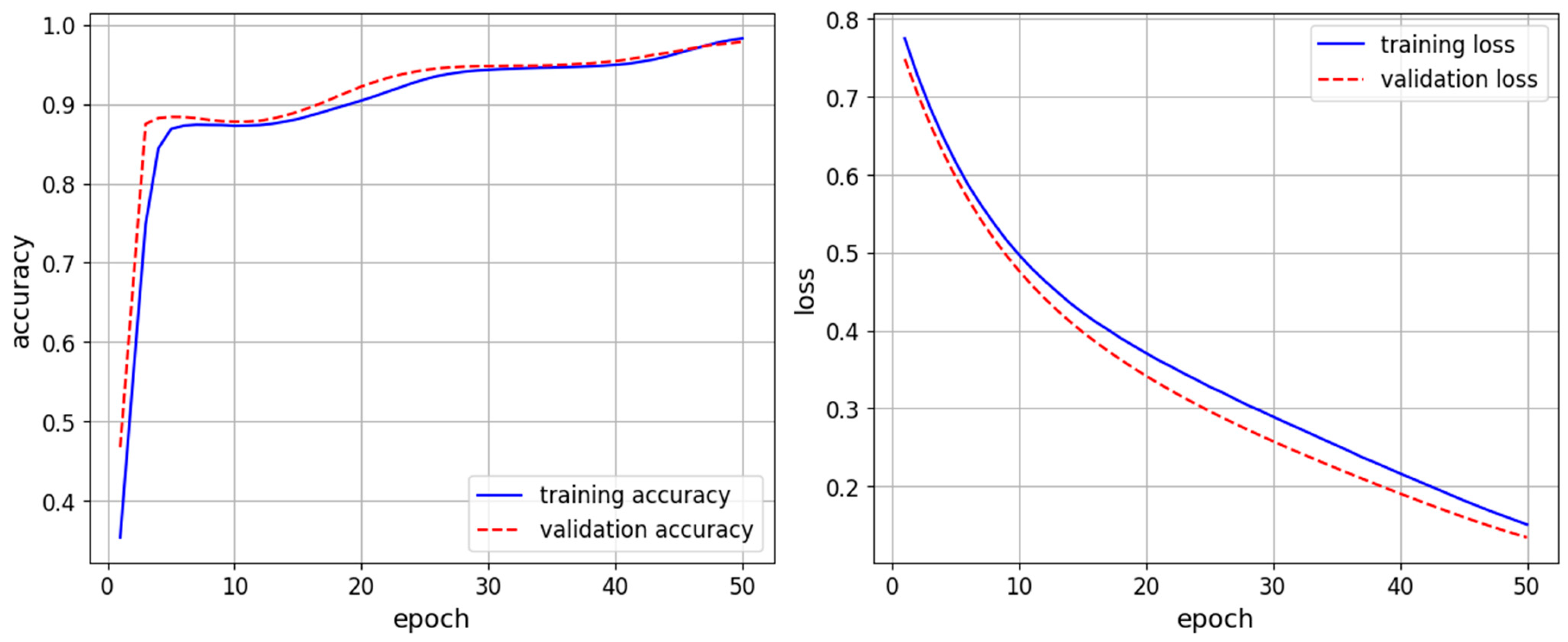
4.1. Training and Learning Curves
4.2. Performance of IBM-BHN for NARW Upcall Classification vs. Five Baseline Models
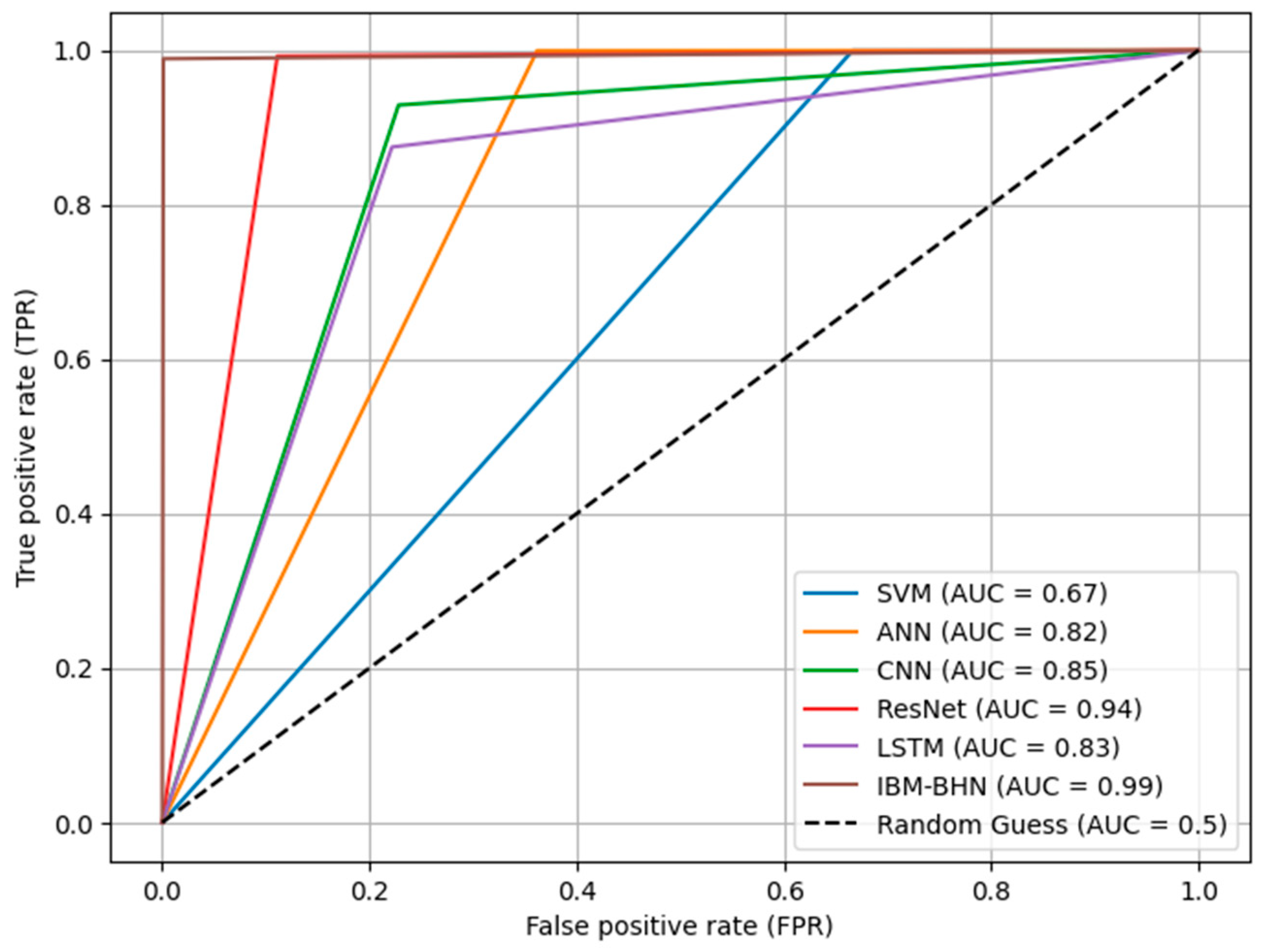
4.3. Receiver Operating Characteristic (ROC) Assessment: Proposed IBM-BHN Model vs. Baseline Models
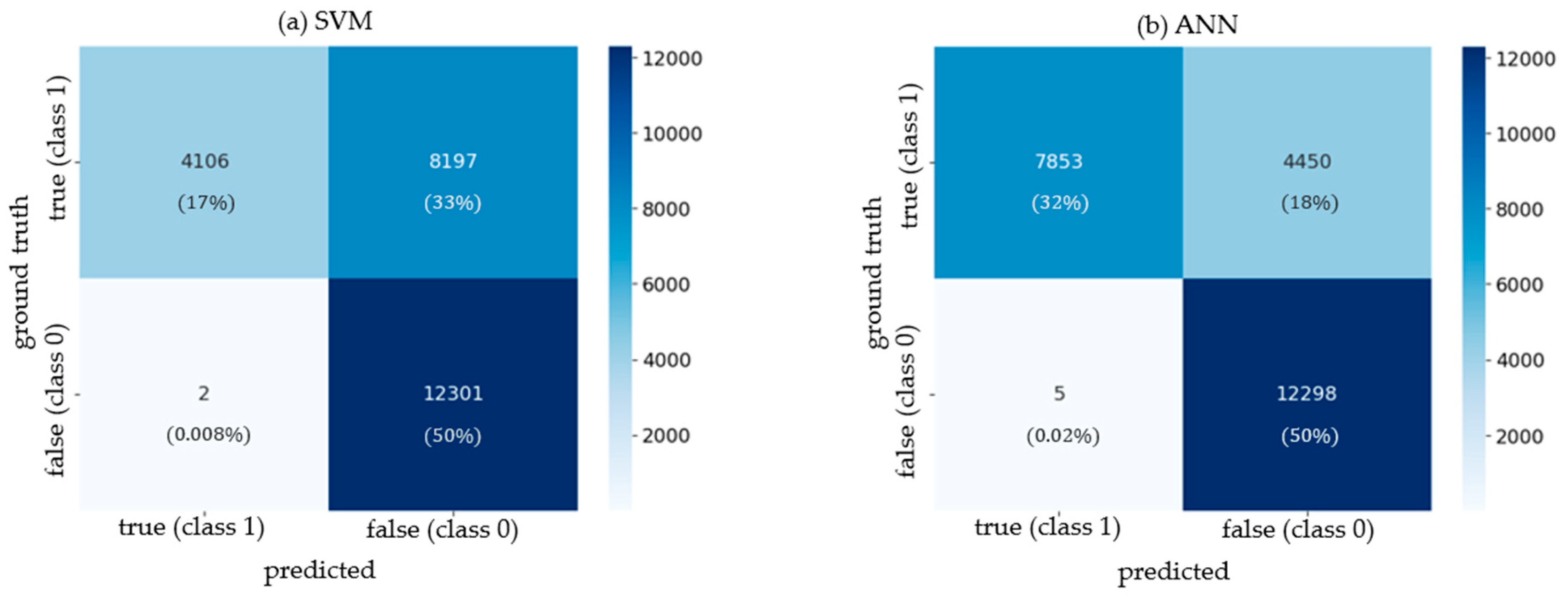
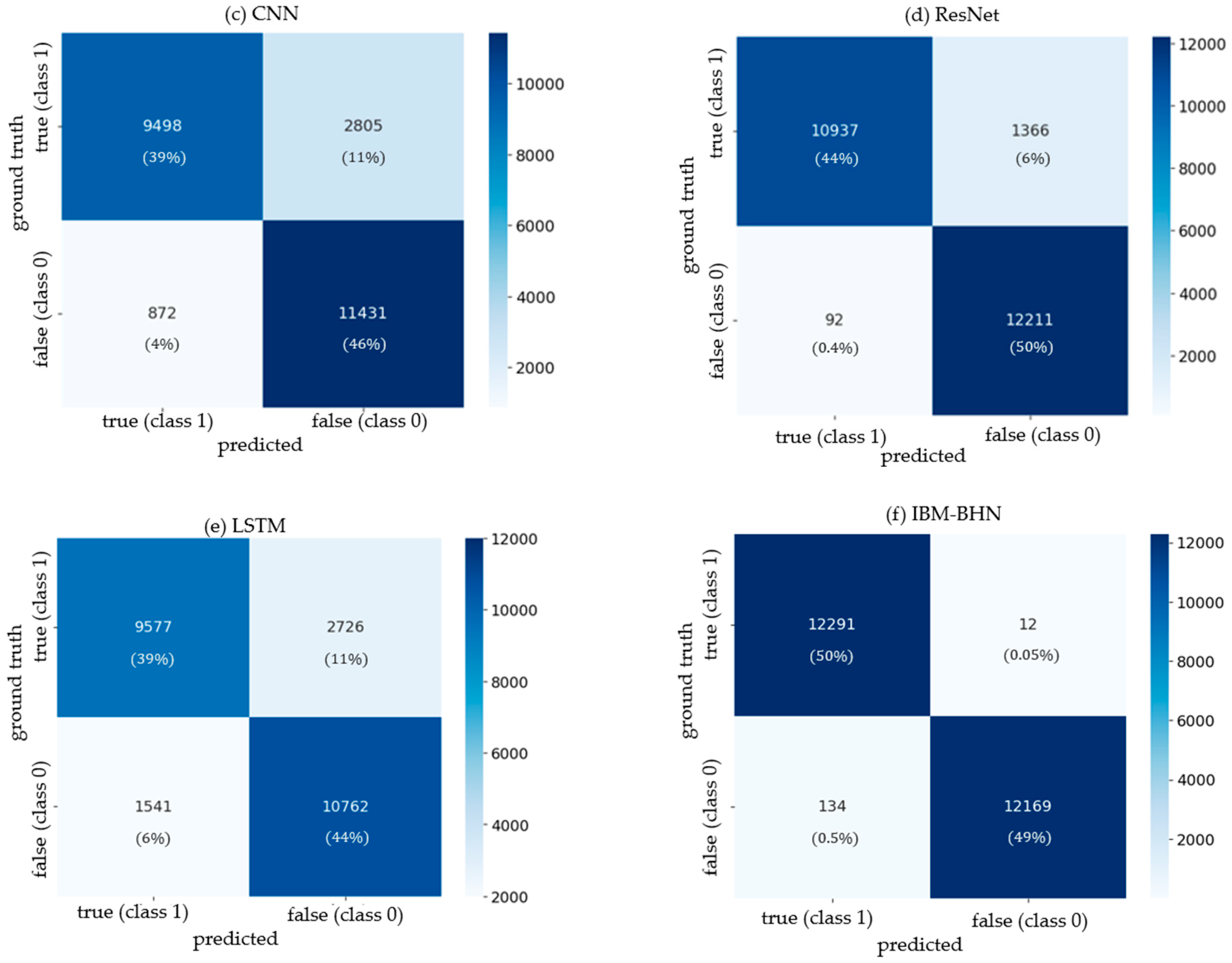
4.4. Error Analysis Comparison of IBM-BHN and the Five Baseline Models Considered
4.5. Comparison of Response Time: Proposed IBM-BHN vs. Baseline Models
4.6. Impact of BiLSTM Units on the IBM-BHN Classifier
4.7. Impact of Imbalanced Evaluation Test Dataset on False Positive and Negative Rates Performance
4.8. IBM-BHN Performance Under Diverse Noise Conditions
5. Discussion
5.1. Training and Learning Curves
5.2. Performance of IBM-BHN for NARW Upcall Classification vs. Five Baseline Models
5.3. Receiver Operating Characteristic (ROC) Assessment: Proposed IBM-BHN Model vs. Baseline Models
5.4. Error Analysis Comparison of IBM-BHN and the Five Baseline Models Considered
5.5. Comparison of Response Time: Proposed IBM-BHN vs. Baseline Methods
5.6. Impact of BiLSTM Units on the IBM-BHN Classifier
5.7. Impact of Imbalanced Evaluation Test Dataset on False Positive and Negative Rates Performance
5.8. IBM-BHN Performance Under Diverse Noise Conditions
5.9. Comparison of the IBM-BHN to Transformer-Based Model
- Targeted feature representation: IBM-BHN excels through explicit feature engineering. By integrating the acoustic characteristics of NARW upcall via hybrid feature input, the model is tuned to the specific bioacoustic target. In contrast, transformer models (e.g., ViTs, animal2vec) [29,30,31,32] are often pre-trained on generic images/birdsongs datasets which could lead to poor representations of marine mammal vocalizations that may render them less effective for detecting NARW upcalls in low-SNR environments.
- Computation efficiency: Unlike transformer models, which requires extensive computation resources due to their large size [62]—often making them impractical for low-resource, near-real-time PAM systems—IBM-BHN employs a lightweight architecture that combines a highway network mechanism with a BiLSTM to reduce computation burden. The highway network enhances the model’s performance and efficiency by optimizing information flow in the network.
5.10. Limitations
6. Conclusions
Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Physical Description | Implementation |
|---|---|---|
| root mean square energy (rms) |
| compute rms value for each frame by summing the squared samples and taking the square root |
| chroma short-time Fourier transform (chroma_stft) |
| compute the magnitude of the STFT coefficients and map them to chroma bins |
| spectral centroid (spec_centroid) |
| multiply each frequency bin by its magnitude and compute the centroid. |
| spectral bandwidth (spec_bw) |
| compute weighted average deviation from the spectral centroid |
| roll-off (roll_off) |
| finds frequency bin with the specified energy percentage |
| 50% roll-off (roll_off50) |
| find frequency bin with specified energy percentage |
| log mel-spectrogram (log_mel) |
| apply mel-filter banks to the magnitude of the STFT coefficients and take the logarithm |
| MFCC |
| compute the discrete cosine transform (DCT) of the log mel-spectrogram |
| magnitude spectrogram (mag_spec) |
| use magnitude of the STFT coefficients |
| mel-frequency (mel) |
| apply mel-filter banks to the magnitude of the STFT coefficients |
| Feature (a) | Feature (b) | Correlation | Description |
|---|---|---|---|
| rms |
|
| strong positive correlation strong negative correlation |
| var |
|
| strong positive correlation |
| chroma_stft_mean |
|
| strong positive correlation strong negative correlation |
| chroma_stft_var |
|
| strong negative correlation |
| spec_centroid_mean |
|
| strong positive correlation strong negative correlation |
| spec_centroid_var |
|
| strong positive correlation |
| spec_bw_mean |
|
| strong positive correlation strong negative correlation |
| spec_bw_var |
|
| strong positive correlation strong negative correlation |
| roll_off_mean |
|
| strong positive correlation strong negative correlation |
| roll_off_var |
|
| strong positive correlation strong negative correlation |
| roll_off50_mean |
|
| strong positive correlation strong negative correlation |
| roll_off50_var |
|
| strong positive correlation |
| log_mel_mean |
|
| strong positive correlation |
| log_mel_var |
|
| strong positive correlation |
| mfcc_mean |
|
| strong positive correlation strong negative correlation |
| mfcc_var |
|
| strong positive correlation strong negative correlation |
| mag_spec_mean |
|
| strong positive correlation strong negative correlation |
| mag_spec_var |
|
| strong positive correlation strong negative correlation |
| mel_mean |
|
| strong positive correlation |
| mel_var |
|
| strong positive correlation |
References
- Cook, D.; Malinauskaite, L.; Davíðsdóttir, B.; Ögmundardóttir, H.; Roman, J. Reflections on the ecosystem services of whales and valuing their contribution to human well-being. Ocean Coast. Manag. 2020, 186, 105100. [Google Scholar] [CrossRef]
- NOAA Fisheries. Laws Policies: Marine Mammal Protection Act. 2022. Available online: https://www.fisheries.noaa.gov/topic/laws-policies/marine-mammal-protection-act (accessed on 2 November 2023).
- Erceg, M.; Palamas, G. Towards Harmonious Coexistence: A Bioacoustic-Driven Animal-Computer. In Proceedings of the Interaction System for Preventing Ship Collisions with North Atlantic Right Whales, ACI, Raleigh, NC, USA, 4–8 December 2023; pp. 1–10. [Google Scholar]
- Roman, J.; Estes, J.A.; Morissette, L.; Smith, C.; Costa, D.M.; Nation, J.B.; Nicol, S.; Pershing, A.; Smetacek, V. Whales as marine ecosystem engineers. Front. Ecol. Environ. 2014, 12, 1201337. [Google Scholar] [CrossRef]
- Olatinwo, D.D.; Seto, M.L. Detection of Marine Mammal Vocalizations in Low SNR Environments with Ideal Binary Mask. In Proceedings of the IEEE OCEANS Conference, Halifax, NS, Canada, 23–26 September 2024; pp. 1–6. [Google Scholar]
- Chami, R.; Cosimano, T.C. Nature’s Solution to Climate Change. 2019. Available online: https://www.imf.org/en/publications/fandd/issues/2019/12/natures-solution-to-climate-change-chami (accessed on 23 September 2024).
- Brunoldi, M.; Bozzini, G.; Casale, A.; Corvisiero, P.; Grosso, D.; Magnoli, N.; Alessi, J.; Bianchi, C.N.; Mandich, A.; Morri, C.; et al. A permanent automated real-time passive acoustic monitoring system for bottlenose dolphin conservation in the mediterranean sea. PLoS ONE 2016, 11, e0145362. [Google Scholar] [CrossRef] [PubMed]
- Marques, T.A.; Thomas, L.; Martin, S.W.; Mellinger, D.K.; Ward, J.A.; Moretti, D.J.; Harris, D.; Peter, L.; Tyack, P.L. Estimating animal population density using passive acoustics. Biol. Rev. 2013, 88, 287–309. [Google Scholar] [CrossRef]
- Gavrilov, A.N.; McCauley, R.D.; Salgado-Kent, C.; Tripovich, J.; Burton, C. Vocal characteristics of pygmy blue whales and their change over time. J. Acoust. Soc. Am. 2011, 130, 3651–3660. [Google Scholar] [CrossRef]
- Gillespie, D.; Hastie, G.; Montabaranom, J.; Longden, E.; Rapson, K.; Holoborodko, A.; Sparling, C. Automated detection and tracking of marine mammals in the vicinity of tidal turbines using multibeam sonar. J. Mar. Sci. Eng. 2023, 11, 2095. [Google Scholar] [CrossRef]
- Dede, A.A. Long-term passive acoustic monitoring revealed seasonal and diel patterns of cetacean presence in the Istanbul strait. J. Mar. Biol. Assoc. United Kingd. 2014, 94, 1195–1202. [Google Scholar] [CrossRef]
- Sherin, B.M.; Supriya, M.H. Selection and Parameter Optimization of SVM Kernel Function for Underwater Target Classification. In Proceedings of the 2015 IEEE Underwater Technology (UT) 2015, Chennai, India, 23 February 2015; pp. 1–5. [Google Scholar]
- Scaradozzi, D.; De Marco, R.; Veli, D.L.; Lucchetti, A.; Screpanti, L.; Di Nardo, F. Convolutional Neural Networks for enhancing detection of Dolphin whistles in a dense acoustic environment. IEEE Access 2024, 12, 127141–127148. [Google Scholar] [CrossRef]
- Abou Baker, N.; Zengeler, N.; Handmann, U.A. Transfer learning evaluation of deep neural networks for image classification. Mach. Learn. Knowl. Extr. 2022, 4, 22–41. [Google Scholar] [CrossRef]
- Premus, V.E.; Abbot, P.A.; Illich, E.; Abbot, T.A.; Browning, J.; Kmelnitsky, V. North Atlantic right whale detection range performance quantification on a bottom-mounted linear hydrophone array using a calibrated acoustic source. J. Acoust. Soc. Am. 2025, 158, 3672–3686. [Google Scholar] [CrossRef]
- Hamard, Q.; Pham, M.T.; Cazau, D.; Heerah, K. A deep learning model for detecting and classifying multiple marine mammal species from passive acoustic data. Ecol. Inform. 2024, 84, 102906. [Google Scholar] [CrossRef]
- Sharma, G.; Umapathy, K.; Krishnan, S. Trends in audio signal feature extraction methods. Appl. Acoust. 2020, 158, 107020. [Google Scholar] [CrossRef]
- Serra, O.M.; Martins, F.P.; Padovese, L.R. Active contourbased detection of estuarine dolphin whistles in spectrogram images. Ecol. Inform. 2020, 55, 101036. [Google Scholar] [CrossRef]
- Ibrahim, A.K.; Zhuang, H.; Erdol, N.; Ali, A.M. A new approach for north atlantic right whale upcall detection. In Proceedings of the IEEE 2016 International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 260–263. [Google Scholar]
- Pourhomayoun, M.; Dugan, P.; Popescu, M.; Risch, D.; Lewis, H.; Clark, C. Classification for Big Dataset of Bioacoustic Signals Based on Human Scoring System and Artificial Neural Network. In Proceedings of the ICML 2013 Workshop on Machine Learning for Bioacoustic, Atlanta, GA, USA, 16–21 June 2013; pp. 1–5. [Google Scholar]
- Bahoura, M.; Simard, Y. Blue whale calls classification using short time fourier and wavelet packet transforms and artificial neural network. Digit. Signal Process. 2010, 20, 1256–1263. [Google Scholar] [CrossRef]
- Choi, R.Y.; Coyner, A.S.; Kalpathy-Cramer, J.; Chiang, M.F.; Campbell, J.P. Introduction to machine learning, neural networks, and deep learning. Transl. Vis. Sci. Technol. 2020, 9, 14. [Google Scholar] [PubMed]
- Wang, D.; Zhang, L.; Lu, Z.; Xu, K. Large-scale whale call classification using deep convolutional neural network architectures. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14 September 2018; pp. 1–5. [Google Scholar]
- Thomas, M.; Martin, B.; Kowarski, K.; Gaudet, B.; Matwin, S. Marine Mammal Species Classification Using Convolutional Neural Networks and a Novel Acoustic Representation. In Machine Learning and Knowledge Discovery in Databases; ECML PKDD, 2019; Brefeld, U., Fromont, E., Hotho, A., Knobbe, A., Maathuis, M., Robardet, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 11908. [Google Scholar] [CrossRef]
- Kirsebom, S.O.; Frazao, F.; Simard, Y.; Roy, N.; Matwin, S.; Giard, S. Performance of a deep neural network at detecting north atlantic right whale upcalls. J. Acoust. Soc. Am. 2020, 147, 2636–2646. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, C.; Bi, Y.; Xue, B.; Vennell, R.; Childe, S.H.; Pine, M.K.; Zhang, M. Deep convolutional neural networks for detecting dolphin echolocation clicks. In Proceedings of the 2021 36th International Conference on Image and Vision Computing New Zealand (IVCNZ), Tauranga, New Zealand, 9 December 2021; pp. 1–6. [Google Scholar]
- Duan, D. Detection method for echolocation clicks based on LSTM networks. Mob. Inf. Syst. 2022, 2022, 4466037. [Google Scholar] [CrossRef]
- Alizadegan, H.; Rashidi, M.B.; Radmehr, A.; Karimi, H.; Ilani, M.A. Comparative study of long short-term memory (LSTM), bidirectional LSTM, and traditional machine learning approaches for energy consumption prediction. Energy Explor. Exploit. 2025, 43, 281–301. [Google Scholar] [CrossRef]
- Makropoulos, D.N.; Filntisis, P.P.; Prospathopoulos, A.; Kassis, D.; Tsiami, A.; Maragos, P. Improving classification of marine mammal vocalizations using vision transformers and phase-related features. In Proceedings of the 2025 25th International Conference on Digital Signal Processing (DSP), Costa Navarino, Greece, 25 June 2025; pp. 1–5. [Google Scholar]
- Gong, Y.; Lai, C.K.; Chung, Y.A. Audio Spectrogram Transformer: General Audio Classification with Image Transformers. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 2049–2063. [Google Scholar]
- You, S.H.; Coyotl, E.P.; Gunturu, S.; Van Segbroeck, M. Transformer-Based Bioacoustic Sound Event Detection on Few-Shot Learning Tasks. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023. [Google Scholar]
- Ahmed, S.A.; Awais, M.; Wang, W.; Plumbley, M.D.; Kittler, J. Asit: Local-global audio spectrogram vision transformer for event classification. IEEE/ACM Trans. Audio Speech Lang. Process. 2024, 32, 3684–3693. [Google Scholar] [CrossRef]
- DCLDE. DCLDE 2013 Workshop Dataset. 2013. Available online: https://research-portal.st-andrews.ac.uk/en/datasets/dclde-2013-workshop-dataset (accessed on 7 April 2025).
- Clark, C.W.; Brown, M.W.; Corkeron, P. Visual and acoustic surveys for North Atlantic right whales, Eubalaena glacialis, in Cape Cod Bay, Massachusetts, 2001–2005: Management implications. Mar. Mammal Sci. 2010, 26, 837–854. [Google Scholar] [CrossRef]
- Thomas, M.; Martin, B.; Kowarski, K.; Gaudet, B.; Matwin, S. Detecting Endangered Baleen Whales within Acoustic Recordings using R-CNNs. In Proceedings of the AI for Social Good Workshop at NeurIPS, Vancouver, VA, Canada, 14 December 2019; pp. 1–5. [Google Scholar]
- Gholamy, A.; Kreinovich, V.; Kosheleva, O. Why 70/30 or 80/20 relation between training and testing sets: A pedagogical explanation. Int. J. Intell. Technol. Appl. Stat. 2018, 11, 105–111. [Google Scholar]
- Pandas. DataFrame—Pandas 2.3.1 Documentation. Available online: https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html (accessed on 8 August 2025).
- Zhang, W.; Li, X.; Zhou, A.; Ren, K.; Song, J. Underwater acoustic source separation with deep Bi-LSTM networks. In Proceedings of the IEEE 4th International Conference on Information Communication and Signal Processing (ICICSP), Shanghai, China, 24–26 September 2021; pp. 254–258. [Google Scholar]
- Wang, D. On ideal binary mask as the computational goal of auditory scene analysis. In Speech Separation by Humans and Machines; Divenyi, P., Ed.; Springer: Boston, MA, USA, 2005; pp. 181–197. [Google Scholar]
- Wang, D.; Chen, J. Supervised speech separation based on deep learning: An overview. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1702–1726. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Wang, D.L. Speech segregation based on pitch tracking and amplitude modulation. In Proceeding of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Platz, NY, USA, 24 October 2001; pp. 1–4. [Google Scholar]
- Hu, G.; Wang, D.L. Monaural speech segregation based on pitch tracking and amplitude modulation. IEEE Trans. Neural Netw. 2004, 15, 1135–1150. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, C.; Xie, J.; An, J.; Huang, N. Time–frequency mask-aware bidirectional lstm: A deep learning approach for underwater acoustic signal separation. Sensors 2022, 15, 5598. [Google Scholar] [CrossRef] [PubMed]
- Ravid, R. Practical Statistics for Educators; Rowman & Littlefield Publishers: Lanham, MD, USA, 2019. [Google Scholar]
- Katthi, J.; Ganapathy, S. Deep correlation analysis for audio-EEG decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2001, 29, 2742–2753. [Google Scholar] [CrossRef] [PubMed]
- Mushtaq, Z.; Su, S.F.; Tran, Q.V. Spectral images based environmental sound classification using CNN with meaningful data augmentation. Appl. Acoust. 2001, 172, 107581. [Google Scholar] [CrossRef]
- Goldwater, M.; Zitterbart, D.P.; Wright, D.; Bonnel, J. Machine-learning-based simultaneous detection and ranging of impulsive baleen whale vocalizations using a single hydrophone. J. Acoust. Soc. Am. 2023, 153, 1094–1107. [Google Scholar] [CrossRef]
- Raju, V.G.; Lakshmi, K.P.; Jain, V.M.; Kalidindi, A.; Padma, V. Study the influence of normalization/transformation process on the accuracy of supervised classification. In Proceedings of the IEEE Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20 August 2020; pp. 729–735. [Google Scholar]
- Ahsan, M.M.; Mahmud, M.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of data scaling methods on machine learning algorithms and model performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Wilkinson, N.; Niesler, T. A hybrid CNN-BiLSTM voice activity detector. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6 June 2021; pp. 6803–6807. [Google Scholar]
- Hendricks, B.; Keen, E.M.; Wray, J.L.; Alidina, H.M.; McWhinnie, L.; Meuter, H.; Picard, C.R.; Gulliver, T.A. Automated monitoring and analysis of marine mammal vocalizations in coastal habitats. In Proceedings of the IEEE OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28 May 2018; pp. 1–10. [Google Scholar]
- Zhu, C.; Seri, S.G.; Mohebbi-Kalkhoran, H.; Ratilal, P. Long-range automatic detection, acoustic signature characterization and bearing-time estimation of multiple ships with coherent hydrophone array. Remote Sens. 2020, 12, 3731. [Google Scholar] [CrossRef]
- Graves, A.; Fernández, S.; Schmidhuber, J. Bidirectional LSTM networks for improved phoneme classification and recognition. In Proceedings of the International Conference on Artificial Neural Networks, Warsaw, Poland, 11–15 June 2005; pp. 799–804. [Google Scholar]
- Li, W.; Qi, F.; Tang, M.; Yu, Z. Bidirectional lstm with self-attention mechanism and multi-channel features for sentiment classification. Neurocomputing 2020, 387, 63–77. [Google Scholar] [CrossRef]
- Liu, G.; Guo, J. Bidirectional lstm with attention mechanism and convolutional layer for text classification. Neurocomputing 2019, 337, 325–338. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Zilly, J.G. Recurrent highway networks. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 17 July 2017; pp. 4189–4198. [Google Scholar]
- Sabiri, B.; El Asri, B.; Rhanoui, M. Mechanism of Overfitting Avoidance Techniques for Training Deep Neural Networks. ICEIS 2022, 2022, 418–427. [Google Scholar]
- Brownlee, J. Better Deep Learning: Train Faster, Reduce Overfitting, And Make Better Predictions; Machine Learning Mastery: San Juan, Puerto Rico, 2018. [Google Scholar]
- Chollet, F. Deep Learning with Python; Simon and Schuster: New York, NY, USA, 2021; pp. 1–504. [Google Scholar]
- Raschka, S. Stat 451: Machine Learning Lecture Notes. 2020. Available online: https://sebastianraschka.com/pdf/lecture-notes/stat451fs20/07-ensembles__notes.pdf (accessed on 9 November 2025).
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intelligence 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Song, G.; Guo, X.; Zhang, Q.; Li, J.; Ma, L. Underwater Noise Modeling and its Application in Noise Classification with Small-Sized Samples. J. Electron. 2023, 12, 2669. [Google Scholar] [CrossRef]
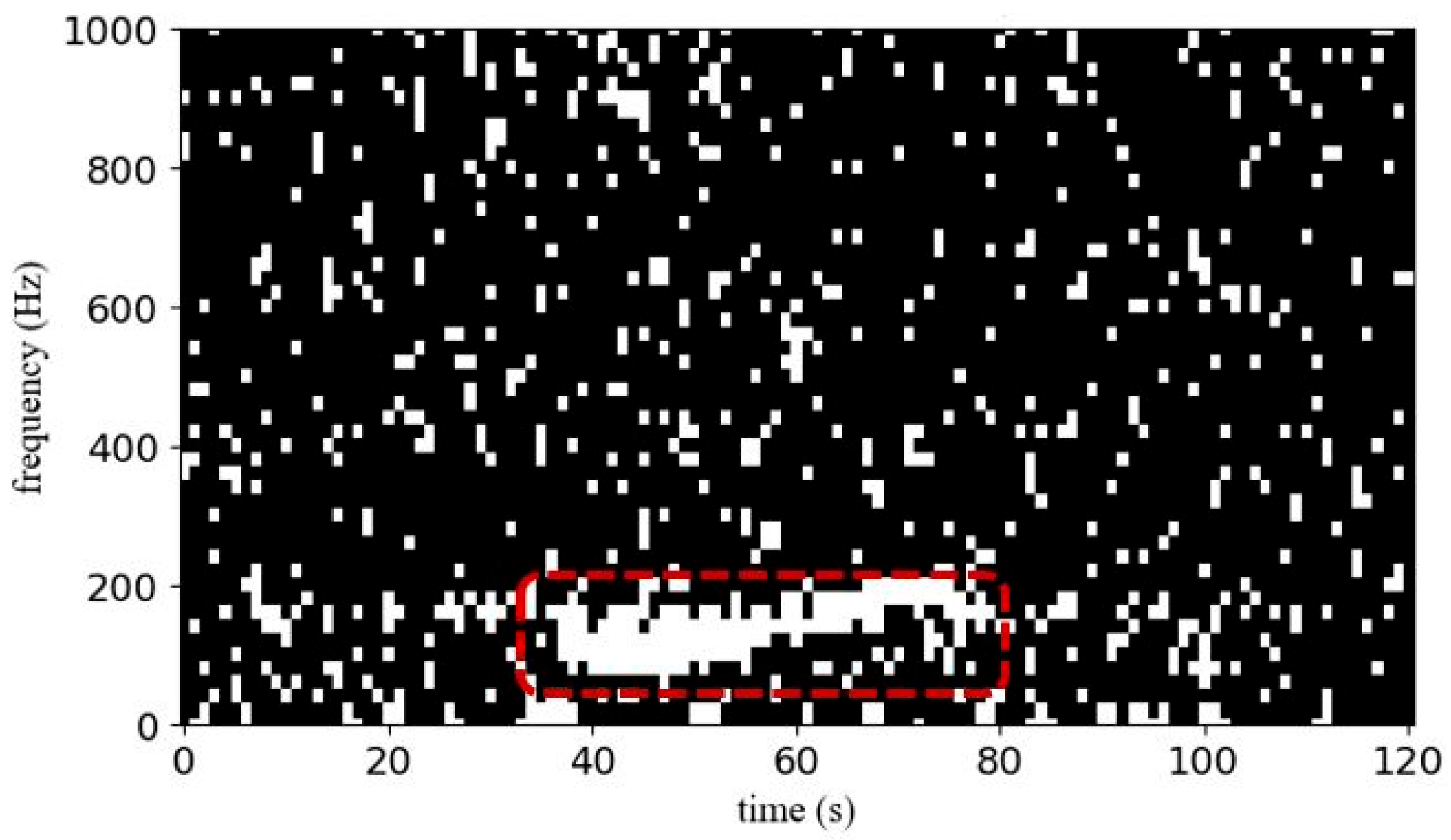
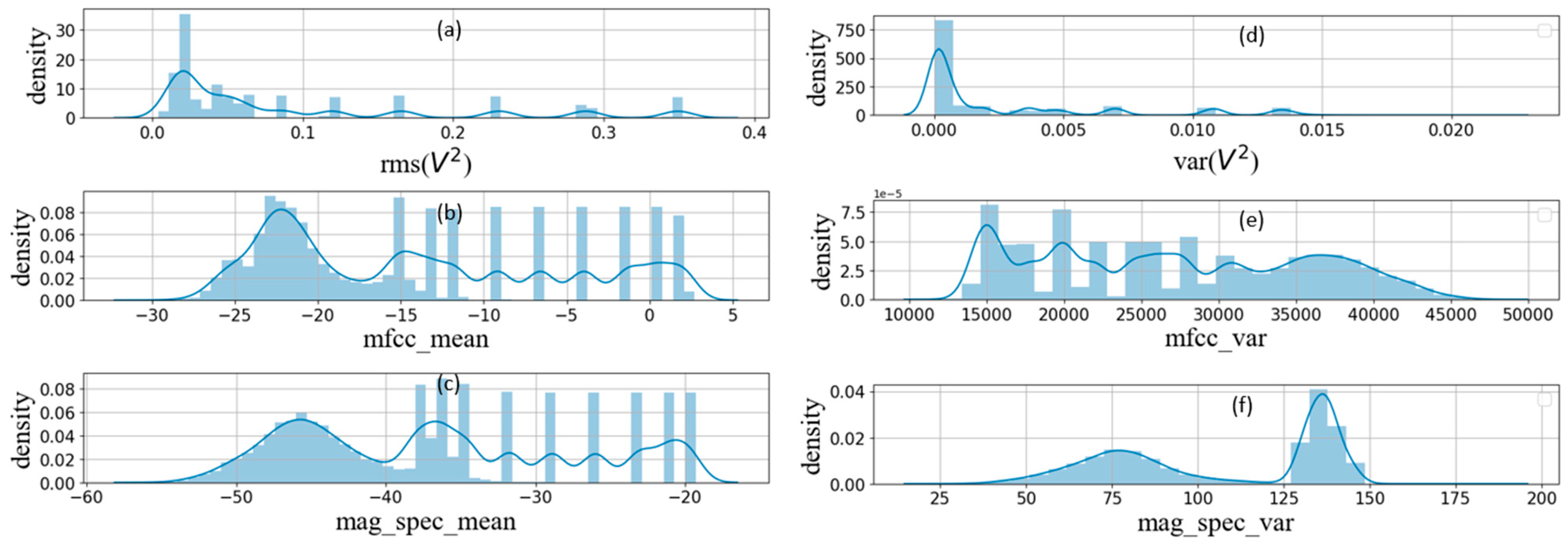
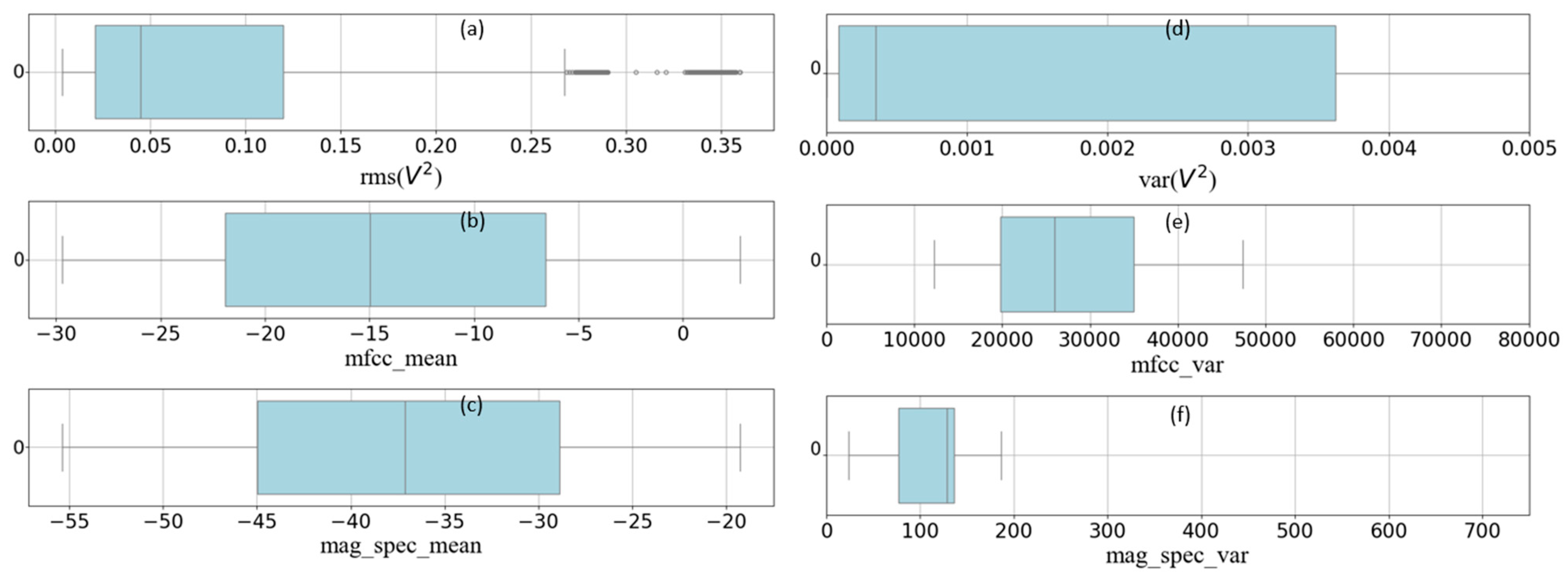
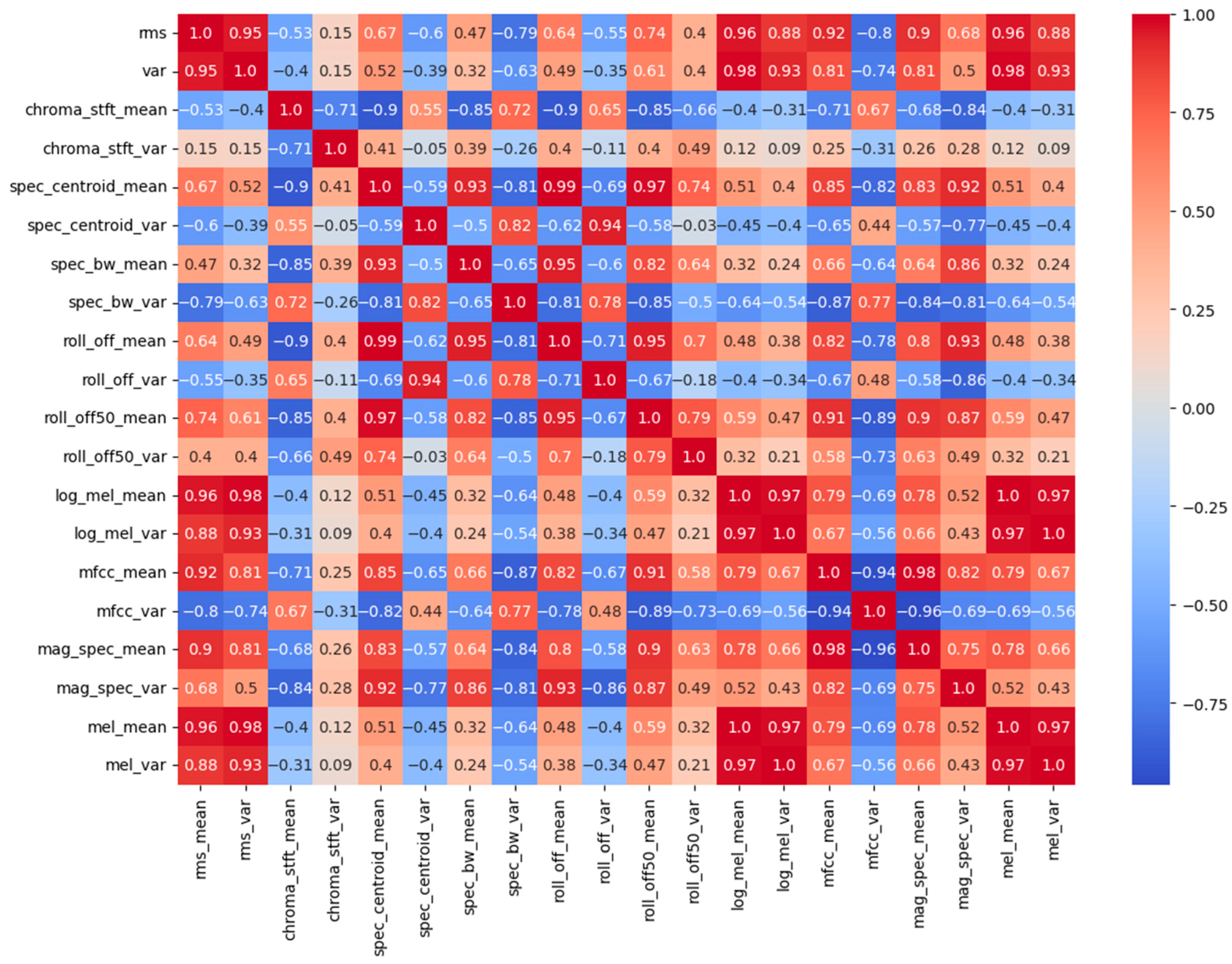


| Ref. | Classifier | Dataset | Feature Extraction | Accuracy | Network Optimization | SNR Ranges (dB) |
|---|---|---|---|---|---|---|
| [19] | SVM | DCLDE | MFCC & DWT | 92% | No | Not specified |
| [20] | ANN | PAM deployed at Stellwagen Bank National Marine Sanctuary. | Spectrogram and human perception features. | 86% | No | SNR > 0 dB |
| [21] | MLP | PAM deployed at St. Lawrence River Estuary. | Short-time Fourier transform (STFT) and wavelet packet transform (WPT). | 86% | No | Not specified |
| [23] | CNN | Kaggle | Mel-filter bank (mel-spectrograms) | 84% | No | Not specified |
| [24] | CNN | PAM deployed at Bay of Fundy. | Spectrogram | 95% | No | Not specified |
| [25] | ResNet | DCLDE | Spectrogram | Recall of 80% and precision of 90%. | No | SNR > 0 dB |
| [26] | LeNet | PAM deployed in New Zealand waters. | Spectrogram | 96% | No | SNR > 0 dB |
| [27] | LSTM | Self-collected dataset. | Spectrogram | 98% | No | Not specified |
| [29] | Swin Transformer | Watkins Marine Mammal Sound Database | Spectrogram and phase-related features. | 95% | No | Not specified |
| [30] | Self-supervised learning and AST | AudioSet and ESC-50 | Spectrogram | An average improvement of 60.9%. | No | Not specified |
| [31] | Transformer-Based Few-Shot | DCASE 2022 task-5 | Spectrogram | 73% | No | Not specified |
| Proposed IBM-BHN | DCLDE | 20 acoustic features across time, frequency, and cepstral domains | Yes | −10 dB to 10 dB |
| Category | Value | Description |
|---|---|---|
| Total audio files | 672 | 15 min long files |
| Total recording duration | 168 h | 672 files |
| Total NARW upcalls | 9063 | Extracted from annotated files, approximately 3 s each. |
| Background noise samples | 672 | 15 min long files |
| SNR range | to | Before noise addition |
| Algorithm 1: Separate Low SNR NARW Upcalls from Noise using IBM |
| 1: initialize: prepare signal 2: apply STFT to to obtain its representation 3: for each bin do Equation (5) 4: if then |
| 5: else 6: 7: end if 8: end 9: apply binary mask to Equation (6) 10: apply inverse STFT to Equation (6) 11: output: and noise |
| No. of Audio Recording (3 s Duration) | Manual Method (s) | Proposed IBM Method (s) |
|---|---|---|
| 10 | 600 | 0.05 |
| 20 | 1200 | 0.08 |
| 30 | 1800 | 0.13 |
| 40 | 2400 | 0.17 |
| 50 | 3000 | 0.18 |
(Equation (1)) | (a) Original Signal | (b) IBM Recovered (Table 1) | (c) Correlate (Equation (8)) | (d) Difference of (a)–(b) | (Equation (3)) | (f) Correlate (Equation (8)) |
|---|---|---|---|---|---|---|
| 10 | 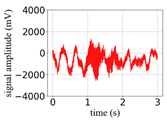 | 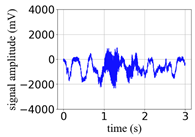 | 0.95 |  | 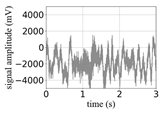 | 0.58 |
| 8 | 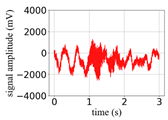 | 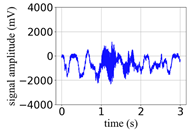 | 0.94 | 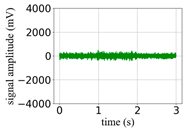 | 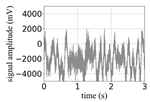 | 0.50 |
| 6 | 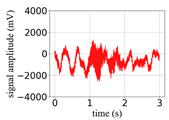 | 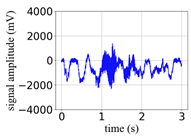 | 0.93 | 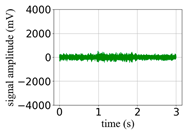 | 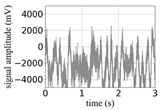 | 0.43 |
| 3 | 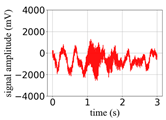 | 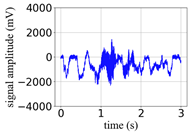 | 0.91 | 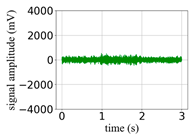 | 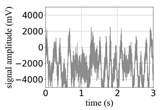 | 0.34 |
| 0 | 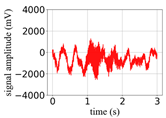 | 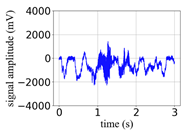 | 0.90 | 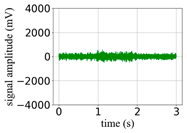 | 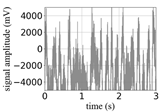 | 0.26 |
| −3 | 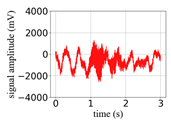 | 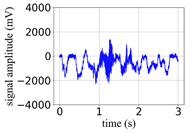 | 0.87 | 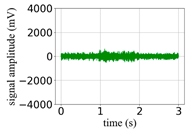 | 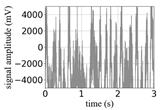 | 0.21 |
| −6 | 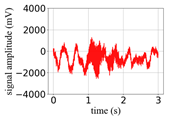 | 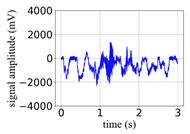 | 0.85 | 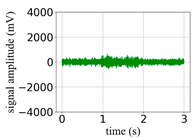 | 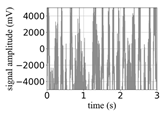 | 0.17 |
| −8 |  | 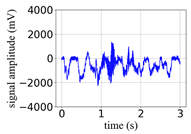 | 0.83 | 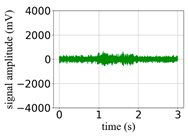 | 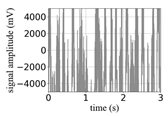 | 0.15 |
| −10 | 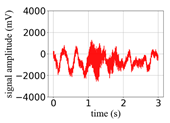 | 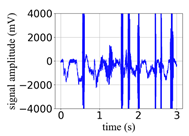 | 0.13 | 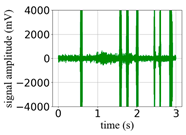 | 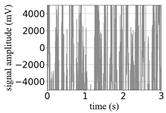 | 0.13 |
| Algorithm 2: Operation of the Proposed IBM-BHN Classifier |
| Require: Given the input sequence as = {, , , …, }, ∈ {0, 1} 1: use BiLSTM to capture contextual information 2: use Equations (11)–(14) to obtain the feature representation 3: feed the output of step 2 into a highway layer 4: flatten the output of step 3 |
| 5: input flattened features into the dense layer with L2 regularization rate 6: pass the output of step 5 into a dropout layer 7: specify 8: pass step 7 into the fully connected layer 9: perform classification using a sigmoid activation function 10: apply binary cross-entropy loss 11: use Adam optimization 12: update the weights and biases of the proposed method |
| Model | Hyperparameter | Value | Optimal |
|---|---|---|---|
| SVM |
|
|
|
|
|
| |
| ANN |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
| __ | 2 (1 hidden dense, 1 output dense) | |
|
|
| |
| CNN |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
| __ | 2 (1 Conv1D, 1 output dense) | |
|
|
| |
| ResNet |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
| __ | 8 (7 Conv1D, 1 output dense) | |
|
|
| |
| LSTM |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
| 64 | |
| __ | 3 (1 LSTM, 1 dense, 1 output dense) | |
|
|
| |
| IBM-BHN |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
| __ | 3 (1 BiLSTM, 1 highway, 1 output dense) | |
|
|
|
| Misclassified by Both Models (Proposed and Baseline): | Misclassified by Proposed IBM-BHN Model Only: |
|---|---|
| misclassified by baseline only: | correctly classified by both models (proposed baseline): |
| Model | Accuracy | Precision | Sensitivity | F1-Score | ||||
|---|---|---|---|---|---|---|---|---|
| Actual (%) | Actual (%) | Actual (%) | Actual (%) | |||||
| SVM | 67 | 31 | 60 | 39 | 99 | −3 | 75 | 23 |
| ANN | 82 | 16 | 73 | 26 | 99 | −3 | 85 | 13 |
| CNN | 85 | 13 | 80 | 19 | 93 | 3 | 86 | 12 |
| ResNet | 94 | 4 | 90 | 9 | 99 | −3 | 94 | 4 |
| LSTM | 83 | 15 | 80 | 19 | 87 | 9 | 83 | 15 |
| IBM-BHN | 98 | 0 | 99 | 0 | 96 | 0 | 98 | 0 |
| Comparison | p-Value | ||
|---|---|---|---|
| BiLSTM vs. SVM | 0.94 | ||
| BiLSTM vs. ANN | 0.85 | ||
| BiLSTM vs. CNN | 0.75 | ||
| BiLSTM vs. ResNet | 0.94 | ||
| BiLSTM vs. LSTM | 0.94 |
| Model | False Positive Rate (%) | False Negative Rate (%) |
|---|---|---|
| SVM | 40 | 0.1 |
| ANN | 27 | 0.1 |
| CNN | 20 | 8 |
| ResNet | 10 | 1 |
| LSTM | 20 | 14 |
| IBM-BHN | 0.1 | 1 |
| Model | Training Time (s) | Response Time (s) |
|---|---|---|
| ANN | 3 | 0.16 |
| CNN | 4 | 0.19 |
| ResNet | 67 | 0.48 |
| LSTM | 11 | 0.20 |
| IBM-BHN | 13 | 0.12 |
| BiLSTM Cells | Precision | Sensitivity |
|---|---|---|
| 96 | 99 | 96 |
| 64 | 99 | 96 |
| 32 | 99 | 96 |
| 16 | 99 | 96 |
| Model | False Positive Rate (%) | False Negative Rate (%) |
|---|---|---|
| SVM | 86 | 0 |
| ANN | 67 | 0 |
| CNN | 23 | 13 |
| ResNet | 7 | 6 |
| LSTM | 14 | 16 |
| IBM-BHN | 6 | 0 |
| SNR (dB) | False Positive Rate (%) | False Negative Rate (%) |
|---|---|---|
| 10 | 0 | 0 |
| 8 | 0 | 0 |
| 6 | 0 | 0 |
| 3 | 0 | 0.1 |
| 0 | 0 | 0.4 |
| −3 | 0.1 | 0.9 |
| −6 | 0.2 | 1.6 |
| −8 | 0.2 | 2.6 |
| −10 | 0.5 | 4.3 |
| Metric | IBM-BHN Score (%) | Best Baseline Score (ResNet) (%) | Improvement Over Baseline (%) |
|---|---|---|---|
| accuracy | 98.0 | 94.0 | 4.3 |
| F1-score | 98.0 | 94.0 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olatinwo, D.D.; Seto, M.L. Low-SNR Northern Right Whale Upcall Detection and Classification Using Passive Acoustic Monitoring to Reduce Adverse Human–Whale Interactions. Mach. Learn. Knowl. Extr. 2025, 7, 154. https://doi.org/10.3390/make7040154
Olatinwo DD, Seto ML. Low-SNR Northern Right Whale Upcall Detection and Classification Using Passive Acoustic Monitoring to Reduce Adverse Human–Whale Interactions. Machine Learning and Knowledge Extraction. 2025; 7(4):154. https://doi.org/10.3390/make7040154
Chicago/Turabian StyleOlatinwo, Doyinsola D., and Mae L. Seto. 2025. "Low-SNR Northern Right Whale Upcall Detection and Classification Using Passive Acoustic Monitoring to Reduce Adverse Human–Whale Interactions" Machine Learning and Knowledge Extraction 7, no. 4: 154. https://doi.org/10.3390/make7040154
APA StyleOlatinwo, D. D., & Seto, M. L. (2025). Low-SNR Northern Right Whale Upcall Detection and Classification Using Passive Acoustic Monitoring to Reduce Adverse Human–Whale Interactions. Machine Learning and Knowledge Extraction, 7(4), 154. https://doi.org/10.3390/make7040154






