Enhancing Cancer Classification from RNA Sequencing Data Using Deep Learning and Explainable AI
Abstract
1. Introduction
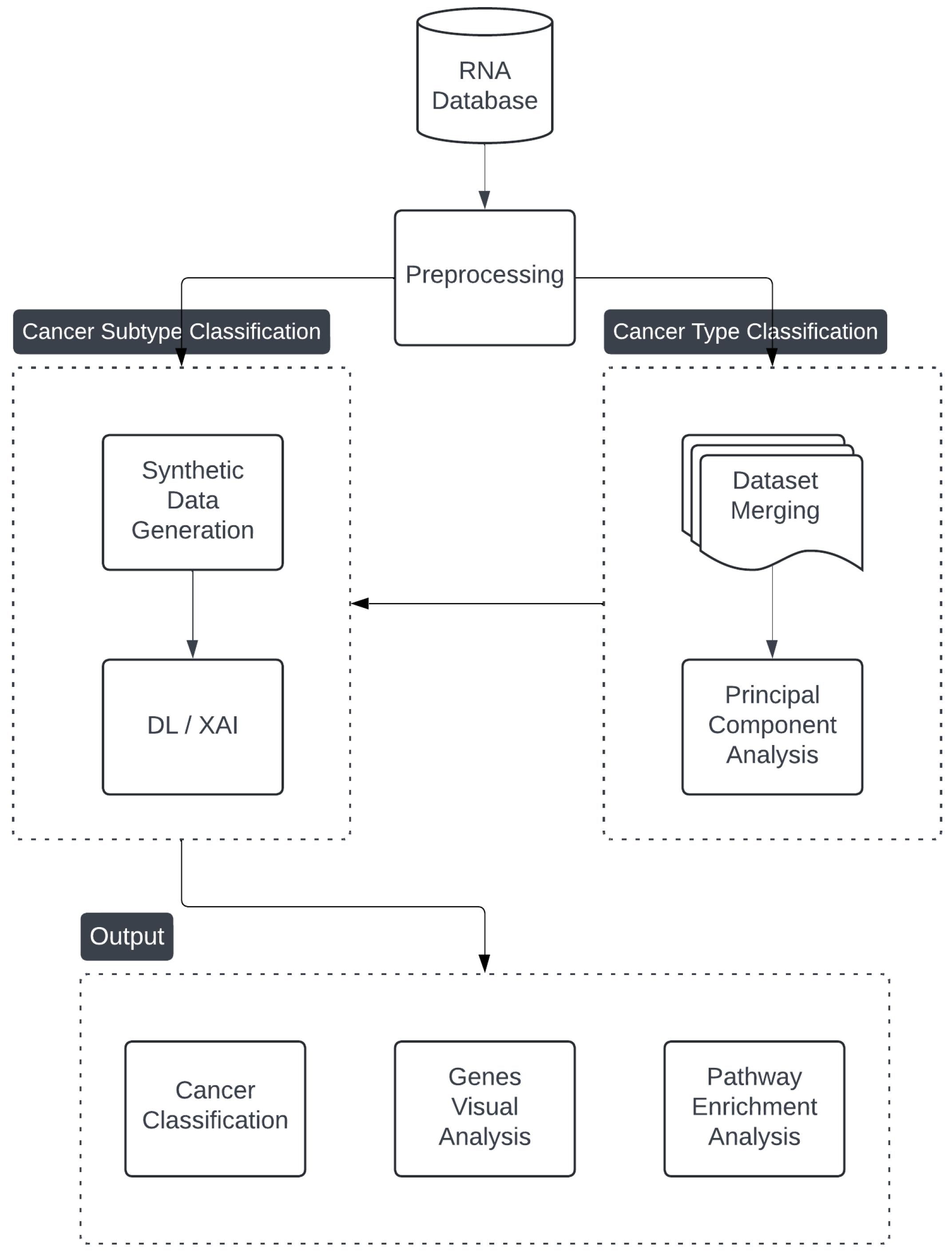
2. Materials and Methods
2.1. Data Preprocessing
2.2. Cancer Classification
2.2.1. SMOTE for Synthetic Data Generation
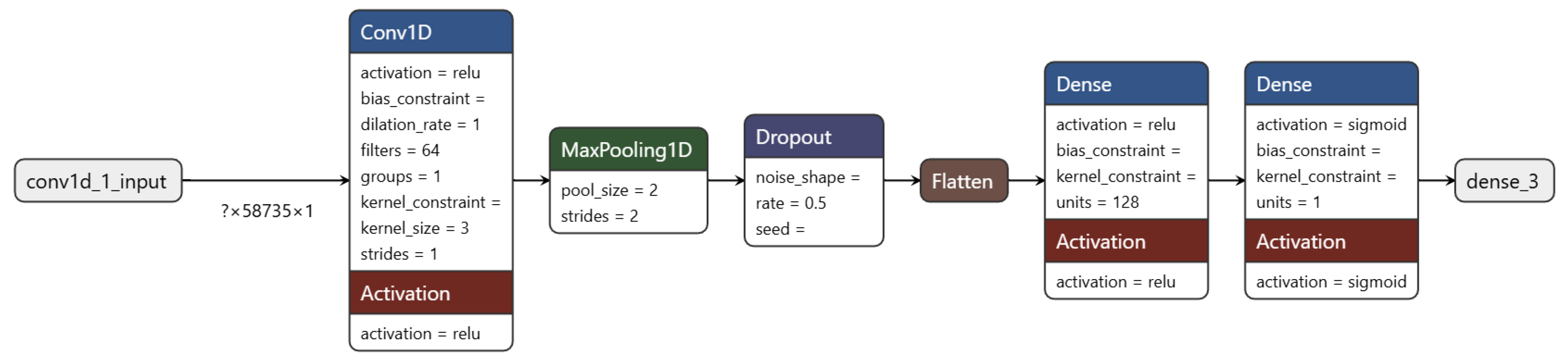
2.2.2. Model for Cancer Subtype Classification
- is the output of the convolution at time step t,
- is the kernel (filter) of the convolution for the ith feature,
- is the input at time step ,
- is the bias term,
- is the activation function, in this case, ReLU (Rectified Linear Unit).
- is the weight matrix of the dense layer,
- is the input to the dense layer,
- is the bias vector,
- is the activation function (ReLU for hidden layers).
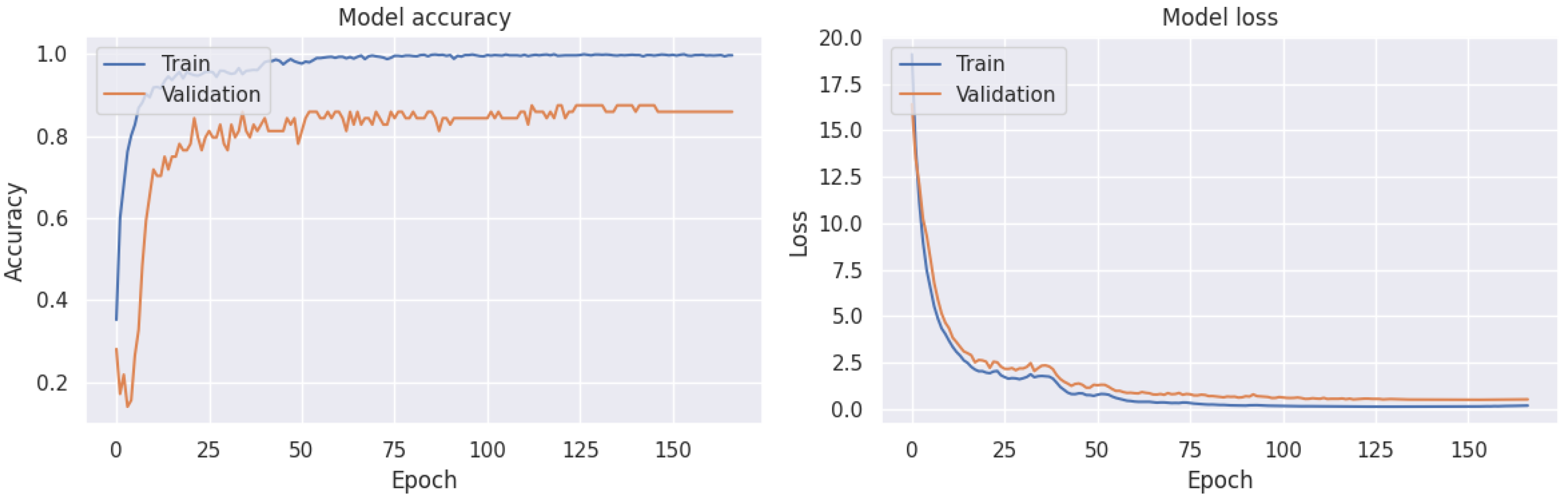
2.2.3. Early Stopping Criteria
2.3. Cancer Type Classification
2.3.1. PCA on RNA Dataset
Centring the Data
- is the matrix of eigenvectors (principal components),
- is the diagonal matrix of eigenvalues, where each eigenvalue represents the variance captured by its corresponding principal component.
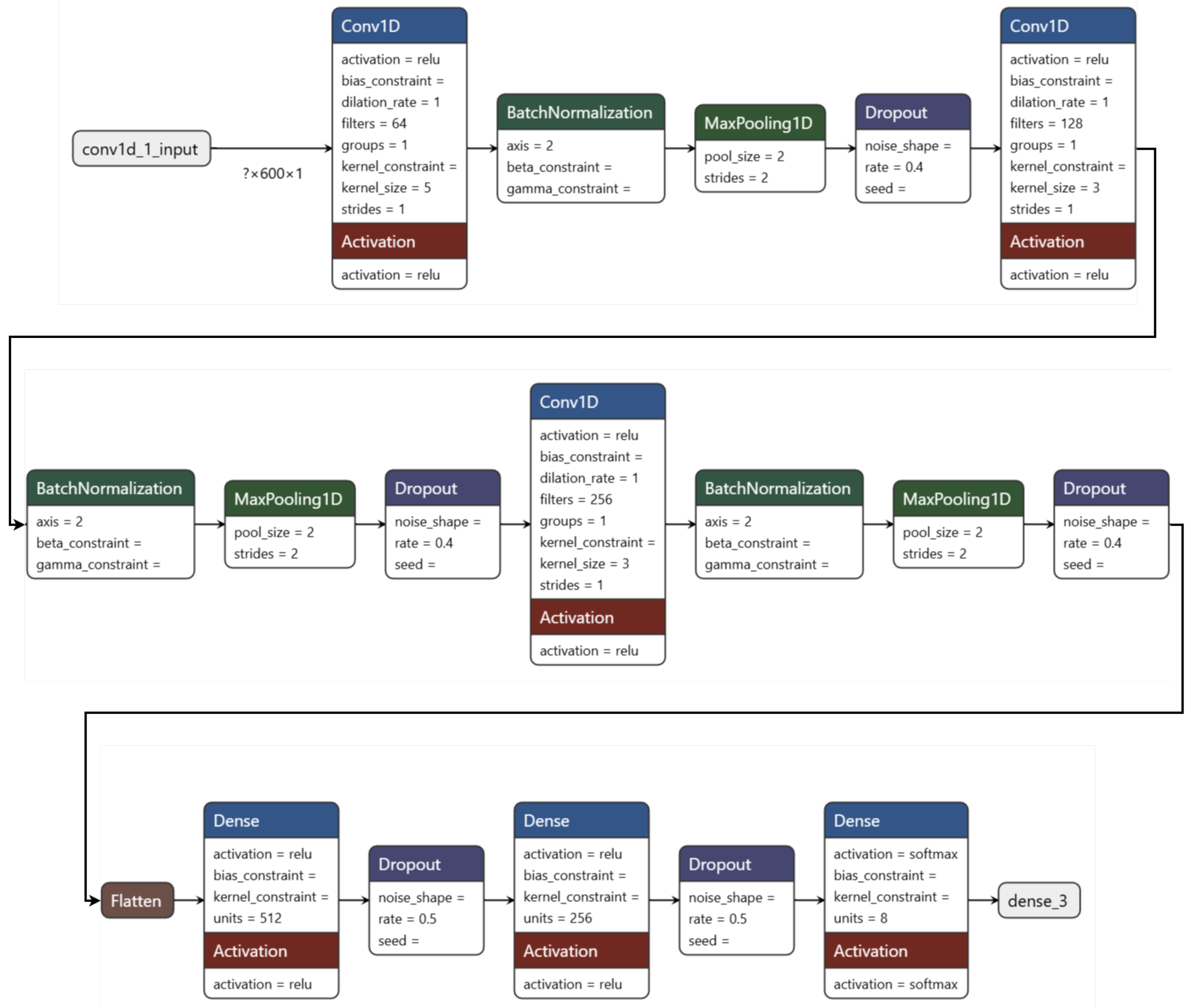
2.3.2. Model for Cancer Type Classification
- -
- The first layer applies a 1D convolution to the input as in Equation (18),
- -
- Batch normalization is applied to normalize the activations as in Equation (20),
- -
- Max pooling is used to reduce the spatial dimensions of the output as in Equation (21),
- -
- Dropout is applied to prevent overfitting by randomly setting 50% of the activations to zero as in Equation (22),
- -
- The second and third convolutional layers are applied similarly to the first layer, with the following transformations as in Equation (23),
- -
- After the last convolutional layer, the output is flattened into a 1D vector as in Equation (24),
- -
- Two fully connected layers are applied, each with ReLU activation and L2 regularization as in Equation (25),
- -
2.3.3. Optimization and Class Balancing
- is the weight for class ,
- is the true label for class (one-hot encoded),
- is the predicted probability for class .
2.4. Explainability and Visual Analysis
2.4.1. XAI Using LIME
- is the distance between the original instance x and the perturbed instance (e.g., using Euclidean distance),
- controls the width of the kernel and the locality of the explanation.
- is the prediction of the original complex model on the perturbed instance ,
- is the prediction of the surrogate model on ,
- is the proximity weighting,
- is a regularization term that controls the complexity of the surrogate model g,
- is a hyperparameter that controls the regularization strength.
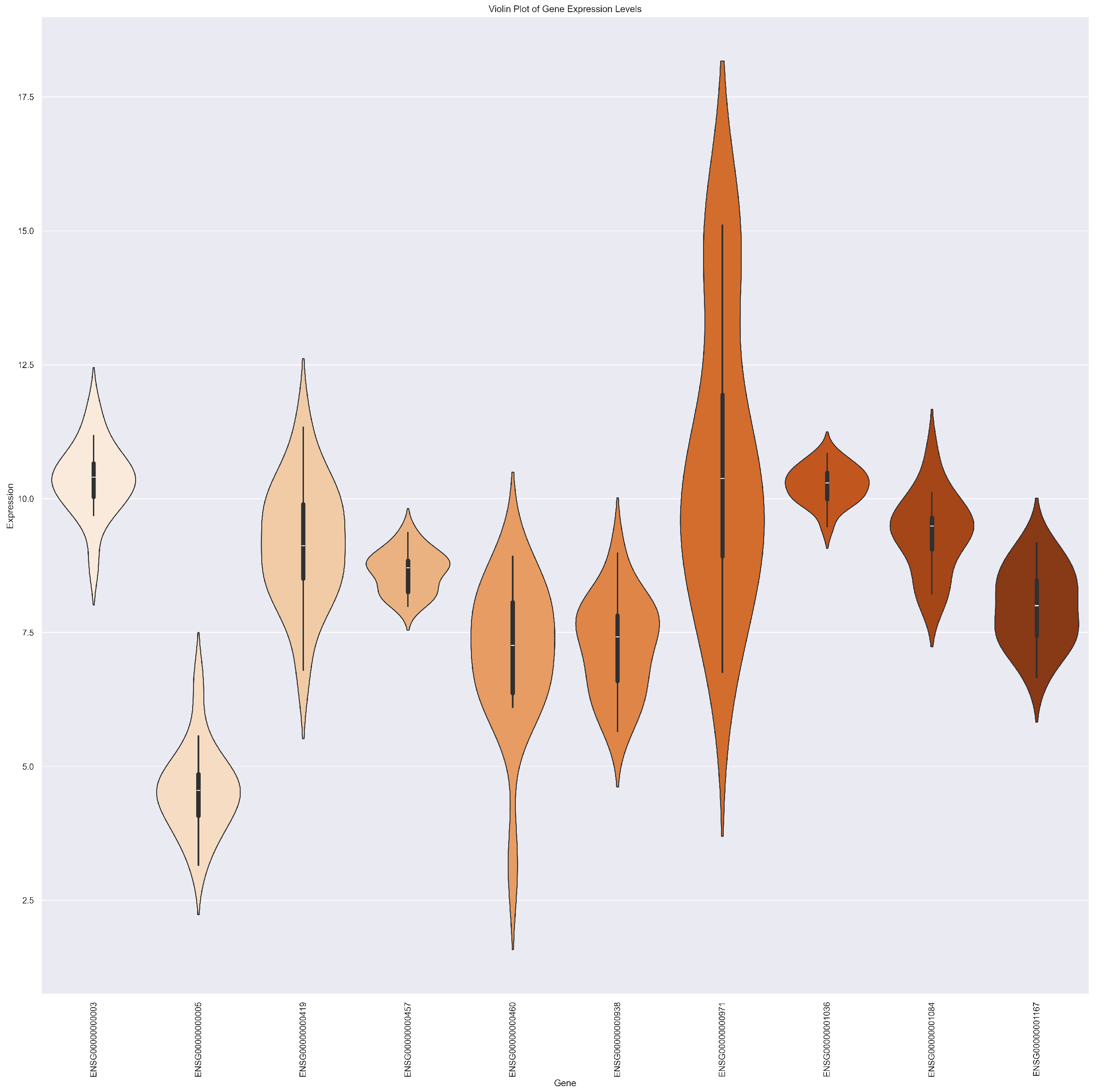
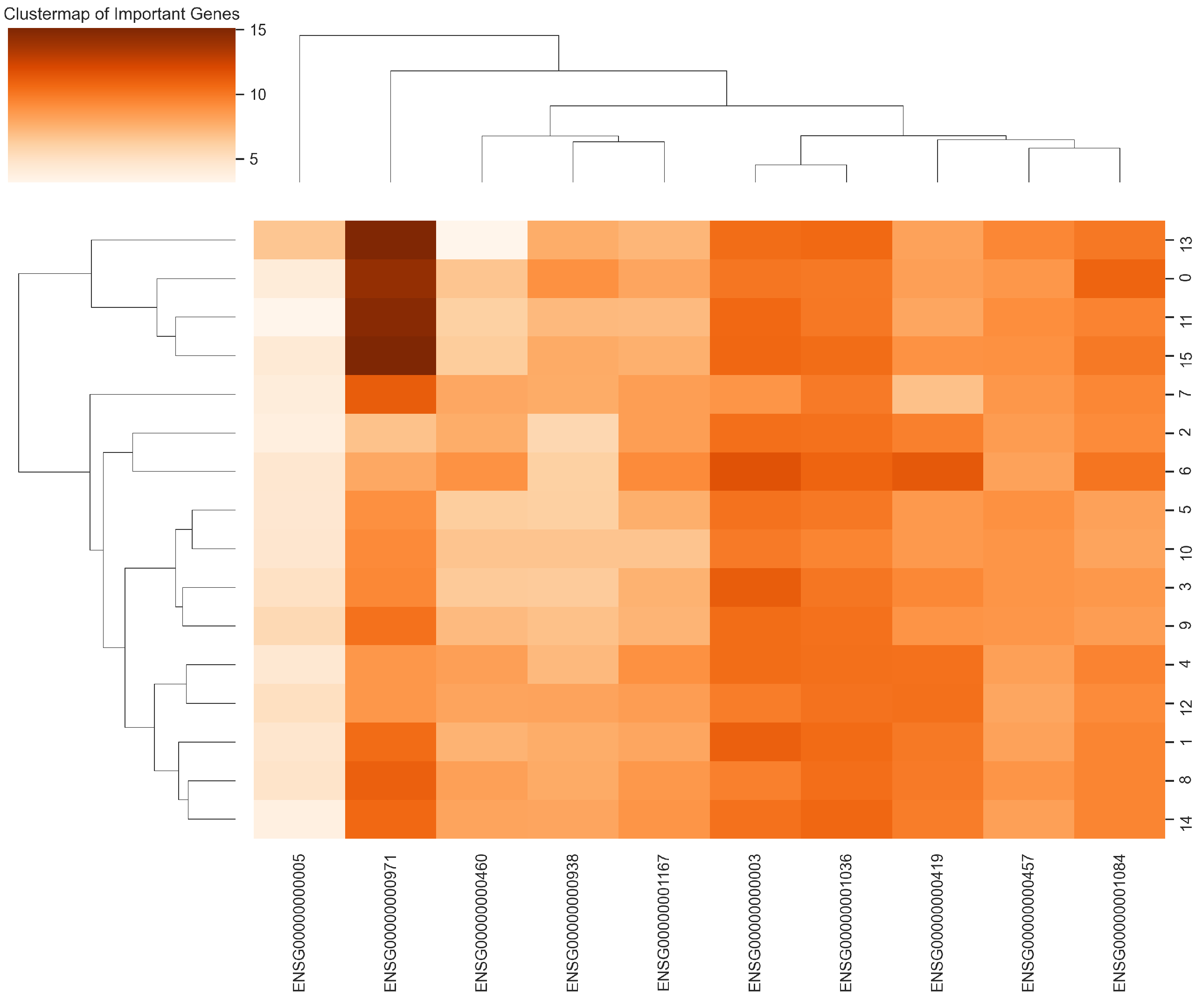
2.4.2. Heatmap
- is the expression value of gene i in sample j,
- is the mean expression value of gene i across all samples,
- is the standard deviation of gene i across all samples.
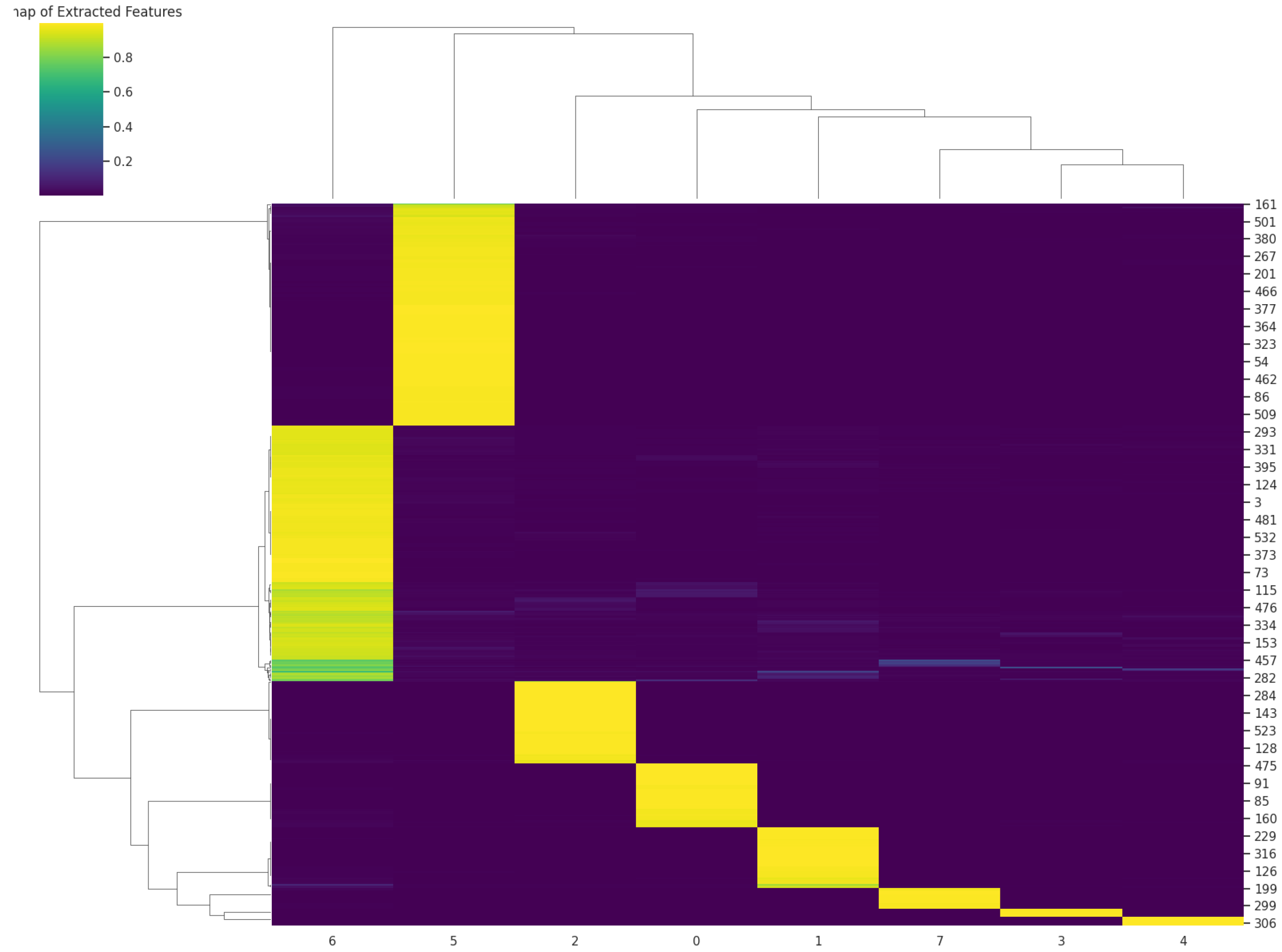
2.4.3. Cluster Map
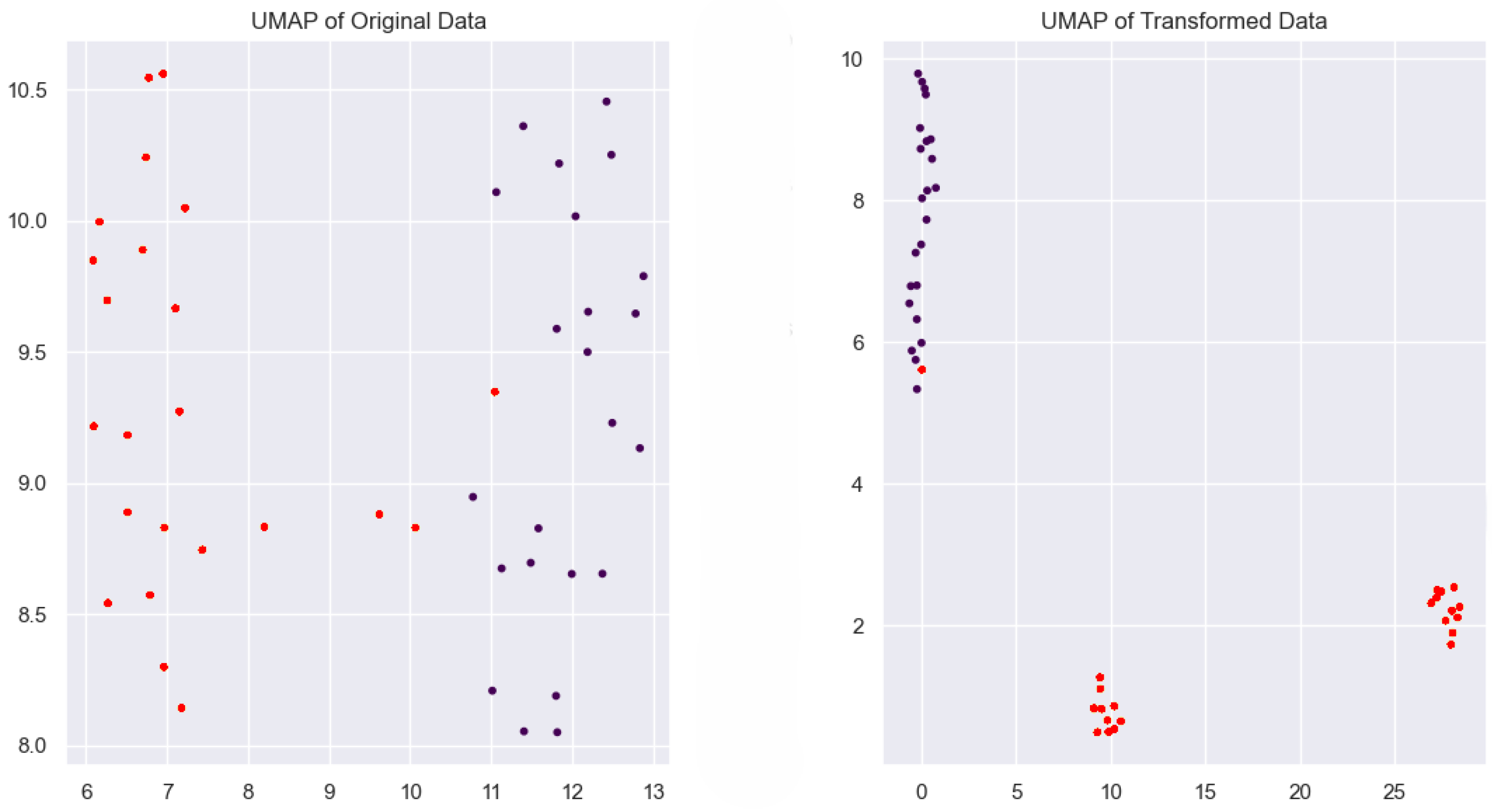
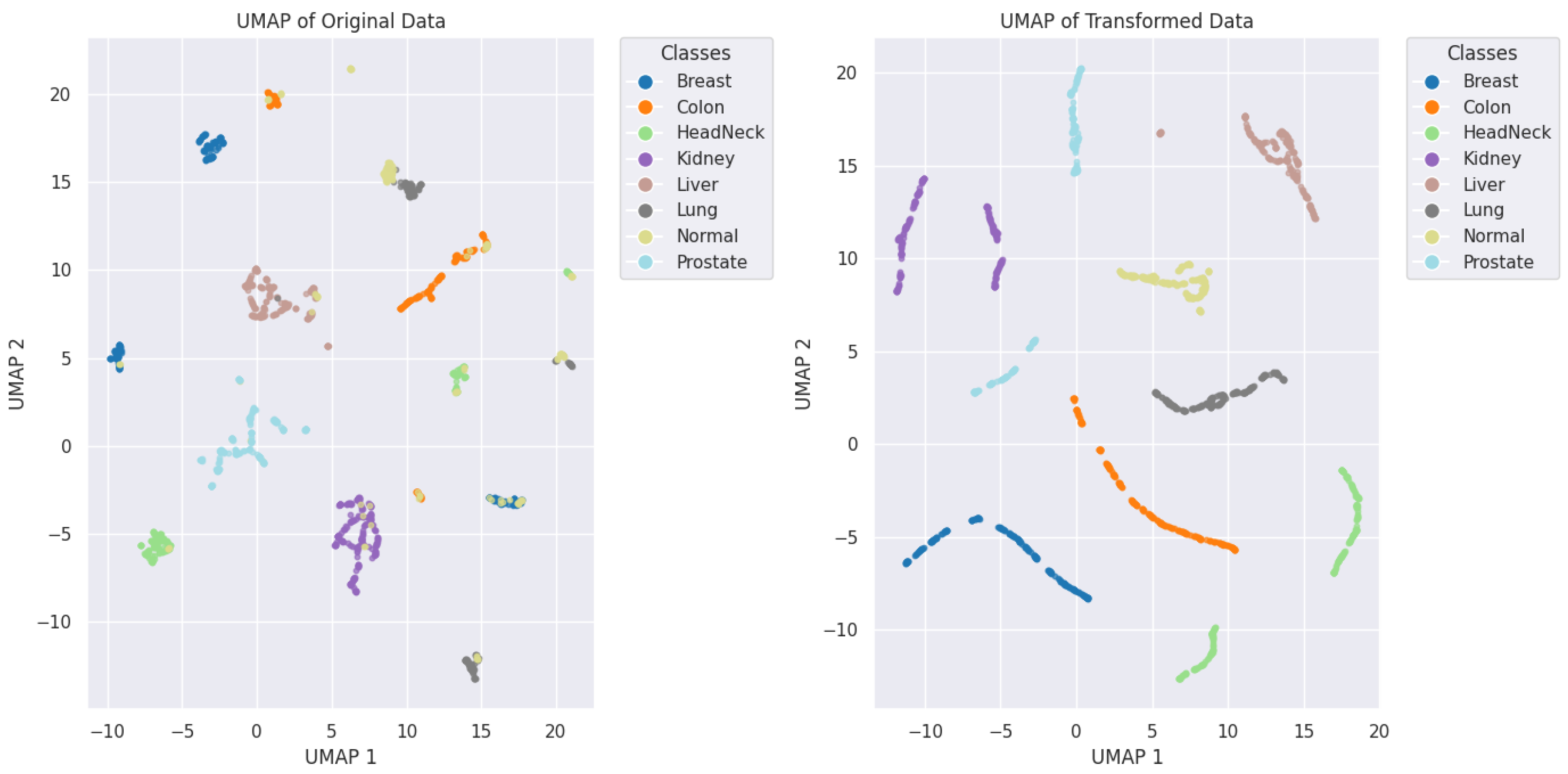
2.4.4. UMAP (Uniform Manifold Approximation and Projection)
- is the distance between points and ,
- is the distance to the nearest neighbor of ,
- is a normalization factor.
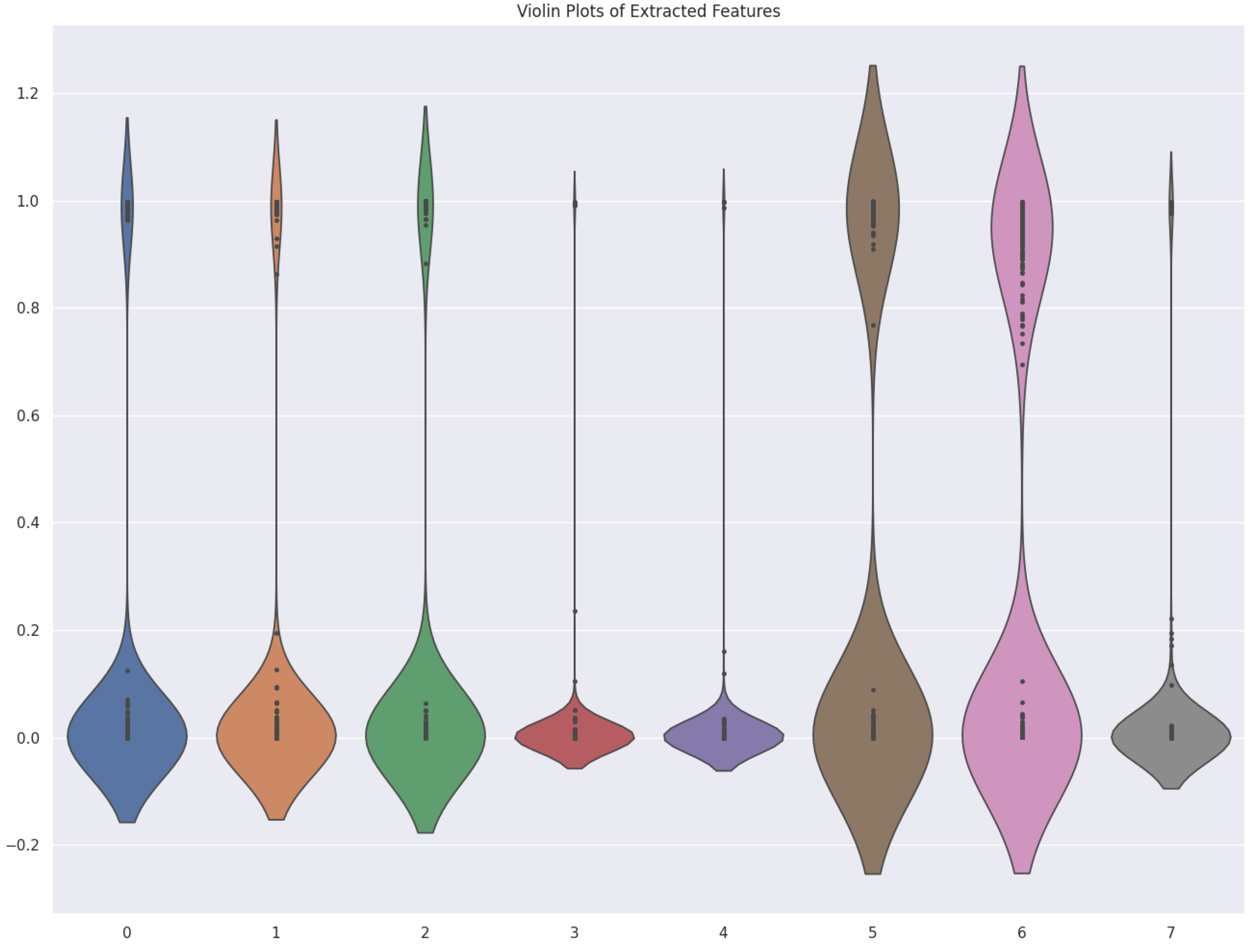
2.4.5. Violin Plot
- is the kernel function (often Gaussian),
- h is the bandwidth parameter,
- n is the number of data points.
2.5. KEGG Pathway Enrichment Analysis
- Organism: Homo sapiens, symbolized by “hsa” in KEGG.
- p-value Adjustment Method: Multiple comparisons were accounted for by applying the Benjamini–Hochberg (BH) method. This method is recommended for high-throughput analyses, such as RNA-seq, because it controls the false discovery rate (FDR).
- q-value Cut-off: A strict q-value threshold of 0.05 was applied to ensure that only highly enriched pathways were retained. Pathways with a q-value greater than 0.05 were considered non-significant and excluded from further analysis.
2.6. GO Enrichment Analysis
- Organism: Homo sapiens (symbolized as ’hsa’).
- p-value adjustment method: Benjamini–Hochberg (BH) to control the false discovery rate (FDR).
- Threshold: Significant GO keywords were found with a p-adjusted value () below 0.05.
Equations for p-Value Adjustment
- p is the original p-value,
- N is the total number of tests,
- is the rank of the p-value among all tests.
3. Results and Discussion
3.1. Experimental Setup
3.2. Dataset Description
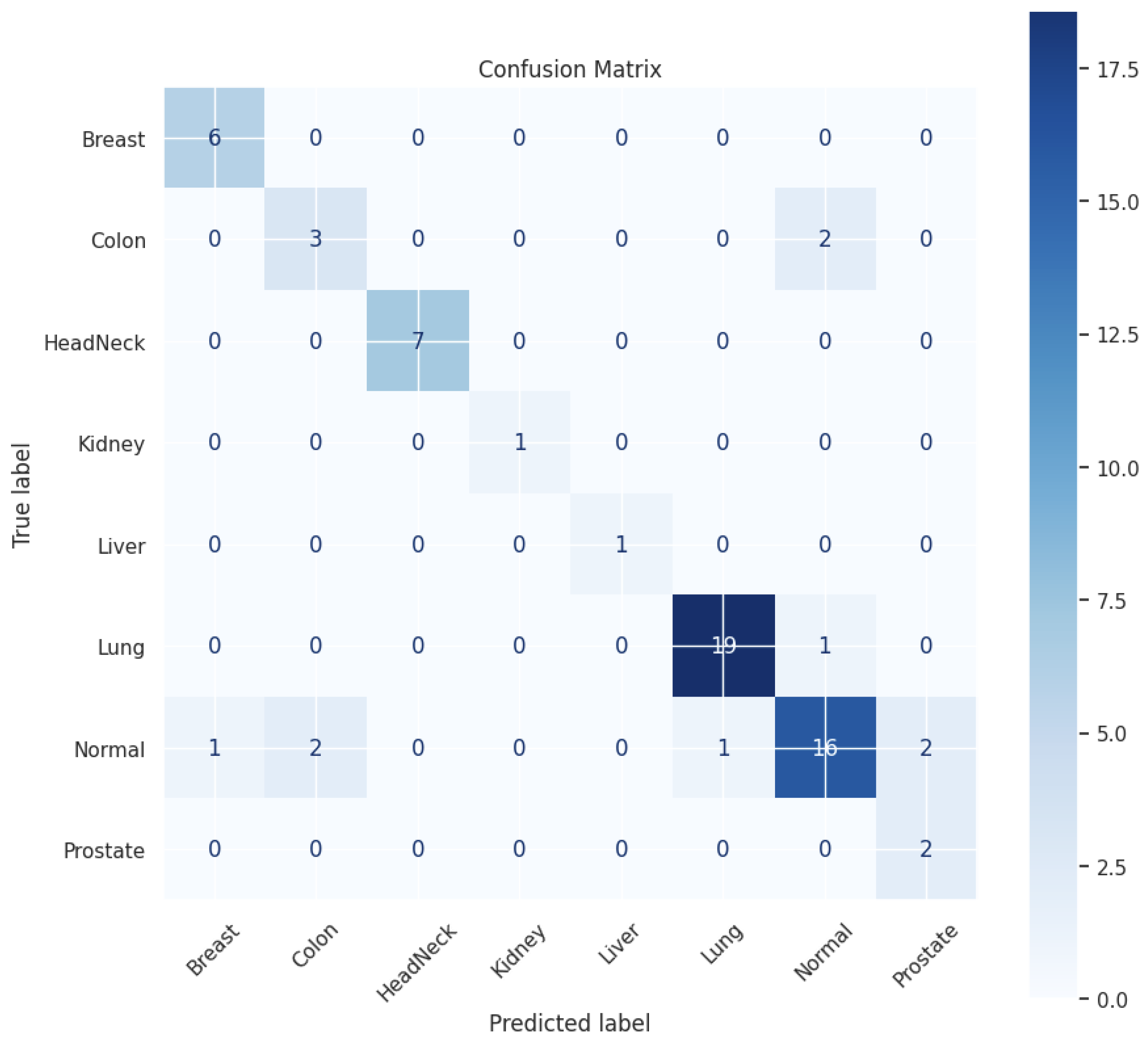
3.3. Evaluation Measures
- TP = Number of correctly classified cancer samples,
- TN = Number of correctly classified healthy samples,
- FP = Number of misclassified cancer samples as healthy,
- FN = Number of misclassified healthy samples as cancer.
3.4. Robustness of Our Methodology
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Cancer WHO Facts-Sheet. 2025. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 1 July 2025).
- World Cancer Research Fund International. Worldwide Cancer Data | World Cancer Research Fund. 2025. Available online: https://www.wcrf.org/preventing-cancer/cancer-statistics/worldwide-cancer-data/ (accessed on 1 July 2025).
- Verma, G.; Luciani, M.L.; Palombo, A.; Metaxa, L.; Panzironi, G.; Pediconi, F.; Giuliani, A.; Bizzarri, M.; Todde, V. Microcalcification morphological descriptors and parenchyma fractal dimension hierarchically interact in breast cancer: A diagnostic perspective. Comput. Biol. Med. 2018, 93, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, E.; Castle, J.; Quirk, A.; Taylor, C.D.; Xu, W.; Prasad, A. Cellular morphological features are predictive markers of cancer cell state. Comput. Biol. Med. 2020, 126, 104044. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Kikuchi, K. Expanding the cytological and architectural spectrum of mucoepidermoid carcinoma: The key to solving diagnostic problems in morphological variants. Semin. Diagn. Pathol. 2024, 41, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Guerroudji, M.A.; Hadjadj, Z.; Lichouri, M.; Amara, K.; Zenati, N. Efficient machine learning-based approach for brain tumor detection using the CAD system. IETE J. Res. 2024, 70, 3664–3678. [Google Scholar] [CrossRef]
- Mallon, E.; Osin, P.; Nasiri, N.; Blain, I.; Howard, B.; Gusterson, B. The basic pathology of human breast cancer. J. Mammary Gland. Biol. Neoplasia 2000, 5, 139–163. [Google Scholar] [CrossRef]
- Allison, K.H. Molecular pathology of breast cancer: What a pathologist needs to know. Am. J. Clin. Pathol. 2012, 138, 770–780. [Google Scholar] [CrossRef]
- Kurman, R.J.; Shih, I.M. Pathogenesis of ovarian cancer: Lessons from morphology and molecular biology and their clinical implications. Int. J. Gynecol. Pathol. 2008, 27, 151–160. [Google Scholar] [CrossRef]
- Beck, A.H.; Sangoi, A.R.; Leung, S.; Marinelli, R.J.; Nielsen, T.O.; Van De Vijver, M.J.; West, R.B.; Van De Rijn, M.; Koller, D. Systematic analysis of breast cancer morphology uncovers stromal features associated with survival. Sci. Transl. Med. 2011, 3, 108ra113. [Google Scholar] [CrossRef]
- Meirovitz, A.; Nisman, B.; Allweis, T.M.; Carmon, E.; Kadouri, L.; Maly, B.; Maimon, O.; Peretz, T. Thyroid hormones and morphological features of primary breast cancer. Anticancer. Res. 2022, 42, 253–261. [Google Scholar] [CrossRef]
- do Nascimento, R.G.; Otoni, K.M. Histological and molecular classification of breast cancer: What do we know? Mastology 2020, 30, 1–8. [Google Scholar] [CrossRef]
- Gamble, P.; Jaroensri, R.; Wang, H.; Tan, F.; Moran, M.; Brown, T.; Flament-Auvigne, I.; Rakha, E.A.; Toss, M.; Dabbs, D.J.; et al. Determining breast cancer biomarker status and associated morphological features using deep learning. Commun. Med. 2021, 1, 14. [Google Scholar] [CrossRef] [PubMed]
- Oyelade, O.N.; Ezugwu, A.E. A novel wavelet decomposition and transformation convolutional neural network with data augmentation for breast cancer detection using digital mammogram. Sci. Rep. 2022, 12, 5913. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, M.; Mwambi, H.; Mboya, I.B.; Elbashir, M.K.; Omolo, B. A stacking ensemble deep learning approach to cancer type classification based on TCGA data. Sci. Rep. 2021, 11, 15626. [Google Scholar] [CrossRef] [PubMed]
- Triantafyllou, A.; Dovrolis, N.; Zografos, E.; Theodoropoulos, C.; Zografos, G.C.; Michalopoulos, N.V.; Gazouli, M. Circulating miRNA expression profiling in breast cancer molecular subtypes: Applying machine learning analysis in bioinformatics. Cancer Diagn. Progn. 2022, 2, 739. [Google Scholar] [CrossRef]
- Almarzouki, H.Z. Deep-learning-based cancer profiles classification using gene expression data profile. J. Healthc. Eng. 2022, 2022, 4715998. [Google Scholar] [CrossRef]
- Aziz, R.M. Nature-inspired metaheuristics model for gene selection and classification of biomedical microarray data. Med. Biol. Eng. Comput. 2022, 60, 1627–1646. [Google Scholar] [CrossRef]
- Ogundokun, R.O.; Misra, S.; Douglas, M.; Damaševičius, R.; Maskeliūnas, R. Medical internet-of-things based breast cancer diagnosis using hyperparameter-optimized neural networks. Future Internet 2022, 14, 153. [Google Scholar] [CrossRef]
- Chowdhary, C.L.; Khare, N.; Patel, H.; Koppu, S.; Kaluri, R.; Rajput, D.S. Past, present and future of gene feature selection for breast cancer classification—A survey. Int. J. Eng. Syst. Model. Simul. 2022, 13, 140–153. [Google Scholar] [CrossRef]
- Amethiya, Y.; Pipariya, P.; Patel, S.; Shah, M. Comparative analysis of breast cancer detection using machine learning and biosensors. Intell. Med. 2022, 2, 69–81. [Google Scholar] [CrossRef]
- Geraci, F.; Saha, I.; Bianchini, M. RNA-Seq analysis: Methods, applications and challenges. Front. Genet. 2020, 11, 220. [Google Scholar] [CrossRef]
- Hrdlickova, R.; Toloue, M.; Tian, B. RNA-Seq methods for transcriptome analysis. Wiley Interdiscip. Rev. RNA 2017, 8, e1364. [Google Scholar] [CrossRef]
- Van den Berge, K.; Hembach, K.M.; Soneson, C.; Tiberi, S.; Clement, L.; Love, M.I.; Patro, R.; Robinson, M.D. RNA sequencing data: Hitchhiker’s guide to expression analysis. Annu. Rev. Biomed. Data Sci. 2019, 2, 139–173. [Google Scholar] [CrossRef]
- Lam, H.Y.; Clark, M.J.; Chen, R.; Chen, R.; Natsoulis, G.; O’huallachain, M.; Dewey, F.E.; Habegger, L.; Ashley, E.A.; Gerstein, M.B.; et al. Performance comparison of whole-genome sequencing platforms. Nat. Biotechnol. 2012, 30, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.A.; Park, J.L.; Park, S.J.; Kim, J.H.; Goh, S.H.; Han, J.Y.; Kim, S.Y. Comparison between MGI and Illumina sequencing platforms for whole genome sequencing. Genes Genom. 2021, 43, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Fouhy, F.; Clooney, A.G.; Stanton, C.; Claesson, M.J.; Cotter, P.D. 16S rRNA gene sequencing of mock microbial populations-impact of DNA extraction method, primer choice and sequencing platform. BMC Microbiol. 2016, 16, 1–13. [Google Scholar] [CrossRef]
- Hu, T.; Chitnis, N.; Monos, D.; Dinh, A. Next-generation sequencing technologies: An overview. Hum. Immunol. 2021, 82, 801–811. [Google Scholar] [CrossRef]
- Gandhi, V.V.; Samuels, D.C. A review comparing deoxyribonucleoside triphosphate (dNTP) concentrations in the mitochondrial and cytoplasmic compartments of normal and transformed cells. Nucleosides Nucleotides Nucleic Acids 2011, 30, 317–339. [Google Scholar] [CrossRef]
- Rai, M.F.; Tycksen, E.D.; Sandell, L.J.; Brophy, R.H. Advantages of RNA-seq compared to RNA microarrays for transcriptome profiling of anterior cruciate ligament tears. J. Orthop. Res. 2018, 36, 484–497. [Google Scholar] [CrossRef]
- Li, W.V.; Li, J.J. Modeling and analysis of RNA-seq data: A review from a statistical perspective. Quant. Biol. 2018, 6, 195–209. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine and Mapping of RNA Modifications Committee. Driving Innovation to Study RNA Modifications. In Charting a Future for Sequencing RNA and Its Modifications: A New Era for Biology and Medicine; National Academies Press (US): Washington, DC, USA, 2024. [Google Scholar]
- Zhao, S.; Fung-Leung, W.P.; Bittner, A.; Ngo, K.; Liu, X. Comparison of RNA-Seq and microarray in transcriptome profiling of activated T cells. PLoS ONE 2014, 9, e78644. [Google Scholar] [CrossRef]
- Zararsız, G. Development and application of novel machine learning approaches for RNA-seq data classification. Int. J. Comput. Trends Tech. 2015, 2017, 62–64. [Google Scholar]
- Gondane, A.; Itkonen, H.M. Revealing the history and mystery of RNA-Seq. Curr. Issues Mol. Biol. 2023, 45, 1860–1874. [Google Scholar] [CrossRef] [PubMed]
- Epstein, C.B.; Butow, R.A. Microarray technology—Enhanced versatility, persistent challenge. Curr. Opin. Biotechnol. 2000, 11, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Blohm, D.H.; Guiseppi-Elie, A. New developments in microarray technology. Curr. Opin. Biotechnol. 2001, 12, 41–47. [Google Scholar] [CrossRef]
- Blalock, E.M. A Beginner’s Guide to Microarrays; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Feltes, B.C.; Chandelier, E.B.; Grisci, B.I.; Dorn, M. Cumida: An extensively curated microarray database for benchmarking and testing of machine learning approaches in cancer research. J. Comput. Biol. 2019, 26, 376–386. [Google Scholar] [CrossRef]
- Verleysen, M.; François, D. The curse of dimensionality in data mining and time series prediction. In Proceedings of the International Work-Conference on Artificial Neural Networks, Barcelona, Spain, 8–10 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 758–770. [Google Scholar]
- Khalsan, M.; Machado, L.R.; Al-Shamery, E.S.; Ajit, S.; Anthony, K.; Mu, M.; Agyeman, M.O. A survey of machine learning approaches applied to gene expression analysis for cancer prediction. IEEE Access 2022, 10, 27522–27534. [Google Scholar] [CrossRef]
- Yuan, F.; Lu, L.; Zou, Q. Analysis of gene expression profiles of lung cancer subtypes with machine learning algorithms. Biochim. Biophys. Acta (BBA) Mol. Basis Dis. 2020, 1866, 165822. [Google Scholar] [CrossRef]
- Wang, D.; Li, J.R.; Zhang, Y.H.; Chen, L.; Huang, T.; Cai, Y.D. Identification of differentially expressed genes between original breast cancer and xenograft using machine learning algorithms. Genes 2018, 9, 155. [Google Scholar] [CrossRef]
- Pisner, D.A.; Schnyer, D.M. Support vector machine. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–121. [Google Scholar]
- Meddouri, N.; Khoufi, H.; Maddouri, M. DFC: A Performant Dagging Approach of Classification Based on Formal Concept. Int. J. Artif. Intell. Mach. Learn. (IJAIML) 2021, 11, 38–62. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New machine learning algorithm: Random forest. In Proceedings of the Information Computing and Applications: Third International Conference, ICICA 2012, Chengde, China, 14–16 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 246–252. [Google Scholar]
- Dramiński, M.; Rada-Iglesias, A.; Enroth, S.; Wadelius, C.; Koronacki, J.; Komorowski, J. Monte Carlo feature selection for supervised classification. Bioinformatics 2008, 24, 110–117. [Google Scholar] [CrossRef]
- Danaee, P.; Ghaeini, R.; Hendrix, D.A. A deep learning approach for cancer detection and relevant gene identification. In Proceedings of the Pacific Symposium on Biocomputing 2017, Waimea, HI, USA, 3–7 January 2017; World Scientific: Singapore, 2017; pp. 219–229. [Google Scholar]
- Jia, D.; Chen, C.; Chen, C.; Chen, F.; Zhang, N.; Yan, Z.; Lv, X. Breast cancer case identification based on deep learning and bioinformatics analysis. Front. Genet. 2021, 12, 628136. [Google Scholar] [CrossRef]
- Clough, E.; Barrett, T. The gene expression omnibus database. In Statistical Genomics: Methods and Protocols; Springer: New York, NY, USA, 2016; pp. 93–110. [Google Scholar]
- Deng, M.; Brägelmann, J.; Schultze, J.L.; Perner, S. Web-TCGA: An online platform for integrated analysis of molecular cancer data sets. BMC Bioinform. 2016, 17, 72. [Google Scholar] [CrossRef]
- Alshareef, A.M.; Alsini, R.; Alsieni, M.; Alrowais, F.; Marzouk, R.; Abunadi, I.; Nemri, N. Optimal deep learning enabled prostate cancer detection using microarray gene expression. J. Healthc. Eng. 2022, 2022, 7364704. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Xu, D. Deep learning shapes single-cell data analysis. Nat. Rev. Mol. Cell Biol. 2022, 23, 303–304. [Google Scholar] [CrossRef] [PubMed]
- Kaveh, M.; Mesgari, M.S. Application of meta-heuristic algorithms for training neural networks and deep learning architectures: A comprehensive review. Neural Process. Lett. 2023, 55, 4519–4622. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Gu, X.; Tang, L.; Yin, Y.; Liu, D.; Zhang, Y. Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: Comprehensive review and future challenge. Gondwana Res. 2022, 109, 1–17. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–231. [Google Scholar]
- Rahman, M.A.; Sokkalingam, R.; Othman, M.; Biswas, K.; Abdullah, L.; Abdul Kadir, E. Nature-inspired metaheuristic techniques for combinatorial optimization problems: Overview and recent advances. Mathematics 2021, 9, 2633. [Google Scholar] [CrossRef]
- Tkatek, S.; Bahti, O.; Lmzouari, Y.; Abouchabaka, J. Artificial intelligence for improving the optimization of NP-hard problems: A review. Int. J. Adv. Trends Comput. Sci. Appl. 2020, 9, 7411–7420. [Google Scholar]
- Mandal, A.K.; Dehuri, S. A survey on ant colony optimization for solving some of the selected np-hard problem. In Proceedings of the Biologically Inspired Techniques in Many-Criteria Decision Making: International Conference on Biologically Inspired Techniques in Many-Criteria Decision Making (BITMDM-2019), Balasore, India, 19–20 December 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 85–100. [Google Scholar]
- Calvet, L.; Benito, S.; Juan, A.A.; Prados, F. On the role of metaheuristic optimization in bioinformatics. Int. Trans. Oper. Res. 2023, 30, 2909–2944. [Google Scholar] [CrossRef]
- Shukla, A.K.; Tripathi, D.; Reddy, B.R.; Chandramohan, D. A study on metaheuristics approaches for gene selection in microarray data: Algorithms, applications and open challenges. Evol. Intell. 2020, 13, 309–329. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mali, K.; Chatterjee, S.; Banerjee, S.; Mazumdar, K.G.; Debnath, M.; Basu, P.; Bose, S.; Roy, K. Detection of skin disease using metaheuristic supported artificial neural networks. In Proceedings of the 2017 8th Annual Industrial Automation and Electromechanical Engineering Conference (IEMECON), Bangkok, Thailand, 16–18 August 2017; pp. 224–229. [Google Scholar] [CrossRef]
- MotieGhader, H.; Masoudi-Sobhanzadeh, Y.; Ashtiani, S.H.; Masoudi-Nejad, A. mRNA and microRNA selection for breast cancer molecular subtype stratification using meta-heuristic based algorithms. Genomics 2020, 112, 3207–3217. [Google Scholar] [CrossRef] [PubMed]
- Onwubolu, G.C.; Mutingi, M. A genetic algorithm approach to cellular manufacturing systems. Comput. Ind. Eng. 2001, 39, 125–144. [Google Scholar] [CrossRef]
- Masoudi-Sobhanzadeh, Y.; Motieghader, H. World Competitive Contests (WCC) algorithm: A novel intelligent optimization algorithm for biological and non-biological problems. Inform. Med. Unlocked 2016, 3, 15–28. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Kaveh, A.; Kaveh, A. Imperialist competitive algorithm. In Advances in Metaheuristic Algorithms for Optimal Design of Structures; Springer: Berlin/Heidelberg, Germany, 2017; pp. 353–373. [Google Scholar]
- Li, W.; Özcan, E.; John, R. A learning automata-based multiobjective hyper-heuristic. IEEE Trans. Evol. Comput. 2017, 23, 59–73. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Ghaemi, M.; Feizi-Derakhshi, M.R. Forest optimization algorithm. Expert Syst. Appl. 2014, 41, 6676–6687. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Prayogo, D. Symbiotic organisms search algorithm: Theory, recent advances and applications. Expert Syst. Appl. 2019, 119, 184–209. [Google Scholar] [CrossRef]
- Kashan, A.H. League Championship Algorithm (LCA): An algorithm for global optimization inspired by sport championships. Appl. Soft Comput. 2014, 16, 171–200. [Google Scholar] [CrossRef]
- Wei, K.; Li, T.; Huang, F.; Chen, J.; He, Z. Cancer classification with data augmentation based on generative adversarial networks. Front. Comput. Sci. 2022, 16, 162601. [Google Scholar] [CrossRef]
- Deng, X.; Li, M.; Deng, S.; Wang, L. Hybrid gene selection approach using XGBoost and multi-objective genetic algorithm for cancer classification. Med. Biol. Eng. Comput. 2022, 60, 663–681. [Google Scholar] [CrossRef] [PubMed]
- Younis, H.; Bhatti, M.H.; Azeem, M. Classification of Skin Cancer Dermoscopy Images using Transfer Learning. In Proceedings of the 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2–3 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Xie, X.; Wang, X.; Liang, Y.; Yang, J.; Wu, Y.; Li, L.; Sun, X.; Bing, P.; He, B.; Tian, G.; et al. Evaluating cancer-related biomarkers based on pathological images: A systematic review. Front. Oncol. 2021, 11, 763527. [Google Scholar] [CrossRef]
- Yadav, S.S.; Jadhav, S.M. Thermal infrared imaging based breast cancer diagnosis using machine learning techniques. Multimed. Tools Appl. 2022, 81, 13139–13157. [Google Scholar] [CrossRef]
- Aljuaid, H.; Alturki, N.; Alsubaie, N.; Cavallaro, L.; Liotta, A. Computer-aided diagnosis for breast cancer classification using deep neural networks and transfer learning. Comput. Methods Programs Biomed. 2022, 223, 106951. [Google Scholar] [CrossRef]
- Karamti, H.; Alharthi, R.; Umer, M.; Shaiba, H.; Ishaq, A.; Abuzinadah, N.; Alsubai, S.; Ashraf, I. Breast cancer detection employing stacked ensemble model with convolutional features. Cancer Biomarkers 2023, 40, 155–170. [Google Scholar] [CrossRef]
- Munshi, R.M.; Cascone, L.; Alturki, N.; Saidani, O.; Alshardan, A.; Umer, M. A novel approach for breast cancer detection using optimized ensemble learning framework and XAI. Image Vis. Comput. 2024, 142, 104910. [Google Scholar] [CrossRef]
- Wani, N.A.; Kumar, R.; Bedi, J. DeepXplainer: An interpretable deep learning based approach for lung cancer detection using explainable artificial intelligence. Comput. Methods Programs Biomed. 2024, 243, 107879. [Google Scholar] [CrossRef]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Comput. Surv. 2023, 55, 1–33. [Google Scholar] [CrossRef]
- Salih, A.M.; Raisi-Estabragh, Z.; Galazzo, I.B.; Radeva, P.; Petersen, S.E.; Lekadir, K.; Menegaz, G. A Perspective on Explainable Artificial Intelligence Methods: SHAP and LIME. Adv. Intell. Syst. 2024, 7, 2400304. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H.; Musirin, I.; Daud, M.R. Barnacles mating optimizer: An evolutionary algorithm for solving optimization. In Proceedings of the 2018 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 20 October 2018; pp. 99–104. [Google Scholar]
- Houssein, E.H.; Abdelminaam, D.S.; Hassan, H.N.; Al-Sayed, M.M.; Nabil, E. A hybrid barnacles mating optimizer algorithm with support vector machines for gene selection of microarray cancer classification. IEEE Access 2021, 9, 64895–64905. [Google Scholar] [CrossRef]
- Karaboga, D. Artificial bee colony algorithm. scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sharma, S.; Saha, A.K.; Saha, A. A novel improved whale optimization algorithm to solve numerical optimization and real-world applications. Artif. Intell. Rev. 2022, 55, 4605–4716. [Google Scholar] [CrossRef]
- Devi, S.S.; Prithiviraj, K. Breast cancer classification with microarray gene expression data based on improved whale optimization algorithm. Int. J. Swarm Intell. Res. (IJSIR) 2023, 14, 1–21. [Google Scholar] [CrossRef]
- Mohamed, T.I.; Ezugwu, A.E.; Fonou-Dombeu, J.V.; Ikotun, A.M.; Mohammed, M. A bio-inspired convolution neural network architecture for automatic breast cancer detection and classification using RNA-Seq gene expression data. Sci. Rep. 2023, 13, 14644. [Google Scholar] [CrossRef]
- JagadeeswaraRao, G.; Sivaprasad, A. An integrated ensemble learning technique for gene expression classification and biomarker identification from RNA-seq data for pancreatic cancer prognosis. Int. J. Inf. Technol. 2024, 16, 1505–1516. [Google Scholar] [CrossRef]
- Wang, J.; Huang, J.; Hu, Y.; Guo, Q.; Zhang, S.; Tian, J.; Niu, Y.; Ji, L.; Xu, Y.; Tang, P.; et al. Terminal modifications independent cell-free RNA sequencing enables sensitive early cancer detection and classification. Nat. Commun. 2024, 15, 156. [Google Scholar] [CrossRef]
- Feltes, B.C.; Poloni, J.D.F.; Dorn, M. Benchmarking and testing machine learning approaches with BARRA: CuRDa, a curated RNA-seq database for cancer research. J. Comput. Biol. 2021, 28, 931–944. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning decision tree classifiers. ACM Computing Surveys (CSUR) 1996, 28, 71–72. [Google Scholar] [CrossRef]
- Larose, D.T.; Larose, C.D. k-nearest neighbor algorithm. In Discovering Knowledge in Data: An Introduction to Data Mining; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). Geomatic Approaches for Modeling Land Change Scenarios; Springer: Cham, Switzerland, 2018; pp. 451–455. [Google Scholar]
- Elbashir, M.K.; Ezz, M.; Mohammed, M.; Saloum, S.S. Lightweight convolutional neural network for breast cancer classification using RNA-seq gene expression data. IEEE Access 2019, 7, 185338–185348. [Google Scholar] [CrossRef]
- Alharbi, F.; Vakanski, A.; Zhang, B.; Elbashir, M.K.; Mohammed, M. Comparative Analysis of Multi-Omics Integration Using Graph Neural Networks for Cancer Classification. IEEE Access 2025, 13, 37724–37736. [Google Scholar] [CrossRef]
- Davis, S.; Meltzer, P.S. GEOquery: A bridge between the Gene Expression Omnibus (GEO) and BioConductor. Bioinformatics 2007, 23, 1846–1847. [Google Scholar] [CrossRef]
- Wingett, S.W.; Andrews, S. FastQ Screen: A tool for multi-genome mapping and quality control. F1000Research 2018, 7, 1338. [Google Scholar] [CrossRef]
- Bolger, A.M.; Lohse, M.; Usadel, B. Trimmomatic: A flexible trimmer for Illumina sequence data. Bioinformatics 2014, 30, 2114–2120. [Google Scholar] [CrossRef]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef]
- Li, B.; Dewey, C.N. RSEM: Accurate transcript quantification from RNA-Seq data with or without a reference genome. BMC Bioinform. 2011, 12, 323. [Google Scholar] [CrossRef] [PubMed]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [PubMed]
- Soneson, C.; Love, M.I.; Robinson, M.D. Differential analyses for RNA-seq: Transcript-level estimates improve gene-level inferences. F1000Research 2015, 4, 1521. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Ige, A.O.; Sibiya, M. State-of-the-art in 1D Convolutional Neural Networks: A survey. IEEE Access 2024, 12, 144082–144105. [Google Scholar] [CrossRef]
- Roeder, L. Netron: Visualizer for Neural Network, Deep Learning and Machine Learning Models. 2025. Available online: https://github.com/lutzroeder/netron (accessed on 22 July 2025).
- Gygi, J.P.; Kleinstein, S.H.; Guan, L. Predictive overfitting in immunological applications: Pitfalls and solutions. Hum. Vaccines Immunother. 2023, 19, 2251830. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Wang, L.G.; Han, Y.; He, Q.Y. clusterProfiler: An R package for comparing biological themes among gene clusters. Omics J. Integr. Biol. 2012, 16, 284–287. [Google Scholar] [CrossRef] [PubMed]
- Ostell, J.M. Entrez: The NCBI search and discovery engine. In Proceedings of the Data Integration in the Life Sciences: 8th International Conference, DILS 2012, College Park, MD, USA, 28–29 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–4. [Google Scholar]
- Chen, L.; Zhang, Y.H.; Lu, G.; Huang, T.; Cai, Y.D. Analysis of cancer-related lncRNAs using gene ontology and KEGG pathways. Artif. Intell. Med. 2017, 76, 27–36. [Google Scholar] [CrossRef]
- Yuan, Y.; Cao, W.; Zhou, H.; Qian, H.; Wang, H. H2A. Z acetylation by lincZNF337-AS1 via KAT5 implicated in the transcriptional misregulation in cancer signaling pathway in hepatocellular carcinoma. Cell Death Dis. 2021, 12, 609. [Google Scholar] [CrossRef]
- Casamassimi, A.; Ciccodicola, A.; Rienzo, M. Transcriptional regulation and its misregulation in human diseases. Int. J. Mol. Sci. 2023, 24, 8640. [Google Scholar] [CrossRef]
- Lowenberg, B.; Downing, J.R.; Burnett, A. Acute myeloid leukemia. N. Engl. J. Med. 1999, 341, 1051–1062. [Google Scholar] [CrossRef]
- DiNardo, C.D.; Erba, H.P.; Freeman, S.D.; Wei, A.H. Acute myeloid leukaemia. Lancet 2023, 401, 2073–2086. [Google Scholar] [CrossRef]
- Kayser, S.; Levis, M.J. The clinical impact of the molecular landscape of acute myeloid leukemia. Haematologica 2023, 108, 308. [Google Scholar] [CrossRef]
- Sánchez-Heras, A.B.; Ramon y Cajal, T.; Pineda, M.; Aguirre, E.; Graña, B.; Chirivella, I.; Balmaña, J.; Brunet, J.; SEOM Hereditary Cancer Working Group; AEGH Hereditary Cancer Committee. SEOM clinical guideline on heritable TP53-related cancer syndrome (2022). Clin. Transl. Oncol. 2023, 25, 2627–2633. [Google Scholar] [CrossRef]
- Mansur, M.B.; Greaves, M. Convergent TP53 loss and evolvability in cancer. BMC Ecol. Evol. 2023, 23, 54. [Google Scholar] [CrossRef]
- Yuzhalin, A.E.; Lowery, F.J.; Saito, Y.; Yuan, X.; Yao, J.; Duan, Y.; Ding, J.; Acharya, S.; Zhang, C.; Fajardo, A.; et al. Astrocyte-induced Cdk5 expedites breast cancer brain metastasis by suppressing MHC-I expression to evade immune recognition. Nat. Cell Biol. 2024, 26, 1773–1789. [Google Scholar] [CrossRef]
- Jäger, D.; Berger, A.; Tuch, A.; Luckner-Minden, C.; Eurich, R.; Hlevnjak, M.; Schneeweiss, A.; Lichter, P.; Aulmann, S.; Heussel, C.P.; et al. Novel chimeric antigen receptors for the effective and safe treatment of NY-BR-1 positive breast cancer. Clin. Transl. Med. 2024, 14, e1776. [Google Scholar] [CrossRef]
- Li, X.; Hu, Z.; Shi, Q.; Qiu, W.; Liu, Y.; Liu, Y.; Huang, S.; Liang, L.; Chen, Z.; He, X. Elevated choline drives KLF5-dominated transcriptional reprogramming to facilitate liver cancer progression. Oncogene 2024, 43, 3121–3136. [Google Scholar] [CrossRef] [PubMed]
- Papin, M.; Bouchet, A.M.; Chantôme, A.; Vandier, C. Ether-lipids and cellular signaling: A differential role of alkyl-and alkenyl-ether-lipids? Biochimie 2023, 215, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Geismann, C.; Hauser, C.; Grohmann, F.; Schneeweis, C.; Bölter, N.; Gundlach, J.P.; Schneider, G.; Röcken, C.; Meinhardt, C.; Schäfer, H.; et al. NF-κB/RelA controlled A20 limits TRAIL-induced apoptosis in pancreatic cancer. Cell Death Dis. 2023, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Solanki, R.; Bhatia, D. Stimulus-responsive hydrogels for targeted cancer therapy. Gels 2024, 10, 440. [Google Scholar] [CrossRef]
- Han, H.; Santos, H.A. Nano-and Micro-Platforms in Therapeutic Proteins Delivery for Cancer Therapy: Materials and Strategies. Adv. Mater. 2024, 36, 2409522. [Google Scholar] [CrossRef]
- Feng, T.Y.; Melchor, S.J.; Zhao, X.Y.; Ghumman, H.; Kester, M.; Fox, T.E.; Ewald, S.E. Tricarboxylic acid (TCA) cycle, sphingolipid, and phosphatidylcholine metabolism are dysregulated in T. gondii infection-induced cachexia. Heliyon 2023, 9, e17411. [Google Scholar] [CrossRef]
- Guerrache, A.; Micheau, O. TNF-Related Apoptosis-Inducing Ligand: Non-Apoptotic Signalling. Cells 2024, 13, 521. [Google Scholar] [CrossRef]
- Benjamin, C.; Crews, R. Nicotinamide Mononucleotide Supplementation: Understanding Metabolic Variability and Clinical Implications. Metabolites 2024, 14, 341. [Google Scholar] [CrossRef]
- Migaud, M.E.; Ziegler, M.; Baur, J.A. Regulation of and challenges in targeting NAD+ metabolism. Nat. Rev. Mol. Cell Biol. 2024, 25, 822–840. [Google Scholar] [CrossRef]
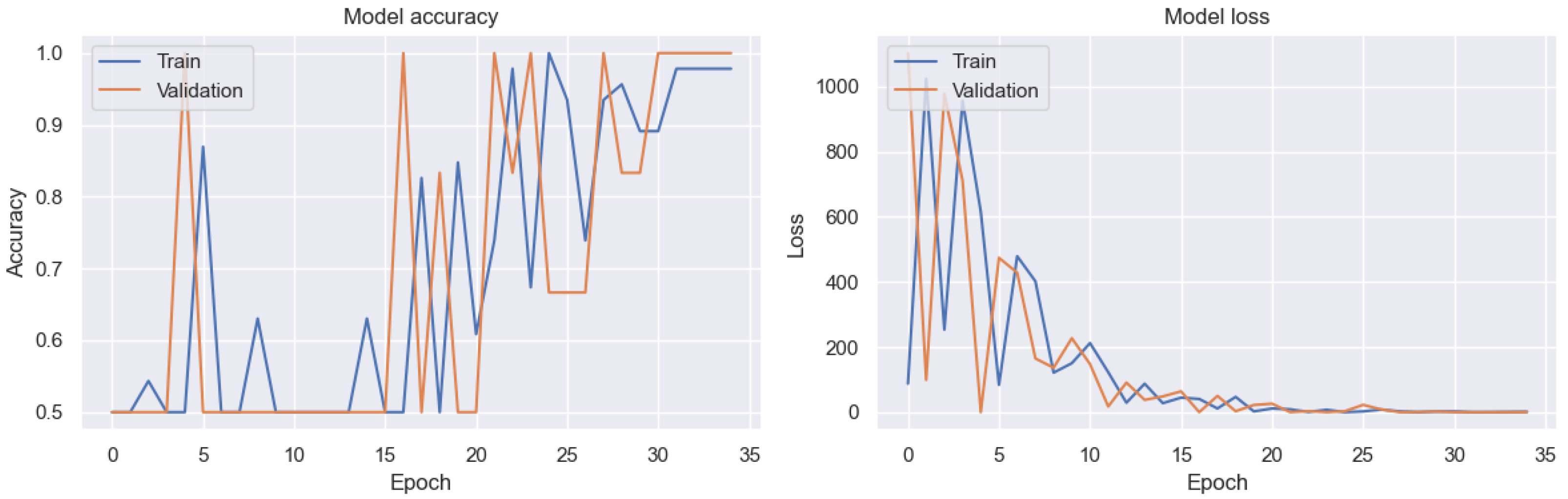

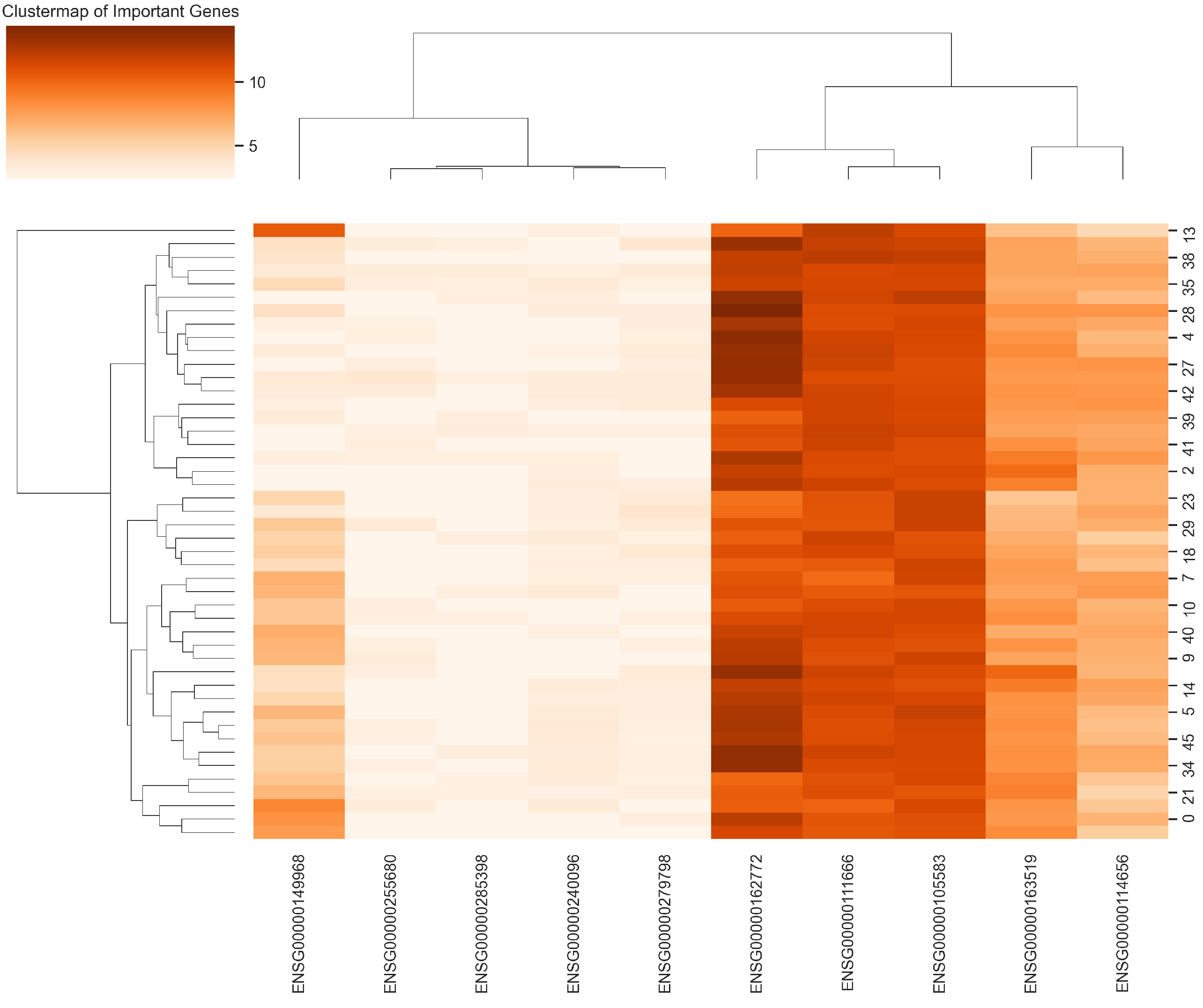
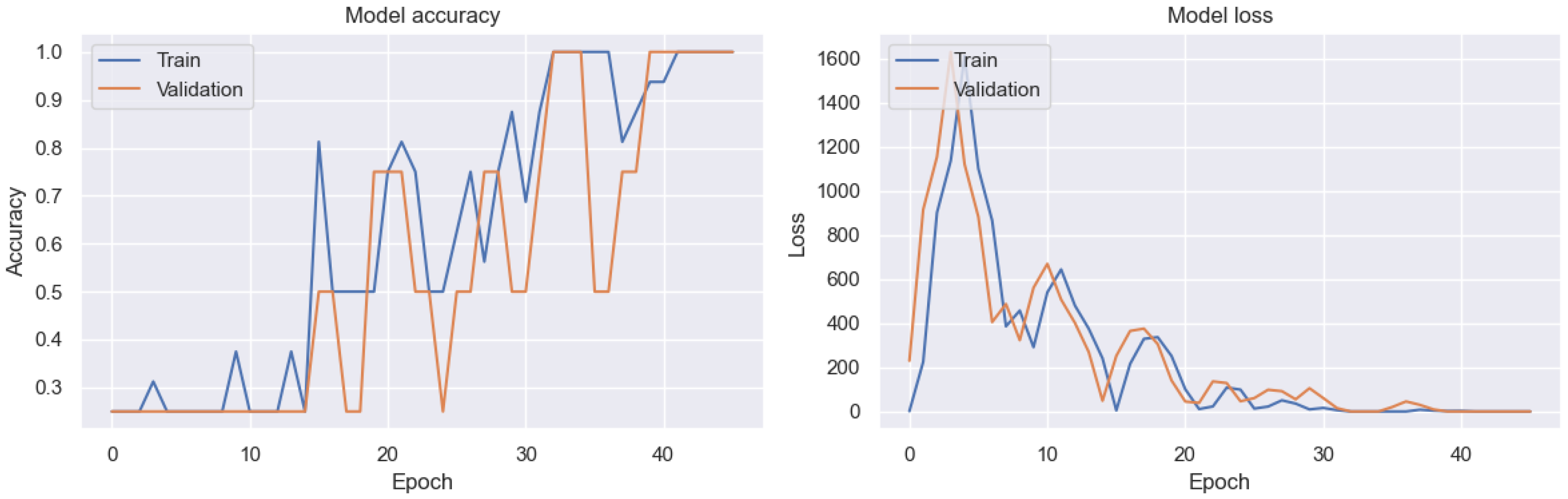
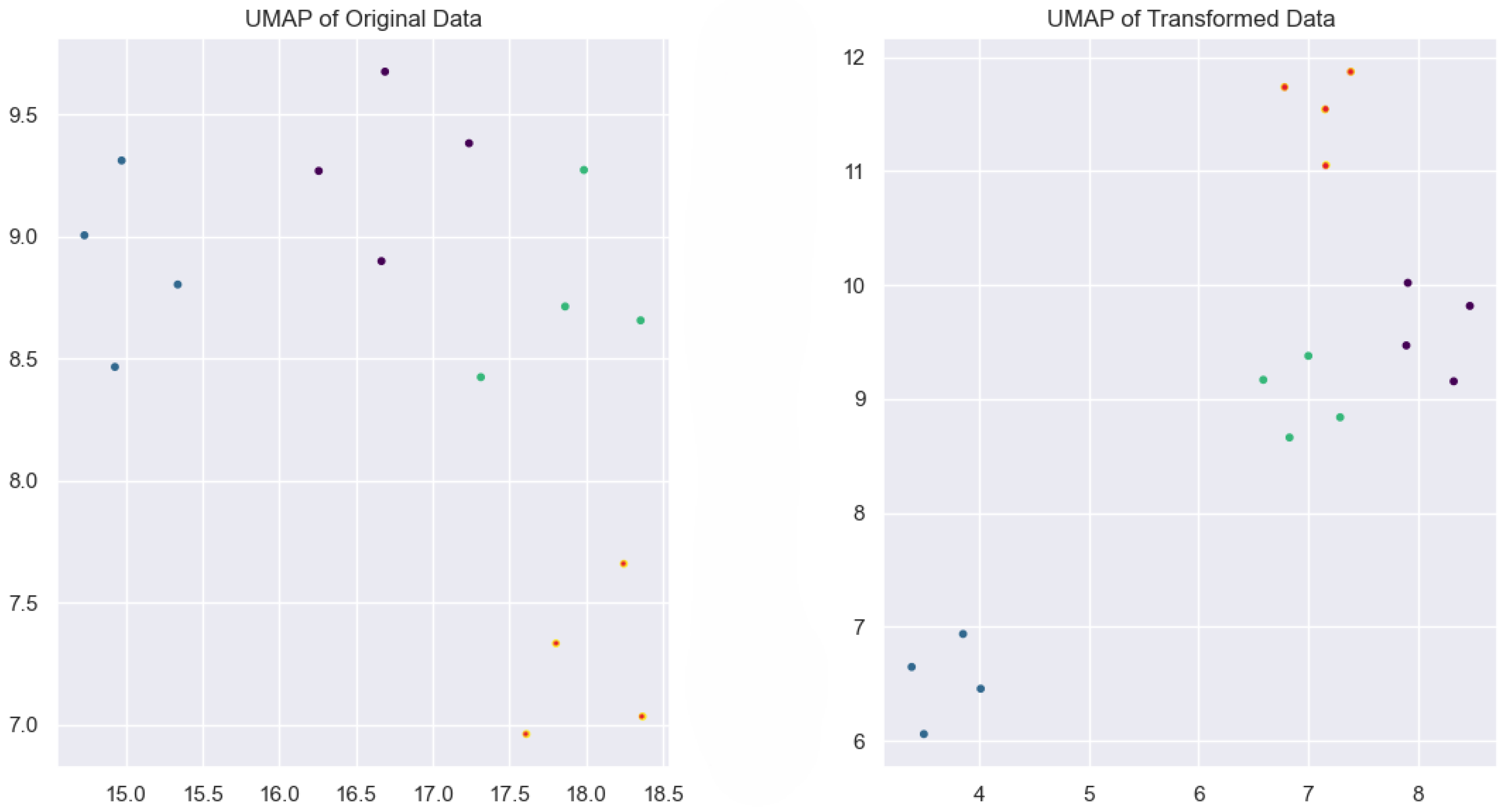


| Year | Study | Method | Result | Optimized | DSA | SD | MCT | SA |
|---|---|---|---|---|---|---|---|---|
| 2017 | Danaee et al. [48] | SDAE | 98.29% Acc | ✗ | ✓ | ✓ | ✗ | ✗ |
| 2018 | Wang et al. [43] | PDX | MCC (0.777) 92.9% Acc | ✗ | ✗ | ✗ | ✗ | ✗ |
| 2019 | Elbashir et al. [99] | CNN | 98.76% Acc | ✗ | ✓ | ✓ | ✗ | ✓ |
| 2020 | Yuan et al. [42] | SVM, RF | 100% Acc | ✗ | ✗ | ✗ | ✗ | ✗ |
| 2020 | MotieGhader et al. [63] | Metaheuristic with SVM | 90% Acc | ✓ | ✗ | ✗ | ✗ | ✗ |
| 2021 | Jia et al. [49] | WGCNA | 97.36% Acc | ✗ | ✓ | ✗ | ✗ | ✓ |
| 2021 | Houssein et al. [87] | BMO-SVM | 99.36% Acc | ✓ | ✗ | ✗ | ✓ | ✗ |
| 2021 | Feltes et al. [95] | RF, SVM, KNN, DT, MLP | 100% Acc | ✓ | ✗ | ✓ | ✓ | ✗ |
| 2022 | Alshareef et al. [52] | IFSDL-PCD | 97.19% Acc | ✗ | ✓ | ✗ | ✗ | ✓ |
| 2022 | Wei et al. [75] | GANs | 92.6% Acc | ✗ | ✓ | ✓ | ✓ | ✓ |
| 2022 | Deng et al. [76] | XGBoost-MOGA | 56.67% Acc | ✓ | ✗ | ✗ | ✓ | ✓ |
| 2023 | Devi et al. [91] | IWOA | 97.7% Acc | ✓ | ✗ | ✗ | ✗ | ✓ |
| 2023 | Mohamed et al. [92] | CNN | 98.3% Acc | ✓ | ✓ | ✓ | ✗ | ✓ |
| 2024 | Jagadeeswararao et al. [93] | RF, SVM, KNN, LR | 96% Acc | ✗ | ✗ | ✓ | ✗ | ✗ |
| 2024 | Wang et al. [94] | SVM, LR | 90.5% AUC | ✗ | ✗ | ✓ | ✓ | ✗ |
| 2025 | Alharbi et al. [100] | LASSO-MOGAT | 95.9% Acc | ✓ | ✓ | ✓ | ✓ | ✗ |
| 2025 | Our Methodology | DL and XAI | 100% Acc | ✓ | ✓ | ✓ | ✓ | ✓ |
| Dataset | Samples [Class Distribution] | Genes | Classes |
|---|---|---|---|
| Kidney_GSE89122 | 13 [7 tumor, 6 normal] | 58,735 | 2 |
| Liver_GSE55758 | 16 [8 tumor, 8 normal] | 58,735 | 2 |
| Prostate_GSE22260 | 28 [19 tumor, 9 normal] | 58,735 | 2 |
| Breast_GSE52194 | 20 [17 tumor, 3 normal] | 58,735 | 2 |
| Breast_GSE69240 | 35 [25 tumor, 10 normal] | 58,735 | 2 |
| Breast_GSE71651 | 33 [15 tumor, 18 normal] | 58,735 | 2 |
| Colon_GSE50760 | 54 [18 primary, 18 metastasis, 18 normal] | 58,148 | 3 |
| Colon_GSE72820 | 14 [7 tumor, 7 normal] | 58,735 | 2 |
| Colon_SRR2089755 | 20 [5 primary, 5 metastasis, 5 normalliver, 5 normal] | 58,148 | 4 |
| HeadNeck_GSE48850 | 11 [6 tumor, 5 normal] | 58,735 | 2 |
| HeadNeck_GSE63511 | 16 [8 tumor, 8 normal] | 58,735 | 2 |
| HeadNeck_GSE64912 | 22 [18 tumor, 4 normal] | 58,735 | 2 |
| HeadNeck_GSE68799 | 45 [41 tumor, 4 normal] | 58,735 | 2 |
| Lung_GSE37764 | 12 [6 tumor, 6 normal] | 58,735 | 2 |
| Lung_GSE40419 | 164 [87 tumor, 77 normal] | 58,735 | 2 |
| Lung_GSE60052 | 86 [79 tumor, 7 normal] | 58,735 | 2 |
| Lung_GSE87340 | 51 [25 tumor, 26 normal] | 58,735 | 2 |
| Class | Precision | Recall | F1 Score | Accuracy |
|---|---|---|---|---|
| Breast | 0.86 | 1.00 | 0.92 | 1.00 |
| Colon | 0.60 | 0.60 | 0.60 | 0.60 |
| HeadNeck | 1.00 | 1.00 | 1.00 | 1.00 |
| Kidney | 1.00 | 1.00 | 1.00 | 1.00 |
| Liver | 1.00 | 1.00 | 1.00 | 1.00 |
| Lung | 0.95 | 0.95 | 0.95 | 0.95 |
| Normal | 0.84 | 0.73 | 0.78 | 0.73 |
| Prostate | 0.50 | 1.00 | 0.67 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Younis, H.; Minghim, R. Enhancing Cancer Classification from RNA Sequencing Data Using Deep Learning and Explainable AI. Mach. Learn. Knowl. Extr. 2025, 7, 114. https://doi.org/10.3390/make7040114
Younis H, Minghim R. Enhancing Cancer Classification from RNA Sequencing Data Using Deep Learning and Explainable AI. Machine Learning and Knowledge Extraction. 2025; 7(4):114. https://doi.org/10.3390/make7040114
Chicago/Turabian StyleYounis, Haseeb, and Rosane Minghim. 2025. "Enhancing Cancer Classification from RNA Sequencing Data Using Deep Learning and Explainable AI" Machine Learning and Knowledge Extraction 7, no. 4: 114. https://doi.org/10.3390/make7040114
APA StyleYounis, H., & Minghim, R. (2025). Enhancing Cancer Classification from RNA Sequencing Data Using Deep Learning and Explainable AI. Machine Learning and Knowledge Extraction, 7(4), 114. https://doi.org/10.3390/make7040114






