Exploring Downscaling in High-Dimensional Lorenz Models Using the Transformer Decoder
Abstract
1. Introduction
2. Materials and Methods
2.1. A Generalized Lorenz Model
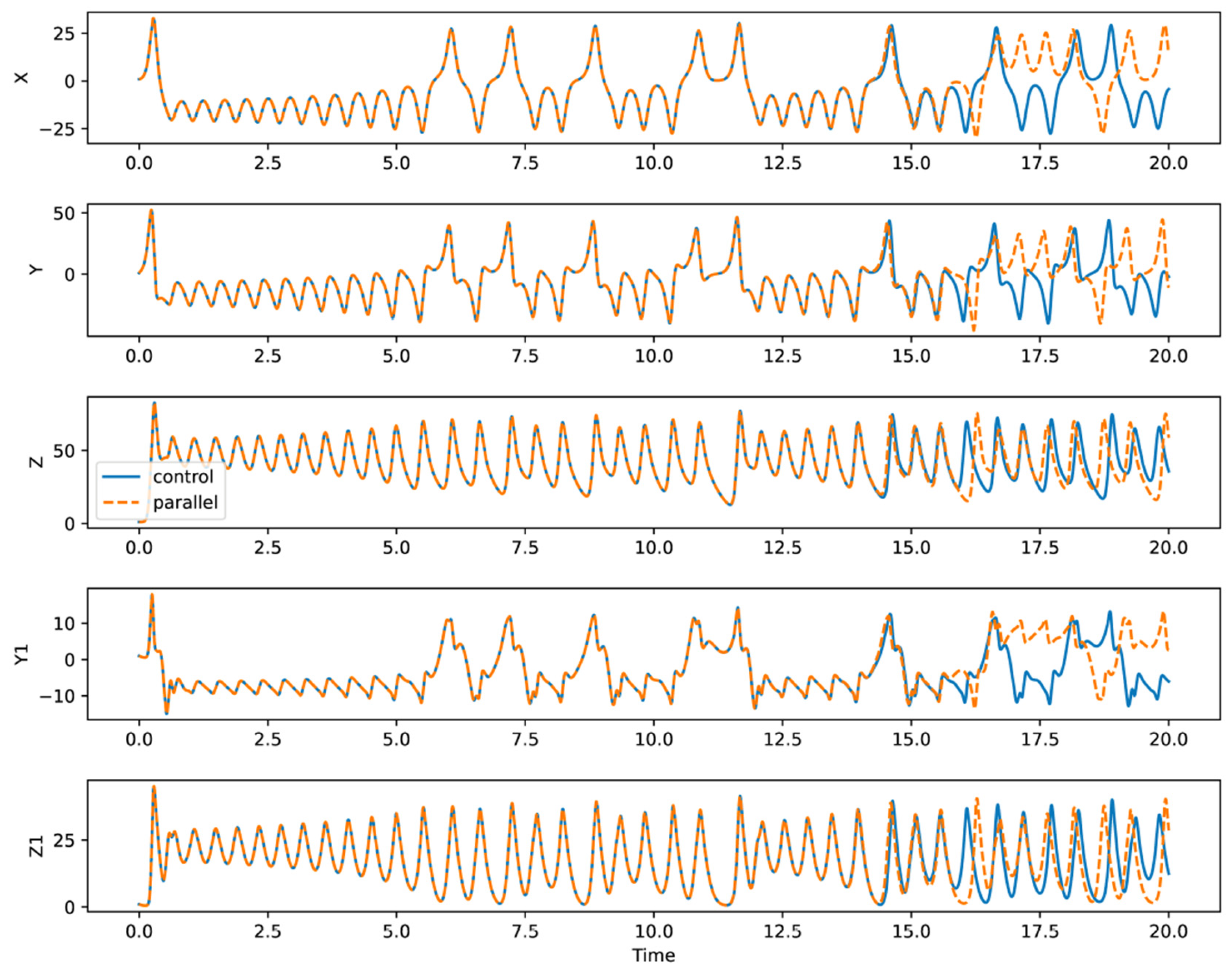
2.2. Chaotic Data Preparation
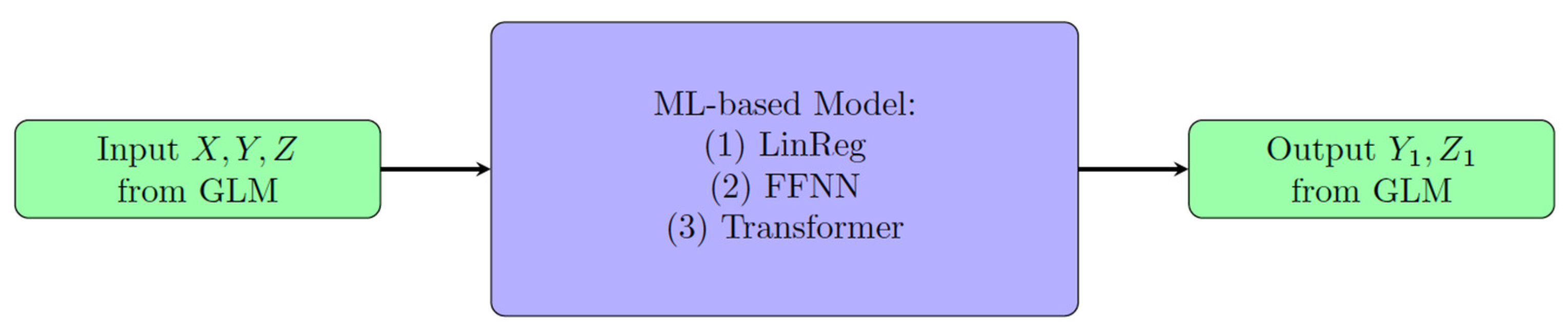
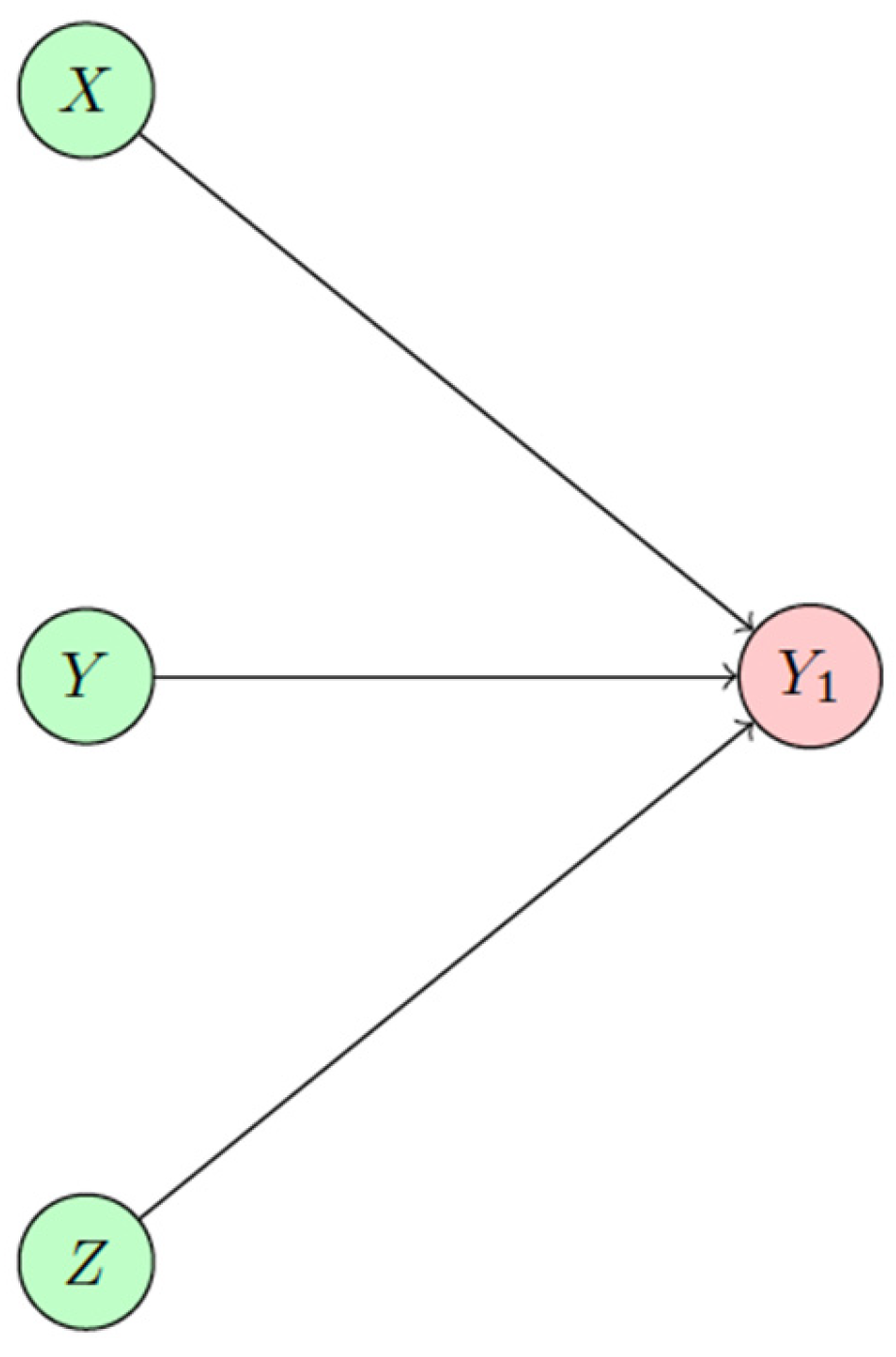
3. ML-Based Empirical Models and Their Performance
3.1. Linear Regression Model
3.2. Feedforward Neural Network (FFNN)
3.3. Transformer Technology
- Embedding Layer:
- ○
- Converts the input time series (X, Y, Z) into a higher-dimensional space, designated as a hidden dimension of 64 (h_dim = 64).
- Positional Encoding:
- ○
- Adds positional encoding to the embedded input to provide temporal information.
- Transformer Decoder Layers:
- ○
- Positionally encoded input is processed through three consecutive transformer decoder layers.
- ○
- Each layer, featuring multi-head attention mechanisms, processes the input and forwards its output to the subsequent layer, as elucidated below.
- FeedForward Neural Network (FFNN):
- ○
- Output from the last transformer decoder layer feeds into a feedforward neural network (i.e., a fully connected layer).
- ○
- This layer reduces dimensionality from the hidden dimension to the output dimensions of Y1 and Z1.
- Output:
- ○
- Final output from the fully connected layer represents the predicted values Y1 and Z1.
- Self-Attention: Enables the model to attend to all positions within the input sequence.
- Feedforward Network: Processes the output from the self-attention mechanism.
- Layer Normalization and Residual Connections (He et al., 2015 [74]): Applied within each sublayer to stabilize and enhance the learning process.
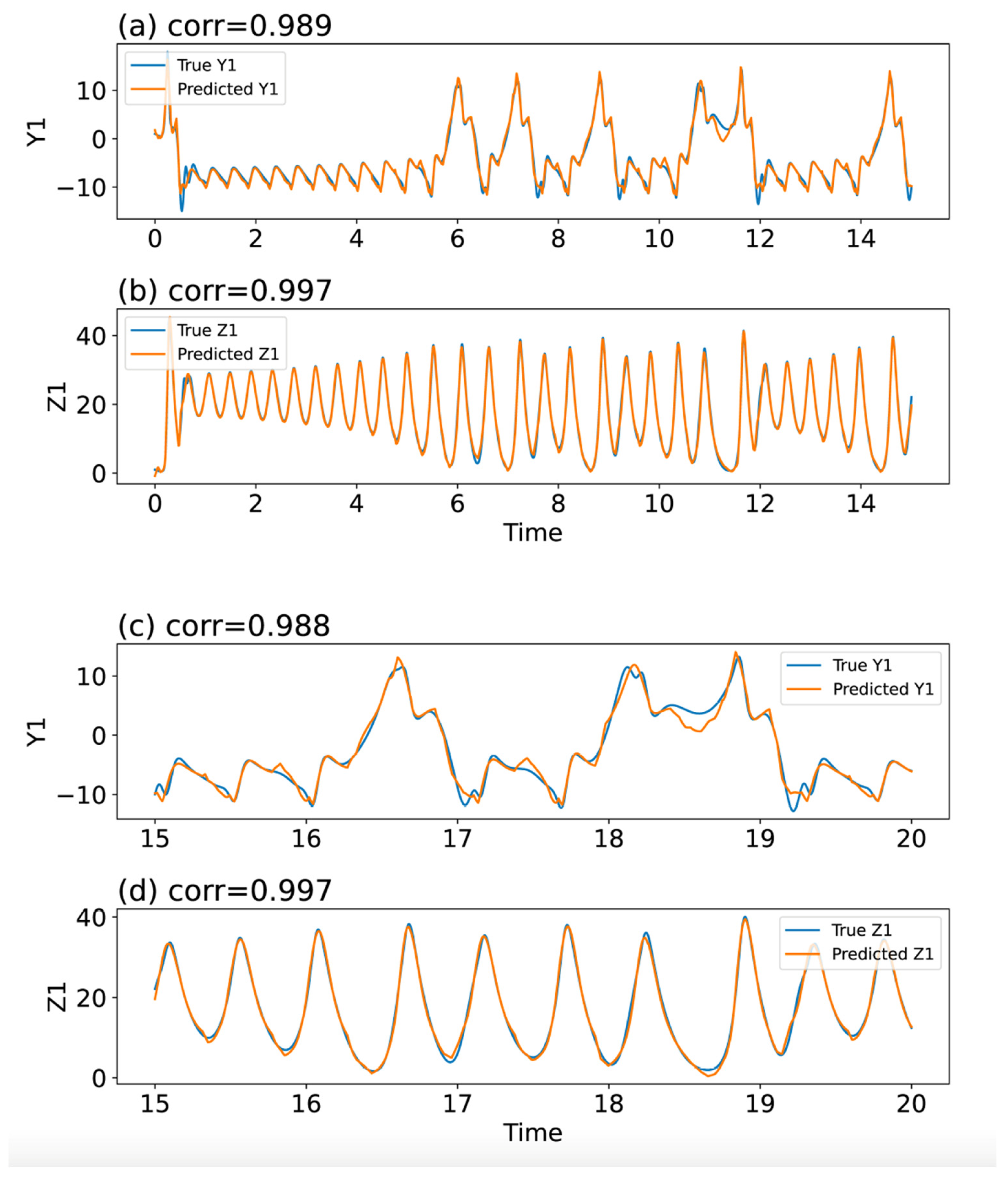
3.4. Additional Verification Using the 7DLM
4. Discussions and Future Directions
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilby, R.L.; Wigley, T.M.L. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Castro, C.L.; Pielke, R.A., Sr.; Leoncini, G. Dynamical downscaling: Assessment of value retained and added using the Regional Atmospheric Modeling System (RAMS). J. Geophys. Res.—Atmos. 2005, 110, D05108. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themessl, M.; et al. Precipitation Downscaling under climate change. Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Pielke, R.A., Sr.; Wilby, R.L. Regional climate downscaling—What’s the point? Eos Forum 2012, 93, 52–53. [Google Scholar] [CrossRef]
- Juang, H.-M.H.; Kanamitsu, M. The NMC Regional Spectral Model. Mon. Weather Rev. 1994, 122, 3–26. [Google Scholar] [CrossRef]
- Von Storch, H.; Langenberg, H.; Feser, F. A spectral nudging technique for dynamical downscaling purposes. Mon. Weather Rev. 2000, 128, 3664–3673. [Google Scholar] [CrossRef]
- Pathak, J.; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. Fourcastnet: A Global Data-Driven High-Resolution Weather Model Using Adaptive Fourier Neural Operators. arXiv 2022, arXiv:2202.11214. [Google Scholar]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Bonev, B.; Kurth, T.; Hundt, C.; Pathak, J.; Baust, M.; Kashinath, K.; Anandkumar, A. Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere. arXiv 2023, arXiv:2306.03838. [Google Scholar] [CrossRef]
- Chen, K.; Han, T.; Gong, J.; Bai, L.; Ling, F.; Luo, J.-J.; Chen, X.; Ma, L.; Zhang, T.; Su, R.; et al. FengWu: Pushing the Skillful Global Medium-range Weather Forecast beyond 10 Days Lead. arXiv 2023, arXiv:2304.02948. [Google Scholar]
- Chen, L.; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for 15-day global weather forecast. NPJ Clim. Atmos. Sci. 2023, 6, 190. [Google Scholar] [CrossRef]
- Nguyen, T.; Brandstetter, J.; Kapoor, A.; Gupta, J.K.; Grover, A. Climax: A Foundation Model for Weather and Climate. In Proceedings of the Workshop “Tackling Climate Change with Machine Learning, ICLR 2023, Virtual, 9 December 2022. [Google Scholar]
- Selz, T.; Craig, G.C. Can artificial intelligence-based weather prediction models simulate the butterfly effect? Geophys. Res. Lett. 2023, 50, e2023GL105747. [Google Scholar] [CrossRef]
- Watt-Meyer, O.; Dresdner, G.; McGibbon, J.; Clark, S.K.; Henn, B.; Duncan, J.; Brenowitz, N.D.; Kashinath, K.; Pritchard, M.S.; Bonev, B.; et al. ACE: A fast, skillful learned global atmospheric model for climate prediction. arXiv 2023, arXiv:2310.02074v1. [Google Scholar] [CrossRef]
- Bouallègue, Z.B.; Clare, M.C.A.; Magnusson, L.; Gascon, E.; Maier-Gerber, M.; Janousek, M.; Rodwell, M.; Pinault, F.; Dramsch, J.S.; Lang, S.T.K.; et al. The rise of data-driven weather forecasting: A first statistical assessment of machine learning-based weather forecasts in an operational-like context. Bull. Am. Meteorol. Soc. 2024, 105, E864–E883. [Google Scholar] [CrossRef]
- Li, H.; Chen, L.; Zhong, X.; Wu, J.; Chen, D.; Xie, S.-P.; Chao, Q.; Lin, C.; Hu, Z.; Lu, B.; et al. A machine learning model that outperforms conventional global subseasonal forecast models. Nat. Portf. 2024. [Google Scholar] [CrossRef]
- Wiener, N. Nonlinear prediction and dynamics. In Proceeding of the Third Berkeley Symposium on Mathematics, Statistics, and Probability, Statistical Laboratory of the University of California, Berkeley, CA, USA, 26–31 December 1954; University of California Press: Berkeley, CA, USA, 1956; Volume III, pp. 247–252. [Google Scholar]
- Charney, J.; Fjørtoft, R.; von Neumann, J. Numerical Integration of the Barotropic Vorticity Equation. Tellus 1950, 2, 237. [Google Scholar] [CrossRef]
- Lorenz, E.N. The statistical prediction of solutions of dynamic equations. In Proceedings of the International Symposium on Numerical Weather Prediction, Tokyo, Japan, 7–13 November 1962; pp. 629–635. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 227p. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Special Issue on Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere 2023, 14, 1279. [Google Scholar] [CrossRef]
- Saltzman, B. Finite Amplitude Free Convection as an Initial Value Problem-I. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lakshmivarahan, S.; Lewis, J.M.; Hu, J. Saltzman’s Model: Complete Characterization of Solution Properties. J. Atmos. Sci. 2019, 76, 1587–1608. [Google Scholar] [CrossRef]
- Lewis, J.M.; Sivaramakrishnan, L. Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method. Atmosphere 2022, 13, 1647. [Google Scholar] [CrossRef]
- Gleick, J. Chaos: Making a New Science; Penguin: New York, NY, USA, 1987; 360p. [Google Scholar]
- Li, T.-Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Curry, J.H. Generalized Lorenz systems. Commun. Math. Phys. 1978, 60, 193–204. [Google Scholar] [CrossRef]
- Curry, J.H.; Herring, J.R.; Loncaric, J.; Orszag, S.A. Order and disorder in two- and three-dimensional Benard convection. J. Fluid Mech. 1984, 147, 1–38. [Google Scholar] [CrossRef]
- Howard, L.N.; Krishnamurti, R.K. Large-scale flow in turbulent convection: A mathematical model. J. Fluid Mech. 1986, 170, 385–410. [Google Scholar] [CrossRef]
- Hermiz, K.B.; Guzdar, P.N.; Finn, J.M. Improved low-order model for shear flow driven by Rayleigh–Benard convection. Phys. Rev. E 1995, 51, 325–331. [Google Scholar] [CrossRef]
- Thiffeault, J.-L.; Horton, W. Energy-conserving truncations for convection with shear flow. Phys. Fluids 1996, 8, 1715–1719. [Google Scholar] [CrossRef]
- Musielak, Z.E.; Musielak, D.E.; Kennamer, K.S. The onset of chaos in nonlinear dynamical systems determined with a new fractal technique. Fractals 2005, 13, 19–31. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. I. Energy-conserving vertical mode truncations. Chaos Solit. Fract. 2007, 32, 1038–1052. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. II. Energyconserving horizontal mode truncations. Chaos Solit. Fract. 2007, 31, 747–756. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. III. Energyconserving horizontal and vertical mode truncations. Chaos Solit. Fract. 2007, 33, 1064–1070. [Google Scholar] [CrossRef]
- Moon, S.; Han, B.-S.; Park, J.; Seo, J.M.; Baik, J.-J. Periodicity and chaos of high-order Lorenz systems. Int. J. Bifurc. Chaos 2017, 27, 1750176. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact Tropical Weather Prediction (CAMVis). IEEE Comput. Sci. Eng. (CiSE) 2011, 13, 56–67. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear Feedback in a Five-dimensional Lorenz Model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.-W. Hierarchical scale dependence associated with the extension of the nonlinear feedback loop in a seven-dimensional Lorenz model. Nonlin. Processes Geophys. 2016, 23, 189–203. [Google Scholar] [CrossRef]
- Shen, B.-W. Aggregated Negative Feedback in a Generalized Lorenz Model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Shen, B.-W. On the Predictability of 30-day Global Mesoscale Simulations of Multiple African Easterly Waves during Summer 2006: A View with a Generalized Lorenz Model. Geosciences 2019, 9, 281. [Google Scholar] [CrossRef]
- Felicio, C.C.; Rech, P.C. On the dynamics of five- and six-dimensional Lorenz models. J. Phys. Commun. 2018, 2, 025028. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Shen, B.-W. Quasi-periodic in the five-dimensional non-dissipative Lorenz model: The role of the extended nonlinear feedback loop. Int. J. Bifurc. Chaos 2018, 28, 1850072. [Google Scholar] [CrossRef]
- Reyes, T.; Shen, B.-W. A Recurrence Analysis of Chaotic and Non-Chaotic Solutions within a Generalized Nine-Dimensional Lorenz Model. Chaos Solitons Fractals 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Cui, J.; Shen, B.-W. A Kernel Principal Component Analysis of Coexisting Attractors within a Generalized Lorenz Model. Chaos Solitons Fractals 2021, 146, 110865. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; pp. 1097–1105. Available online: https://papers.nips.cc/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html (accessed on 4 July 2024).
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Atienza, R. Advanced Deep Learning with Tensorflow 2 and Keras, 2nd ed.; Packt Publishing Ltd.: Brimingham, UK, 2020; 491p. [Google Scholar]
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective, 2nd ed.; Ellsevier Ltd.: London, UK, 2020; 1131p. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need; Advances in Neural Information Processing Systems. 30; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Available online: https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 4 July 2024).
- Raschka, S.; Liu, Y.H.; Mirjalili, V. Machine Learning with Pytorch and Scikit-Learn; Packt Publishing Ltd.: Brimingham, UK, 2022; 741p. [Google Scholar]
- Bommasani, R.; Hudson, D.A.; Adeli, E.; Altman, R.; Arora, S.; von Arx, S.; Bernstein, M.S.; Bohg, J.; Bosselut, A.; Brunskill, E.; et al. On the Opportunities and Risks of Foundation Models. arXiv 2022, arXiv:2108.07258. [Google Scholar] [CrossRef]
- OpenAI. ChatGPT 3.5: Language Model [Computer Software]. OpenAI. 2023. Available online: https://chat.openai.com/ (accessed on 4 July 2024).
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-Training of Deep Bidirectional Transformers for Language Understanding; Association for Computational Linguistics (ACL): Kerrville, TX, USA, 2019; pp. 4171–4186. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. arXiv 2019, arXiv:1910.10683. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 8. [Google Scholar]
- Yin, P.; Neubig, G.; Yih, W.-t.; Riedel, S. TaBERT: Pretraining for Joint Understanding of Textual and Tabular Data. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 8413–8426. [Google Scholar]
- Chen, M.; Radford, A.; Child, R.; Wu, J.; Jun, H.; Luan, D.; Sutskever, I. Generative Pretraining from Pixels. In Proceedings of the 37th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 119), Online, 12–18 July 2020; Daumé, H., III, Singh, A., Eds.; PMLR: Boston, MA, USA, 2020; pp. 1691–1703. Available online: http://proceedings.mlr.press/v119/chen20s.html (accessed on 4 July 2024).
- Rives, A.; Meier, J.; Sercu, T.; Goyal, S.; Lin, Z.; Liu, J.; Guo, D.; Myle Ott, C.; Zitnick, L.; Ma, J.; et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA 2021, 118, 15. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? Coexistence of chaos and order within a generalized Lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. [Google Scholar] [CrossRef]
- Pedlosky, J. Finite-amplitude baroclinic waves with small dissipation. J. Atmos. Sci. 1971, 28, 587597. [Google Scholar] [CrossRef]
- Pauli, V.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Atlas, R. Three Kinds of Butterfly Effects Within Lorenz Models. Encyclopedia 2022, 2, 1250–1259. [Google Scholar] [CrossRef]
- Pielke, R.A.; Shen, B.-W.; Zeng, X. Butterfly Effects. Phys. Today 2024, 77, 10. [Google Scholar] [CrossRef]
- Lighthill, J. The recently recognized failure of predictability in Newtonian dynamics. Proc. R. Soc. Lond. A 1986, 407, 35–50. [Google Scholar]
- Shen, B.-W. A Review of Lorenz’s Models from 1960 to 2008. Int. J. Bifurc. Chaos 2023, 33, 2330024. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Shen, B.-W.; Nelson, B.; Cheung, S.; Tao, W.-K. Improving the NASA Multiscale Modeling Framework’s Performance for Tropical Cyclone Climate Study. Comput. Sci. Eng. 2013, 5, 56–67. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Shen, B.-W. An Evaluation of the Parallel Ensemble Empirical Mode Decomposition Method in Revealing the Role of Downscaling Processes Associated with African Easterly Waves in Tropical Cyclone Genesis. J. Atmos. Oceanic Technol. 2016, 33, 1611–1628. [Google Scholar] [CrossRef]
- Frank, W.M.; Roundy, P.E. The role of tropical waves in tropical cyclogenesis. Mon. Weather Rev. 2006, 134, 2397–2417. [Google Scholar] [CrossRef]
- Kaplan, J.; McCandlish, S.; Henighan, T.; Brown, T.B.; Chess, B.; Child, R.; Gray, S.; Radford, A.; Wu, J.; Amodei, D. Scaling Laws for Neural Languages Models. arXiv 2020, arXiv:2001.08361. [Google Scholar] [CrossRef]
- Llama Team. The Llama 3 Herd of Models. 2024. Available online: https://llama.meta.com/ (accessed on 4 July 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present; Copernicus Climate Change Service (C3S), Climate Data Store (CDS): Reading, UK, 2018; p. 10. [Google Scholar]
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Observations of the 40–50-Day Tropical Oscillation—A Review. Mon. Weather Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef]
- Charney, J.G.; Fleagle, R.G.; Lally, V.E.; Riehl, H.; Wark, D.Q. The feasibility of a global observation and analysis experiment. Bull. Am. Meteorol. Soc. 1966, 47, 200–220. [Google Scholar]
- GARP. GARP topics. Bull. Am. Meteorol. Soc. 1969, 50, 136–141. [Google Scholar]
- Lorenz, E.N. Three approaches to atmospheric predictability. Bull. Am. Meteorol. Soc. 1969, 50, 345–351. [Google Scholar]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 19. [Google Scholar]
- Reeves, R.W. Edward Lorenz Revisiting the Limits of Predictability and Their Implications: An Interview from 2007. Bull. Am. Meteorol. Soc. 2014, 95, 681–687. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Zeng, X. Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s. Atmosphere 2024, 15, 837. [Google Scholar] [CrossRef]



| Model | Training Period | Validation Period |
|---|---|---|
| LinReg | 0.920 | 0.910 |
| FFNN | 0.989 | 0.988 |
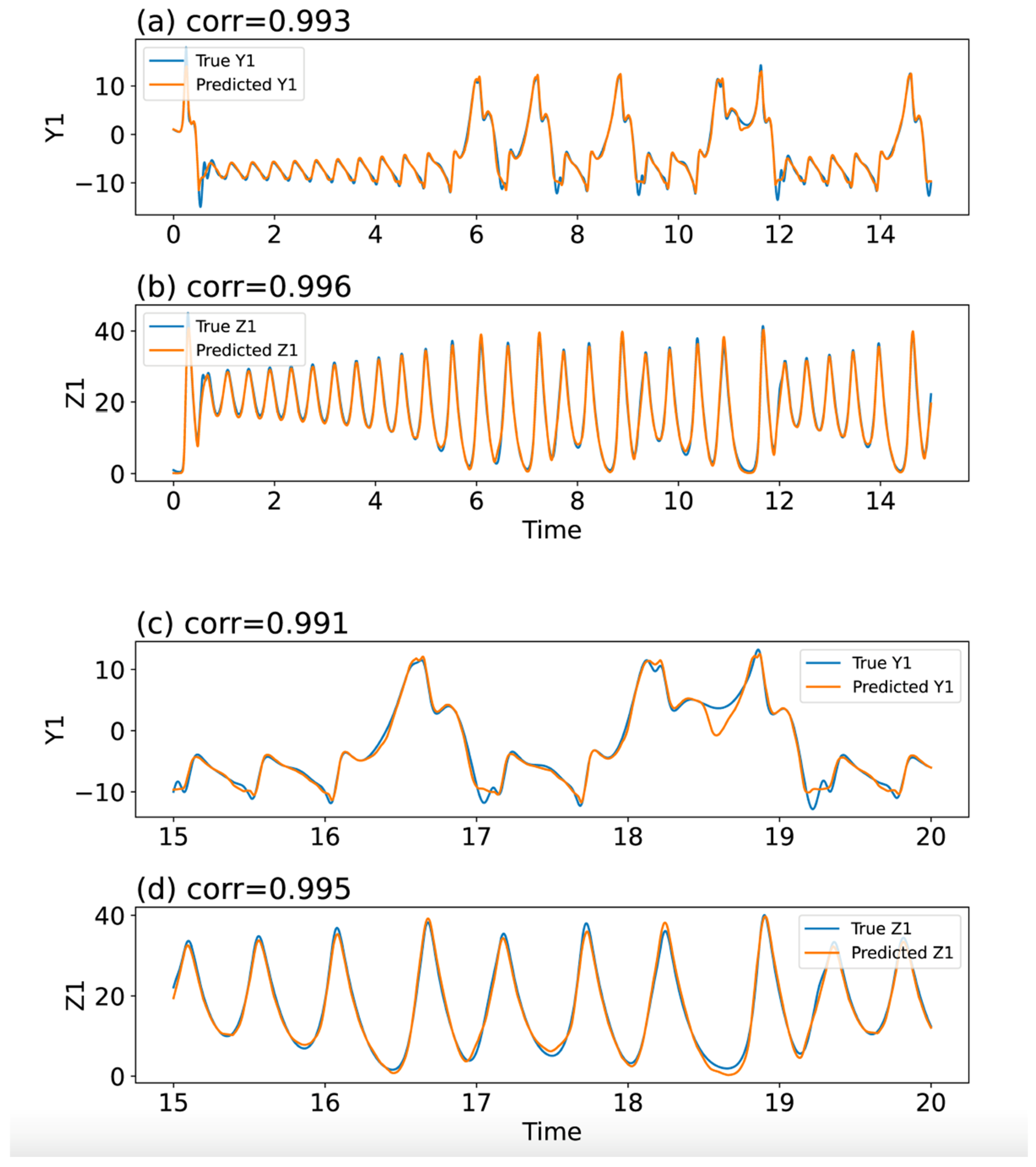
| Transformer | 0.993 | 0.991 |
| Model | Training Period |
|---|---|
| LinReg | 0.07065 |
| FFNN | 0.02673 |
| Transformer | 0.02107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.-W. Exploring Downscaling in High-Dimensional Lorenz Models Using the Transformer Decoder. Mach. Learn. Knowl. Extr. 2024, 6, 2161-2182. https://doi.org/10.3390/make6040107
Shen B-W. Exploring Downscaling in High-Dimensional Lorenz Models Using the Transformer Decoder. Machine Learning and Knowledge Extraction. 2024; 6(4):2161-2182. https://doi.org/10.3390/make6040107
Chicago/Turabian StyleShen, Bo-Wen. 2024. "Exploring Downscaling in High-Dimensional Lorenz Models Using the Transformer Decoder" Machine Learning and Knowledge Extraction 6, no. 4: 2161-2182. https://doi.org/10.3390/make6040107
APA StyleShen, B.-W. (2024). Exploring Downscaling in High-Dimensional Lorenz Models Using the Transformer Decoder. Machine Learning and Knowledge Extraction, 6(4), 2161-2182. https://doi.org/10.3390/make6040107






