Correlating Histopathological Microscopic Images of Creutzfeldt–Jakob Disease with Clinical Typology Using Graph Theory and Artificial Intelligence
Abstract
1. Introduction
2. Background and Materials
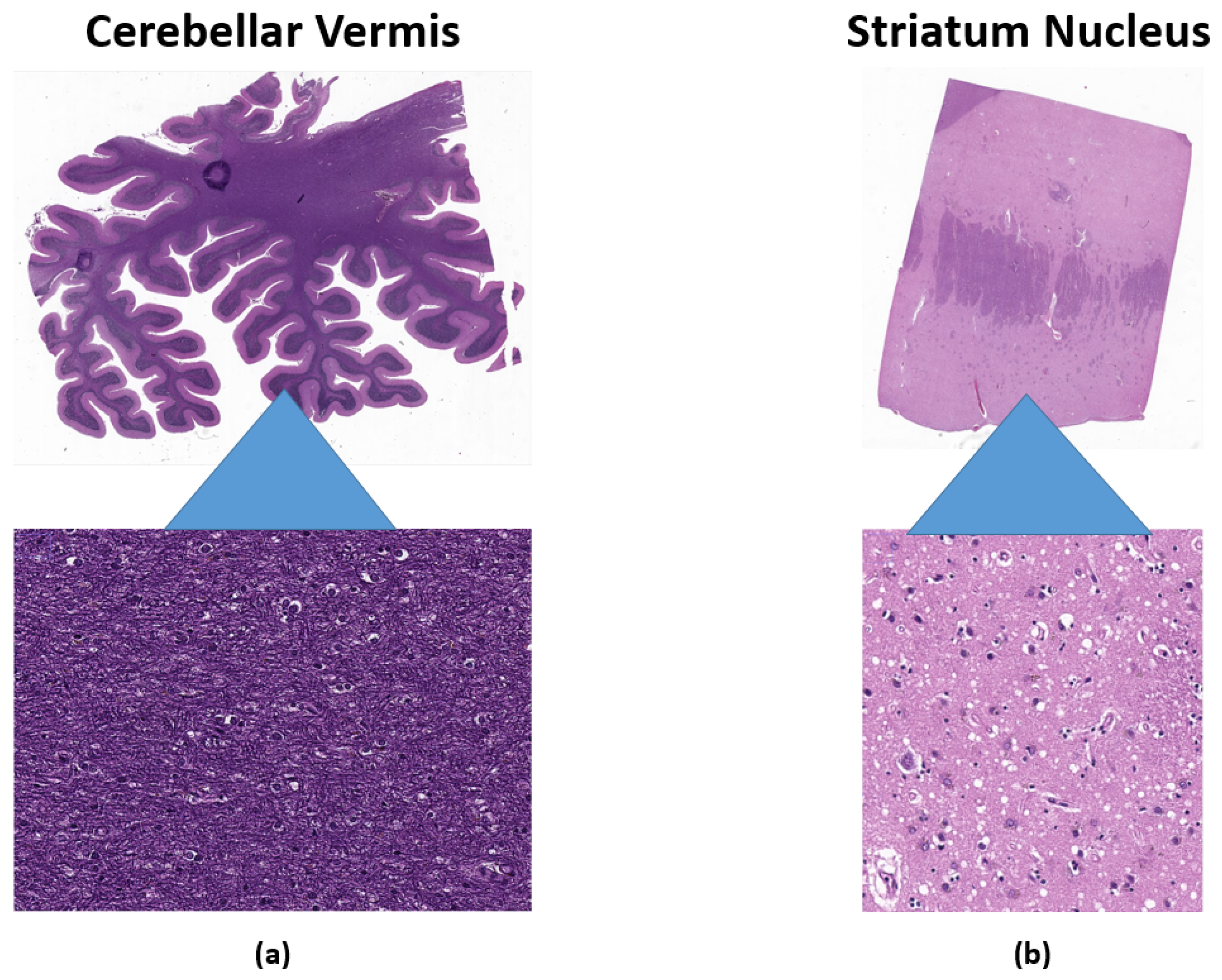
2.1. Dataset
2.2. Pipeline Components for Feature Extraction
2.2.1. Gaussian Filter
2.2.2. Roundness Criteria
- Circularity Ratio:
- Aspect Ratio:
- Fill Ratio:
2.3. Graph Theory for Feature Extraction
- Average clustering coefficient: This metric assesses the degree to which the neighbors of a node are interconnected, offering insights into the propensity for vacuoles to cluster together [16].
- Average degree of connectivity: This metric quantifies the mean number of connections each node has within the network, offering insight into the graph’s overall connectivity density. To avoid the unrealistic scenario wherein every node is considered connected to all others, it is essential to establish a maximum distance criterion for connections. In this study, we employ the Euclidean distance as the threshold to determine the connectivity between vacuoles.
- Global efficiency: This indicator measures the graph’s overall efficiency in information transfer, illustrating how swiftly information can traverse the network from one node to another [16].
- Modularity: Modularity evaluates the graph’s division into modules or communities; a high modularity score signifies a clear delineation between densely connected clusters of nodes and their weaker inter-cluster connections [16].
- Degree assortativity coefficient (degree correlation): By examining the tendency of nodes to connect with others possessing a similar degree of connections, this measure provides insight into the structural hierarchy and clustering tendencies among the nodes [16].
3. A New Method for the Automatic Feature Extraction and Classification of Creutzfeldt–Jakob Disease
3.1. Image Processing Pipeline
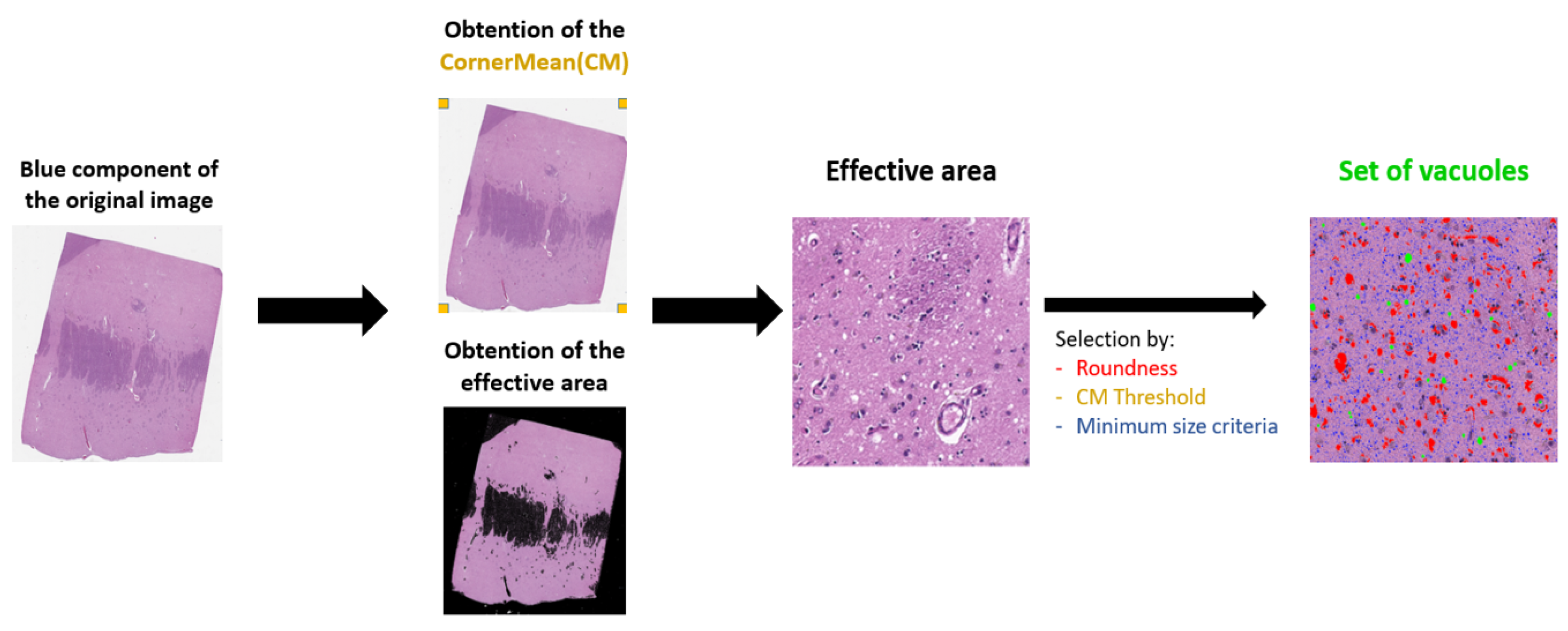
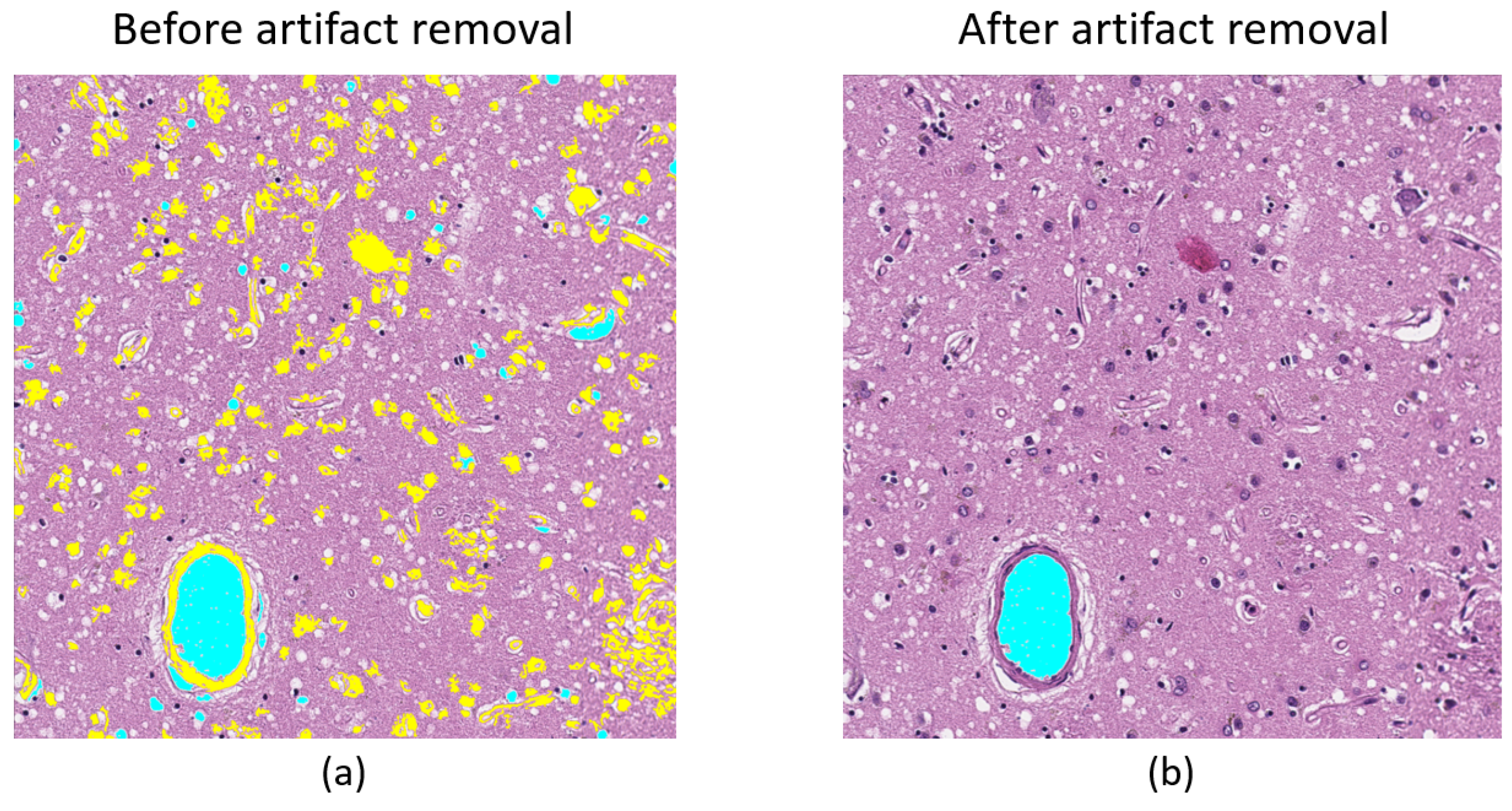
3.1.1. Preprocessing
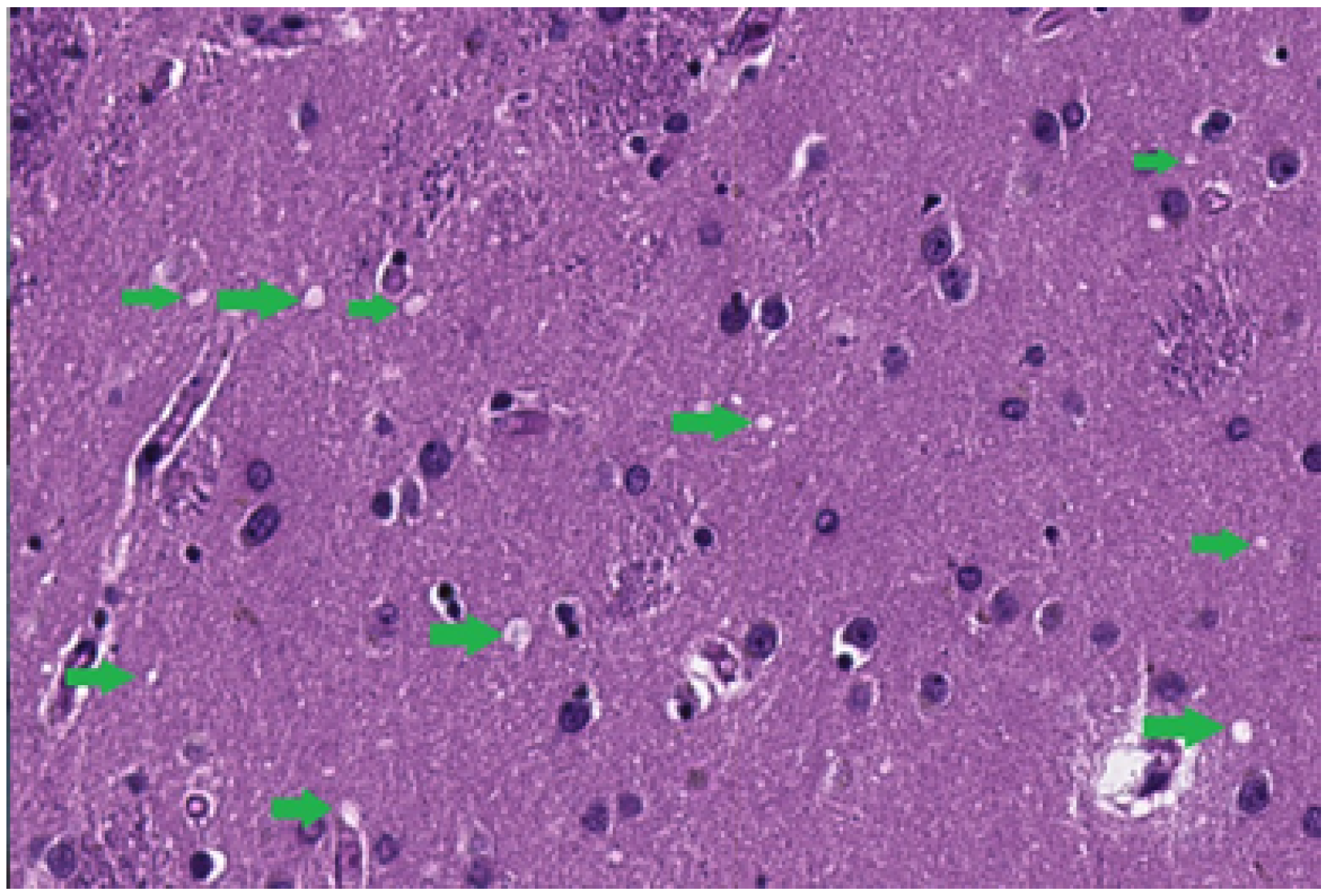
3.1.2. Identification of a Set of Vacuoles
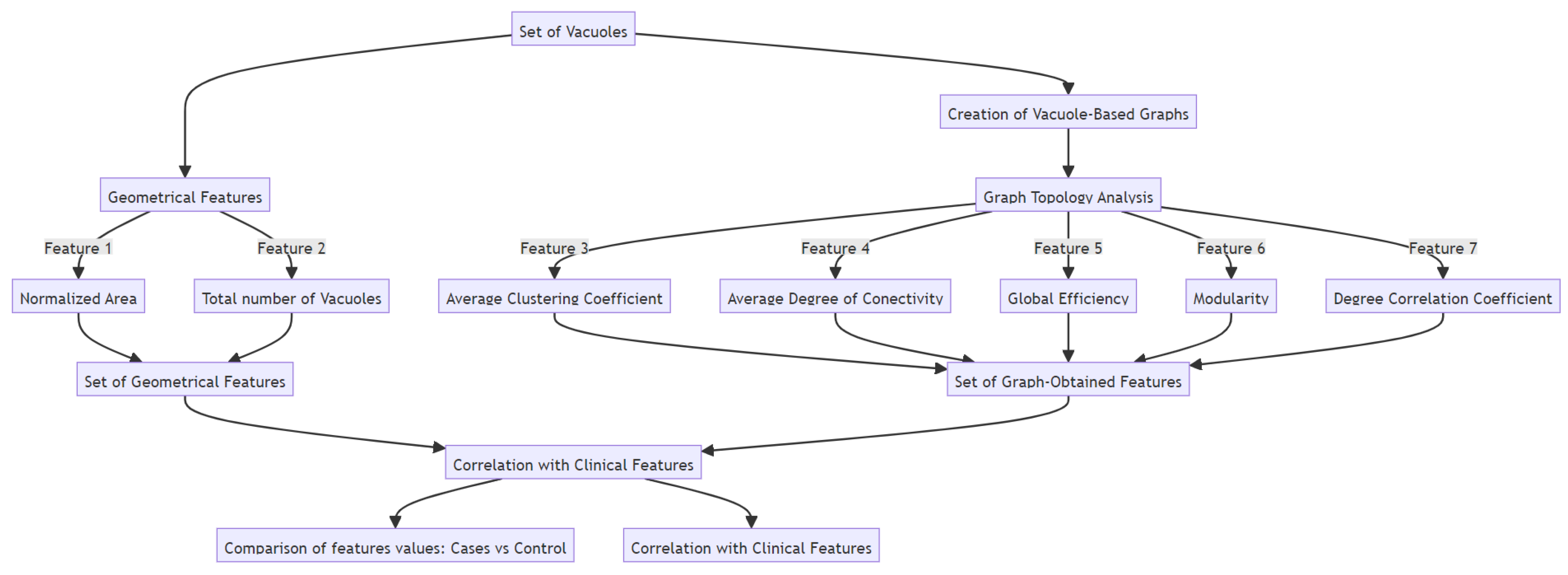
3.2. Feature Extraction
- Normalized area: the area of the vacuoles relative to the total tissue area in the image, providing an indicator of the severity of the spongiosis.
- Total number of vacuoles: the number of vacuoles found in the image.
- Creation of Vacuole-Based Graphs:
- Graph Feature Extraction and Topology Analysis:
- Community detection: Through community detection algorithms, we identify groups of vacuoles that show significant clustering patterns. This clustering may indicate areas of greater affection by or severity of spongiosis, providing valuable clues about the progression of CJD.
- Centrality and graph density: We analyze centrality measures to identify nodes (vacuoles) that play critical roles in the structure of the affected tissue. The graph’s density offers information about the generality of spongiosis in the analyzed sample.
3.3. Coding Details
4. Results
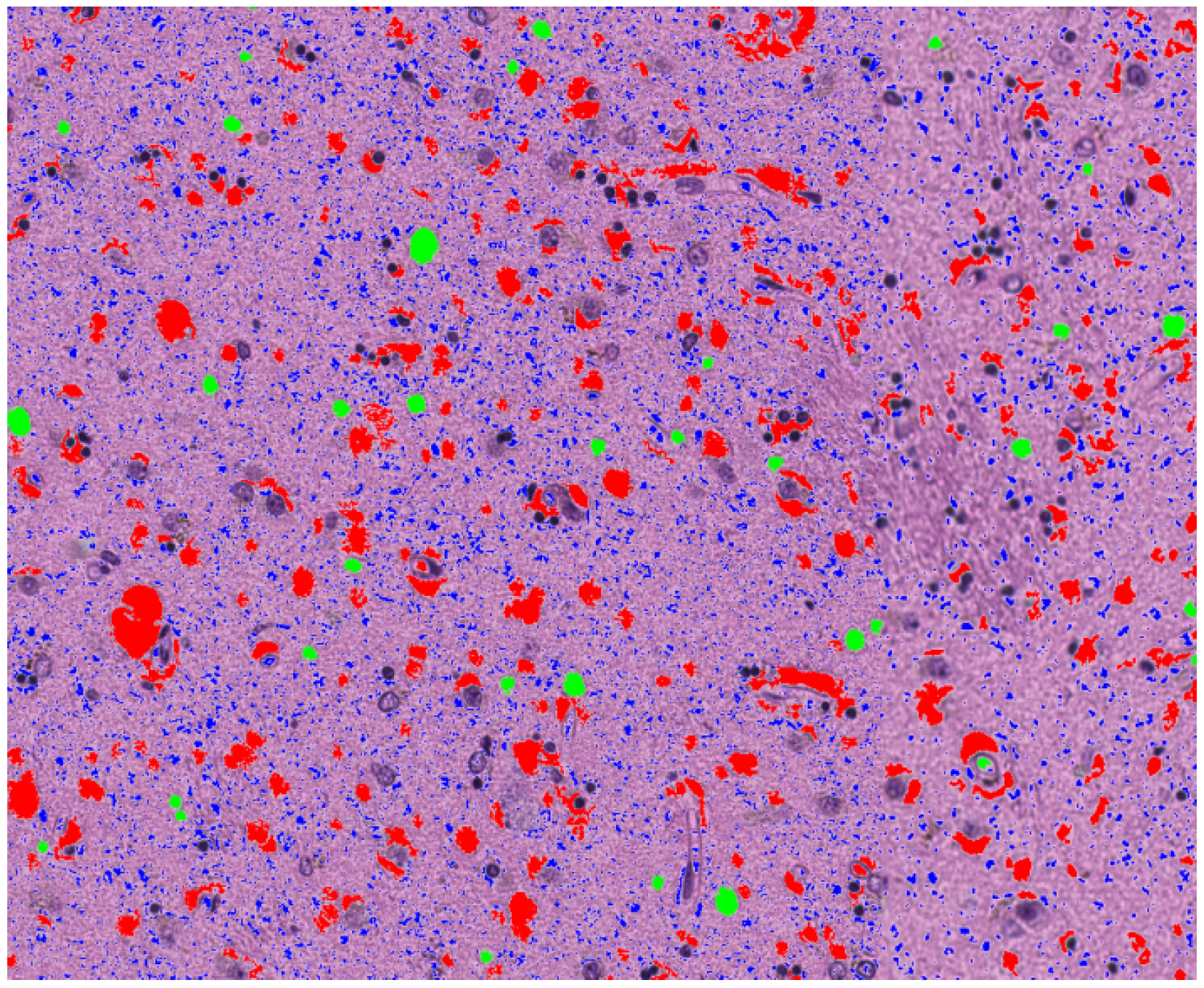
4.1. Spongiosis Segmentation
4.2. Feature Extraction
4.3. Correlation of Features with Clinical Variables
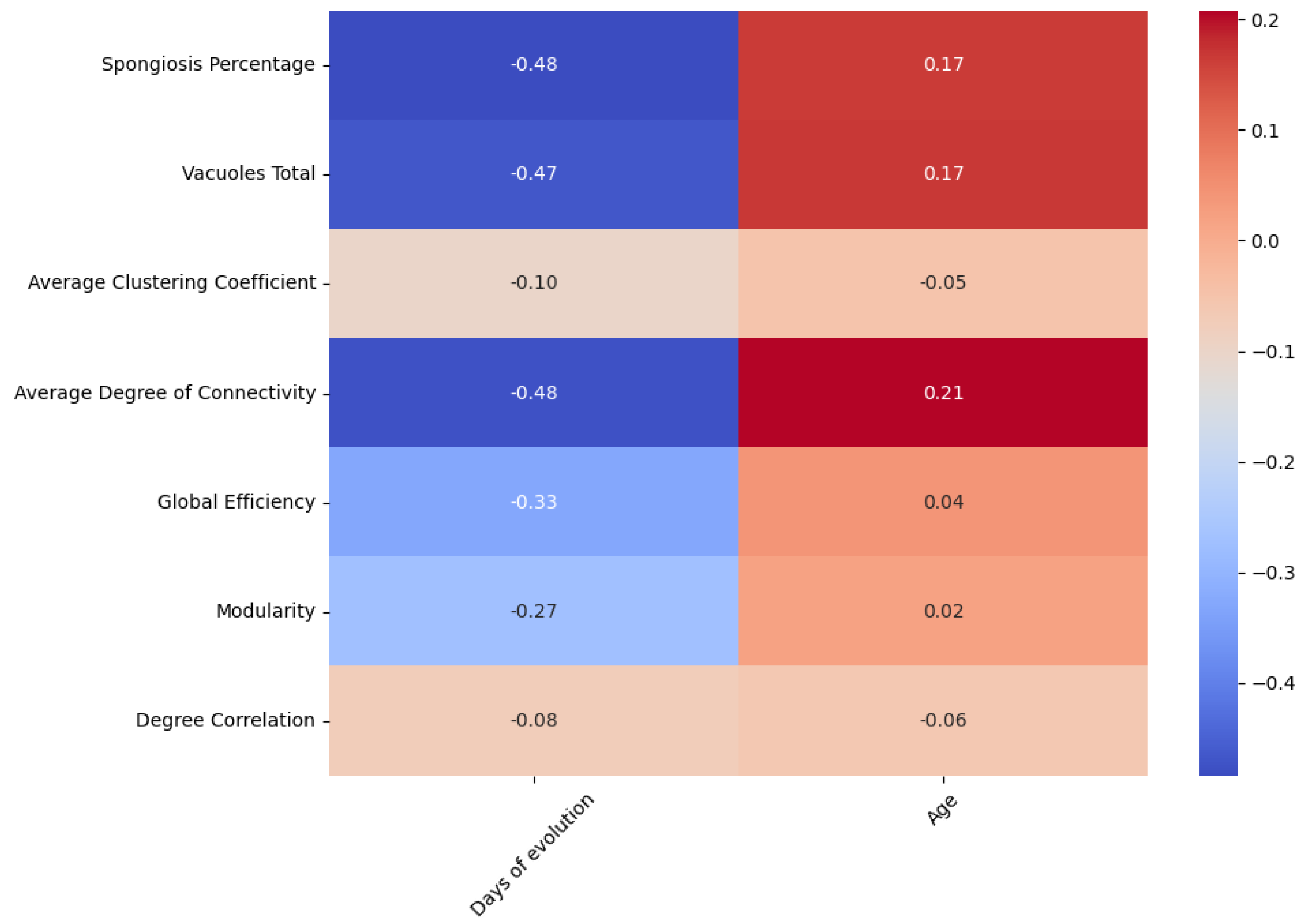
4.3.1. Age and Days of Evolution
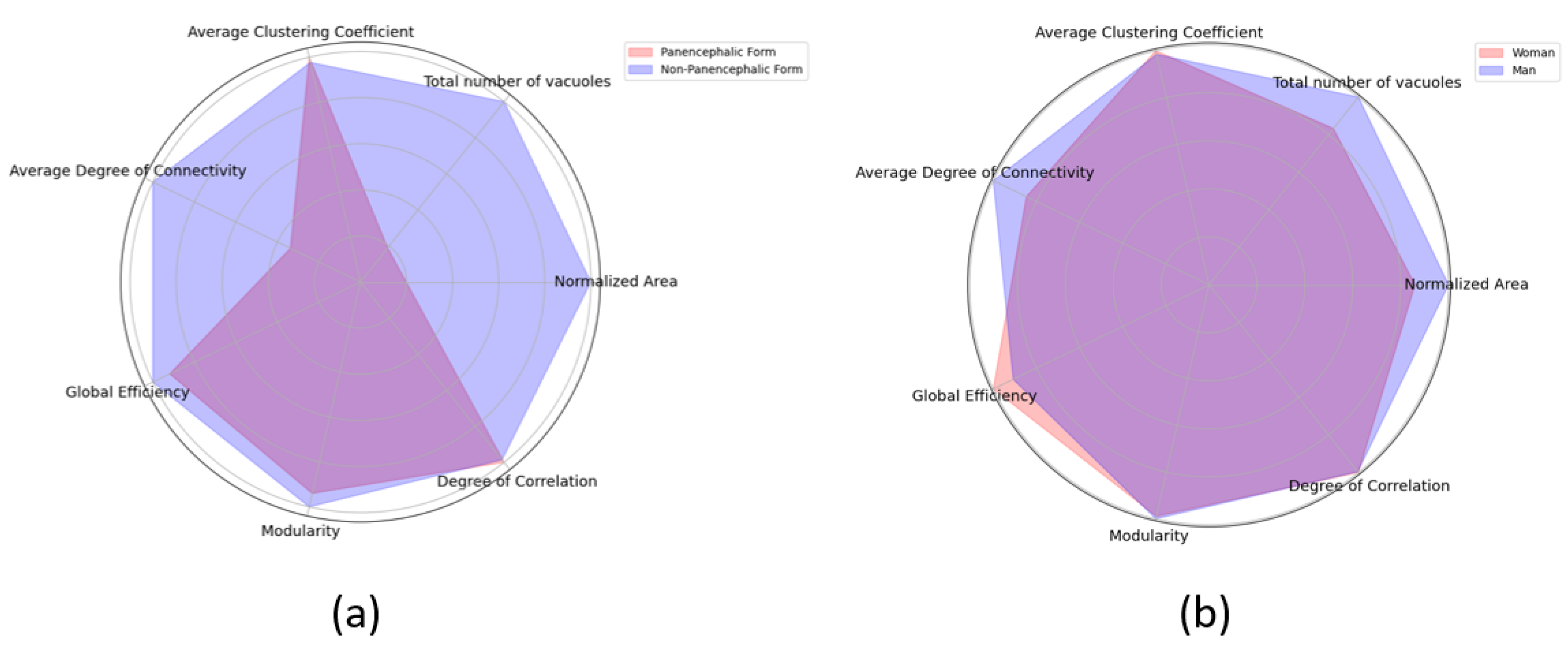
4.3.2. Sex and Panencephalic Form
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CJD | Creutzfeldt–Jakob Disease |
| PRP | Prion Protein |
| WSI | Whole Slide Image |
| TSE | Transmissible Spongiform Encephalopathy |
References
- Johnson, R.T.; Gibbs, C.J., Jr. Creutzfeldt–Jakob disease and related transmissible spongiform encephalopathies. N. Engl. J. Med. 1998, 339, 1994–2004. [Google Scholar] [CrossRef] [PubMed]
- Uttley, L.; Carrol, C.; Wong, R.; Hilton, D.A. Creutzfeldt-Jakob disease: A systematic review of global incidence, prevalence, infectivity, and incubation. Lancet Inf. Dis. 2020, 20, E2–E10. [Google Scholar] [CrossRef] [PubMed]
- Prusiner, S.B. Scrapie prions. Annu. Rev. Microbiol. 1989, 43, 345–374. [Google Scholar] [CrossRef] [PubMed]
- Wall, C.A.; Rummans, T.A.; Aksamit, A.J.; Krahn, L.E.; Pankratz, V.S. Psychiatric Manifestations of Creutzfeldt-Jakob Disease: A 25-Year Analysis. J. Neuropsychiatry Clin. Neurosci. 2005, 17, 489–495. [Google Scholar] [CrossRef] [PubMed]
- Zerr, I.; Parchi, P. Chapter 9—Sporadic Creutzfeldt–Jakob disease. In Handbook of Clinical Neurology; Pocchiari, M., Manson, J., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 2018; pp. 155–174. [Google Scholar]
- Hermann, P.; Appleby, B.; Brandel, J.P.; Caughey, B.; Collins, S.; Geschwind, M.; Green, A.; Haïk, S.; Kovacs, G.; Ladogana, A.; et al. Biomarkers and Diagnostic Guidelines for Sporadic Creutzfeldt-Jakob Disease. Lancet Neurol. 2021, 20, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Budka, H.; Aguzzi, A.; Brown, P.; Brucher, J.M.; Bugiani, O.; Gullotta, F.; Haltia, M.; Hauw, J.J.; Ironside, J.W.; Jellinger, K.; et al. Neuropathological diagnostic criteria for Creutzfeldt-Jakob disease (CJD) and other human spongiform encephalopathies (prion diseases). Brain Pathol. 1995, 5, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Jahn, S.; Plass, M.; Moinfar, F. Digital Pathology: Advantages, Limitations and Emerging Perspectives. J. Clin. Med. 2018, 9, 3697. [Google Scholar] [CrossRef] [PubMed]
- Manners, D.; Parchi, P.; Tonon, C.; Capellari, S.; Strammiello, R.; Testa, C.; Tani, G.; Malucelli, E.; Spagnolo, C.; Cortelli, P.; et al. Pathologic correlates of diffusion MRI changes in Creutzfeldt-Jakob disease. Neurology 2009, 72, 1425–1431. [Google Scholar] [CrossRef] [PubMed]
- Lechpammer, M.; Clegg, M.; Muzar, Z.; Huebner, P.; Jin, L.W.; Gospe, S., Jr. Pathology of inherited manganese transporter deficiency. Ann. Neurol. 2014, 75, 608–612. [Google Scholar] [CrossRef] [PubMed]
- Haddad, R.; Akansu, A. A Class of Fast Gaussian Binomial Filters for Speech and Image Processing. IEEE Trans. Signal Process. 1991, 39, 723–727. [Google Scholar] [CrossRef]
- Takashimizu, Y.; Iiyoshi, M. New parameter of roundness R: Circularity corrected by aspect ratio. Prog. Earth Planet. Sci. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Sanfeliu, A.; Alquézar, R.; Andrade, J.; Climent, J.; Serratosa, F.; Vergés, J. Graph-based representations and techniques for image processing and image analysis, Pattern Recognition. Pattern Recognit. 2002, 35, 639–650. [Google Scholar] [CrossRef]
- Mamatha, S.K.; Krishnappa, H.K.; Shalini, N. Graph Theory Based Segmentation of Magnetic Resonance Images for Brain Tumor Detection. Pattern Recognit. Image Anal. 2022, 32, 153–161. [Google Scholar] [CrossRef]
- Leskovec, J.; Lang, K.; Mahoney, M. Empirical comparison of algorithms for network community detection. In Proceedings of the WWW, Raleigh, NC, USA, 26–30 April 2010; pp. 631–640. [Google Scholar]
- Hagberg, A.; Schult, D.; Swart, P. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Van Rossum, G.; Drake, F. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Van der Walt, S.; Schönberger, J.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.; Yager, N.; Gouillart, E.; Yu, T.; Contributors, T.S.I. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, J.; Nicewander, W. Thirteen Ways to Look at the Correlation Coefficient. Am. Statiscian 1998, 42, 59–66. [Google Scholar] [CrossRef]

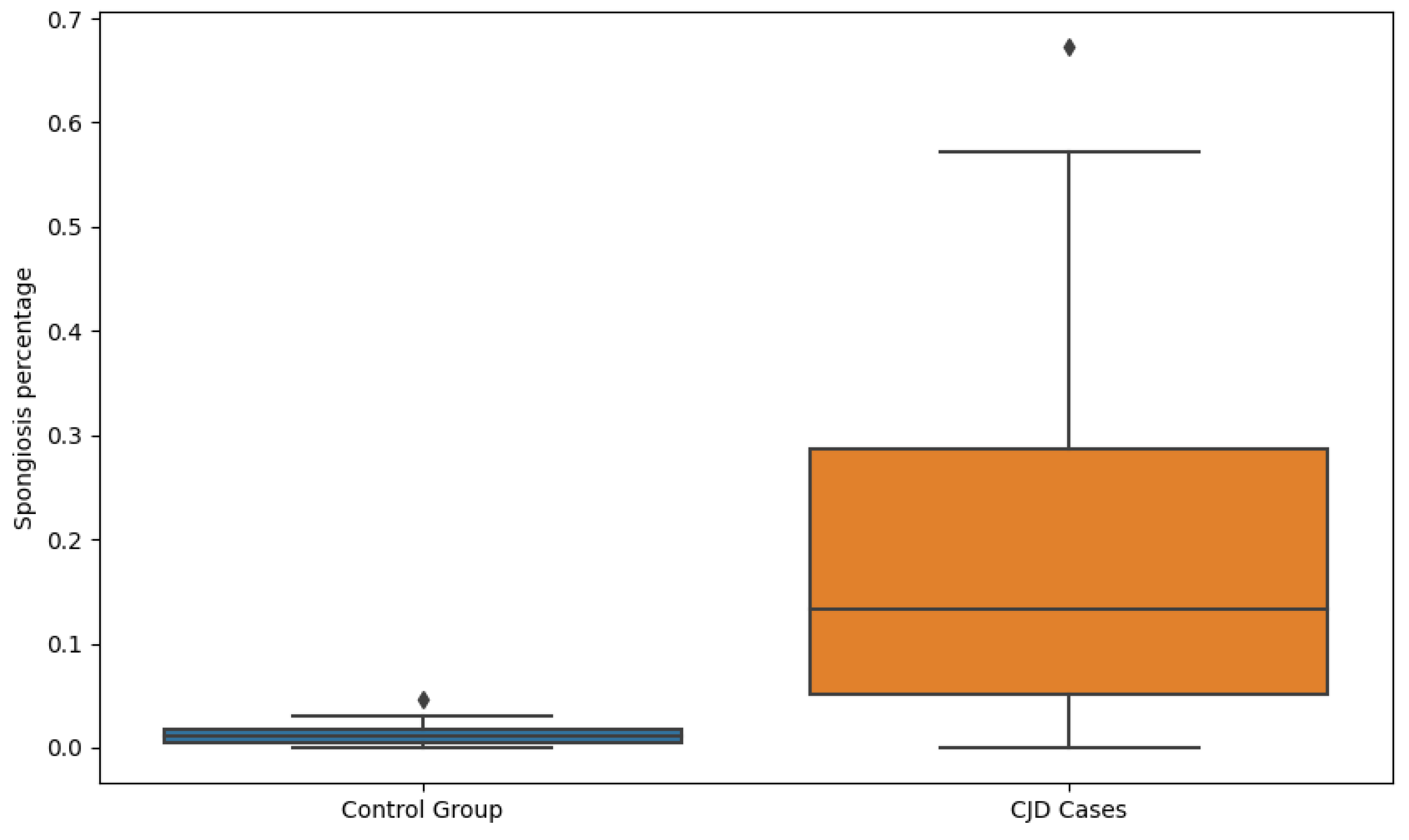
| Group | Normalized Area Mean | Normalized Area Std | Total Number of Vacuoles Mean | Total Number of Vacuoles Std |
|---|---|---|---|---|
| Control group | 0.0128 | 0.0120 | 1868.08 | 1781.64 |
| CJD cases | 0.1778 | 0.1548 | 14,079.36 | 12,459.91 |
| Group | Average Clustering Coefficient | Average Degree of Connectivity | Global Efficiency | Modularity | Degree of Correlation |
|---|---|---|---|---|---|
| Control group | 0.5129 | 9.9677 | 0.0531 | 0.7532 | 0.7319 |
| CJD cases | 0.6091 | 85.6109 | 0.0792 | 0.8485 | 0.8433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, C.; Teijeira, S.; Domínguez, P.; Campanioni, S.; Busto, L.; González-Nóvoa, J.A.; Alonso, J.; Poveda, E.; San Millán, B.; Veiga, C. Correlating Histopathological Microscopic Images of Creutzfeldt–Jakob Disease with Clinical Typology Using Graph Theory and Artificial Intelligence. Mach. Learn. Knowl. Extr. 2024, 6, 2018-2032. https://doi.org/10.3390/make6030099
Martínez C, Teijeira S, Domínguez P, Campanioni S, Busto L, González-Nóvoa JA, Alonso J, Poveda E, San Millán B, Veiga C. Correlating Histopathological Microscopic Images of Creutzfeldt–Jakob Disease with Clinical Typology Using Graph Theory and Artificial Intelligence. Machine Learning and Knowledge Extraction. 2024; 6(3):2018-2032. https://doi.org/10.3390/make6030099
Chicago/Turabian StyleMartínez, Carlos, Susana Teijeira, Patricia Domínguez, Silvia Campanioni, Laura Busto, José A. González-Nóvoa, Jacobo Alonso, Eva Poveda, Beatriz San Millán, and César Veiga. 2024. "Correlating Histopathological Microscopic Images of Creutzfeldt–Jakob Disease with Clinical Typology Using Graph Theory and Artificial Intelligence" Machine Learning and Knowledge Extraction 6, no. 3: 2018-2032. https://doi.org/10.3390/make6030099
APA StyleMartínez, C., Teijeira, S., Domínguez, P., Campanioni, S., Busto, L., González-Nóvoa, J. A., Alonso, J., Poveda, E., San Millán, B., & Veiga, C. (2024). Correlating Histopathological Microscopic Images of Creutzfeldt–Jakob Disease with Clinical Typology Using Graph Theory and Artificial Intelligence. Machine Learning and Knowledge Extraction, 6(3), 2018-2032. https://doi.org/10.3390/make6030099







