Abstract
Accurate aboveground vegetation biomass forecasting is essential for livestock management, climate impact assessments, and ecosystem health. While artificial intelligence (AI) techniques have advanced time series forecasting, a research gap in predicting aboveground biomass time series beyond single values persists. This study introduces RECMO and DirRecMO, two multi-output methods for forecasting aboveground vegetation biomass. Using convolutional neural networks, their efficacy is evaluated across short-, medium-, and long-term horizons on six Kenyan grassland biomass datasets, and compared with that of existing single-output methods (Recursive, Direct, and DirRec) and multi-output methods (MIMO and DIRMO). The results indicate that single-output methods are superior for short-term predictions, while both single-output and multi-output methods exhibit a comparable effectiveness in long-term forecasts. RECMO and DirRecMO outperform established multi-output methods, demonstrating a promising potential for biomass forecasting. This study underscores the significant impact of multi-output size on forecast accuracy, highlighting the need for optimal size adjustments and showcasing the proposed methods’ flexibility in long-term forecasts. Short-term predictions show less significant differences among methods, complicating the identification of the best performer. However, clear distinctions emerge in medium- and long-term forecasts, underscoring the greater importance of method choice for long-term predictions. Moreover, as the forecast horizon extends, errors escalate across all methods, reflecting the challenges of predicting distant future periods. This study suggests advancing hybrid models (e.g., RECMO and DirRecMO) to improve extended horizon forecasting. Future research should enhance adaptability, investigate multi-output impacts, and conduct comparative studies across diverse domains, datasets, and AI algorithms for robust insights.
1. Introduction
Forecasting aboveground vegetation biomass is crucial in many domains, including for assessing livestock-carrying capacity, understanding the consequences of climate change, monitoring drought conditions, and preserving ecosystem health [1,2,3]. This predictive capability is useful not only in optimizing land management practices, but also in protecting biodiversity and advancing sustainable development goals [4,5]. Furthermore, accurate biomass estimation aids in assessing ecosystem resilience to environmental stressors and identifying areas prone to degradation [6]. It also serves as an important tool for evaluating the effectiveness of conservation interventions and restoration efforts, enabling evidence-based decision making [3,7]. Furthermore, by quantifying grasslands’ carbon storage capacity, biomass forecasting contributes to global carbon cycle models, which inform regional and global climate change mitigation strategies [8,9]. In essence, the early prediction of grassland biomass promotes environmental conservation while also ensuring food security, water resource management, and sustainable development around the world.
Despite substantial efforts using field data, remote sensing, statistical modeling, and machine learning [10,11,12,13], a research gap remains in predicting near-term biomass time series, defined as forecasting periods from one month to one year [14,15]. The temporal dynamics of biomass time series pose significant challenges for accurate predictions over varying time horizons. Artificial intelligence (AI), known for its impact in environmental sciences [16] (offers robust forecasting capabilities. Time series forecasting strategies using artificial intelligence (AI) can bridge existing gaps in early biomass prediction and provide critical early warning systems for planners and stakeholders.
Existing AI methodologies for multi-step time series forecasting employ various strategies, ranging from repeated single-step predictions to simultaneous multi-step forecasts (multi-output) [17,18,19]. The recursive method iteratively predicts a single future value, incorporating the previously predicted value as an input for subsequent predictions using the same AI forecasting model. Referred to as a “sliding window”, this technique maintains a constant input string length while progressing through time [20]. The direct method predicts values within the target horizon independently using a different AI model tuned for each specific value, maintaining the same input subseries values while forecasting various target horizon values [20]. The direct-recursive (DirRec) method combines the recursive concept with the direct concept, expanding the input substring recursively and incorporating prior forecasts in each iteration [21]. The Multiple-Input Multiple-Output (MIMO) method predicts all target horizon values at once using a single fitted AI model [22], thus achieving multiple-output prediction, with the output length matching the target horizon [23,24,25]. The DIRect-MIMO (DIRMO) method combines concepts from the direct and MIMO methods, partitioning target horizon values into multiple segments, each predicted independently using a specifically tuned AI model, akin to the direct method [23].
Each of these prediction methods, as applied in various disciplines like economics, finance, climatology, and health sciences, exhibit strengths and weaknesses [26,27,28]. The recursive method is simple and has proven effective for time series forecasting using various algorithms, including neural networks [29,30,31,32]; however, this method is less accurate for long-term forecasting because its iterative approach leads to error accumulation. The direct method prevents error accumulation by discarding previous predictions in subsequent forecasts. This method has, in some studies, performed well for time series modeling with AI algorithms [23]; however, predicting target horizon values independently introduces conditional independence, neglecting the complex dependencies between consecutive values and thereby reducing forecast accuracy [25,29,33]. The direct method also requires significant computational time, as the number of models to learn matches the size of the horizon. The DirRec (Direct-Recursive) method combines simplicity, flexibility, and efficiency in time series forecasting, especially for short-term tasks using neural networks. However, it may also face issues like error accumulation in long-term predictions, a limited consideration of complex dependencies, an increased computational complexity, and sensitivity to initial predictions. The MIMO method maintains stochastic dependence between forecasted values in time series, eliminating the independence assumption of the direct method and avoiding the error accumulation seen in the recursive method. It has proven effective in various time series forecasting scenarios, particularly for horizons beyond one step ahead. Preserving stochastic dependencies with a single model can, however, limit forecasting flexibility. The DIRMO method, with its multi-output forecasting strategy, may mitigate this constraint.
In addition to the five existing forecasting methods discussed above, this study introduces and assesses two novel methodologies for multi-output time series modeling. The first new methodology, termed “RECMO”, combines aspects of the recursive and MIMO methods. Unlike the existing DIRMO method, which independently predicts partitioned segments and, therefore, fails to consider the complex dependencies between them, the RECMO method incorporates the iterative approach of the recursive method. Furthermore, because the number of iterations corresponds to the number of segments (below the horizon’s length), error accumulation may be less significant than that with the recursive method. The second new method, named the “DirRec-MO” method, combines aspects of the DirRec and MIMO methods. This integrated approach involves trade-offs among the strengths and liabilities of the direct, recursive, and MIMO techniques and offers a unique perspective on multi-step forecasting.
This paper has two purposes: (1) addressing the pressing need for accurate aboveground vegetation biomass forecasting and (2) introducing innovative forecasting methodologies that use AI algorithms to enhance prediction capabilities. The effectiveness of the existing and proposed forecasting methods was assessed using Kenyan grassland biomass time series data and the Convolutional Neural Network (CNN) algorithm, recognized for its effectiveness in biomass prediction [34]. The evaluation spanned various target horizons, ranging from short-term (one month) to long term (twelve months). We compared the results of the two novel methodologies with those of five existing forecasting methods to enable a more comprehensive assessment of the proposed methods’ performance. Our work aims to contribute practical solutions to the existing challenges of biomass forecasting, recognizing the significance of accurate vegetation biomass estimation for optimized vegetation management, biodiversity conservation, and sustainable development.
2. Methodology
2.1. Aboveground Biomass Database
Funded by the United States Agency for International Development (USAID) and the Global Livestock Collaborative Research Support Program (GL-CRSP), a network of monitoring sites was installed in Kenya beginning in 1999 onward as an integral component of the broader Livestock Early Warning System (LEWS) for East Africa [35]. The network in Kenya was expanded beginning in 2015 as part of a collaboration among the Food and Agriculture Organization (FAO), Texas A&M AgriLife Research (TAMU), and the Kenya National Drought Management Authority (KNDMA), and became part of the Predictive Livestock Early Warning System in East Africa [4,36]. The main objectives of the monitoring network were to provide near real-time assessments of aboveground biomass that could be grazed by livestock and to enable the near-term (30–90 days) and mid-term (90–180 day) forecasting of aboveground biomass to aid pastoralists and other stakeholders in assessing risk. At monitoring sites, field data were collected to parameterize and calibrate the Phytomass Growth Model (PHYGROW) [4] and generate near real-time aboveground biomass time series at the monitoring sites throughout Kenya [4,35,37]. While the present study is distinct from the PHYGROW model and the Predictive Livestock Early Warning System, it leverages the model’s generated time series data to conduct near-term biomass forecasts. The dataset used in this study is available at: https://github.com/noayarae/multi_output_time_series_forecasting_methods_with_CNN (accessed on 21 May 2024).
For this study, we selected six time series that represent aboveground biomass, comprising the model outputs at 15-day intervals from 14 January 2002 to 31 August 2022. As a result, each time series comprises a total of 496 aboveground biomass estimates in kg/ha. To ensure data quality, these chosen time series underwent meticulous visual examination for any irregularities or unusual patterns, whether isolated events or chronological sequences. Figure 1 illustrates the assessed time series of aboveground vegetation biomass for the selected monitoring sites. It is noteworthy that the selected time series effectively capture a wide spectrum of regional aboveground biomass production rates within the study area, ranging from an average low of 104.5 kg/ha to an average high of 3171.5 kg/ha.
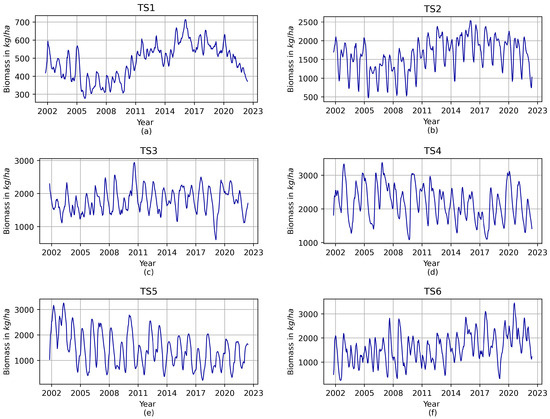
Figure 1.
Time series of aboveground vegetation biomass (kg/ha) derived from calibrated PHYGROW model simulations at six rangeland locations in Kenya. Each subfigure (a–f) represents time series data from a representative location.
2.2. Data Preprocessing
The time series underwent preprocessing aimed at enhancing the efficiency of the model training process and mitigating potential complications, such as vanishing gradients, which could otherwise speed up model convergence. In this regard, normalization played a pivotal role in minimizing the model’s susceptibility to variations in the scale of input features, ultimately bolstering its capacity for generalization. The normalization procedure was executed by rescaling the data within the range from 0 to 1 using the following equation:
where is the time series value, is the normalized value, is the highest value of the time series, and is the lowest value of the time series. Applying this normalization procedure ensured consistent data scaling, improving training, convergence, and model generalization—all crucial for research success.
In transforming the time series data into a supervised dataset, the time series was partitioned into two subseries. The first 472 data points were utilized for training the model, while the remaining 24 data points (one year of data) were designated for model testing. The training time subseries was then structured into a supervised database with predictor and response values to facilitate the application of the CNN algorithm. This structuring process primarily involved extracting short subsequences from the training series, with each subsequence containing one segment designated as predictor values (w) and another segment designated as response values (k). The length of the predictor segments (representing independent variables) was consistently set at 24 values, while the length of the response segments (representing dependent variables) varied between 1 and 24, depending on the multi-output case under consideration. For instance, if we considered the scenario of multi-output forecasting where three values were predicted simultaneously (k = 3), the subsequences would consist of 27 data points , with the first 24 designated as predictors and the remaining 3 as response values. Subsequently, the process repeated, shifting forward one time step within the training time subseries, until the last data point of the training subseries () was reached/included (Figure 2). Thus, the total number of subsequences obtained was determined as .
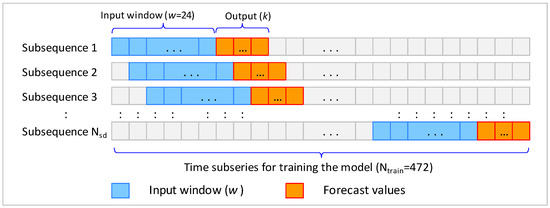
Figure 2.
Conversion of time series data into a supervised dataset. Blue squares: predictor subsequences inputted to the model (window size w). Orange squares: predicted values.
2.3. Methods for Multi-Output Time Series Forecasting
Existing methodologies for time series forecasting using AI algorithms can be categorized into single-step forecasting methods and multi-step forecasting methods. For target horizons beyond a single step, single-step methods typically involve repeated predictions until the target horizon is attained, whereas multi-step methods directly forecast either all or a portion of the target horizon values. The first category includes the recursive, direct, and DirRec methods, and the second category includes the MIMO and DIRMO approaches. Additionally, our work introduces two novel methods in the latter category: RECMO and DirRecMO. Each of these existing and novel methods are described in greater detail below. Figure 3 provides an overview of each of these forecasting methods specifically for a target horizon of 24 (H = 24).

Figure 3.
Overview of the examined and prospective forecasting methods. Blue squares: predictor subsequences inputted to the model (window size w). Orange squares: predicted values.
- Recursive Method
The recursive, also called iterative, approach entails step-by-step forecasting. This method typically advances one time step at a time until the target forecast horizon () is attained, thus requiring a total of iterations (Equation (2)) [20]. In each iteration, the previously forecasted value is included in the input for the next prediction, while the most remote past value is excluded. This ensures that the input window size () remains constant across all iterations; thus, this technique is often characterized as the “sliding window” approach (Figure 3a). Using a single forecast model in all iterations makes this method fast and practical. However, any errors in a prediction carry forward and accumulate in subsequent forecasts.
where is the forecast value and represents the single forecast model.
- Direct Method
The direct method predicts each time point within the horizon independently, using a different AI model specifically fitted for each point value [29]. As a result, the number of prediction models equals the length of the target horizon () (Equation (3)). Because there is no recursive feeding of predicted values into the input for subsequent predictions, this technique prevents error accumulation over the predicted time points. This approach maintains a constant window size and input values for all predictions (Figure 3c).
where with () represents the distinct prediction models.
- Direct-Recursive Method
The direct-recursive (DirRec) method represents a hybrid of the direct (Dir) and recursive (Rec) methods. Like the direct method, the DirRec method applies a distinct model at each time point within the forecast horizon [21] and the total number of models matches the length of the target horizon. As in the recursive (iterative) method, these models incorporate previous predictions. Because each prediction is included in the input for the subsequent forecast without excluding any past values, the input window length expands with each iteration; thus, this method is known as the “expanding window” approach (Figure 3b).
More generally, it is:
- MIMO Method
The Multiple-Input Multiple-Output (MIMO) method is a forecasting approach where the model predicts multiple output values simultaneously. This entails configuring the model’s output layer to align with the target forecast horizon, facilitating the concurrent prediction of multiple data points. Particularly valuable for capturing dependencies in time series forecasting, this method overcomes the limitations of single-step models that assume stochastic independence, mitigating bias in longer horizons [23]. Due to its multi-output nature, the method requires only one model for a given target horizon, thereby reducing the number of models and iterations as compared to single-step models (Figure 3g). All future values within the target horizon are predicted by:
- DIRMO Method
The DIRMO method integrates aspects of the DIRect and the miMO strategies by decomposing the forecast horizon into numerous multi-outcome segments [23,38]. This strategy balances the flexibility of multiple models with the stochastic dependencies within each multi-output model. This is equivalent to extending the direct model to forecast several values at the same time (e.g., 2, 3, or more consecutive steps ahead), effectively decreasing the requirement for multiple models (Figure 3f). The DIRMO method considers the parameter ‘k’ to define the number of steps ahead predicted at each pace (multi-output), resulting in a total of models, where and 1 < k < H. At range edges, when k = 1, it becomes the direct method; when k = H, it becomes MIMO. The multi-output DIRMO forecasting method is expressed as:
where is the iteration number and is computed by . As an illustration, when , , and , we find that , resulting in being and being . Therefore, we will utilize three models for multi-output forecasting, where each model simultaneously predicts eight values to achieve the total length of the target horizon.
- RECMO Method
This method integrates the concepts of the RECursive and miMO strategies, breaking down the forecast horizon into multi-output segments and processing them recursively. Similar to DIRMO, the RECMO method incorporates the parameter to specify the number of steps ahead predicted in each iteration. During each iteration, the forecast model predicts the next k-steps (where ). These predicted k-steps become part of the input window for subsequent iterations. By including the previously predicted k values and excluding the most remote k value from the input window, the window size remains constant across all iterations but shifts in k time steps, resembling the “sliding window” of the recursive method (Figure 3d). With this modification, the number of iterations (n) is scaled down to the quotient between the target horizon and the k-steps predicted ahead at each time (). At k’s limits, it is recursive for k = 1 and MIMO for k = H. In such instances, Equation (2) can be extended to Equation (7):
where is the iteration number and is computed by . As an illustration, when , , and , we find that , resulting in being and being . Therefore, the equations for multi-step (eight-step) iterative forecasting are provided by the following three expressions:
- DirRecMO Method
The DirRecMO method integrates the Direct, Recursive, and MIMO strategies, essentially extending the DirRec method by predicting multi-output values (k) in each iteration (where ). Like the recursive method, it uses the predicted multi-output values as inputs for subsequent predictions until the target horizon is reached; however, the input window does not slide, but instead expands with each iteration, as in the DirRec method (Figure 3e). Like the Direct method, AI models are distinct at each iteration. With k output values predicted per iteration (), the number of models is . At k’s limits, it becomes the DirRec method for k = 1 and the MIMO method for k = H. Thus, all future values within the target horizon are predicted by:
For example, for , , and , we have , and , and the forecasting equations simplify to:
2.4. Modeling, Prediction, and Experimental Baselines
The main settings included the AI model, input window size (w), prediction horizon (H), multi-output size (k), number of models (m), and replications. The forecasting methods were assessed using the AI CNN model, known for its performance in reliably predicting biomass time series [34]. To mitigate randomness, 20 replications were conducted for each combination of horizon and k value, ensuring robust outcomes. The input window size for the forecasting methods with no expanding window, (i.e., Recursive, Direct, MIMO, RECMO, and DIRMO) was fixed at 24, in accordance with prior studies suggesting an input length akin to the horizon length. In methods with an expanding window (i.e., DirRec and DirRecMO), the input size varied from 24 to 47 based on the multi-output size, horizon length, and method used. The target horizons (H) evaluated were 2, 6, 12, and 24 data values ahead, corresponding to 1, 3, 6, and 12 months, respectively. These horizons were strategically selected to align with the practical needs of early warning system stakeholders. For instance, planners frequently demand forecasts of six and twelve months (long-term) to facilitate comprehensive planning. Pastoralists and ranchers, on the other hand, are interested in one-month forecasts (short-term) and three-month forecasts (medium-term) to make informed decisions on critical issues like forage scarcity related to drought duration and intensity. The multi-output sizes were set to the maximum allowable number based on the target horizon. For instance, when considering a horizon of 24 values, we assessed eight multi-output sizes (), which are all divisors of 24. For one-month horizons, only two multi-output sizes were assessed (. The number of models (m) varied based on the forecasting method, horizon, and multi-output size. For instance, for a horizon of 12 and k = 4, the recursive method uses one model, while DIRMO requires three. Table 1 summarizes the methods’ key parameters and settings.

Table 1.
Parameters and settings of the forecasting methods.
- Convolutional Neural Network (CNN) Model
The CNN algorithm, designed for complex data processing, has proven effective in simulating time series data [39]. CNNs integrate advanced data preprocessing techniques, including convolution layers and pooling layers, preceding the fully connected layers. These networks excel in capturing hierarchical patterns and spatial correlations within data, increasing their proficiency in image recognition and feature extraction and enabling them to capture temporal patterns in sequential data [40]. Figure 4 outlines the structure of the CNN algorithm, beginning with an input layer subjected to a convolution process [34]. The input time subseries corresponds to the input window of each subsequence obtained during data preprocessing (Section 2.2). Each subsequence is represented as a subseries of length . This subseries is convoluted using a 1D kernel of size (), resulting in a new subseries of length . Thus, with kernels applied, subseries are obtained, each of length . To retain information in these short subseries, the pooling size is set to 1 (), so the number and length of the subseries remain and (), respectively. Each subseries is then flattened to form the flatten layer (NN input layer), with the number of nodes computed as , followed by a set of fully interconnected nodes in hidden layers [41]. The flattened and hidden layers generate the output layer. The output layer varies for single-output tasks, and it has one node; for multi-output tasks, it matches the multi-output size , as detailed in Table 1. The manual fine-tuning of hyperparameters in the CNN model aimed to minimize prediction errors, with the specific values detailed in Table 2.
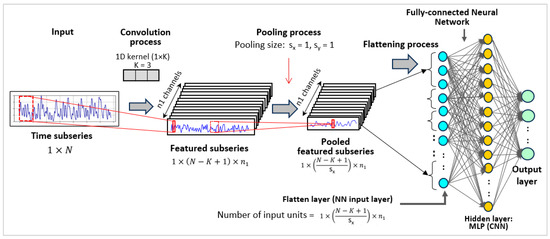
Figure 4.
Architecture of the Convolutional Neural Network.

Table 2.
Hyperparameters of the CNN model.
- Software and Computer Tools
The CNN models were implemented using the Python platform v3.9.13 [42]. Codes were built using open-access libraries, including scipy, keras, and tensorflow [43]. The codes developed for this study are available at https://github.com/noayarae/multi_output_time_series_forecasting_methods_with_CNN, accessed on 1 May 2023.
2.5. Model Performance Evaluation
Model performance was evaluated using several metrics. First, we employed the Root Mean Square Error (RMSE), which is calculated as:
In this equation, represents the observed time series value at time i, is the estimated/forecast time series value at time i, and is the number of data points. RMSE values can range from zero to infinity, with zero indicating a perfect model with no prediction error.
To systematically compare the RMSE values both among different methods and within methods across various multi-outputs, we conducted statistical analyses using Analysis of Variance (ANOVA) and Multivariate Analysis of Variance (MANOVA). We sought to identify significant differences in the RMSE values due to both the forecasting model (Recursive, Direct, DirRec, MIMO, DIRMO, RECMO, or DirRecMO) and the multi-output size (i.e., the different multi-output values considered when predicting the target horizon).
- Coefficient of Variation
The variability in the RMSE across forecast replications employing different multi-output values (k) and methods was quantified using coefficients of variation (CVs). These coefficients represent the relationship between the standard deviation and the mean. In essence, this ratio measures the extent to which RMSE values carry across forecasting replications, offering insights into the model’s reproducibility and the degree of uncertainty in its replicability. We classified reproducibility as excellent (<10% CV), good (10–20% CV), acceptable (20–30% CV), and poor (>30% CV), based on established recommendations [44].
3. Results
3.1. Method Performance in Forecasting
Figure 5 illustrates the Root Mean Square Error (RMSE) values for predictions from the six time series using the diverse forecasting methods, projected over a horizon of 24 future steps (H = 24). Both the single-output methods (Recursive, Direct, and DirRec) and MIMO (Multiple-Input Multiple-Output) method yielded a single outcome per time series. In contrast, the multi-output methods (DIRMO, RECMO, and DirRecMO) presented six results per time series (k = 2, 3, 4, 6, 8, and 12). These values correspond to the possible multi-output variations assessed for the 24-step horizon, where each k value represents a divisor of the target horizon length under evaluation.
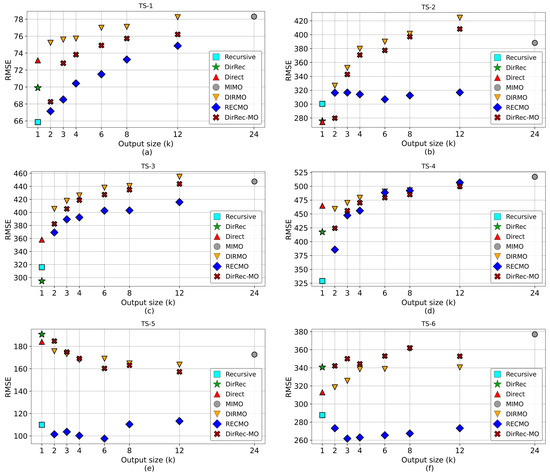
Figure 5.
Average RMSE values across different forecasting methods for aboveground vegetation biomass (kg/ha) across a horizon (H) of 24. Each subfigure from (a–f) displays the results of each time series data from a representative study location.
The MANOVA analysis of individual time series for the target horizon (H = 24) yielded statistically significant differences (p < 0.05) among the RMSE metrics. This analysis considered the k values (including k = 1 and k = 24) as the number of variables (eight variables when H = 24) and the type of approach (Recursive, Direct and DirRec) as the number of groups (three groups). Detailed p-values and Wilks’ values for each time series can be found in Table S1 of the Supplementary Materials accompanying this study.
Despite the differences in the model outcomes, no method consistently outperformed the others across all six time series. The recursive and RECMO (k = 6 in TS5 and k = 3 in TS6) methods each excelled in two cases, while the DirRec and Direct methods each outperformed the other methods once. The MIMO method consistently produced less accurate results. Among the multi-output methods, RECMO was more accurate than the other two methods (DIRMO and DirRecMO) across all multi-output sizes (k) evaluated, with no significant difference between DIRMO and DirRecMO.
For each multi-output method (RECMO, DIRMO, and DirRec-MO), the ANOVA analysis considered the k values (excluding k = 1 and k = target horizon) as the number of variables (six variables when H = 24). The p- and F-values for each time series are listed in Table S2 in the Supplementary Materials. The ANOVA analysis of the RMSE values corresponding to the six multi-output RECMO outcomes showed significant differences (p < 0.001) among them. A similar analysis of DIRMO and DirRecMO’s RMSE values also revealed significant differences among their multi-output outcomes. The findings indicated that, for multi-output methods, the choice of multi-output size (k) significantly impacted the accuracy of the predictions. Therefore, the optimization of the multi-output size parameter is essential in identifying the most effective multi-output method configuration.
For H = 12, the recursive and RECMO methods (with k = 2 and k = 3) had the lowest average RMSE in two time series each, while the DirRec and DirRecMO methods had the lowest average RMSE in one time series each (Table 3). The evaluation of multi-output methods included four multi-output sizes (k = 2, 3, 4, and 6), which are all divisors of the target horizon. ANOVA analysis revealed statistically significant differences among the outcomes of the four multi-output variants, mirroring the findings for the H = 24 horizon. This consistency further emphasized that the value of k significantly influenced the performance of the multi-output model. The p- and F-values for each time series can be found in Table S3 of the Supplementary Materials.

Table 3.
Average RMSE values for aboveground vegetation biomass (kg/ha) across different methods for the forecasting horizon of 12 (H = 12). The best-performing methods’ RMSE values are highlighted and italicized.
In medium-term forecasts (H = 6), the single-output methods outperformed the multi-output methods. The recursive method had the lowest average RMSE in four time series, while DirRec and MIMO had the lowest average RMSE in one time series each (Table 4). In these forecasts, the multi-output methods assessed only two multi-output sizes (k = 2 and 3), the exclusive divisors of the target horizon (H = 6). Iin the longer-term forecasts (H = 12 and H = 24), ANOVA showed significant differences between the outcomes of the two multi-output variants. The p- and F-values for each time series can be found in Table S4 of the Supplementary Materials.

Table 4.
Average RMSE values for aboveground vegetation biomass (kg/ha) across different methods for a forecasting horizon of 6 (H = 6). Best-performing methods’ RMSE values are highlighted and italicized.
In the short-term forecasts (H = 2), the direct method had the lowest average RMSE in four time series, while the recursive and MIMO methods achieved the lowest RMSE in one time series each (Table 5). Despite the seemingly remarkable performance of the direct method, the ANOVA and MANOVA analyses indicated that, in five of the six time series, the differences in the RMSE values of the various methods were non-significant (p > 0.05), suggesting that the performances of the forecasting methods were comparable, with no clear standout.

Table 5.
Average RMSE values for aboveground vegetation biomass (kg/ha) across different methods for a forecasting horizon of 2 (H = 2). Best-performing methods’ RMSE values are highlighted and italicized.
Table 6 provides a summary of the number of times each method achieved the minimum average of RMSE across all six times series and four target horizons evaluated. As discussed above, the single-output methods excelled in short- and medium-term forecasts, while the recursive (single-output) and RECMO (multi-output) methods outperformed the other methods in long-term forecasts. These results indicate that the multi-output forecasting methods developed in this study—and especially the RECMO method—are quite useful, particularly for long-term predictions. This corresponds to the increased number of multi-output sizes that can be examined across large time horizons.

Table 6.
Number of times each method achieved the minimum average RMSE across all the time series (TS) and target horizons (H) evaluated. For instance, at H = 24, Recursive and RECMO methods prevailed in two instances each, while Direct and DirRec methods each prevailed in one instance.
3.2. Forecast Accuracy Variation with the Horizon
This study also considered how the length of the forecast horizon affects the accuracy of a time series forecast. We averaged and relativized the RMSE values of all of the various methodologies for a particular forecast horizon, or time series (TS), for comparison. This approach captures the overall trends in accuracy, independent of the specific forecasting methods. The results, plotted in Figure 6, reveal that the prediction error increased with the length of the forecast horizon, although this link was not monotonic.
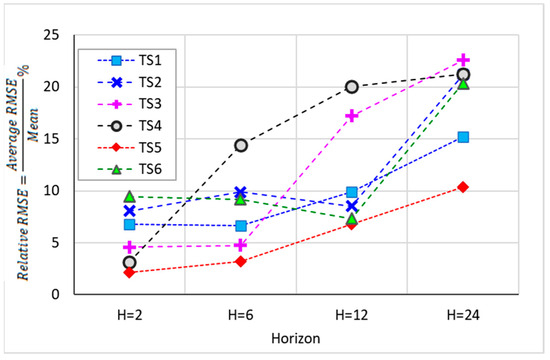
Figure 6.
Relative RMSE values of aboveground vegetation biomass (kg/ha) across different forecasting methods in relation to forecast horizons. Relative RMSE is calculated as a percentage by dividing the average RMSE by the time series mean.
Figure 6 also illustrates the disparity in the relativized RMSE values among the different TS datasets. These disparate outcomes indicated that the different characteristics of the TS data sets could impact the results of the forecast models. Factors such as the data trends and noise levels within each data set can affect the performance of forecasting methods. For example, TS4 could have unique characteristics that make it more difficult to model accurately compared to the other TSs, particularly for horizons H = 6 and H = 12, resulting in differences in model performance. Additionally, TS4 exhibited pronounced seasonal fluctuations with notable peaks and troughs, introducing substantial variability in biomass levels that could cause difficulties for the predictive model across different forecasting strategies. Furthermore, TS4 showed abrupt changes around 2003, 2010, and 2020, adding further complexity to the learning models. The abrupt and non-regular changing characteristics of these time series require more attention in longer time series. Due to the limited scope of this study and the focus on introducing new forecasting methodologies, a detailed analysis of the individual characteristics of each TS data set was not performed. However, recognizing the potential influence of these characteristics on model results is important for future research.
3.3. RMSE Variability of Methods
As the prediction horizon increased (H = 2, 6, 12, and 24), the mean CV for the RMSE values decreased (16.3, 9.4, 7.1, and 3.6). This negative correlation indicated reduced variability in the RMSE values—or more consistent, stable results—for longer forecast horizons. This has practical implications for decision makers, in that they can more confidently select the optimal method for longer-term forecasts, even though forecasting error increased with longer horizons for all of the methods studied.
4. Discussion
This study introduced RECMO and DirRecMO, two multi-output methods for forecasting aboveground vegetation biomass using a CNN. We compared these novel methodologies with existing single-output forecasting methods (Recursive, Direct, and DirRec) and multi-output forecasting methods (MIMO and DIRMO) across short-, medium-, and long-term horizons. While the single-output forecasting methods performed slightly better than the multi-output methods in short-term predictions, both the single-output and multi-output methods demonstrated a comparable efficacy in long-term forecasts. Notably, RECMO exhibited significant performance improvements compared to the established DIRMO and MIMO multi-output methods. While the DIRMO and MIMO methods have been effective in other disciplines in prior research [38], they proved less accurate in long-term biomass prediction.
The results indicated that time series characteristics, including factors like data trends and noise levels, may significantly influence forecast model outcomes. Given the limited scope of this study and its focus on introducing new forecasting methodologies, we did not extensively analyze the interactions of individual time series characteristics and forecasting models. Future research should delve deeper into the impacts of these characteristics on forecast outcomes. Additionally, expanding datasets and incorporating diverse environmental conditions and AI algorithms such as multilayer neurocontrol techniques in future studies would enhance findings’ robustness and applicability. Moreover, a larger sample size would provide a more reliable assessment of method performance and offer valuable insights for future research endeavors.
This study also revealed that the multi-output size has a significant impact on the forecast error rate of multi-output methods. Therefore, determining the optimal size for each time series is crucial to the performance of multi-output methods. Furthermore, with longer prediction horizons, the number of possible multi-output sizes increases, enabling a broader evaluation of various multi-output values and enhancing the flexibility of multi-output methods. Furthermore, this range of multi-output size options allows for a more thorough evaluation of methods that use multiple outputs when making long-range forecasts. This finding is consistent with previous studies emphasizing the importance of the calibration of the multi-output step to achieve an optimal value, especially in long-term predictions [23,29].
This study observed a consistent trend in forecast accuracy as the prediction horizon extended. In a pattern consistent with prior research and with the inherent complexity of predicting distant events, the forecasting accuracy consistently decreased with the length of the forecast horizon across all time series, although this did not always follow a monotonic trajectory [34,45]. In recursive methods, accuracy loss is primarily linked to the accumulation of errors in iterative forecasting steps. Conversely, in the direct method, accuracy loss is rooted in the diminishing correlation between the target future value, which extends further into the future, and the input values of the time series. In the DirRec method, a fusion of the direct and recursive methods, the accuracy loss as horizons lengthen can be ascribed to a combination of the causes described above. By contrast, in the MIMO method, accuracy loss is due to inherent limitations of the method. The use of a single-model structure for the entire forecast horizon restricts the method’s adaptability to dynamic changes in biomass over time. Thus, as the horizon increases, the model may encounter difficulties in capturing and predicting these changes accurately. This lack of flexibility becomes more evident in long-term horizons, where the complexity of forecasting distant events amplifies the challenges for a singular model structure. The RECMO and DirRecMO methods introduced in this study, along with DIRMO, represent hybrid models combining single-output and MIMO approaches. They inherit both the strengths and shortcomings of each method, contributing to the observed accuracy loss of these hybrids over the prediction horizon.
In terms of short-term forecasts, differences between methodologies were generally not significant. As noted above, short-term errors tended to be smaller than long-term errors, regardless of the method used. Accordingly, relative errors remained low for any approach, resulting in frequently insignificant differences among the model outcomes. Thus, even though the single-output methods generally performed better than their multi-output counterparts (as noted in the beginning of this section) and had a slightly higher average RMSE, it was difficult to pinpoint the best method for short-term forecasts. In contrast, when examining medium- and long-term predictions, significant disparities in the model outcomes became evident. As noted above, accuracy declined as the prediction horizon expanded. For long-term projections, errors increased significantly, and disparities between the outcomes of different methods were notable. This implies that the choice of forecasting method is more significant in long-term forecasts than short-term forecasts, where the differences across forecasting methods were less pronounced.
From an operational standpoint, a livestock early warning system must consider both the generalizability of forecasting models across monitoring sites and the specificity of each site’s characteristics. While running a single forecasting model for all monitoring sites might offer logistical simplicity, it may not yield the most accurate results, due to potential variations in environmental conditions, vegetation dynamics, and other site-specific factors. Therefore, it is advisable to assess which forecasting model works best for each individual monitoring site to ensure tailored and accurate predictions. This approach acknowledges the potential heterogeneity among sites and allows for the optimization of forecasting methods based on the unique characteristics of each location, ultimately enhancing the effectiveness of livestock early warning systems.
This study indicates that the RECMO and DirRecMO methods perform competitively in long-term biomass forecasting and offer valuable insights applicable across diverse disciplines, despite certain limitations. Multi-output methods are sensitive to output step size, leading to increased forecast errors over extended horizons. Future research should explore adaptive strategies to address these limitations and enhance model applicability. The flexibility of multi-output sizes and a thorough understanding of these methods improve long-term prediction accuracy, extending beyond biomass forecasting. Notably, data size poses a limitation in our study. Validation across diverse datasets is necessary to comprehensively assess the effectiveness of these methods. It is also worth noting that these proposed methodologies can be implemented using various AI algorithms, such as Random Forest (RF), XGBoost, Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU). The core architecture of the AI model is not under scrutiny; rather, the focus is on how the prediction horizon is approached.
5. Conclusions
This study introduced two multi-output methods (RECMO and DirRecMO) for the time series forecasting of aboveground biomass data and compared the forecasting outcomes of these methods with those of existing single-output methods (Recursive, Direct, and Dir-Rec) and multi-output methods (MIMO and DIRMO). The performances of these methods were systematically evaluated across short-, medium-, and long-term horizons using the CNN algorithm and six aboveground vegetation biomass time series datasets from Kenyan grasslands, comprising values at 15-day intervals over a 20-year span. In the multi-output methods, the impact of varying multi-output sizes on forecasts across multiple horizons was also examined. The RMSE was used to compare method performance, while the coefficient of variability assessed forecast replication robustness.
The findings suggested that the single-output methods performed slightly better than their multi-output counterparts in short-term predictions, but that both were comparably effective for long-term forecasts. Of the two introduced methods, RECMO outperformed the established multi-output methods MIMO and DIRMO, whereas DirRecMO exhibited only a moderate efficacy relative to its established counterparts. Nevertheless, both of these novel methodologies show potential for biomass forecasting and warrant further investigation.
This study’s findings also indicated that the forecast accuracy of multi-output methods was substantially affected by the multi-output step size, emphasizing the need for optimal size adjustments. Additionally, as the forecast horizon extended, errors escalated across all methods, indicating a consistent, albeit not strictly monotonic, trend. This growing error pattern can be attributed to the inherent challenges of predicting more distant future periods, underscoring the complexities associated with long-term forecasting.
Future research should focus on improving the accuracy and robustness of the RECMO and DirRecMO methods, particularly for extended prediction horizons. Evaluating these models across diverse domains will improve their generalizability. Future studies should also investigate the effects of different multi-output sizes and develop optimal calibration strategies. Comparative studies using varied datasets, environmental conditions, and AI algorithms will provide valuable insights into the robustness and versatility of the proposed forecasting approaches.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/make6030079/s1, Table S1: Results of the MANOVA analysis for RMSE values across different time series; Table S2: ANOVA results for RMSE values at horizon H = 24; Table S3: ANOVA results for RMSE values at horizon H = 12; Table S4: ANOVA results for RMSE values at horizon H = 6.
Author Contributions
J.M.O.L. and E.N.-Y. conceptualized the research question. E.N.-Y. designed the methodology, while E.N.-Y. and J.M.O.L. gathered the data. J.M.O.L. and J.P.A. conducted the simulations with PHYGROW. E.N.-Y. conducted the modeling and analysis. All authors discussed and contributed to the results and gave critical feedback on the paper. E.N.-Y. primarily authored the paper, incorporating inputs from all co-authors. All authors have read and agreed to the published version of the manuscript.
Funding
The support for this research has been provided by The Food and Agriculture Organization of the United Nations (FAO) under the project Establishing and Strengthening Predictive Livestock Early Warning System (PLEWs) in Kenya, Somalia, Sudan, and Uganda as part of the delivery of the project Food and Nutrition Security Resilience Programme (FNS-REPRO) (TAMU M-2002133—Account 408999-96610). Support for JPA was provided by the U.S. Department of Agriculture’s Agriculture Research Service. The U.S. Department of Agriculture is an equal opportunity lender, provider, and employer.
Data Availability Statement
The aboveground vegetation biomass time series data used in this study, as well as all code for training and testing the CNN models are available at https://github.com/noayarae/multi_output_time_series_forecasting_methods_with_CNN, accessed on 1 May 2023.
Acknowledgments
This study has been sponsored by The Food and Agriculture Organization of the United Nations (FAO) under the project Establishing and Strengthening Predictive Livestock Early Warning System (PLEWs) in Kenya, Somalia, Sudan, and Uganda as part of the delivery of the project Food and Nutrition Security Resilience Programme (FNS-REPRO): Building food system resilience in protracted crises funded by the government of Netherland and establishment of Livestock Feed Security System in Kenya, Somalia, and Uganda, funded by the government of Sweden. The views and opinions expressed in this paper are those of the authors and not necessarily the views and opinions of the Food and Agriculture Organization of the United Nations. We extend our gratitude to Erin Camody for her valuable contributions to the writing and proofreading of this document.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- He, L.; Li, A.; Yin, G.; Nan, X.; Bian, J. Retrieval of Grassland Aboveground Biomass through Inversion of the PROSAIL Model with MODIS Imagery. Remote Sens. 2019, 11, 1597. [Google Scholar] [CrossRef]
- Bernhardt-Römermann, M.; Römermann, C.; Sperlich, S.; Schmidt, W. Explaining grassland biomass—The contribution of climate, species and functional diversity depends on fertilization and mowing frequency. J. Appl. Ecol. 2011, 48, 1088–1097. [Google Scholar] [CrossRef]
- Das, B.; Patnaik, S.K.; Bordoloi, R.; Paul, A.; Tripathi, O.P. Prediction of forest aboveground biomass using an integrated approach of space-based parameters, and forest inventory data. Geol. Ecol. Landsc. 2022, 8, 1–13. [Google Scholar] [CrossRef]
- Matere, J.; Simpkin, P.; Angerer, J.; Olesambu, E.; Ramasamy, S.; Fasina, F. Predictive Livestock Early Warning System (PLEWS): Monitoring forage condition and implications for animal production in Kenya. Weather Clim. Extrem. 2020, 27, 100209. [Google Scholar] [CrossRef]
- Braimoh, A.; Manyena, B.; Obuya, G.; Muraya, F. Assessment of Food Security Early Warning Systems for East and Southern Africa; World Bank: Washington, DC, USA, 2018; p. 20433. Available online: http://hdl.handle.net/10986/29269 (accessed on 5 February 2023).
- Zang, P.; Zhang, Y.; Chen, Z.; Hou, G.; Liu, Z.; Lu, X. The inversion modeling and aboveground biomass mapping of withered grass changes in the western grassland of Northeast China. Front. Earth Sci. 2023, 10, 1031098. [Google Scholar] [CrossRef]
- Hanrahan, L.; Geoghegan, A.; O’Donovan, M.; Griffith, V.; Ruelle, E.; Wallace, M.; Shalloo, L. PastureBase Ireland: A grassland decision support system and national database. Comput. Electron. Agric. 2017, 136, 193–201. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P.; Taylor, S.; Alqurashi, A.F. Review of the use of remote sensing for biomass estimation to support renewable energy generation. J. Appl. Remote Sens. 2015, 9, 097696. [Google Scholar] [CrossRef]
- Jiang, F.; Deng, M.; Tang, J.; Fu, L.; Hua, S. Integrating spaceborne LiDAR and Sentinel-2 images to estimate forest aboveground biomass in Northern China. Carbon Balance Manag. 2022, 17, 12. [Google Scholar] [CrossRef]
- Bazzo, C.O.G.; Kamali, B.; Hütt, C.; Bareth, G.; Gaiser, T. A Review of Estimation Methods for Aboveground Biomass in Grasslands Using UAV. Remote Sens. 2023, 15, 639. [Google Scholar] [CrossRef]
- Bu, L.; Lai, Q.; Qing, S.; Bao, Y.; Liu, X.; Na, Q.; Li, Y. Grassland Biomass Inversion Based on a Random Forest Algorithm and Drought Risk Assessment. Remote Sens. 2022, 14, 5745. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, R.; Cheng, H.; Liang, T.; Zhang, K.; Chai, N.; Gao, J.; Feng, Q.; Hou, M.; Liu, J.; et al. Can Machine Learning Algorithms Successfully Predict Grassland Aboveground Biomass? Remote Sens. 2022, 14, 3843. [Google Scholar] [CrossRef]
- Morais, T.G.; Teixeira, R.F.M.; Figueiredo, M.; Domingos, T. The use of machine learning methods to estimate aboveground biomass of grasslands: A review. Ecol. Indic. 2021, 130, 108081. [Google Scholar] [CrossRef]
- Huntington, T.; Cui, X.; Mishra, U.; Scown, C.D. Machine learning to predict biomass sorghum yields under future climate scenarios. Biofuels Bioprod. Biorefin. 2020, 14, 566–577. [Google Scholar] [CrossRef]
- Maddison, A.L.; Camargo-Rodriguez, A.; Scott, I.M.; Jones, C.M.; Elias, D.M.O.; Hawkins, S.; Massey, A.; Clifton-Brown, J.; McNamara, N.P.; Donnison, I.S.; et al. Predicting future biomass yield in Miscanthus using the carbohydrate metabolic profile as a biomarker. GCB Bioenergy 2017, 9, 1264–1278. [Google Scholar] [CrossRef]
- Noa-Yarasca, E. A Machine Learning Model of Riparian Vegetation Attenuated Stream Temperatures. Oregon State University: Corvallis, OR, USA, 2021. Available online: https://ir.library.oregonstate.edu/downloads/0r967b65c#page=137 (accessed on 10 April 2024).
- An, N.H.; Anh, D.T. Comparison of Strategies for Multi-Step-Ahead Prediction of Time Series Using Neural Network. In Proceedings of the 2015 International Conference on Advanced Computing and Applications (ACOMP), Ho Chi Minh City, Vietnam, 23–25 November 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 142–149. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.-J.; Chang, L.-C.; Kao, I.-F.; Wang, Y.-S. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2019, 209, 134–145. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Q.; Wang, J.; Gao, Y. A novel interval forecasting system for uncertainty modeling based on multi-input multi-output theory: A case study on modern wind stations. Renew. Energy 2021, 163, 88–104. [Google Scholar] [CrossRef]
- Hamzaçebi, C.; Akay, D.; Kutay, F. Comparison of direct and iterative artificial neural network forecast approaches in multi-periodic time series forecasting. Expert Syst. Appl. 2009, 36, 3839–3844. [Google Scholar] [CrossRef]
- Sorjamaa, A.; Lendasse, A. Time Series Prediction using DirRec Strategy. In Proceedings of the 14th European Symposium on Artificial Neural Networks, Bruges, Belgium, 26–28 April 2006; pp. 143–148, ISBN 2-930307-06-4. [Google Scholar]
- Bao, Y.; Xiong, T.; Hu, Z. Multi-step-ahead time series prediction using multiple-output support vector regression. Neurocomputing 2014, 129, 482–493. [Google Scholar] [CrossRef]
- Taieb, S.B.; Sorjamaa, A.; Bontempi, G. Multiple-output modeling for multi-step-ahead time series forecasting. Neurocomputing 2010, 73, 1950–1957. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.-D.; Chang, P.-C.; Yang, J.-W.; Li, F.-Z. Iterated time series prediction with multiple support vector regression models. Neurocomputing 2013, 99, 411–422. [Google Scholar] [CrossRef]
- Kline, D.M. Methods for Multi-Step Time Series Forecasting Neural Networks. In Neural Networks in Business Forecasting; Zhang, G.P., Ed.; IGI Global: Hershey, PE, USA, 2004; pp. 226–250. [Google Scholar] [CrossRef]
- Fox, I.; Ang, L.; Jaiswal, M.; Pop-Busui, R.; Wiens, J. Deep Multi-Output Forecasting. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, ACM, New York, NY, USA, 19–23 August 2018; pp. 1387–1395. [Google Scholar] [CrossRef]
- Niu, T.; Wang, J.; Lu, H.; Du, P. Uncertainty modeling for chaotic time series based on optimal multi-input multi-output architecture: Application to offshore wind speed. Energy Convers. Manag. 2018, 156, 597–617. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Chiong, R.; Xiong, T. Mid-term interval load forecasting using multi-output support vector regression with a memetic algorithm for feature selection. Energy 2015, 84, 419–431. [Google Scholar] [CrossRef]
- Bontempi, G. Long Term Time Series Prediction with Multi-Input Multi-Output Local Learning. In Proceedings of the 2nd European Symposium on Time Series Prediction (TSP), ESSP08, Helsinki, Finland, 17–19 September 2008. [Google Scholar]
- Weigend, A.S. Time Series Prediction; Routledge: London, UK, 2018. [Google Scholar] [CrossRef]
- Murray, C.; Chaurasia, P.; Hollywood, L.; Coyle, D. A Comparative Analysis of State-of-the-Art Time Series Forecasting Algorithms. In Proceedings of the 9th International Conference on Computational Science and Computational Intelligence (CSCI), IEEE, Las Vegas, NV, USA, 14–16 December 2022; pp. 89–95. [Google Scholar] [CrossRef]
- Marcellino, M.; Stock, J.H.; Watson, M.W. A comparison of direct and iterated multistep AR methods for forecasting macroeconomic time series. J. Econom. 2006, 135, 499–526. [Google Scholar] [CrossRef]
- Bontempi, G.; Taieb, S.B.; Le Borgne, Y.-A. Machine Learning Strategies for Time Series Forecasting. In Business Intelligence; Aufaure, M.-A., Zimanyi, E., Eds.; eBISS: Brussels, Belgium, 2013; pp. 62–77. [Google Scholar] [CrossRef]
- Noa-Yarasca, E.; Leyton, J.M.O.; Angerer, J.P. Deep Learning Model Effectiveness in Forecasting Limited-Size Aboveground Vegetation Biomass Time Series: Kenyan Grasslands Case Study. Agronomy 2024, 14, 349. [Google Scholar] [CrossRef]
- Stuth, J.W.; Angerer, J. Livestock Early Warning System for Africa’s Rangelands. In Monitoring and Predicting Agricultural Drought; Boken, V.K., Cracknell, A.P., Heathcote, R.L., Eds.; Oxford University Press: Oxford, UK, 2005. [Google Scholar] [CrossRef]
- Opio, P.; Makkar, H.P.S.; Tibbo, M.; Ahmed, S.; Sebsibe, A.; Osman, A.B.; Olesambu, E.; Ferrand, C.; Munyua, S. Opinion paper: A regional feed action plan—One-of-a-kind example from East Africa. Animal 2020, 14, 1999–2002. [Google Scholar] [CrossRef]
- Rhodes, E.C.; Tolleson, D.R.; Angerer, J.P. Modeling Herbaceous Biomass for Grazing and Fire Risk Management. Land 2022, 11, 1769. [Google Scholar] [CrossRef]
- Taieb, S.B.; Bontempia, G.; Atiyac, A.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2011, 39, 7067–7083. [Google Scholar] [CrossRef]
- Koprinska, I.; Wu, D.; Wang, Z. Convolutional Neural Networks for Energy Time Series Forecasting. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Ghosh, A.; Sufian, A.; Sultana, F.; Chakrabarti, A.; De, D. Fundamental Concepts of Convolutional Neural Network. In Recent Trends and Advances in Artificial Intelligence and Internet of Things; Balas, V.E., Kumar, R., Srivastava, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 519–567. [Google Scholar] [CrossRef]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Keras. GitHub. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 May 2023).
- Aronhime, S.; Calcagno, C.; Jajamovich, G.H.; Arezki, H.; Philip, D.; Douglas, R.; Isabel, D.M.; Valérie, F.; Chatterji, M.-L.M. DCE-MRI of the liver: Effect of linear and nonlinear conversions on hepatic perfusion quantification and reproducibility. J. Magn. Reson. Imaging 2014, 40, 90–98. [Google Scholar] [CrossRef]
- Noa-Yarasca, E.; Leyton, J.M.O.; Angerer, J. Biomass Time Series Forecasting Using Deep Learning Techniques. Is the Sophisticated Model Superior. In Biometry and Statistical Computing; SSSA International Annual Meeting; ASA: St. Louis, MO, USA; CSSA: St. Louis, MO, USA, 2023; Available online: https://scisoc.confex.com/scisoc/2023am/meetingapp.cgi/Paper/151648 (accessed on 10 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).