Abstract
Despite increasing digitalization and automation, complex production processes often require human judgment/decision-making adaptability. Humans can abstract and transfer knowledge to new situations. People in production are an irreplaceable resource. This paper presents a new concept for digitizing human expertise and their ability to make knowledge-based decisions in the production area based on ontologies and causal Bayesian networks for further research. Dedicated approaches for the ontology-based creation of Bayesian networks exist in the literature. Therefore, we first comprehensively analyze previous studies and summarize the approaches. We then add the causal perspective, which has often not been an explicit subject of consideration. We see a research gap in the systematic and structured approach to ontology-based generation of causal graphs (CGs). At the current state of knowledge, the semantic understanding of a domain formalized in an ontology can contribute to developing a generic approach to derive a CG. The ontology functions as a knowledge base by formally representing knowledge and experience. Causal inference calculations can mathematically imitate the human decision-making process under uncertainty. Therefore, a systematic ontology-based approach to building a CG can allow digitizing the human ability to make decisions based on experience and knowledge.
1. Introduction
In production companies, human capital is an indispensable asset, comprising knowledge, experience, and expertise that defy easy replacement. Diverse expert systems have emerged to augment human endeavors within these contexts. Our inquiry delves into the intricacies of human knowledge and its capacity for abstraction, essential for transference to novel situations. In contrast, machine learning methodologies hinge on extensive datasets and associative principles, although evolving trends toward individualization suggest potential flexibility in such solutions.
Human experts distinguish themselves through adaptive responsiveness and the execution of causal decision-making processes. The departure of personnel from a company invariably leads to a loss of both expertise and knowledge, underscoring the urgency of digitalizing human expertise—an objective we pursue. Humans think in causal chains and create causal relationships from existing knowledge and experience. In conclusion, an application that supports the expert should consider the causality principle.
This study presents a semi-autonomous combinatorial approach based on an ontology for inferring a CG. The ontology acts as a foundation by representing formalized and semantic knowledge. The CG is derived from this knowledge model and uses inference calculation to allow various causal conclusions reminiscent of human decision-making processes. Humans think in causal chains and create causal relationships from existing knowledge and experience. In conclusion, an application that supports the expert should consider the causality principle. We elucidate the theoretical underpinnings of ontologies and causality in Section 2.
While ontological knowledge modeling is already used within production domains, CG adoption lags, albeit with a burgeoning corpus of literature. Existing endeavors, including ontology-based bayesian networks (BNs), incorporate CG representation sporadically but often disregard ontology standards. Noteworthy applications suc h as “BNTab” [1,2,3], “BN Domain Explorer” [4,5], and “BayesOWL” [6,7,8,9] are explored in Section 3.
Our paper introduces a conceptual framework for the ontology-driven creation of a CG, leveraging the international standard of basic formal ontology (BFO). We delineate the procedural intricacies and identify potential research domains; see Section 4. Initial conceptual approaches are part of this paper. While production is our primary application domain, the framework’s adaptability extends to diverse fields.
Creating ontologies and CGs demands substantial manual effort, which is why the prospect of exploiting synergistic effects offers immense appeal. The research advances of ontologies in production can complement the application of CGs, benefiting both theory and practice. Ontologies facilitate logical consistency checks, adaptive extensions, and versatile utility through SPARQL queries, while CGs enable inquiries into hypothetical scenarios, such as retroactively assessing operational parameter changes.
2. Ontology and (Causal) Bayesian Network—Two (Directed) Graph Models
2.1. Ontology as Knowledge Model
Ontology, originating from philosophy, explores and categorizes existence, reality, and possibility, organizing them into distinct categories governed by specific laws [10]. In artificial intelligence, ontology refers to the formal modeling of knowledge in computers, representing a conceptualization of the world as an explicit specification [11,12]. Essentially, an ontology catalogs types within a domain, encompassing properties, and word meanings [13]. Various approaches to ontology specification share a common foundation, involving a vocabulary for domain entities and a logical specification of term meanings [14].
In the Semantic Web context, ontologies are primarily defined using Resource Description Framework Schema (RDFS) and Web Ontology Language (OWL), based on description logic principles [15,16]. RDFS describes class hierarchies, properties, and data types for literals, while OWL extends these capabilities to include set-oriented class interpretation and fine-grained property definitions [17,18]. The newer Shapes Constraint Language (SHACL) [19] addresses the validation and consistency of Resource Description Framework (RDF) graphs. It does this by allowing us to define a set of constraints or conditions that data in an RDF graph must satisfy. These constraints can range from simple datatype checks to complex structural requirements. Although SHACL and OWL have some similarities in their semantics [20], the main purpose of SHACL is data validation, whereas OWL enables the definition of ontologies by specifying the vocabulary and relationships between terms in a knowledge domain.
Figure 1 depicts core elements of an OWL ontology, employing a graphical notation to present terms and their relationships. The example contains classes, superclass–subclass relationships, and applicable object properties. The graphical representation makes it obvious that an ontology describes a graph of terms that are organized within a taxonomy and have typed relationships with particular directions. We argue that it is possible to use this directed graph structure as a base to identify the causal semantics of ontological relationships. The resulting causal models are also representable as graph structures and can be used for causal inferencing, as described in the next section.
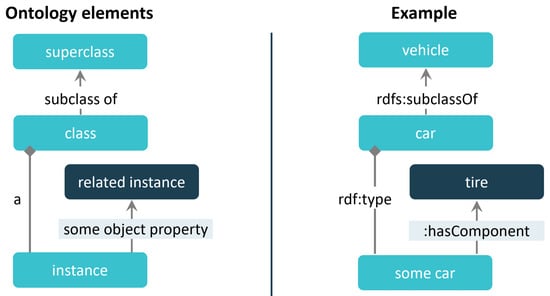
Figure 1.
Basic ontological elements applied to an example of cars and their components.
2.2. Causal Bayesian Network as Inference Models
Despite the early causal, graphical models at the beginning of the 20th century, for a long time, they received little attention compared to (exclusively) statistical methods. There was a change when Judea Pearl received the Turing Award for his work on artificial intelligence [21]. His main work included theoretical considerations on causal inference and the advantages of directed graph notation [22]. Today’s machine learning approaches use various statistical calculation methods, thus serving associative inference. One of the advantages of causal models is their adaptive capability. Causal relationships in intelligent applications simplify the verification of machine decisions by humans. In their position paper for robust and explainable AI (in the medical field), Holzinger et al. listed causal graphical models and counterfactuals as one of three pioneering research areas [23].
As the naming suggests, both RDF graphs, like ontologies and CGs, are graphical representation forms. However, CGs focus on representing cause–effect relationships. Furthermore, it is possible to perform more comprehensive analytical calculations. Figure 2 illustrates notable disparities between the two graphs regarding representation type and extent in the context of the ontological example concerning cars. The depiction on the left-hand side delineates an expanded simple ontology. Beyond the portrayal of the car’s physical constituents, it also illustrates a person’s involvement in a vehicle accident related to this car. Furthermore, the elements within the ontological model, namely “tire”, “car”, and “person”, are endowed with respective qualitative attributes. The graph on the right shows a causal graph derived for this situation. In the graph, the edges do not have a semantic specification beyond their causal meaning. Nevertheless, the human reader associates a semantic meaning with an edge relationship. Three of the four nodes merge two ontological concepts, as indicated by a dashed border. According to the nodes and edges in the causal graph in this simple example, the occurrence of a car accident is causally dependent on the driver’s experience and the car’s roadworthiness. The tire profile, in turn, has a causal influence on the latter.
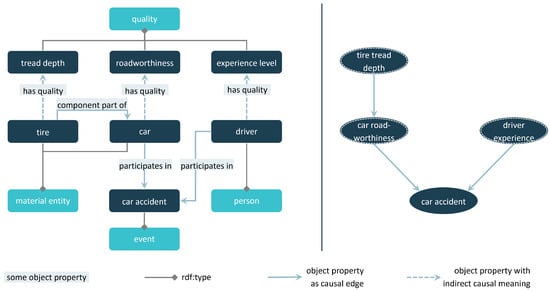
Figure 2.
The derivation of a CG using ontological model elements in the example of the involvement of a car in an accident.
The causal frameworks proposed by Pearl and Rubin are two well-known modeling concepts. The analytical examination of similarities and differences is part of the scientific discourse. In the following, we base our causal analysis on Pearl’s approach. Pearl [24] used the term “blueprint of reality” in his book to describe a causal model. It is based on a directed acyclic graph (DAG) and defined here as follows:
Definition 1.
A DAG is an acyclic, graphical representation of nodes and directed edges. Its modeling reflects the assumption about a situation by setting or predefining edge relationships (in the form of arrows). The direction of the arrow expresses the (causal) direction of action from cause to effect, which can be direct () or via a mediator ().
Figure 3 shows an example of a CG composed of labeled nodes connected with arrows called edges. Three basic structures exist: the collider, the mediator, and the confounder. The expression represents a causal influence from A to B. Another path exists via node D through and is referred to as a backdoor path. Node D is called a collider, as it influences A and B. Confounders also have a triangular structure. The causal effect is shown here by . The backdoor path exists via . Thus, a causal relationship exists not only via the direct route but also via H. If the backdoor by the confounder paths is open, non-causal correlation phenomena are the result; see Simpson’s paradox [25]. The aim is to determine direct causal influences and avoid distortions. With colliders, the way is closed per se but is opened by manipulating D. With confounders, on the other hand, it is first necessary to close the backdoor path to determine the causal influence of I on J. The third graph form is the mediator. The example shows no direct causal effect from C to G, but the node E acts as a mediator. When conditioning the mediator, the value of C is irrelevant to the influence on G.
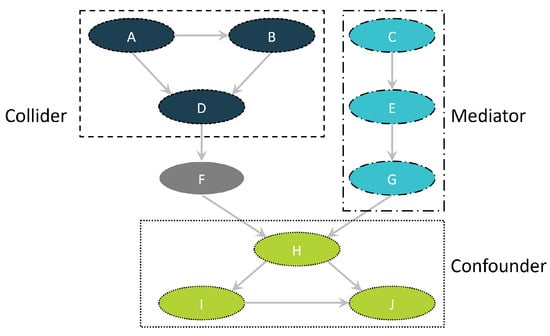
Figure 3.
The three graphical structures in a directed acyclic graph are shown here in the following color coding: collider in dark blue, mediator in light blue, and confounder in green.
Pearl further distinguished between three levels of causality: the association, the intervention, and the counteraction; see Figure 4. The association considers statistical correlations. For example, statistically, one can determine the deviation from the expected value and the exceeding of limit values for machine data. On the other hand, level two of the intervention looks at the causal relationship and considers observations. For example, the worker observes the condition of a machine component under specific operating parameters. This observation already allows conclusions to be drawn about other nodes in the graph. During the intervention, this knowledge is included in the recalculation, known as the do-operator. What happens if I increase a parameter from X to Y when Z has already been observed? Level three addresses retrospective topics and, thus, questions such as “What if I had acted differently?”, for example, whether a machine error would also have occurred with other parameter settings. The following is a syntactic description of the three levels:
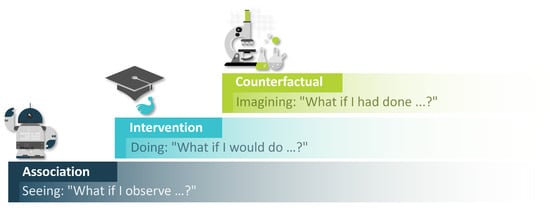
Figure 4.
The three stages according to Pearl’s Ladder of Causation [22,26].
- The association in the form of expresses the probability p of under the condition that the event has occurred.
- In the intervention, the probability of is expressed in the form of the “do-operator” in if was observed after the intervention of the variable value X on x.
- In the context of the counterfactual consideration, ) expresses the probability that the event would have been observed if , although and were observed.
3. Studies on Previous Ontology-Based Bayesian Networks
This section delineates the current research endeavors in our study domain. Initially, we outline the criteria employed for study selection. Subsequently, we explore ontology-based methodologies for constructing (causal) BNs. Our analysis encompasses seven distinct research domains. Moreover, we present a nuanced summary incorporating supplementary facets that warrant further examination within the existing literature.
3.1. Selection of Studies
We used the Scopus database for the study research to find peer-reviewed papers. We also assumed they were English-language (and, therefore, international) publications and advanced papers in the final publication phase. We did not take the year of publication into account. The reason for this was the limited number of studies insofar as we considered the application domain of production and the BFO standard in ontology modeling. Expanding the search space to include the search terms listed below revealed matches in the database. We also applied individual restrictions, such as excluding studies from medicine or limiting to specific keywords.
- TITLE-ABS-KEY (ontology-based OR ontology-driven OR ontological)
- TITLE-ABS-KEY (“bayesian * network”)
- LIMIT-TO (EXACTKEYWORD, “Bayesian Network”) OR LIMIT -TO (EXACTKEYWORD, “Bayesian Networks”) OR LIMIT-TO (EXACTKEYWORD, “Causal Bayesian Network”) OR LIMIT-TO (EXACTKEYWORD,“ Causal Inference”) OR LIMIT-TO (EXACTKEYWORD, “Causal Inferences”) OR LIMIT-TO (EXACTKEYWORD, “Ontology-based”))
- AND NOT (medical)
3.2. Analysis of the Studies
The edge relationships considered in the studies are not necessarily causal but can be. We justify the need for more explicit consideration of causality because research on CGs in production is still relatively young. Nevertheless, the ontology-based approaches shown in the studies allow conclusions to be drawn about the procedure and its advantages.
3.2.1. Scientific Publications
We want to emphasize and explain three studies in particular. The first paper by Chen et al. [27] is the most recent example to date and also an example from production, contrary to the majority of the other publications identified. Another study is Messaoud [28], which focused on causal discovery in conjunction with an ontological model. Finally, we would like to highlight the work of Fenz [1], who has published several papers on the topic of ontology-based BN creation. At the same time, his development resulted in a plug-in that can be used in the well-known ontology software Protégé (Stanford Center for Biomedical Informatics Research. Open-Source Plattform, v5.5.0. Available online: https://protege.stanford.edu/, accessed on 10 March 2024). Some publications have strived for the inverse transformation, i.e., from CG to ontologies (similar to Hu et al. [29]). However, such investigations are different from the subject of this paper.
Chen et al. [27] analyzed the interactions between the design, the process, and the structural properties in additive manufacturing. Existing data still need to be used comprehensively for quality assessment and control in this use case. The challenge lies in determining the causal influence of process parameters on product quality. Structural learning is performed using a combinatorial approach consisting of score- and constraint-based algorithms. For the authors, the advantage of using ontologies lies in integrating the expert knowledge formalized there into an algorithmic approach. The domain knowledge of the individuals was utilized in two ways. Firstly, the persons initially restricted possible edges between the nodes. Secondly, discretization of continuous data was carried out with the help of the persons. How the knowledge formalized in the ontology was integrated into the algorithm must be explained in detail. For this reason, it is also challenging to understand what causal conclusions the authors drew from the semantic modeling. The study also pointed out that the approach developed needs to be customized if other parameters are to be considered.
Messaoud et al. [28] used ontology for causal discovery and to improve visualization. The application example and the data should be presented in detail. However, the explanations suggest that it concerns bio-medicine. The authors extended the greedy approach with ontological knowledge. The result was the MyDaDo algorithm, which reduces the edge reduction to the relations modeled in the ontology. The advantage of this is that fewer interventions and, thus, calculations are required. The authors emphasized that the connections between ontologies and a BN should be investigated and used more intensively.
Fenz’s work [1,2,3] presented a four-stage approach to an ontology-based creation BN: (1) select classes, instances, and relations; (2) create a graphical skeleton; (3) create a condition probability table (CPT); and finally (4) integrate existing knowledge. The work was explained using examples from information security. The BN was used here to determine the probability of a possible attack. The data basis was the ontology with knowledge about the nodes’ state or the domain’s relevant concepts. The BN was based on the classes and instances modeled in the ontology and connected by relations. When selecting ontological concepts, ensuring they do not create redundant relationships was essential. If, for example, a transitive relationship is modeled from A to B and from B to C, an edge from A to C is superfluous. The ontology also serves as a model for storing edge weights for the BN. The author provided a calculation formula to determine the conditional probabilities, which has also been taken up by other works, such as Zheng et al. [30].
Table 1 contains an overview of further studies, briefly describing the data, methods, findings, and research needs. We were able to identify the following motivations in the studies on the use of ontologies in the creation of a BN:

Table 1.
Further studies with ontology-based approaches for the creation of (causal) BNs.
- Reduced effort compared to otherwise manual creation;
- Support in the visualization;
- The extension or adaptation of existing algorithmic approaches through the knowledge in ontologies;
- Securing information of a BN in the ontological model;
- The consideration of uncertainties that are otherwise not part of ontologies.
3.2.2. Applications
To the best of our knowledge, there is a limited number of generic approaches in the form of an application, especially not for the production domain. We want to point out that we use the notation (causal) BN because the approaches do not necessarily specify the aspect of causality.
BNGen is available as a Protégé plug-in and is similar to BNTab from Fenz [1,2,3]. The intention is to support the classification of vague data (specifically spatial data). According to Melchior [35], human judgment allows for inaccuracy in the data. The ontology functions as a categorization and classification model. The BN determines the degree of agreement with the ontological concepts. Instead of an “if-or-if-not” statement, they use a categorization based on probability.
ByNowLife is an abbreviation for “Bayesian Network and OWL Integration Framework”. It is a framework to transform ontologies to BNs and vice versa. Setiawan et al. [36] took the view that both models are a knowledge base. The motivation of ByNowLife is unification to be able to reason both logically and probabilistically. The authors developed an algorithmic transformation approach to convert an existing model (BN or ontology) into another form. Consequently, it is more of a mapping rather than a conceptual approach.
BayesOWL, on the other hand, contains structural translation rules and (algorithmic) mechanisms for determining CPT. The aim is to integrate a probabilistic framework for representing uncertainty into an ontology. The authors focused on the ontological class concepts but did not consider relationships between individuals or datatype properties. The so-called bridge and concept nodes are novel in this approach. They act as Bayesian counterparts to classes linked in the ontology by logical operators (for example, AND-operator: ∧).
Kalet et al. [5] developed the Bayesian Network Domain Explorer based on a hub-and-spoke system in the application context of radiology. The ontology is represented as the Hub (a radiation ontology), which represents knowledge of the domain. The spoke is a software tool [4] and enables ontology-based reasoning to create a BN. A core component of the approach is the object relation “dependsOn”. There are four versions of this relation (“dependsOn1”, “dependsOn2”, “dependsOn3”, “dependsOn4”), depending on the level of validity in tmarhe form of limit values). The BN is created based on the defined context.
BNTab is known as a prototypical plug-in for the ontology editor Protégé. The author Fenz used a BN to determine the probability of occurrence of events. His work has already been presented in connection with the studies above. His four-step approach begins with manually selecting relevant observation variables from the ontology. All further steps build autonomously on this.
Table 2 shows the use of logical and linguistic aspects in ontologies in these five frameworks. We want to show to what extent logic and language are already part of the investigations and recognize whether generic approaches exist.

Table 2.
Use of RDFS and OWL in ontology-based frameworks to create (causal) BN in the respective applications, marked with a cross.
A component of RDFS is the representation of sets through sub-relationships and, thus, term hierarchies. Relationships are specified by rdfs:domain and rdfs:range restrictions. A distinction between these RDFS expressions is recognizable in the table. Classes and relations are used in all the applications presented. This emphasizes the idea of the visual similarity of both graphs. Classes or instances in an ontology appear as counterparts to nodes in the BN. Respectively, relations correspond to edges. There are different procedures for sub-specifications. The situation is even more differentiated with domain range restrictions, which are only part of BNTab.
Only a few applications go further in their approach, including the linguistic aspect with OWL. The inversion is partially taken into account and thus allows the conclusion that a distinction is made about the direction of the relationship. Transitivity or symmetry is not the subject of the analyses. Although Fenz [1] addressed the importance of transitive relations in the manual selection of edge relations in his work, he did not integrate it methodically. Only BNTab and BayesOWL take object restrictions and class specifications into account. Fenz [1] checked restrictions in the form of universal (owl:allValuesFrom) or existential (owl:someValuesFrom) restrictions. Regarding cardinality restrictions, n nodes are added to the graph according to the min or max values. The intersection, union, or complement is only modeled in BayesOWL as independent nodes. However, we would like to point out that the motivation in Ding et al. [7] lay in operating with uncertainty in an ontology. The purpose of this consideration is the differentiated judgment about the membership of a class and thus differs from the objective presented here in the ontology-based creation BN.
The applications of OWL require object characteristics and relation restriction, as well as the specification of classes, sometimes sporadically, as seen in Table 2. Most ontology-based applications primarily use RDFS to support graph creation. Consequently, we would like to claim that RDFS and OWL have not yet been fully considered in their entirety, and therefore, the applications presented do not represent a generic approach.
The listed ontology-based framework does not consider SHACL. Except for ByNowLife [36], it became part of the W3C standard after the publications. However, we could not find any scientific papers in our Scopus research with the terms “causal graph” and “SHACL” in the abstracts, titles, or keywords. Table 2, therefore, focuses on the aspects of OWL and RDFS.
3.3. Research Gaps
In the comprehensive analysis of the studies, we were able to identify a total of seven research gaps (G) in the ontology-based creation of (causal) Bayesian networks:
- G1:
- Node concepts—selectionof causally relevant domain concepts [1], including their verification or other study-specific approaches for the inclusion of domain concepts;
- G2:
- Causal relationships—investigation of induced (causal) correlations in ontologies to create a DAG [27,28];
- G3:
- Semantics—exploring the integration possibilities of ontological knowledge [28,32];
- G4:
- Node expression—research into the number of node expressions, sometimes limited to two [1], accompanied by a possible loss of information [31];
- G5:
- Probabilities—inaccurate or erroneous estimation with historical data [31], NP problem when calculating with large numbers of data [5], values are not integrated in the ontology [2,35];
- G6:
- Transferability—extension to applications that are relevant in the domain [31];
- G7:
- Generalizability—application to another database of a similar example [30,31].
The studies provided insight into the approach and an overview of the procedure. We supplemented the analysis with application-orientated frameworks. Figure 5 shows an overview for categorization. Table 3, on the other hand, shows which works have named which research fields, with the studies at the top and the frameworks at the bottom The author Fenz [1,2,3], who published both studies and a plug-in, is listed at the bottom. In the horizontal view, it becomes clear that each paper names between one and three research topics, most in Cao et al. [31].
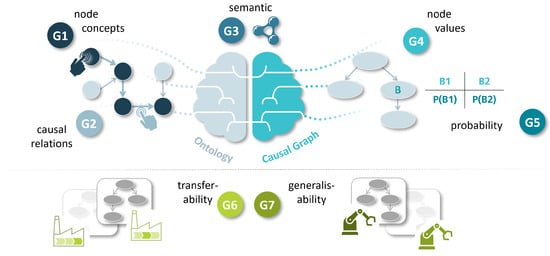
Figure 5.
Graphic classification of the research gaps (G) of the studies in a coherent context.

Table 3.
Identified research needs in ontology-based approaches for creating (causal) BN, marked with a cross.
There is a tendency toward G1 (node concepts) and G5 (probabilities) in the framework-based approaches. We justify this with the fact that the focus there is on the application. At the same time, the authors do not consider G3 (semantics) or G6 (transferability). Thus, the representation of uncertainty in ontological modeling (including BayesOWL or BNGen), probabilistic reasoning (as in BNTab and Bayesian Network Domain Explorer), or the creation of a uniform knowledge base (see ByNowLife) is the subject of investigation. Simplified, one can say that the extension of an ontology is in the foreground. The causal meaning of concepts and relations provides the incentive for a closer analysis of semantic modeling.
Only Cao et al. [31] named the transferability to similar or tangential applications in the domain under consideration (corresponding to G6) as a field of research. All studies only considered one application example. There is a need to investigate how the methodological approaches developed can be transferred to other use cases. G6, therefore, requires a cross-study analysis. We want to mention that there is a thematic proximity to G7 (generalizability). The difference is that G7 addresses reproducibility, while G6 refers to the ability to abstract. We want to illustrate this using the fictitious example of predictive maintenance. The application of predictive maintenance to a different machine (different data and parameters) corresponds to G7, while G6 refers to a different production stage, such as quality control.
We want to add two aspects to the seven research fields mentioned: standards in ontology modeling, such as the BFO, or references such as the Industrial Ontology Foundry (IOF) Core and the consideration of causality in the creation of a BN.
Existing concepts from top-level or mid-level ontologies are only sometimes the basis when modeling ontologies. Individual knowledge models or so-called isolated solutions lack interoperability and comparability. The ontology-based approaches presented here also do not consider any standards or other references in the ontology model. In particular, the research needs G1, G2, G4, G6, and G7 related to the ontological concepts. Extending the perspective to include standardization is logical.
We discuss three approaches for combining BN and CG in framework-oriented efforts. We exclude the representation of uncertainty in ontology models (1) because we assume a reliable knowledge base. Work such as ByNowLife assumes an existing probabilistic or ontological model (2). The motivation lies in the transformation from one form to the other. Probabilistic (causal) reasoning based on ontological, formalized knowledge is the third intention and shows the most significant correspondence to the motivation of our work.
In order to make a contribution to the digitization of human expertise with the help of ontologies and CGs, it is necessary to include standards and references in ontology modeling in combination with the causal perspective in the previous research fields according to Table 3. It includes the derivation of nodes based on the ontology concepts and the investigation of the causal meaning of the relations according to BFO or IOF Core. Studies have occasionally highlighted causal relations in ontological modeling (see G2), for example, in Chen et al. [27] and Messaoud et al. [28]. However, selecting causal ontological concepts (see G1) is also directly related to causal relations.
G3 is related to G1. Table 2 shows the extent to which framework-based approaches take individual linguistic and logical contents from ontologies into account. Symmetrical relations contradict the directionality of causality relations. Consequently, researchers must check whether this and other exclusion criteria exist in ontology standards and references.
The fourth research aspect addresses the formalization of node expressions. In contrast to structured causal models, the research must show to what extent discrete node values can adequately represent the causal observation context in combination with ontologies. Furthermore, the question arises regarding which requirements can be derived in reverse for the conformal modeling of IOF Core and BFO.
G5 considers the number of data and its informative value when performing causal calculations. Research must show whether the RDF representation of data improves or simplifies the calculation through semantic expressivity. To the best of the author’s knowledge, no studies perform causal inference calculations based on triples.
G6 raises the question of which ontological concepts of ontology standards and references are required for modeling the various scenarios in production. As a consequence, the research can then show based on which model elements causal derivations are possible. In the narrow context, G6 focuses on the generic (causal) concepts in the BFO and the IOF Core of a production area.
The result of the research from G1 to G7 in connection with ontology standards and references, as well as the causal perspective, can be a concept for the ontology-based creation of causal BN. Content can represent transformation principles and guided procedures. Conversely, we ask ourselves the question of the extent to which causal insights influence modeling. The question is whether ontological modeling can be detached from a causal perspective and thus possibly a “distortion”. It can also be recognized that there is a research gap concerning the production domain. The studies presented in this paper showed applications from various areas, such as medicine, information security, and insurance. Only Chen et al. [27] with quality control for additive manufacturing showed thematic proximity, even if this work did not consider other application examples.
Considering the ontology as the basis, we see G1, G2, and G3 prioritized over G4 and G5. According to Figure 5, G6 and G7 require a data basis or various practical examples. We can see that a chronological order accompanies the highlighted research aspects. It first requires a conceptual approach, including G1 to G3, before we can analyze G4 to G7. It is also logical to examine G4 and G5 before G6 and G7 so that the assessment of transferability and generalizability can be incorporated into the causal model side.
4. Conceptual Model for the Generic Derivation of Causal Bayesian Networks Based on Ontologies
4.1. General Consideration about the Basic Idea
The knowledge of professionals is the cornerstone of their ability to act, and they are constantly gaining new experiences and learning. In contrast to machine learning applications, humans can abstract their knowledge and transfer it to new situations. People use their experience and expertise in different decision-making situations. It is well known that humans think in causal chains [37,38]; see Assumption 1. They use this specialized knowledge adaptively in new environments.
Assumption 1.
Humans think in causal chains and create theoretical connections from existing knowledge and experience. The ability to abstract and transfer these makes them unique compared to machine applications, as these generally require a large number of data.
At the center of Figure 6 is a triangle of variables consisting of production as an application domain, people as carriers of experience and knowledge, and the combinatorial view of the two models. The human being forms another triangle as an expert on the left-hand side. Knowledge forms the basis of the human ability to act. New experiences expand this wealth of knowledge. Specialists in a domain have the knowledge and the ability to use it correctly. On the right-hand side of the illustration is the digital counterpart to the specialist in this variable production environment. It shows the research area of deriving a concept for the ontology-based creation of a CG based on formalized knowledge. Here, the ontology contains the knowledge by formally representing the knowledge and experience values. The inference model in the form of a CG in the second instance enables the answering of hypothetical questions; see Figure 4. The potential in the combinatorial consideration of both models lies in deriving adaptive conclusions using experience and knowledge.
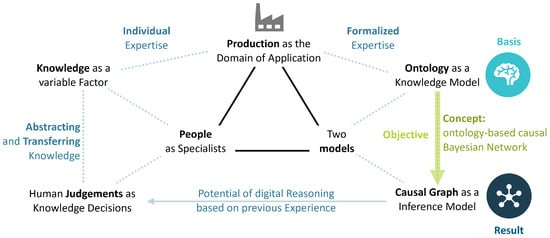
Figure 6.
The human ability to make abstract decisions based on individual knowledge compared to the combination of ontologies and CGs. The framework is the application domain of production.
A basic idea in the use of ontologies to create a BN is the graphical similarity of RDF to DAG. However, there is a difference in the modeling. While a CG focuses solely on modeling causal relationships, ontologies aim to formalize knowledge in general. The idea is that an ontology allows the creation of different CGs, depending on the focus of observation. Researchers must investigate to what extent and under what conditions deductions are possible. As a first step, we consider it necessary to investigate the formal description logic regarding causal exclusion criteria to investigate application-related causal model elements based on the BFO standard in a second step; see Assumption 2.
Assumption 2.
Ontologies and CGs address different aspects despite a certain similarity in the form of presentation. While ontologies focus on the formal conceptualization of an area of reality without exclusive reference to causality, CGs consider causal relationships in an observation domain exclusively without semantic specification of the edges.
The emergence of knowledge can represent a further aspect of research in this conceptual application. The same applies to the meaning of language as a form of the verbalization of knowledge. The Semantic Web Stack with its elements such as RDF, RDFS, and OWL can be viewed as a digital counterpart to the semantic understanding of humans. The application domain characterizes not only human language but also the digital form of representation in the form of application-specific model concepts.
4.2. Approach and Research Proposal
A catalog of measures with a structured procedure and defined modeling rules is required. Reference examples can help with understanding. If it is possible to derive a CG based on a standardized ontology, such as the BFO, it can be possible to achieve comparability with an CG. To what extent we can transfer the standard in the ontology modeling to the CG must be investigated. The following aspects play a role:
- The logic and language of ontologies: If we look at the logic and language, we are talking about the formal description logic SROIQ and with RDF, RDFS, and OWL also components of the Semantic Web Stack, according to Tim Berners Lee [39]. It seems logical that some aspects exclude causal edges, such as symmetrical relations. The extent to which further conclusions are possible is a subject of research. However, it is already a fact that the subject-predicate-object structure (S-P-O for short) of triples is similar to a CG. According to this, the predicate indicates the edge, while the subject and the object represent the node. This also means determining which relation has a causal meaning in inverse relation pairs. The fact is that there can only be one causal direction.
- The semantic context: Causal analyses are dedicated to questions in a specific domain. Consequently, the ontology-based derivation of a CG must be considered in the context of domain-specific modeling. While the BFO, as a standard top-level ontology, has no domain reference, the IOF Core serves as a reference for representing the industry.
The illustration of two examples elucidates the conceptual framework, as depicted in Figure 7 and Figure 8. On the left side, simple ontological production examples are presented, while the corresponding causal counterpart is portrayed on the right. Object relations with causal significance are highlighted in light blue, with solid connections representing explicit causal edges. Dashed relations, on the other hand, indirectly contribute to the CG by amalgamating the associated ontological concepts into a single causal node.
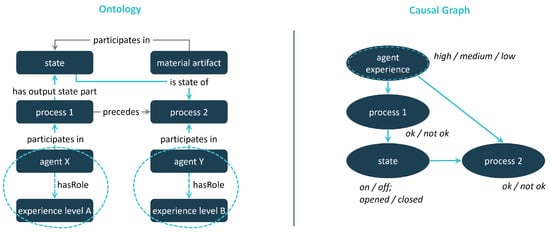
Figure 7.
Ontology-based creation of a CG using the simplified example of a process impact chain.
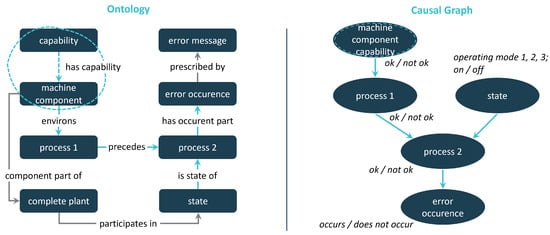
Figure 8.
Ontology-based creation of a CG using the simplified example of root cause analysis.
The ontological relations are model elements according to the BFO and the IOF Core. Individual connections, such as “is state of”, are specifications of the relation taxonomy there. For clarity, we have omitted the representation of the inverse relation on the left-hand side of the model. The connections are also partially simplified; see “participates in” according to the IOF Core modeling “participates in at all times”. Compared to its ontological counterpart, the CG on the right side exhibits graphical reduction. The edges within the CG symbolize causal relationships without undergoing additional semantic specification. Examples of potential variables within the CG are denoted in italicized font next to their respective nodes. This representation aims to capture and differentiate the causal connections, providing insights into the complex interplay of variables and their impact on the overall system dynamics.
In Figure 7, a precedence relationship between two processes is discernible, each executed by individuals with varying expertise levels. The first process induces a change in the state of a material artifact, which, in its modified form, becomes a prerequisite for the subsequent process. The CG representation encompasses nodes corresponding to the processes, the material state, and the worker’s expertise. Notably, the two processes are not directly linked by a single edge; instead, the state of the material artifact acts as a causal mediator. Both processes are causally influenced by the individual executing them. For instance, the success of process two, indicated by being “ok”, depends, among other factors, on the worker’s level of expertise. However, it is plausible that despite a high level of expertise, process two may only be executed properly if the necessary prerequisites, such as the material state form illustrated in the example, are met. This nuanced causal interplay, as captured in the CG, provides a comprehensive understanding of how the material state, worker expertise, and the sequential order of processes contribute to the overall dynamics of the system.
The second example mirrors the structure of the first, featuring two processes and a material state form within the ontology; see Figure 8. Additionally, the ontology represents a machine component’s capability and the occurrence of a fault event described by an associated notification text. In contrast to Figure 7, the causal counterpart on the right side now exhibits a causal edge connecting both processes. The second process emerges as a collider in this simplified analysis, serving as the cause of the fault event. Conversely, the process is influenced by two independent causal nodes: the preceding process step and the machine’s state form. Examples of time-dependent state forms may include operational modes such as automatic or manual. Process one, conversely, is influenced by the proper functionality of a machine component.
It is conceivable that the ontology contains detailed information about the application domain, including its relevance for the CG. An ontology can serve as a basis for several CGs, depending on the focus of consideration. We only consider the nodes and edge relationships relevant to the analysis to minimize the CPT calculation effort; see G4.
Including an ontology as a knowledge base, the sequence of steps to create a KG consists of four stages. Step one creates the foundation with the ontological model creation based on the IOF Core. Figure 9 shows a simple example in which a person executes a process and assigns a process value to it. The result is a product with a quality property. A CG can express that the operating parameter influences the product quality; see causal edge from “process value” to “product quality” in step four. There exists a procedural bridge between foundational elements and resultant outcomes, involving the systematic selection of causal model components within the ontology. These selected elements are subsequently translated into a causal skeleton.
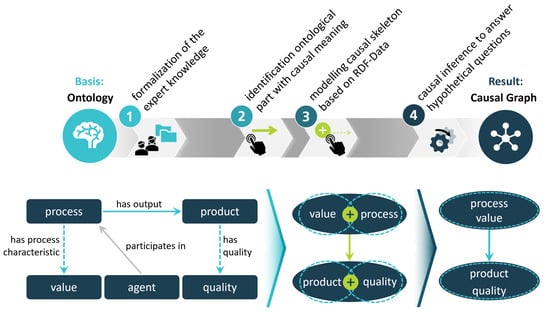
Figure 9.
Transformation of ontologies into causal skeletons.
We have yet to examine the merging of concepts, as shown in the middle representation of the simple example in Figure 9, with “process parameter” and “product quality”. First, there is a difference in the granularity of information modeling in ontologies and CGs. It, therefore, appears necessary to merge ontological concepts. Since ontology modeling follows a structure, we assume a schema can also be worked out during the merge. The extent to which this is limited to an application domain must be investigated during development. The relations “has output”, “has quality”, or “has process characteristic” are not assigned any properties, such as transitivity or symmetry, by IOF Core modeling. We derive the causal significance from the semantic meaning we associate with the relation by definition. In practice, there are similar concepts for one domain. The IOF Core can provide a reproducible set of concepts and relations to describe production with its knowledge-bound processes. If research succeeds in identifying the causal meaning in the logical and linguistic aspects, achieving a degree of comparability in ontology-based causal BN will be possible. Furthermore, according to the idea, the one-time effort in analyzing causal structures in ontological modeling according to the IOF Core model will be offset by a structured procedure that can be transferred in many ways to transform ontologies into CGs. Overall, the development effort for CGs can be considerably reduced.
The latest valid version of the IOF Core (at the time of writing: version one released on May 2022 [40]) contains 103 object relations and 93 classes. A class or its associated instances can occur as a cause or effect node. In addition, almost every relation has an inverse relationship. If you were to theoretically create a matrix from the object relations and the classes, this would result in 9579 pair combinations. Whether it is necessary and appropriate to check each of these connections is questionable. Instead, we assume that it is sufficient to include more abstract concepts in the class taxonomy in consideration. There is a further reduction if researchers consider the ontology’s domain and range restrictions. As can be seen from Table 2, the studies have so far only partially utilized OWL for the creation of BN. We see great and so far untapped potential in developing causal meaning in semantic modeling. The extension of the consideration to the production domain creates an application reference and the possibility of creating an application-related set of rules with defined derivation rules.
5. Summary and Discussion
We summarized seven research areas in the comprehensive study analysis of ontology-based approaches. We then supplemented these topics with two further aspects for further consideration. The CG is still a relatively new field of research, especially in production. Unsurprisingly, the potential in the combination of ontologies and BN under the condition of causal edge relations has not yet been the subject of extensive research. We presented a conceptual research approach and showed which steps are necessary. We also pointed out tangential research endeavors. We developed an initial ontological model concept based on the BFO standard and the IOF Core reference. We want to use this to develop a concept based on reference examples. We initially see the research focus on analyzing the logical and linguistic aspects of the ontology, especially in the application context of production. We must determine whether restrictions arise from the causal findings in modeling ontology by implication. We also ask ourselves what consequences, if any, ontological deviations can have on the resulting CG. The closer examination of causal edge relations in ontological relations leads to further application-related challenges. For example, there are relations whose domain and range restrictions include the exact class concepts, such as part–whole relationships. It is then necessary to analyze the integration of a generic differentiation into a concept. Finally, the basic assumption must be discussed, according to which an existing ontology model is assumed. The idea is that this ontology formally represents the knowledge of an application. In practice, however, modeling is an iterative development process between domain and ontology experts. The conditions under which logical (ontology) and probabilistic reasoning for which (CGs) make sense in an application must be explained. If a formal knowledge representation in an ontology model is unnecessary, users should prefer the direct creation of a CG.
People think in causal chains and create theoretical connections from existing knowledge and lived experience. A feeling of explainability and predictability of events is conveyed. Predictability is limited. The world is complex, and predictions are accompanied by an objective ignorance of influencing factors, especially as the time horizon under consideration increases. The human intellect is also selective as a measuring instrument. While the formalization and semantic representation of knowledge are possible with ontologies, relations in these models can represent causality but do not have to. Knowledge representation is essential in developing AI applications, as are causal graphical models with counterfactual analysis.
6. Outlook
There have already been several years of intensive research in creating ontology references. The field of ontological knowledge models in production has also been researched more intensively than that of CGs. If we succeed in transferring existing research achievements to the young field of CGs, we believe this will only advance development. The transfer to other application domains can also be further investigated.
The development of a concept for deriving CGs based on ontologies using BFO and ontological references such as IOF Core is the subject of one of the author’s doctoral thesis, corresponding to G1, G2, and G3. Reference examples were derived from real-world applications within the production domain. Data were collected and serialized as RDF. We also analyzed the concept–relation combinations and their causal meaning. As part of further research, a framework is created that enables an individual CG to be created directly using an ontology upload, including categorizing data values according to G4 and exporting. The presentation of this work will be the subject of forthcoming publications.
The authors plan to test the concept and the framework in further research projects. The aim is to verify or improve the concept. Current tests show that a high number of triples influence the performance of the framework. Further research content currently uses semantic meaning to support the calculation of CPT, corresponding to G5. The final goal is the integration into a software application. As an expert system, this application is intended to support workers in carrying out individual production activities by having the bundled formalized knowledge of the employees at its disposal and being able to conclude adaptive production environments under uncertainty.
Author Contributions
Conceptualization, M.M.-L.P.-K. and K.W.; methodology, M.M.-L.P.-K.; formal analysis, M.M.-L.P.-K.; investigation, M.M.-L.P.-K. and K.W.; writing—original draft preparation, M.M.-L.P.-K. and K.W.; writing—review and editing, M.M.-L.P.-K. and K.W.; visualization, M.M.-L.P.-K.; supervision, K.W. and S.I.; project administration, M.M.-L.P.-K.; funding acquisition, M.M.-L.P.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. However, the study is based on data collected in research project funded by the European Commission (European Regional Development Fund) and by the Free State of Saxony under the grant number 100365076.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
We do not provide any data, as this work focuses on highlighting research fields and new approaches in the ontology-based creation of causal BN.
Acknowledgments
We want to thank the small and medium-sized enterprises for the intensive discussions and the support provided during the company processes as part of the research project. This work gave us a comprehensive overview of the challenges in knowledge-based process steps.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BFO | basic formal ontology |
| BN | bayesian network |
| CG | causal graph |
| CPT | condition probability table |
| DAG | directed acyclic graph |
| IOF | Industrial Ontology Foundry |
| OWL | Web Ontology Language |
| RDF | Resource Description Framework |
| RDFS | Resource Description Framework Schema |
| SHACL | Shapes Constraint Language |
References
- Fenz, S. An ontology-based approach for constructing Bayesian networks. Data Knowl. Eng. 2012, 73, 73–88. [Google Scholar] [CrossRef]
- Fenz, S.; Tjoa, A.M.; Hudec, M. Ontology-Based Generation of Bayesian Networks. In Proceedings of the 2009 International Conference on Complex, Intelligent and Software Intensive Systems, Fukuoka, Japan, 16–19 March 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 712–717. [Google Scholar] [CrossRef]
- Settas, D.; Cerone, A.; Fenz, S. Enhancing ontology-based antipattern detection using Bayesian networks. Expert Syst. Appl. 2012, 39, 9041–9053. [Google Scholar] [CrossRef]
- Kalet, A.M. Bayesian Network Domain Explorer. 2014. Available online: https://ont2bn.radonc.washington.edu/amkalet-apps/Ont2BNapp/ (accessed on 7 December 2022).
- Kalet, A.M. Bayesian Networks from Ontological Formalism in Radiation Oncology. Ph.D. Dissertation, University of Washington, Washington, DC, USA, 2015. [Google Scholar]
- Ding, Z. BayesOWL: Website. 2008. Available online: https://redirect.cs.umbc.edu/~ypeng/BayesOWL/index.html (accessed on 7 December 2022).
- Ding, Z.; Peng, Y.; Pan, R. (Eds.) A Bayesian Approach to Uncertainty Modeling in OWL Ontology. In Proceedings of the International Conference on Advances in Intelligent Systems-Theory and Applications, Luxembourg, 15–18 November 2004. [Google Scholar]
- Peng, Y.; Ding, Z. Modifying Bayesian Networks by Probability Constraints. arXiv 2012, arXiv:1207.1356. [Google Scholar]
- Ding, Z.; Peng, Y.; Pan, R. BayesOWL: Uncertainty Modeling in Semantic Web Ontologies. In Soft Computing in Ontologies and Semantic Web; Ma, Z., Ed.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2006; Volume 204, pp. 3–29. [Google Scholar] [CrossRef]
- Grossmann, R. The Existence of the World, An Introduction to Ontology; Routledge: London, UK, 1992. [Google Scholar] [CrossRef]
- Gruber, T.R. A translation approach to portable ontology specifications. Knowl. Acquis. 1993, 5, 199–220. [Google Scholar] [CrossRef]
- Gruber, T.R. Toward principles for the design of ontologies used for knowledge sharing? Int. J. Hum.-Comput. Stud. 1995, 43, 907–928. [Google Scholar] [CrossRef]
- Sowa, J.F. Knowledge Representation: Logical, Philosophical, and Computational Foundations, 1st ed.; Brooks/Cole: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Uschold, M.; Gruninger, M. Ontologies and semantics for seamless connectivity. ACM SIGMOD Rec. 2004, 33, 58–64. [Google Scholar] [CrossRef]
- Baader, F. Description Logics. In Reasoning Web. Semantic Technologies for Information Systems, Proceedings of the 5th International Summer School 2009, Brixen-Bressanone, Italy, 30 August–4 September 2009; Tessaris, S., Franconi, E., Eiter, T., Gutierrez, C., Handschuh, S., Rousset, M.C., Schmidt, R.A., Eds.; Tutorial Lectures; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–39. [Google Scholar] [CrossRef]
- Baader, F. (Ed.) The Description Logic Handbook: Theory, Implementation, and Applications, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Horrocks, I.; Patel-Schneider, P.F.; Van Harmelen, F. From SHIQ and RDF to OWL: The making of a Web Ontology Language. J. Web Semant. 2003, 1, 7–26. [Google Scholar] [CrossRef]
- Hitzler, P.; Krötsch, M.; Parsia, B.; Patel-Schneider, P.F.; Rudolph, S. OWL 2 Web Ontology Language Primer, 2nd ed.; W3C Recommendation 11 December 2012; Available online: http://www.w3.org/TR/owl2-primer/ (accessed on 10 March 2024).
- Pareti, P.; Konstantinidis, G. A Review of SHACL: From Data Validation to Schema Reasoning for RDF Graphs. In Reasoning Web. Declarative Artificial Intelligence, Proceedings of the 17th International Summer School 2021, Leuven, Belgium, 8–15 September 2021; Šimkus, M., Varzinczak, I., Eds.; Tutorial Lectures; Springer International Publishing: Cham, Switzerland, 2022; pp. 115–144. [Google Scholar] [CrossRef]
- Bogaerts, B.; Jakubowski, M.; van den Bussche, J. SHACL: A Description Logic in Disguise. In Logic Programming and Nonmonotonic Reasoning; Gottlob, G., Inclezan, D., Maratea, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 75–88. [Google Scholar]
- Cunningham, S. Causal Inference: The Mixtape; Yale University Press: New Haven, CT, USA; London, UK, 2021. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Holzinger, A.; Dehmer, M.; Emmert-Streib, F.; Cucchiara, R.; Augenstein, I.; Ser, J.D.; Samek, W.; Jurisica, I.; Díaz-Rodríguez, N. Information fusion as an integrative cross-cutting enabler to achieve robust, explainable, and trustworthy medical artificial intelligence. Inf. Fusion 2022, 79, 263–278. [Google Scholar] [CrossRef]
- Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect, 1st ed.; Basic Books: New York, NY, USA, 2018. [Google Scholar]
- Pearl, J. Comment: Understanding Simpson’s Paradox. Am. Stat. 2014, 68, 8–13. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Chen, R.; Lu, Y.; Witherell, P.; Simpson, T.W.; Kumara, S.; Yang, H. Ontology-Driven Learning of Bayesian Network for Causal Inference and Quality Assurance in Additive Manufacturing. IEEE Robot. Autom. Lett. 2021, 6, 6032–6038. [Google Scholar] [CrossRef]
- Ben Messaoud, M.; Leray, P.; Ben Amor, N. Integrating Ontological Knowledge for Iterative Causal Discovery and Visualization. In Symbolic and Quantitative Approaches to Reasoning with Uncertainty; Sossai, C., Chemello, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5590, pp. 168–179. [Google Scholar] [CrossRef]
- Hu, H.; Kerschberg, L. Evolving Medical Ontologies Based on Causal Inference. In Proceedings of the 2018 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Barcelona, Spain, 28–31 August 2018; Brandes, U., Reddy, C.K., Tagarelli, A., Eds.; IEEE: Piscataway, NJ, USA, 2018; pp. 954–957. [Google Scholar] [CrossRef]
- Zheng, H.T.; Kang, B.Y.; Kim, H.G. An Ontology-Based Bayesian Network Approach for Representing Uncertainty in Clinical Practice Guidelines. In Uncertainty Reasoning for the Semantic Web I; da Costa, P.C.G., d’Amato, C., Fanizzi, N., Laskey, K.B., Laskey, K.J., Lukasiewicz, T., Nickles, M., Pool, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5327, pp. 161–173. [Google Scholar] [CrossRef]
- Cao, S.; Bryceson, K.; Hine, D. An Ontology-based Bayesian network modelling for supply chain risk propagation. Ind. Manag. Data Syst. 2019, 119, 1691–1711. [Google Scholar] [CrossRef]
- Ben Ishak, M.; Leray, P.; Ben Amor, N. Ontology-Based Generation of Object Oriented Bayesian Networks. In Proceedings of the 8th Bayesian Modeling Applications Workshop (BMWA-11), Workshop of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence (UAI 2011), Barcelona, Spain, 14 July 2011; Volume 818, pp. 9–17. [Google Scholar]
- Friedman, N. The Bayesian Structural EM Algorithm. In Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, Madison, WI, USA, 24–26 July 1998; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 129–138. [Google Scholar]
- Zhang, N.L.; Poole, D. Exploiting Causal Independence in Bayesian Network Inference. arXiv 1996, arXiv:cs/9612101. [Google Scholar]
- Melchior, A. Data Enrichment of Spatial Databases Using Ontologies and Bayesian Networks. Master’s Thesis, Utrecht University, in Collaboration with the University of Edinburgh, Utrecht, The Netherlands, 2013. [Google Scholar]
- Setiawan, F.; Budiardjo, E.; Wibowo, W. ByNowLife: A Novel Framework for OWL and Bayesian Network Integration. Information 2019, 10, 95. [Google Scholar] [CrossRef]
- Kahneman, D. Schnelles Denken, Langsames Denken, 1st ed.; Siedler: München, Germany, 2012. [Google Scholar]
- Kahneman, D.; Sibony, O.; Sunstein, C.R. Noise: Was Unsere Entscheidungen Verzerrt—Und Wie Wir Sie Verbessern Können, 1st ed.; Siedler: München, Germany, 2021. [Google Scholar]
- Berners-Lee, T. Weaving the Web: The Past, Present and Future of the World Wide Web by Its Inventor; Orion Business: London, UK, 1999. [Google Scholar]
- The Industrial Ontologies Foundry Core Ontology: Version 1 Beta, 6 May 2022. Available online: https://github.com/iofoundry/Core (accessed on 20 November 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).