4.1. Datasets and Experiment Settings
Environment: We carried out the experiments on a desktop computer running Ubuntu Linux with an AMD Ryzen 3700x 3.6Ghz CPU, 32GB of RAM memory, and an NVIDIA GeForce GTX 1070 GPU (8GB).
Datasets: Our experiments were conducted on four different datasets: two mono-lingual datasets, D-W-15K-LP(generated) and DBP-FB [
28]; and two multi-lingual datasets, CN3l (EN-DE) and WK3l-15k (EN-FR) [
29]. All of the datasets we chose were originally designed for benchmarking entity alignment algorithms; thus, seed alignments between KGs are readily available. The detailed statistics about the datasets can be found in
Table 1. In D-W-15K-LP and DBP-FB, 70% of the triples are reserved for the training set, 10% for the validation set, and 20% for the test set. In CN3l (EN-DE) and WK3l-15k (EN-FR), the percentages are 60%, 20%, and 20% for the training, validation, and test sets, respectively. Relation alignments are available in the two multilingual datasets, but not in the two mono-lingual datasets.
D-W-15K-LP generation: D-W-15K-LP is a dataset generated from the entity alignment benchmarking dataset D-W-15K [
17]. The sources of the two KGs are DBPedia and WikiData, with 15,000 entities in each KG. However, because D-W-15K was generated for the entity alignment task, every entity has an alignment across KGs. We argue that such a scenario is extremely rare in the real world because KGs from different sources rarely exhibit a large proportion of overlaps, and seed alignment annotations between KGs are very expensive, given the size and scale of real-world KGs. Therefore, we decided to employ the sampling strategy proposed in the work of Sun et al. [
18] to create dangling entities (entities without alignment across KGs) within KGs. In the sampling process, triples containing removed entities are excluded by removing part of the alignments from KGs. This results in a more sparse dataset with dangling entities in KGs. Concretely, we created 30% dangling entities in our base dataset D-W-15K; only 30% of the remaining 70% aligned entities (3150 entities) were used as seed alignments to create a more life-like scenario for the experiment.
Settings: The problem set of the experiment is consistent with what we discussed in
Section 3: for knowledge graphs
and
, the goal is to improve the knowledge graph embedding and its performance on LP tasks for
with information from
and seed alignments between them. We chose to compare our IPPT4KRL method against ATransN [
15] and MD-MKB [
14]. To the best of our knowledge, these two open-source methods achieve state-of-the-art performance in multi-KG KRL settings. In addition, two baseline models,
Individual and
Connected, were also included in the experiment. For the baseline
Individual, we simply trained the knowledge graph embeddings on
and evaluated the embeddings with their performance on the LP task with test triples in
. The baseline
Individual was also used as the pre-trained embeddings for the post-processing stage of our IPPT4KRL method. The second baseline
Connected was generated by connecting two KGs with seed alignments. Concretely, if there exists entity seed alignment
, where
and
, we then merge two entities and replace all entity occurrences
in triples
with entity
. Knowledge graph embeddings are then trained on the connected KG and evaluated on the LP task with test triples in
. We used TransE as the knowledge graph embedding model for all methods in the experiments for the fairness of comparison. However, all the multi-KG KRL methods in the experiments can be extended to incorporate other triple-based embedding methods for knowledge representation. The pre-training and baseline experiments were conducted using the OpenKE framework [
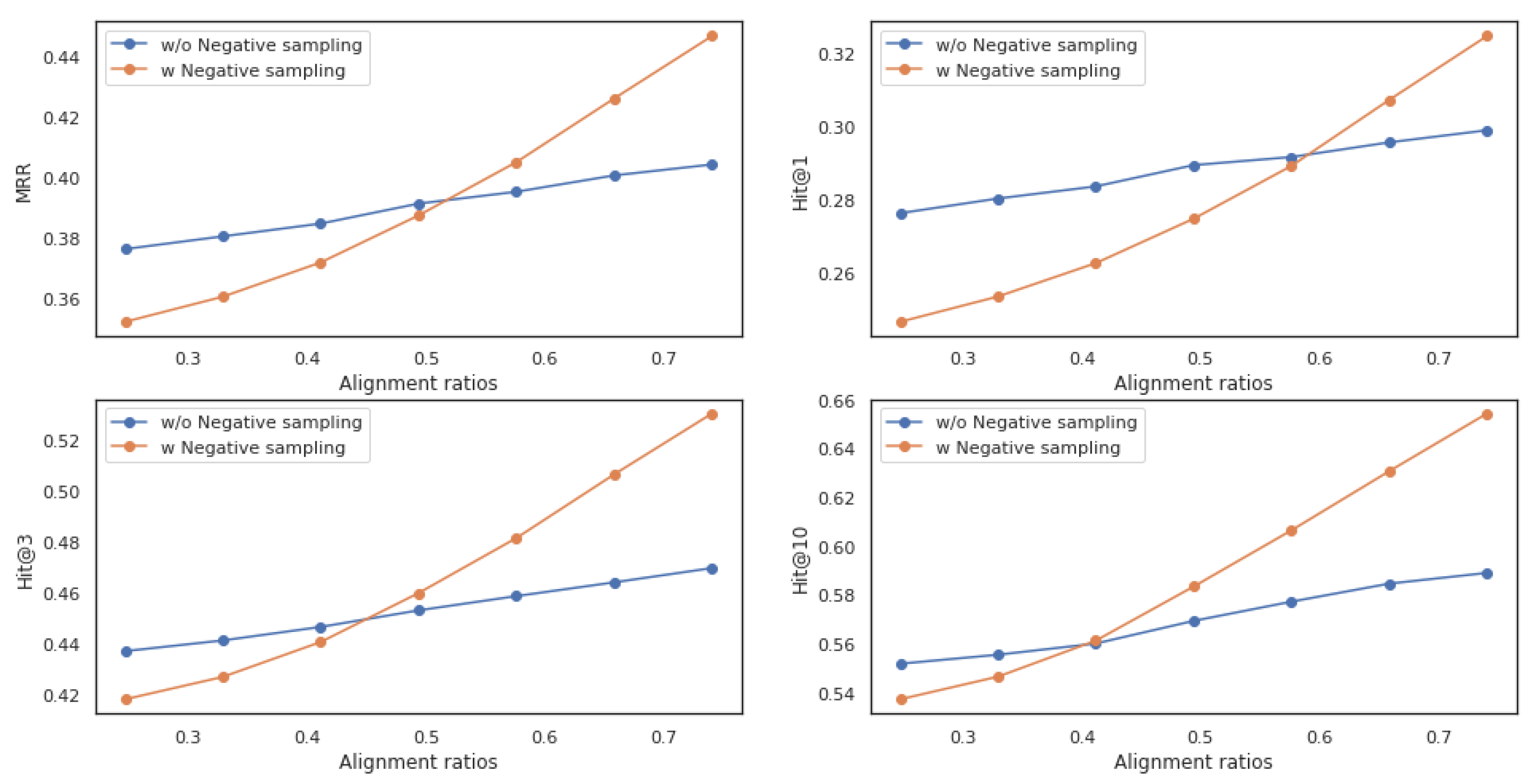
30] with uniform negative sampling.
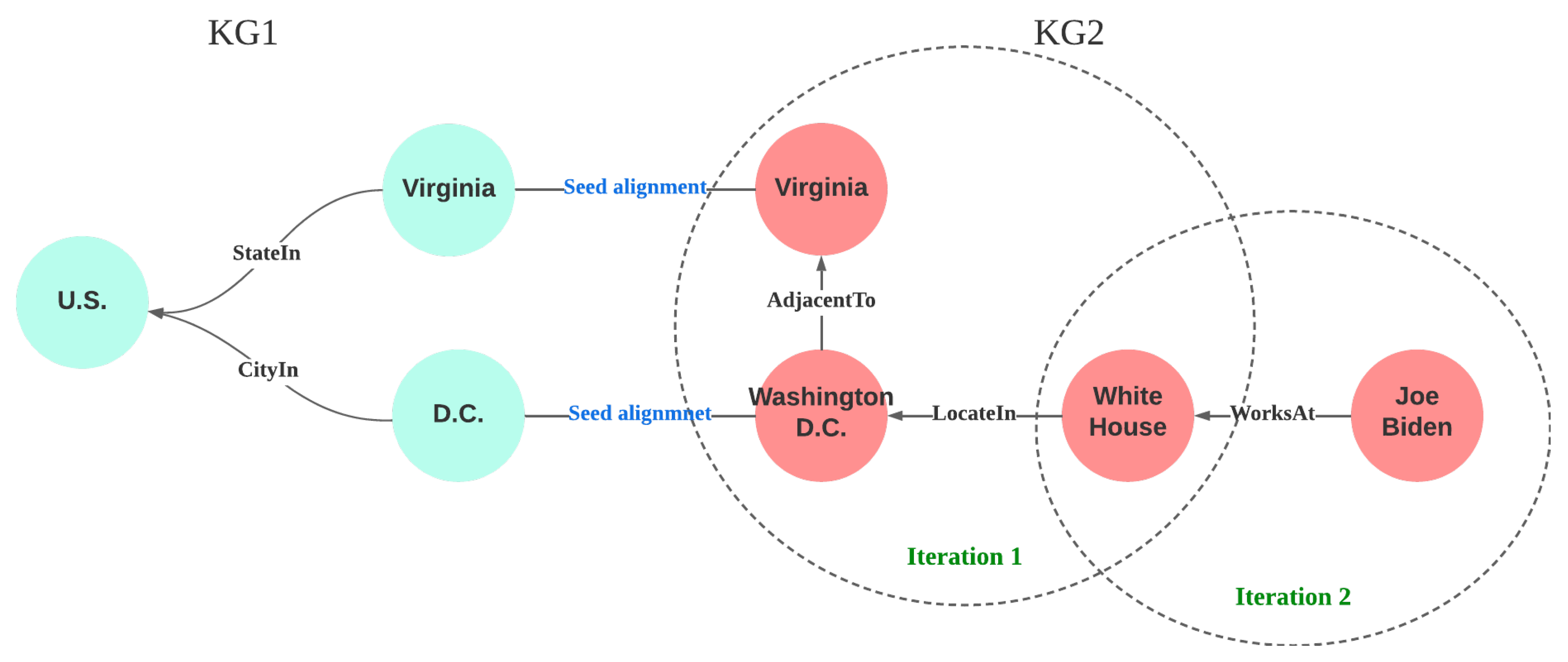
In the D-W-15K-LP dataset, the DBpedia KG is , and the Wikidata KG is added into the post-processing following an iterative manner. In DBP-FB, we chose the DBpedia KG to be and the Freebase KG to be . The German and French KGs were selected to be for CN3l (EN-DE) and WK3l-15k (EN-FR), respectively, while the English KGs of each dataset were included to provide knowledge transfer in the IPPT4KRL. Because ATransN employs a teacher–student setting in the training, naturally, in our setting was regarded as the “student” KG in ATransN. KD-MKB treats each KG equally. Hence, no special configuration was needed in our benchmarking experiments.
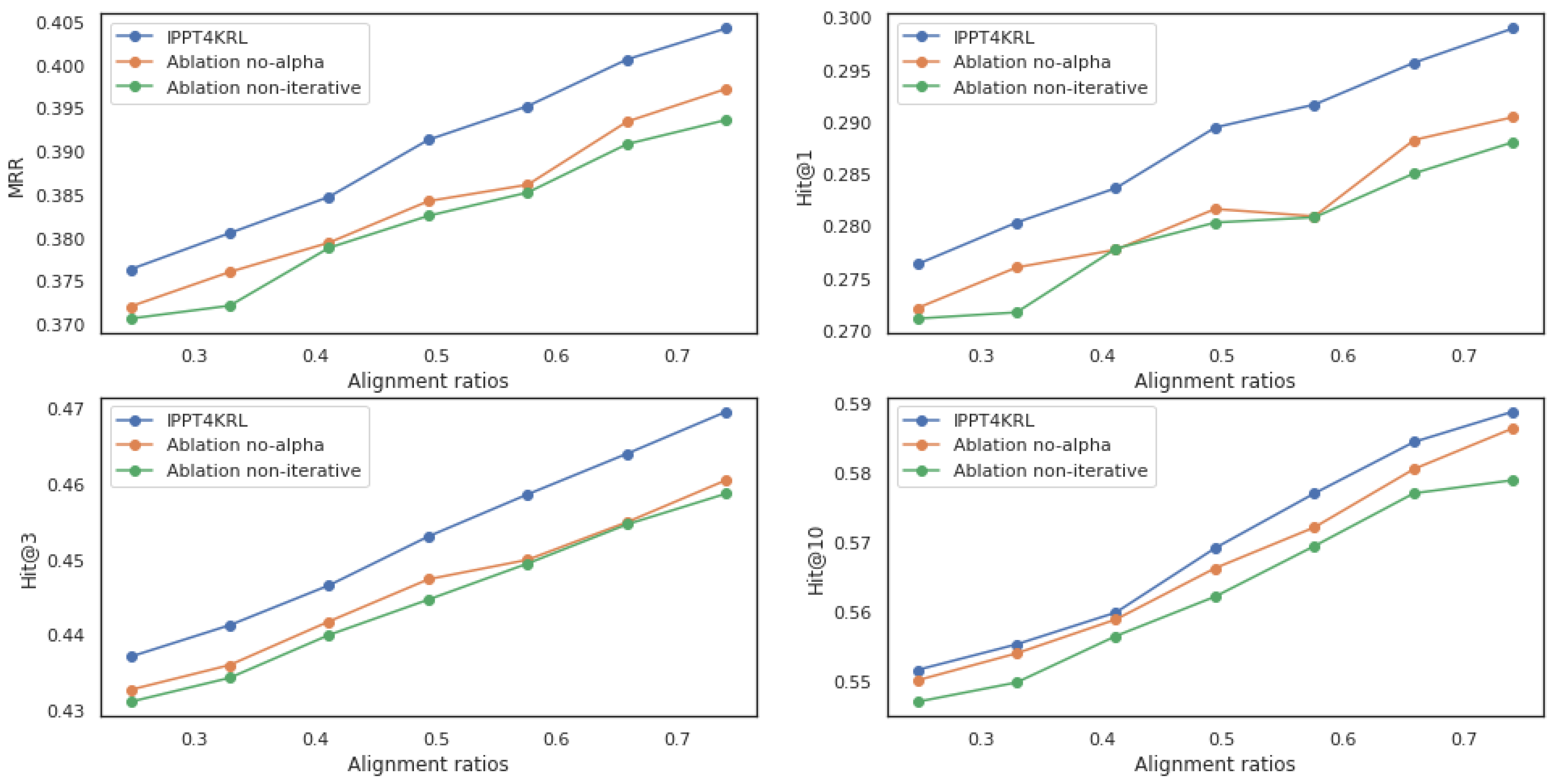
Hyper-parameters: For the fairness of comparison, we set the embedding dimension to be the same across all models for a dataset. The embedding size dimension n was set to be 100 for D-W-15K-LP, 200 for DBP-FB, and 200 for CN3l (EN-DE) and Wk3l-15k (EN-FR) (CN3l(EN-DE) and Wk3l-15k (EN-FR) were also reported in the experiments in the ATransN paper. Thus, we set the embedding dimension to be 200 for the ease of reproducing their best model performance on these two datasets). denotes the learning rate for the overall knowledge representation. The best learning rate for D-W-15K-LP (DBP-FB, WK3l-15K, CN3l) is . For D-W-15K-LP, the best-performing IPPT4KRL model employed hyper-parameters , , , and ; for DBP-FB, , , , and ; for WK3l-15K, , , , and ; and for CN3l, , , , and . In the iterative inclusion of the k-hop neighbours of , the triple-based margin loss would consider more entities as k increases. As a result, triple-based margin loss increases the most every time the neighbour size is increased. We tried to assign different for each hop, to account for the change in the trade-off between loss terms as k iteratively increases. However, in our experiment, assigning different for each hop only provided marginal gains in performance.
Evaluation: We used a link prediction task to evaluate and compare the performance of the trained embeddings. The Entity Ranking (ER) protocol was employed for this evaluation: for a test triple , the ER protocol uses the embedding model to rank all possible answers to link prediction queries and and employs the rank of the correct answer for embedding evaluation. The standard filtered Hit@m(m = 1, 3, 10), Mean Ranks (MRs), and Mean Reciprocal Rank (MRR) metrics are reported in the result tables. The reported results were averaged across multiple runs of the fine-tuned models. (Although we used the two datasets from the ATransN paper in our evaluation, we do not report the results from the ATransN paper. This is because we found a small issue in the open-sourced ATransN code for computing the filtered metrics on the link prediction tasks. Therefore, we followed the hyper-parameters provided in the ATransN paper to generate the embeddings and evaluate them against the corrected, filtered metrics.) The best entries for each metric are highlighted in bold in each of the table.
4.2. Results and Analysis
From the result
Table 2 and
Table 3, we can observe that our IPPT4KRL model achieved comparable and even superior results against the best performers in each dataset.
Table 2 shows the experimental results on the generated D-W-15K-LP and DBP-FB. On these two monolingual datasets with no relation alignment available, we extended the original KD-MKB and created KD-MKB*, in which we share the relation knowledge between embedding models of each KG. A more detailed description of the modification can be found in the
Appendix B. On D-W-15K-LP, IPPT4KRL outperformed all the baseline models across all metrics. Compared to other multi-KG KRL methods, IPPT4KRL achieved the best performances on the MRR, Hit@1, and Hit@3 while producing a very similar performance against the top performer KD-MKB* on the MR and Hit@10. An important aspect is that IPPT4KRL achieved this comparable performance while requiring less than
of the training time of KD-MKB*. Concretely, one complete run of the training process for KD-MKB* on this dataset took 12 hrs on our workstation, while the training for IPPT4KRL only took 1.5 hr, including the pre-training of individual embeddings on
. D-W-15K-LP is a scenario that was deliberately generated to mimic real-life mono-lingual multi-KG learning. The significant margin that IPPT4KRL produced against the baselines indicated that our model could facilitate positive knowledge transfer even when the seed alignment ratio is low. At the same time, ATransN’s performance on this dataset was unsatisfactory. One possible reason is that ATransN usually performed well when the teacher KG in their model holds richer information than their student KG, which is not the case for our generated dataset D-W-15K-LP. On DBP-FB, we observed similar performance trends: IPPT4KRL achieved the best performance on the MRR, MR Hit@1, and Hit@3 metrics, while having comparable performance against the top performers on Hit@10. An interesting observation is that, although the alignment ratio was larger in DBP-FB than in D-W-15K-LP, the margins gained by the multi-KG KRL methods were smaller and inconsistent. This indicates that is is “harder” to transfer knowledge between KGs for the dataset DBP-FB. We believe the main driver behind this observation is that DBpedia and Freebase, two KGs, are constructed by two isolated parties, while for D-W-15K-LP, DBpedia and Wikidata practically come from very similar sources. This observation provided a meaningful indicator for our plans for the next steps, which we will discuss more in
Section 6.
Table 3 shows the experiment results on CN3l (EN-DE) and WK3l-15K (EN-FR). On CN3l (EN-DE), we can observe that IPPT4KRL outperformed the rest of the models on the MRR, MR, and Hit@1 metrics, while also achieving similar performance on the other metrics compared to the top performers. CN3l (EN-DE) has a relatively large alignment ratio compared to the other three datasets, which usually implies a smaller difference between KGs. IPPT4KRL was also able to match and even outperform the top performers in this case as well. WK3l-15K is one of the harder datasets for multi-KG KRL in the work of Wang et al. [
15], mainly because of (1) the lack of alignments and (2) the relatively dense and rich information already existing in the French KG. From
Table 3, we can still observe a similar trend that IPPT4KRL achieved a similar performance level compared to other multi-KG KRL methods. However, on WK3l-15K (EN-FR), the margins between all multi-KG KRL methods and the baselines were minimal, which is fairly consistent with the findings in the ATransN paper. The fact that WK3l-15K contains many more relations than the other two datasets might also contribute to this result.
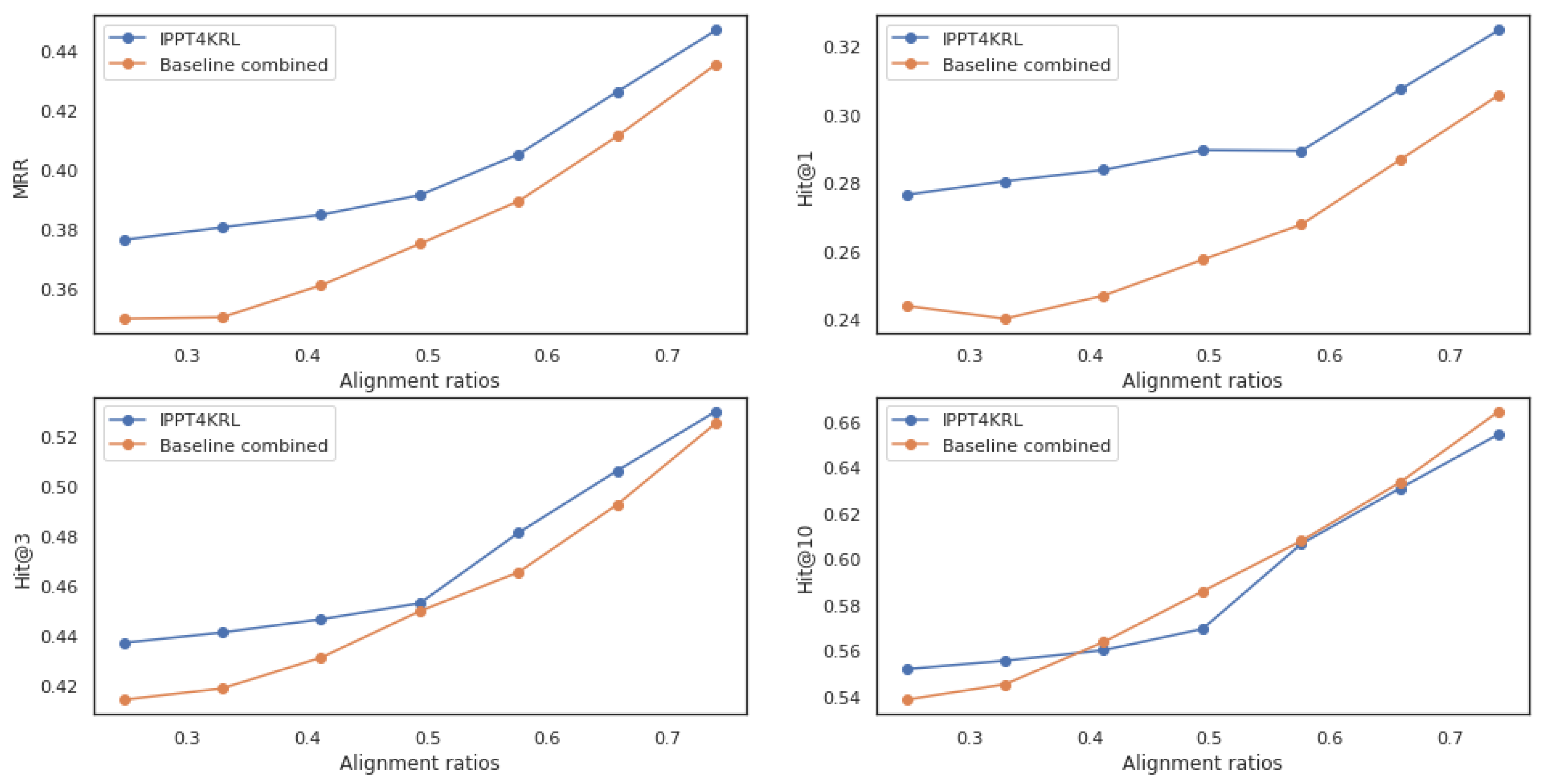
An interesting observation from the performance of the baseline Connected is that it outperformed the baseline Individual by a significant margin on the CN3l dataset, but the same trend was not observed on the generated D-W-15K-LP. Compared to the CN3l dataset, D-W-15K-LP has a relatively smaller alignment ratio and several aligned entities not visible to the models during training. We view the difference in the baseline performances as evidence showing that the D-W-15K-LP dataset provides a more “life-like” scenario and is better suited for benchmarking multi-KG representation learning.
To test the generality of IPPT4KRL, we also experimented with our method on the D-W-15K-LP dataset with the roles of
and
flipped. From
Table 4, we can see that after flipping the KGs, our method still consistently outperformed all of the baselines, showing consistent success in facilitating positive knowledge transfer across KGs in both directions.