InvMap and Witness Simplicial Variational Auto-Encoders
Abstract
:1. Introduction
2. Notions of Computational Topology
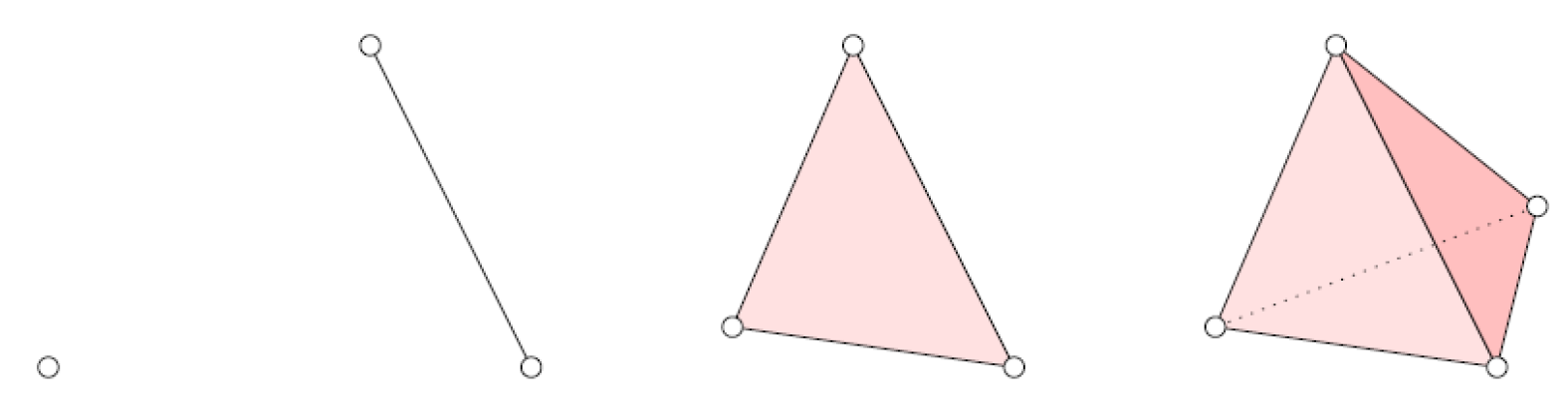
2.1. Simplicial Complexes
- Each face of any simplex of K is also a simplex of K.
- The intersection of any two simplices of K is either empty or a face of both simplices.
2.2. Betti Numbers
3. Related Work
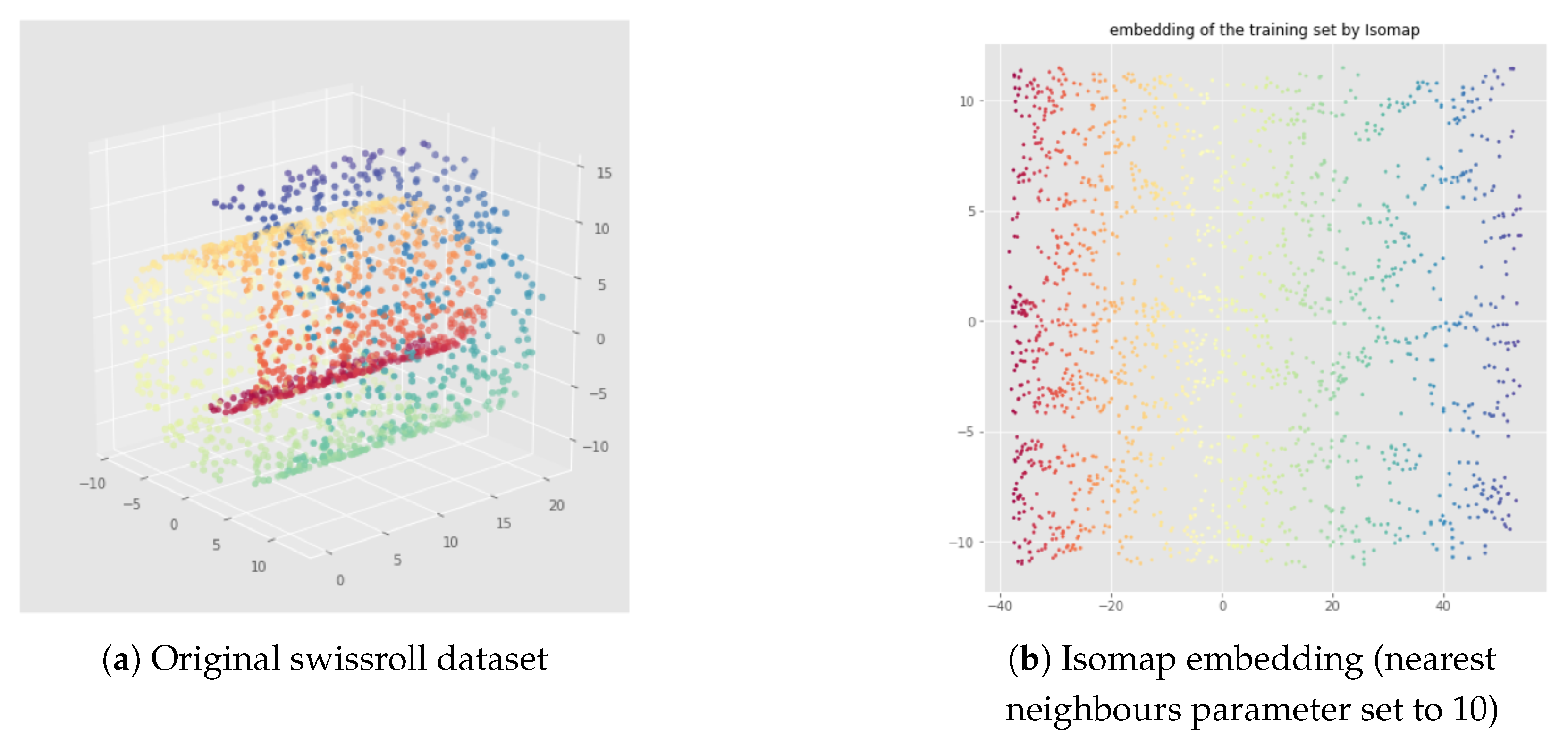
3.1. Non-Linear Dimensionality Reduction
3.2. Variational Auto-Encoder
3.3. Topology and Auto-Encoders
4. Implementation Details
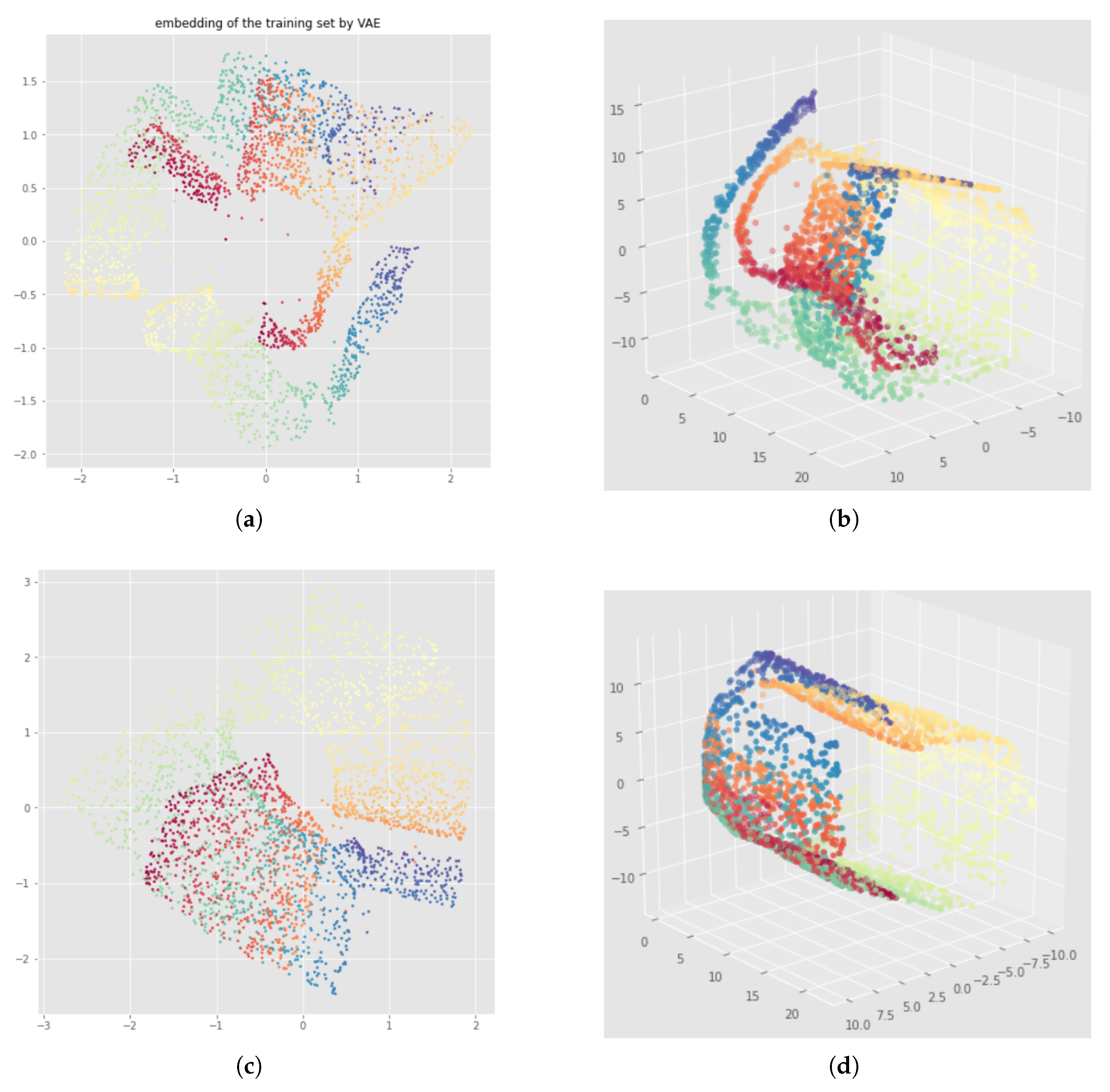
5. Problem Formulation
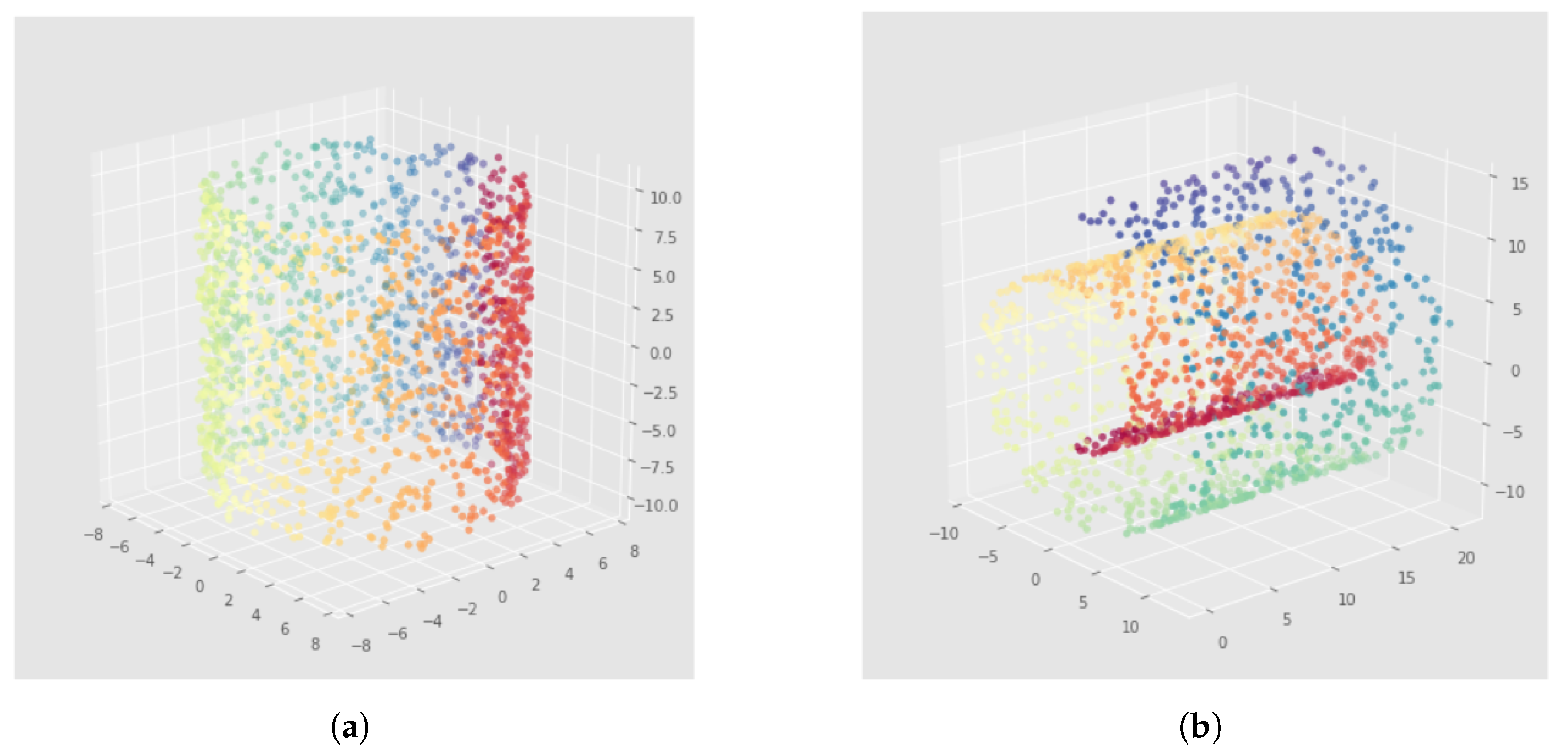
5.1. Datasets
5.2. Illustration of the Problem
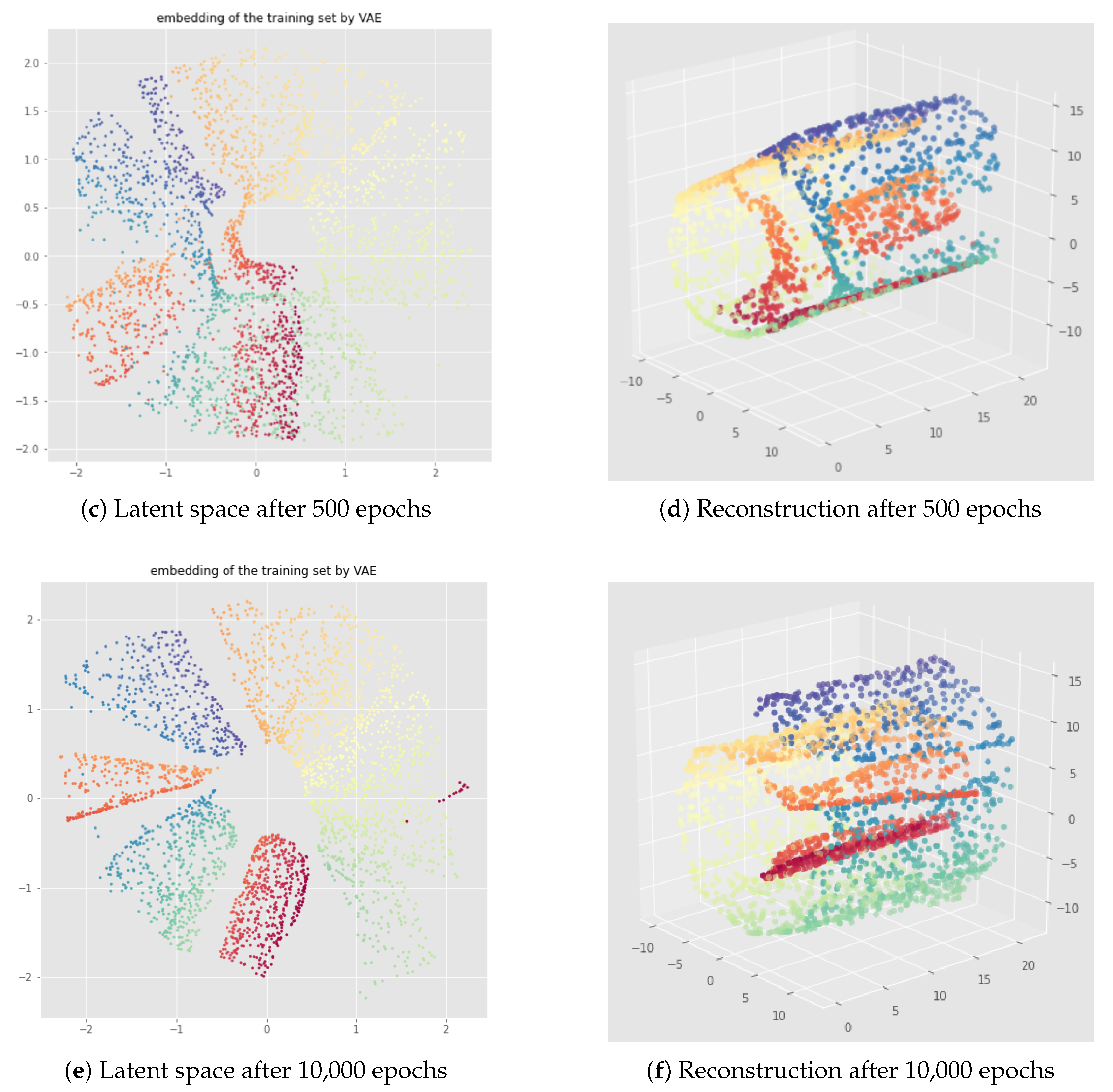
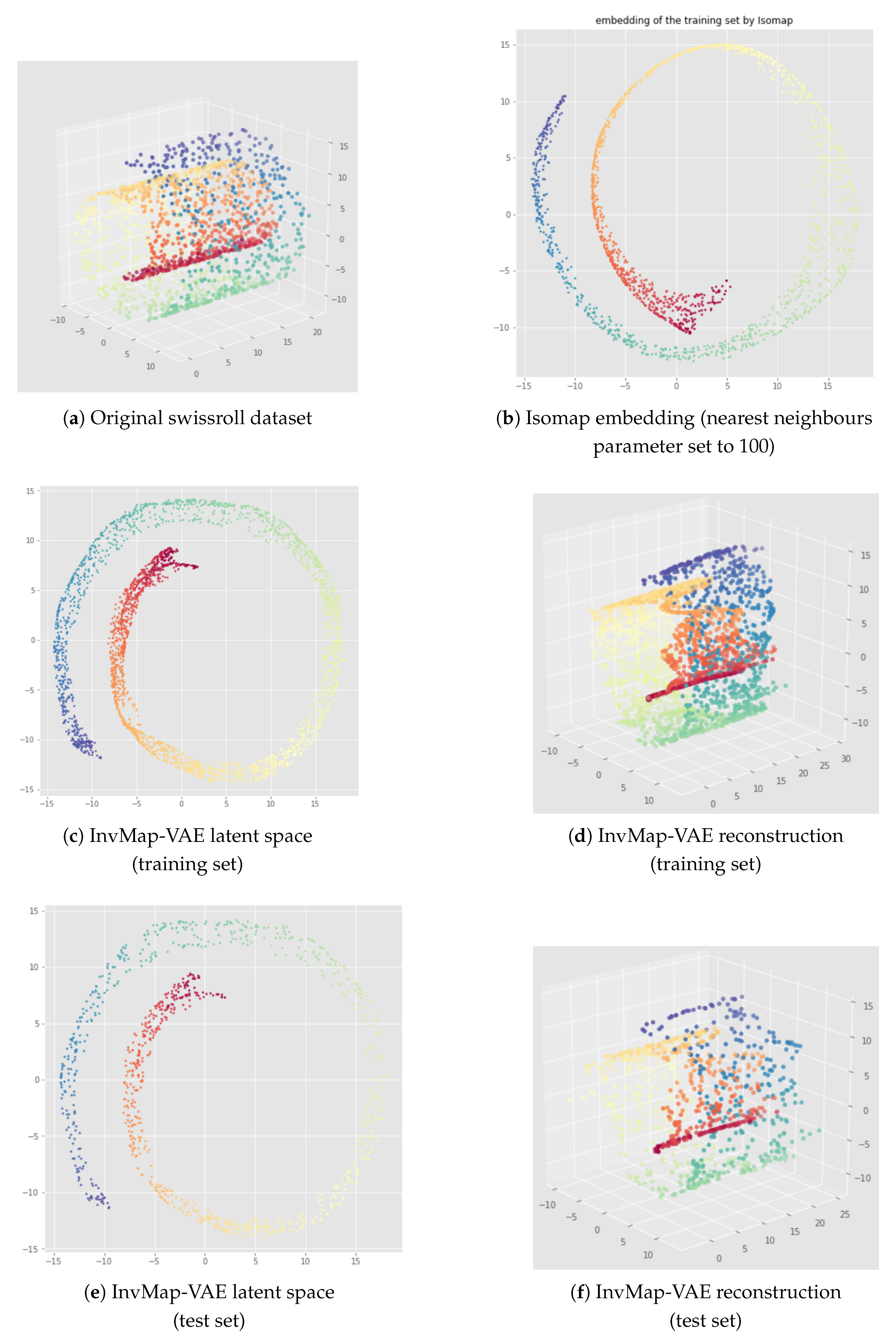
6. InvMap VAE
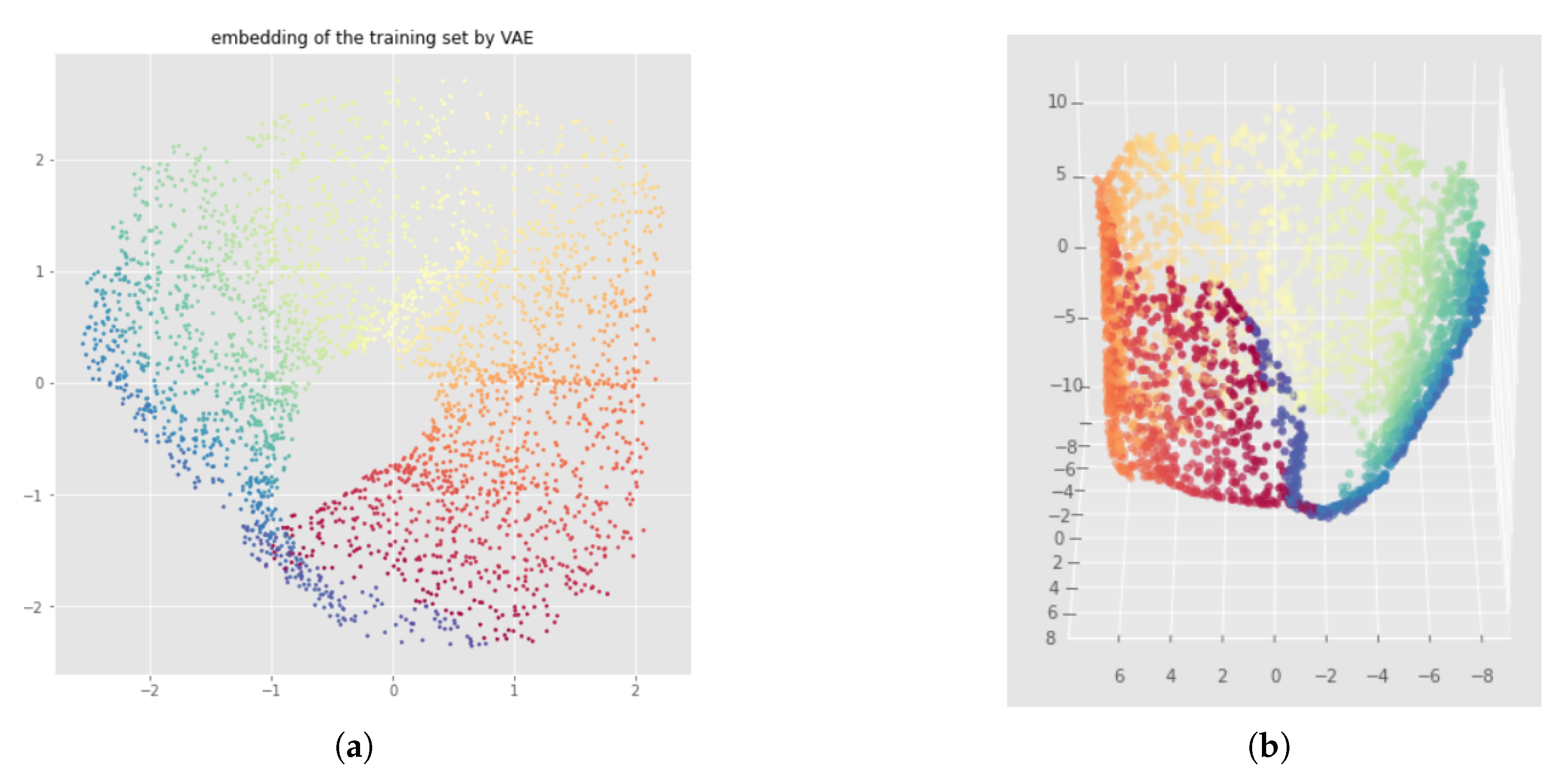
6.1. Method
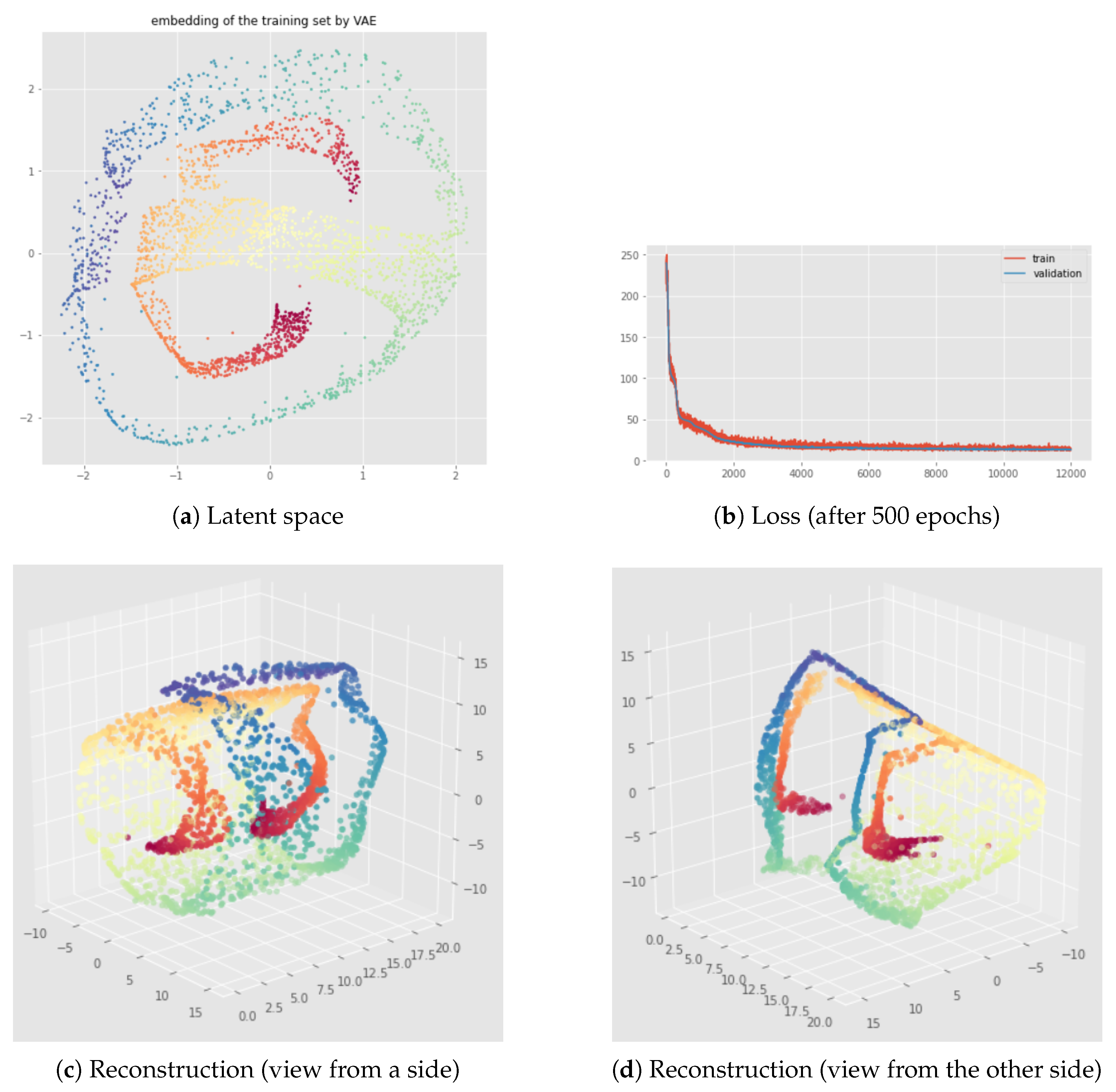
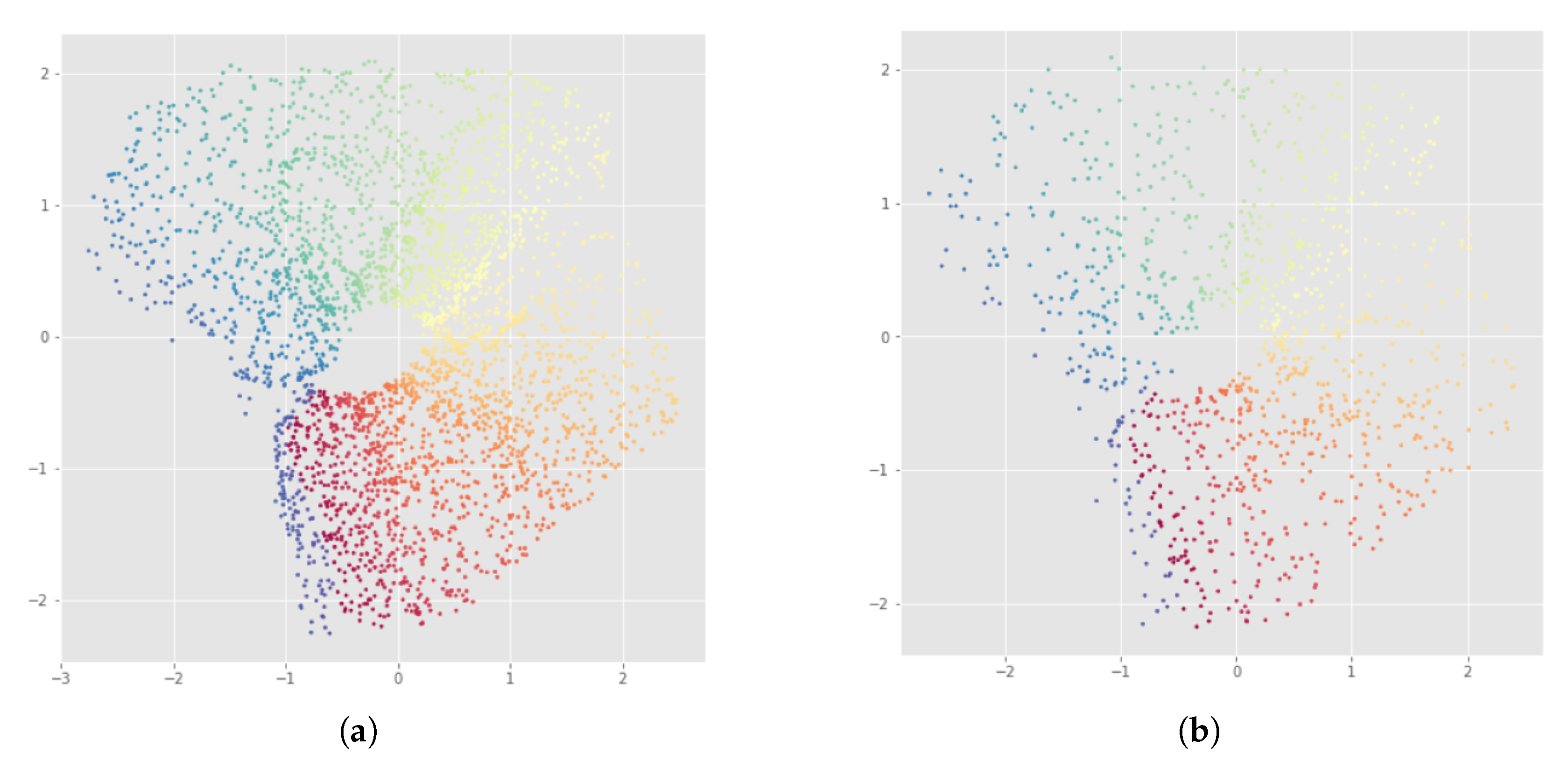
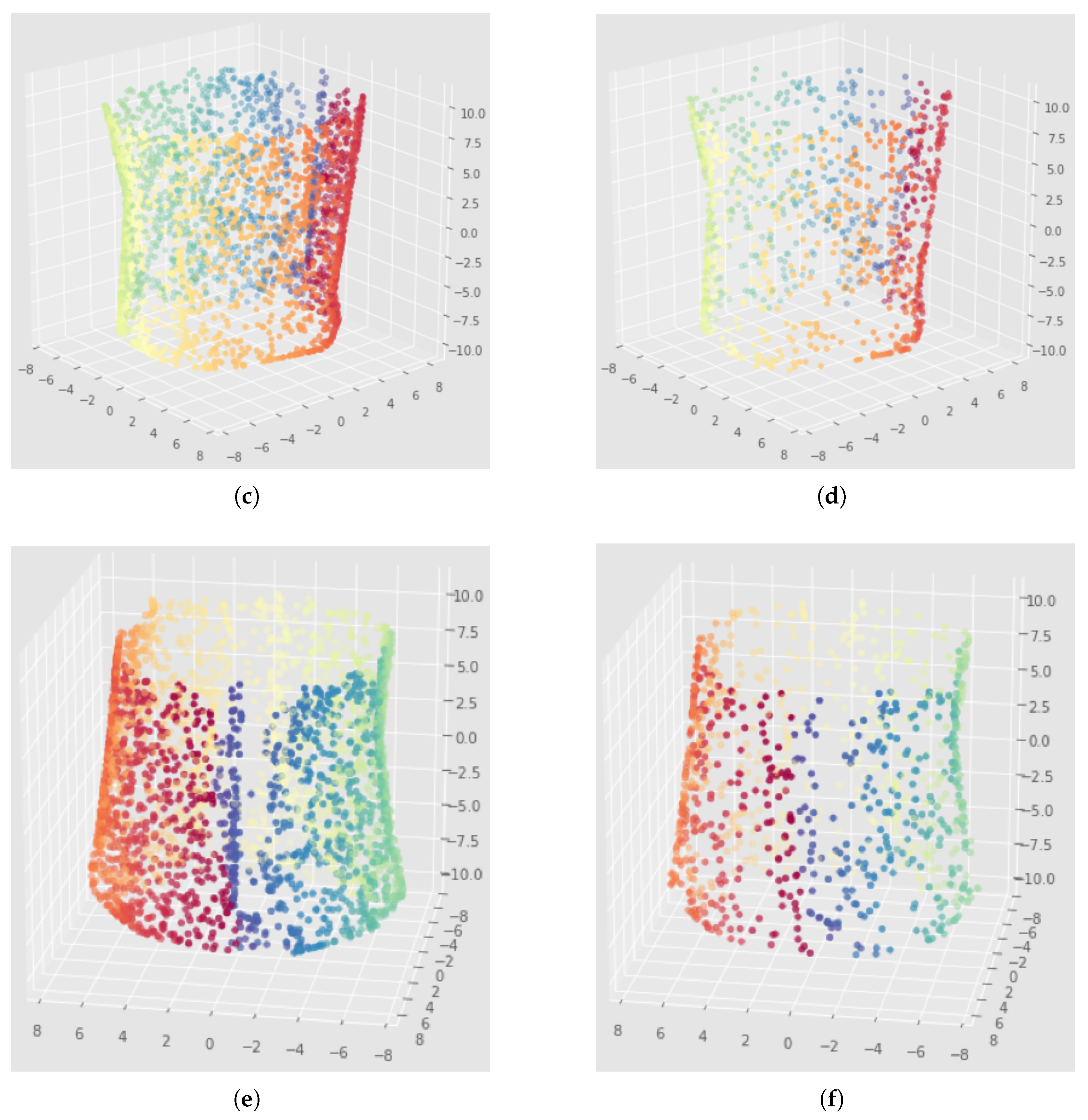
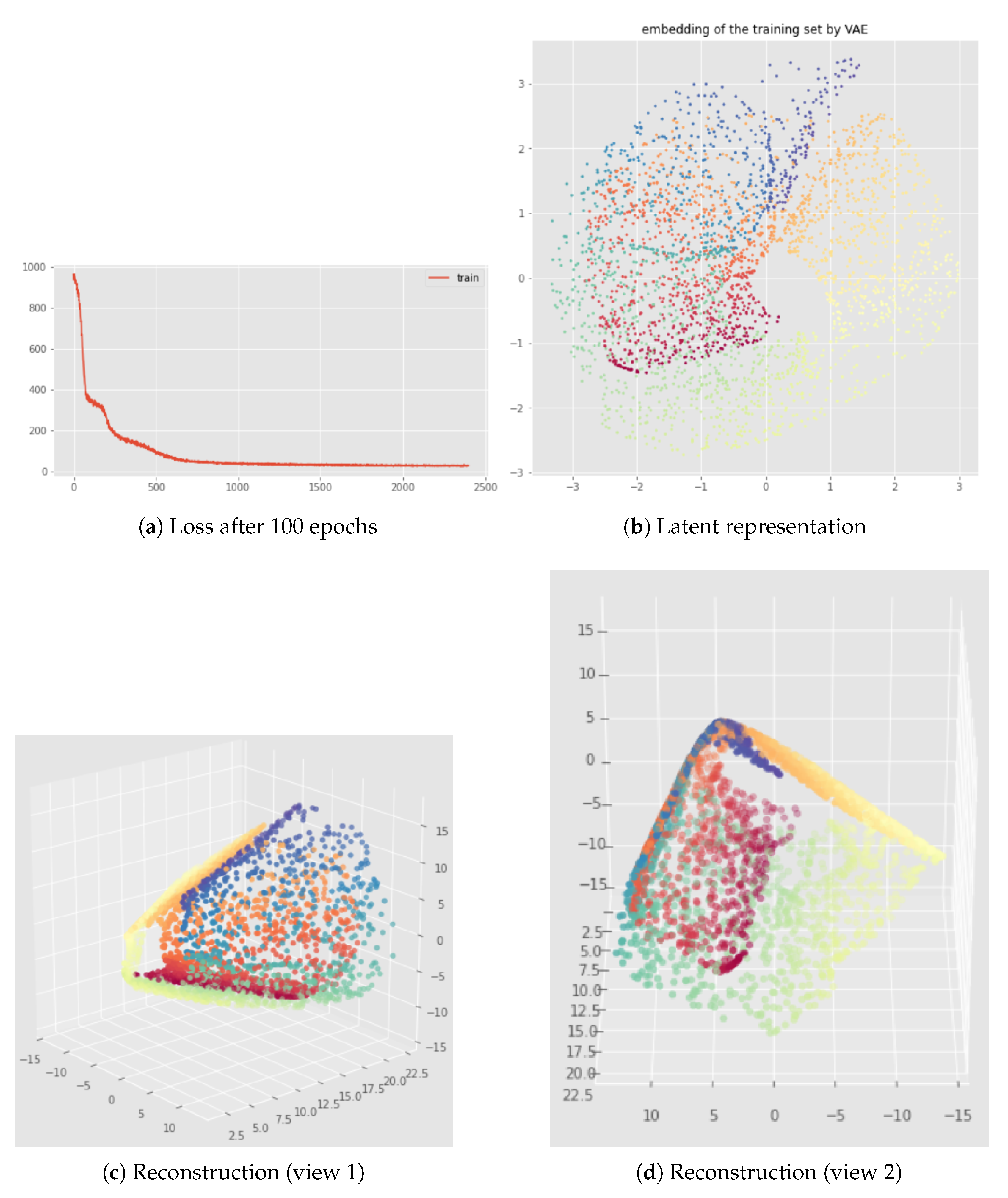
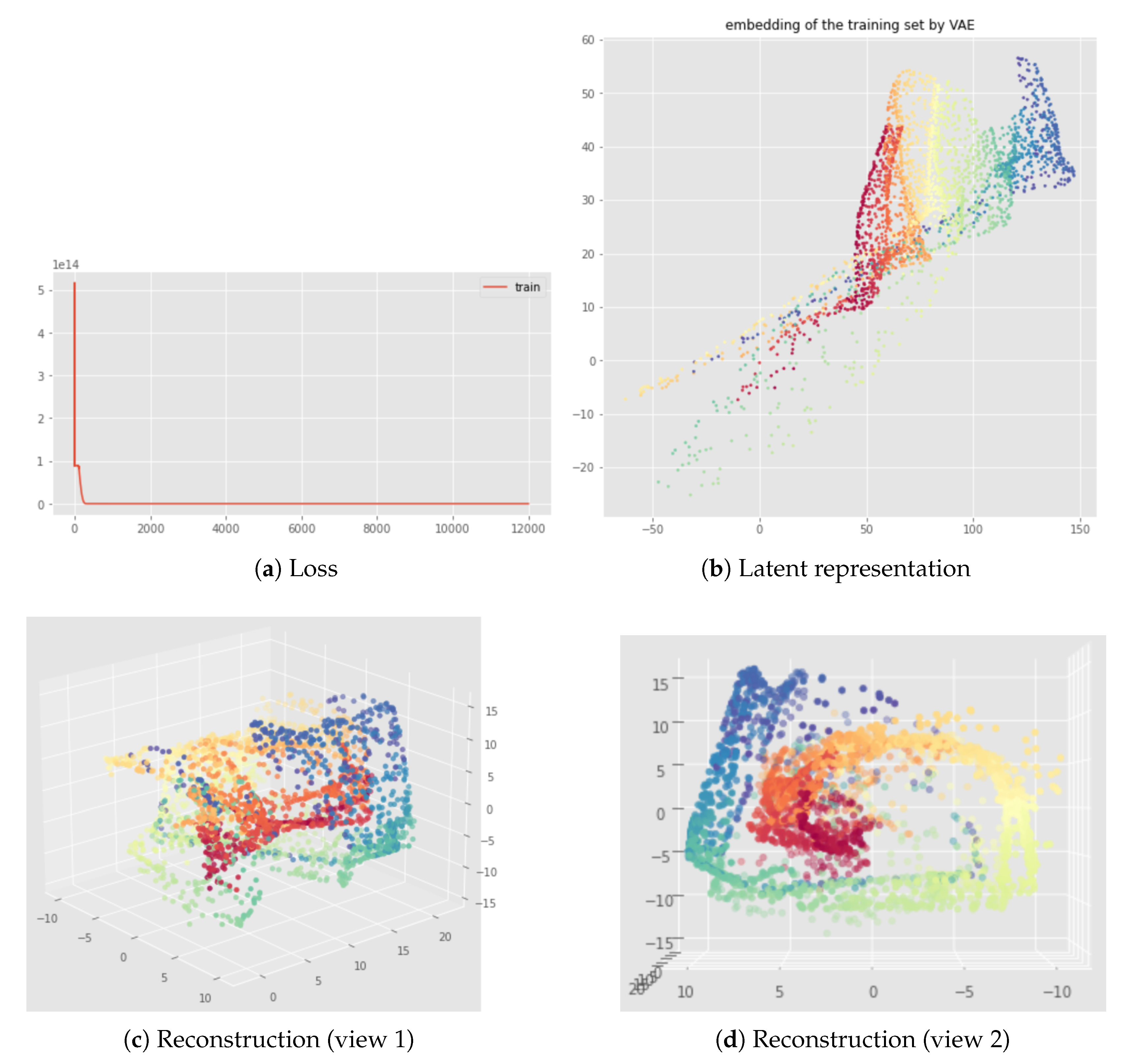
6.2. Results
7. Witness Simplicial VAE
7.1. Method
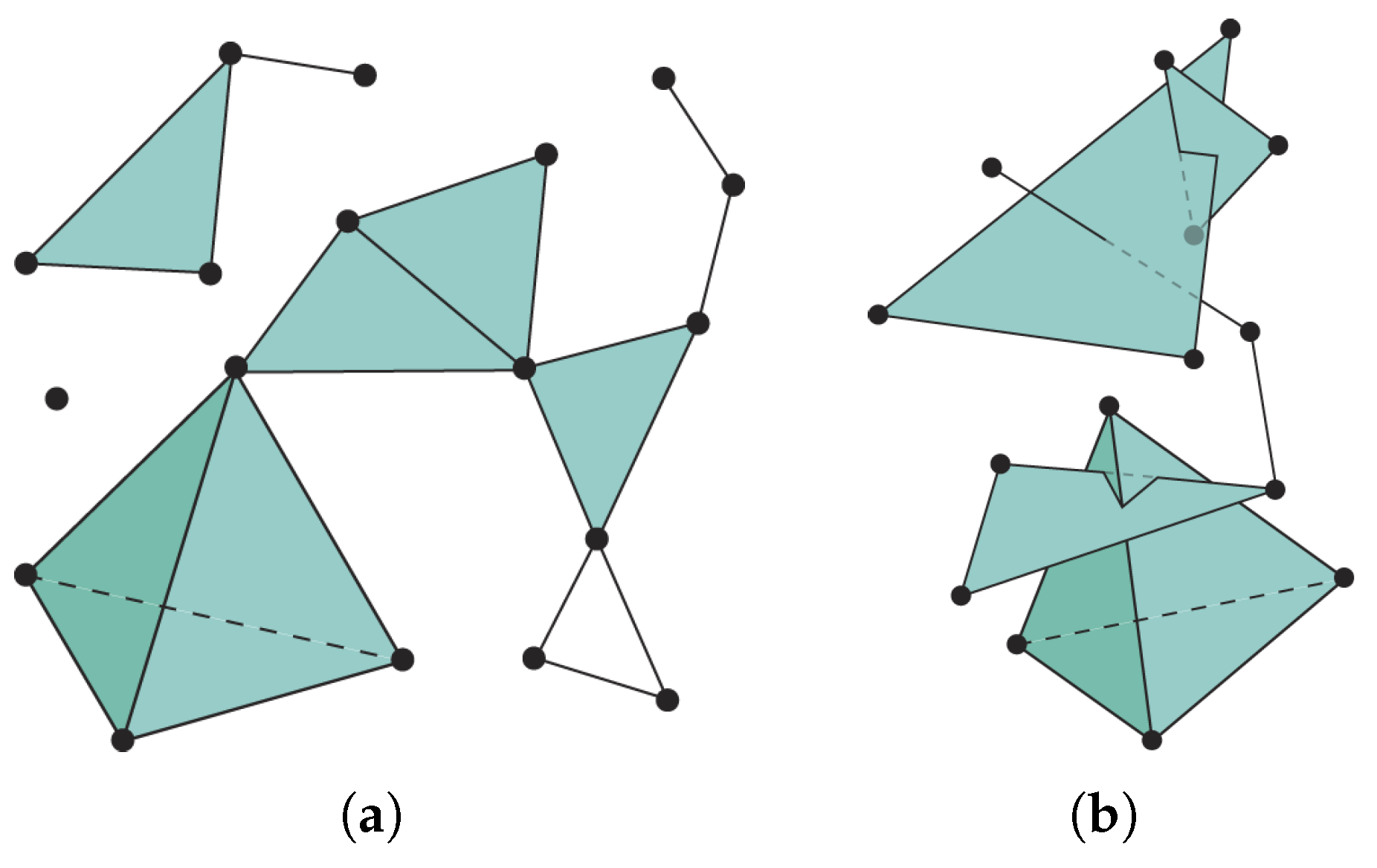
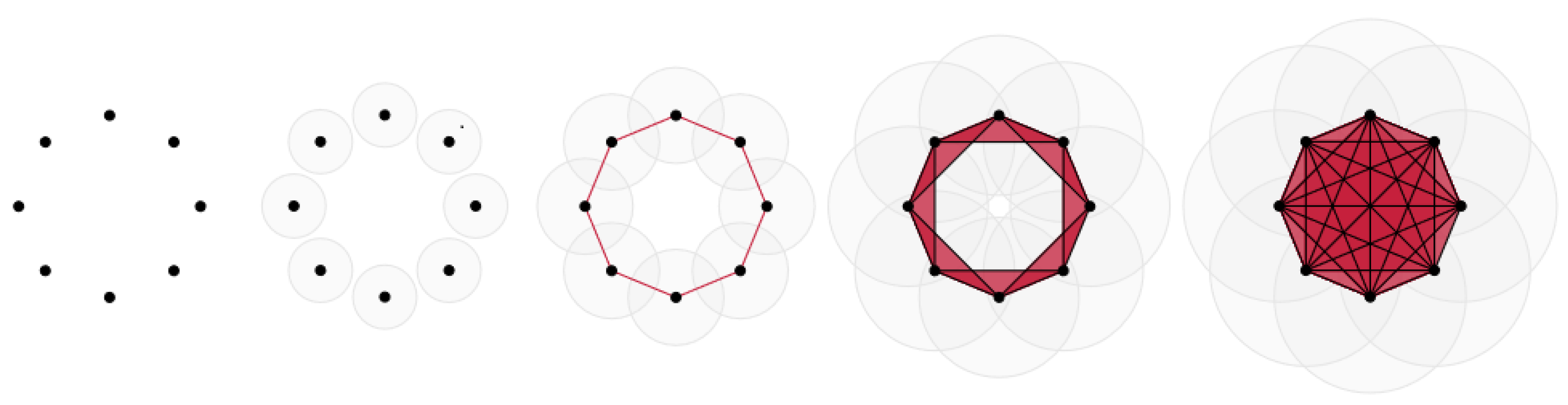
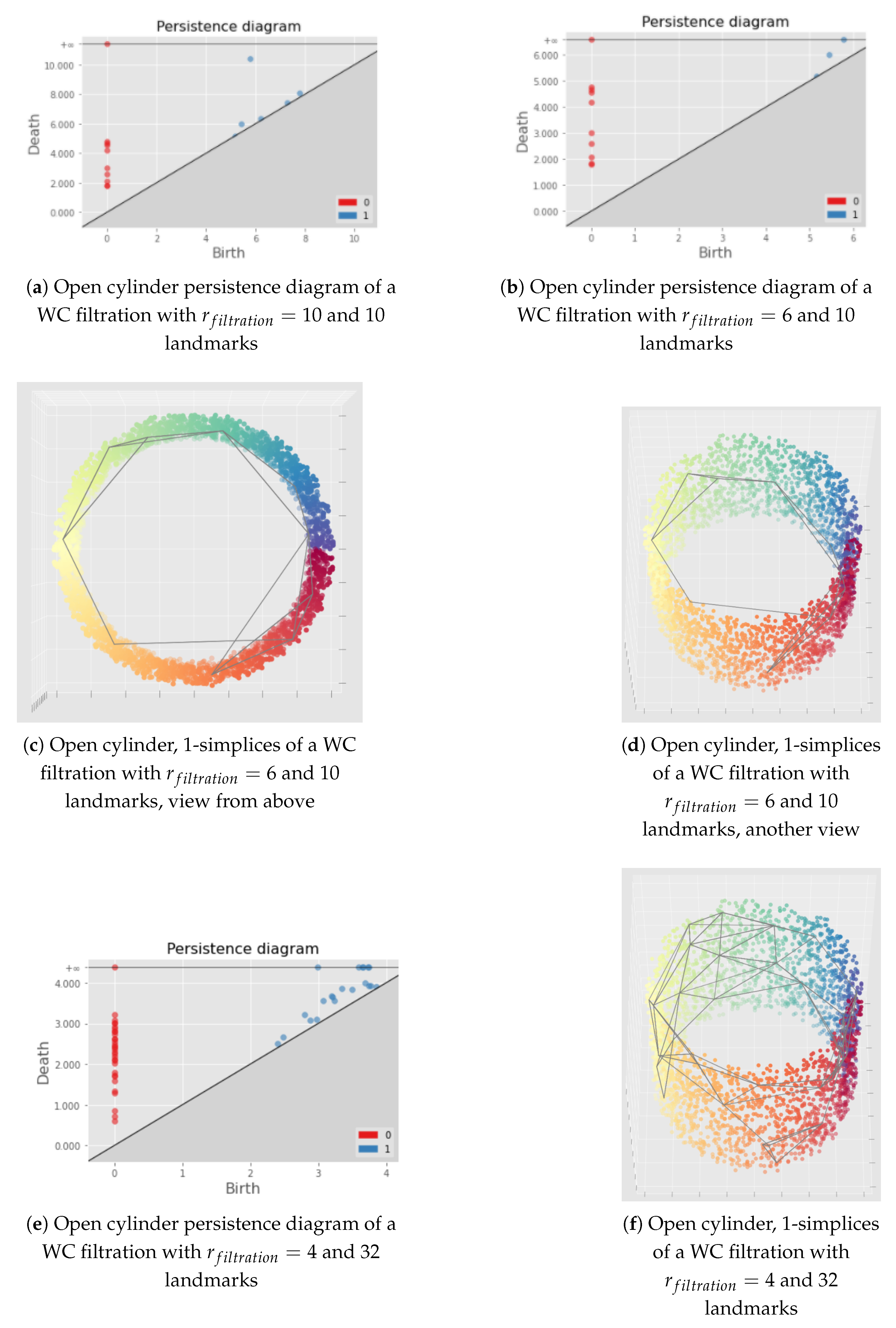
7.1.1. Witness Complex Construction
7.1.2. Witness Complex Simplicial Regularization
- It does not depend on any embedding whereas in [28] the author was relying on a UMAP embedding for his simplicial regularization of the decoder.
- We use only one witness simplical complex built from the input data whereas the author of [28] was using one fuzzy simplicial complex built from the input data and a second one built from the UMAP embedding and both were built via the fuzzy simplicial set function provided with UMAP (keeping only simplices with highest probabilities).
- the simplicial regularization term for the encoder.
- the simplicial regularization term for the decoder.
- e and d, respectively, the (probabilistic) encoder and decoder.
- K a (witness) simplicial complex built from the input space.
- a simplex belonging to the simplicial complex K.
- the vertex number j of the -simplex which has exactly vertices. is, thus, a data point in the input space X.
- the Mean Square Error between a and b.
- the expectation for the following a symmetric Dirichlet distribution with parameters and . When , which is what we used in practice, the symmetric Dirichlet distribution is equivalent to a uniform distribution over the -simplex , and as tends towards 0, the distribution becomes more concentrated on the vertices.
7.1.3. Witness Simplicial VAE
- Perform a witness complex filtration of the input data to obtain a persistence diagram (or a barcode).
- Build a witness complex given the persistence diagram (or the barcode) of this filtration, and potentially any additional information on the Betti numbers which should be preserved according to the problem (number of connected components, 1-dimensional holes…).
- Train the model using this witness complex to compute the loss of Equation (5).
7.1.4. Isolandmarks Witness Simplicial VAE
- the loss of the Witness Simplicial VAE.
- l the number of landmarks.
- the Frobenius norm.
- the approximate geodesic distance matrix of the landmarks points in the input space computed once before learning.
- D the Euclidean distance matrix of the encodings of the landmarks points computed at each batch.
- K the Isomap kernel defined as with I the identity matrix and A the matrix composed only by ones.
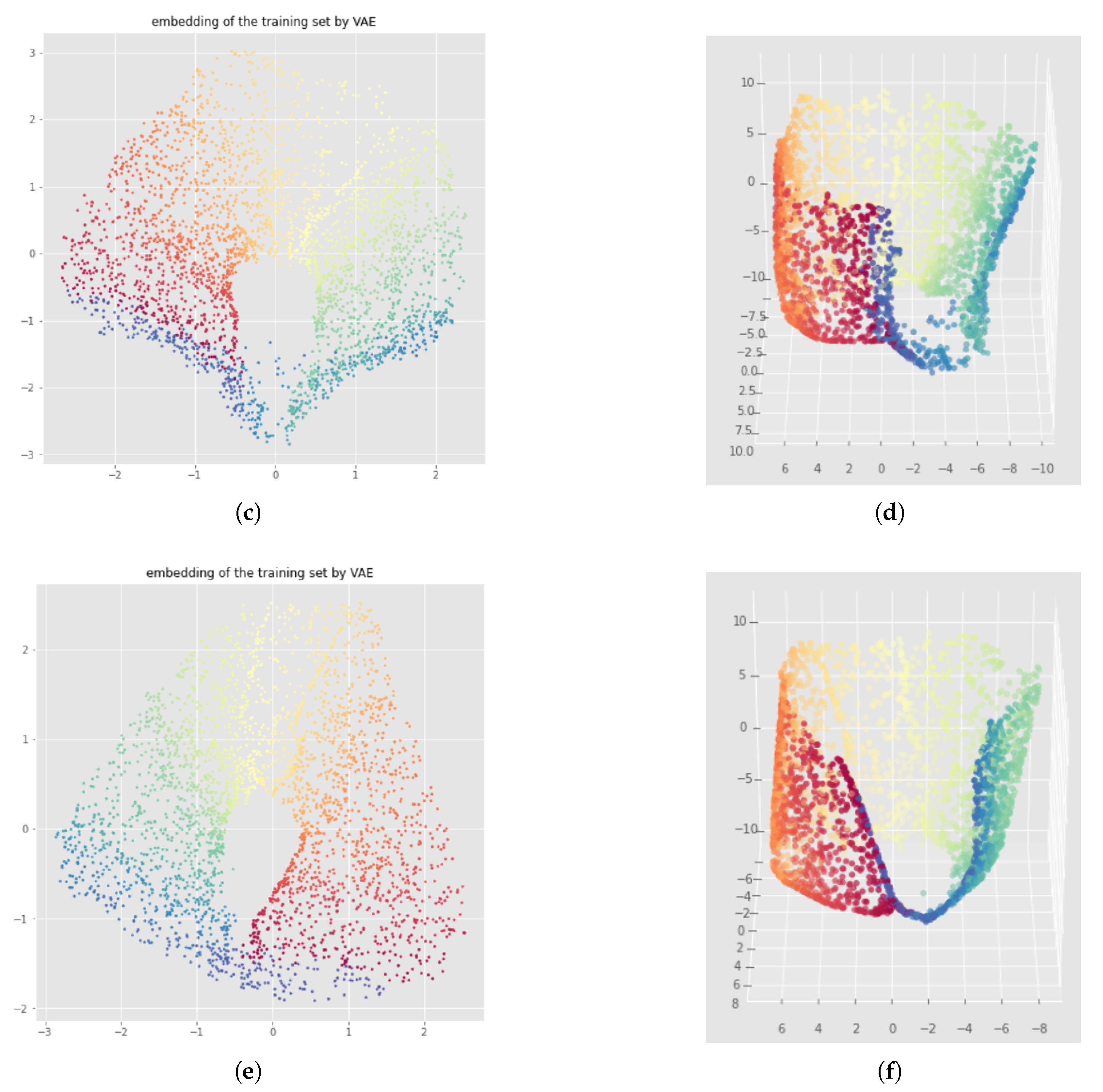
7.2. Results
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Auto-Encoder |
| i.i.d. | independent and identically distributed |
| ELBO | Evidence lower bound |
| Isomap | Isometric Mapping |
| k-nn | k-nearest neighbours |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MSE | Mean Square Error |
| s.t. | such that |
| TDA | Topological Data Analysis |
| UMAP | Uniform Manifold Approximation and Projection |
| VAE | Variational Auto-Encoder |
| WC | Witness complex |
Appendix A. Variational Auto-Encoder Derivations
Appendix A.1. Derivation of the Marginal Log-Likelihood
Appendix A.2. Derivation of the ELBO
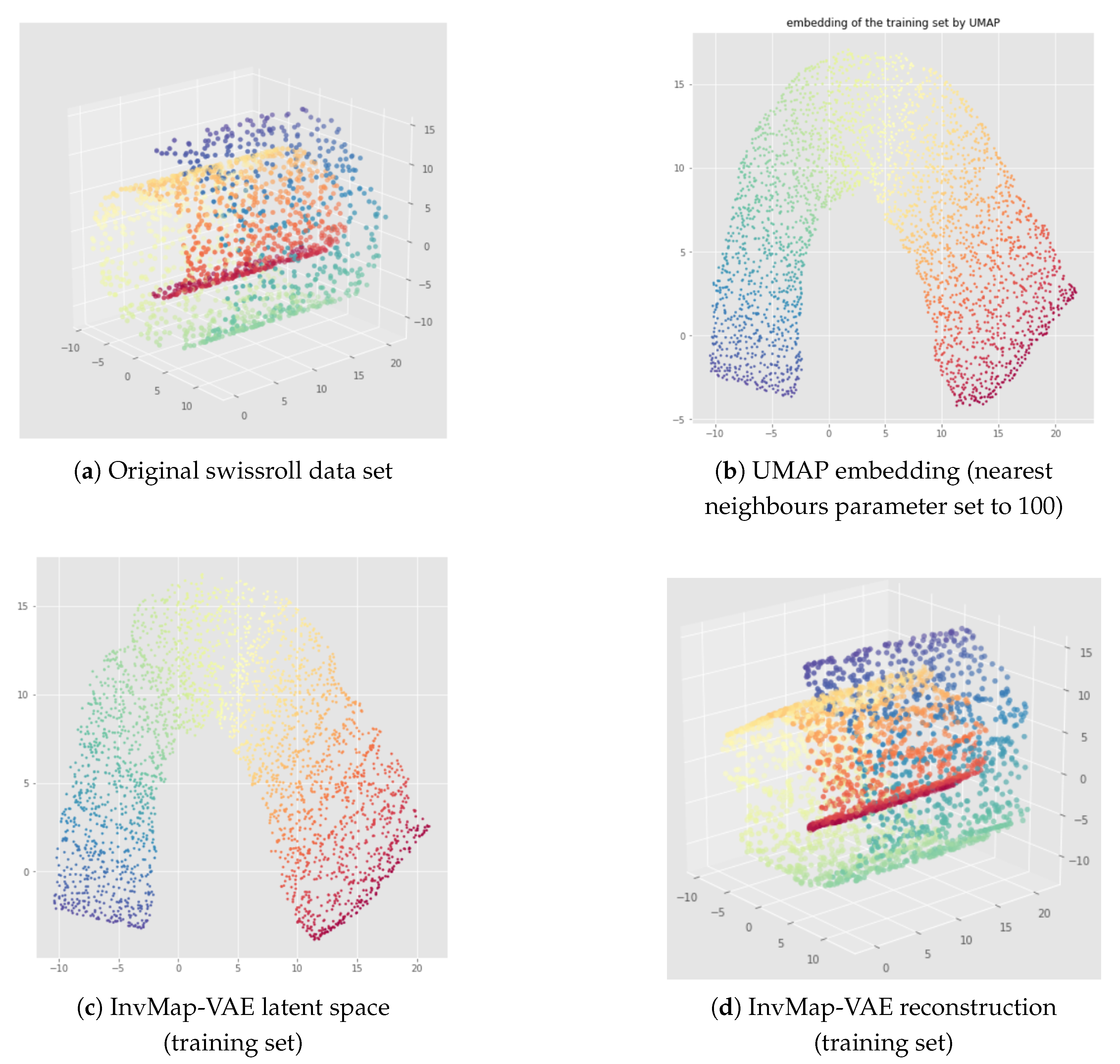
Appendix B. UMAP-Based InvMap-VAE Results

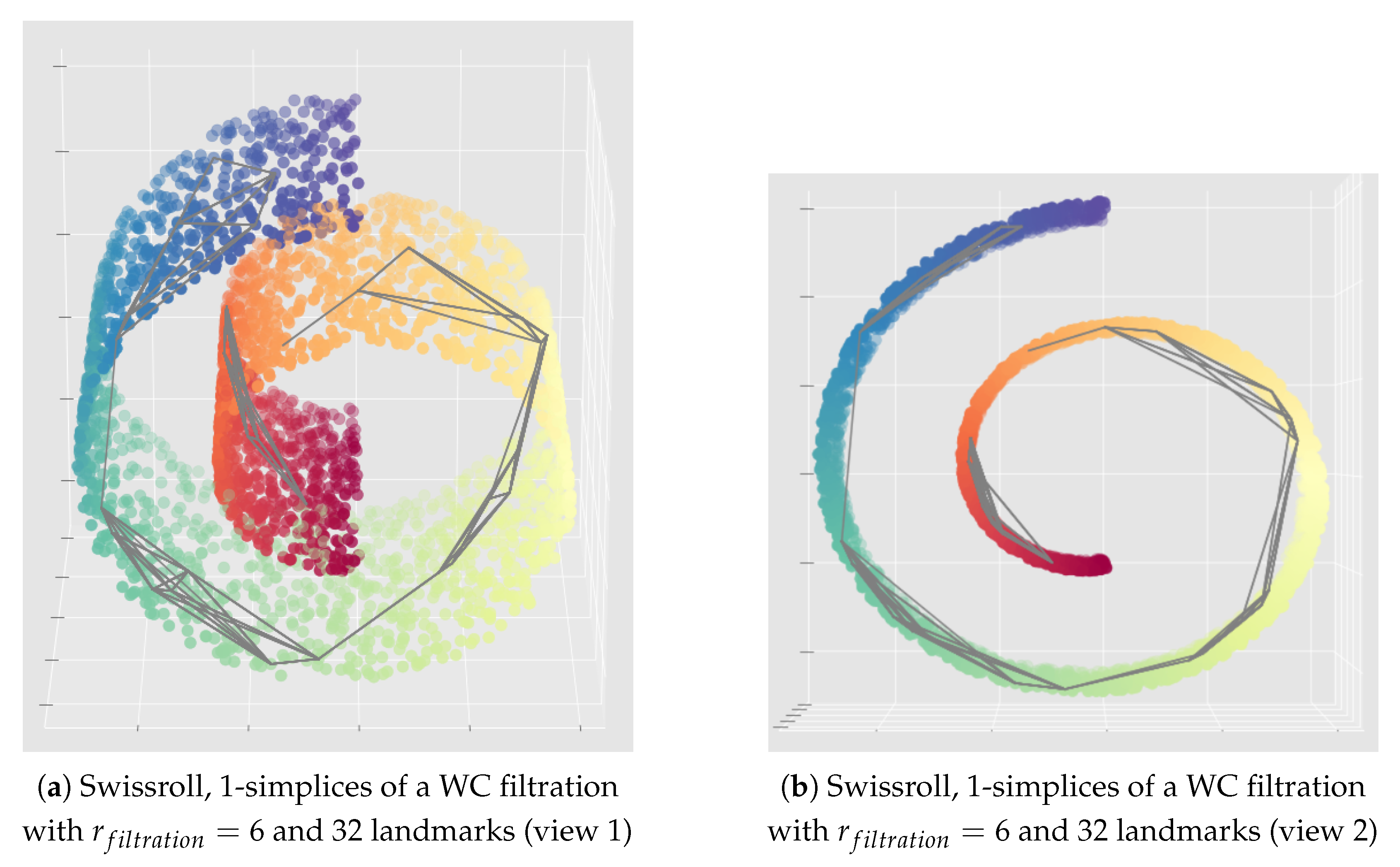
Appendix C. Illustration of the Importance of the Choice of the Filtration Radius Hyperparameter for the Witness Complex Construction

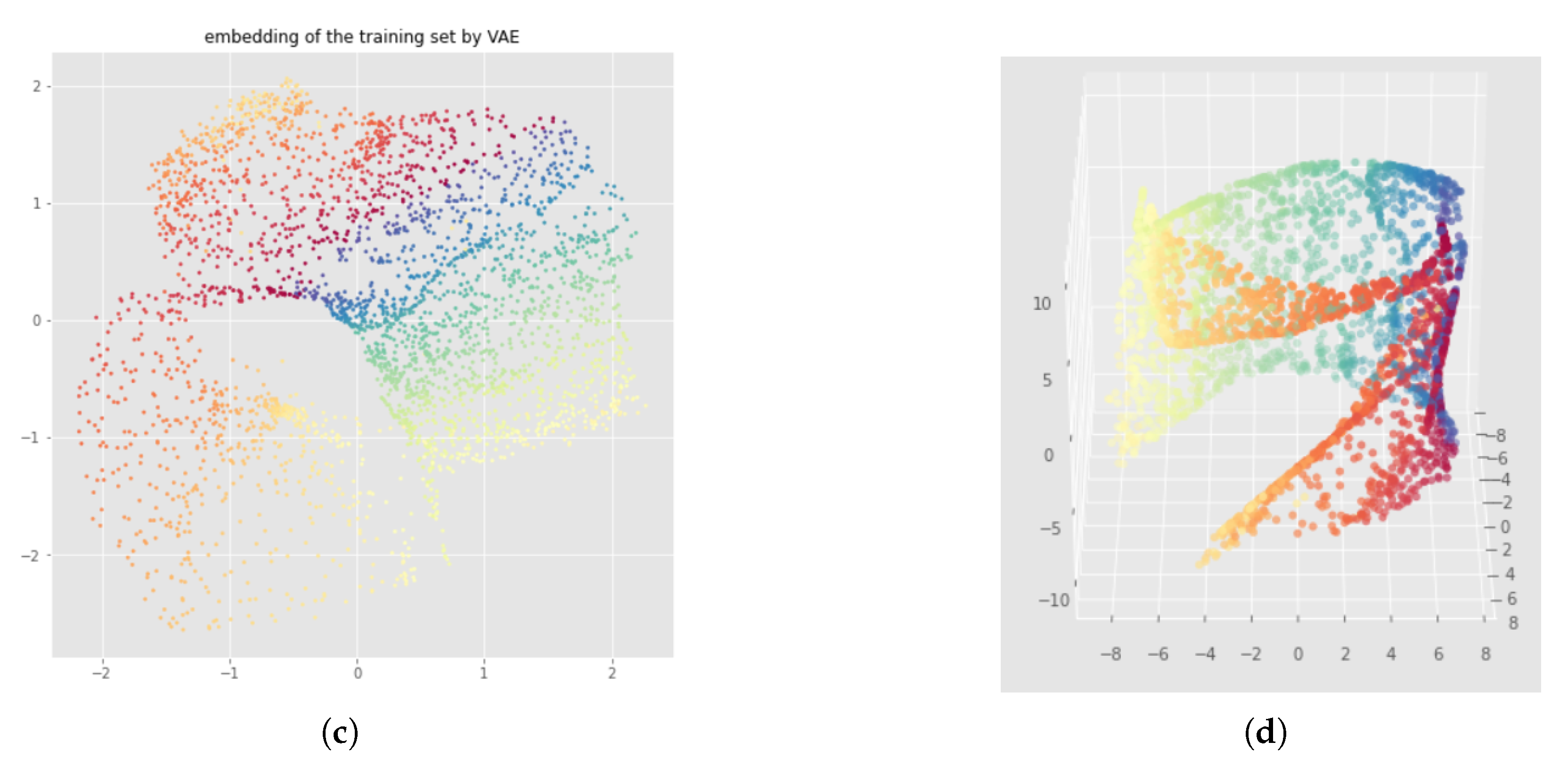
Appendix D. Bad Neural Network Weights Initialization with Witness Simplicial VAE

References
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27 (NIPS 2014); Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the ICLR, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Xing, E.P., Jebara, T., Eds.; PMLR: Bejing, China, 2014; Volume 32, pp. 1278–1286. [Google Scholar]
- Medbouhi, A.A. Towards Topology-Aware Variational Auto-Encoders: From InvMap-VAE to Witness Simplicial VAE. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]
- Hensel, F.; Moor, M.; Rieck, B. A Survey of Topological Machine Learning Methods. Front. Artif. Intell. 2021, 4, 52. [Google Scholar] [CrossRef] [PubMed]
- Ferri, M. Why Topology for Machine Learning and Knowledge Extraction? Mach. Learn. Knowl. Extr. 2019, 1, 115–120. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Computational Topology-an Introduction; American Mathematical Society: Providence, RI, USA, 2010; pp. I–XII, 1–241. [Google Scholar]
- Wikipedia, the Free Encyclopedia. Simplicial Complex Example. 2009. Available online: https://en.wikipedia.org/wiki/File:Simplicial_complex_example.svg (accessed on 18 March 2021).
- Wikipedia, the Free Encyclopedia. Simplicial Complex Nonexample. 2007. Available online: https://commons.wikimedia.org/wiki/File:Simplicial_complex_nonexample.png (accessed on 18 March 2021).
- Wilkins, D.R. Algebraic Topology, Course 421; Trinity College: Dublin, Ireland, 2008. [Google Scholar]
- de Silva, V.; Carlsson, G. Topological estimation using witness complexes. IEEE Symp. Point-Based Graph. 2004, 4, 157–166. [Google Scholar]
- Rieck, B. Topological Data Analysis for Machine Learning, Lectures; European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases. 2020. Available online: https://bastian.rieck.me/outreach/ecml_pkdd_2020/ (accessed on 12 November 2020).
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Relations Between Two Sets of Variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Lee, J.A.; Verleysen, M. Nonlinear Dimensionality Reduction, 1st ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2007. [Google Scholar]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319. [Google Scholar] [CrossRef] [PubMed]
- Kruskal, J. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Kruskal, J. Nonmetric multidimensional scaling: A numerical method. Psychometrika 1964, 29, 115–129. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P. Modern Multidimensional Scaling: Theory and Applications; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hinton, G.E.; Roweis, S. Stochastic Neighbor Embedding. In Advances in Neural Information Processing Systems 15 (NIPS 2002); Becker, S., Thrun, S., Obermayer, K., Eds.; MIT Press: Cambridge, MA, USA, 2002; Volume 15. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Kingma, D.P.; Welling, M. An Introduction to Variational Autoencoders. Found. Trends Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Gabrielsson, R.B.; Nelson, B.J.; Dwaraknath, A.; Skraba, P.; Guibas, L.J.; Carlsson, G.E. A Topology Layer for Machine Learning. arXiv 2019, arXiv:1905.12200. [Google Scholar]
- Polianskii, V. An Investigation of Neural Network Structure with Topological Data Analysis. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Moor, M.; Horn, M.; Rieck, B.; Borgwardt, K.M. Topological Autoencoders. arXiv 2019, arXiv:1906.00722. [Google Scholar]
- Hofer, C.D.; Kwitt, R.; Dixit, M.; Niethammer, M. Connectivity-Optimized Representation Learning via Persistent Homology. arXiv 2019, arXiv:1906.09003. [Google Scholar]
- Gallego-Posada, J. Simplicial AutoEncoders: A connection between Algebraic Topology and Probabilistic Modelling. Master’s Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2018. [Google Scholar]
- Gallego-Posada, J.; Forré, P. Simplicial Regularization. In Proceedings of the ICLR 2021 Workshop on Geometrical and Topological Representation Learning, Virtual, 3–7 May 2021. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Verma, V.; Lamb, A.; Beckham, C.; Courville, A.C.; Mitliagkas, I.; Bengio, Y. Manifold Mixup: Encouraging Meaningful On-Manifold Interpolation as a Regularizer. arXiv 2018, arXiv:1806.05236. [Google Scholar]
- Khrulkov, V.; Oseledets, I.V. Geometry Score: A Method For Comparing Generative Adversarial Networks. arXiv 2018, arXiv:1802.02664. [Google Scholar]
- Perez Rey, L.A.; Menkovski, V.; Portegies, J. Diffusion Variational Autoencoders. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, Yokohama, Japan, 11–17 July 2020; pp. 2704–2710. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Simon, S. Witness Complex. 2020. Available online: https://github.com/MrBellamonte/WitnessComplex (accessed on 20 December 2022).
- Maria, C.; Boissonnat, J.D.; Glisse, M.; Yvinec, M. The Gudhi Library: Simplicial Complexes and Persistent Homology; Technical Report; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Maria, C. Filtered Complexes. In GUDHI User and Reference Manual, 3.4.1th ed.; GUDHI Editorial Board: San Francisco, CA, USA, 2021. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Marsland, S. Machine Learning-An Algorithmic Perspective; Chapman and Hall/CRC Machine Learning and Pattern Recognition Series; CRC Press: Boca Raton, FL, USA, 2009; pp. I–XVI, 1–390. [Google Scholar]
- Arvanitidis, G.; Hansen, L.K.; Hauberg, S. Latent Space Oddity: On the Curvature of Deep Generative Models. In Proceedings of the ICLR (Poster), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Schönenberger, S.T.; Varava, A.; Polianskii, V.; Chung, J.J.; Kragic, D.; Siegwart, R. Witness Autoencoder: Shaping the Latent Space with Witness Complexes. In Proceedings of the NeurIPS 2020 Workshop on Topological Data Analysis and Beyond, Virtual, 6–12 December 2020. [Google Scholar]
- Jang, U.; Jha, S.; Jha, S. On the Need for Topology-Aware Generative Models for Manifold-Based Defenses. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medbouhi, A.A.; Polianskii, V.; Varava, A.; Kragic, D. InvMap and Witness Simplicial Variational Auto-Encoders. Mach. Learn. Knowl. Extr. 2023, 5, 199-236. https://doi.org/10.3390/make5010014
Medbouhi AA, Polianskii V, Varava A, Kragic D. InvMap and Witness Simplicial Variational Auto-Encoders. Machine Learning and Knowledge Extraction. 2023; 5(1):199-236. https://doi.org/10.3390/make5010014
Chicago/Turabian StyleMedbouhi, Aniss Aiman, Vladislav Polianskii, Anastasia Varava, and Danica Kragic. 2023. "InvMap and Witness Simplicial Variational Auto-Encoders" Machine Learning and Knowledge Extraction 5, no. 1: 199-236. https://doi.org/10.3390/make5010014
APA StyleMedbouhi, A. A., Polianskii, V., Varava, A., & Kragic, D. (2023). InvMap and Witness Simplicial Variational Auto-Encoders. Machine Learning and Knowledge Extraction, 5(1), 199-236. https://doi.org/10.3390/make5010014








