Abstract
Machine unlearning is the task of updating machine learning (ML) models after a subset of the training data they were trained on is deleted. Methods for the task are desired to combine effectiveness and efficiency (i.e., they should effectively “unlearn” deleted data, but in a way that does not require excessive computational effort (e.g., a full retraining) for a small amount of deletions). Such a combination is typically achieved by tolerating some amount of approximation in the unlearning. In addition, laws and regulations in the spirit of “the right to be forgotten” have given rise to requirements for certifiability (i.e., the ability to demonstrate that the deleted data has indeed been unlearned by the ML model). In this paper, we present an experimental study of the three state-of-the-art approximate unlearning methods for logistic regression and demonstrate the trade-offs between efficiency, effectiveness and certifiability offered by each method. In implementing this study, we extend some of the existing works and describe a common unlearning pipeline to compare and evaluate the unlearning methods on six real-world datasets and a variety of settings. We provide insights into the effect of the quantity and distribution of the deleted data on ML models and the performance of each unlearning method in different settings. We also propose a practical online strategy to determine when the accumulated error from approximate unlearning is large enough to warrant a full retraining of the ML model.
1. Introduction
Machine unlearning is the task of updating a machine learning (ML) model after the partial deletion of data on which the model had been trained so that the model reflects the remaining data. The task arises in the context of many database applications that involve training and using an ML model while allowing data deletions to occur. For example, consider an online store that maintains a database of ratings for its products and uses the database to train a model that predicts customer preferences (e.g., a logistic regression model that predicts what rating a customer would assign to a given product). If part of the database is deleted (e.g., if some users request their accounts to be removed), then a problem arises: how to update the ML model to “unlearn” the deleted data. It is crucial to address this problem appropriately so that the computational effort for unlearning is in proportion to the effect of the deletion. A tiny amount of deletion should not trigger a full retraining of the ML model, leading to potentially huge data-processing costs, but at the same time, data deletions should not be ignored to such extent that the ML model does not reflect the remaining data anymore.
In this work, we perform a comparative analysis of the existing methods for machine unlearning. In doing so, we are motivated both by the practical importance of the task and the lack of a comprehensive comparison in the literature. Our goal is to compare the performance of existing methods in a variety of settings in terms of certain desirable qualities.
What are those qualities? First, machine unlearning should be efficient (i.e., achieving small running time) and effective (i.e., achieving good accuracy). Moreover, machine unlearning is sometimes required to be certifiable (i.e., guarantee that after data deletion the ML model operates as if the deleted data had never been observed). Such a requirement may be stipulated by laws (e.g., in the spirit of the right to be forgotten [1] or the right of erasure [2] in EU laws) or even offered voluntarily by the application in order to address privacy concerns. In the example of the online store, consider the case where some users request their data to be removed from its database. The online store should not only delete the data in the hosting database but also ensure that the data are unlearned by any ML model that was built from them. Essentially, if an audit was performed, the employed ML models should be found to have unlearned the deleted data as well as a model that is obtained with a brute-force full retraining of the remaining data, even if full retraining was not actually performed to unlearn the deleted data.
The aforementioned qualities exhibit pairwise trade-offs. There is a trade-off between efficiency on one hand and effectiveness or certifiability on the other because it takes time to optimize a model so as to reflect the underlying data or unlearn the deleted data. Moreover, there is a trade-off between certifiability and effectiveness. That’s because unlearning the deleted data, thus ensuring certifiability, corresponds to learning from fewer data, thus decreasing accuracy. In this study, we observe the three trade-offs experimentally and find that because the compared methods involve different processing costs for different operations, they offer better or worse trade-offs in different settings.
For the experimental evaluation, we implement a common unlearning pipeline (Figure 1) for the compared methods. The first stage trains an initial ML model from the data. To limit the variable parts of our experimentation, we will be focusing on logistic regression, which represents a large class of models that are commonly used in a wide range of settings. In addition, we will be assuming that the initial model is trained with stochastic gradient descent (SGD), since SGD and its variants are the standard algorithms for training general ML models. The second stage employs the initial ML model for inference (i.e., for classification). During this stage, if data deletion occurs, then the pipeline proceeds to the third stage to unlearn the deleted data and produce an updated model. After every such model update, the updated model is evaluated for certifiability. If it fails, then the pipeline restarts and trains a new model from scratch on the remaining data; otherwise, it is employed in the inference stage, and the pipeline resumes. When an audit is requested by an external auditor (not shown in Figure 1), a full retraining of the ML model is executed on the remaining data, and the fully retrained model is compared to the currently employed model. If the employed model is found to have unlearned the deleted data as well as the fully retrained model (within a threshold of disparity), then the audit is successful, meaning the pipeline has certifiably unlearned the deleted data thus far and is allowed to resume.
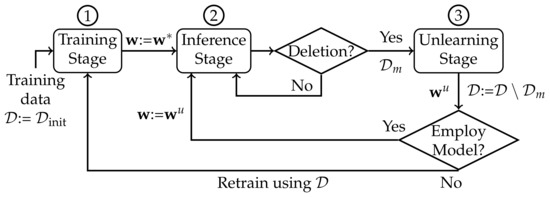
Figure 1.
The common unlearning pipeline with the three stages of training, inference and unlearning. First, an initial model w* is trained on all data and used for inference. Subsequently, whenever a part of the data is deleted, an updated model wu is obtained via machine unlearning. The pipeline restarts if the updated model is deemed inadequate.
Given this pipeline, we evaluate three methods, namely Fisher [3], Influence [4], and DeltaGrad [5], that follow largely different approaches for machine unlearning and represent the state of the art for our setting (linear classification models trained with SGD). Fisher, proposed by Golatkar et al. [3], updates the initial ML model using the remaining data to perform a corrective Newton step. Influence, proposed by Guo et al. [4], updates the initial ML model using the deleted data to perform a corrective Newton step. Finally, DeltaGrad, proposed by Wu et al. [5], updates the initial ML model by correcting the SGD steps that led to the initial model. Note that, in this work, we extend the original algorithms of [3,5] to ensure that all the evaluated methods are equipped with mechanisms to control the trade-offs between efficiency, effectiveness and certifiability.
For the experimental evaluation, we implement the three methods and compare them in a large range of settings that adhere to the pipeline described above. The aim of the experiments is to demonstrate the trade-offs that the three methods offer in terms of efficiency, effectiveness and certifiability. First, we demonstrate that the trade-offs are much more pronounced for certain worst-case deletion distributions than for random deletions. Subsequently, we observe that Fisher offers the overall best certifiability, along with good effectiveness at a lower efficiency than Influence, especially for larger datasets. In addition, Influence offers the overall best efficiency, along with good effectiveness at lower levels of certifiability, and DeltaGrad offers stable albeit lower performance across all qualities. Moreover, we observe that the efficiency of Fisher and Influence is much higher for datasets of lower dimensionality. The patterns we observe in these experiments have a beneficial by-product: they allow us to define a practical approach to determine in online fashion (i.e., as the pipeline unfolds) when the accumulated error from approximate unlearning is large enough to require restarting the pipeline to perform a full retraining of the ML model.
To summarize, we make the following contributions:
- We define a novel framework to compare machine unlearning methods in terms of effectiveness, efficiency, and certifiability.
- We extend the methods of [3,5] with mechanisms to control performance trade-offs.
- We offer the first experimental comparison of the competing methods in a large variety of settings. As an outcome, we obtain novel empirical insights about (1) the effect of the deletion distribution on the performance trade-offs and (2) the strengths of each method in terms of performance trade-offs.
- We propose a practical online strategy to determine an optimal time for when to restart the training pipeline.
As for future work, a similar experimental study would address model updates for data addition rather than deletion. For this work, we opted to focus on deletion to keep the paper well-contained, because certifiability is typically required in the case of deletion (e.g., when users request their data to be deleted from an application), and the methods we evaluate are tailored to certifiable deletion.
2. Related Work
Unlearning methods are classified as exact or approximate.
- Exact unlearning methods produce ML models that perform as fully retrained models. By definition, these methods offer the highest certifiability, as the produced models are effectively the same as ones obtained with retraining. There exist several exact unlearning methods, typically for training algorithms that are model-specific and deterministic in nature. For instance, ML models such as support vector machines [6,7,8], collaborative filtering, naive Bayes [9,10], k-nearest neighbors and ridge regression [9] possess exact unlearning methods. The efficiency for such exact methods varies.
For stochastic training algorithms such as SGD, an exact unlearning approach, under the assumption that learning is performed in federated fashion, was proposed in [11]. In federated learning, separate ML models are trained on separate data partitions, and their predictions are aggregated during inference. This partitioning of data allows for efficient retraining of ML models on smaller fragments of data, leading to efficient unlearning when data are deleted. However, for general ML models trained with SGD, the setting of federated learning comes with a potential cost of effectiveness that is difficult to quantify and control because model optimization is not performed jointly on the full dataset.
- Approximate unlearning methods produce ML models that are an approximation of the fully retrained model. These methods typically aim to offer much larger efficiency through relaxation of the effectiveness and certifiability requirements. Most of them can be categorized into one of three groups.
The first group [3,12,13] uses the remaining data of the training dataset to update the ML model and control certifiability. These methods use Fisher information [14] to retain the information of the remaining data and inject optimal noise in order to unlearn the deleted data. The second group [4,15,16] uses the deleted data to update ML models during unlearning. They perform a Newton step [17] to approximate the influence of the deleted data on the ML model and remove it. To trade off effectiveness for certifiability, they inject random noise into the training objective function [16]. The third group [5,18,19,20] stores data and information during training and then utilizes this when deletion occurs to update the model. Specifically, these methods focus on approximating the SGD steps that would have occurred if full retraining was performed. To aid in this approximation, they store the intermediate quantities (e.g., gradients and model updates) produced by each SGD step during training. The amount of stored information and the approximation process raise an effectiveness vs. efficiency trade-off.
Methods from the above three groups can be used to perform unlearning for classification models with SGD, as long as the relevant quantities (e.g., the model gradients) are easy to compute for the model at hand. Apart from the above three groups, there are other approximate unlearning methods that do not fit the same template (e.g., methods for specific ML models, such as [21] for random forest models, or for Bayesian modeling, such as [22] for Bayesian learning), and so we consider them outside the scope of this paper.
In this paper, we focus on approximate unlearning methods, because they are applicable to general ML models, when training is performed with general and widely used optimization algorithms such as SGD. We implement three methods—Fisher, Influence and DeltaGrad—which correspond to state-of-the-art unlearning methods from each of the aforementioned groups ([3,4,5], respectively).
3. Machine Unlearning
Section 3.1 below will present the stages of the unlearning pipeline and how each method implements them. Each unlearning method we consider is equipped with mechanisms to navigate trade-offs between efficiency, effectiveness and certifiability. Therefore, to facilitate presentation, let us first provide a high-level description of those mechanisms along with some related terms and notation.
In what follows, effectiveness is measured as the model’s accuracy on the test dataset Acctest (i.e., the fraction of the test data that it classifies correctly). Certifiability is measured as the disparity AccDis in accuracy of the deleted data between the updated model (i.e., the model that results from the (possibly approximate) unlearning of the deleted data) and the fully retrained ML model. This metric is a normalized version of the “error on the cohort to be forgotten” metric seen in Golatkar et al. [3]. Intuitively, AccDis quantifies how well the updated model “remembers” the deleted data. If it is small, then the updated model has “unlearned” the deleted data almost as well as if fully retrained.
The first mechanism trades efficiency for effectiveness on one hand and certifiability on the other via an efficiency parameter τ, which is specified separately for each unlearning method. Lower values of τ indicate lower efficiency, thus allowing longer running times to improve the effectiveness and certifiability of the updated model.
The second mechanism trades effectiveness (high accuracy Acctest) for certifiability (low disparity AccDis) via noise injection. Simply expressed, noise injection deliberately adds randomness to an ML model both during training and unlearning. A noise parameter controls the amount of injected noise, defined for a model of d features as
On one end of this trade-off, large amounts of noise ensure that the fully retrained and unlearned model are both essentially random, thus leading to high certifiability (low disparity AccDis) at the cost of low effectiveness (low accuracy). On the other end, when no noise is injected, the unlearning method strives to readapt the model to the remaining data, thus possibly sacrificing in favor of effectiveness some of the certifiability it would achieve on the first end of this trade-off. We note that this trade-off, along with noise injection as a control mechanism, has already been introduced as concepts in the differential privacy literature [4,16,23].
3.1. Unlearning Pipeline and Methods
The unlearning pipeline represents the lifecycle of the ML models in our study (Figure 1). Below, we describe how each unlearning method we consider executes each stage of the pipeline, with a summary shown in Table 1.

Table 1.
Overview of the chosen unlearning methods.
3.2. Training Stage
This stage produces an ML model from the training dataset . In what follows, we assume that the ML model is a logistic regression, a simple and widely used model for classification. Each data point is accompanied by a categorical label , and there are data points initially. At any time, will denote the currently available training dataset, which is a subset of the initial training dataset due to possible deletions (i.e., ). The fitness of an ML model’s parameters on a dataset is measured via an objective function, such as
with binary cross entropy ℓ in the first term and ridge regularization in the second term for a fixed value .
Moreover, we use SGD for training [24]. SGD iteratively minimizes the objective function over the training data. First, it initializes the model parameters to a random value , and it improves them iteratively:
where is the learning rate at iteration t and the iterations repeat until convergence. Following common practice, we execute SGD in mini-batch fashion (i.e., only a subset of is used in each execution of Equation (3)).
The training algorithms for each unlearning method are presented in the second column of Table 1. The Fisher and DeltaGrad methods obtain the model that optimizes L and subsequently adds to it random noise proportionally to the noise parameter . Here, the random noise is directly added to by the DeltaGrad method, while the Fisher method adds noise in the direction of the fisher matrix F, which for logistic regression is the Hessian of the objective L. On the other hand, the Influence method optimizes a modified objective function , which adds random noise to the standard objective L rather than directly adding noise to the model parameters. Furthermore, in the DeltaGrad method, after every iteration of the SGD algorithm (Equation (3)), the parameters and the objective function gradients are stored to the disk.
A model obtained from the training stage of the pipeline is denoted by . When it is obtained using the initial dataset , then is referred to as the initial trained model, and when it is obtained using a subset of the training dataset, it is referred to as the fully retrained model. This model is sent to the second stage to be employed for inference.
For further details on the training algorithm, see from Appendix A.1, Appendix A.2 and Appendix A.3.
3.3. Inference Stage
This stage uses the available model to predict the class of arbitrary data points specified as queries. As soon as a subset of the data is deleted, the pipeline moves to the third stage.
3.4. Unlearning Stage
This stage executes the unlearning algorithm so as to “unlearn” the deleted data and produce an updated model (third column of Table 1).
The Fisher and Influence methods use corrective Newton steps in their unlearning algorithms (terms and , respectively). These Newton steps compute the inverse Hessian of the objective L on the remaining data . However, while the Fisher method also computes the gradient on the remaining data, the Influence method computes the gradient on the deleted data. Furthermore, the Fisher method adds random noise in the direction of the Fisher matrix, similar to the training algorithm. Both the Fisher and Influence unlearning algorithms can be performed in mini-batches of size , which leads to multiple smaller corrective Newton steps. Smaller unlearning mini-batch sizes lead to a more effective ML model at the cost of efficiency, and therefore, serves as the efficiency parameter for the Fisher and Influence methods. Refer to Algorithms A1 and A2 for the mini-batch versions of the unlearning algorithms.
The DeltaGrad unlearning algorithm proceeds in two steps. The first step of the algorithm aims to obtain the approximate ML model that would have resulted from SGD if the subset had never been used for training. This is achieved by approximating the objective function gradient on the remaining data points using the L-BFGS algorithm [25,26,27] and the stored terms and from the training stage. However, to reduce the error from consecutive L-BFGS approximations, the gradient is computed explicitly after every SGD iterations. Larger values of lead to more consecutive approximations steps, resulting in higher efficiency, though at the cost of a less effective model. Therefore, the periodicity serves as the efficiency parameter . The second step adds random noise similar to the training algorithm. Please see Appendix A.3 and Algorithm A3 for further details.
3.5. Evaluation
During evaluation the updated model is assessed for certifiability as soon as it is produced using the test dataset . If the disparity AccDis is below some threshold (e.g., determined by the administrator of this pipeline), then the pipeline returns to the second stage and employs the updated model := for inference; otherwise, it returns to the first stage for a full retraining over the remaining data. In Section 7, we discuss a practical online strategy for evaluation.
A properly conducted evaluation ensures that the pipeline will successfully pass a certifiability audit at any point. In other words, if an auditor were to perform a full retraining on the available data and compare the resulting model to the currently employed model, then the two models should be found to be within the threshold of disparity.
4. Experimental Setup
In this section, we describe the datasets, the implementation of the pipeline and the metrics used for evaluation.
4.1. Datasets
We performed experiments over six datasets retrieved from the public LIBSVM repository [28]. The datasets cover a large range of size and dimensionality, as summarily shown in Table 2. In addition, we focused on the task of binary classification, and therefore, most datasets were chosen to include two target classes (or, if the original dataset contained more classes, the experiments focused on two of them, as reported in Table 2). Nevertheless, we also included one multi-class dataset (mnist, with 10 classes).

Table 2.
Datasets.
In more detail, mnist [29] consists of black and white images of handwritten digits (0–9), each digit corresponding to one class. mnistb is the binary class subset of the mnist dataset, consisting only of digits “3” and “8” for both the training and test data. cifar2 consists of RGB color images, belonging to the “cat” or “ship” categories from the original 10-category CIFAR-10 [30] dataset. covtype [31] consists of 54 features used to categorize forest cover into 2 types. The higgs [32] dataset consists of kinematic features from the Monte Carlo simulation of particle detectors for binary classification. epsilon [33] was obtained from the PASCAL Large Scale Learning Challenge 2008.
4.2. Unlearning Pipeline
We now provide implementation details for the pipeline (Figure 1). The pipeline is designed so that it is suitable for all the three chosen unlearning methods discussed in Section 3. The pipeline was implemented in Python 3.6 using PyTorch 1.8 [34]. All experiments were run on a machine with 24 CPU cores and 180 GB RAM. Our full code base is publicly available (https://version.helsinki.fi/mahadeva/unlearning-experiments (accessed on 26 May 2022)).
4.2.1. Preprocessing
The Influence unlearning method requires all data points of a dataset to have a Euclidean norm of at most one (i.e., ) (see Guo et al. [4]). To satisfy this requirement, we performed a max- normalization for all datasets as a preprocessing step, where we divided each data point by the largest norm of any data point in the dataset. This normalization does not affect the performance of other unlearning methods.
4.2.2. Training
As mentioned in Section 3, we used the mini-batch SGD algorithm for training. In all cases, we use a fixed learning rate and ridge regularization parameter . Moreover, we used standard SGD since DeltaGrad does not support momentum-based SGD algorithms such as Adam [35]. Note that both the Fisher and Influence unlearning algorithms require a positive definite Hessian matrix to compute its inverse (see Table 1). This is ensured by a sufficiently large number of SGD iterations during training to achieve convergence. Toward this end, we used a small subset of the training data as a validation dataset to identify an optimal mini-batch size and the total number of SGD iterations. Moreover, we controlled the data points selected in each mini-batch by fixing the random seed used to produce mini-batches in the SGD algorithm. This ensured reproducibility of the experiments across various unlearning methods. Finally, for multi-class classification with classes on the mnist dataset, we trained k independent binary logistic regression classifiers in a One vs. Rest (OVR) fashion.
4.2.3. Unlearning
We modified and extended the code of Guo et al. [4] to implement the Influence and Fisher mini-batch unlearning algorithms as described in Algorithms A1 and A2. For the DeltaGrad method, we used the code of Wu et al. [5] and modified it to add the noise injection mechanism seen in Table 1 to trade off effectiveness for certifiability.
4.3. Evaluation Metrics
In this section, we define the metrics we used to report the performance of different unlearning methods in terms of effectiveness, certifiability and efficiency. For uniformity of presentation, we reported the performance achieved by a given model as relative to the performance of a baseline model. Toward this end, we used the Symmetric Absolute Percentage Error (SAPE), defined as
where a is the baseline value and b is the value compared against the baseline. Furthermore, we defined .
4.3.1. Effectiveness
It is measured in terms of the predictive accuracy of a given ML model on a particular dataset. Let Acctest denote the accuracy on the test dataset . Specifically, let be the accuracy of the updated model on the test dataset and be the optimal test data accuracy of a fully trained model, with obtained via logistic regression on the available data. We reported AccErr as the error in the test accuracy of the updated model compared with the optimal one, where
A low value for AccErr implies that the updated model is more effective (i.e., the predictive accuracy of the updated model is close to optimal for the available data).
4.3.2. Certifiability
It is measured in terms of how well the updated model has unlearned the deleted data relative to a fully retrained model with the same method. Let be the accuracy of the deleted data . Specifically, let and be the accuracy of the deleted data for the updated model and the fully retrained model, respectively, for the same noise value . We reported AccDis as the disparity in accuracy of the two models, where
The deleted data are the union of all the subsets of the initial dataset that were deleted since the initialization of the pipeline. A lower value of AccDis implies that the updated model has higher certifiability (i.e., the updated model is more similar to the fully retrained model, which never saw the deleted data). Note that the symmetry of is essential here, because both under- and over-performance of the updated model contributes toward a disparity with respect to the fully retrained model.
4.3.3. Efficiency
It is measured as the speed-up in running time to obtain the updated model relative to the running time to obtain the fully retrained model . A speed-up of 2× indicates that the unlearning stage is able to produce an updated model twice as fast as it takes for the training stage to produce a fully retrained model.
5. Effect of Deletion Distribution
Before we compare the unlearning methods, let us explore how the volume and distribution of the deleted data affect the accuracy of fully trained models. This will allow us to separate the effects of data deletion from the effects of a specific unlearning method.
We implemented a two-step process to generate different deletion distributions. The process was invoked once for each deleted data point for a predetermined number of deletions. In the first step, one class is selected. For example, for binary class datasets (see Table 2), the first step selects one of the two classes. The selection may be either uniform, where one of the k classes is selected at random, each with a probability , or targeted, where one class is randomly predetermined and subsequently always selected.
The second step selects a data point from the class chosen in the previous step. The selection may be either random, where one data point is selected uniformly at random, or informed, where the point that decreases the model’s accuracy the most is selected. Ideally, for the informed selection and for each data point, we would compute the exact drop in the accuracy of a fully trained model on the remaining data after the single-point removal, and we would repeat this computation after every single selection. In practice, however, such an approach is extremely heavy computationally, even for experimental purposes. Instead, for the informed selection, we opted to heuristically select the outliers in the dataset, as quantified by the norm of each data point. This heuristic is inspired by [15], who stated that deleting data points with a large norm negatively affects the approximation of Hessian-based unlearning methods. We note that the informed selections are highly adversarial and are not practically feasible. We included it in our experiments to study the worst-case effects of data deletion on unlearning methods.
The two-step process described above yields four distinct deletion distributions, namely uniform-random, uniform-informed, targeted-random and targeted-informed. In the experiments that follow, we vary the distribution and volume of deletions performed. For each set of deleted data, we report the accuracy of the fully trained model after deletion (i.e., the accuracy achieved by the model that optimizes Equation (2) using SGD).
The results are shown in Figure 2. Each plot in the figure corresponds to one dataset. The first row of plots reports the accuracy on the test dataset, and the second row shows the accuracy on the deleted data. Accuracy values correspond to the y-axis, while the volume of deletion (as a fraction of the original dataset size) corresponds to the x-axis. Different deletion distributions are indicated with different markers and colors. The variance seen in Figure 2 is a consequence of the randomness in the selection of deleted points (two random runs were performed). There are three main takeaways from these results.
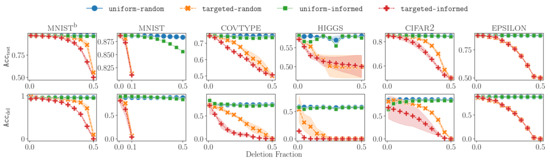
Figure 2.
Effect of different deletion distributions on the test accuracy () and deleted data accuracy (), as the fraction of deleted data was varied for different datasets.
- 1.
- Uniform deletion distributions are unimpactfuluniform-random and uniform-informed do not adversely affect the test accuracy of a fully retrained ML model even at deletion fractions close to . This is due to the clear separation of classes encountered in many real-world datasets. Therefore, evaluating unlearning methods on deletions from uniform distributions will not offer significant insights into the effectiveness and efficiency trade-offs.
- 2.
- Targeted deletion distributions are the worst casetargeted-random and targeted-informed deletions lead to large drops in test accuracy. This is because deleting data points from one targeted class eventually leads to class imbalance, causing ML models to be less effective in classifying data points from that class. Therefore, to validate the performance of unlearning methods, one should test them on targeted distributions, where data deletions reduce the accuracy of the learned model.In addition, we observed that the variance resulting from the selection of the deleted class was low in all datasets apart from higgs. We postulate that this is because of the particular way that missing values were treated for this dataset: data points that had missing feature values disproportionately belonged to class 1. Therefore, this tended to cause a steeper drop in accuracy when data from class 1 was targeted. Moreover, between the two targeted distributions, we observed that targeted-informed led to quicker accuracy drops.
- 3.
- Metrics and are correlatedWe see across deletion fractions that the values of the accuracy on the test and deleted dataset were highly correlated. Hence, the test accuracy , which can always be computed for a model on the test data, can be used as a good proxy for the of an ML model, which may be impossible to compute after data deletion but is required in order to assess certifiability. This observation will be useful in deciding when to trigger a model retrained in the pipeline (Section 7).Additionally, we note that the drop rate in and with respect to the deletion fraction varied with the dataset.
6. Experimental Evaluation
In this section, we demonstrate the trade-offs exhibited by the unlearning methods in terms of the qualities of interest (effectiveness, efficiency and certifiability) for different values of their parameters and . For each dataset, we experimented with three volumes of deleted data points—small, medium and large—measured as a fraction of the initial training data. The deletion volumes corresponded to a 1%, 5% and 10% drop in for a fully retrained model when using a targeted-informed deletion distribution, with class 0 as the deleted class (see Figure 2). Here, we present the results for the large volumes of deletion, which were 4493, 2000, 4500, 78,436, 100,000 and 990,000 deletions for the datasets in Table 2, respectively. Furthermore, we grouped the datasets presented in Table 2 into three categories (low, moderate and high) based on their dimensionality. Please see Appendix D for the results corresponding to the small and medium deletion volumes.
6.1. Efficiency vs. Certifiability
In this experiment, we studied how varying the efficiency parameter trades off certifiability and efficiency for a fixed noise parameter . The efficiency parameter for Fisher and Influence was the size of the unlearning mini-batch, and we varied , where m is the volume of deleted data. For DeltaGrad, the efficiency parameter is the periodicity of the unlearning algorithm, and we varied . The noise parameter was set at for all methods, and we obtained the updated model and the fully retrained model for each unlearning method as described in Table 1.
The results are shown in Figure 3a. For each plot in the figure, the y-axis reports certifiability (AccDis), and the x-axis reports efficiency (speed-up). Different unlearning methods and values of are indicated with different colors and markers, respectively, in the legend.
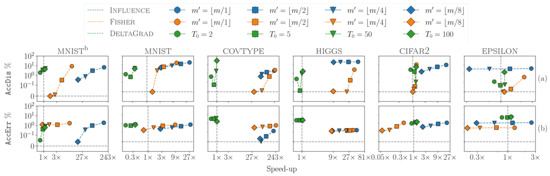
Figure 3.
Trade-offs between efficiency and (a) certifiability and (b) effectiveness for at the largest volume of deletion as is varied. The y-axis reports (a) certifiability (AccDis) and (b) effectiveness (AccErr), while the x-axis reports the efficiency (speed-up).
We observed two main trends. First, for the general trade-off between efficiency and certifiability, higher efficiency (i.e., a higher speed-up) was typically associated with lower certifiability (i.e., a higher AccDis) in the plots. Some discontinuity in the plotlines, especially for DeltaGrad, was largely due to the convergence criteria, particularly since DeltaGrad employs SGD not only for training but also for unlearning.
Second, the efficiency of Influence and Fisher had a roughly similar trend for each dataset. For the low-dimensional datasets, Influence and Fisher provided large speed-ups of nearly 200× and 50× for each dataset, respectively, when , while DeltaGrad provided a speed-up of less than 1× (i.e., requiring more time than the fully retrained model). This was because when the dimensionality was low, the cost of computing the inverse Hessian matrix for Influence and Fisher (see Section 3) was much lower compared with the cost of approximating a large number of SGD iterations for the DeltaGrad method. Conversely, for the high-dimensional datasets, Influence and Fisher provided a smaller speed-up. When was decreased to , the efficiency reduced to 2.2× and 1× for cifar2 and 0.3× and 1.2× for epsilon, respectively, whereas DeltaGrad at provided better speed-ups of 1.3× and 1.1×, respectively, along with comparable values of AccDis.
6.2. Efficiency vs. Effectiveness
In this experiment, we studied how varying the efficiency parameter trades off efficiency and effectiveness for a fixed and volume of deleted data. The range of for each unlearning method was the same as the previous experiment and . In Figure 3b, each plot reports effectiveness as the test accuracy error AccErr and efficiency as the speed-up in running time. We observed the following trends. First, there was the general trade-off: higher efficiency (i.e., a higher speed-up) was associated with slightly higher accuracy error (i.e., AccErr) for each method. Furthermore, for Influence, decreasing in the unlearning algorithm led to lower test accuracy error because the noise was injected only in the training algorithm (see Table 1).
Second, Influence offered the best efficiency and effectiveness trade-off among all the methods. Especially for the high-dimensional datasets, the highest efficiency offered was 20× and 2.5× compared with 0.4× and 1.3× for Fisher, respectively, at a slightly larger test accuracy error. For the low-dimensional datasets, Influence and Fisher offered similar efficiency while the former had a lower AccErr. Lastly, for the moderate dimensional datasets, the largest efficiency Influence offered was 168× and 29× compared with 9× and 8.5× for Fisher, respectively, at a lower test accuracy error.
Third, we saw that DeltaGrad was mostly stable in terms of both efficiency and effectiveness. However, note that the test accuracy error for all datasets was larger compared with the other methods due to the direct noise injection and hence offered lower effectiveness even at .
6.3. Effectiveness vs. Certifiability
In this experiment, we studied how varying the noise parameter traded off effectiveness and certifiability for a fixed efficiency parameter .
The efficiency parameter was set as follows: for Influence and Fisher, we set the size of the unlearning mini-batch to , and for DeltaGrad, we set the periodicity . For different values of the noise parameter , we obtained the updated models corresponding to each unlearning method as described in Section 3. For the baselines, we first obtained the fully retrained model at the same to measure certifiability and a second fully retrained model at to measure effectiveness, as per Section 4.3.
The results are shown in Figure 4, where for each plot the left y-axis reports the certifiability (AccDis), and the right y-axis reports effectiveness (AccErr) as is varied from to for the different unlearning methods. We observed the trade-off between effectiveness and certifiability: higher effectiveness (lower AccErr) was typically associated with lower certifiability (higher AccDis).
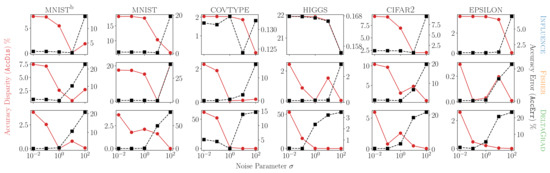
Figure 4.
Effectiveness and certifiability trade-offs for largest volume of deletion. Each row corresponds to an unlearning method. Efficiency parameter is fixed at for Influence and Fisher and at for DeltaGrad. The left y-axis reports certifiability (AccDis), the right y-axis reports effectiveness (AccErr), and the x-axis varies the noise parameter . Lower is better for both y-axes.
Another clear observation is that for the Influence method, the test accuracy error AccErr increased only at higher values of (≥10). Moreover, we saw that its largest AccErr was lower than that for other methods across all datasets. For example, in the mnist dataset, the maximum AccErr (at ) was approximately , and for Influence, Fisher and DeltaGrad, respectively. At the same time, however, improved certifiability (i.e., decreased AccDis) was achieved for high values of . Therefore, to obtain a good combination of effectiveness and certifiability, one must select higher values of based on the dataset.
Moreover, for Fisher, near , the trade-off between AccErr and AccDis was the best among all methods, having values of at most and , respectively, across all datasets, as seen in Figure 4. If a good effectiveness and certifiability trade-off is required, then the Fisher method appears to be a very suitable method.
Note that because Influence and Fisher shared the same efficiency parameter , their results in this section are directly comparable. However, that is not the case with DeltaGrad. As we saw earlier in this section, DeltaGrad was typically quite slower than the other methods. Therefore, for these experiments, we used it with the largest value of so that its running time was small and closer to the running time of the other two methods (being, in fact, comparable for the high-dimensional datasets).
7. Online Strategy for Retraining
When the updated model is obtained after data deletion (see Figure 1), a decision is made on whether to employ the model for inference. Specifically, if the disparity AccDis of the updated model is below a certain predetermined threshold for certifiability, then the model is employed for inference; otherwise, the pipeline restarts, training a new model on the remaining data. However, measuring AccDis using Equation (6) would require the full retrained model , which was not readily available. In fact, computing after every batch of deletions would defeat the purpose of using an approximate unlearning method in the first place.
Therefore, in practice, AccDis needs to be estimated. To this end, we propose an online estimation strategy based on the empirical observation (see Table A5) that, as more data are deleted, the disparity AccDis grows proportionally to the drop in test accuracy relative to the initial model :
where and are the test accuracies for the initial and updated model, respectively. In more detail, we measured the correlations between AccDis and for targeted-random deletions while varying the deletion fraction from to ( for mnist) while utilizing the Fisher unlearning method (). We observed that, apart from the higgs dataset, the Pearson correlation [36] for all other datasets was greater than , suggesting a strong correlation between AccDis and . Note that this observation is related to the correlation of accuracy on the test and deleted data that we mentioned in Section 5.
Building upon this observation, we estimated AccDis as
where c is a constant proportion learned from the data before the pipeline starts as follows. First, we obtained the test accuracy for the model trained on the initial dataset. Second, we obtained an updated model and a fully retrained model for a large deletion fraction , such as . Third, the proportion c was calculated as follows:
An example run of the pipeline using the estimation strategy for the threshold is shown in Figure 5. At each timestep, batches of data points from a targeted-informed distribution were chosen for deletion. Then, the Fisher unlearning algorithm (see Table 1) was used with the efficiency parameter set as to obtain an updated model . Next, the of was measured using the stored , and the certifiability disparity was estimated using Equation (8). If the estimated exceeds the threshold , then the pipeline restarts; a new initial model is trained from scratch on the remaining data, and the is updated, while c remains unchanged. The dotted green lines in Figure 5 correspond to the times when the pipeline restarted. Then, the pipeline resumes receiving further batches of deletions until the next restart is determined by the estimation strategy or the pipeline ends.
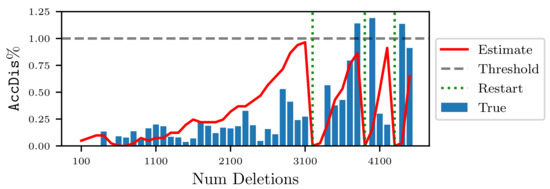
Figure 5.
Pipeline run at for the mnistb dataset. Fisher unlearning with and targeted-informed deletions.
To evaluate the strategy, we selected three thresholds for each dataset: and 50 for higgs and and 5 for the other datasets. Next, the number of deletions m was 100 for the mnistb, mnist and cifar2 datasets and and 10,000 for the for the epsilon, covtype and higgs datasets, respectively. In Figure 5, we observe that the initial estimate was larger than the true AccDis, and as more data were deleted, the true AccDis exceeded the threshold, leading to errors in the estimation. We define the relative percentage estimation error of the true AccDis for a given threshold at a given time as
where the true AccDis is computed by obtaining a fully retrained model on the remaining data at that time. For each individual run of the pipeline, we computed the mean across the duration of the pipeline (e.g., in Figure 5, the mean is ). Then, we collected multiple individual runs corresponding to different random seeds (six for and two for the random deletion distributions) and computed the pooled mean (i.e., the mean of the mean for each threshold ).
In Table 3, we report the pooled mean of for different datasets and deletion distributions at different thresholds. We observe that the pooled mean for all thresholds was lower than . The larger estimation errors for the higgs dataset were a result of the lower Pearson correlation of discussed earlier. However, the Spearman correlation [36] was , indicating that the estimation error may have been reduced by using a non-linear estimation strategy. Note that the pooled mean was larger for the targeted-informed distribution, indicating that the estimated using the proportion c computed from targeted-random deletions tended to underestimate the true disparity for the more adversarial targeted-informed deletions. Therefore, based on Table 3, for a pipeline to be certifiable at threshold , the estimation strategy should be employed with a threshold , ensuring a large buffer for possible estimation errors.

Table 3.
Pooled mean of % for the AccDis strategy at different thresholds . Noise parameter .
In Figure 6, we report the speed-up of the pipeline with respect to retraining at every timestep for different datasets and deletion distributions at different thresholds . The observed drops in the speed-up for the targeted-informed distribution correspond to the restarts of the pipeline triggered by the estimation strategy. Notice how smaller thresholds resulted in more frequent restarts and therefore larger drops in the speed-up for targeted-informed deletions. Furthermore, the estimation strategy was adaptive; in the less adversarial uniform-random distribution, fewer restarts were triggered, thereby resulting in larger speed-ups.
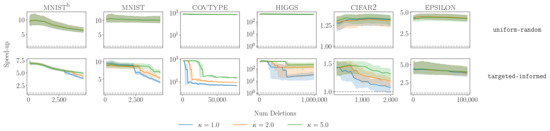
Figure 6.
Speed-up of AccDis estimation strategy at different thresholds . Rows correspond to different deletion distributions. Dashed line indicates speed-up of 1×. Note: for the higgs dataset, .
In summary, we found that the proposed strategy to estimate the disparity and restart the pipeline, albeit a heuristic, provided a significant speed-up in running time. Furthermore, as evidenced by our experiments, the strategy performed well for different distributions of deletions and could effectively be used to ensure that the pipeline was certifiable at a given disparity threshold . The design of more sophisticated strategies to better estimate the disparity is left for future work.
8. Conclusions
We highlighted the impact of different deletion distributions on the performance of retrained ML models and identified that the trade-offs offered by the unlearning methods must be evaluated in a worst-case scenario of targeted deletions. We studied experimentally three state-of-the-art unlearning methods for logistic regression. We found that for the right parameterization, Fisher offered the overall best certifiability, Influence offered the overall best efficiency along with good effectiveness at lower levels of certifiability, and DeltaGrad offered stable albeit lower performance across all qualities. Third, we found that the efficiency of Fisher and Influence was much higher for the low-dimensional datasets. Furthermore, we showcased an online strategy to determine when a full retraining on the remaining data is required.
For future work, several possibilities are open. One direction is to extend the study to methods for more complex models. While the proposed unlearning pipeline can be extended to non-linear ML models such as neural networks with appropriate unlearning methods [37,38,39], extending the experimental evaluation (Section 6) is non-trivial. This is due to the stochasticity of learning [11] for non-linear ML models, which results in many local minima (i.e., several equally valid, fully retrained models with different accuracies). Another research direction is to develop more elaborate mechanisms to determine when a full retraining of the updated models is needed.
Author Contributions
Conceptualization, A.M. and M.M.; data curation, A.M. and M.M.; formal analysis, A.M. and M.M.; funding acquisition, M.M.; investigation, A.M. and M.M.; methodology, A.M. and M.M.; project administration, M.M.; resources, M.M.; software, A.M.; supervision, M.M.; validation, A.M. and M.M.; visualization, A.M. and M.M.; writing—original draft, A.M. and M.M.; writing—review and editing, A.M. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the University of Helsinki and the Academy of Finland Projects MLDB (322046) and HPC-HD (347747).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All our experiments were conducted with publicly available datasets. Our full code base is available at https://version.helsinki.fi/mahadeva/unlearning-experiments (accessed on 26 May 2022).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Unlearning Methods
Appendix A.1. Fisher Unlearning Method
The Fisher unlearning method is described in [3].
Appendix A.1.1. Training Algorithm
The training algorithm for this method proceeds in two steps. In the first step, it invokes SGD to optimize the objective L (Equation (2)), and in the second step, it performs noise injection. The output model is expressed as
where
As shown in Equation (A2), is the model that optimizes the objective function L using SGD. Moreover, F is the Fisher matrix of L, defined as the covariance of the objective function. For logistic regression, F is equal to the Hessian of L, as reflected in Equation (A3). The second term in Equation (A1) corresponds to the noise injection that adds standard normal noise (see Equation (A4)) to the optimal model in the direction of the Fisher matrix.
Appendix A.1.2. Unlearning Algorithm
The unlearning algorithm takes as input the currently employed model , the deleted subset of the training data , and outputs an updated model given by
where
where is the same as in. As shown in Equation (A6), is the gradient of the objective function L (Equation (2)), and similar to Equation (A1), F is the Fisher matrix, now computed on the remaining training data after deletion (). The first term in Equation (A5) corresponds to the corrective Newton step that aims to unlearn the deleted data . The second term corresponds to noise injection and adds standard normal noise (see Equation (A4)) to the updated model in the direction of the Fisher matrix (see Equation (A7).
As defined in Equation (A5), the unlearning algorithm computes an updated model in a single step. A more elaborate approach is to split the deleted data in mini-batches of size and use Equation (A5) sequentially for each of them. This approach leads to multiple and smaller corrective Newton steps, which in turn lead to a more effective ML model at the cost of efficiency. For this experimental study, we used this mini-batch version of the unlearning algorithm, as shown in Algorithm A1.
| Algorithm A1:Fisher mini-batch |
 |
Appendix A.1.3. Trade-Off Parameters
As explained earlier (Section 3.1), the noise parameter controls the trade-off between effectiveness and certifiability. Moreover, the size of the mini-batches τfisher serves as the efficiency parameter that controls the trade-offs between efficiency on one hand and effectiveness and certifiability on the other. The lowest efficiency is achieved when (i.e., unlearning one deleted data point at a time incrementally). However, this comes at the massive cost of recomputing the Fisher matrix after every single deleted data point. The highest efficiency is achieved when (i.e., unlearning all deleted data at once), which comes at the cost of effectiveness due to a single crude, corrective Newton step. In typical real settings, one would choose a value between the two extremes.
Appendix A.2. Influence Unlearning Method
The Influence unlearning method is as follows [4]. Its approach is based on ML influence theory [17]. At a high level, unlearning is performed by computing the influence of the deleted data on the parameters of the trained ML model and then updating the parameters to remove that influence. Moreover, it uses a modified objective function that incorporates noise injection:
where L and are the same as in Equations (2) and (A4), respectively. The second term in Equation (A8) describes the noise injection, where is the noise parameter. The amount of noise is scaled with respect to the size of the training data .
Appendix A.2.1. Training Algorithm
This uses SGD to optimize the noisy objective:
Note that when is increased, the effectiveness of the ML model decreases, as the SGD algorithm prioritizes minimizing the second term in Equation (A8) rather than the original objective function captured by the first term.
Appendix A.2.2. Unlearning Algorithm
The unlearning algorithm approximates the influence of the deleted subset on the parameters of the currently employed model and performs the update as follows:
where
As seen in Equations (A11) and (A12), is the gradient of the objective function L (see Equation (2)) computed on the deleted data, and H is the Hessian matrix computed on the remaining training data. The second term in Equation (A10) is known as the influence function of the deleted data on the model parameters .
Similar to Fisher, when the unlearning algorithm is performed in mini-batches of , we obtain a more effective ML model at the cost of the efficiency. This is because we compute the influence function on smaller mini-batches of deleted data multiple times. For this experimental study, we used this mini-batch version of the unlearning algorithm as shown in Algorithm A2.
Appendix A.2.3. Trade-Off Parameters
The trade-off parameters for the Influence unlearning method are similar to those in the Fisher method. The size of serves as the efficiency parameter, and serves as the noise parameter.
| Algorithm A2:Influence mini-batch |
 |
Appendix A.3. DeltaGrad Unlearning Method
The DeltaGrad unlearning method is described in [5]. Its approach is to approximate the SGD steps that would have happened if the deleted data had not been present using the information from the initial SGD training steps.
Appendix A.3.1. Training Algorithm
It uses SGD followed by noise injection:
where is defined as in Equation (A4)). This noise injection mechanism is a Gaussian version of the one described in [18] using the results from [23]. In contrast to Fisher method’s noise injection (Equation (A5)), there is no Fisher matrix to guide the random Gaussian noise in this mechanism. Therefore, a large value of will indiscriminately remove information from the employed model, which in turn drastically reduces the effectiveness of the ML model.
At every iteration of the SGD algorithm (Equation (3)), the parameters and objective function gradients are stored to the disk.
Appendix A.3.2. Unlearning Algorithm
For this method the unlearning algorithm proceeds in two steps: in the first step, it approximately updates the stored sequence of parameters computed by SGD; in the second step, it injects noise. In summary, and slightly abusing notation, we write
The first term corresponds to the approximate update of SGD steps, and the second corresponds to noise injection, with defined as in Equation (A4).
Let us provide more details about how the first term is computed. Upon the deletion of the current subset of the training data , the unlearning algorithm aims to obtain the approximate ML model that would have resulted from SGD if had never been used for training. By definition, in the absence of , the gradient of the objective function at every step of the SGD algorithm would have been
Using Equation (A15), the SGD step from Equation (3) can be rewritten as
These SGD steps lead to a different sequence of model parameters than the one obtained before deletion from Equation (3). Consequently, the value of differs between the executions of Equation (3) (before deletion) and Equation (A16) (after deletion). DeltaGrad’s approach is to obtain a fast approximation of the latter from the former, thus approximately unlearning the deleted data without performing a full-cost SGD on the remaining data.
The unlearning algorithm is shown for reference in Algorithm A3. As seen in line 9, the term is approximated using the quasi-Newton L-BFGS optimization algorithm with the terms and , which were stored during training. However, there exist two issues with this approximation. First, the L-BFGS algorithm requires a history of accurate computations to produce an effective approximation. Second, consecutive approximations lead to errors accumulating after several iterations in SGD. The first issue is addressed by using a burn-in period of iterations, during which the exact gradient on the remaining dataset is computed. The latter issue is addressed by periodically computing the exact gradient after every iterations (following the burn-in period). These are seen from lines 3 to 7. Moreover, in order to use the above DeltaGrad algorithm for subsequent data deletions, the terms and that were previously stored in the disk are updated after unlearning the deleted data . This is described in lines 6 and 7 and lines 13 and 14.
| Algorithm A3:DGApprox |
 |
Appendix A.3.3. Trade-Off Parameters
As described in Table 1, the primary parameter chosen for the DeltaGrad method was the periodicity . Based on the discussion of the hyper-parameter of the DeltaGrad in [5], the ideal parameter would be the training mini-batch size. However, this would result in a non-standard training stage in the unlearning pipeline for the DeltaGrad, which in turn would prevent any comparison with the other unlearning methods. Therefore, upon fixing the common training stage, we choose the hyper-parameter that best represents the trade-off between effectiveness and efficiency. The remaining candidate parameters are the burn-in period and the size of the history for the L-BFGS algorithm h. Following [5], we fix for all datasets, and the values of are presented in Table A1.

Table A1.
Values of DeltaGrad burn-in period parameter .
Table A1.
Values of DeltaGrad burn-in period parameter .
| Dataset | MNISTb | MNIST | COVTYPE | HIGGS | CIFAR2 | EPSILON |
|---|---|---|---|---|---|---|
| 10 | 20 | 10 | 500 | 20 | 10 |
Appendix B. Experimental Set-Up
In this section, we discuss the additional details regarding the experiments and the implementation of the common unlearning pipeline.
Training
Ensuring the training phase of the common unlearning pipeline, especially the optimization of each unlearning method, is a difficult task. As mentioned in Section 4.2, Influence and Fisher require SGD convergence, and DeltaGrad can only use vanilla SGD. The additional constraints come from the DeltaGrad method. In [5], it is described that a smaller mini-batch size leads to lower approximation and hence lower effectiveness. However, choosing a full-batch gradient descent update as described in Equation (3) to ensure the best performance of the DeltaGrad method leads to the requirement of a large number of epochs to achieve convergence for Influence and Fisher. This is computationally expensive both in the calculation of full-batch gradients for the large datasets such as epsilon and higgs and the number of epochs required in total to reach convergence. Ideally, to reduce the impact of the latter, we would fix a number of epochs and then select a larger learning rate to compensate for the slower average gradient updates. However, we experimentally found that increasing the learning rate beyond one has a significant impact on the performance of DeltaGrad. This is primarily because the error in the approximate SGD step is amplified as the learning rate is increased beyond the optimal learning rate (which results in an increased number of epochs to achieve the same convergence). These constraints and limitations led us to fix the learning rate to one and choose large enough mini-batches (for DeltaGrad performance) while keeping the number of epochs low (for computational effort) while using a small validation dataset of the initial training data . The chosen values of the mini-batch size and the number of epochs for each dataset are described in Table A2.

Table A2.
Values of training parameters common for all unlearning methods.
Table A2.
Values of training parameters common for all unlearning methods.
| Dataset | Epochs | Mini-Batch Size |
|---|---|---|
| mnistb | 1000 | 1024 |
| mnist | 200 | 512 |
| covtype | 200 | 512 |
| higgs | 20 | 512 |
| cifar2 | 500 | 512 |
| epsilon | 60 | 512 |
Appendix C. Extended Deletion Distribution Results
We present the extended results for the uniform-random and uniform-informed deletion distributions in Figure A1. We increased the fraction of data deleted from to . We see that the drop in both and only occurred when we deleted beyond of the initial training data. We also clearly see that the drop in both metrics was much steeper for the uniform-informed distribution compared with the uniform-random distribution. This indicates that the informed deletions were deleting outliers that were required by the ML model to effectively classify samples.
Appendix D. Extended Experimental Results
In this section, we provide the extended results of the experiments discussed in Section 4.
Appendix D.1. Deletion Volumes
As mentioned in Section 4, we evaluated the unlearning methods for three volumes of deletion corresponding to different drops in test accuracy of the retrained model. In Table A3, we present both the fraction and the volume of deletion corresponding to , and drops in test accuracy when targeted-informed deletions were used. They are named small, medium and large volumes of deletion, respectively.
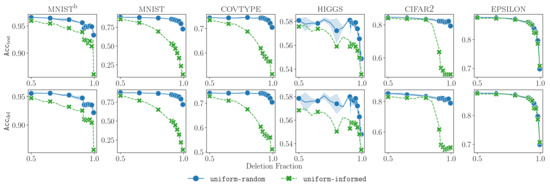
Figure A1.
Extended deletion distribution results. Deletion fraction varied from to . Only uniform-random and uniform-informed deletion distribution results are reported.

Table A3.
Fraction and volume of deleted data of initial data volume, corresponding to different drops in for fully retrained model and targeted-informed deletion.
Table A3.
Fraction and volume of deleted data of initial data volume, corresponding to different drops in for fully retrained model and targeted-informed deletion.
| Dataset | Small 1% Drop | Medium 5% Drop | Large 10% Drop | |||
|---|---|---|---|---|---|---|
| Fraction | Fraction | Fraction | ||||
| mnistb | 0.2 | 2396 | 0.3 | 3594 | 0.375 | 4493 |
| mnist | 0.01 | 600 | 0.05 | 3000 | 0.075 | 6000 |
| covtype | 0.05 | 26,145 | 0.10 | 52,291 | 0.15 | 78,436 |
| higgs | 0.01 | 99,000 | 0.05 | 495,000 | 0.10 | 990,000 |
| cifar2 | 0.05 | 500 | 0.125 | 1250 | 0.2 | 2000 |
| epsilon | 0.1 | 4000 | 0.2 | 8000 | 0.25 | 10,000 |
Appendix D.2. Efficiency and Certifiability Trade-Off
Here, we present the extended results for all volumes of deletion and as the efficiency parameter is varied in Figure A2. The legend for is the same as that displayed in Figure 3. The key takeaway here is that the trends described in Section 6 were similar for the small and medium volumes of deletion.
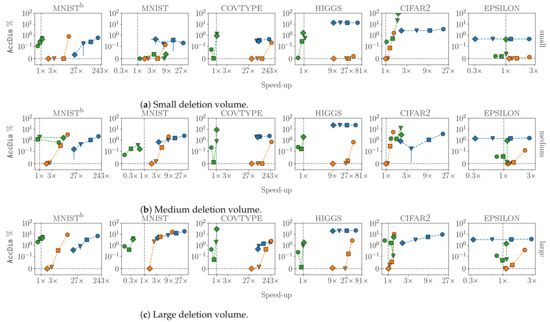
Figure A2.
Efficiency and certifiability trade-off results for at different volumes of deletion: (a) small, (b) medium and (c) large. AccDis is reported on the y-axis and the speed-up in running time on the x-axis. The legend is the same as in Figure 3.
Appendix D.3. Efficiency and Certifiability Trade-Off
Appendix E. When to Retrain Strategies
The implementation details for the pipeline experiments are shown in Table A4.

Table A4.
Batch sizes and thresholds for the pipeline experiments.
Table A4.
Batch sizes and thresholds for the pipeline experiments.
| Dataset | Batch Size | for AccErr | for AccDis |
|---|---|---|---|
| mnistb | 100 | ||
| mnist | 100 | ||
| covtype | 1000 | ||
| higgs | 10,000 | ||
| cifar2 | 100 | ||
| epsilon | 500 |
Appendix E.1. AccDis Strategy
The empirical correlations between AccDis and when targeted-random deletions were performed and the Fisher unlearning method () while the deletion ratio was varied are shown in Table A5. As noted in Section 7, the Pearson correlations are high for all datasets excluding higgs. The low Pearson correlation values for the higgs dataset can be attributed to the the variance resulting from the selection of the deleted class seen in Figure 2. We postulate that this is because of the particular way that missing values have been treated for the higgs dataset. Data points that have missing feature values disproportionately belong to class 1. Therefore, this tends to cause a steeper drop in accuracy when data from class 1 is targeted. In turn, this leads to the lower predictive capability of the linear estimation strategy described in Equation (8).
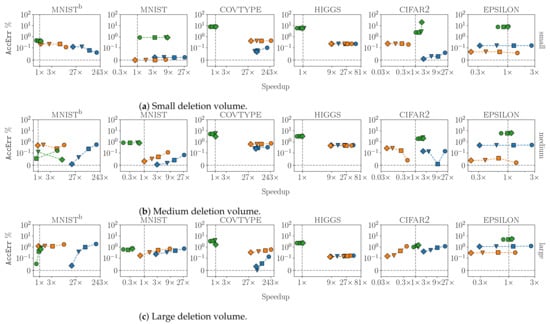
Figure A3.
Efficiency and effectiveness trade-off results for at different volumes of deletion: (a) small, (b) medium and (c) large. AccErr is reported on the y-axis and the speed-up in running time on the x-axis. The legend is the same as in Figure 3.
The extended results of the pooled mean and the speed-up are shown in Table A6 and Figure A5, respectively. In Figure A5, we observe that for the uniform-informed deletion distribution, more pipeline restarts were triggered compared with uniform-random, a consequence of the deletion of more informative samples, leading to a larger estimated disparity .

Table A5.
Correlation between and AccDis with targeted-random deletion distribution for the Fisher method.
Table A5.
Correlation between and AccDis with targeted-random deletion distribution for the Fisher method.
| Dataset | Pearson Corr. | Spearman Corr. |
|---|---|---|
| mnistb | 0.963 | 0.612 |
| mnist | 0.999 | 1 |
| covtype | 0.881 | 0.964 |
| higgs | 0.478 | 0.892 |
| cifar2 | 0.938 | 0.976 |
| epsilon | 0.8787 | 0.891 |
Appendix E.2. AccErr Strategy
Here, we describe a strategy to monitor and trigger the pipeline to restart based on the effectiveness of the updated model .
When a subset of the existing data is deleted, the updated model is obtained from the unlearning stage of the pipeline. We propose an estimate of AccErr using the test accuracy of initial model , defined in Equation (7). The is stored during the initialization of the pipeline, when is obtained after training on the initial dataset . If the computed does not exceed the predefined threshold, then is employed for inference; otherwise, the pipeline restarts, obtaining a new by training on the remaining dataset . The is also recomputed and updated, and the pipeline resumes.
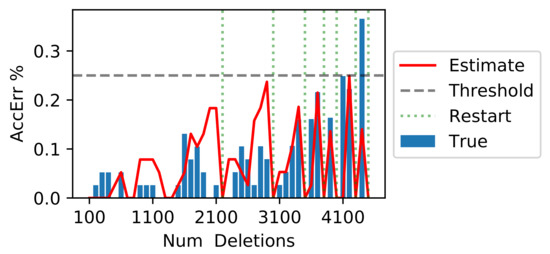
Figure A4.
AccErr strategy pipeline run at for the mnistb dataset, as well as Fisher method with and targeted-informed deletions.
An example of the pipeline’s execution is shown in Figure A4 for the mnistb dataset and targeted-random deletions at a predefined threshold of . We must note that the pipeline estimate of the AccErr is zero, corresponding to the restarts of the pipeline. This indicates that at that iteration, the updated model’s was exceeding the threshold, and a restart was triggered. These pipeline restarts require retraining from scratch and hence increase the running time of the pipeline.
In Figure A6, we report the speed-up for different values of and deletion distributions as a function of the number of deletions. Here, a speed-up of 1× corresponds to retraining at every iteration of the pipeline. Observe how the lower values of lead to earlier drops in the speed-up, indicating the pipeline has been reset. Moreover, we observed this decrease in speed-up more significantly for the more adversarial deletion distributions (targeted-random and targeted-informed). In the less adversarial deletion distribution (uniform-random and uniform-informed), we observed only the smallest led to drops in the speed-up, indicating that the strategy was adaptive. Lastly, even for the lowest value of and the most adversarial deletion distribution of targeted-informed, we observed for all datasets a significant speed-up compared with always retraining.
In Figure A4, we observe that as the number of deletions increased, the underestimated the true AccErr of the model. We quantified these relative estimation errors of AccErr for a given threshold as
where AccErr is the true AccErr computed using the fully retrained model . A relative estimation error percentage of for implies that the true AccErr was . For each run of the pipeline, we computed the mean (e.g., the mean was for the pipeline run in Figure A4). Then, for multiple pipeline runs for different random seeds of and the deletion distributions, we reported the mean of the relative estimation error. In Table A7, we report the mean of for each dataset and the value of for different deletion distributions. The largest mean corresponded to the smallest value of , while larger values of had very small mean values across deletion distributions. We note that the higgs dataset had significantly larger mean values as a result of the larger number of deletions in each batch size. Selecting a larger threshold resulted in lower estimation errors.

Table A6.
Pooled mean of % for the AccDis strategy at different thresholds . Noise parameter .
Table A6.
Pooled mean of % for the AccDis strategy at different thresholds . Noise parameter .
| Dataset | Uniform Random | Uniform Informed | Targeted Random | Targeted Informed | |
|---|---|---|---|---|---|
| mnistb | 1.0 | ||||
| 2.0 | |||||
| 5.0 | |||||
| mnist | 1.0 | ||||
| 2.0 | |||||
| 5.0 | |||||
| covtype | 1.0 | ||||
| 2.0 | |||||
| 5.0 | |||||
| higgs | 10.0 | ||||
| 20.0 | |||||
| 50.0 | |||||
| cifar2 | 1.0 | ||||
| 2.0 | |||||
| 5.0 | |||||
| epsilon | 1.0 | ||||
| 2.0 | |||||
| 5.0 |
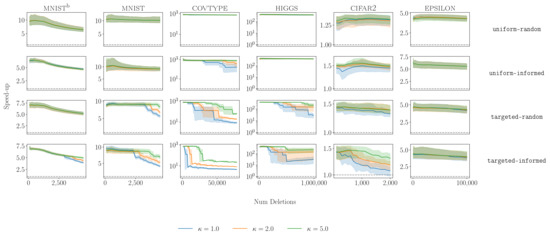
Figure A5.
Speed-up of AccDis strategy at different thresholds . Rows correspond to different deletion distributions. Dashed line indicates speed-up of 1×. Note that for higgs, .

Table A7.
Pooled mean of % of the AccErr strategy for each threshold . Noise parameter .
Table A7.
Pooled mean of % of the AccErr strategy for each threshold . Noise parameter .
| Dataset | Uniform Random | Uniform Informed | Targeted Random | Targeted Informed | |
|---|---|---|---|---|---|
| mnistb | 0.25 | ||||
| 0.50 | |||||
| 1.00 | |||||
| mnist | 0.25 | ||||
| 0.50 | |||||
| 1.00 | |||||
| covtype | 0.25 | ||||
| 0.50 | |||||
| 1.00 | |||||
| higgs | 0.25 | ||||
| 0.50 | |||||
| 1.00 | |||||
| cifar2 | 0.25 | ||||
| 0.50 | |||||
| 1.00 | |||||
| epsilon | 0.25 | ||||
| 0.50 | |||||
| 1.00 |
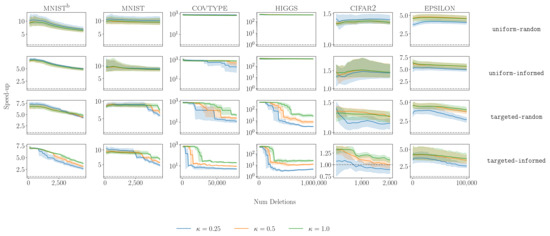
Figure A6.
Speed-up of AccErr strategy at different thresholds . Rows correspond to different deletion distributions. Dashed line indicates speed-up of 1×.
References
- Mantelero, A. The EU Proposal for a General Data Protection Regulation and the roots of the “right to be forgotten”. Comput. Law Secur. Rev. 2013, 29, 229–235. [Google Scholar] [CrossRef] [Green Version]
- Council of European Union. 2018 Reform of EU Data Protection Rules. Available online: https://ec.europa.eu/commission/sites/beta-political/files/data-protection-factsheet-changes_en.pdf (accessed on 26 May 2022).
- Golatkar, A.; Achille, A.; Soatto, S. Eternal Sunshine of the Spotless Net: Selective Forgetting in Deep Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Guo, C.; Goldstein, T.; Hannun, A.; Van Der Maaten, L. Certified Data Removal from Machine Learning Models. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Volume 119, pp. 3832–3842. [Google Scholar]
- Wu, Y.; Dobriban, E.; Davidson, S. DeltaGrad: Rapid retraining of machine learning models. In Proceedings of the 37th International Conference on MachineLearning, Virtual, 13–18 July 2020; Volume 119, pp. 10355–10366. [Google Scholar]
- Tsai, C.H.; Lin, C.Y.; Lin, C.J. Incremental and Decremental Training for Linear Classification. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 343–352. [Google Scholar] [CrossRef]
- Cauwenberghs, G.; Poggio, T. Incremental and Decremental Support Vector Machine Learning. In Proceedings of the 13th International Conference on Neural Information Processing Systems, Virtual, 6–14 December 2021; MIT Press: Cambridge, MA, USA, 2000; pp. 388–394. [Google Scholar]
- Karasuyama, M.; Takeuchi, I. Multiple Incremental Decremental Learning of Support Vector Machines. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–12 December 2009; Volume 22. [Google Scholar]
- Schelter, S. “Amnesia”—Towards Machine Learning Models That Can Forget User Data Very Fast. In Proceedings of the Conference on Innovative Data Systems Research (CIDR), Amsterdam, The Netherlands, 12–15 January 2020; p. 4. [Google Scholar]
- Cao, Y.; Yang, J. Towards Making Systems Forget with Machine Unlearning. In Proceedings of the 2015 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 17–21 May 2015; pp. 463–480. [Google Scholar] [CrossRef]
- Bourtoule, L.; Chandrasekaran, V.; Choquette-Choo, C.A.; Jia, H.; Travers, A.; Zhang, B.; Lie, D.; Papernot, N. Machine Unlearning. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 141–159. [Google Scholar] [CrossRef]
- Golatkar, A.; Achille, A.; Soatto, S. Forgetting Outside the Box: Scrubbing Deep Networks of Information Accessible from Input-Output Observations. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 383–398. [Google Scholar]
- Golatkar, A.; Achille, A.; Ravichandran, A.; Polito, M.; Soatto, S. Mixed-Privacy Forgetting in Deep Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 792–801. [Google Scholar]
- Martens, J. New Insights and Perspectives on the Natural Gradient Method. J. Mach. Learn. Res. 2020, 21, 1–76. [Google Scholar]
- Izzo, Z.; Anne Smart, M.; Chaudhuri, K.; Zou, J. Approximate Data Deletion from Machine Learning Models. Proceedings of The 24th International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; Volume 130, pp. 2008–2016. [Google Scholar]
- Chaudhuri, K.; Monteleoni, C. Privacy-preserving logistic regression. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 2–12 December 2009; Volume 21. [Google Scholar]
- Koh, P.W.; Liang, P. Understanding Black-box Predictions via Influence Functions. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1885–1894. [Google Scholar]
- Wu, Y.; Tannen, V.; Davidson, S.B. PrIU: A Provenance-Based Approach for Incrementally Updating Regression Models. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; ACM: Portland, OR, USA, 2020; pp. 447–462. [Google Scholar] [CrossRef]
- Neel, S.; Roth, A.; Sharifi-Malvajerdi, S. Descent-to-Delete: Gradient-Based Methods for Machine Unlearning. In Proceedings of the 32nd International Conference on Algorithmic Learning Theory, Paris, France, 16–19 March 2021; Volume 132, pp. 931–962. [Google Scholar]
- Graves, L.; Nagisetty, V.; Ganesh, V. Amnesiac Machine Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11516–11524. [Google Scholar]
- Brophy, J.; Lowd, D. Machine Unlearning for Random Forests. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 1092–1104. [Google Scholar]
- Nguyen, Q.P.; Low, B.K.H.; Jaillet, P. Variational Bayesian Unlearning. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 16025–16036. [Google Scholar]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Byrd, R.H.; Nocedal, J.; Schnabel, R.B. Representations of quasi-Newton matrices and their use in limited memory methods. Math. Program. 1994, 63, 129–156. [Google Scholar] [CrossRef]
- Mokhtari, A.; Ribeiro, A. Global convergence of online limited memory BFGS. J. Mach. Learn. Res. 2015, 16, 3151–3181. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C. MNIST Handwritten Digit Database 2010. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 26 May 2022).
- Krizhevsky, A.; Nair, V.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Available online: citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf (accessed on 26 May 2022).
- Collobert, R.; Bengio, S.; Bengio, Y. A Parallel Mixture of SVMs for Very Large Scale Problems. Neural Comput. 2002, 14, 1105–1114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baldi, P.; Sadowski, P.; Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 2014, 5, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, G.X.; Ho, C.H.; Lin, C.J. An Improved GLMNET for L1-regularized Logistic Regression. J. Mach. Learn. Res. 2012, 13, 1999–2030. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Freedman, D.; Pisani, R.; Purves, R. Statistics (International Student Edition), 4th ed.; WW Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Tarun, A.K.; Chundawat, V.S.; Mandal, M.; Kankanhalli, M. Fast Yet Effective Machine Unlearning. arXiv 2021, arXiv:2111.08947. [Google Scholar]
- Baumhauer, T.; Schöttle, P.; Zeppelzauer, M. Machine unlearning: Linear filtration for logit-based classifiers. arXiv 2020, arXiv:2002.02730. [Google Scholar]
- Felps, D.L.; Schwickerath, A.D.; Williams, J.D.; Vuong, T.N.; Briggs, A.; Hunt, M.; Sakmar, E.; Saranchak, D.D.; Shumaker, T. Class Clown: Data Redaction in Machine Unlearning at Enterprise Scale. arXiv 2020, arXiv:2012.04699. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).