Abstract
Datasets with thousands of features represent a challenge for many of the existing learning methods because of the well known curse of dimensionality. Not only that, but the presence of irrelevant and redundant features on any dataset can degrade the performance of any model where training and inference is attempted. In addition, in large datasets, the manual management of features tends to be impractical. Therefore, the increasing interest of developing frameworks for the automatic discovery and removal of useless features through the literature of Machine Learning. This is the reason why, in this paper, we propose a novel framework for selecting relevant features in supervised datasets based on a cascade of methods where speed and precision are in mind. This framework consists of a novel combination of Approximated and Simulate Annealing versions of the Maximal Information Coefficient (MIC) to generalize the simple linear relation between features. This process is performed in a series of steps by applying the MIC algorithms and cutoff strategies to remove irrelevant and redundant features. The framework is also designed to achieve a balance between accuracy and speed. To test the performance of the proposed framework, a series of experiments are conducted on a large battery of datasets from SPECTF Heart to Sonar data. The results show the balance of accuracy and speed that the proposed framework can achieve.
1. Introduction
The current capacity of cloud services has allowed the storage of large quantities of data about any possible phenomenon. However, as always, the quality of such data is not the best that can be achieved [1,2,3]. Thus, there is interest in improving such data [4,5,6,7], given that it is simpler to improve its quality than produce complex algorithms to handle low quality datasets. Furthermore, techniques such as Machine Learning have played a fundamental role in exploiting the potential of such datasets. These techniques consist mainly of identifying patterns on the data to generate valuable insights to solve problems where Machine Learning is applied to [8,9,10]. However, despite its success, Machine Learning algorithms depend on various pre-processing algorithms to reduce important issues in learning such datasets. One of the most important is known as the curse of dimensionality, which refers to the fact that, when you have a high number of dimensions in your data, the more complex the interactions are and the more data you need [11,12]. Basically, such interactions become internal noise in the datasets, decreasing the performance of Machine Learning algorithms. Thus, the need to select the most informative features, dimensionality reduction, in such datasets in order to improve performance on the Machine Learning algorithms.
There are three kinds of features in a dataset: relevant, irrelevant, and redundant [4]. Therefore, dimensionality reduction is one of the most popular techniques to remove noisy and unnecessary features. Dimensionality reduction techniques can be categorized into feature extraction and feature selection [13]. Feature extraction approaches attempt to generate new features from the original features such that they are more informative. On the other hand, feature selection aims to select a small subset of features minimizing possible redundancies and maximizing relevant features without incurring a loss of information. Feature extraction and selection methods are capable of improving learning performance on many models by lowering computational complexity, building better generalizations and decreasing required storage. Next, we will chronologically mention some of the most important algorithms to deal with the curse dimensionality.
Principal Component Analysis (PCA) [14] was developed by Karl Pearson in 1901. This proposal was the first known unsupervised feature extraction method. A couple of years earlier, Pearson also introduced the Pearson correlation coefficient [15], which allows us to find a linear relationship between two variables and could be considered one of the first steps for supervised feature selection.
Around 1936, Fisher developed the linear discriminant analysis (LDA) [16], which is the first supervised feature extraction method, but it was only designed for two classes. In 1948, C.R. Rao [17] extended the algorithms’ LDA to generalize for multi-class linear discriminant analysis in order to treat problems in biological classification. A couple of years later, the kernel discriminant analysis would establish the idea of linear discriminant analysis.
ST Roweis and LK Saul, in 2000, developed locally linear embedding [18] for nonlinear dimensionality reduction. In the same year, De Silva, V. Langford and J.C developed a manifold-based reduction method called Isomap [19]. In 2003, M. Belkin and P. Niyogi successfully applied Laplacian eigenmaps [20] for dimensionality reduction in data representation.
In 2005, Hanchuan Peng proposed the feature selection algorithm called minimum redundancy maximum relevance (mRMR) [21] that introduces the importance of removing not only irrelevant but also redundant features.
Finally, Van der Maaten introduced t-SNE in 2008 [22], a feature extraction technique that reduces the number of dimensions preserving the local structure, something very useful for visualizing datasets with large feature sets. In 2018, Leland McInnes introduced UMAP [23], an improvement of t-SNE, a technique that also preserves global structure.
This work proposes a method of feature selection using two general approaches: the first one is called individual evaluation, also known as feature ranking, and the second is a subset evaluation [24]. In feature ranking, the weight of every feature is assigned according to its relevance and in subset evaluation, candidate feature subsets are constructed using heuristic search strategies. The optimal subset is selected by some pre-selected filter function and, typically, this function tries to measure the discriminating ability of a single or subset of features to distinguish the different class labels of a problem [6]. Thus, in this paper, we present a novel framework that employs different measures in order to accelerate the process of ranking features. The main contributions of the proposed framework are:
- The use of a cascade of Mutual Information Correlation (MIC) algorithms and the Pearson Correlation to balance speed with accuracy in the process of feature selection;
- A search strategy based in the MIC Score to remove irrelevant and redundant features by a novel combination of the previous algorithms;
- All this packed in a framework for easy deployment and use.
All this makes the proposed framework a useful tool for feature selection in many possible setups.
2. Background
Generally, the feature selection measures are categorized into two groups: The first ones measure the possible dependence and correlation between two features [21,25,26], and the second ones consist of using metrics to measure possible similarities or dissimilarities between them [7,27]. In this work, we take the decision to use the first approach by developing a fast framework for feature selection that identifies relevant features, and remove redundant and irrelevant ones. This choice is based on the fact that it is simpler to calculate dependence and correlation between features than first calculating a representative subspace of a feature space, then to define a metric on it. A classic example of the use of correlation is the Pearson Correlation [28,29], and a natural evolution of it is the MIC [30]. Thus, in the following sections, we review all the basic methods behind the proposed framework.
2.1. Pearson Correlation
The Pearson correlation [28,29] coefficient has been widely used to understand relationships between pairs of variables. Given its ease to calculate and interpret, the Pearson correlation is widely used by statisticians to calculate linear correlation between features. The simplicity of the Pearson correlation r can be observed in (Equation (1)).
Unfortunately, the Pearson correlation is not a useful metric in general when non-linearities are involved. Actually, the Pearson correlation is limited to the detection of linear relationships between variables, and it is not suitable for detecting variable dependencies that are not linear. Fortunately, its computation is quite fast and produces similar results to MIC (Section 2.3) when there is a linear relationship and low noise [5] on the features. For example, (Figure 1) shows an example of two variables with a linear relationship and its corresponding Pearson score.
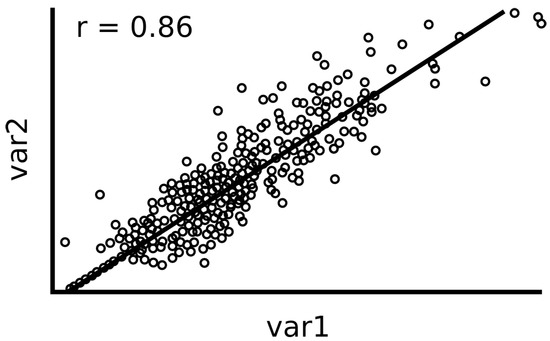
Figure 1.
A noisy linear relation and its corresponding Pearson score.
2.2. Mutual Information (MI)
Equation (2) is a well-known correlation measure that uses the Shannon entropy [31] to obtain a wider range of relations between random variables.
Although this measure is not normalized in the interval , there are versions of it where their outputs are bounded into such interval. For example, Equation (3) is a normalized version of the Mutual Information.
where is the entropy of X.
2.3. Maximal Information Coefficient
The MIC [5,30] is a measure of correlation among two variables. Its general idea is to establish whether two variables (features) are related linearly or not linearly. For this, a grid is generated and drawn over their dispersion graph to compute the degree of relationship between them by square grid. Since the number of possible grids can be large, it is necessary to find the best number of grid partitions (grid resolution) and their best location (partition placements). Thus, to compute MIC efficiently, all the grids are explored using the following constraint , where n is the total amount of points representing the data of the tuple. This restriction has been shown to work well in practice for several problems [5]. Similarly, for each resolution explored, the partition positions that produce the higher mutual information must be found (Figure 2). Then, the indicator of mutual information is computed by using the following equation (Equation (4)).
where X and Y represent random variables, is the joint probability for the regions x and y, respectively, while and are their marginal probability distributions [5]. (Figure 3) shows a possible partition. The regions marked in blue correspond to the column and row , respectively. The quadrant for the intersection of column x and row y is highlighted in yellow with data points. With this information, it is easy to compute the following probabilities , and . Substituting these probabilities in (Equation (4)), the mutual information of the grid can be calculated. The following figure (Figure 4) shows the complete procedure to compute the mutual information for this example.
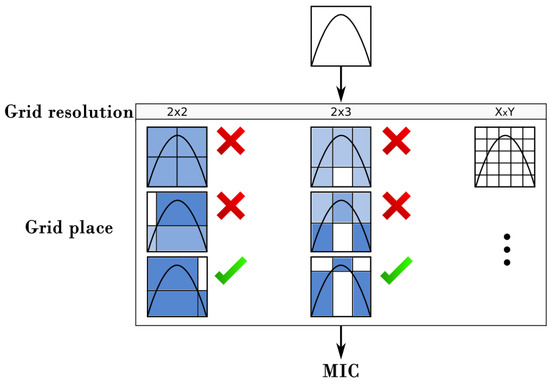
Figure 2.
Partition and placement for the computation of the MIC metric.
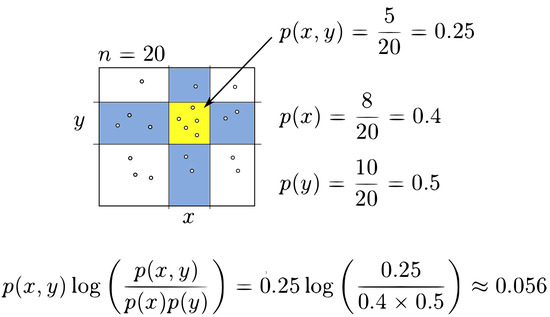
Figure 3.
Partial mutual information computation for a grid.
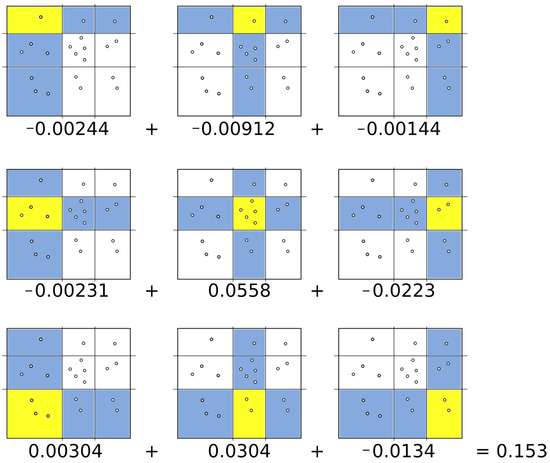
Figure 4.
Mutual information computation for a grid.
This operation is repeated for each resolution saving the higher value obtained. Then the higher mutual information score is normalized between and stored in a characteristic matrix . Finally, the value of MIC is considered as the higher normalized mutual information value contained in matrix M. Thus, the MIC metric is a value in the interval .
Unfortunately, the exhaustive computation of MIC is unpractical for large datasets. Therefore, it is preferable to use approximation algorithms to estimate the MIC metric. These algorithms are significantly faster than the use of exhaustive computation. However, usually slower estimation algorithms have better accuracy than the faster ones. Thus, we propose, in this framework, an equilibrium between slow and fast algorithms for the MIC to obtain a better performance.
2.4. Fast and Accurate MIC Estimation
With the intention of finding a good balance between accuracy and speed, we proposed a method that uses a sequence of algorithms to speed up the computation of the MIC metric. Each algorithm of the sequence excels at dealing with a special case of correlation. When analyzing the correlation of all the possible pairs of features in the dataset, the sequence is applied from the fastest algorithm to the slowest one. At each step of the sequence, some feature pairs are pruned when a reasonably good estimation of its MIC metric is achieved. This prevents unnecessary computation of the slower algorithms over all the pairs; thus, accelerating the MIC estimation while retaining a good amount of accuracy. The MIC estimation sequence is composed of the following algorithms: Pearson Correlation, ParallelMIC and SAMIC.
Section 3 shows the complete criteria used to prune feature pairs on each process stage. The next subsections detail the nature of the algorithms tested and their role in the final computation of the MIC metric.
2.4.1. ApproxMaxMI
ApproxMaxMI [5] is a heuristic algorithm to approximate the optimal value of the MIC metric. The idea behind this heuristic is to consider one axis of the analyzed grids as being equally partitioned while optimizing the partition placement of the other axis. The optimization made for each grid axis is performed using a dynamic programming approach. Then, by repeating the process, the previously unfixed axis is refitted and equipartitioned. At the end, the maximum of the two obtained scores is used as the final MIC approximation [5]. In the context of ApproxMaxMI, an axis is equipartitioned if all of the regions induced by its partitions contain the same number of data points. Finally, ApproxMaxMI has been implemented on various software packages including Minerva for R and MINEPY for Python [32].
2.4.2. ParallelMIC
ParallelMIC is a parallelized version of ApproxMaxMI, and accelerates the computation of MIC by calculating the score for various feature pairs in parallel. To some extent, ParallelMIC is based on RapidMIC [33]. The difference between the ParallelMIC and RapidMIC is that it computes MIC by calculating multiple grid resolutions at the same time. However, the performance of ParallelMIC is slightly better than RapidMIC and, actually, both algorithms are equivalent when included in the MIC estimation sequence.
For the purpose of this framework, an open source implementation of ParallelMIC available at https://github.com/ivangarcia88/ffselection, has been written in C++. RapidMIC is also an open source implementation, and it is available in the following URL: https://github.com/HelloWorldCN/RapidMic (accessed on: 15 March 2021), and it is part of MICTools software discussed in section (Section 4). Further, table (Table 1) compares RapidMIC and ParallelMIC against software packages that compute MIC by using ApproxMaxMI implementations. There, N determines the number of samples in each dataset, and M the amount of records in each variable. The time reported does not include the reading time of the dataset into the main memory.

Table 1.
Performance comparison (in seconds) for MIC calculations over several software packages.
2.5. SAMIC
SAMIC is an MIC estimation algorithm based on Simulated Annealing. Just as ApproxMaxMI, SAMIC tries to find MIC by optimizing every possible grid resolution (Section 2.3 and Section 2.4.1). It is based on Simulated Annealing [34] by using random choices over a temperature decay function to enforce the exploration of the whole solution space. In its simplest form, SAMIC will proceed as follows at every grid resolution while keeping track of the maximum mutual information score found at every step:
- Set temperature and equipartition grid in both axes;
- Compute the mutual information score of the current grid placement;
- Generate a random neighboring grid placement and compute its new score (more neighbors can be generated at this step if more precision is needed);
- Compare both and :
- If , then .
- If , generate a random choice and make if and only if .
- Update temperature where c is a cooling factor between 0; and
- Repeat steps 2 to 6 until .
Algorithm (1) shows the complete pseudocode of SAMIC when running over a single pair of variables.
In the context of SAMIC, given any grid G placement, a neighbor grid placement is a new placement with one and only one differently placed partition for each axis. Thus, Simulated Annealing guarantees finding the optimal solution to the optimization problem if the temperature decay is sufficiently slow, and the amount of neighbors explored at each temperature change is vast. However, in a practical setup, the decay ratio and number of explored neighbors are constrained to ensure the termination of the algorithm in a reasonable time. SAMIC is way slower than ParallelMIC, but is in fact more precise.
3. A Novel Approach for Feature Selection
In this section, we explain in more detail the proposed framework for feature selection. For this, we present the following figure (Figure 5) that shows the steps of the proposed framework.

Figure 5.
MIC based feature selection process.
The proposed framework works in the following way to obtain the selected features:
- First, feature are ranked by the ParallelMIC score (Section 2.3). This is done to be able to select possible relevant features;
- Second, these features are pruned by the use of cut strategies to remove the irrelevant ones (Section 3.3). Although this allows us to remove irrelevant features, it is necessary to remove redundant features that can provide the same information;
- Third, the use of the Pearson Correlation, ParallelMIC and SAMIC to remove the redundant features at the pipeline by the use of mutual information (Section 3.1) and the idea of clustering.
The final result of this process is the set of features with relevant and non-redundant information. This results in a fast feature selection pipeline to improve classification problems.
3.1. Ranking Features
The first step is feature scoring; this step compares every feature with the target to determine which features are relevant. If a feature has a high score it is considered relevant, otherwise it is considered irrelevant. Even MIC Score is limited to the value between the range [0, 1] and it is not trivial to determine a threshold to define if a feature is relevant or not.
| Algorithm 1: SAMIC One Pair |
 |
3.2. Removing Irrelevant Features
Search strategies such as forward selection and sequential backward elimination [35] could be useful to determine a candidate subset of features, but they could be quite time consuming. A faster option to obtain a good (but not optimal) feature subset is to cut; these strategies require that features are ranked. The following cuts methods are implemented in our framework:
- Cut based in a selected number of features. It returns the n best features according to MIC {, …}, where n is a number selected by the user;
- Cut based on biggest distance correlation. It compares the score of every variable with the subsequent and makes the cut where the biggest difference between them is presented;
- Cut based on the best evaluation using classifiers. In addition to the last two methods R these techniques use classifiers algorithms in order to compare subsets given by cuts, then selects the best of them;
- -
- Cut distance with validation. This cut method is based on the biggest distance correlation. Then, it generates multiple subsets based on the n-biggest score difference and selects the best of them using a classifier;
- -
- Binary Cut. This method tries to reach an optimal cut using binary search over the set R returning the best subset according to a particular classifier;
- -
- Optimal Cut. It is based on a selected number of features, red but in this case n change its value in every iteration from 1 to x and returns the best subset according to the selected classifier.
3.3. Removing Redundant Features
MIC is symmetric; this means . This property is very useful because, when comparing if two features are related, the order of the arguments using MIC does not matter. MIC is not transitive in general, but when scores are close to 1, the behavior is similar to a transitive property. In other words if is close to 1 and is close to 1, then is more likely close to 1. This provides the opportunity of grouping features where the features in group are highly correlated. Creating groups and selecting only the feature with a higher correlation to the target is how our framework deals with redundant features. The full process is described in Algorithm 3.
In this step the number of pair features could be quadratic to the number of relevant features, which is the reason in this step we used a cascade of scores to improve the speed performance. The main idea is to apply the following algorithm from the fastest to the slowest with each step pruning some pair computation. The sequence is composed of the following algorithms:
- Pearson Correlation.
- ParallelMIC.
- SAMIC.
The process is described in Algorithm 4. This is a heuristic process based on the correlation of the comparative between Pearson score vs MIC score [5]. The cascade of Algorithm 2 is mainly a sequential filter that tries to avoid using computationally expensive algorithms, pruning pairs of features on each step. Figure 6 illustrates the process.
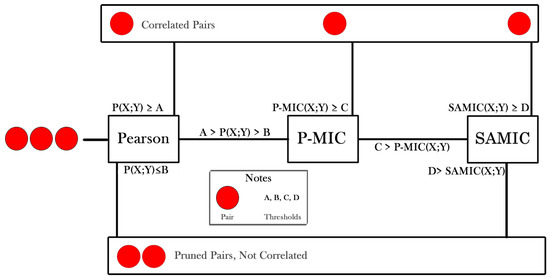
Figure 6.
Algorithm cascade for scoring redundant features.
The red circles refer to a pair of features. A,B,C,D are thresholds, used to prune pairs. It is important to notice that this process could lead to a false negative correlation; it is the price to speed up this process. We notice experimentally that keeping redundant features is less sensitive than removing redundant features when dealing with the curse of dimensionality to tune up a machine learning model.
| Algorithm 2: MIC Estimation Sequence |
 |
| Algorithm 3: Detect Groups |
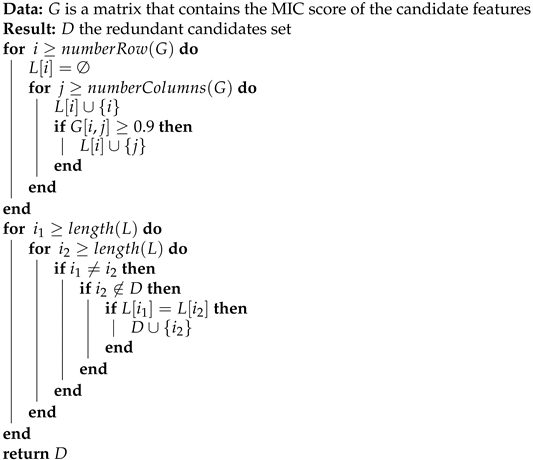 |
| Algorithm 4: Feature Selection |
 |
4. MICTools and MICSelect Software Architecture
In order to test and refine the feature selection and MIC estimation techniques presented in this project, a pair of software packages were developed. MICTools and MICSelect are computer programs to perform efficient MIC calculations and feature selection, respectively.
MICTools is implemented in C++ and allows the parallel execution of the previous algorithm sequence (Pearson, ParallelMIC and SAMIC). MICSelect is implemented in Python and performs the feature selection tasks; it relies heavily on MICTools to perform its required MIC calculations. The communication between MICSelect and MICTools is achieved by a Python wrapper, which is written with the Boost Python library and the Distutils build system. Even though MICSelect integrates MICTools, it can be used independently and is compiled as a standalone application.
In order to unify and guarantee the correct execution of both MICTools and MICSelect, a software architecture has been developed, which is detailed in (Figure 7).
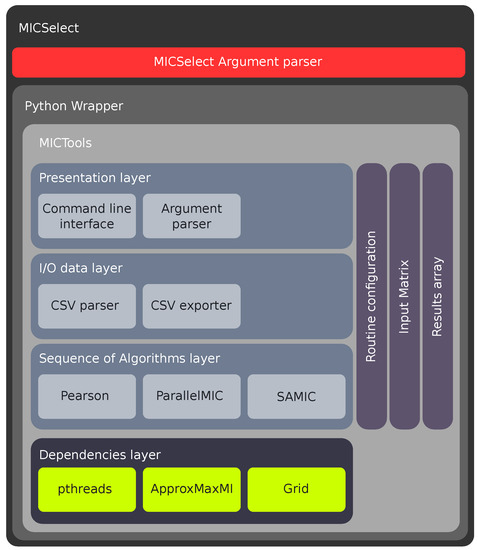
Figure 7.
Architecture overview.
This architecture defines a common set of patterns and data structures to handle the data between algorithms and manage their results. It also allows MICSelect to make use of MICTools transparently through a Python wrapper.
The architecture design is composed of four layers. Each layer provides a specific function. The communication between layers is done through shared data structures, including execution configuration, input matrix and results array. The architecture layers are: MICSelect layer, Python wrapper layer and MICTools layer.
The architecture allows us to run each of the MIC estimation algorithms sequentially. However, each algorithm can run independently from the others. Furthermore, each algorithm of the sequence has been completely parallelized using POSIX threads (pthreads) and lock free policies [36,37]. The parallelization model used to implement Pearson correlation, ParallelMIC and SAMIC relies on a Single Instruction Multiple Data (SIMD) design over a Uniform Memory Access model (UMA) [38]. In practice, this means that every thread of the CPU will operate over a different set of feature pairs without overlapping. Figure 8 gives an intuition of how the parallelization model works.
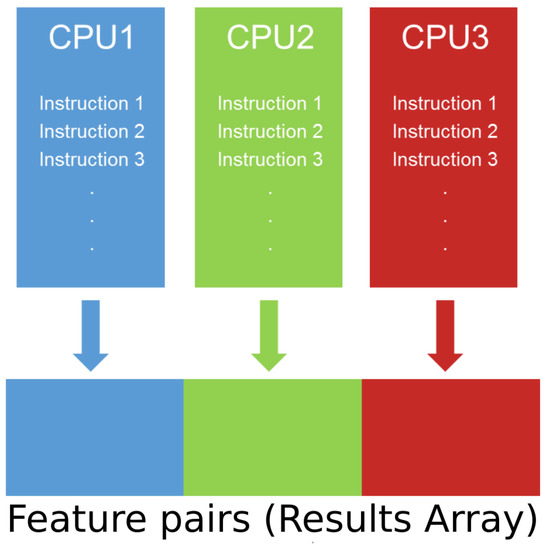
Figure 8.
Single Instruction Multiple Data (SIMD) model.
Communication between layers is done by the following data structures: routine configuration, input matrix and results array.
The next subsections explain in detail the role and functions of each architecture’s component.
4.1. MICSelect Layer
The MICSelect layer performs the feature selection method described in algorithm (Algorithm 3). This layer relies on MICTools to read the datasets and to perform the required MIC operations. In addition, it deals with the process of cutting, ordering, grouping and selecting the relevant features of the dataset. A user or program can interact with this layer by sending instructions to its argument parser. Table (Table 2) shows the available commands recognized by MICSelect. This layer is implemented in Python as it allows easy data slicing and filtering.

Table 2.
Parameters of MICSelect.
4.2. Python Wrapper Layer
This layer consents to the communication between MICSelect and MICTools. It is implemented as a Python module meaning that MICTools can be included in any Python program. The wrapper functions are the following:
- Instructions passing from MICSelect to MICTools;
- Results parsing to Python standard data structures;
- Automatic handling of memory allocation.
This layer is implemented in C++ using the Boost Python libraries and the Distutils build system.
4.3. MICTools Layer
The MICTools layer performs the MIC algorithms estimation sequence explained in Section 3.1. It contains several sub-layers that perform simple tasks, these layers are: presentation layer, I/O layer, sequence of algorithm layer and dependencies layer.
Since the performance of this layer is critical, it is implemented in C++ with POSIX Threads as parallelization library. This library ensures portability between Unix compliant operative systems. This layer can also be compiled as a standalone application independent of the rest of the architecture.
4.3.1. Presentation Layer
This layer provides the input interface for the MICTools program. A user or application can utilize this layer to specify commands, arguments, and parameters to MICTools. These instructions may be introduced as a single command and interpreted by an argument parser. Table 3 shows the different options accepted as input by MICTools.

Table 3.
MICTools supported parameters.
4.3.2. I/O Layer
This layer provides the input and output operations to interact with data sources; for example, datasets contained in CSV files or databases (not implemented). This layer guarantees the correct reading of datasets and the writing of the resulting data.
4.3.3. Sequence of Algorithms Layer
This layer contains the parallel implementations of the MIC estimation algorithms supported by MICTools. It allows every algorithm to process any pair of features based on the algorithm sequence described in Section 3.1.
4.3.4. Dependencies Layer
This layer contains all the libraries needed by the Algorithms Layer. The libraries provide functionalities such as parallelization routines, grid management, thread safe random number, generators, a sequential implementation of ApproxMaxMI (implemented in C++ from scratch), and other functionalities required by the Algorithms Layer.
4.4. MICTools Auxiliary Data Structures
The auxiliary data structures in MICTools provide a way of communicating for all of its layers. These datasets mainly contain algorithms’ execution parameters, results, and common input data.
4.4.1. Execution Configuration
This data structure contains the settings for the current planned execution of MICTools. It includes all the algorithms that are going to be executed in the current run as well as their pertinent parameters. The configurations comprise: input data source, output data source and algorithms’ execution parameters.
4.4.2. Mutual Input Matrix
This data structure contains reading registers acquired by the data source input. In addition, it provides the input data to all the algorithms in execution.
4.4.3. Array of Results
This data structure encloses the computed pairs of variables, as well as the results obtained by each of the performed algorithms over them. When running any of the parallel algorithms in MICTools, this data structure is segmented in many pieces as threads are available for the computation. Then, each thread will operate over its corresponding piece, reading the stored pairs and writing the results to the data structure.
5. Results & Evaluations
In order to evaluate the framework, twelve classification datasets from UCI MLR [39] and LIBSVM [40] were used. We compare our method against three different algorithms; STG [41], Random Forest [42] and M1-GA [43]. In every test, we used three models, SVM, KNN, and Logistic Regression, to get the AUC Score (average). In addition, the implementation of these models is taken from SciKit-Learn [44] (0.24.2) for Python 3.6. Table 4 shows the configurations and parametrization of the models used as testing methods.

Table 4.
Configurations and Parametrization of Testing Methods.
The time (seconds) showed in the Table 5, only considers the feature selection process. Thus, the proposed framework achieves a better balance in accuracy and time complexity. Our proposal has an execution time quite similar to the random forest algorithm but the performance is significantly better, almost the same as that of STG.

Table 5.
Table of results.
Table 6 shows the average scores for a stratified five-fold cross-validation with AUC, F1 Accuracy, Recall and Precision metrics among the testing datasets in our proposal for the Top 10 Feature Selection method.

Table 6.
Scores for Stratified 5-Fold Cross-Validation.
Moreover, Figure 9, Figure 10 and Figure 11 shows the performance among each testing datasets, with the mean score of three models SVM, KNN and LR using stratified 5-fold cross-validation and both methods top 10 Feature Selection and Stepwise Feature Selection.
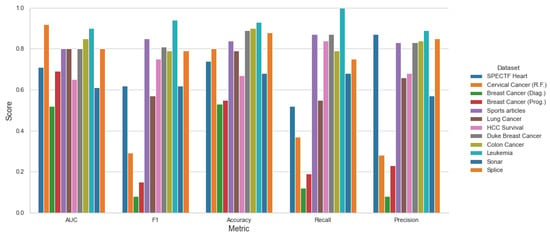
Figure 9.
Original Features—Mean Metrics Scores for LR, KNN, SVC.
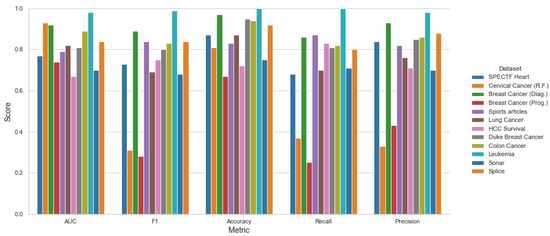
Figure 10.
Top 10 Features—Mean Metrics Scores for LR, KNN, SVC.
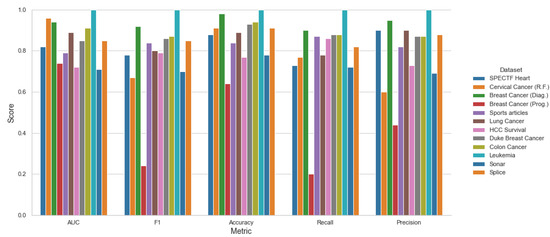
Figure 11.
Stepwise Features—Mean Metrics Scores for LR, KNN, SVC.
The software–hardware configurations to run the experiments were the following: Ryzen 5800×, 4 × 16 GB Kingston DDR4, Samsung 1TB 970 Evo Pro, Ubuntu Desktop 18.04 × x86-64. It is clear that the proposed framework can obtain better results over the testing algorithms. However, we can see that on the Lung Caner and Sonar datasets, for example, the other algorithms obtain a better AUC, but the time complexities are higher.
6. Conclusions
In this work, we present a feature selection framework for large datasets based on a correlation capable of detecting nonlinear relationships between two features. This correlation was handled by the smart combination of MIC, Pearson Correlation, ParallelMIC and SAMIC algorithms to obtain precision and speed on the feature selection task. The experiments reveal that the proposed framework shows better accuracy with lower computational complexity when applied to different datasets. Therefore, the proposed framework is capable of detecting the relation between a pair of features at good speeds and accuracies. However, there are more complex associations between more than two features that need to be studied to obtain a better way to detect such complex relations. For this, we are conducting research on the use of meta-learning to acquire knowledge on already studied data sets, the use of Deep Learning for feature generation and Bayesian causality to extend the proposed framework into more complex capabilities but maintaining the balance between speed and accuracy.
Author Contributions
Conceptualization, I.-A.G.-R. and A.M.-V.; methodology, A.C.-M.; software, I.-A.G.-R.; validation, A.M.-V. and S.O.-C.; formal analysis, A.C.-M.; investigation, I.-A.G.-R.; resources, I.-A.G.-R. and I.R.-A.; data curation, I.-A.G.-R.; writing—original draft preparation, A.C.-M.; writing—review and editing, I.-A.G.-R. and I.R.-A.; visualization, A.C.-M.; supervision, A.M.-V.; project administration, A.M.-V.; funding acquisition, A.M.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets and the code related to this work could be found on: https://github.com/ivangarcia88/ffselection (accessed on 15 June 2021).
Conflicts of Interest
The authors declare no conflict of interest. The founders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Siddiqa, A.; Karim, A.; Gani, A. Big data storage technologies: A survey. Front. Inf. Technol. Electron. Eng. 2017, 18, 1040–1070. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.K.; Nirantar, S.; Yew, W.S.; Poh, C.L. Novel modalities in DNA data storage. Trends Biotechnol. 2021, 39, 990–1003. [Google Scholar] [CrossRef]
- Oakden-Rayner, L. Exploring large-scale public medical image datasets. Acad. Radiol. 2020, 27, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Chao, G.; Luo, Y.; Ding, W. Recent advances in supervised dimension reduction: A survey. Mach. Learn. Knowl. Extr. 2019, 1, 341–358. [Google Scholar] [CrossRef] [Green Version]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [Green Version]
- Dash, M.; Liu, H.; Motoda, H. Consistency based feature selection. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Kyoto, Japan, 18–20 April 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 98–109. [Google Scholar]
- Liul, H.; Motoda, H.; Dash, M. A monotonic measure for optimal feature selection. In Proceedings of the 10th European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 101–106. [Google Scholar]
- McCoy, J.T.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Burton, H.V.; Huang, H. Machine learning applications for building structural design and performance assessment: State-of-the-art review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Secaucus, NJ, USA, 2006. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Kumar, V.; Minz, S. Feature selection: A literature review. SmartCR 2014, 4, 211–229. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. London Edinburgh Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Britain, R.S.G. Proceedings of the Royal Society of London; Taylor & Francis: Abingdon, UK, 1895. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Rao, C.R. The utilization of multiple measurements in problems of biological classification. J. R. Stat. Soc. Ser. Methodol. 1948, 10, 159–203. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, M.; Schwartz, E.L.; Tenenbaum, J.B.; de Silva, V.; Langford, J.C. The isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. A review of feature selection methods on synthetic data. Knowl. Inf. Syst. 2013, 34, 483–519. [Google Scholar] [CrossRef]
- Mengle, S.S.; Goharian, N. Ambiguity measure feature-selection algorithm. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 1037–1050. [Google Scholar] [CrossRef]
- Liping, W. Feature selection algorithm based on conditional dynamic mutual information. Int. J. Smart Sens. Intell. Syst. 2015, 8, 316–337. [Google Scholar] [CrossRef] [Green Version]
- Shin, K.; Xu, X.M. Consistency-based feature selection. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Santiago, Chile, 28–30 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 342–350. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Clark, M. A Comparison of Correlation Measures; Center for Social Research, University of Notre Dame: Notre Dame, IN, USA, 2013; Volume 4. [Google Scholar]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef] [Green Version]
- Gray, R.M. Entropy and Information Theory; Springer: New York, NY, USA, 1990. [Google Scholar]
- Albanese, D.; Filosi, M.; Visintainer, R.; Riccadonna, S.; Jurman, G.; Furlanello, C. Minerva and minepy: A C engine for the MINE suite and its R, Python and MATLAB wrappers. Bioinformatics 2012, 29, bts707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, D.; Wang, M.; Zheng, W.; Wang, H. RapidMic: Rapid Computation of the Maximal Information Coefficient. Evol. Bioinform. Online 2014, 10, 11. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Herlihy, M.; Shavit, N. The Art of Multiprocessor Programming; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2008. [Google Scholar]
- Williams, A. C++ Concurrency in Action: Practical Multithreading; Manning Pubs Co Series; Manning: Shelter Island, NY, USA, 2012. [Google Scholar]
- Hennessy, J.L.; Patterson, D.A. Computer Architecture: A Quantitative Approach, 5th ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2011. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository 2017. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 15 June 2021).
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 1 June 2021). [CrossRef]
- Yamada, Y.; Lindenbaum, O.; Negahban, S.; Kluger, Y. Feature Selection using Stochastic Gates. Proc. Mach. Learn. Syst. 2020, 2020, 8952–8963. [Google Scholar]
- Rogers, J.; Gunn, S. Identifying feature relevance using a random forest. In International Statistical and Optimization Perspectives Workshop “Subspace, Latent Structure and Feature Selection"; Springer: Berlin/Heidelberg, Germany, 2005; pp. 173–184. [Google Scholar]
- Bonidia, R.P.; Machida, J.S.; Negri, T.C.; Alves, W.A.L.; Kashiwabara, A.Y.; Domingues, D.S.; De Carvalho, A.; Paschoal, A.R.; Sanches, D.S. A Novel Decomposing Model With Evolutionary Algorithms for Feature Selection in Long Non-Coding RNAs. IEEE Access 2020, 8, 181683–181697. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).