Abstract
This paper explores the use of Private Aggregation of Teacher Ensembles (PATE) in a setting where students have their own private data that cannot be revealed as is to the ensemble. We propose a privacy model that introduces a local differentially private mechanism to protect student data. We implemented and analyzed it in case studies from security and health domains, and the result of the experiment was twofold. First, this model does not significantly affecs predictive capabilities, and second, it unveiled interesting issues with the so-called data dependency privacy loss metric, namely, high variance and values.
1. Introduction
Boosted by the growth of available data and computing power, progress in the field of artificial intelligence is leading to significant improvements in the ability to solve a variety of tasks with the help of intelligent artifacts powered by machine learning algorithms. This is the case in critical domains such as health and security, where researchers are actively working towards developing increasingly accurate algorithms for tackling problems like disease diagnosis [1] and intrusion detection [2,3,4,5].
Particularly, but not exclusively in these two domains, the opportunity to build intelligent predictive systems brings along, however, difficult challenges that must be addressed. Typically, substantial amounts of training data are required to learn predictive models to achieve satisfactory performance, but this requirement may not be fulfilled by a single organization alone. Howevr, this shortcoming could be overcome by organizations sharing raw data or predictive models trained with such data. As an example along this line, the last decade has seen a push from NGOs and research institute. for the broader release of open government data [6].
In the case of Europe, for instance, access to public data is legislated by Directive (EU) 2019/1024 on open data and the re-use of public sector information [7].
Certainly, data sharing is not only a function of the legislation on open data, but also of the need to make it freely available to public and private actors who have the technical ability to use this data for scientific innovation [8].
However, despite the benefits of sharing, in most cases data can neither be easily published nor transferred [6,9]. Indeed, most data gathered by organizations, whether public or private, contain information about citizens, clients, users or patients who are the real owners of that data, such as, ID, passwords, and social security, bank account and credit card numbers. Obviously, regardless of the problem-solving value it may have for an organizations or external third parties, that data does not belong to them.
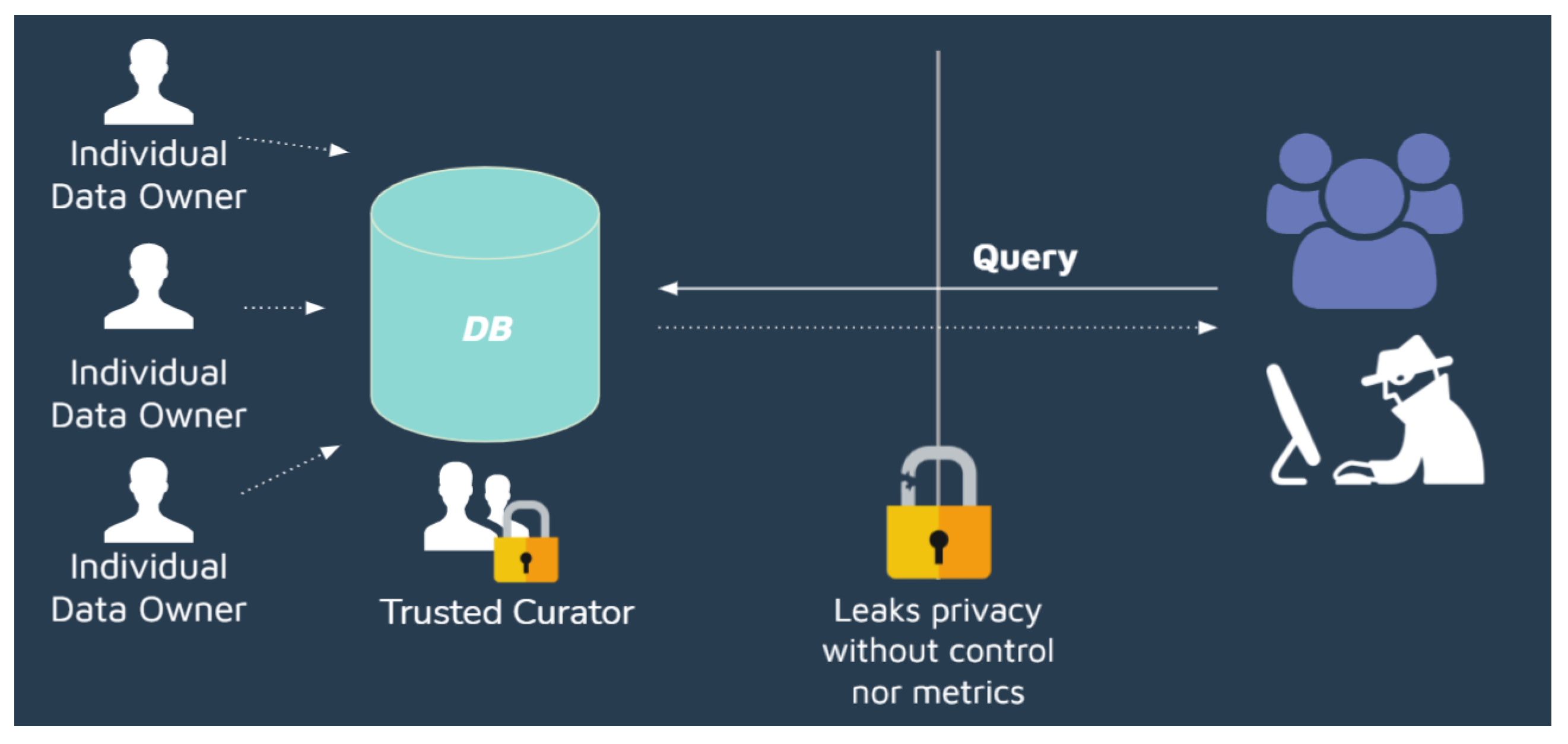
Figure 1 illustrates a situation where privacy is neglected. Here, data from a number of clients data owners are stored in the database of an e-commerce company trusted curator that allows a data analytics service provider (third party) to query its database. Without appropriate protection measures, such queries, not necessarily intentional, may reveal sensitive owner data, such as the person’s identity. To avoid this loss of privacy, appropriate measures must be taken when allowing access to an organization’s database, notwithstanding any anonymization technique that removes personally identifiable information [10]. Indeed, several attacks capable of reidentifying individuals in this context have been described [11,12,13,14]. Furthermore, private information from unpublished data can be exposed by allowing third parties to query predictive models by so-called model inversion attacks [15].
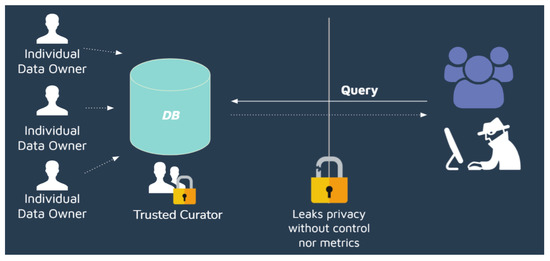
Figure 1.
Context without privacy.
Therefore, sharing information, either as raw data or trained models, must ensure appropriate levels of privacy. This issue is not only technical but also legal, as there are laws regarding the privacy of data within databases.
For instance, Europe’s General Data Protection Regulation (GDPR) defines a normative framework of data protection that applies to all EU organizations independent of where they are located [16]. Hence, there exists a clear tension between the ability to provide access to data and maintain privacy.
Clearly, it is essential to install mechanisms for protecting private information contained in data that is made available to third parties. Such mechanisms must be applied irrespective of how the data is shared, whether by publishing a dataset or by allowing external stakeholders to query a database. Moreover, data protection mechanisms should be able to keep enough useful information to solve tasks [17].
The motivation of this work is to study a scenario where several organizations are involved in sharing models, each one of which is exculsively trained to use its own organization’s database. The Private Aggregation of Teacher Ensembles (PATE) [18,19] has been proposed for such purpose. It consists of building an ensemble model that adds random noise to the outputs of the predictors (teachers) before aggregating them. PATE provides differential privacy (DP) [20] protection to the databases of the organizations participating in the ensemble, but does not provide any protection for the third party (student) who queries the ensemble to train its own model with its own data.
This paper proposes and experimentally evaluates an approach consisting of protecting the third party’s data by adding a DP mechanism before sending the query to the ensemble in the context of the PATE. This technique is implemented and analyzed in two examples of critical domains: cybersecurity and health. The former concerns the detection of malicious web requests, while the latter is focused on cardiopathy classification based on hearbeat data.
2. Differential Privacy
Dwork defines DP as the data curator’s promise to an individual that he or she will not be affected in any way as the result of a database query by a third party [20]. Another way of putting it is that DP allows the acquisition of information of the overall population but not any specific information about individuals. More precisely, DP is a general mathematical framework based upon quantifying privacy loss as a random variable. The goal is to enable the design of specific mechanisms that provide data protection through the establishment of a desired quantity of privacy loss within a given confidence .
2.1. Formalizing Differential Privacy
Let be the universe of databases. We do not assume here any particular representation of databases, but we do require to be equipped with a distance . In this context, two databases are called “adjacent” or “neighbor”, if .
A randomized algorithm, or mechanism with output domain takes as input a database , and possibly other parameters, and outputs some , according to some probability distribution.
DP does not define a particular mechanism for privacy. In this paper we used the Laplace mechanism based on the Laplace distribution centered at 0 with scale b and probability density function given by
Given any function , the Laplace mechanism is defined as:
where are i.i.d random variables with distribution . That is, this mechanism returns a noisy response which consists in adding a random perturbation to the result of the evaluating function f on database d.
DP defines the privacy loss as a random variable as follows. For a given mechanism , databases , and output , the privacy loss at o, denoted , is:
Given , is said to be -“differentially private” if for all adjacent databases it holds that:
To simplify the notation, we denote L the random variable distributed as whose values are given by evaluating ℓ at outcomes sampled from , and write
For example, the Laplace mechanism is -differentially private, where is the -sensitivity of function f, defined as
DP ensures that there is no further privacy loss after applying a mechanism . This property is called “post-processing”. Formally, if is -differentially private, then for any arbitrary randomized mapping , is -differentially private as well.
Moreover, DP has the strength of having a composition theorem that limits the privacy loss through repeated queries to the database independently of the type of query or mechanism. Formally, let be -differentially private mechanisms for . Then the mechanism is -differentially private.
2.2. Privacy Models
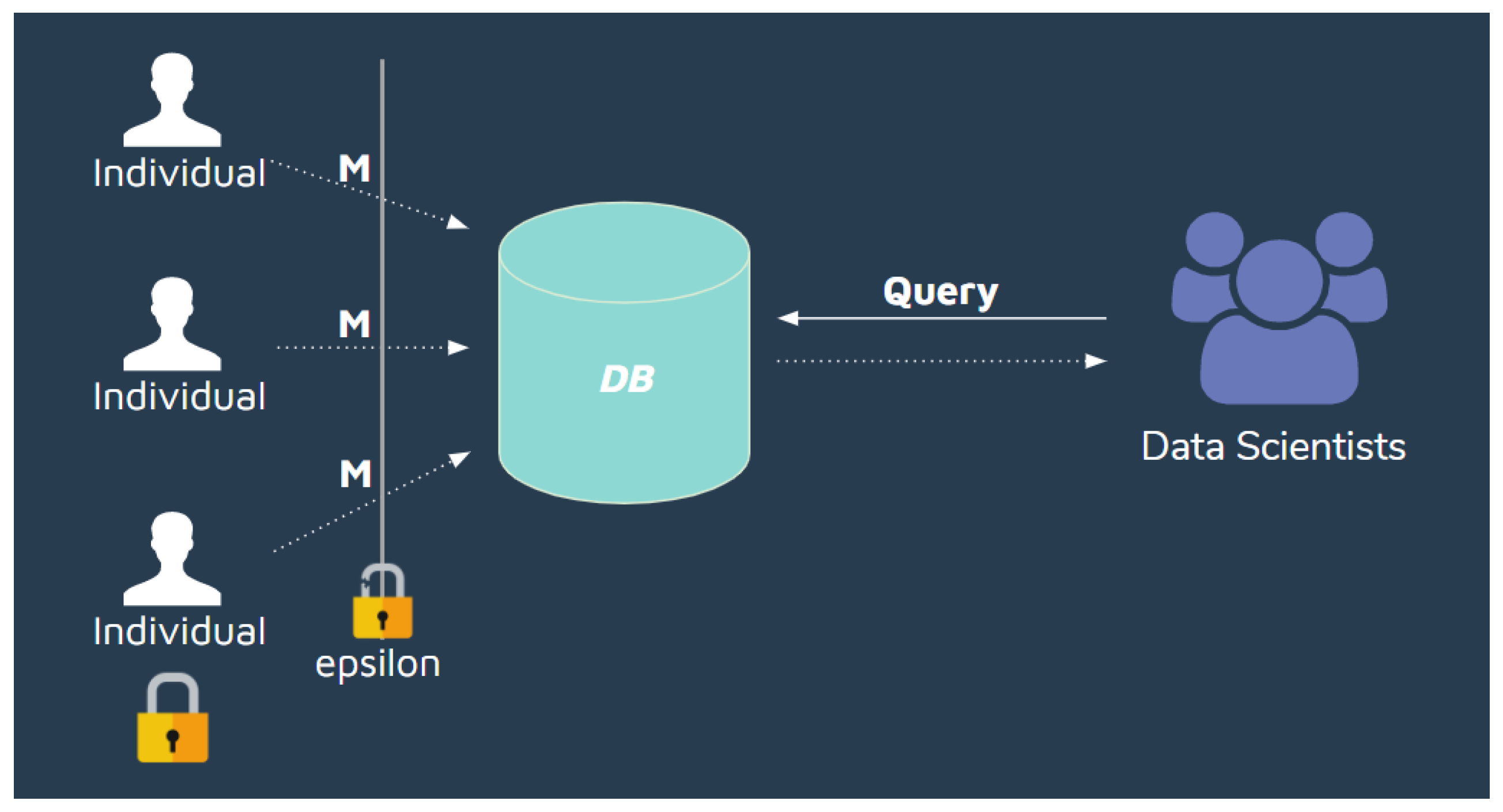
Differential privacy proposed two main types of privacy models that we took into consideration when implementing our privacy compliant architecture. The local model (Figure 2), also known as the non-interactive or offline model, consists of creating a database with data already privatized. This means that a randomized mechanism is applied to the data recollected from the individuals before it is stored in the database by the Trusted Curator. Privatization and its leakage takes place when recollecting the individual information, not when querying the database. This model takes advantage of the post-processing property of differential privacy so that data scientists can send as many queries to the database as they desire without worrying about leakage composition. The database is privatized only once, and this model allows the database to be released entirely under (, )-differentially private guarantees.
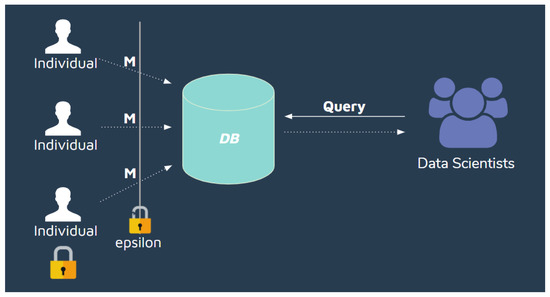
Figure 2.
Local model.
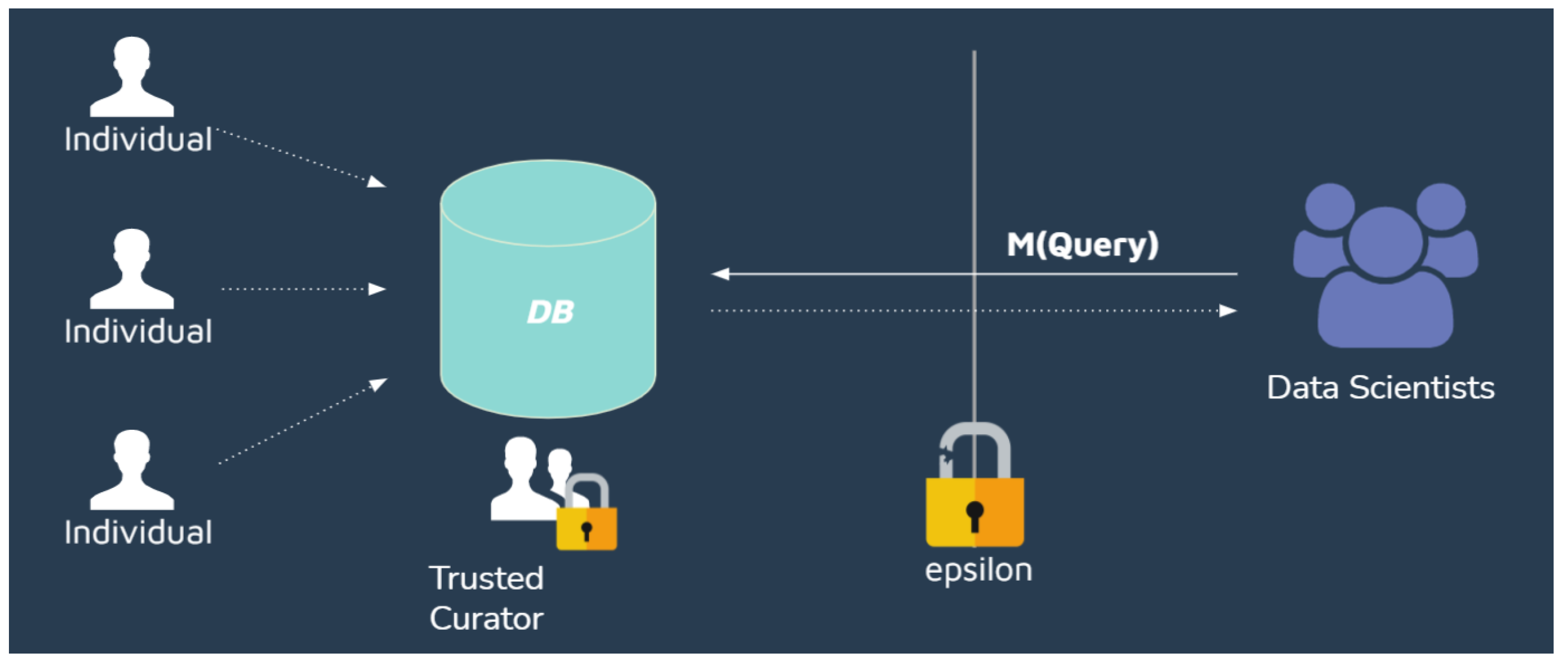
The centralized model (Figure 3), also known as interactive or online model, consists of the data scientists’ sending n queries to the database, which is owned or protected by a Trusted Curator. The query is a function applied to the database, and then the result of the function is privatized with some mechanism M, such as some (, )-differentially private mechanism. This model allows, for example, a second database query based on previous responses. However, each query has to be considered as a composition of mechanisms, and the accumulated leakage has to be taken into account. Each query to the database has an upper bound leakage of while k queries has an upper bound of leakage due to composition.
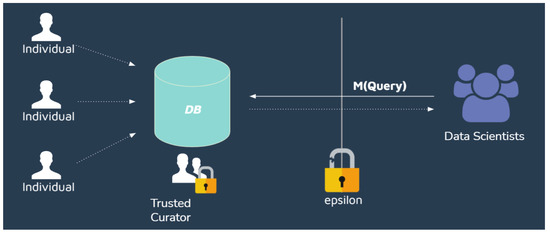
Figure 3.
Centralized model.
3. Private Aggregation of Teacher Ensembles
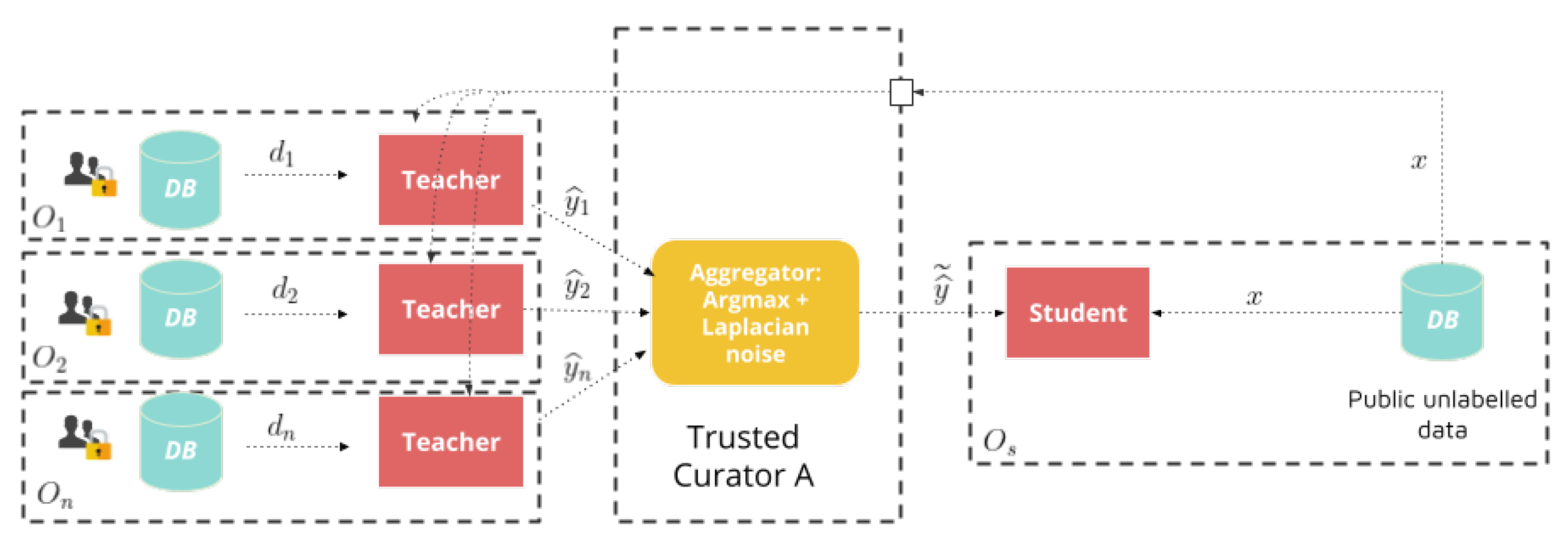
Private Aggregation of Teacher Ensembles (PATE) [18,19], is a technique that enables the training of machine-learning models of arbitrary architecture isuch that privacy guarantees can be described through differential privacy. The technique proposes to train multiple “teacher” models on sets of sensitive private data, and then use an ensemble of these teachers to guide the training of a “student” model with public, unlabeled data. The student training data is sent through each teacher model to obtain a label prediction, and a noisy aggregation of predictions is used as the training sample label (Figure 4). The PATE implements a centralized model of privacy.
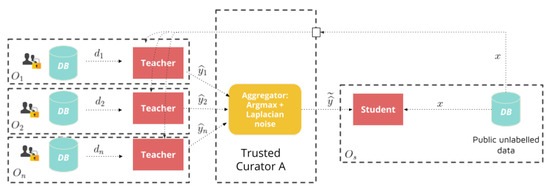
Figure 4.
Private Aggregation of Teacher Ensembles (PATE).
The thinking behind the PATE’s privacy guarantees is that if multiple distinct teacher models agreed on an input label, no private data of their training examples wereleaked since the conclusion was arrived at by consensus, and no particular model revealed too much information. If, however, there was a strong disagreement among the teachers and the most probable class was likely to be defined by a single model’s prediction, the random noise added by the aggregation mechanism would play a bigger role in defining the output, thereby protecting the individual model predictions.
Although the aggregation mechanisms can vary, the general idea often consists in counting how many teacher models predict each class as being the most probable, adding noise to this count, and then picking the most probable one. The aggregation mechanism employed in this work is the one proposed in [18], which consists in adding noise sampled from a Laplace distribution to the teachers’ class prediction count. For a given student training sample x, given the label count of teacher predictions for class c, the aggregation mechanism that outputs the noisy prediction of the ensemble is defined as
3.1. Analysis of PATE Privacy Loss
We provide here a detailed but simplified analysis of PATE privacy loss. The PATE with the aggregation mechanism given in Equation (5) provided -differential privacy [18]. Therefore, a direct application of the DP composition theorem resulted in T queries to the teacher ensemble yield -DP. However, the privacy leakage could have been reduced if we had reduced the confidence in the DP guarantees, that is, to have . To do this would have meant fixing the desired bound on the tail probability of the privacy loss random variable L and then finding the smallest to satisfy Equation (3). To do this, we applied the moment-generating function method to derive the following bound on the tail probability:
where is the logarithm of the moment-generating function of L:
This means that was guaranteed to be smaller than any such that
Now, we can rewrite the above equation as follows:
Hence, by fixing , we obtained the minimum bound of the privacy loss that could be ensured with such :
It follows from [18] that the PATE with the aggregation mechanism defined in Equation (5), satisfied:
By the composability theorem of [18], the moment-generating function of the mechanism obtained by applying the PATE T times is . Therefore, after T queries, we had a data-independent privacy guarantee of , where
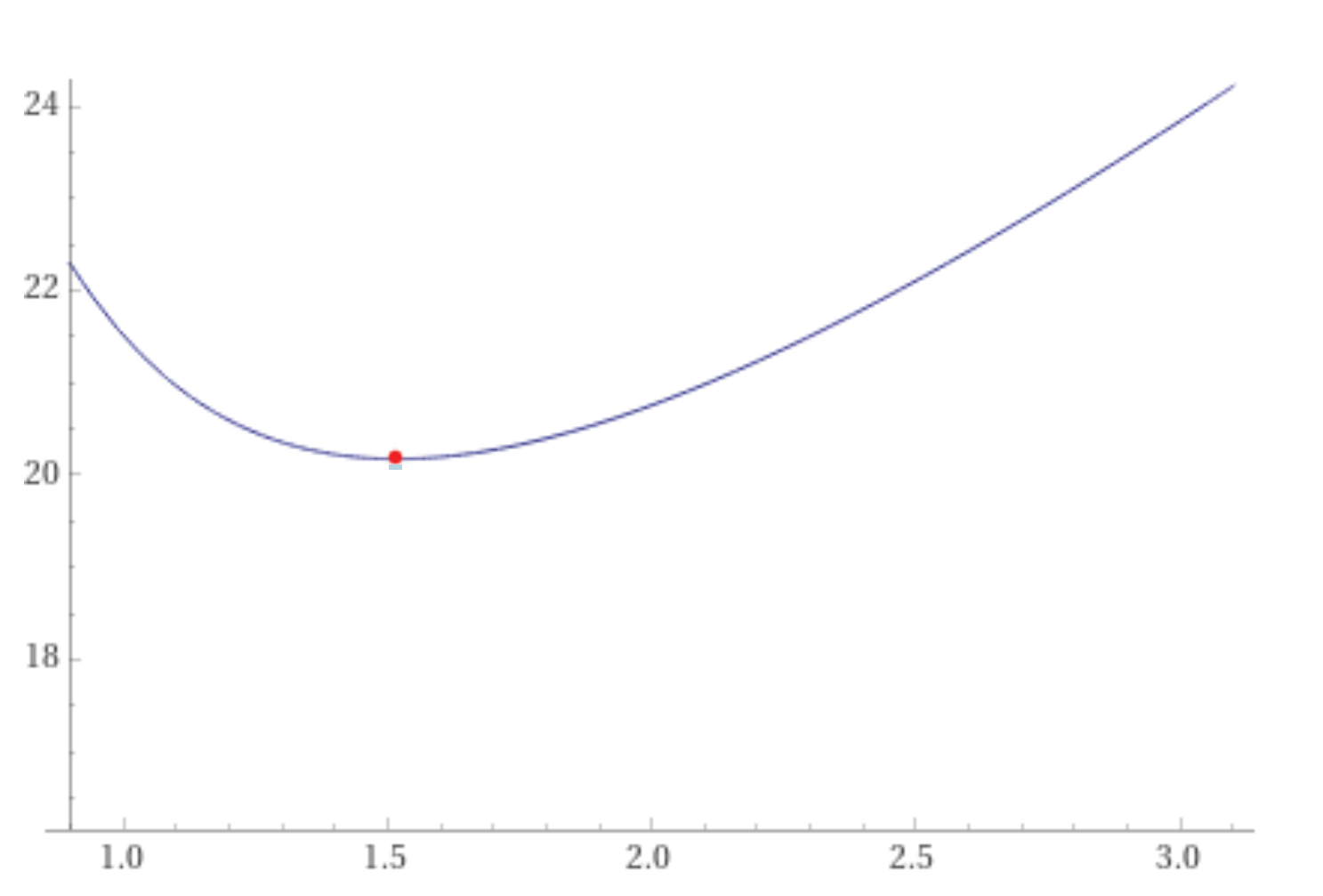
We will refer to as the “data independent epsilon”. Figure 5 gives an example of the data-independent epsilon for , and , computed using Wolfram Alpha.
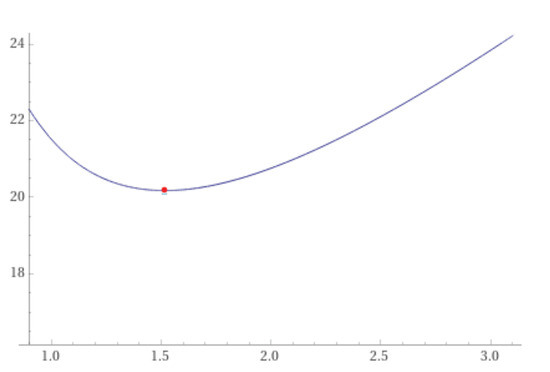
Figure 5.
Graph of . Data independent epsilon is at .
Indeed, the epsilon bound on the privacy loss could have been made smaller if we had brought into the picture the actual predictions delivered by the ensemble of teachers. This bound is called the “data dependent epsilon” [18]. A tighter bound on the moment-generating function could have been computed if we had taken into account the fact that when the quorum among the teachers was strong, the majority outcome was overwhelmingly likely, so the privacy loss was smaller when this outcome occurred. The following theorem, proved in [18], provides a data-dependent bound on as a function of the most probable predicted class of the teacher ensemble:
For this result to be applied, an upper bound of was computed in [18]. For the sake of readability, we omit the details here. Thanks to this bound that depends on the teacher agreement, a tighter tail bound was computed for specific responses of the ensemble to a sequence of T student queries:
3.2. Sensitive Student Data Scenario
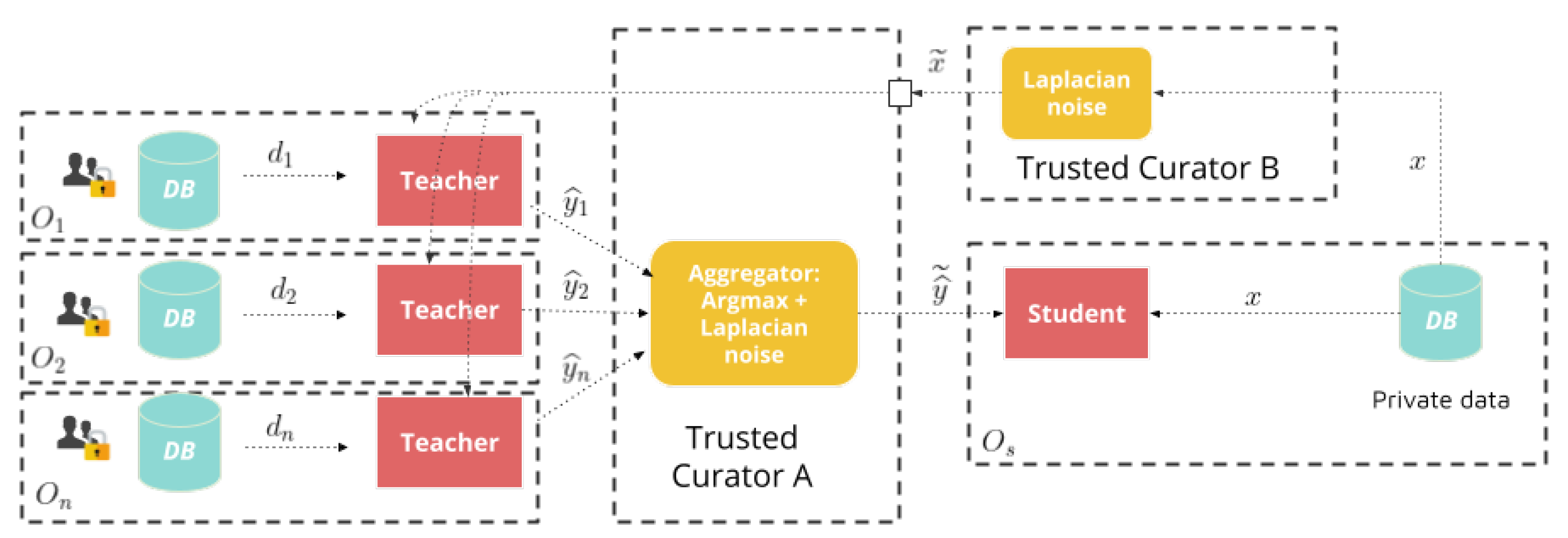
In this paper we were concerned with the case where the student did not have access to a public dataset but had its own private data. In this scenario, the student was not able or willing to share its private data with the teacher ensemble or trusted curator (Trusted Curator A). For this case, we proposed a framework where the student relied on another curator, which we called Trusted Curator B, the role of which was to privatize student data by using a randomized (e.g., Laplace) Mechanism to grant the student differential privacy guarantees over its data. Here, Trusted Curator A provided a centralized privacy model, which protected the data used to train teachers, while Trusted Curator B provided a local privacy model, by granting DP guarantees for each individual data point in the student organization sent to Trusted Curator A to be labelled by the teacher ensemble. This scenario is illustrated in Figure 6.
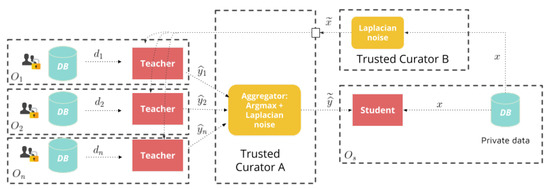
Figure 6.
PATE with protected student data.
It is worth mentioning that several works have experimentally shown that ensembles are robust to noise in data [21,22]. Therefore, based on that evidence and the PATE’s being an ensemble model, it was reasonable to think that the predictive capacity of the PATE would not suffer much from the controlled noise added by Trusted Curator B.
4. Experimental Results
In this section we describe the experimental setup and apply the approach presented in the previous section to two case studies representative of the domains of interest: security and health. Following the same strategy as the original PATE paper [18], teacher models were trained and used to generate labels for the student training samples, using an ensemble based on a Laplace aggregation mechanism with . Every teacher was presented with a labelled independent dataset , which was used for training. The student was presented with an unlabelled independent dataset x. Trusted Curator B privatized student data with a Laplace mechanism with distribution . To analyze this setting different values of were used. In both case studies, database elements were vectors of real numbers having an -norm equal to 1. Thus, the distance iwas-norm. Moreover, the fact that the vectors had a norm equal to 1 ensured that the -sensitivity of the Laplace mechanism applied by Trusted Curator B was 2, resulting in a -DP mechanism. For each value of , 10 student models were trained, each one on a different random sample of student datapoints labelled by the teacher ensemble. Each random sample was privatized by Trusted Curator B with noise from a Laplace distribution . Both the student and teachers were assumed to have had access to a labelled validation dataset, which was used only to evaluate performance and privacy loss metrics in the context of this work. In a real world scenario, such validation data may not be available. However, it did not pose any drawback to the applicability of this approach.
4.1. Cardiopathy Classification
In this experiment we analyzed the case of cardiopathy classification based on electrocardiogram (ECG) data. The ECG dataset contained 109,446 beats [23] extracted from signals in the MIT–BIH Arrhythmia Database [24]. The sampling frequency of each beat was 125 Hz, and they were categorized into five classes.
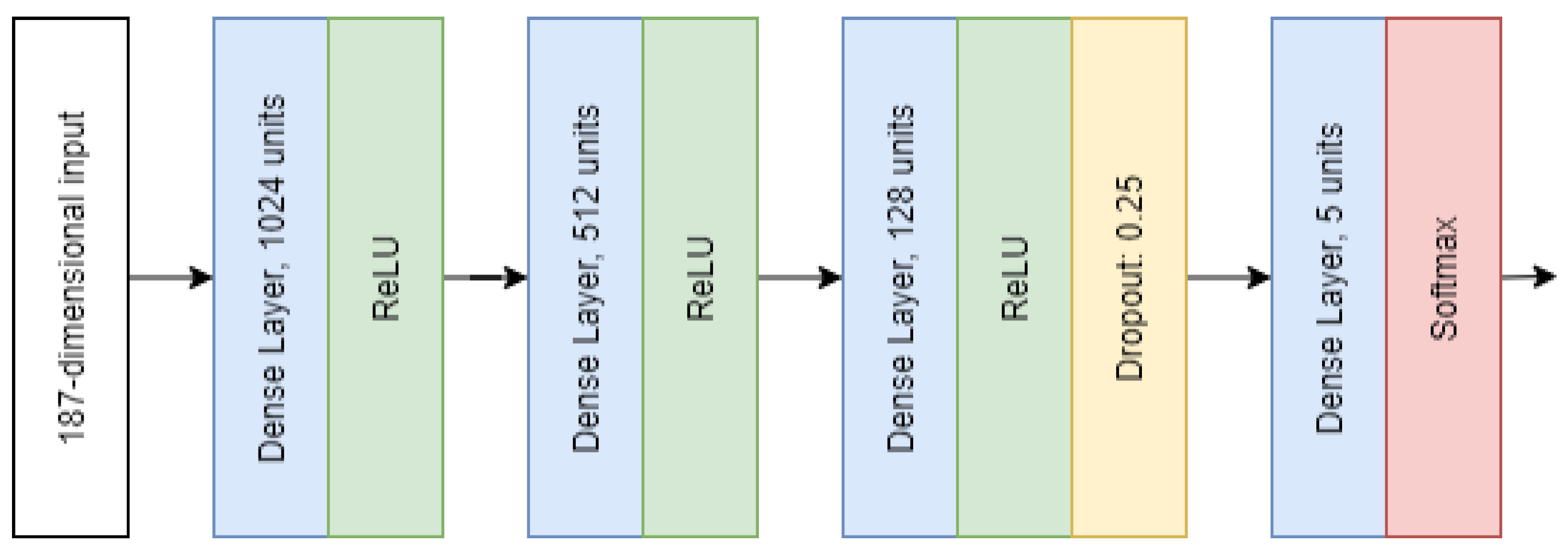
For simplicity, we used a multi-layer perceptron architecture both for the teacher and student models, see Figure 7. The number of teachers in the ensemble for this example was 200. Every teacher was trained with 5000 datapoints. The validation dataset contained 500 samples. For the student, 900 datapoints were used for training and 100 for validation.
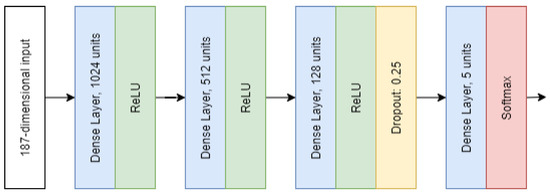
Figure 7.
Neural network architecture used for teachers and student in the ECG example.
First, we analyzed the performance of the teacher ensemble on the 900 student queries for different values of the student privacy paramenter . Figure 8 presents the accuracy of the ensemble before adding noise in the teacher aggregator; that is, the in Equation (5) was computed using unperturbed label counts. The experimental results showed that this ensemble has a mild accuracy decay of 4–5% with respect to unperturbed data. Furthermore, Figure 9 depicted the accuracy on the same queries but after privatizing through the Laplace aggregator. Here, the accuracy obtained after applying the PATE aggregation exhibited an expected larger gap in the case of perturbed data, but it was consistently around 10–12% across all values of . These experiments were aligned with the argument that ensembles are robust to perturbations in input data.
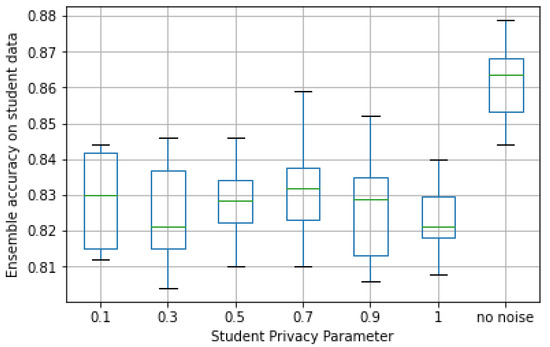
Figure 8.
Ensemble accuracy evaluated on student data by privacy parameter in ECG dataset.
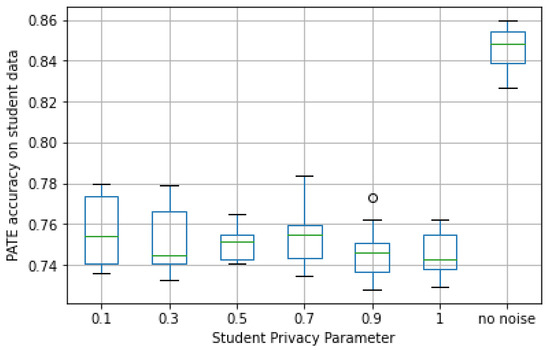
Figure 9.
PATE accuracy evaluated on student data by privacy parameter in ECG dataset.
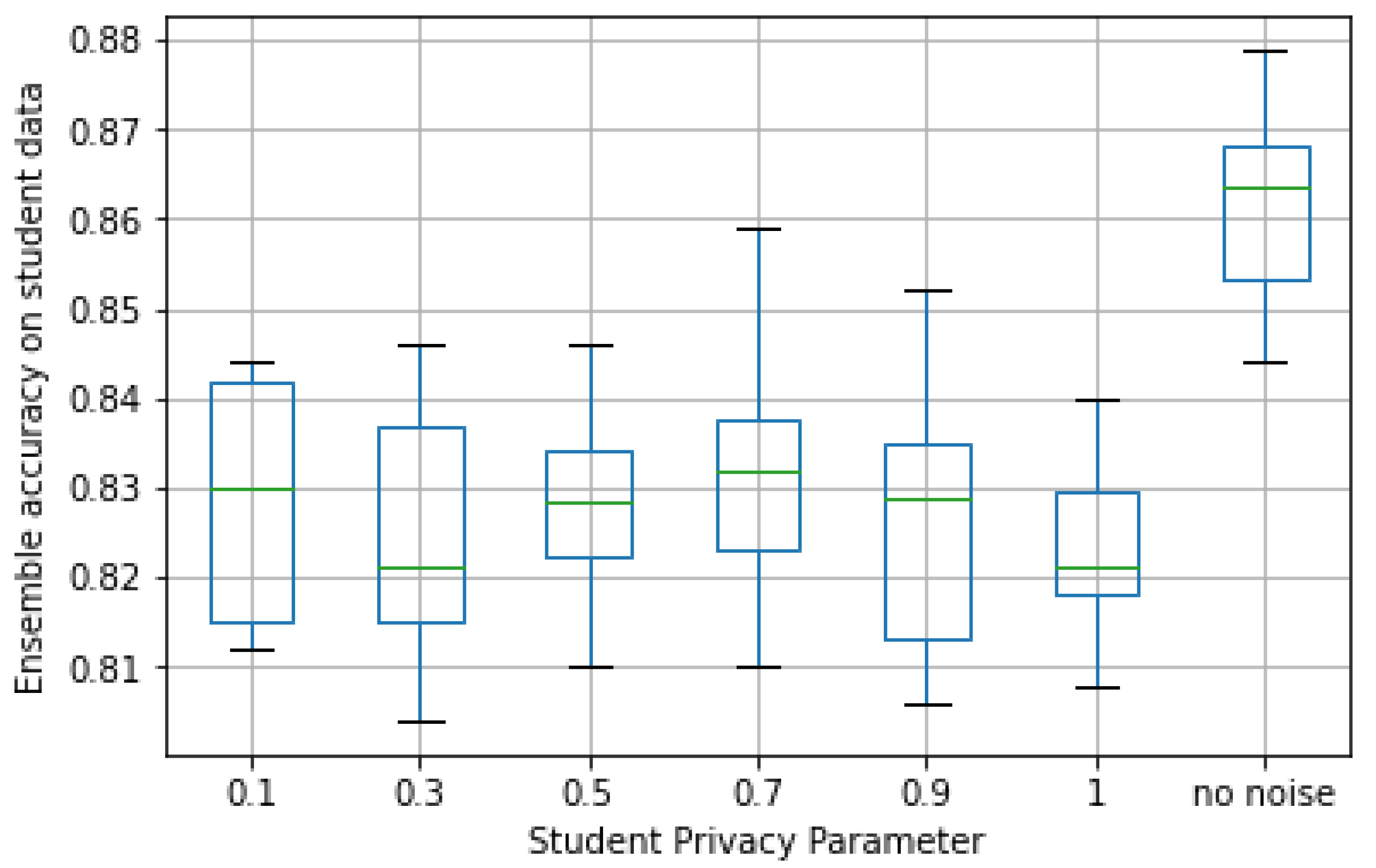
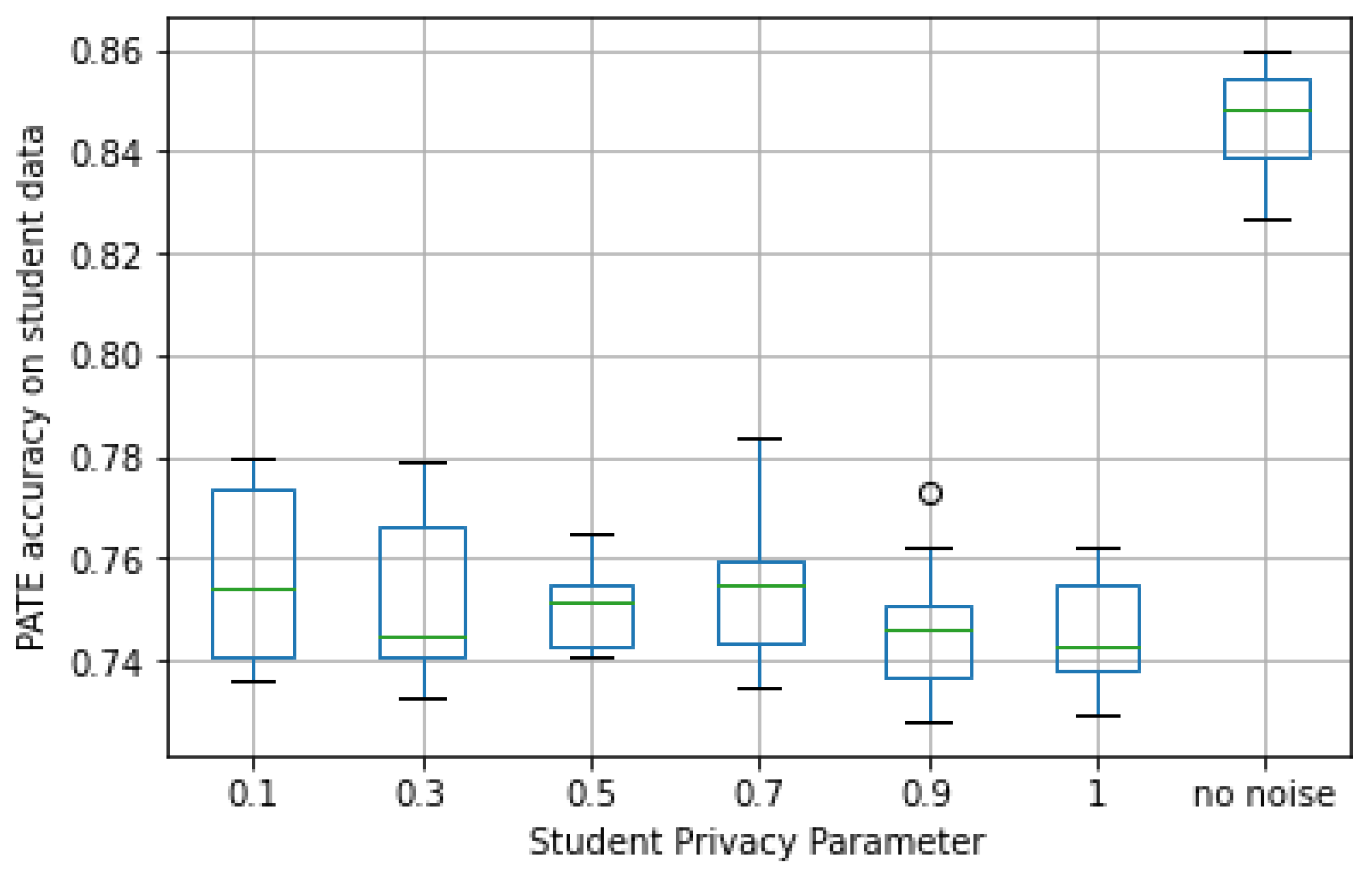
Second, we looked at student accuracy and privacy loss. In Figure 10, the accuracy observed in the validation set for different values is plotted. As can be seen, despite the loss in accuracy of the teacher ensemble, the median student accuracy for all cases was not significantly smaller (7–8%) than the one observed in the case of no noise. In particular, it came closer to the latter for larger values of (i.e., less noise).
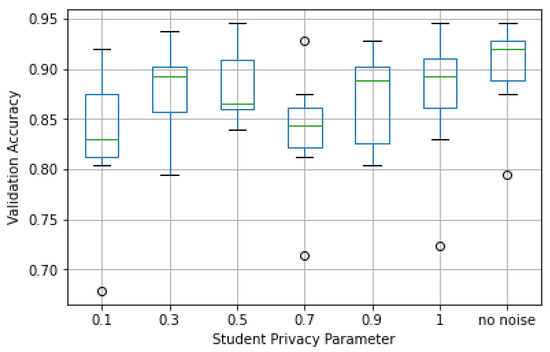
Figure 10.
Validation accuracy by student privacy parameter in ECG dataset.
In Figure 11 the data-dependent privacy loss for different values was compared with the data-independent privacy loss, and a confidence parameter was used. The computed data-independent privacy loss is , represented by the dashed red line.
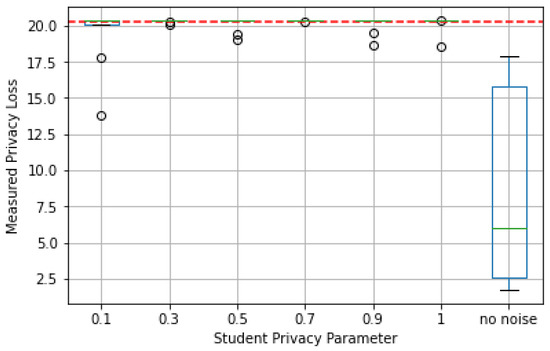
Figure 11.
Privacy loss by student privacy parameter in ECG dataset.
As Figure 11 shows, presents more variability when the student does not privatize its data. Table 1 shows that the worst case interquartile range (IQR) for the student with privatized data was 0.32 for (the largest perturbation), while the no-noise example presented a very large IQR of 13.12. At the same time, the median for every different to the no-noise version was larger than three times the median of the no-noise case.

Table 1.
Median and IQR of data-dependent privacy loss for student privacy parameter ρ.
4.2. Malicious Web Request Detection
To classify web requests, a dataset of 651,602 labeled requests was assembled from several public datasets, namely, Malicious-URLs [25], PKDD [26], and CSIC 2010 [27]. To merge the datasets, only the URL of each web request was used. To construct a feature vector to train the networks, each URL was tokenized in unigrams following a bag-of-words approach. For each URL, the values of the unigrams were computed using term frequency–inverse document frequency (TF–IDF) [28]. Each URL was represented by an -normalized vector composed of the 500 most frequent tokens across the entire dataset.
An ensemble of 250 teacher models was trained to generate labels for the student training samples using the Laplace aggregation mechanism. Every teacher was trained with 930 datapoints and the validation dataset contained 500 samples. Given the unbalanced distribution of the training set where 95% of samples were not malicious, a threshold of 0.5 to split the model’s output between positive and negative samples might have yielded poor accuracy results. Therefore, the receiver operating characteristic curve was calculated for a subset of samples, and the threshold that maximized the difference between the true positive and false positive rates was picked as the best one. Every teacher used 800 samples to calculate the best threshold for considering the classifier’s output as a positive prediction. For the student, random samples of 1000 datapoints were used for training and 200 for calculating the optimal threshold. For validation, 5000 datapoints were used.
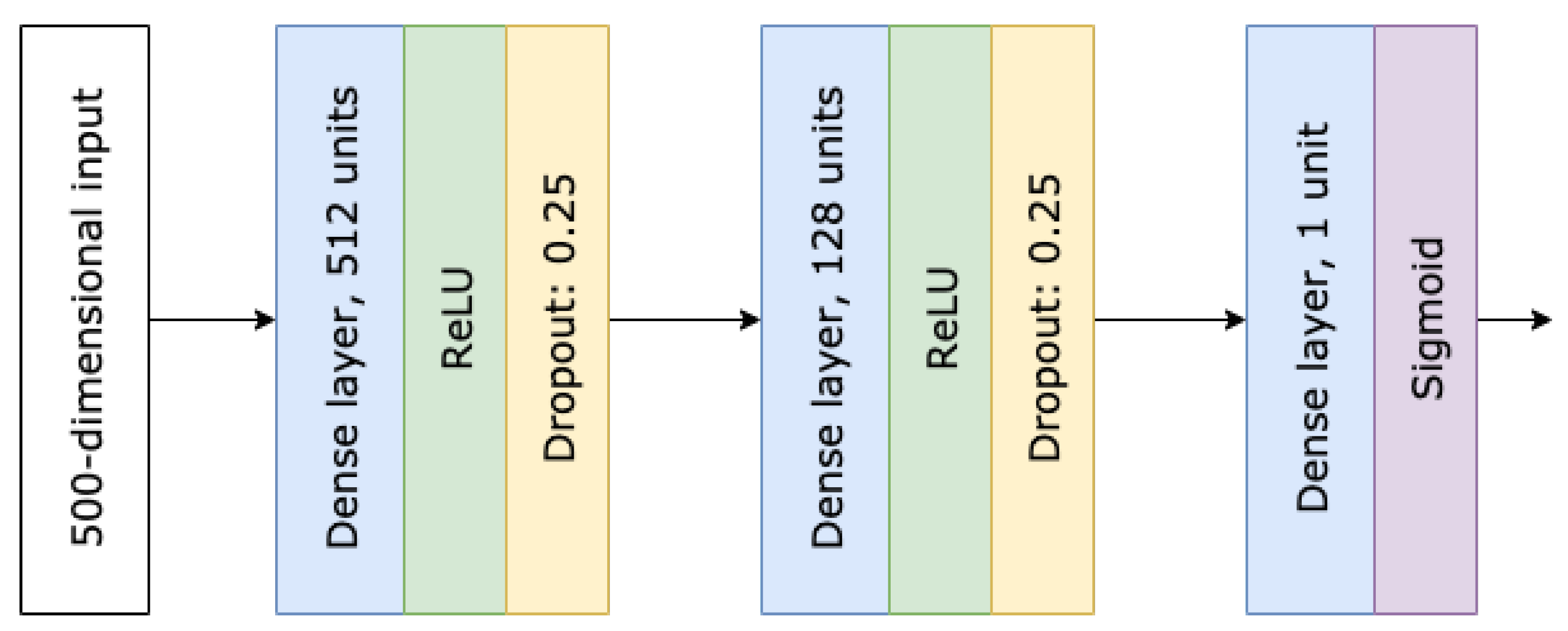
A simple, fully connected neural network architecture with a single real-valued output (see Figure 12) was used for both the teacher and student models.
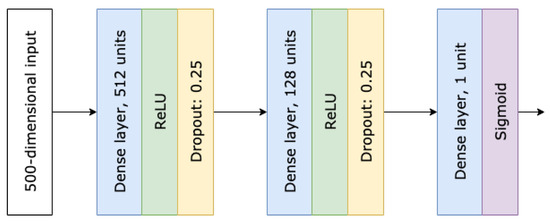
Figure 12.
Neural network architecture used for teachers and student in Web Request example.
The data dependent privacy loss of the teacher ensemble is computed for every case as described in Section 3 for . The data independent privacy loss of the teacher ensemble computed using WolframAlpha resulted in a value of 20.1743.
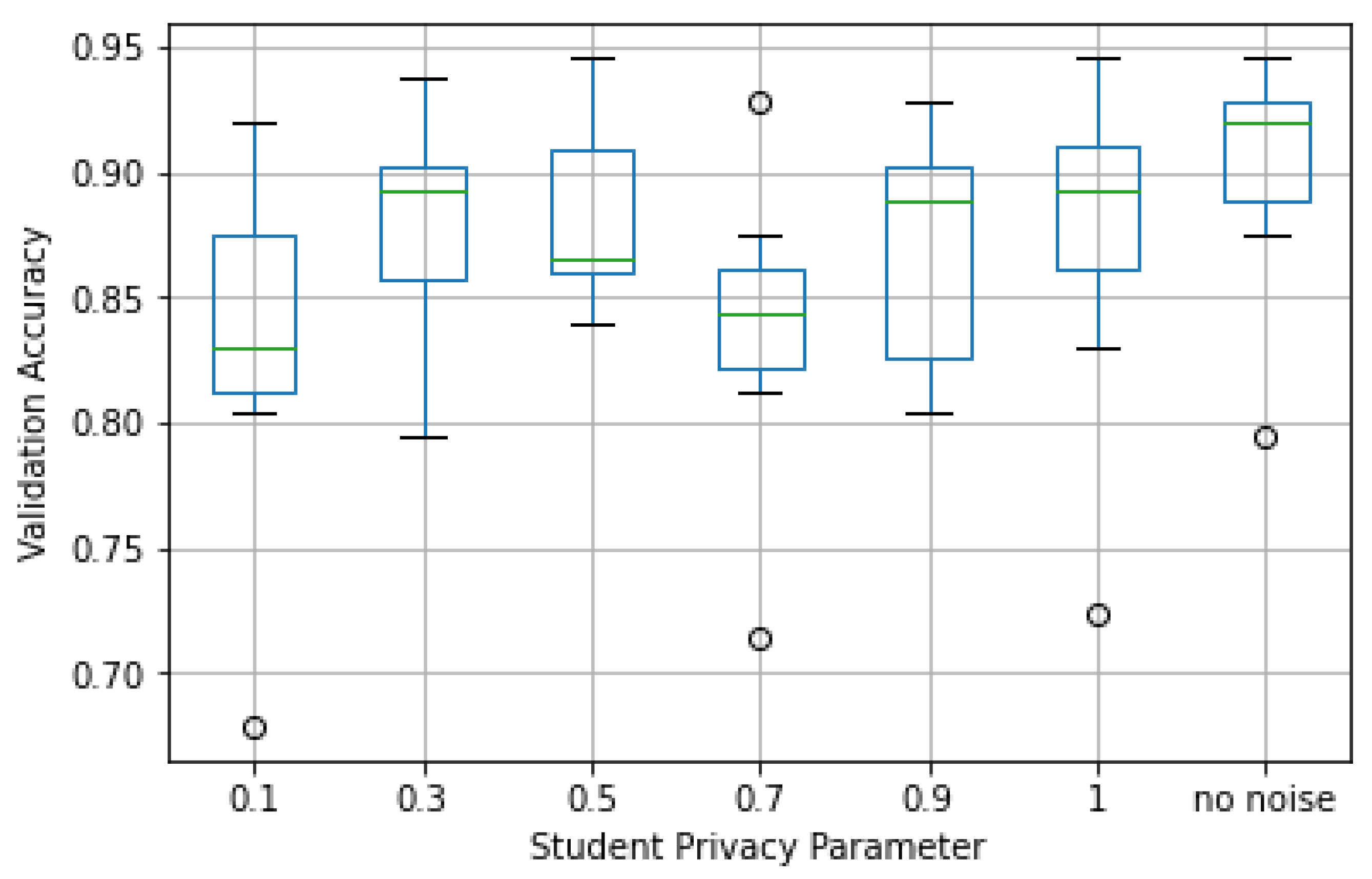
As presented in Figure 13 and Figure 14, the median of both the TPR and TNR performance metrics was similar for all values of with relatively low dispersion in most cases. This showed that the predictive capacity of a student that privatized its data was close to the one observed for student models trained with non-privatized data; that is, the experiments showed that privatizing student data led to no significant loss in predictive value.
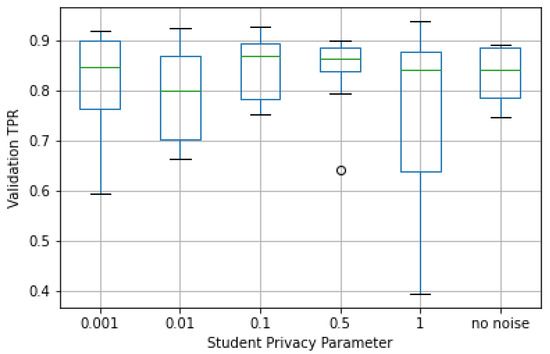
Figure 13.
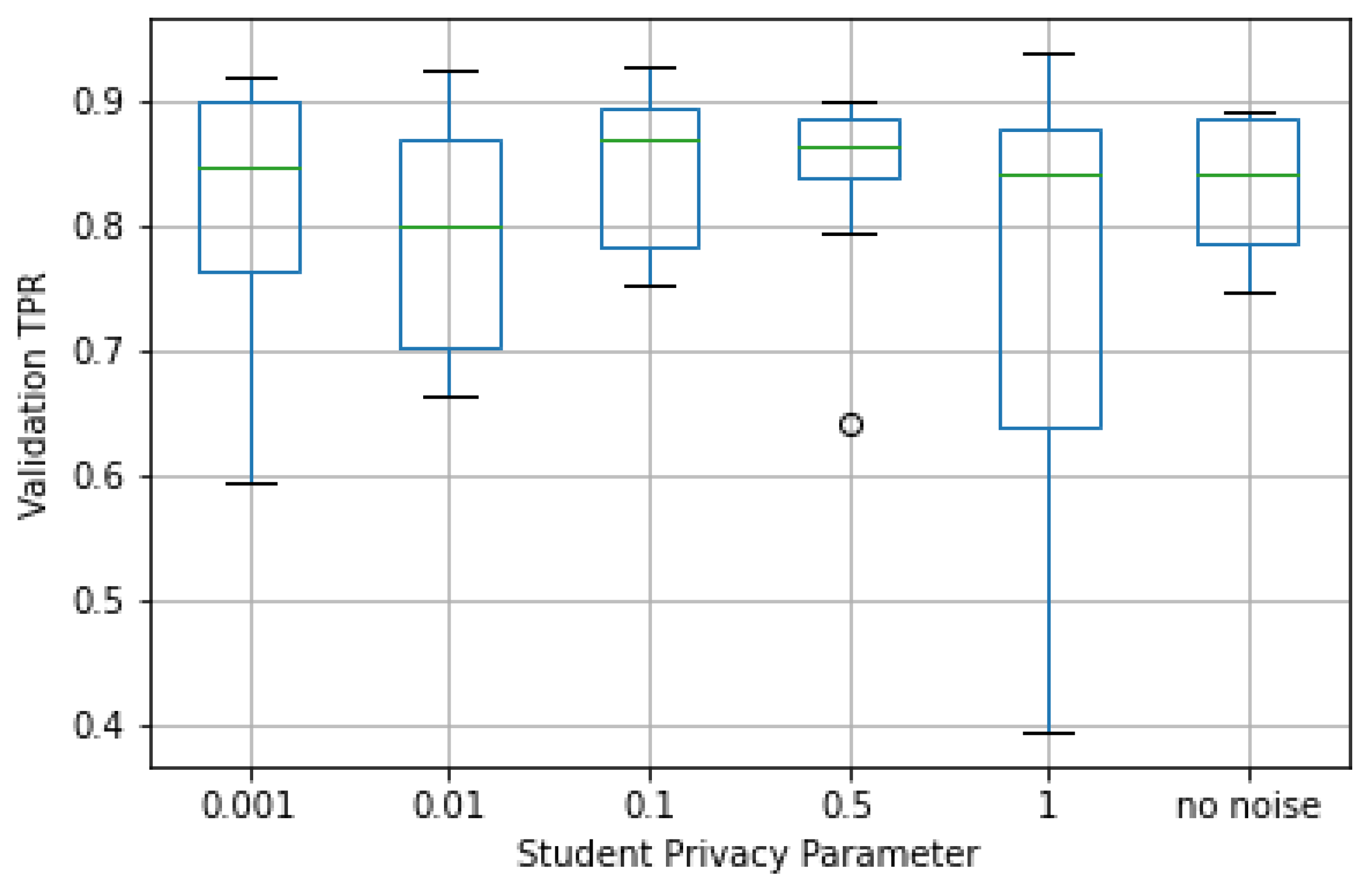
Validation TPR by student privacy parameter in Web Requests dataset.
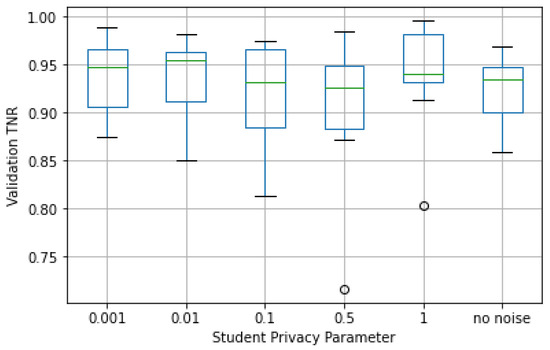
Figure 14.
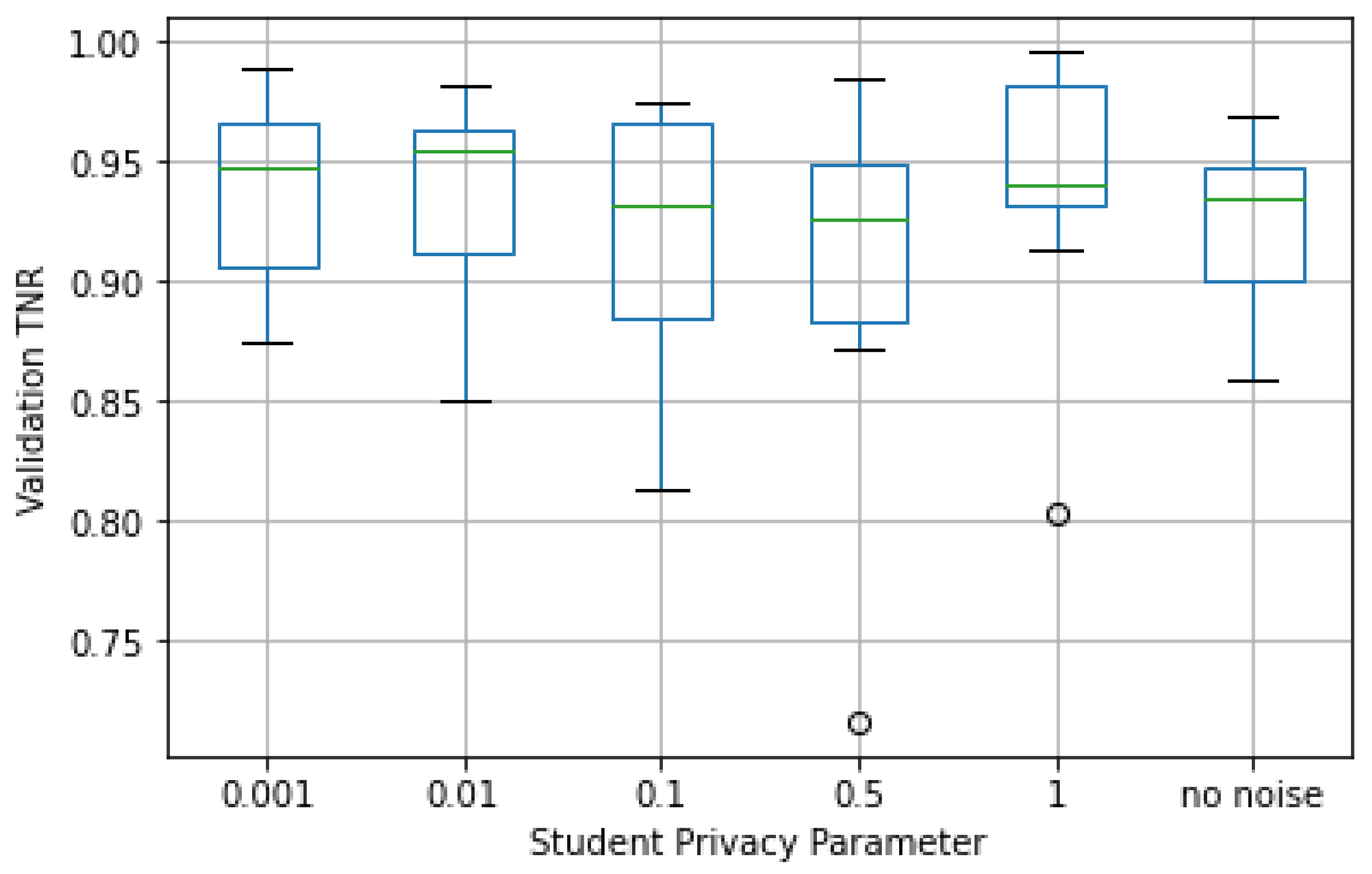
Validation TNR by student privacy parameter in Web Requests dataset.
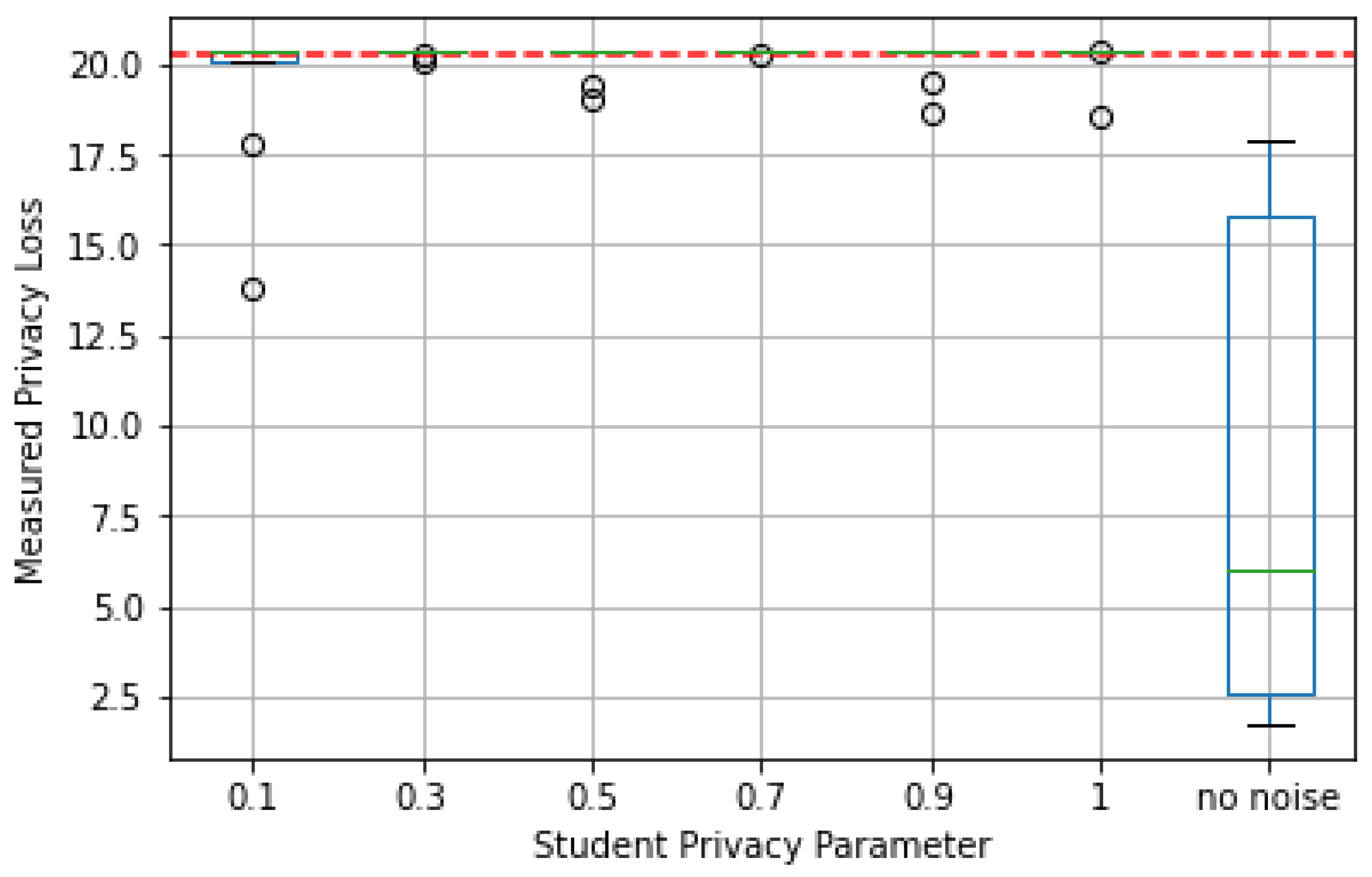
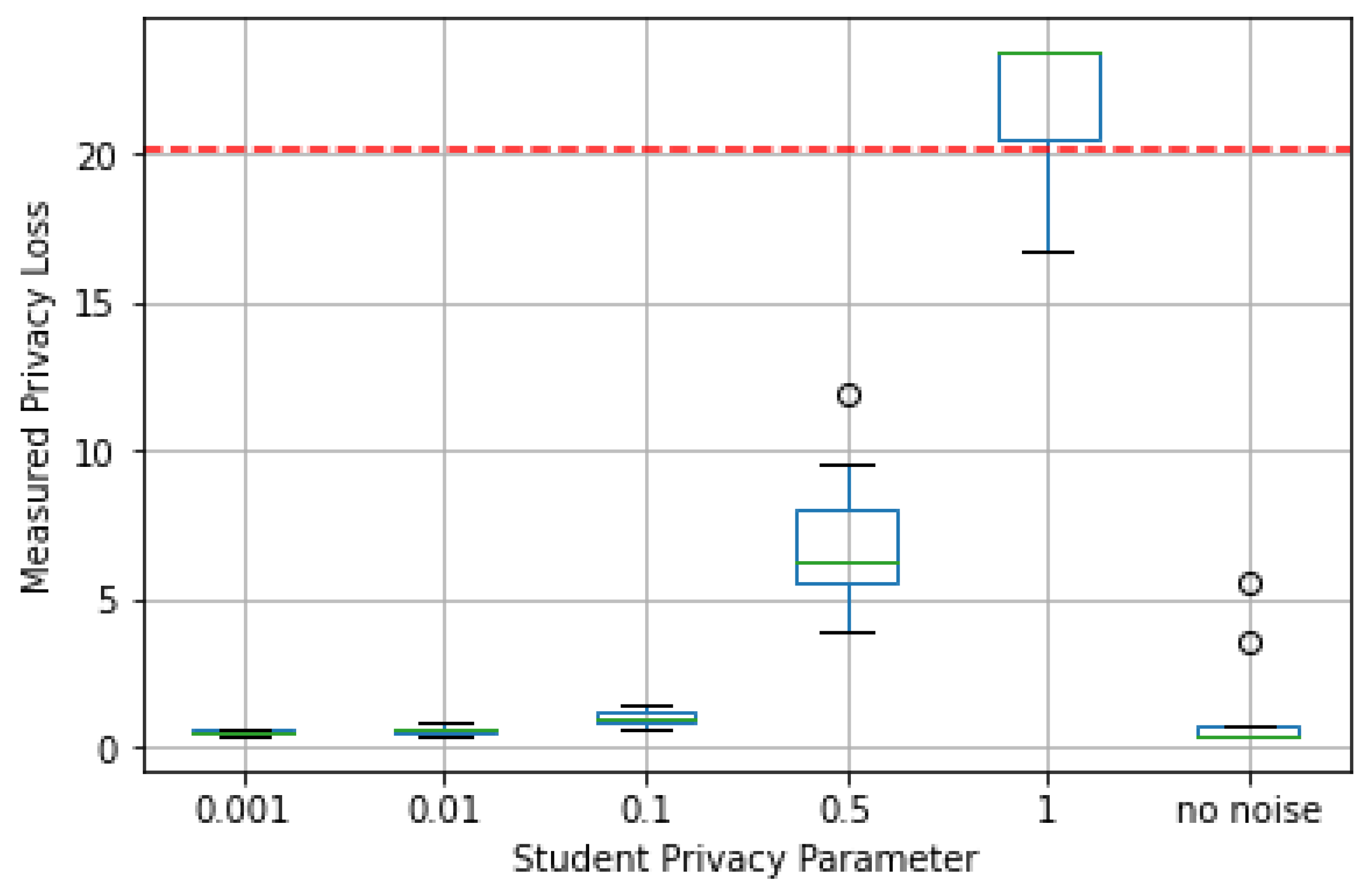
On the other hand, Figure 15 presents data-dependent privacy loss for the different values of . The dashed red line represents the data-independent privacy loss . As can be seen, the data-dependent privacy loss in some cases turned out to be higher than for the experiment where noise was not applied to student data. In one case, it happened to be even higher than for the data-independent privacy loss .
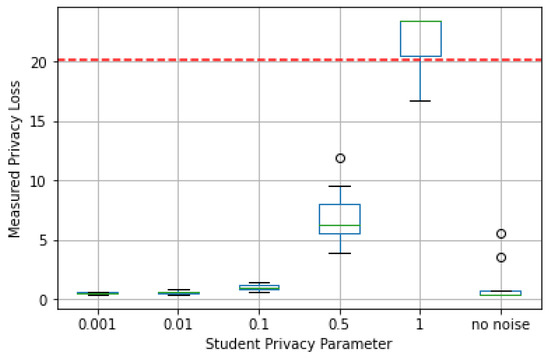
Figure 15.
Privacy loss by student privacy parameter in Web Requests dataset.
5. Conclusions
This paper exploredthe problem of using the PATE in more realistic scenarios where students were not allowed, or willing, to share private data with the teacher ensemble.
To cope with this constraint, we introduced a trusted curator that implemented a local DP model that added noise to student data before it was sent to the teacher ensemble. This approach was implemented and evaluated in case studies security and health. The experimental setup consisted of training students for several values of privacy parameters and measuring model predictive capacity and the data dependent privacy loss of the teacher ensemble.
The key result of this work is that the introduction of controlled noise, to ensure DP in student data, yielded no important reductions in predictive model performance compared with using unperturbed (non privatized) student data. This provided experimental evidence that using the PATE while preserving students’ privacy is feasible.
Tangentially, those experiments helped uncover some features of data-dependent privacy loss proposed in [18] that, to the best of our knowledge, had not been reported. In short, data-dependent privacy loss may be subject to high variance, as shown in the ECG case study with unperturbed data, and it may be very sensitive to noise in data, as observed in both case studies, which could be the subject of further research.
Author Contributions
S.Y. proposed the idea of protecting student data, the theoretical analysis, and supervised the research. S.Y., R.V. and F.M. contributed to the experimental results and writing. S.Y. and F.M. jointly developed the health case study. S.S. contributed to prototyping and the security case study. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by ICT4V—Information and Communication Technologies for Verticals grant number POS_ICT4V_2016_1_15, and ANII—Agencia Nacional de Investigación e Innovación grant numbers FSDA_1_2018_1_154419 and FMV_1_2019_1_155913.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sources used in this work were referenced throughout the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Iqbal, M.J.; Javed, Z.; Sadia, H.; Qureshi, I.A.; Irshad, A.; Ahmed, R.; Malik, K.; Raza, S.; Abbas, A.; Pezzani, R.; et al. Clinical applications of artificial intelligence and machine learning in cancer diagnosis: Looking into the future. Cancer Cell Int. 2021, 21, 270. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Thi Thu, H.L.; Kim, H. Long Short Term Memory Recurrent Neural Network Classifier for Intrusion Detection. In Proceedings of the 2016 International Conference on Platform Technology and Service (PlatCon), Jeju, Korea, 15–17 February 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Bontemps, L.; Cao, V.L.; McDermott, J.; Le-Khac, N. Collective Anomaly Detection Based on Long Short-Term Memory Recurrent Neural Networks. In International Conference on Future Data and Security Engineering; Dang, T.K., Wagner, R.R., Küng, J., Thoai, N., Takizawa, M., Neuhold, E.J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 10018, pp. 141–152. [Google Scholar] [CrossRef]
- Thi, N.N.; Cao, V.L.; Le-Khac, N. One-Class Collective Anomaly Detection Based on LSTM-RNNs. Trans. Large Scale Data Knowl. Centered Syst. 2017, 36, 73–85. [Google Scholar] [CrossRef]
- Yin, C.; Zhu, Y.; Fei, J.; He, X. A Deep Learning Approach for Intrusion Detection Using Recurrent Neural Networks. IEEE Access 2017, 5, 21954–21961. [Google Scholar] [CrossRef]
- Ruijer, E.; Détienne, F.; Baker, M.; Groff, J.; Meijer, A. The Politics of Open Government Data: Understanding Organizational Responses to Pressure for More Transparency. Am. Rev. Public Adm. 2020, 50, 260–274. [Google Scholar] [CrossRef] [Green Version]
- Directive (EU) 2019/1024 of the European Parliament and of the Council of 20 June 2019 on Open Data and the Re-Use of Public Sector Information. Available online: https://eur-lex.europa.eu/legal-content/en/TXT/?uri=CELEX%3A32019L1024 (accessed on 5 August 2021).
- Irvin, J.; Rajpurkar, P.; Ko, M.; Yu, Y.; Ciurea-Ilcus, S.; Chute, C.; Marklund, H.; Haghgoo, B.; Ball, R.L.; Shpanskaya, K.S.; et al. CheXpert: A Large Chest Radiograph Dataset with Uncertainty Labels and Expert Comparison. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 590–597. [Google Scholar] [CrossRef]
- Gruschka, N.; Mavroeidis, V.; Vishi, K.; Jensen, M. Privacy Issues and Data Protection in Big Data: A Case Study Analysis under GDPR. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 5027–5033. [Google Scholar] [CrossRef] [Green Version]
- Rocher, L.; Hendrickx, J.; de Montjoye, Y. Estimating the success of re-identifications in incomplete datasets using generative models. Nat. Commun. 2019, 10, 3069. [Google Scholar] [CrossRef]
- Harmanci, A.; Gerstein, M. Quantification of private information leakage from phenotype-genotype data: Linking attacks. Nat. Methods 2016, 13, 251–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narayanan, A.; Shmatikov, V. Robust de-anonymization of large sparse datasets. In Proceedings of the 2008 IEEE Symposium on Security and Privacy (sp 2008), Oakland, CA, USA, 18–21 May 2008; pp. 111–125. [Google Scholar]
- Sweeney, L.; Abu, A.; Winn, J. Identifying participants in the personal genome project by name (a re-identification experiment). arXiv 2013, arXiv:1304.7605. [Google Scholar]
- De Montjoye, Y.A.; Hidalgo, C.A.; Verleysen, M.; Blondel, V.D. Unique in the crowd: The privacy bounds of human mobility. Sci. Rep. 2013, 3, 1376. [Google Scholar] [CrossRef] [Green Version]
- Fredrikson, M.; Jha, S.; Ristenpart, T. Model Inversion Attacks that Exploit Confidence Information and Basic Countermeasures. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015. [Google Scholar] [CrossRef]
- General Data Protection Regulation. Available online: https://gdpr-info.eu/ (accessed on 10 May 2021).
- Chen, B.; Kifer, D.; LeFevre, K.; Machanavajjhala, A. Privacy-Preserving Data Publishing. Found. Trends Databases 2009, 2, 1–167. [Google Scholar] [CrossRef]
- Papernot, N.; Abadi, M.; Erlingsson, U.; Goodfellow, I.; Talwar, K. Semi-supervised knowledge transfer for deep learning from private training data. arXiv 2016, arXiv:1610.05755. [Google Scholar]
- Papernot, N.; Song, S.; Mironov, I.; Raghunathan, A.; Talwar, K.; Erlingsson, Ú. Scalable private learning with pate. arXiv 2018, arXiv:1802.08908. [Google Scholar]
- Dwork, C.; Roth, A. The Algorithmic Foundations of Differential Privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Melville, P.; Shah, N.; Mihalkova, L.; Mooney, R.J. Experiments on ensembles with missing and noisy data. In International Workshop on Multiple Classifier Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3077, pp. 293–302. [Google Scholar]
- Strauss, T.; Hanselmann, M.; Junginger, A.; Ulmer, H. Ensemble Methods as a Defense to Adversarial Perturbations against Deep Neural Networks. arXiv 2017, arXiv:1709.03423. [Google Scholar]
- Kachuee, M.; Fazeli, S.; Sarrafzadeh, M. ECG Heartbeat Classification: A Deep Transferable Representation. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 443–444. [Google Scholar] [CrossRef] [Green Version]
- Moody, G.; Mark, R. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, H.; Wei, Z. The weighted word2vec paragraph vectors for anomaly detection over HTTP traffic. IEEE Access 2020, 8, 141787–141798. [Google Scholar] [CrossRef]
- LIRMM. Analyzing Web Traffic: ECML/PKDD 2007 Discovery Challenge. 2007. Available online: http://www.lirmm.fr/pkdd2007-challenge/ (accessed on 21 September 2021).
- Torrano-Gimenez, C.; Perez-Villegas, A.; Alvarez, G. An anomaly-based approach for intrusion detection in web traffic. J. Inf. Assur. Secur. 2010, 5, 446–454. [Google Scholar]
- Salton, G.; Buckley, C. Term-weighting approaches in automatic text retrieval. Inf. Process. Manag. 1988, 24, 513–523. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).