Confidence Intervals for Class Prevalences under Prior Probability Shift

Abstract

Point estimation of class prevalences in the presence of dataset shift has been a popular research topic for more than two decades. Less attention has been paid to the construction of confidence and prediction intervals for estimates of class prevalences. One little considered question is whether or not it is necessary for practical purposes to distinguish confidence and prediction intervals. Another question so far not yet conclusively answered is whether or not the discriminatory power of the classifier or score at the basis of an estimation method matters for the accuracy of the estimates of the class prevalences. This paper presents a simulation study aimed at shedding some light on these and other related questions.

1. Introduction

In a prevalence estimation problem, one is presented with a sample of instances (the test sample), each of which belongs to exactly one of a finite number of classes but has not been labelled with the class. The task is to estimate the distribution of the class labels in the sample. If the problem sits in a binary two-class context, all instances belong to exactly one of two possible classes and, accordingly, can be labelled either positive or negative. The distribution of the labels then is characterised by the prevalence (i.e., proportion) of the positive labels (“class prevalence” for short) in the test sample. However, the labels are latent at estimation time such that the class prevalence cannot be determined by simple inspection of the labels. Instead, the class prevalence can only be inferred from the features of the instances in the sample, i.e., from observable covariates of the labels. The interrelationship between features and labels must be learnt from a training sample of labelled instances in another step before the class prevalence of the positive labels in the test sample can be estimated.

This whole process is called “supervised prevalence estimation” [1], “quantification” [2], “class distribution estimation” [3] or “class prior estimation” [4] in the literature. See the work of González et al. [5] for a recent overview of the quantification problem and approaches to deal with it. The emergence of further recent papers with new proposals of prevalence estimation methods suggests that the subject is still of high interest for both researchers and practitioners [6,7,8,9].

A variety of different methods for prevalence point estimation has been proposed and a considerable number of comparative studies for such methods has been published in the literature [5]. However, the question of how to construct confidence and prediction intervals for class prevalences seems to have attracted less attention. Hopkins and King [10] routinely provided confidence intervals for their estimates “via standard bootstrapping procedures”, without commenting much on details of the procedures or on any issues encountered with them. Keith and O’Connor [7] proposed and compared a number of methods for constructing such confidence intervals. Some of these methods involve Monte-Carlo simulation and some do not. In addition, Daughton and Paul [11] proposed a new method for constructing bootstrap confidence intervals and compared its results with the confidence intervals based on popular prevalence estimation methods. Vaz et al. [9] introduced the “ratio estimator” for class prevalences and used its asymptotic properties for determining confidence intervals without involving Monte-Carlo techniques.

This paper presents a simulation study that seeks to illustrate some observations from these previous papers on confidence intervals for class prevalences in the binary case and to provide answers to some questions begged in the papers:

• Would it be worthwhile to distinguish confidence and prediction intervals for class prevalences and deploy different methods for their estimation? This question is raised against the backdrop that, for instance, Keith and O’Connor [7] talked about estimating confidence intervals but in fact constructed prediction intervals which are conceptionally different [12].
• Would it be worthwhile to base class prevalence estimation on more accurate classifiers? The background for this question are conflicting statements in the literature as to the benefit of using accurate classifiers for prevalence estimation. On the one hand, Forman [2] stated on p. 168: “A major benefit of sophisticated methods for quantification is that a much less accurate classifier can be used to obtain reasonably precise quantification estimates. This enables some applications of machine learning to be deployed where otherwise the raw classification accuracy would be unacceptable or the training effort too great.” As an example for the opposite position, on the other hand, Barranquero et al. [13] commented on p. 595 with respect to prevalence estimation: “We strongly believe that it is also important for the learner to consider the classification performance as well. Our claim is that this aspect is crucial to ensure a minimum level of confidence for the deployed models.”
• Which prevalence estimation methods show the best performance with respect to the construction of as short as possible confidence intervals for class prevalences?
• Do non-simulation approaches to the construction of confidence intervals for class prevalences work?

In addition, this paper introduces two new methods for class prevalence estimation that are specifically designed for delivering as short as possible confidence intervals.

Deploying a simulation study for finding answers to the above questions has some advantages compared to working with real-world data:

• The true class prevalences are known and can even be chosen with a view to facilitate obtaining clear answers.
• The setting of the study can be freely modified—e.g., with regard to samples sizes or accuracy of the involved classifiers—to more precisely investigate the topics in question.
• In a simulation study, it is easy to apply an ablation approach to assess the relative impact of factors that influence the performance of methods for estimating confidence intervals.
• The results can be easily replicated.
• Simulation studies are good for delivering counter-examples. A method performing poorly in the study reported in this paper may be considered unlikely to perform much better in complex real-world settings.

Naturally, these advantages are bought at the cost of accepting certain obvious drawbacks:

• Most findings of the study are suggestive and illustrative only. No firm conclusions can be drawn from them.
• Important features of the problem which only occur in real-world situations might be overlooked.
• The prevalence estimation problem primarily is caused by dataset shift. For capacity reasons, the scope of the simulation study in this paper is restricted to prior probability shift, a special type of dataset shift. In the literature, prior probability shift is known under a number of different names, for instance “target shift” [14], “global drift” [15], or “label shift” [16] (see Moreno-Torres et al. [17] for a categorisation of types of dataset shift).

With these qualifications in mind, the main findings of this paper can be summarised as follows:

• Extra efforts to construct prediction intervals instead of confidence intervals for class prevalences appear to be unnecessary.
• “Error Adjusted Bootstrapping” as proposed by Daughton and Paul [11] for the construction of prevalence confidence or prediction intervals may fail in the presence of prior probability shift.
• Deploying more accurate classifiers for class prevalence estimation results in shorter confidence intervals.
• Compared to the other estimation methods considered in this paper, straight-forward “adjusted classify and count” methods for prevalence estimation [2] (called “confusion matrix method” in [18]) without any further tuning produce the longest confidence intervals and, hence, given identical coverage, perform worst. Methods based on minimisation of the Hellinger distance [3] (with different numbers of bins) produce much shorter confidence intervals, but sometimes do not guarantee sufficient coverage. The maximum likelihood approach (with bootstrapping for the confidence intervals) and “adjusted probabilistic classify and count” ([19], called there “scaled probability average”) appear to stably produce the shortest confidence intervals among the methods considered in the paper.

In this paper, instead of accuracy, also the term “discriminatory power” is used; similarly, instead of “accurate” the adjective “powerful” is employed.

The paper is organised as follows:

• Section 2 describes the conception and technical details of the simulation study, including in Section 2.2 a list of the prevalence estimation methods in scope.
• Section 3 provides some tables with results of the study and comments on the results, in order to explore the questions stated above. The results in Section 3.3 show that certain standard non-simulation approaches cannot take into account estimation uncertainty in the training sample and that bootstrap-based construction of confidence intervals could be used instead.
• Section 4 wraps up and closes the paper.
• In Appendix A, the mathematical details needed for coding the simulation study are listed.
• In Appendix B, the appropriateness for prior probability shift of the approach proposed by Daughton and Paul [11] is investigated.

The calculations of the simulation study were performed by making use of the statistical software R [20]. The R-scripts utilised can be downloaded from the URL https://www.researchgate.net/profile/Dirk_Tasche under the heading “Rscripts and data for paper Confidence Intervals for Class Prevalences under Prior Probability Shift”.

2. Setting of the Simulation Study

The set-up of the simulation study is intended to reflect the situation that occurs when a prevalence estimation problem as described in Section 1 has to be solved:

• There is a training sample $(x_{1,\mathrm{P}},y_{1,\mathrm{P}}),\dots ,$$(x_{m,\mathrm{P}},y_{m,\mathrm{P}})$ of observations of features $x_{i,\mathrm{P}}$ and class labels $y_{i,\mathrm{P}}\in \{-1,1\}$ for m instances. Instances with label $-1$ belong to the negative class, instances with label 1 belong to the positive class. By assumption, this sample was generated from a joined distribution $\mathrm{P}(X,Y)$ (the training population distribution) of the feature random variable X and the label (or class) random variable Y.
• There is a test sample $x_{1,\mathrm{Q}},\dots ,x_{n,\mathrm{Q}}$ of observations of features $x_{i,\mathrm{Q}}$ for n instances. By assumption, each instance has a latent class label $y_{i,\mathrm{Q}}\in \{-1,1\}$, and both the features and the labels were generated from a joined distribution $\mathrm{Q}(X,Y)$ (the test population distribution) of the feature random variable X and the label random variable Y.

The prevalence estimation or quantification problem is then to estimate the prevalence $q=\mathrm{Q}[Y=1]$ of the positive class labels in the test population. Of course, this is only a problem if there is dataset shift, i.e., if $\mathrm{P}(X,Y)\ne \mathrm{Q}(X,Y)$ and as a likely consequence $p=\mathrm{P}[Y=1]\ne q$.

This paper deals only with the situation where the training population distribution $\mathrm{P}(X,Y)$ and the test population distribution $\mathrm{Q}(X,Y)$ are related by prior probability shift, which means in mathematical terms that

$$\mathrm{Q}[X\in A|Y=-1]=\mathrm{P}[X\in A|Y=-1]\mathrm{and}\mathrm{Q}[X\in A|Y=1]=\mathrm{P}[X\in A|Y=1],$$

(1)

for all subsets A of the feature space such that $\mathrm{P}[X\in A]$ and $\mathrm{Q}[X\in A]$ are well-defined.

2.1. The Model for the Simulation Study

The classical binormal model with equal variances fits well into the prior probability shift setting for prevalence estimation of this paper. Kawakubo et al. [21] used it as part of their experiments for comparing the performance of prevalence methods. Logistic regression is a natural and optimal approach to the estimation of the binormal model with equal variances ([22] Section 6.1). Hence, when logistic regression is used for the estimation of the model in the simulation study, there is no need to worry about the results being invalidated by the deployment of a sub-optimal regression or classification technique. The binormal model is specified by defining the two class-conditional feature distributions $\mathrm{P}(X|Y=-1)$ and $\mathrm{P}(X|Y=1)$, respectively.

Training population distribution. Both class-conditional feature distributions are normal, with equal variances, i.e.,

$$\mathrm{P}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2),\mathrm{P}(X|Y=1)=\mathcal{N}(\nu ,{\sigma }^2),$$

(2a)

with $\mu <\nu$ and $\sigma >0$.

Test population distribution. This is the same as the training population distribution, with $\mathrm{P}$ replaced by $\mathrm{Q}$, in order to satisfy the assumption in Equation (1) on prior probability shift between training and test times.

For the sake of brevity, in the following, the setting with Equation (2a) for both the training and the test samples is referred to as “double” binormal setting.

Given the class-conditional population distributions as specified in Equation (2a), the unconditional training and test population distributions can be represented as

$$\begin{array}{cc}\hfill \mathrm{P}\left(X\right)& =p\mathrm{P}(X|Y=1)+(1-p\left)\mathrm{P}\right(X|Y=-1)\mathrm{and}\hfill \\ \hfill \mathrm{Q}\left(X\right)& =q\mathrm{P}(X|Y=1)+(1-q\left)\mathrm{Q}\right(X|Y=-1),\hfill \end{array}$$

(2b)

with $p=\mathrm{P}[Y=1]$ and $q=\mathrm{Q}[Y=1]$ as parameters whose values in the course of the simulation study are selected depending on the purposes of the specific numerical experiments.

Control parameters. For this paper’s numerical experiments, the values for the parameterisation of the model are selected from the ranges specified in the following list:

• $p\in \{0.33,0.5,0.67\}$ is the prevalence of the positive class in the training population.
• $m\in \{100,\infty \}$ is the size of training sample. In the case $m=\infty$, the training sample is considered identical with the training population and learning of the model is unnecessary. In the case of a finite training sample, the number of instances with positive labels is non-random in order to reflect the fact that for model development purposes a pre-defined stratification of the training sample might be desirable and can be achieved by under-sampling of the majority class or by over-sampling of the minority class. $m^{+}$ then is the size of the training sub-sample with positive labels, and $m^{-}$ is the size of the training sub-sample with negative labels. Hence, it holds that $m=m^{+}+m^{-}$, $m^{+}=pm$ und $m^{-}=(1-p)m$ for finite m.
• $q\in \{0.05,0.2\}$ is the prevalence of the positive class in the test population.
• $n\in \{50,500\}$ is the size of the test sample. In the test sample, the number of instances with positive labels is random.
• The population distribution underlying the features of the negative-class training sub-sample is always $\mathrm{P}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2)$ with $\mu =0$ and $\sigma =1$. The population distribution underlying the features of the positive-class training sub-sample is $\mathrm{P}(X|Y=1)=\mathcal{N}(\nu ,{\sigma }^2)$ with $\nu \in \{1,2.5\}$ and $\sigma =1$.
• The population distribution underlying the features of the negative-class test sub-sample is always $\mathrm{Q}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2)$ with $\mu =0$ and $\sigma =1$. The population distribution underlying the features of the positive-class test sub-sample is $\mathrm{Q}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2)$ with $\nu \in \{1,2.5\}$ and $\sigma =1$.
• The number of simulation runs in all of the experiments is $n_{\mathrm{sim}}=100$, i.e., $n_{\mathrm{sim}}$-times a training sample and a test sample as specified above are generated and subjected to some estimation procedures.
• The number of bootstrap iterations where needed in any of the interval estimation procedures is always $R=999$ [23].
• All confidence and prediction intervals are constructed at $\alpha =90\%$ confidence level.

Choosing $\nu =1$ in one of the following simulation experiments reflects a situation where no accurate classifier can be found, as it is suggested by the fact that then the AUC (area under the curve) of the feature X taken as a soft classifier is $\Phi \left(\frac{\nu -\mu }{\sigma \sqrt{2}}\right)=76.02\%$ (where $\Phi$ denotes the standard normal distribution function). In the case $\nu =2.5$, the same soft classifier X is very accurate with an AUC of $\Phi \left(\frac{\nu -\mu }{\sigma \sqrt{2}}\right)=96.15\%$. The different performance of the classifier depending on the value of parameter $\nu$ is also demonstrated in Figure 1 by the ROCs (receiver operating characteristics) corresponding to the two values $\nu =1$ (“low power”) and $\nu =2.5$ (“high power”).

For the sake of completeness, it is also noted that the feature-conditional class probability $\mathrm{P}[Y=1|X]$ under the training population distribution is given by

$$\mathrm{P}[Y=1|X]\left(x\right)=\frac{1}{1+exp(ax+b)},x\in \mathbb{R},$$

(3a)

with $a=\frac{\mu -\nu }{{\sigma }^2}<0$ and $b=\frac{{\nu }^2-{\mu }^2}{2{\sigma }^2}+log\left(\frac{1-\mathrm{P}[Y=1]}{\mathrm{P}[Y=1]}\right)$.

For the density ratio R under both the training and test population distributions, one obtains

$$R\left(x\right)=\frac{{\varphi }_{\nu ,\sigma }\left(x\right)}{{\varphi }_{\mu ,\sigma }\left(x\right)}=exp\left(x\frac{\nu -\mu }{{\sigma }^2}+\frac{{\mu }^2-{\nu }^2}{2{\sigma }^2}\right),x\in \mathbb{R}.$$

(3b)

${\varphi }_{\gamma ,\tau }$ denotes the density function of the one-dimensional normal distribution with mean $\gamma$ and standard deviation $\tau$.

2.2. Methods for Prevalence Estimation Considered in this Paper

The following criteria were applied for the selection of the methods deployed in the simulation study:

• The methods must be Fisher consistent in the sense of Tasche [24]. This criterion excludes, for instance, “classify and count” [2], the “Q-measure” approach [1] and the distance-minimisation approaches based on the Inner Product, Kumar–Hassebrook, Cosine, and Harmonic Mean distances mentioned in [8].
• The methods should enjoy some popularity in the literature.
• Two new methods based on already established methods and designed to minimise the lengths of confidence intervals are introduced and tested.

According to these criteria, the following prevalence estimation methods were included in the simulation study:

• ACC50: Adjusted Classify and Count (ACC: [2,18,25]), based on the Bayes classifier that minimises accuracy. The number “50” indicates that, when the Bayes classifier is represented by means of the posterior probability of the positive class and a threshold, the threshold has to be 50%.
• ACCp: Adjusted Classify and Count, based on the Bayes classifier that maximises the difference of TPR (true positive rate) and FPR (false positive rate). “p” because if the Bayes classifier is represented by means of the posterior probability of the positive class and a threshold, the threshold needs to be p, the a priori probability (or prevalence) of the positive class in the training population. ACCp is called “method max” in Forman [2].
• ACCv: New version of ACC where the threshold for the classifier is selected in such a way that the variance of the prevalence estimates is minimised among all ACC-type estimators based on classifiers represented by means of the posterior probability of the positive class and some threshold.
• MS: “Median sweep” as proposed by Forman [2].
• APCC: “Adjusted probabilistic classify and count” ([19], there called “scaled probability average”).
• APCCv: New version of APCC where the a priori positive class probability parameter in the posterior positive class probability is selected in such a way that the variance of the prevalence estimates is minimised among all APCC-type estimators based on posterior positive class probabilities where the a priori positive class probability parameter varies between 0 and 1.
• H4: Hellinger distance approach with four bins [3,6].
• H8: Hellinger distance approach with eight bins [3,6].
• Energy: Energy distance approach [6,21].
• MLinf/MLboot: ML is the maximum likelihood approach to prevalence estimation [26]. Note that the EM (expectation maximisation) approach of Saerens et al. [18] is one way to implement ML. “MLinf” refers to construction of the prevalence confidence interval based on the asymptotic normality of the ML estimator (using the Fisher information for the variance). “MLboot” refers to construction of the prevalence confidence interval solely based on bootstrap sampling.

For the readers’ convenience, the particulars needed to implement the methods in this list are presented in Appendix A. Note that ACC50, ACCp, ACCv, APCC und APCCv are all special cases of the “ratio estimator” discussed by Vaz et al. [9].

On the basis of the general asymptotic efficiency of maximum likelihood estimators ([27] Theorem 10.1.12), the maximum likelihood approach for class prevalences is a promising approach for achieving minimum confidence intervals lengths. In addition, the ML approach may be considered a representative of the class of entropy-related estimators and, as such, is closely related to the Topsøe approach which was found to perform very well by Maletzke et al. [8].

2.3. Calculations Performed in the Simulation Study

The calculations performed as part of the simulation study serve the purpose of providing facts for answers to the questions listed in Section 1 “Introduction”.

Calculations for constructing confidence intervals. Iterate $n_{\mathrm{sim}}$ times the following steps:

• Create the training sample: Simulate $m^{+}$ times from $\mathrm{P}(X|Y=1)=\mathcal{N}(\nu ,{\sigma }^2)$ features $x_{1,{\mathrm{P}}^{+}}$, …, $x_{m^{+},{\mathrm{P}}^{+}}$ of positive instances and $m^{-}$ times from $\mathrm{P}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2)$ features $x_{1,{\mathrm{P}}^{-}}$, …, $x_{m^{-},{\mathrm{P}}^{-}}$ of negative instances.
• Create the test sample: Simulate the number $N^{+}$ of positive instances as a binomial random variable with size n and success probability q. Then, simulate $N^{+}$ times from $\mathrm{Q}(X|Y=1)=\mathcal{N}(\nu ,{\sigma }^2)$ features $x_{1,\mathrm{Q}}$, …, $x_{N^{+},\mathrm{Q}}$ of positive instances and $N^{-}=n-N^{+}$ times from $\mathrm{Q}(X|Y=-1)=\mathcal{N}(\mu ,{\sigma }^2)$ features $x_{N^{+}+1,\mathrm{Q}}$, …, $x_{n,\mathrm{Q}}$ of negative instances. The information of whether a feature $x_{i,\mathrm{Q}}$ was sampled from $\mathrm{Q}(X|Y=1)$ or from $\mathrm{Q}(X|Y=-1)$ is assumed to be unknown in the estimation step. Therefore, the generated features are combined in a single sample $x_{1,\mathrm{Q}}$, …, $x_{n,\mathrm{Q}}$.
• Iterate R times the bootstrap procedure: Generate by stratified sampling with replications bootstrap samples $x_{1,{\mathrm{P}}^{+}}^{\prime }$, …, $x_{m^{+},{\mathrm{P}}^{+}}^{\prime }$ of features of positive instances, $x_{1,{\mathrm{P}}^{-}}^{\prime }$, …, $x_{m^{-},{\mathrm{P}}^{-}}^{\prime }$ of features of negative instances from the training subsamples, and $x_{1,\mathrm{Q}}^{\prime }$, …, $x_{n,\mathrm{Q}}^{\prime }$ of features with unknown labels from the test sample. Calculate, based on the three resulting bootstrap samples, estimates of the positive class prevalence in the test population according to all the estimation methods listed in Section 2.2.
• For each estimation method, the bootstrap procedure from the previous step creates a sample of R estimates of the positive class prevalence. Based on this sample of R estimates, construct confidence intervals at level $\alpha$ for the positive class prevalence in the test population.

Tabulated results of the simulation algorithm for confidence intervals.

• For each estimation method, $n_{\mathrm{sim}}$ estimates of the positive class prevalence are calculated. From this set of estimates, the following summary results were derived and tabulated:

  −

  the average of the prevalence estimates;

  −

  the average absolute deviation of the prevalence estimates from the true prevalence parameter;

  −

  the percentage of simulation runs with failed prevalence estimates; and

  −

  the percentage of estimates equal to 0 or 1;

• For each estimation method, $n_{\mathrm{sim}}$ confidence intervals at level $\alpha$ for the positive class prevalence are produced. From this set of confidence intervals, the following summary results were derived and tabulated:

  −

  the average length of the confidence intervals; and

  −

  the percentage of confidence intervals that contain the true prevalence parameter (coverage rate).

For the construction of the bootstrap confidence intervals in Step 4 of the list of calculations, the method “perc” ([23] Section 5.3.1) of the function boot.ci of the R-package “boot” was used. More accurate methods for bootstrap confidence intervals are available, but these tend to require more computational time and to be less robust. Given that the performance of “perc” in the setting of this simulation study can be controlled via checking the coverage rates, the loss in performance seems tolerable. In the cases where calculations resulted in coverage rates of less than $\alpha$, the calculations were repeated with the “bca” method ([23] Section 5.3.2) of boot.ci in order to confirm the results.

Step 1 of the calculations can be omitted in the case $m=\infty$, i.e., when the training sample is identical with the training population distribution. However, in this case, some quantities of relevance for the estimates have to be pre-calculated before the entrance into the loop for the $n_{\mathrm{sim}}$ simulation runs. The details for these pre-calculations are provided in Appendix A. In addition, in the case $m=\infty$, for the prevalence estimation methods ACC50, ACCp, ACCv, APCC und APCCv, the bootstrap confidence intervals for the prevalences were replaced by “conservative binomial intervals” ([12] Section 6.2.2), computed with the “exact” method of the R-function binconf. Moreover, as explained in Section 2.2, in the case $m=\infty$, the method MLinf was applied instead of MLboot for the construction of the maximum likelihood confidence interval.

As mentioned in Section 1, one of the purposes of the simulation study was to illustrate the differences between confidence and prediction intervals. Conceptionally, the difference may be described by their definitions as given in Meeker et al. [12] (“$1-\alpha$” as used by Meeker et al. [12] corresponds to “$\alpha$” as used in this paper):

• “A $100(1-\alpha )\%$ confidence interval for an unknown quantity $\theta$ may be formally characterized as follows: If one repeatedly calculates such intervals from many independent random samples, $100(1-\alpha )\%$ of the intervals would, in the long run, correctly include the actual value $\theta$. Equivalently, one would, in the long run, be correct $100(1-\alpha )\%$ of the time in claiming that the actual value of $\theta$ is contained within the confidence interval.” ([12] Section 2.2.5)
• “If from many independent pairs of random samples, a $100(1-\alpha )\%$ prediction interval is computed from the data of the first sample to contain the value(s) of the second sample, $100(1-\alpha )\%$ of the intervals would, in the long run, correctly bracket the future value(s). Equivalently, one would, in the long run, be correct $100(1-\alpha )\%$ of the time in claiming that the future value(s) will be contained within the prediction interval.” ([12] Section 2.3.6)

To construct prediction intervals instead of confidence intervals in the simulation runs, Step 4 of the calculations was modified as follows:

4*.

For each estimation method, the bootstrap procedure from the previous step creates a sample of R estimates of the positive class prevalence. For each estimate, generate a virtual number of realisations of positive instances by simulating an independent binomial variable with size n and success probability given by the estimate. Divide these virtual numbers by n to obtain (for each estimation method) a sample of relative frequencies of positive labels. Based on this additional size-R sample of relative frequencies, construct prediction intervals at level $\alpha$ for the percentage of instances with positive labels in the test sample.

As in the case of the construction of confidence intervals, for the construction of the prediction intervals, again the method “perc” of the function boot.ci of the R-package “boot” was deployed.

Tabulated results of the simulation algorithm for prediction intervals.

• For each estimation method, $n_{\mathrm{sim}}$ virtual relative frequencies of positive labels in the test sample were simulated under the assumption that the estimated positive class prevalence equals the true prevalence. From this set of frequencies, the following summary results are derived and tabulated:

  −

  the average of the virtual relative frequencies;

  −

  the average absolute deviation of the virtual relative frequencies from the true prevalence parameter;

  −

  the percentage of simulation runs with failed prevalence estimates and hence also failed simulations of virtual relative frequencies of positive labels; and

  −

  the percentage of virtual relative frequencies equal to 0 or 1.

• For each estimation method, $n_{\mathrm{sim}}$ prediction intervals at level $\alpha$ for the realised relative frequencies of positive labels are produced. From this set of prediction intervals, the following summary results were derived and tabulated:

  −

  the average length of the prediction intervals; and

  −

  the percentage of prediction intervals that contain the true relative frequencies of positive labels (coverage rate).

3. Results of the Simulation Study

All simulation procedures were performed with parameter setting $n_{\mathrm{sim}}=100$, $Rseed=17$ and $R=999$ (see Section 2.1 for the complete list of control parameters). In each table in the following, the values selected for the remaining control parameters are listed in the captions or within the table bodies.

In all the simulation procedures run for this paper, the R-boot.ci method for determining the statistical intervals (both confidence and prediction) was the method “perc”. In cases where the coverage found with “perc” is significantly lower than 90% (for $n_{\mathrm{sim}}=100$ at 5% significance level this means lower than 85%), the calculation was repeated with the R-boot.ci method “bca” for confirmation or correction.

The naming of the table rows and table columns has been standardized. Unless mentioned otherwise, the columns always display results for all or some of the prevalence estimation methods listed in Section 2.2. Short explanations of the meaning of the row names are given in

Table 1. Explanation of the row names in the result tables in Section 3.

Row Name	Explanation
“Av prev”	Average of the prevalence estimates (for confidence intervals)
“Av freq”	Average of the relative frequencies of simulated positive class labels (for prediction intervals)
“Av abs dev”	Average of the absolute deviation of the prevalence estimates
	or the simulated relative frequencies from the true prevalence
“Perc fail est”	Percentage of simulation runs with failed prevalence estimates
“Av int length”	Average of the confidence or prediction interval lengths
“Coverage”	Percentage of confidence intervals containing the true prevalence or
	of prediction intervals containing the true realised relative frequencies of positive labels
“Perc 0 or 1”	Percentage of prevalence estimates or simulated fequencies with value $\le {10}^{-7}$ or $\ge 1-{10}^{-7}$

. A more detailed explanation of the row names can be found in Section 2.3.

3.1. Prediction vs. Confidence Intervals

In the simulation study performed for this paper, the values of the true positive class prevalences of the test samples—understood in the sense of the a priori positive class prevalences of the populations from which the samples were generated (see Section 2)—are always known. In contrast, when one is working with real-world datasets, there is no way to know with certainty the true positive class prevalences of the test samples. Inevitably, therefore, in studies of prevalence estimation methods on real-world datasets, the performance has to be measured by comparison between the estimates and the relative frequencies of the positive labels observed in the test samples.

This was stated explicitly, for instance, by Keith and O’Connor [7]. The authors said in the section “Problem definition” of the paper that they estimated “prevalence confidence intervals” with the property that “$(1-\alpha )\%$ of the predicted intervals ought to contain the true value ${\theta }^{*}$”. For this purpose, Keith and O’Connor [7] defined the “true value” as follows: “For each group $\mathcal{D}$, let ${\theta }^{*}\equiv \left(1/n\right){\sum }_i^n{y}_i$ be the true proportion of positive labels (where $n=|\mathcal{D}|$).” As “group” was used by Keith and O’Connor [7] as equivalent to sample and $y_i$ was 1 for positive labels and 0 otherwise, it is clear that Keith and O’Connor [7] estimated rather prediction intervals than confidence intervals (see Section 2.3 for the definitions of both types of intervals).

Hence, as asked in Section 1: Would it be worthwhile to distinguish confidence and prediction intervals for class prevalences and deploy different methods for their estimation?

By assumption (see Section 2), the test sample $x_{1,\mathrm{Q}},\dots ,x_{n,\mathrm{Q}}$ is interpreted as the feature components of independent, identically distributed random variables $(X_{1,\mathrm{Q}},Y_{1,\mathrm{Q}})$, …, $(X_{n,\mathrm{Q}},Y_{n,\mathrm{Q}})$. While the positive class prevalence in the test population is given by the constant $\mathrm{Q}[Y=1]=q$, the relative frequency of the positive labels in test sample is represented by the random variable

$${\widehat{Y}}_{n,\mathrm{Q}}=\frac{1}{n}\sum _{i=1}^{n}I(Y_{i,\mathrm{Q}}=1),$$

(4)

where $I(Y_{i,\mathrm{Q}}=1)=1$ if $Y_{i,\mathrm{Q}}=1$ and $I(Y_{i,\mathrm{Q}}=1)=0$ otherwise.

The simulation procedures for the panels in

Table 2. Illustration of coverage of positive class frequencies in the test sample by means of prediction and confidence intervals. Control parameter for all panels: $n=50$.

${\mathit{m}}^{+}=33$,${\mathit{m}}^{-}=67$,$\mathit{\nu }=2.5$,$\mathit{q}=0.2$, Prediction Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av freq	19.26	20.70	16.02	20.72	20.42	18.74	18.92	19.72	19.76	19.38
Av abs dev	7.50	8.82	9.02	7.60	7.58	7.58	7.40	7.24	7.28	7.50
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	32.20	33.30	29.98	30.36	30.04	29.68	30.32	29.86	30.00	29.88
Coverage	100.0	99.0	94.0	100.0	99.0	98.0	99.0	99.0	99.0	98.0
Perc 0 or 1	1.0	2.0	6.0	1.0	2.0	2.0	4.0	1.0	3.0	1.0
${\mathit{m}}^{+}=\mathbf{33}$, ${\mathit{m}}^{-}=\mathbf{67}$, $\mathit{\nu }=\mathbf{2.5}$, $\mathit{q}=\mathbf{0.2}$, Confidence Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av prev	20.34	21.05	17.01	20.50	20.54	20.34	20.63	20.31	20.55	20.65
Av abs dev	6.68	7.23	7.61	6.22	6.12	6.13	6.06	5.88	6.18	6.00
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	28.27	28.98	26.13	25.67	25.15	24.55	25.57	25.10	25.10	24.83
Coverage	97.0	97.0	89.0	98.0	97.0	96.0	98.0	95.0	97.0	98.0
Perc 0 or 1	0.0	2.0	1.0	0.0	0.0	1.0	1.0	0.0	0.0	1.0
${\mathit{m}}^{+}=\mathbf{67}$, ${\mathit{m}}^{-}=\mathbf{33}$, $\mathit{\nu }=\mathbf{1}$, $\mathit{q}=\mathbf{0.2}$, Prediction Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av freq	18.96	22.30	23.72	21.33	17.08	18.20	22.80	28.76	19.12	17.48
Av abs dev	19.00	16.98	17.32	15.56	15.16	14.32	15.12	17.20	15.04	14.48
Perc fail est	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	71.69	58.92	72.82	54.15	47.88	49.96	56.24	59.32	49.44	47.38
Coverage	95.0	94.0	99.0	95.0	92.0	94.0	92.0	87.0	93.0	91.0
Perc 0 or 1	43.0	26.0	19.0	17.2	32.0	24.0	20.0	9.0	24.0	24.0
${\mathit{m}}^{+}=\mathbf{67}$, ${\mathit{m}}^{-}=\mathbf{33}$, $\mathit{\nu }=\mathbf{1}$, $\mathit{q}=\mathbf{0.2}$, Confidence Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av prev	21.36	22.90	21.16	23.61	19.25	20.93	23.65	28.81	21.26	19.59
Av abs dev	19.28	16.45	15.21	14.60	14.63	13.91	15.64	15.53	14.56	13.37
Perc fail est	0.0	0.0	0.0	4.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	66.65	57.89	69.97	51.98	47.20	49.07	54.25	54.26	48.45	47.08
Coverage	97.0	95.0	98.0	96.0	90.0	95.0	90.0	77.0	94.0	96.0
Perc 0 or 1	36.0	24.0	22.0	15.6	27.0	22.0	19.0	7.0	22.0	16.0
${\mathit{m}}^{+}=\mathbf{67}$, ${\mathit{m}}^{-}=\mathbf{33}$, $\mathit{\nu }=\mathbf{1}$, $\mathit{q}=\mathbf{0.05}$, Prediction Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
AAv freq	13.90	10.78	12.48	12.02	10.50	10.96	13.74	19.86	11.80	8.48
Av abs dev	13.06	10.34	11.84	10.94	10.36	10.44	12.88	16.52	11.12	8.44
Perc fail est	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	62.61	44.90	59.71	44.94	39.12	41.48	46.78	52.30	41.30	35.30
Coverage	98.0	97.0	97.0	94.0	93.0	92.0	90.0	75.0	92.0	93.0
Perc 0 or 1	41.0	42.0	42.0	36.4	47.0	42.0	39.0	13.0	38.0	47.0
${\mathit{m}}^{+}=\mathbf{67}$, ${\mathit{m}}^{-}=\mathbf{33}$, $\mathit{\nu }=\mathbf{1}$, $\mathit{q}=\mathbf{0.05}$, Confidence Intervals
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av prev	13.43	11.88	11.65	12.15	9.52	10.40	12.77	18.30	10.70	8.33
Av abs dev	13.79	11.11	11.03	10.68	9.56	9.71	11.44	15.43	10.01	8.34
Perc fail est	0.0	0.0	0.0	4.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	58.34	45.14	55.64	41.20	34.38	37.22	43.41	48.10	37.30	32.95
Coverage	98.0	93.0	96.0	93.0	89.0	91.0	83.0	62.0	94.0	92.0
Perc 0 or 1	52.0	40.0	42.0	31.2	42.0	36.0	34.0	17.0	37.0	44.0

are intended to gauge the impact of using a confidence interval instead of a prediction interval for capturing the relative frequency of positive labels in the test sample as defined in Equation (4). By the law of large numbers, the difference of ${\widehat{Y}}_{n,\mathrm{Q}}$ and q should be small for large n. Therefore, if there were any impact of using a confidence interval when a prediction interval would be needed, it should rather be visible for smaller n.

The algorithm devised in this paper for the construction of prediction intervals (see Section 2.3) involves the simulation of binomial random variables with the prevalence estimates as success probabilities which are independent of the test samples. This procedure, however, is likely to exaggerate the variance of the relative frequencies of the positive labels because the prevalence estimates and the test samples are not only not independent but even by design should be strongly dependent. The dependence between prevalence estimate and the test sample should be stronger when the classifier underlying the estimator is more accurate. This implies that, for prevalence estimation, differences between prediction and confidence intervals should rather be discernible for lower accuracy of the classifiers deployed.

Table 2 shows a number of simulation results, all for test sample size $n=50$, i.e., for small size of the test sample:

• Top two panels: Simulation of a “benign” situation, with not too much difference of positive class prevalences (33% vs. 20%) in training and test population distributions, and high power of the score underlying the classifiers and distance minimisation approaches. The results suggest “overshooting” by the binomial prediction interval approach, i.e., intervals are so long that coverage is much higher than requested, even reaching 100%. The confidence intervals clearly show sufficient coverage of the true realised percentages of positive labels for all estimation methods. Interval lengths are quite uniform, with only the straight ACC methods ACC50 and ACCp showing distinctly longer intervals. In addition, in terms of average absolute deviation from the true positive class prevalence, the performance is rather uniform. However, it is interesting to see that ACCv which has been designed for minimising confidence interval length among the ACC estimators shows the distinctly worst performance with regard to average absolute deviation.
• Central two panels: Simulation of a rather adverse situation, with very different (67% vs. 20%) positive class prevalences in training and test population distributions and low power of the score underlying the classifiers and distance minimisation approaches. There is still overshooting by the binomial prediction interval approach for all methods but H8. For all methods but H8, sufficient coverage by the confidence intervals is still clearly achieved. H8 coverage of relative positive class frequency is significantly too low with the confidence intervals but still sufficient with the prediction intervals. However, H8 also displays heavy bias of the average relative frequency of positive labels, possibly a consequence of the combined difficulties of there being eight bins for only 50 points (test sample size) and little difference between the densities of the score conditional on the two classes. In terms of interval length performance MLboot is best, closely followed by APCC and Energy. However, even for these methods, confidence interval lengths of more than 47% suggest that the estimation task is rather hopeless.
• Bottom two panels: Similar picture to the central panels, but even more adverse with a small test sample prevalence of 5%. The results are similar, but much higher proportions of 0% estimates for all methods. H8 now has insufficient coverage with both prediction and confidence intervals, and also H4 coverage with the confidence intervals is insufficient. Note the strong estimation bias suggested by all average frequency estimates, presumably caused by the clipping of negative estimates (i.e., replacing such estimates by zero). Among all these bad estimators, MLboot is clearly best in terms of bias, average absolute deviation and interval lengths.
• General conclusion: For all methods in Section 2.2 but the Hellinger methods, it suffices to construct confidence intervals. No need to apply special prediction interval techniques.
• Performance in terms of interval length (with sufficient coverage in all circumstances): MLboot best, followed by APCC and Energy.

Daughton and Paul [11] proposed “Error Adjusted Bootstrapping” as an approach to constructing “confidence intervals” (prediction intervals, as a matter of fact) for prevalences and showed by example that its performance in terms of coverage was sufficient. However, theoretical analysis of “Error Adjusted Bootstrapping” presented in Appendix B suggests that this approach is not appropriate for constructing prediction intervals in the presence of prior probability shift. Indeed,

Table 3. Illustration of difference between binomial approach and approach by Daughton and Paul [11] to prediction intervals for positive class prevalences. Control parameters for both panels: $n=50$, $\nu =2.5$, and $q=0.2$. Columns “ACC50” and “ACCp” show results for confidence intervals with methods as explained in Section 2.2. All other columns show prediction intervals and average relative frequencies of positive labels. In all columns, coverage refers to containing the realised relative frequency of positive labels in the test sample. “DnPACC50” and “DnPACCp” are determined according to the “error-corrected bootstrapping”, as  proposed by Daughton and Paul [11].

${\mathit{m}}^{+}=33$,${\mathit{m}}^{-}=67$
	ACC50	predACC50	ACCp	predACCp	DnPACC50	DnPACCp
Av prev or freq	19.97	20.22	19.49	19.78	24.32	25.40
Av abs dev	6.19	7.70	6.56	8.54	5.68	6.80
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	27.91	32.84	29.28	33.90	21.68	21.78
Coverage	100.0	100.0	99.0	100.0	95.0	93.0
Perc 0 or 1	0.0	0.0	1.0	2.0	0.0	0.0
${\mathit{m}}^{+}=\mathbf{67}$, ${\mathit{m}}^{-}=\mathbf{33}$
	ACC50	predACC50	ACCp	predACCp	DnPACC50	DnPACCp
Av prev	19.69	19.38	19.58	20.28	38.06	39.26
Av abs dev	9.91	9.82	9.03	10.32	18.18	19.26
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	32.41	36.34	30.49	34.72	26.28	26.32
Coverage	98.0	99.0	95.0	98.0	22.0	14.0
Perc 0 or 1	12.0	12.0	3.0	5.0	0.0	0.0

demonstrates that “Error Adjusted Bootstrapping” intervals based on the classifiers ACC50 and ACCp (see Section 2.2) achieve sufficient coverage if the difference between the training and test sample prevalences is moderate (33% vs. 20%) but breaks down if the difference is large (67% vs. 20%).

3.2. Does Higher Accuracy Help for Shorter Confidence Intervals?

As mentioned in Section 1, views in the literature differ on whether or not the performance of prevalence estimators is impacted by the discriminatory power of the score underlying the estimation method.

Table 4. Illustration of length of confidence intervals for different degrees of accuracy (or discriminatory power) of the score or classifier underlying the prevalence estimation methods.

$\mathit{n}=500$, ${\mathit{m}}^{+}=\mathit{\infty }$, ${\mathit{m}}^{-}=\mathit{\infty }$, $\mathit{\nu }=2.5$, $\mathit{p}=0.5$, $\mathit{q}=0.2$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLinf
Av prev	20.28	20.28	19.68	20.34	20.35	20.27	20.27	20.33	20.34	20.35
Av abs dev	1.97	1.97	1.90	1.79	1.79	1.72	1.81	1.76	1.80	1.72
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	8.47	8.47	8.04	7.74	7.71	7.50	7.54	7.42	7.72	7.35
Coverage	91.0	91.0	93.0	90.0	89.0	92.0	89.0	89.0	89.0	91.0
Perc 0 or 1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
$\mathit{n}=\mathbf{500}$, ${\mathit{m}}^{+}=\infty$, ${\mathit{m}}^{-}=\infty$, $\mathit{\nu }=\mathbf{1}$, $\mathit{p}=\mathbf{0.5}$, $\mathit{q}=\mathbf{0.2}$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLinf
Av prev	20.71	20.71	18.60	20.74	20.53	20.00	20.47	20.47	20.66	20.41
Av abs dev	4.68	4.68	4.21	3.64	3.37	3.23	3.65	3.30	3.39	3.19
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	19.08	19.08	18.47	16.70	15.73	15.15	16.14	15.50	15.91	15.05
Coverage	92.0	92.0	93.0	94.0	94.0	94.0	96.0	95.0	95.0	94.0
Perc 0 or 1	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
$\mathit{n}=\mathbf{50}$, ${\mathit{m}}^{+}=\infty$, ${\mathit{m}}^{-}=\infty$, $\mathit{\nu }=\mathbf{2.5}$, $\mathit{p}=\mathbf{0.33}$, $\mathit{q}=\mathbf{0.05}$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLinf
Av prev	4.96	5.49	2.75	4.99	5.14	4.60	5.07	4.56	5.15	5.09
Av abs dev	3.63	4.03	3.26	3.32	3.47	2.92	3.33	2.93	3.54	3.06
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	16.75	17.98	14.44	12.65	12.73	10.88	12.95	12.03	12.84	16.96
Coverage	95.0	98.0	97.0	90.0	86.0	85.0	88.5	94.4	88.0	97.0
Perc 0 or 1	24.0	24.0	27.0	16.0	18.0	11.0	18.0	10.0	18.0	13.0
$\mathit{n}=\mathbf{50}$, ${\mathit{m}}^{+}=\infty$, ${\mathit{m}}^{-}=\infty$, $\mathit{\nu }=\mathbf{1}$, $\mathit{p}=\mathbf{0.33}$, $\mathit{q}=\mathbf{0.05}$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLinf
Av prev	8.37	9.56	2.77	8.07	7.74	6.56	7.86	7.37	7.93	7.26
Av abs dev	8.31	9.28	5.70	7.78	7.64	7.00	7.73	7.47	7.68	7.50
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	38.27	35.30	29.85	27.52	25.46	24.98	27.63	25.80	26.30	47.01
Coverage	96.0	92.0	90.0	89.0	86.0	86.0	89.0	86.3	89.0	97.0
Perc 0 or 1	38.0	44.0	65.0	32.0	41.0	48.0	41.0	45.0	43.0	48.0
$\mathit{n}=\mathbf{50}$, ${\mathit{m}}^{+}=\mathbf{33}$, ${\mathit{m}}^{-}=\mathbf{67}$, $\mathit{\nu }=\mathbf{2.5}$, $\mathit{q}=\mathbf{0.05}$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av prev	5.72	6.91	3.62	5.67	5.88	5.72	5.53	5.65	5.97	5.59
Av abs dev	4.46	5.10	3.54	4.11	4.11	3.97	4.00	3.95	4.18	3.55
Perc fail est	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	16.62	18.68	11.35	14.96	14.92	13.90	14.22	13.44	15.09	13.95
Coverage	89.0	87.0	91.0	88.0	86.0	87.0	84.8	82.0	85.0	85.0
Perc 0 or 1	24.0	22.0	24.0	18.0	17.0	17.0	18.0	15.0	17.0	14.0
$\mathit{n}=\mathbf{50}$, ${\mathit{m}}^{+}=\mathbf{33}$, ${\mathit{m}}^{-}=\mathbf{67}$, $\mathit{\nu }=\mathbf{1}$, $\mathit{q}=\mathbf{0.05}$
	ACC50	ACCp	ACCv	MS	APCC	APCCv	H4	H8	Energy	MLboot
Av prev	10.49	11.59	6.54	10.43	8.50	8.38	10.96	12.12	9.50	8.39
Av abs dev	10.47	10.94	6.58	9.55	8.30	7.88	10.00	10.43	8.83	7.72
Perc fail est	0.0	0.0	0.0	4.0	0.0	0.0	0.0	0.0	0.0	0.0
Av int length	52.48	46.04	40.00	36.00	32.37	31.70	39.38	39.11	32.85	32.96
Coverage	97.0	95.0	96.0	94.0	91.0	90.0	91.0	92.0	92.0	92.0
Perc 0 or 1	43.0	37.0	43.0	32.3	41.0	38.0	36.0	28.0	40.0	38.0

shows a number of simulation results, for a variety of sets of circumstances, both benign and adverse. The results for high and low power are juxtaposed:

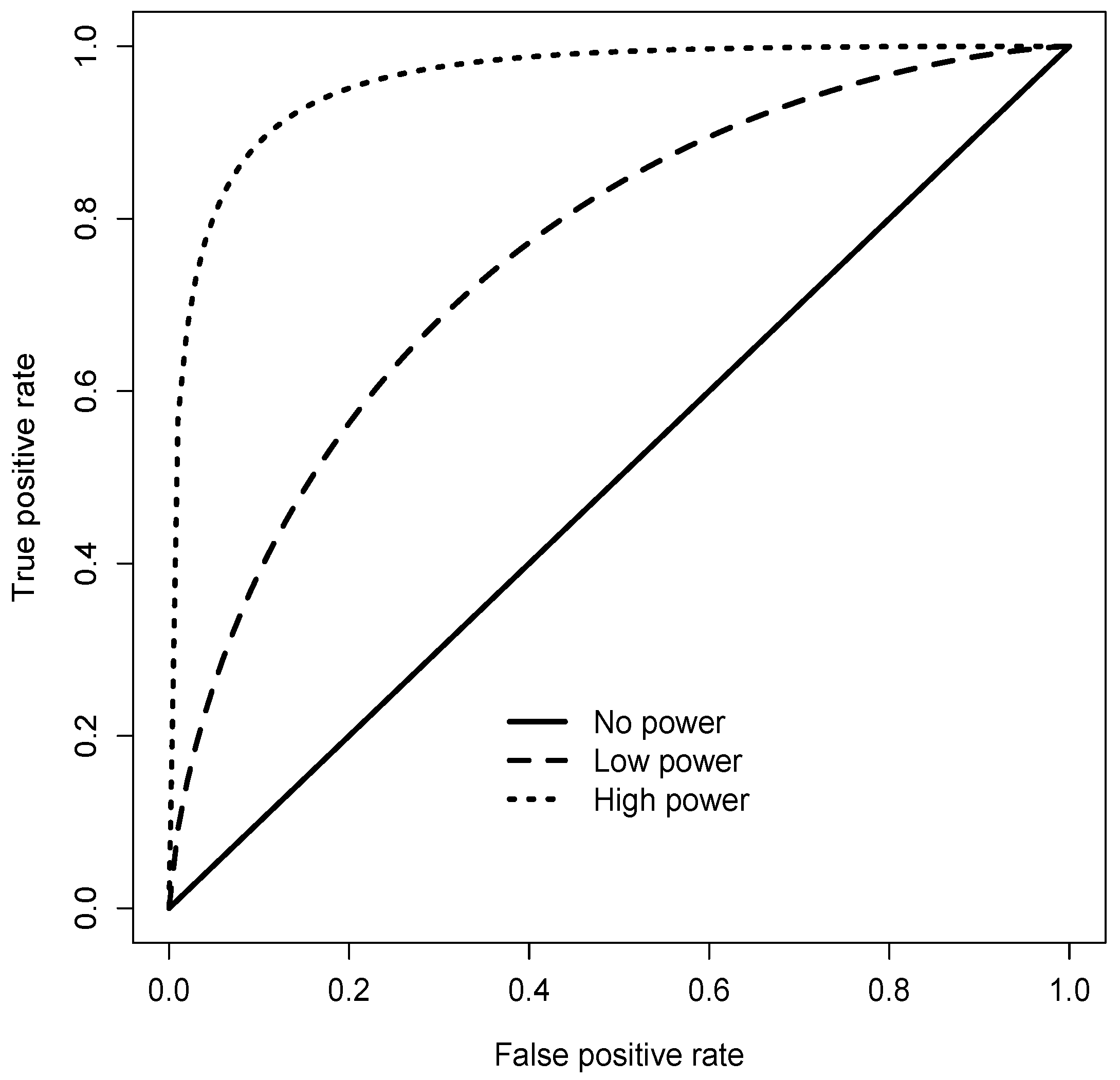
• Top two panels: Simulation of a “benign” situation, with moderate difference of positive class prevalences (50% vs. 20%) in training and test population distributions, no estimation uncertainty on the training sample and a rather large test sample with $n=500$. The results for all estimation methods suggest that the lengths of the confidence intervals are strongly dependent upon the discriminatory power of the score which is the basic building block of all the methods. Coverage is accurate for the high power situation, whereas there is even slight overshooting of coverage in the low power situation.
• Central two panels: Simulation of a less benign situation, with small test sample size and low true positive class prevalence in the test sample but still without uncertainty on the training sample. There is nonetheless again evidence for the strong dependence of the lengths of the confidence intervals upon the discriminatory power of the score. For all estimation methods, low power leads to strong bias of the prevalence estimates. The percentage of zero estimates jumps between the third and the fourth panel. Hence, decrease of power of the score entails much higher rates of zero estimates. For the maximum likelihood method, the interval length results in both panels show that constructing confidence intervals based on the central limit theorem for maximum likelihood estimators may become unstable for small test sample size and small positive class prevalence.
• Bottom two panels: Simulation of an adverse situation, with small test and training sample sizes and low true positive class prevalence in the test sample. The results show qualitatively very much the same picture as in the central panels. The impact of estimation uncertainty in the training sample which marks the difference to the situation for the central panels, however, is moderate for high power of the score but dramatic for low power of the score. Again, there is a jump of the rate of zero estimates between the two panels differentiated by different levels of discriminatory power. For the Hellinger methods, results of the high power panel suggest a performance issue with respect to the coverage rate. This observation is not confirmed by a repetition of the calculations for Panel 5 with deployment of R-boot.ci method “bca” instead of “perc”; however, the “better” results are accompanied by a high rate of failures of the confidence interval construction. In contrast to MLinf, MLboot (using only bootstrapping for constructing the confidence intervals) performs well, even with relatively low bias for the prevalence estimate in the low power case.
• General conclusion: The results displayed in Table 4 suggest that there should be a clear benefit in terms of shorter confidence intervals when high power scores and classifiers are deployed for prevalence estimation. In addition, the results illustrate the statement on the asymptotic variance of ratio estimators like ACC50, ACCp, APCv, APCC and APCCv in Corollary 11 of Vaz et al. [9].
• Performance in terms of interval length (with sufficient coverage in all circumstances): Both APCC estimation methods show good and stable performance when compared to all other methods. Energy and MLboot follow closely. The Hellinger methods also produce short confidence lengths but may have insufficient coverage.

3.3. Do Approaches to Confidence Intervals without Monte Carlo Simulations Work?

For the prevalence estimation methods ACC50, ACCp, ACCv, MS, and MLinf, confidence intervals can be constructed without bootstrapping and, therefore, much less numerical effort. For ACC50, ACCp, ACCv, and MS, conservative binomial intervals by means of the “exact” method of R-function binconf can be deployed ([12] Section 6.2.2). For the maximum likelihood approach, an asymptotically most efficient normal approximation with variance expressed in terms of the Fisher information can be used ([27] Theorem 10.1.12). This approach is denoted by “MLinf” in order to distinguish it from “MLboot”, maximum likelihood estimation combined with bootstrapping for the confidence intervals.

However, it can be shown by examples that these non-simulation approaches fail in the sense of producing insufficient coverage rates if training sample sizes are finite, i.e., if parameters such as true positive and false positive rates needed for the estimators have to be estimated (e.g., by means of regression) before being plugged in.

Table 5. Illustration of failure of non-simulation approaches to confidence intervals when training sample is finite. Control parameters for all panels: $p=0.33$, $\nu =2.5$, $q=0.2$, and $n=500$.

No Bootstrap, ${\mathit{m}}^{+}=\mathit{\infty }$, ${\mathit{m}}^{-}=\mathit{\infty }$
	ACC50	ACCp	ACCv	MS	MLinf
Av prev	20.15	20.28	19.40	20.14	20.27
Av abs dev	2.25	2.24	2.18	2.22	2.02
Perc fail est	0.0	0.0	0.0	0.0	0.0
Av int length	8.11	8.46	8.02	8.17	7.33
Coverage	92.0	86.0	88.0	87.0	92.0
Perc 0 or 1	0.0	0.0	0.0	0.0	0.0
No Bootstrap, ${\mathit{m}}^{+}=\mathbf{33}$, ${\mathit{m}}^{-}=\mathbf{67}$
	ACC50	ACCp	ACCv	MS	MLinf
Av prev	19.95	19.48	19.01	19.76	20.06
Av abs dev	3.23	3.88	2.98	3.35	2.57
Perc fail est	0.0	0.0	0.0	0.0	0.0
Av int length	8.13	8.47	7.60	8.16	7.22
Coverage	69.0	64.0	66.0	66.0	75.0
Perc 0 or 1	0.0	0.0	0.0	0.0	0.0
Bootstrap, ${\mathit{m}}^{+}=\mathbf{33}$, ${\mathit{m}}^{-}=\mathbf{67}$
	ACC50	ACCp	ACCv	MS	MLboot
Av prev	19.79	19.94	18.63	20.18	20.34
Av abs dev	3.11	3.38	3.17	2.79	2.67
Perc fail est	0.0	0.0	0.0	0.0	0.0
Av int length	15.13	16.96	14.18	12.94	12.07
Coverage	95.0	93.0	91.0	91.0	92.0
Perc 0 or 1	0.0	0.0	0.0	0.0	0.0

with panels juxtaposing results for infinite sample and finite sample sizes of the training sample, provides such an example.

The estimation problem whose results are shown in Table 5 is pretty well-posed, with a large test sample, a high power score underlying the estimation methods and moderate difference between training and test sample positive class prevalences. Panel 1 shows that without estimation uncertainty on the training sample (infinite sample size) the non-simulation approaches produce confidence intervals with sufficient coverage. In contrast, Panel 2 demonstrates that for all five methods coverage breaks down when estimation uncertainty is introduced into the training sample (finite sample size). According to Panel 3, this issue can be remediated by deploying bootstrapping for the construction of the confidence intervals.

4. Conclusions

The simulation study whose results are reported in this paper was intended to shed some light on certain questions from the literature regarding the construction of confidence or prediction intervals for the prevalence of positive labels in binary quantification problems. In particular, the results of the study should help to provide answers to the questions on:

• whether estimation techniques for confidence intervals are appropriate if in practice most of the time prediction intervals are needed; and
• whether the discriminatory power of the soft classifier or score at the basis of a prevalence estimation method matters when it comes to minimizing the confidence interval for an estimate.

The answers suggested by the results of the simulation study are subject to a number of qualifications. Most prominent among the qualifications are:

• the fact that the findings of the paper apply only for problems where it is clear that training and test samples are related by prior probability shift; and
• the general observation that the scope of a simulation study necessarily is rather restricted and therefore findings of such studies can be suggestive and illustrative at best.

Hence, the findings from the study do not allow firm or general conclusions. As a consequence, the answers to the questions suggested by the simulation study have to be ingested with caution:

• For not too small test sample sizes, such as 50 or more, there is no need to deploy special techniques for prediction intervals.
• It is worthwhile to base prevalence estimation on powerful classifiers or scores because this way the lengths of the confidence intervals can be much reduced. The use of less accurate classifiers may entail confidence intervals so long that the estimates have to be considered worthless.

In most of the experiments performed as part of the simulation study, the maximum likelihood approach (method MLboot) to the estimation of the positive class prevalence turned out to deliver on average the shortest confidence intervals. As shown in Appendix A.2.3, application of the maximum likelihood approach requires that in a previous step the density ratio or the posterior class probabilities are estimated on the training samples. To achieve this with sufficient precision is a notoriously hard problem. Note, however, the promising recent progress made on this issue [28]. Not much worse and in a few cases even superior was the performance of APCC (Adjusted Probabilistic Classify and Count). In contrast the performance of the Energy distance and Hellinger distance estimation methods was not outstanding and, in the case of the latter methods, even insufficient in the sense of not guaranteeing the required coverage rates of the confidence intervals.

Clearly, it would be desirable to extend the scope of the simulation study in order to obtain more robust answers to the questions mentioned above.

One way to do so would be to look at a larger range of prevalence estimation methods. Recent research by Maletzke et al. [8] singled out prevalence estimation methods based on minimising distances related to the Earth Mover’s distance as very well and robustly performing. Earlier research by Hofer [29] already found that prevalence estimation by minimising the Earth Mover’s distance worked well in the presence of general dataset shift (“local drift”). Hence, it might be worthwhile to compare the performance of such estimators with respect to the length of confidence intervals to the performance of other estimators such as the ones considered in this paper.

Another way to extend the scope of the simulation study would be to generalise the “double binormal” framework the study described in this paper is based on. Such an extension could be constructed along the lines described in Section 4 of Tasche [24].