A Novel Heterogeneous Swarm Reinforcement Learning Method for Sequential Decision Making Problems
Abstract
1. Introduction
- it consists of many individuals;
- the individuals are relatively homogeneous, i.e., they are either identical of they belong to a small number of typologies;
- the individuals exhibit stigmergy, i.e., they interact based on simple behavioral rules that exploit solely local information that the individuals exchange directly or via their environment;
- the overall behavior of the system self-organizes, i.e., it results from the interactions of the individuals with each other or with the environment.
- Age-structured swarms, in which heterogeneity arises when motion or sensing capabilities vary significantly with age.
- Predator–prey swarming, where there are distinct time-scale differences in the motion of predator and prey animals.
- Segregation of intermingled cell types during growth and development of an organism by introducing heterogeneity in inter cell adhesion properties.
2. Markov Decision Processes (MDPs)
2.1. Formal MDP Definition
- is a set of agent-environment states.
- is a set of actions the agent can take.
- is a state transition function which gives the probability that taking action in state results in state .
- is a reward function that quantifies the reward the agent gets for taking action in state resulting in state .
- is a discount factor that trades off between immediate reward and potential future reward.
2.2. The Exploitation–Exploration Trade-Off
2.3. Action–Selection Strategies
3. RL Methods for MDPs (Single-Agent, MARL, Swarm RL)
3.1. Q-Learning
3.2. Q-Learning for Agent-Based Systems
- is the number of agents.
- is the set of the environment states.
- are the set of actions that available to the agents, yielding the joint action set .
- is the state transition probability function.
- are reward functions of agents.
- is a discount factor that trades off between immediate reward and potential future reward.
4. A Novel Heterogeneous Swarm Reinforcement Learning (HetSRL) Method
- is a set of agent-environment states.
- is a set of profiles that for each state indicates its visitors collective profile.
- is a set of actions the agent can take.
- is a state transition function which gives the probability that taking action in state results in state .
- is a reward function that quantifies the reward the agent gets for taking action in state resulting in state .
- is a discount factor that trades off between immediate reward and potential future reward.
5. The Application of Affinity-Based HetSRL Method to the Shortest Path Problem
6. Holonic-Q-Learning: A Practical Application of the Affinity-Based HetSRL Method
6.1. The Holonic Medical Diagnosis System (HMDS)
6.2. Learning in HMDS
6.3. Simulation: A New DDx for Arthritis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons, Inc.: New York, NY, USA, 1994; p. 684. [Google Scholar]
- Littman, M.L. Algorithms for Sequential Decision Making. Ph.D. Thesis, Department of Computer Science, Brown University, Providence, RI, USA, 1996. [Google Scholar]
- Beni, G.; Wang, J. Swarm Intelligence in Cellular Robotic Systems. Robot. Biol. Syst. A New Bionics 1989, 102, 703–712. [Google Scholar] [CrossRef]
- Dorigo, M.; Floreano, D.; Gambardella, L.M.; Mondada, F.; Nolfi, S.; Baaboura, T.; Birattari, M.; Bonani, M.; Brambilla, M.; Brutschy, A.; et al. Swarmanoid: A novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 2013, 20, 60–71. [Google Scholar] [CrossRef]
- Akbari, Z.; Unland, R. A Holonic Multi-Agent Based Diagnostic Decision Support System for Computer-Aided History and Physical Examination. In Proceedings of the Advances in Practical Applications of Agents, Multi-Agent Systems, and Complexity: The PAAMS Collection (PAAMS 2018), Lecture Notes in Computer Science, Toledo, Spain, 20–22 June 2018; Volume 10978, pp. 29–41. [Google Scholar]
- UNANIMOUS AI. Available online: https://unanimous.ai/ (accessed on 11 March 2019).
- Dorigo, M.; Birattari, M. Swarm intelligence. 2007. Available online: http://www.scholarpedia.org/article/Swarm_intelligence (accessed on 11 March 2019).
- Montes de Oca, M.A.; Pena, J.; Stützle, T.; Pinciroli, C.; Dorigo, M. Heterogeneous Particle Swarm Optimizers. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Trondheim, Norway, 18–21 May 2009; pp. 698–705. [Google Scholar]
- Szwaykowska, K.; Romero, L.M.-y.-T.; Schwartz, I.B. Collective motions of heterogeneous swarms. IEEE Trans. Autom. Sci. Eng. 2015, 12, 810–818. [Google Scholar] [CrossRef]
- Ferante, E. A Control Architecture for a Heterogenous Swarm of Robots; Université Libre de Bruxelles: Brussels, Belgium, 2009. [Google Scholar]
- Kumar, M.; Garg, D.P.; Kumar, V. Segregation of heterogeneous units in a swarm of robotic agents. IEEE Trans. Autom. Control 2010, 55, 743–748. [Google Scholar] [CrossRef]
- Pinciroli, C.; O’Grady, R.; Christensen, A.L.; Dorigo, M. Coordinating heterogeneous swarms through minimal communication among homogeneous sub-swarms. In Proceedings of the International Conference on Swarm Intelligence, Brussels, Belgium, 8–10 September 2010; pp. 558–559. [Google Scholar]
- Engelbrecht, A.P. Heterogeneous particle swarm optimization. In Proceedings of the International Conference on Swarm Intelligence (ANTS 2010), Brussels, Belgium, 8–10 September 2010; pp. 191–202. [Google Scholar]
- Ma, X.; Sayama, H. Hierarchical heterogeneous particle swarm optimization: algorithms and evaluations. Intern. J. Parallel Emergent Distrib. Syst. 2015, 31, 504–516. [Google Scholar] [CrossRef]
- van Hasselt, H.P. Insights in Reonforcment Learning; Wöhrmann Print Service: Zutphen, The Netherlands, 2011; p. 278. [Google Scholar]
- Tandon, P.; Lam, S.; Shih, B.; Mehta, T.; Mitev, A.; Ong, Z. Quantum Robotics: A Primer on Current Science and Future Perspectives; Morgan & Claypool Publichers: San Rafael, CA, USA, 2017; p. 149. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; p. 322. [Google Scholar]
- Poole, D.; Mackworth, A. Artificial Intelligence: Foundations of Computational Agents; Cambridge University Press: New York, NY, USA, 2010; p. 682. [Google Scholar]
- Mitchell, T.M. Chapter 13: Reinforcement Learning. In Machine Learning; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1997. [Google Scholar]
- Vrancx, P. Decentralised Reinforcement Learning in Markov Games. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2010. [Google Scholar]
- Coggen, M. Exploration and Exploitation in Reinforcement Learning; CRA-W DMP Project at McGrill University: Montreal, QC, Canada, 2004. [Google Scholar]
- Barto, A.G.; Sutton, R.S.; Anderson, C.W. Neuronlike adaptive elements that can solve difficult learning control problems. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 834–846. [Google Scholar] [CrossRef]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H. Learning from delayed rewards. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1989. [Google Scholar]
- Schwartz, A. A reinforcement learning method for maximizing undiscounted rewards. In Proceedings of the 10th International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 298–305. [Google Scholar]
- Rummery, G.A.; Niranjan, M. On-Line Q-Learning Using Connectionist Systems; Department of Engineering, University of Cambridge: Cambridge, UK, 1994; pp. 1–20. [Google Scholar]
- Wiering, M.A.; van Hasselt, H. Two novel on-policy reinforcement learning algortihms based on TD(λ)-methods. In Proceedings of the Approximate Dynamic Programming and Reinforcement Learning, ADPRL 2007, Honolulu, HI, USA, 1–5 April 2007. [Google Scholar]
- Hoffman, m.; Doucet, A.; de Freitas, N.; Jasra, A. Trans-dimensional MCMC for Bayesian Policy Learning. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 665–672. [Google Scholar]
- Buşoniu, L.; Babuška, R.; Schutter, B.D. Multi-agent reinforcement learning: An overview. Innov. Multi-Agent Syst. Appl. 2010, 310, 183–221. [Google Scholar] [CrossRef]
- Tuyls, K.; Weiss, G. Multiagent Learning: Basics, Challenges, and Prospects. AI Mag. 2012, 33, 41–52. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 1992. [Google Scholar]
- Gambardella, L.M.; Dorigo, M. Ant-Q: A Reinforcement Learning approach to the traveling salesmn problem. In Proceedings of the ML-95, 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 252–260. [Google Scholar]
- Monekosso, N.; Remagnino, A.P. Phe-Q: A pheromone based Q-learning. In Proceedings of the Australian Joint Conference on Artificial Intelligence: AI 2001, LNAI 2256, Adelaide, SA, Australia, 10–14 December 2001; pp. 345–355. [Google Scholar]
- Iima, H.; Kuroe, Y.; Matsuda, S. Swarm reinforcement learning method based on ant colony optimization. In Proceedings of the 2010 IEEE International Conference on Systems Man and Cybernetics (SMC), Istanbul, Turkey, 10–13 October 2010; pp. 1726–1733. [Google Scholar]
- Hong, M.; Jung, J.J.; Camacho, D. GRSAT: A novel method on group recommendation by social affinity and trustworthiness. Cybern. Syst. 2017, 140–161. [Google Scholar] [CrossRef]
- Hong, M.; Jung, J.J.; Lee, M. Social Affinity-Based Group Recommender System. In Proceedings of the International Conference on Context-Aware Systems and Applications, Vung Tau, Vietnam, 26–27 November 2015; pp. 111–121. [Google Scholar]
- APA Dictionary of Psychology. Available online: https://dictionary.apa.org (accessed on 11 March 2019).
- Hill, C.; O’Hara O’Connor, E. A Cognitive Theory of Trust. 84 Wash. U. L. Rev. 2005, 84, 1717–1796. [Google Scholar] [CrossRef]
- Chatterjee, K.; Majumdar, R.; Henzinger, T.A. Markov decision processes with multiple objectives. In Proceedings of the Annual Symposium on Theoretical Aspects of Computer Science, Marseille, France, 23–25 February 2006; pp. 325–336. [Google Scholar]
- Lizotte, D.J.; Laber, E.B. Multi-Objective Markov Decision Processes for Data-Driven Decision Support. J. Mach. Learn. Res. 2016, 17, 1–28. [Google Scholar]
- Roijers, D.M.; Vamplew, P.; Whiteson, S.; Dazeley, R. A survey of multi-objective sequential decision-making. J. Artif. Intell. Res. 2013, 48, 67–113. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Masud, A.S.M. Multiple Objective Decision Making, Methods and Application: A State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1979; p. 351. [Google Scholar]
- Melo, F. Convergence of Q-learning: A simple proof; Institute Of Systems and Robotics, Tech. Rep (2001); Institute of Systems and Robotics: Lisbon, Portugal, 2001; pp. 1–4. [Google Scholar]
- Jaakkola, T.; Jordan, M.I.; Singh, S. Convergence of stochastic iterative dynamic programming algorithms. In Proceedings of the 6th International Conference on Neural Information Processing Systems, Denver, CO, USA, 29 November–2 December 1993; pp. 703–710. [Google Scholar]
- Jaakkola, T.; Jordan, M.I.; Singh, S. On the convergence of stochastic iterative dynamic programming algorithms. Neural Comput. 1994, 6, 1185–1201. [Google Scholar] [CrossRef]
- Akbari, Z.; Unland, R. A Holonic Multi-Agent System Approach to Differential Diagnosis. In Proceedings of the Multiagent System Technologies. MATES 2017, Leipzig, Germany, 23–26 August 2017; pp. 272–290. [Google Scholar]
- GAMA Platform. Available online: https://gama-platform.github.io/ (accessed on 11 March 2019).
- Gerber, C.; Siekmann, J.H.; Vierke, G. Holonic Multi-Agent Systems; DFKI-RR-99-03: Kaiserslautern, Germany, 1999. [Google Scholar]
- Merriam-Webster. Differential Diagnosis. Available online: https://www.merriam-webster.com/dictionary/differential%20diagnosis (accessed on 11 March 2019).
- Maude, J. Differential diagnosis: The key to reducing diagnosis error, measuring diagnosis and a mechanism to reduce healthcare costs. Diagnosis 2014, 1, 107–109. [Google Scholar] [CrossRef] [PubMed]
- Koestler, A. The Ghost in the Machine; Hutchinson: London, UK, 1967; p. 384. [Google Scholar]
- Rodriguez, S.A. From Analysis to Design of Holonic Multi-Agent Systems: A Framework, Methodological Guidelines and Applications. Ph.D. Thesis, University of Technology of Belfort-Montbéliard, Sevenans, France, 2005. [Google Scholar]
- Lavendelis, E.; Grundspenkis, J. Open holonic multi-agent architecture for intelligent tutoring system development. In Proceedings of the IADIS International Conference on Intelligent Systems and Agents, Amsterdam, The Netherlands, 22–24 July 2008. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discoverey and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Akbari, Z.; Unland, R. Automated Determination of the Input Parameter of the DBSCAN Based on Outlier Detection. In Proceedings of the Artificial Intelligence Applications and Innovations (AIAI 2016), IFIP Advances in Information and Communication Technology, Thessaloniki, Greece, 16–18 September 2016; Volume 475, pp. 280–291. [Google Scholar]
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 11 March 2019).
- Mayo Clinic. Available online: https://www.mayoclinic.org/ (accessed on 11 March 2019).
- Lemaire, O.; Paul, C.; Zabraniecki, L. Distal Madelung-Launois-Bensaude disease: An unusual differential diagnosis of acromalic arthritis. Clin. Exp. Rheumatol. 2008, 26, 351–353. [Google Scholar] [PubMed]
- Polikar, R. Ensemble learning. 2009. Available online: http://www.scholarpedia.org/article/Ensemble_learning (accessed on 11 March 2019).
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive mixtures of local experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Jordan, M.I.; Jacobs, R.A. Hierarchical mixtures of experts and the EM algorithm. In Proceedings of the 1993 International Conference on Neural Networks (IJCNN-93-Nagoya, Japan), Nagoya, Japan, 25–29 October 1993; pp. 181–214. [Google Scholar]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier Chains for Multi-label Classification. In Proceedings of the 13th European Conference on Principles and Practice of Knowledge Discovery in Databases and the 20th European Conference on Machine Learning, Bled, Slovenia, 7–11 September 2009; pp. 254–269. [Google Scholar]
- Liu, W.; Tsang, I.W. On the optimality of classifier chain for multi-label classification. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 712–720. [Google Scholar]
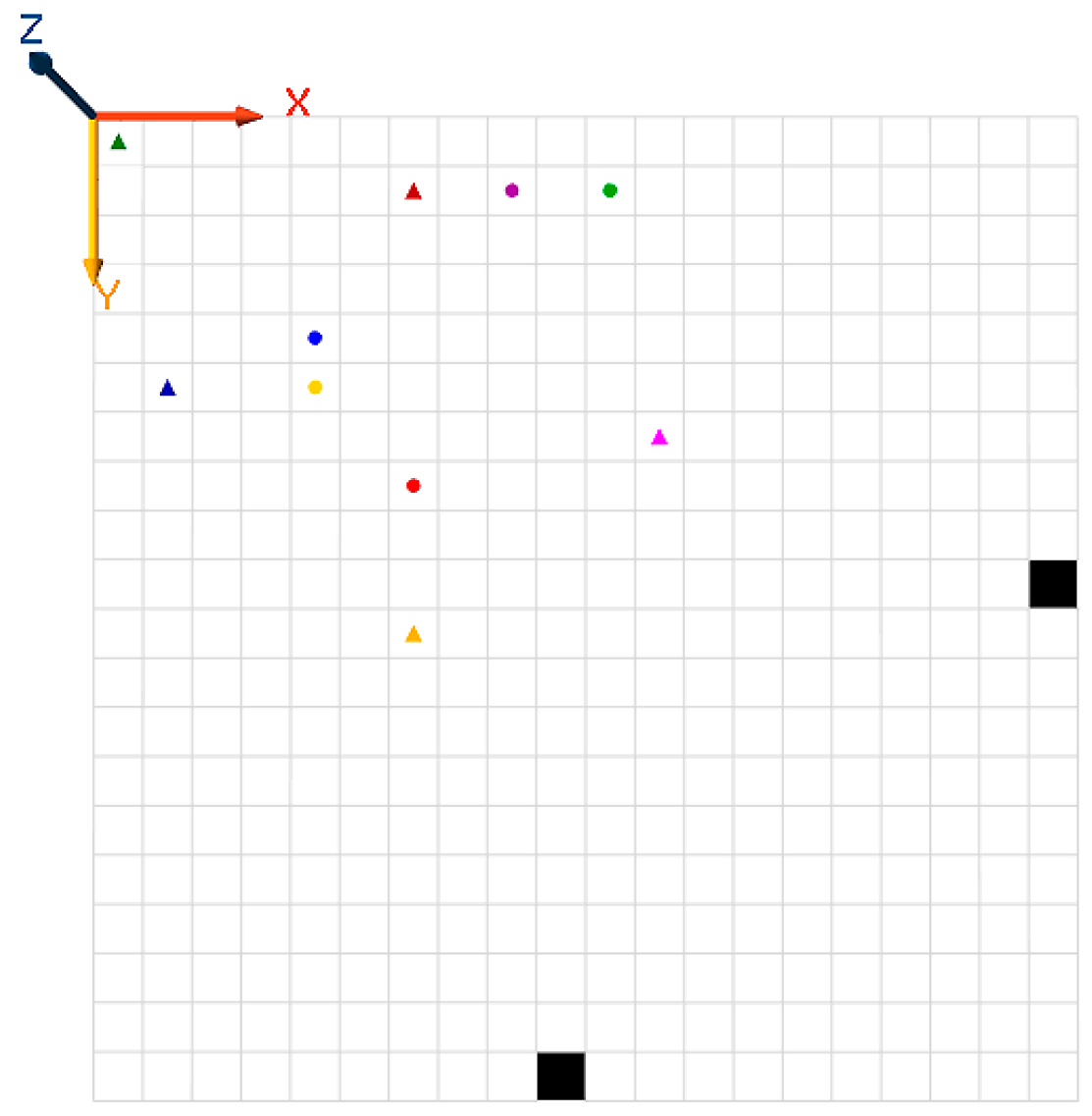
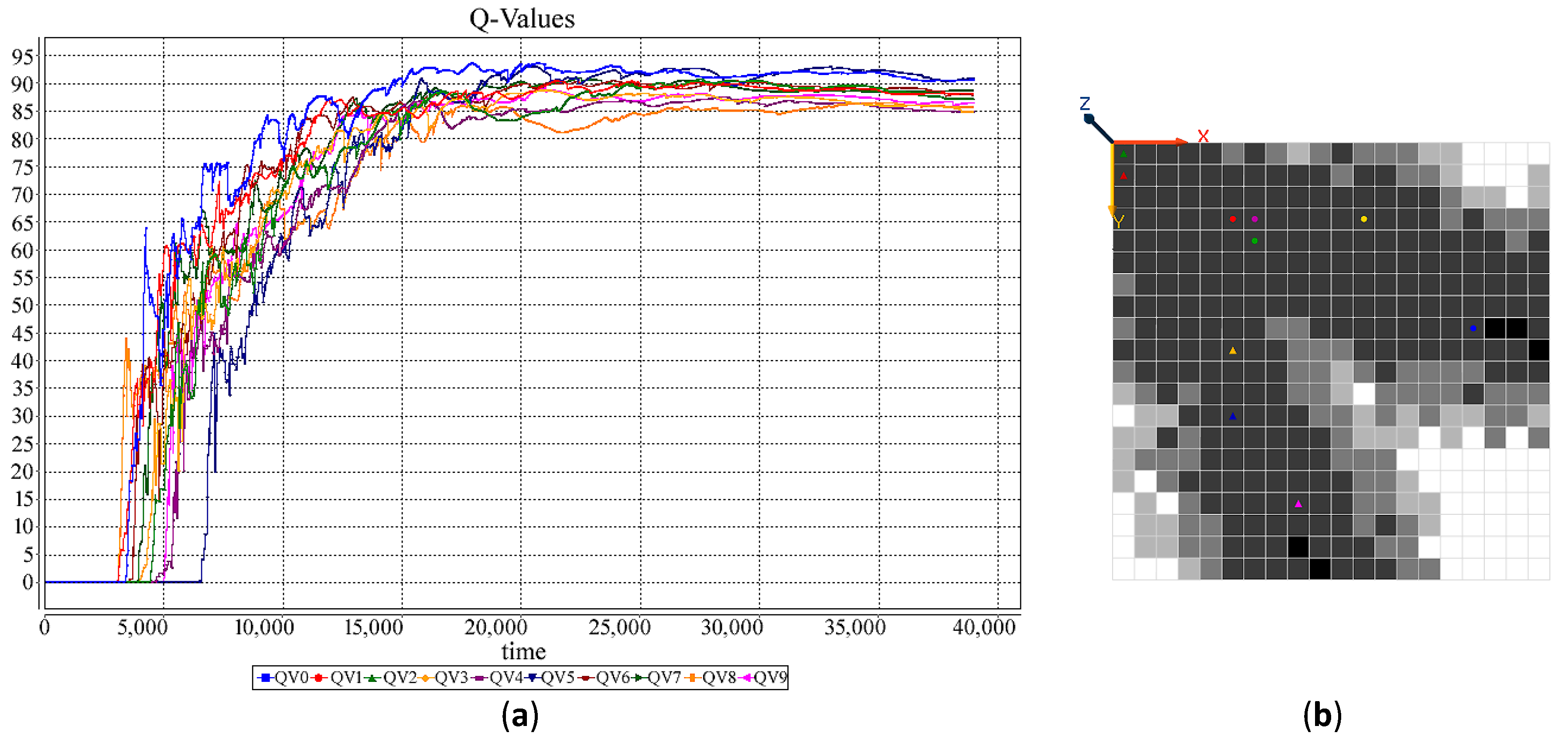
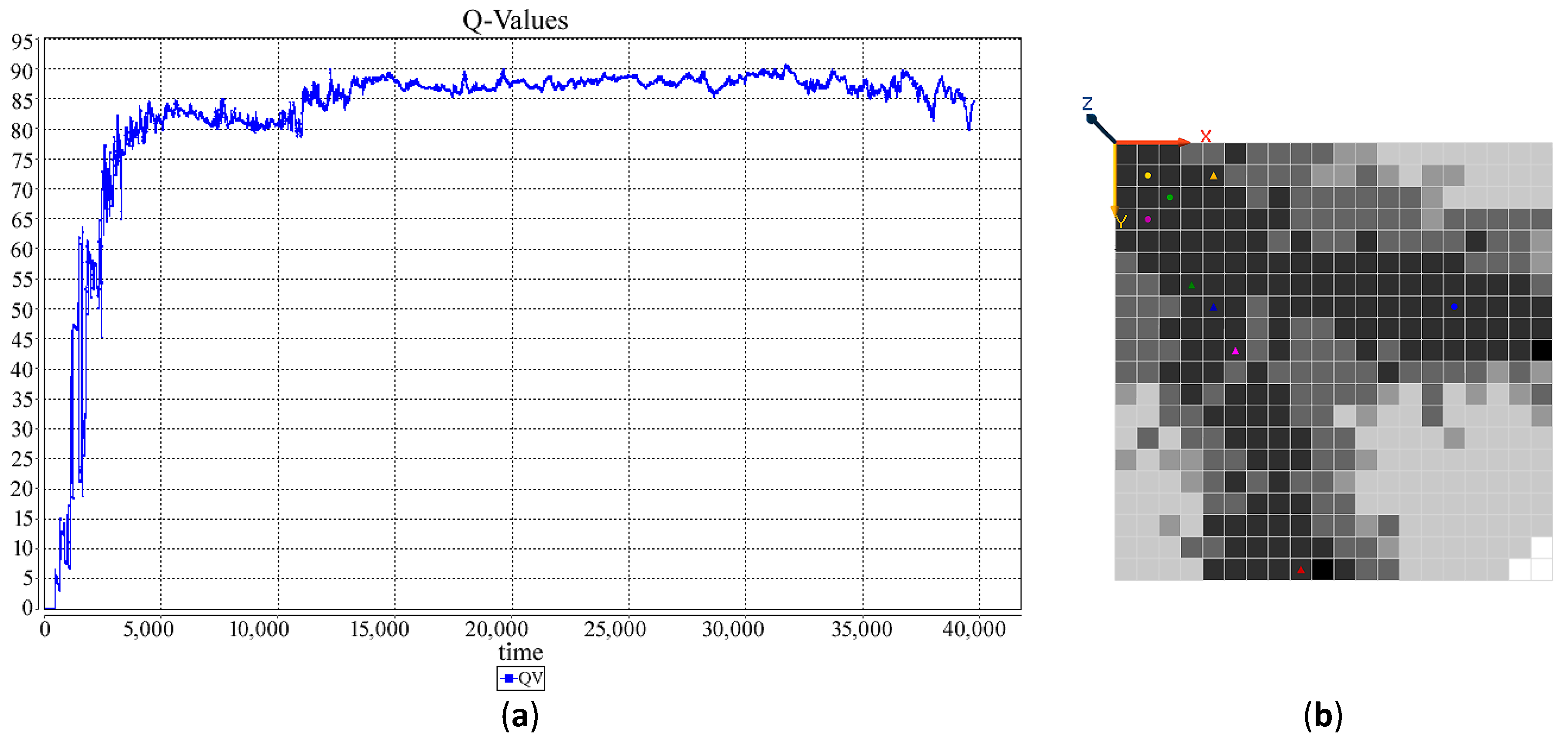
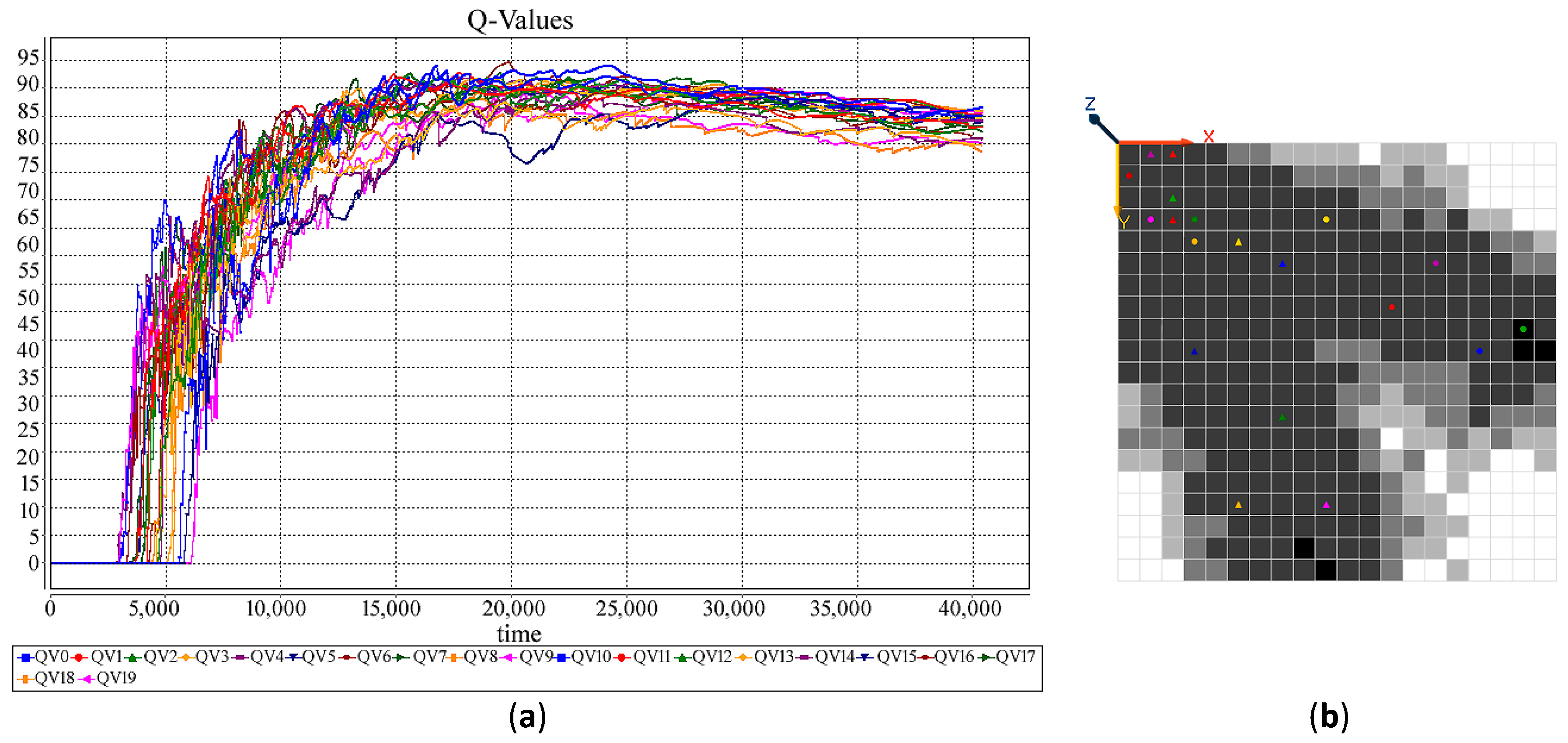
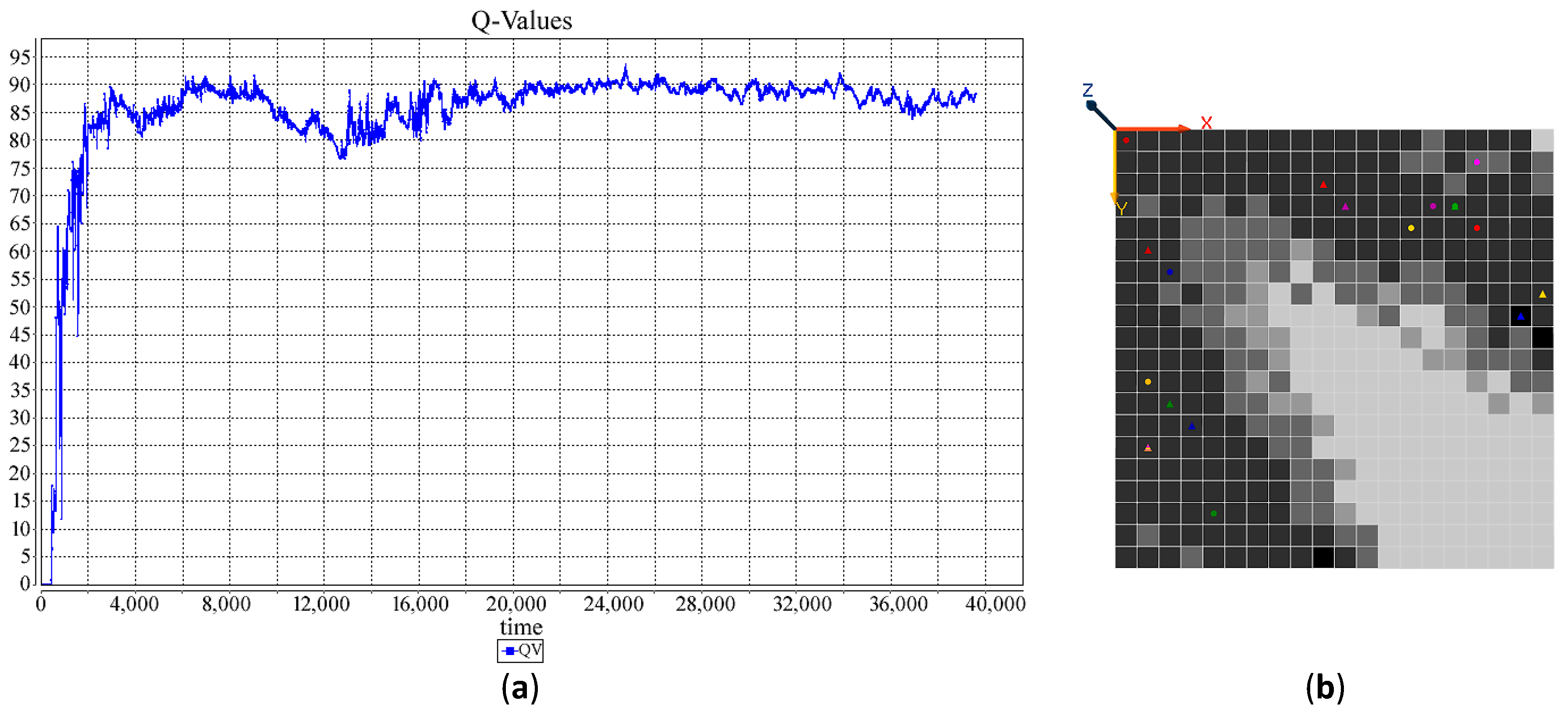
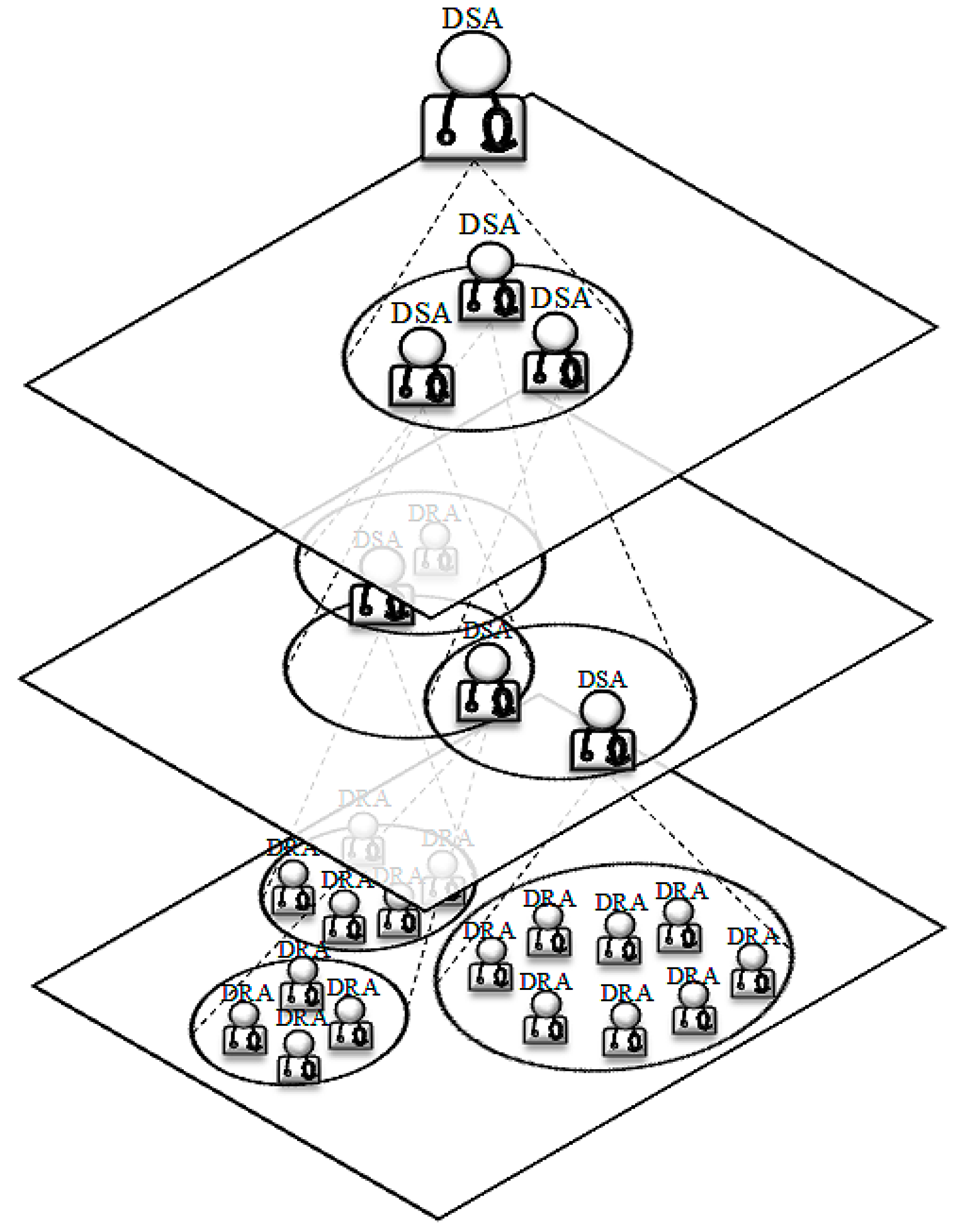
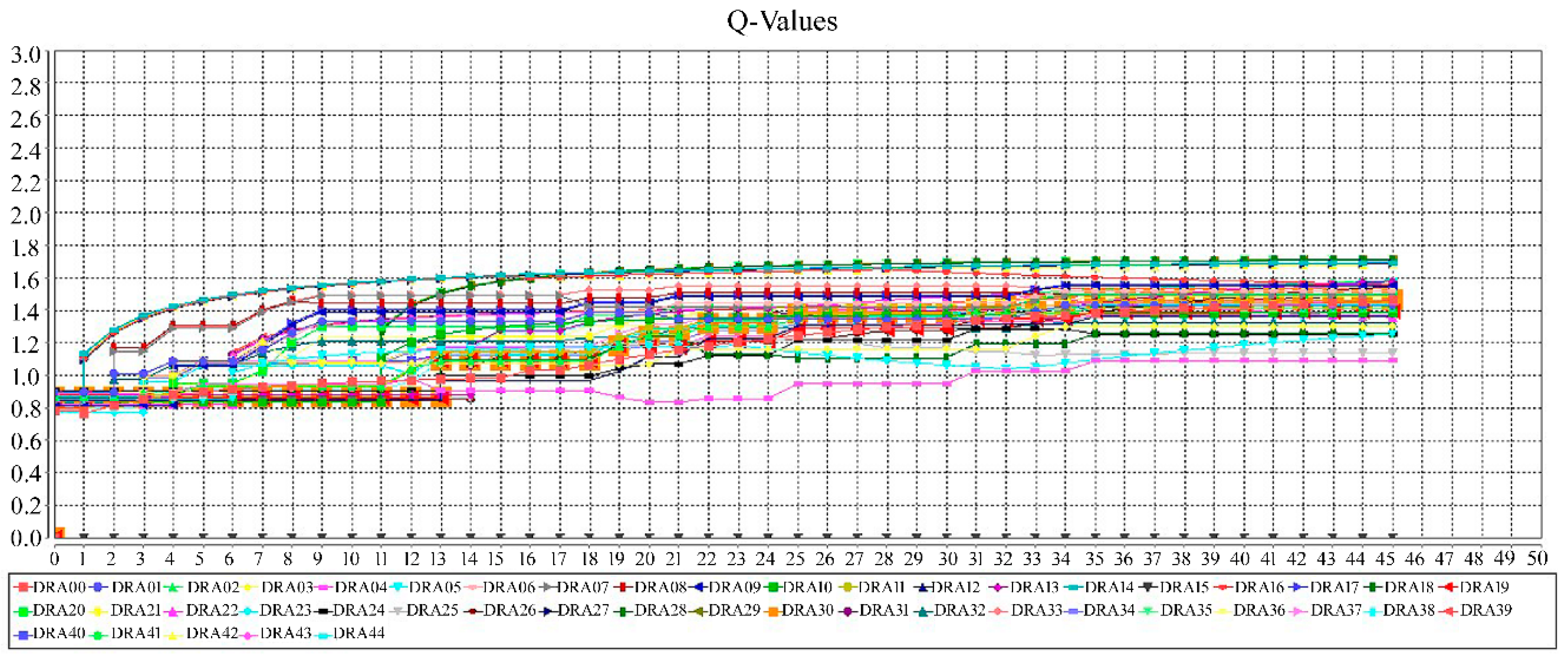
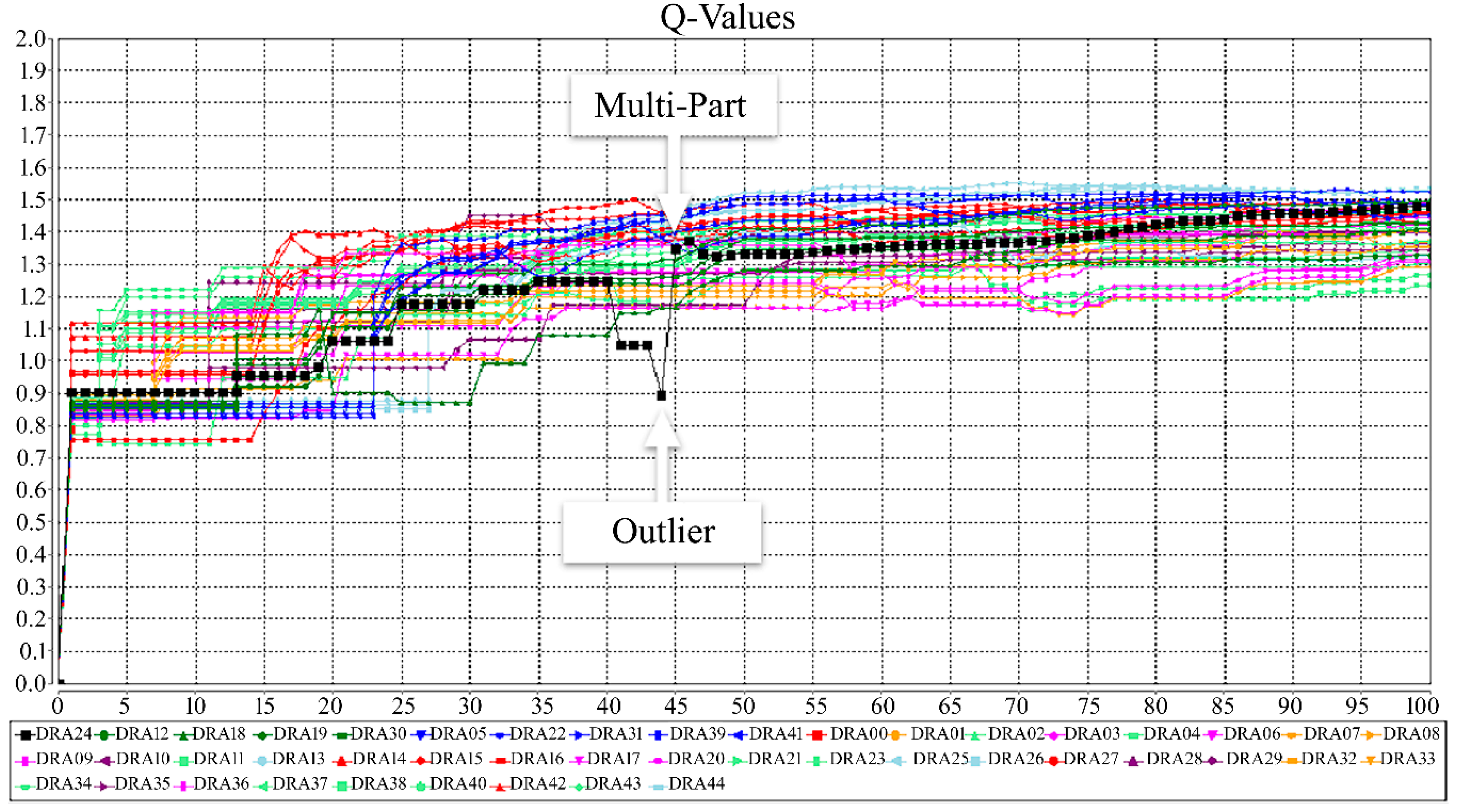
| RL Technique | Policy | Year | Reference |
|---|---|---|---|
| Actor-Critic (AC) | on-policy | 1983 | [22] |
| Temporal Difference (TD) | on-policy | 1988 | [23] |
| Q-Learning | off-policy | 1989 | [24] |
| R-Learning | off-policy | 1993 | [25] |
| State-Action-Reward-State-Action (SARSA) | on-policy | 1994 | [26] |
| Actor Critic Learning Automaton (ACLA) | on-policy | 2007 | [27] |
| QV(λ)-Learning | on-policy | 2007 | [27] |
| Monte Carlo (MC) for RL | on-policy | 2008 | [28] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbari, Z.; Unland, R. A Novel Heterogeneous Swarm Reinforcement Learning Method for Sequential Decision Making Problems. Mach. Learn. Knowl. Extr. 2019, 1, 590-610. https://doi.org/10.3390/make1020035
Akbari Z, Unland R. A Novel Heterogeneous Swarm Reinforcement Learning Method for Sequential Decision Making Problems. Machine Learning and Knowledge Extraction. 2019; 1(2):590-610. https://doi.org/10.3390/make1020035
Chicago/Turabian StyleAkbari, Zohreh, and Rainer Unland. 2019. "A Novel Heterogeneous Swarm Reinforcement Learning Method for Sequential Decision Making Problems" Machine Learning and Knowledge Extraction 1, no. 2: 590-610. https://doi.org/10.3390/make1020035
APA StyleAkbari, Z., & Unland, R. (2019). A Novel Heterogeneous Swarm Reinforcement Learning Method for Sequential Decision Making Problems. Machine Learning and Knowledge Extraction, 1(2), 590-610. https://doi.org/10.3390/make1020035





