Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer
Abstract
:1. Introduction
2. Theoretical Reference
2.1. Breast Cancer
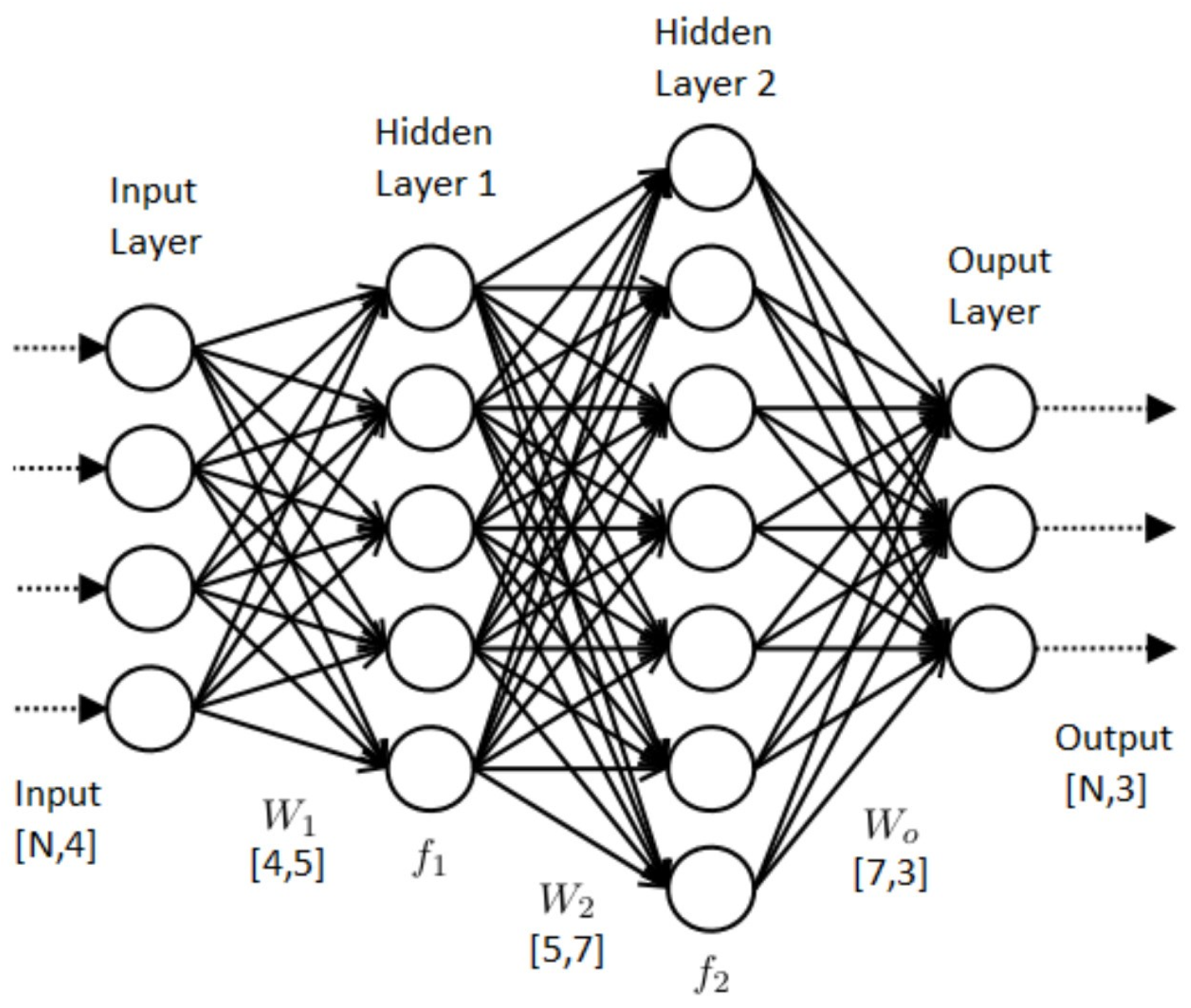
2.2. Artificial Neural Networks
2.3. Fuzzy Systems
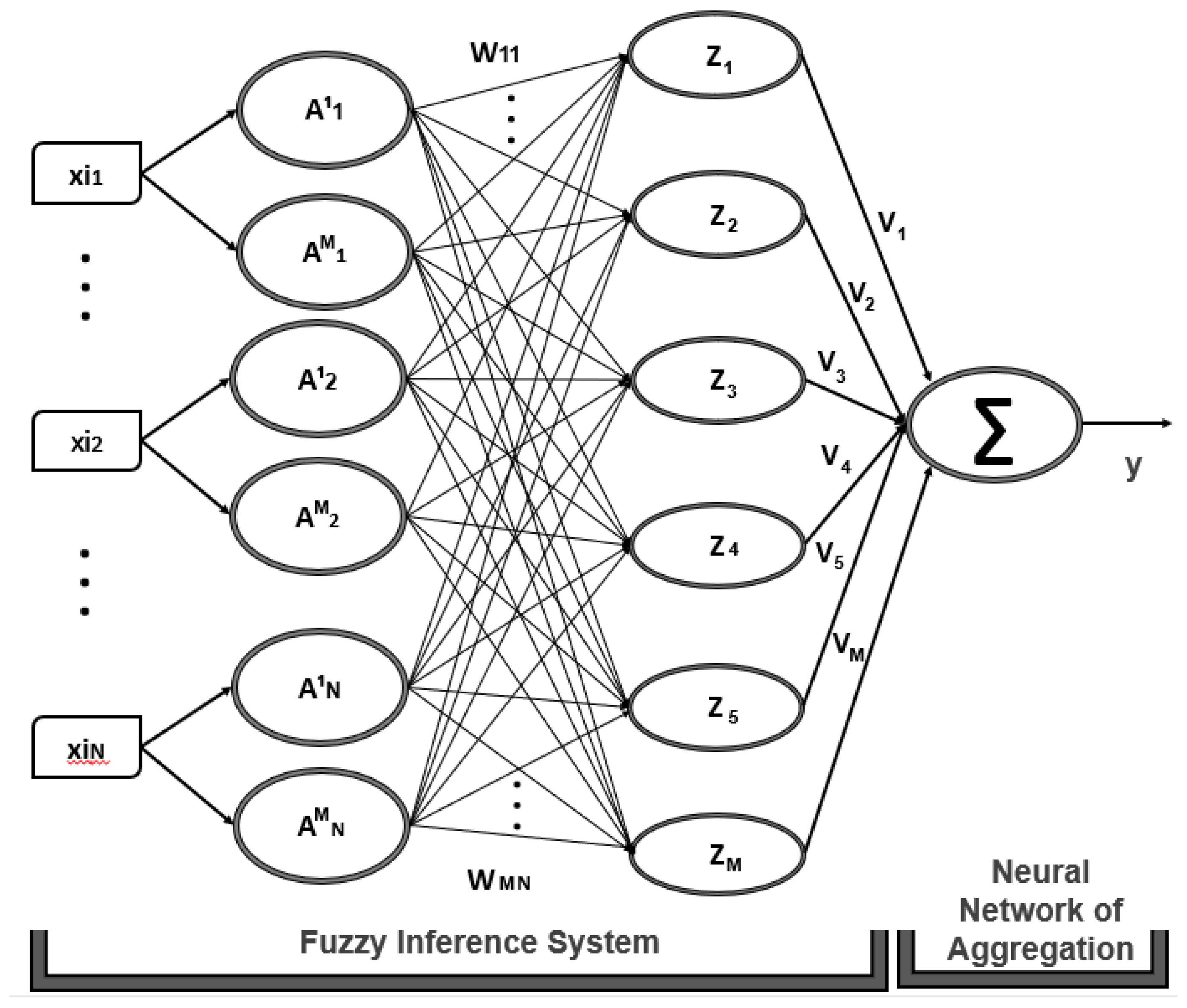
2.4. Fuzzy Logic Neurons
- Transform each pair () into a single value = h ();
- Calculate the unified aggregation of the transformed values U (), where n is the number of input.
2.5. Related Work
3. Fuzzy Neural Network for Detection of Breast Cancer
Neural Network Neural Network Architecture and Training for Binary Classification Problems
- the number of membership functions, M;
- the type of fuzzy logic neuron, unineuron, andneuron or orneuron;
| Algorithm 1: FNN- Training |
| (1) Define the number os membership functions, M. (2) Calculate M neurons for each characteristic in the first layer using Anfis. (3) Construct L fuzzy neurons with Gaussian or Triangular membership functions constructed with center and values derived from ANFIS (Using genfis1 approach). (4) Define the weights and bias of the fuzzy neurons randomly. (5) Construct L fuzzy logical neurons with random weights and bias on the second layer of the network by welding the L fuzzy neurons of the first layer. (6) Use f-scores to define the most significant neurons to the problem (). (7) For all K input do (7.1) Calculate the mapping using logical neurons end for (8) Estimate the weights of the output layer using Equation (6). (9) Calculate output y using Equation (5). |
4. Patient Classification Tests Using Fuzzy Neural Network
4.1. Dabase on Breast Cancer Prediction Research
- V1 = Glucose
- V2 = Resistin
- V3 = Age
- V4 = BMI − body mass
- V5 = HOMA − evaluation of the homeostasis model for insulin resistance
- V6 = Leptin
- V7 = Insulin
- V8 = Adiponectin
- V9 = MCP-1 − monocyte-1 chemotactic protein.
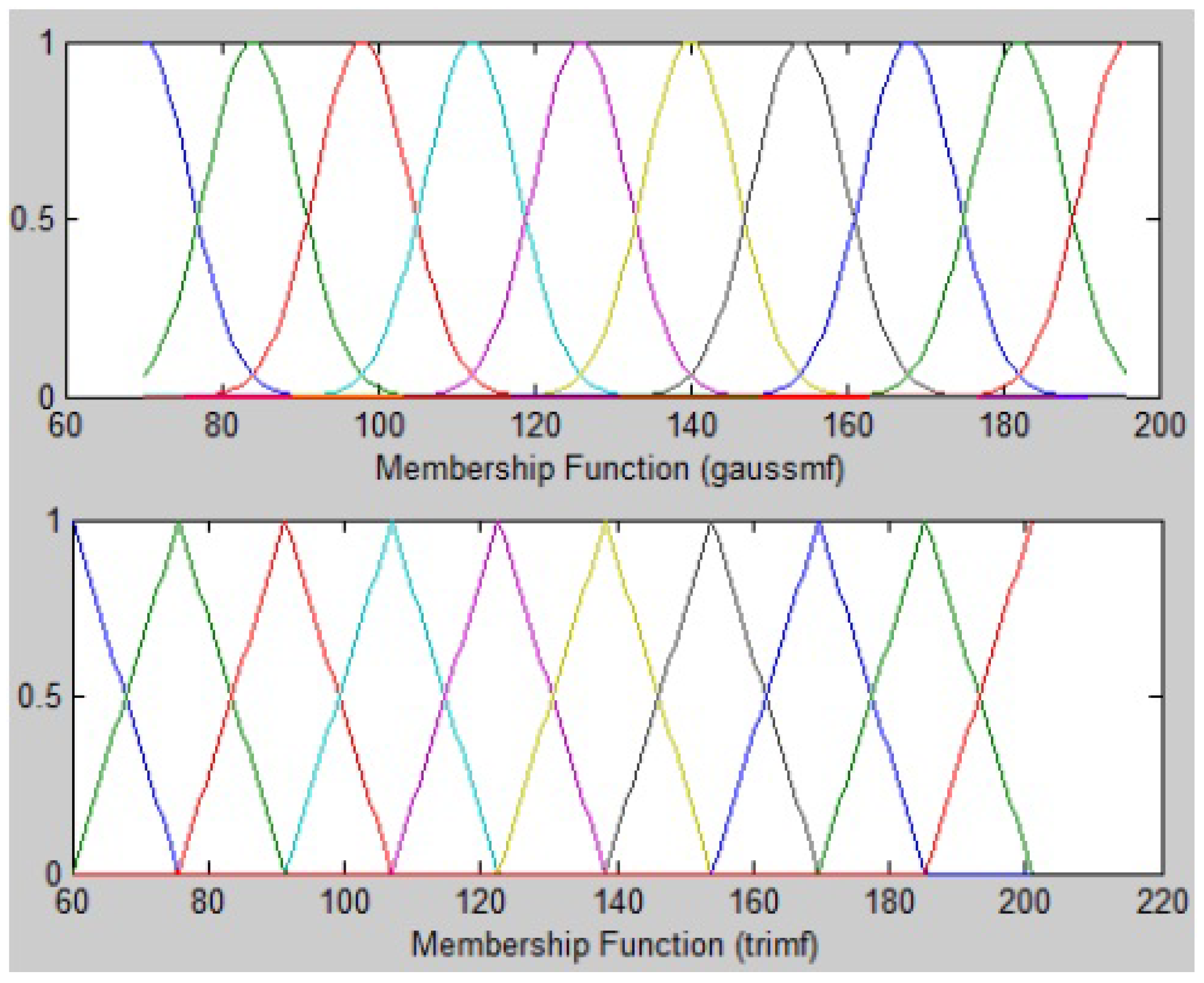
4.2. Test Configuration
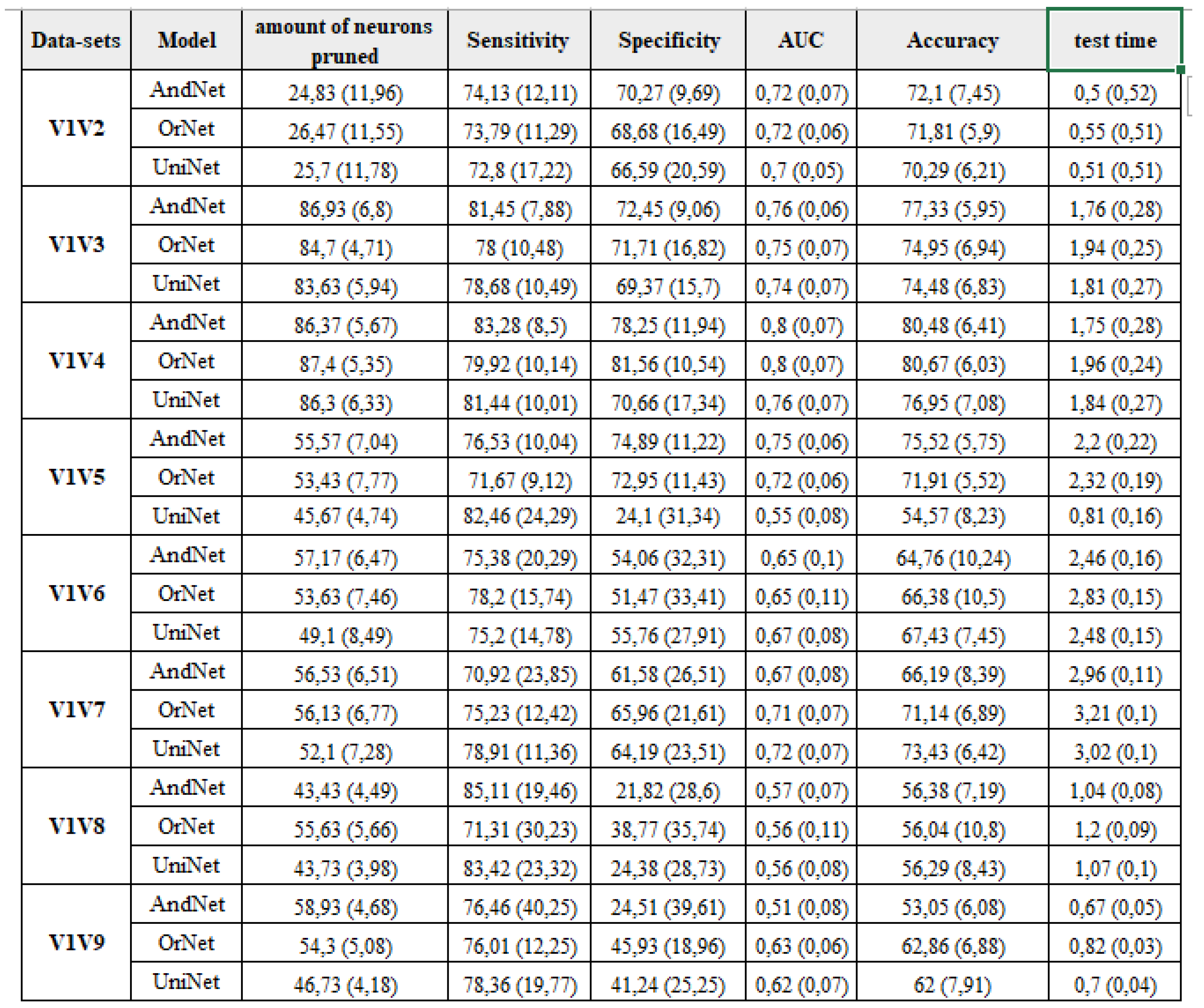
4.3. Patient Classification Tests
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FNN | Fuzzy Neural Network |
| AUC | Area Under Curve |
| UNI | unineuron |
| AND | andneuron |
References
- Brabletz, T.; Jung, A.; Spaderna, S.; Hlubek, F.; Kirchner, T. Migrating cancer stem cells—An integrated concept of malignant tumour progression. Nat. Rev. Cancer 2005, 5, 744. [Google Scholar] [CrossRef] [PubMed]
- Van’t Veer, L.J.; Dai, H.; Van De Vijver, M.J.; He, Y.D.; Hart, A.A.; Mao, M.; Peterse, H.L.; Van Der Kooy, K.; Marton, M.J.; Witteveen, A.T.; et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature 2002, 415, 530. [Google Scholar]
- Kerlikowske, K.; Grady, D.; Rubin, S.M.; Sandrock, C.; Ernster, V.L. Efficacy of screening mammography: A meta-analysis. JAMA 1995, 273, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Veronesi, U.; Paganelli, G.; Galimberti, V.; Viale, G.; Zurrida, S.; Bedoni, M.; Costa, A.; De Cicco, C.; Geraghty, J.G.; Luini, A.; et al. Sentinel-node biopsy to avoid axillary dissection in breast cancer with clinically negative lymph-nodes. Lancet 1997, 349, 1864–1867. [Google Scholar] [CrossRef]
- Giunti, G.; Giunta, D.; Guisado-Fernandez, E.; Bender, J.; Fernández-Luque, L. A biopsy of Breast Cancer mobile applications: State of the practice review. Int. J. Med. Informat. 2018, 110, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Vlahou, A.; Laronga, C.; Wilson, L.; Gregory, B.; Fournier, K.; McGaughey, D.; Perry, R.R.; Wright, G.L., Jr.; Semmes, O.J. A novel approach toward development of a rapid blood test for breast cancer. Clin. Breast Cancer 2003, 4, 203–209. [Google Scholar] [CrossRef]
- Patrício, M.; Pereira, J.; Crisóstomo, J.; Matafome, P.; Gomes, M.; Seiça, R.; Caramelo, F. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC Cancer 2018, 18, 29. [Google Scholar] [CrossRef]
- Zadeh, L.A. A fuzzy-algorithmic approach to the definition of complex or imprecise concepts. In Systems Theory in the Social Sciences; Springer: Berlin, Germany, 1976; pp. 202–282. [Google Scholar]
- Pedrycz, W. Fuzzy neural networks and neurocomputations. Fuzzy Sets Syst. 1993, 56, 1–28. [Google Scholar] [CrossRef]
- Moreno, J.; Ortúzar, M.E.; Dixon, J.W. Energy-management system for a hybrid electric vehicle, using ultracapacitors and neural networks. IEEE Trans. Ind. Electron. 2006, 53, 614–623. [Google Scholar] [CrossRef]
- Cireşan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. arXiv, 2012; arXiv:1202.2745. [Google Scholar]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Yang, Y.; Pedersen, J.O. A comparative study on feature selection in text categorization. Icml 1997, 97, 412–420. [Google Scholar]
- Guimarães, A.J.; Araujo, V.J.S.; de Campos Souza, P.V.; Araujo, V.S.; Rezende, T.S. Using Fuzzy Neural Networks to the Prediction of Improvement in Expert Systems for Treatment of Immunotherapy. In Ibero-American Conference on Artificial Intelligence; Springer: Berlin, Germany, 2018; pp. 229–240. [Google Scholar]
- Lin, F.J.; Chen, S.G.; Hsu, C.W. Intelligent Backstepping Control Using Recurrent Feature Selection Fuzzy Neural Network for Synchronous Reluctance Motor Position Servo Drive System. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Sharifian, A.; Ghadi, M.J.; Ghavidel, S.; Li, L.; Zhang, J. A new method based on Type-2 fuzzy neural network for accurate wind power forecasting under uncertain data. Renew. Energy 2018, 120, 220–230. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, L.; Zhao, H.S.; Huang, X.Y. Fuzzy neural network and LLE Algorithm for forecasting precipitation in tropical cyclones: Comparisons with interpolation method by ECMWF and stepwise regression method. Nat. Hazards 2018, 91, 201–220. [Google Scholar] [CrossRef]
- García, F.; Guijarro, F.; Oliver, J.; Tamošiūnienė, R. Hybrid fuzzy neural network to predict price direction in the German DAX-30 index. Technol. Econ. Dev. Econ. 2018, 24, 2161–2178. [Google Scholar] [CrossRef]
- De Campos Souza, P.V.; Torres, L.C.B. Regularized fuzzy neural network based on or neuron for time series forecasting. In North American Fuzzy Information Processing Society Annual Conference; Springer: Berlin, Germany, 2018; pp. 13–23. [Google Scholar]
- Vitor de Campos Souza, P. Pruning fuzzy neural networks based on unineuron for problems of classification of patterns. J. Intell. Fuzzy Syst. 2018, 35, 1–9. [Google Scholar]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Chen, Y.W.; Lin, C.J. Combining SVMs with various feature selection strategies. In Feature Extraction; Springer: Berlin, Germany, 2006; pp. 315–324. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Stewart, B.; Wild, C.P. World Cancer Report 2014; WHO: Geneva, Switzerland, 2014. [Google Scholar]
- Al-Hajj, M.; Wicha, M.S.; Benito-Hernandez, A.; Morrison, S.J.; Clarke, M.F. Prospective identification of tumorigenic breast cancer cells. Proc. Natl. Acad. Sci. USA 2003, 100, 3983–3988. [Google Scholar] [CrossRef]
- Cassileth, B.R.; Lusk, E.J.; Strouse, T.B.; Bodenheimer, B.J. Contemporary unorthodox treatments in cancer medicine: A study of patients, treatments, and practitioners. Ann. Intern. Med. 1984, 101, 105–112. [Google Scholar] [CrossRef] [PubMed]
- DeSantis, C.; Ma, J.; Bryan, L.; Jemal, A. Breast cancer statistics, 2013. CA Cancer J. Clin. 2014, 64, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Giordano, S.H.; Buzdar, A.U.; Hortobagyi, G.N. Breast cancer in men. Ann. Intern. Med. 2002, 137, 678–687. [Google Scholar] [CrossRef] [PubMed]
- Breast Cancer. Available online: https://pt.wikipedia.org/wiki/Ficheiro:Diagram_1_of_2_showing_stage_2A_breast_cancer_CRUK_003.svg (accessed on 11 February 2019).
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- The Artificial Neural Networks Handbook: Part 1. Available online: https://medium.com/coinmonks/the-artificial-neural-networks-handbook-part-1-f9ceb0e376b4 (accessed on 11 February 2019).
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Cherri, A.C.; Junior, D.J.A.; da Silva, I.N. Inferencia fuzzy para o problema de corte de estoque com sobras aproveitaveis de material. 2011. Available online: http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0101-74382011000100011 (accessed on 11 February 2019).
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Englewood Cliffs, NJ, USA, 1997. [Google Scholar]
- Savic, D.A.; Pedrycz, W. Evaluation of fuzzy linear regression models. Fuzzy Sets Syst. 1991, 39, 51–63. [Google Scholar] [CrossRef]
- Pedrycz, W. Neurocomputations in relational systems. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 289–297. [Google Scholar] [CrossRef]
- Lemos, A.; Caminhas, W.; Gomide, F. New uninorm-based neuron model and fuzzy neural networks. In Proceedings of the 2010 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Uren, R.F.; Howman-Giles, R.B.; Thompson, J.F.; Malouf, D.; Ramsey-Stewart, G.; Niesche, F.W.; Renwick, S.B. Mammary lymphoscintigraphy in breast cancer. J. Nuclear Med. Off. Publ. Soc. Nuclear Med. 1995, 36, 1775–1780. [Google Scholar]
- Vyborny, C.J.; Giger, M.L. Computer vision and artificial intelligence in mammography. Am. J. Roentgenol. 1994, 162, 699–708. [Google Scholar] [CrossRef] [PubMed]
- Robertson, S.; Azizpour, H.; Smith, K.; Hartman, J. Digital image analysis in breast pathology—From image processing techniques to artificial intelligence. Transl. Res. 2018, 194, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Hosny, A.; Parmar, C.; Quackenbush, J.; Schwartz, L.H.; Aerts, H.J. Artificial intelligence in radiology. Nat. Rev. Cancer 2018, 18, 500–510. [Google Scholar] [CrossRef] [PubMed]
- Abbass, H.A. An evolutionary artificial neural networks approach for breast cancer diagnosis. Artif. Intell. Med. 2002, 25, 265–281. [Google Scholar] [CrossRef]
- Delen, D.; Walker, G.; Kadam, A. Predicting breast cancer survivability: A comparison of three data mining methods. Artif. Intell. Med. 2005, 34, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Setiono, R. Generating concise and accurate classification rules for breast cancer diagnosis. Artif. Intell. Med. 2000, 18, 205–219. [Google Scholar] [CrossRef]
- Marcano-Cedeño, A.; Quintanilla-Domínguez, J.; Andina, D. WBCD breast cancer database classification applying artificial metaplasticity neural network. Expert Syst. Appl. 2011, 38, 9573–9579. [Google Scholar] [CrossRef]
- Liu, Y.; Kohlberger, T.; Norouzi, M.; Dahl, G.E.; Smith, J.L.; Mohtashamian, A.; Olson, N.; Peng, L.H.; Hipp, J.D.; Stumpe, M.C. Artificial Intelligence–Based Breast Cancer Nodal Metastasis Detection: Insights Into the Black Box for Pathologists. Arch. Pathol. Lab. Med. 2018. [Google Scholar] [CrossRef]
- Khan, M.M.; Mendes, A.; Chalup, S.K. Evolutionary Wavelet Neural Network ensembles for breast cancer and Parkinson’s disease prediction. PLoS ONE 2018, 13, e0192192. [Google Scholar] [CrossRef]
- Pena-Reyes, C.A.; Sipper, M. A fuzzy-genetic approach to breast cancer diagnosis. Artif. Intell. Med. 1999, 17, 131–155. [Google Scholar] [CrossRef]
- Colaluca, I.N.; Basile, A.; Freiburger, L.; D’Uva, V.; Disalvatore, D.; Vecchi, M.; Confalonieri, S.; Tosoni, D.; Cecatiello, V.; Malabarba, M.G.; et al. A Numb–Mdm2 fuzzy complex reveals an isoform-specific involvement of Numb in breast cancer. J. Cell Biol. 2018, 217, 745–762. [Google Scholar] [CrossRef] [PubMed]
- Akay, M.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
- Polat, K.; Güneş, S. Breast cancer diagnosis using least square support vector machine. Dig. Signal Process. 2007, 17, 694–701. [Google Scholar] [CrossRef]
- Cireşan, D.C.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Mitosis detection in breast cancer histology images with deep neural networks. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin, Germany, 2013; pp. 411–418. [Google Scholar]
- Chan, H.; Helvie, M. Deep Learning for Mammographic Breast Density Assessment and Beyond. Radiology 2019, 290, 59. [Google Scholar] [CrossRef] [PubMed]
- Guimaraes, A.J.; Araújo, V.J.; de Oliveira Batista, L.; Souza, P.V.C.; Araújo, V.; Rezende, T.S. Using Fuzzy Neural Networks to Improve Prediction of Expert Systems for Detection of Breast Cancer. In Proceedings of the XV Encontro Nacional de Inteligência Artificial e Computacional (ENIAC), Sao Paulo, SP, Brazil, 22–25 October 2018; Volume 1, pp. 799–810. [Google Scholar]
- Li, Y.; Chen, Z. Performance Evaluation of Machine Learning Methods for Breast Cancer Prediction. Appl. Comput. Math. 2018, 7, 212–216. [Google Scholar]
- Polat, K.; Sentürk, U. A Novel ML Approach to Prediction of Breast Cancer: Combining of mad normalization, KMC based feature weighting and AdaBoostM1 classifier. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–4. [Google Scholar]
- Dular, L. Statistical Comparison of Machine Learning Algorithms with Respect to Multiple Performance Measures: Master’s Thesis. Ph.D. Thesis, Univerza v Ljubljani, Fakulteta za Matematiko in Fiziko, Ljubljana, Slovenia, 2018. [Google Scholar]
- Livieris, I. Improving the Classification Efficiency of an ANN Utilizing a New Training Methodology. Informatics 2019, 6, 1. [Google Scholar] [CrossRef]
- Patterson, D.W. Redes Neurais Artificiais: Teoria e Aplicações; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Souza, P.V.C. Regularized Fuzzy Neural Networks for Pattern Classification Problems. Int. J. Appl. Eng. Res. 2018, 13, 2985–2991. [Google Scholar]
- Gao, J.; Wang, Z.; Yang, Y.; Zhang, W.; Tao, C.; Guan, J.; Rao, N. A novel approach for lie detection based on F-score and extreme learning machine. PLoS ONE 2013, 8, e64704. [Google Scholar] [CrossRef] [PubMed]
- Güneş, S.; Polat, K.; Yosunkaya, Ş. Multi-class f-score feature selection approach to classification of obstructive sleep apnea syndrome. Expert Syst. Appl. 2010, 37, 998–1004. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Albert, A. Regression and the Moore-Penrose Pseudoinverse; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- De Campos Souza, P.V.; Guimaraes, A.J.; Araújo, V.S.; Rezende, T.S.; Araújo, V.J.S. Method of pruning the hidden layer of the extreme learning machine based on correlation coefficient. In Proceedings of the 5th IEEE Latin American Conference on Computational Intelligence LA-CCI, Guadalajara, Mexico, 7–9 November 2018; Volume 5. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhou, G.; Jin, J.; Wang, B.; Wang, X.; Cichocki, A. Multi-kernel extreme learning machine for EEG classification in brain-computer interfaces. Expert Syst. Appl. 2018, 96, 302–310. [Google Scholar] [CrossRef]
- Sun, Z.L.; Choi, T.M.; Au, K.F.; Yu, Y. Sales forecasting using extreme learning machine with applications in fashion retailing. Decis. Support Syst. 2008, 46, 411–419. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Aghaei, J.; Shafie-khah, M.; Catalão, J.P. Probabilistic Load Forecasting using an Improved Wavelet Neural Network Trained by Generalized Extreme Learning Machine. IEEE Trans. Smart Grid 2018, 9, 6961–6971. [Google Scholar] [CrossRef]
- Das, P.; Bisoi, R.; Dash, P. Data decomposition based fast reduced kernel extreme learning machine for currency exchange rate forecasting and trend analysis. Expert Syst. Appl. 2018, 96, 427–449. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Li, L. Wavelet transform and Kernel-based extreme learning machine for electricity price forecasting. Energy Syst. 2018, 9, 113–134. [Google Scholar] [CrossRef]
- Janahiraman, T.V.; Ahmad, N.; Nordin, F.H. Extreme Learning Machine and Particle Swarm Optimization in optimizing CNC turning operation. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 342, p. 012086. [Google Scholar]
- Hu, Q.; Qin, A.; Zhang, Q.; He, J.; Sun, G. Fault Diagnosis Based on Weighted Extreme Learning Machine With Wavelet Packet Decomposition and KPCA. IEEE Sens. J. 2018, 18, 8472–8483. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, M.; Ye, L.; Zhu, Q.; Geng, Z.; He, Y.L.; Han, Y. A novel prediction intervals method integrating an error & self-feedback extreme learning machine with particle swarm optimization for energy consumption robust prediction. Energy 2018, 164, 137–146. [Google Scholar]
- Pan, H.; Lü, Z.; Wang, H.; Wei, H.; Chen, L. Novel battery state-of-health online estimation method using multiple health indicators and an extreme learning machine. Energy 2018, 160, 466–477. [Google Scholar] [CrossRef]
- Eshtay, M.; Faris, H.; Obeid, N. Improving extreme learning machine by competitive swarm optimization and its application for medical diagnosis problems. Expert Syst. Appl. 2018, 104, 134–152. [Google Scholar] [CrossRef]
- Rongjun, X.; Khalil, I.; Badsha, S.; Atiquzzaman, M. Collaborative extreme learning machine with a confidence interval for P2P learning in healthcare. Comput. Netw. 2019, 149, 127–143. [Google Scholar]
- De Campos Souza, P.V.; Guimarães, A.J. Utilizando redes neurais nebulosas para melhoria na predição de sistemas especialistas para tratamento de crioterapia. In Proceedings of the Anais- I Congresso Internacional Cidadania, Ciência, Direito e Saúde: Reflexões Transdisciplinares, Barreiro, Brazil, 2–4 May 2018. (In Portuguese). [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Rish, I. An empirical study of the naive Bayes classifier. In IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence; IBM: New York, NY, USA, 2001; Volume 3, pp. 41–46. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-exploring random trees: A new tool for path planning. In Computer Science Dept. Research Report 9811; CiteSeerX: Ames, LA, USA, 1998. [Google Scholar]
- Witten, I.H.; Frank, E.; Trigg, L.E.; Hall, M.A.; Holmes, G.; Cunningham, S.J. Weka: Practical Machine Learning Tools and Techniques with Java Implementations; Citeseer: Pennsylvania, PA, USA, 1999. [Google Scholar]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]


| Models | Accuracy | AUC | Sensitivity | Specificity | Time |
|---|---|---|---|---|---|
| AndNet | 80.01 (6.98) | 0.8052 (0.1011) | 0.7841 (0.1124) | 0.7905 (0.1003) | 1.94 (0.03) |
| OrNet | 81.04 (4.85) | 0.8019 (0.0918) | 0.8193 (0.1024) | 0.8118 (0.1203) | 1.89 (0.02) |
| UniNet | 78.49 (4.97) | 0.7624 (0.1207) | 0.8248 (0.1412) | 0.7105 (0.0311) | 2.19 (0.06) |
| MLP | 73.80 (11.38) | 0.7409 (0.1206) | 0.4187 (0.2102) | 0.7803 (0.1018) | 15.62 (6.04) |
| J48 | 71.83 (14.27) | 0.7114 (0.1243) | 0.5276 (0.1206) | 0.7895 (0.1032) | 0.78 (0.01) |
| NB | 69.71 (12.61) | 0.6925 (0.1213) | 0.3687 (0.1786) | 0.7112 (0.2142) | 15.22 (0.76) |
| ZR | 55.15 (3.10) | 0.5004 (0.0012) | 0.5500 (0.0021) | 0.5500 (0.0016) | 7.12 (0.43) |
| RT | 79.67 (11.67) | 0.7421 (0.1120) | 0.5301 (0.1703) | 0.8718 (0.0613) | 8.21 (0.01) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva Araújo, V.J.; Guimarães, A.J.; de Campos Souza, P.V.; Rezende, T.S.; Araújo, V.S. Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer. Mach. Learn. Knowl. Extr. 2019, 1, 466-482. https://doi.org/10.3390/make1010028
Silva Araújo VJ, Guimarães AJ, de Campos Souza PV, Rezende TS, Araújo VS. Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer. Machine Learning and Knowledge Extraction. 2019; 1(1):466-482. https://doi.org/10.3390/make1010028
Chicago/Turabian StyleSilva Araújo, Vinícius Jonathan, Augusto Junio Guimarães, Paulo Vitor de Campos Souza, Thiago Silva Rezende, and Vanessa Souza Araújo. 2019. "Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer" Machine Learning and Knowledge Extraction 1, no. 1: 466-482. https://doi.org/10.3390/make1010028
APA StyleSilva Araújo, V. J., Guimarães, A. J., de Campos Souza, P. V., Rezende, T. S., & Araújo, V. S. (2019). Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer. Machine Learning and Knowledge Extraction, 1(1), 466-482. https://doi.org/10.3390/make1010028






