Introduction to MAchine Learning & Knowledge Extraction (MAKE)
Abstract
:1. Executive Summary: Why MAchine Learning & Knowledge Extraction (MAKE)?
2. Machine Learning
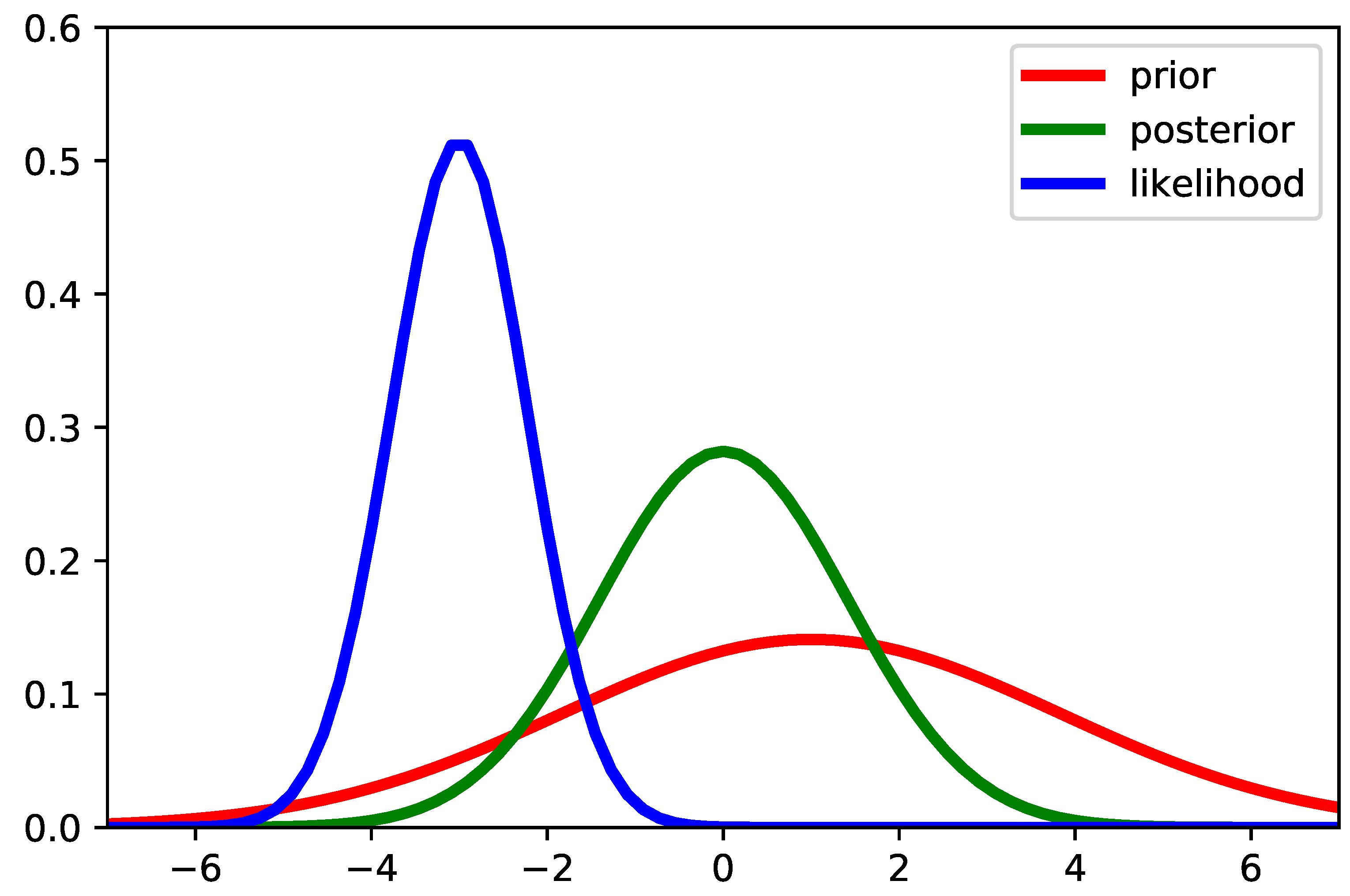
- (1) engineer’s acceptance of the concept of probable information in an uncertain world [2];
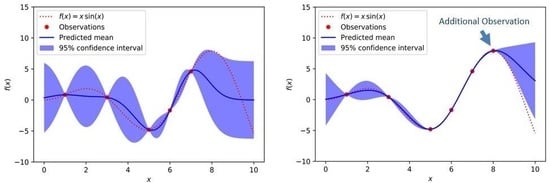
- (2) the power and applicability of statistical learning theory (see a few notes below); and
- (1) the ability to draw values at random from probability distributions, and
- (2) the ability to condition values of variables in a program via observations.
3. Knowledge Extraction (KE)
4. Selected three Future Research Challenges
5. Benefits of the New Journal MAKE
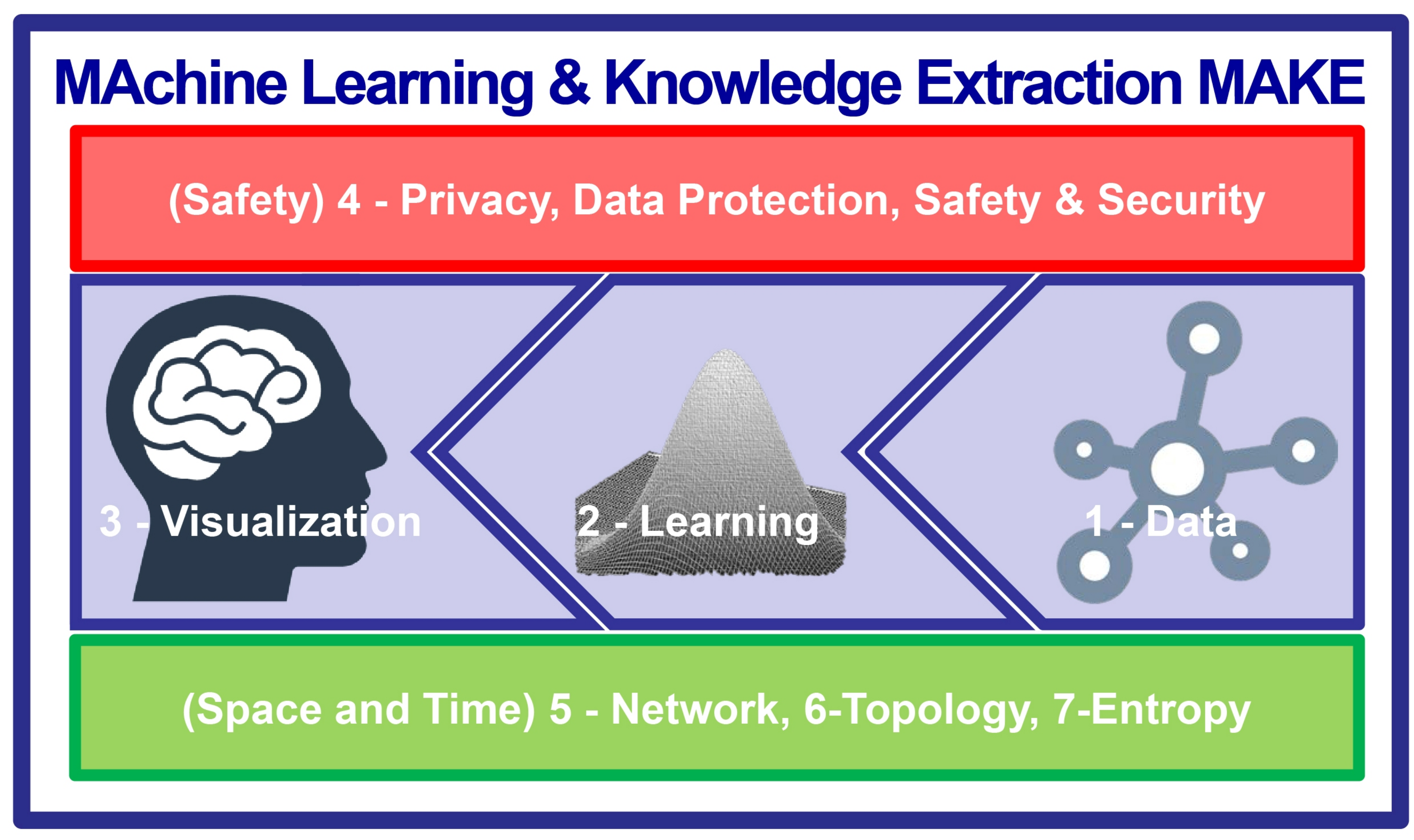
- Promotion of a cross-disciplinary integrated machine learning approach addressing seven sections to concert international efforts without boundaries, supporting collaborative, trans-disciplinary, and cross-domain collaboration between experts from these seven disciplines (see next section for details);
- Appraisal of these different fields shall foster diverse perspectives and opinions, hence offering a platform for the exchange of novel ideas and a fresh look on methodologies to put crazy ideas into business for the benefit of the human; additionally to foster education (see details below);
- Stimulation of replications and further research by inclusion of data and/or software regarding the full details of experimental work as supplementary material, if unable to be published in a standard way, or by providing links to repositories (e.g., Github) shall provide a benefit for the international research community (see issues of availability, usability and acceptance, below).
- (1) availability of open source code associated with research papers [117];
- (2) reproducibility of available methods and tools which is a cornerstone in fundamental science;
- (3) usability and usefulness of that code for solving real-world problems.
6. Integrative Machine Learning
7. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| aML | Automatic Machine Learning |
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| EWC | Elastic Weight Consolitation |
| FMA | Foundational Model of Anatomy |
| FB | |
| GO | Gene Ontology |
| GP | Gaussian Processes |
| HCI–KDD | Human–Computer Interaction & Knowledge Discovery from Data |
| iML | Interactive Machine Learning |
| ICD | International Classification of Diseases |
| ML | Machine Learning |
| MAKE | MAchine Learning & Knowledge Discovery |
| MCMC | Markov Chain Monte Carlo |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MTL | Multi Task Learning |
| NP | Nondeterministic Polynomial time |
| NELL | Never Ending Language Learning |
| NLU | Natural Language Understanding |
| OMIM | Online Mendelian Inheritance in Man |
| PAC | Probable Approximate Correct |
| Probability Density Function | |
| RNN | Recurrent Neural Network; alternatively: Recursive Neural Network |
| SNAP | Stanford Network Analysis Platform |
| SVM | Support Vector Machine |
| SLT | Statistical Learning Theory |
| SNOMED | Systematized Nomenclature of Medicine |
| TSP | Traveling Salesman Problem |
| UMLS | Unified Medical Language System |
References
- Meijer, E. Making money using math. Commun. ACM 2017, 60, 36–42. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V.N.; Chervonenkis, A.Y. On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities. Theory Probab. Appl. 1971, 16, 264–280. [Google Scholar] [CrossRef]
- Bousquet, O.; Boucheron, S.; Lugosi, G. Introduction to Statistical Learning Theory. In Advanced Lectures on Machine Learning; Bousquet, O., von Luxburg, U., Raetsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 169–207. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Bayes, T. An Essay towards solving a Problem in the Doctrine of Chances (communicated by Richard Price). Philos. Trans. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Laplace, P.S. Mémoire sur les probabilités. Mémoires de l’Académie Royale des sciences de Paris 1781, 1778, 227–332. (In French) [Google Scholar]
- Kolmogorov, A. Interpolation und extrapolation von stationaeren zufaelligen Folgen. Izv. Akad. Nauk SSSR Ser. Mat. 1941, 5, 3–14. (In German) [Google Scholar]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Knill, D.C.; Pouget, A. The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 2004, 27, 712–719. [Google Scholar] [CrossRef] [PubMed]
- Chater, N.; Tenenbaum, J.B.; Yuille, A. Probabilistic models of cognition: Conceptual foundations. Trends Cogn. Sci. 2006, 10, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Doya, K.; Ishii, S.; Pouget, A.; Rao, R. Bayesian Brain: Probabilistic Approaches to Neural Coding; MIT Press: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Wood, F.; van de Meent, J.-W.; Mansinghka, V. A new approach to probabilistic programming inference. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics (AISTATS) 2014, Reykjavik, Iceland, 22–25 April 2014; pp. 1024–1032. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Gordon, A.D.; Henzinger, T.A.; Nori, A.V.; Rajamani, S.K. Probabilistic programming. In Proceedings of the on Future of Software Engineering, Hyderabad, India, 31 May–7 June 2014; pp. 167–181. [Google Scholar] [CrossRef]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Kemp, C.; Griffiths, T.L.; Goodman, N.D. How to grow a mind: Statistics, structure, and abstraction. Science 2011, 331, 1279–1285. [Google Scholar] [CrossRef] [PubMed]
- Bell, G.; Hey, T.; Szalay, A. Beyond the Data Deluge. Science 2009, 323, 1297–1298. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Henke, N.; Bughin, J.; Chui, M.; Manyika, J.; Saleh, T.; Wiseman, B.; Sethupathy, G. The Age of Analytics: Competing in a Data-Driven World; Mckinsey Company: New York, NY, USA, 2016. [Google Scholar]
- Holzinger, A.; Dehmer, M.; Jurisica, I. Knowledge Discovery and interactive Data Mining in Bioinformatics—State-of-the-Art, future challenges and research directions. BMC Bioinform. 2014, 15 (Suppl. 6), I1. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Holzinger, A. Knowledge Discovery from Complex High Dimensional Data. In Solving Large Scale Learning Tasks. Challenges and Algorithms, Lecture Notes in Artificial Intelligence, LNAI 9580; Michaelis, S., Piatkowski, N., Stolpe, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 148–167. [Google Scholar] [CrossRef]
- Simovici, D.A.; Djeraba, C. Mathematical Tools for Data Mining; Springer: London, UK, 2014. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ghahramani, Z. Bayesian non-parametrics and the probabilistic approach to modelling. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.; Huang, S.; Marthaler, D.E.; Kersting, K. pyGPs: A Python library for Gaussian process regression and classification. J. Mach. Learn. Res. 2015, 16, 2611–2616. [Google Scholar]
- Domingos, P. The Role of Occam’s Razor in Knowledge Discovery. Data Min. Knowl. Discov. 1999, 3, 409–425. [Google Scholar] [CrossRef]
- Wilson, A.G.; Dann, C.; Lucas, C.G.; Xing, E.P. The Human Kernel. arXiv, 2015; arXiv:1510.07389. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Sonnenburg, S.; Rätsch, G.; Schaefer, C.; Schoelkopf, B. Large scale multiple kernel learning. J. Mach. Learn. Res. 2006, 7, 1531–1565. [Google Scholar]
- Holzinger, A. Biomedical Informatics: Computational Sciences Meets Life Sciences; BoD: Norderstedt, Germany, 2012; p. 368. [Google Scholar]
- Hofmann, T.; Schoelkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Lucas, C.; Williams, J.; Kalish, M.L. Modeling human function learning with Gaussian processes. In Advances in Neural Information Processing Systems (NIPS 2008); Koller, D., Schuurmans, D., Bengio, Y., Bottou, L., Eds.; NIPS: San Diego, CA, USA, 2009; Volume 21, pp. 553–560. [Google Scholar]
- Holzinger, A. Interactive Machine Learning for Health Informatics: When do we need the human-in-the-loop? Brain Inform. 2016, 3, 119–131. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, A.; Plass, M.; Holzinger, K.; Crisan, G.C.; Pintea, C.M.; Palade, V. Towards interactive Machine Learning (iML): Applying Ant Colony Algorithms to solve the Traveling Salesman Problem with the Human-in-the-Loop approach. In Springer Lecture Notes in Computer Science LNCS 9817; Springer: Berlin/Heidelberg, Germany, 2016; pp. 81–95. [Google Scholar] [CrossRef]
- Crescenzi, P.; Goldman, D.; Papadimitriou, C.; Piccolboni, A.; Yannakakis, M. On the complexity of protein folding. J. Comput. Biol. 1998, 5, 423–465. [Google Scholar] [CrossRef] [PubMed]
- Macgregor, J.N.; Ormerod, T. Human performance on the traveling salesman problem. Percept. Psychophys. 1996, 58, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Napolitano, F.; Raiconi, G.; Tagliaferri, R.; Ciaramella, A.; Staiano, A.; Miele, G. Clustering and visualization approaches for human cell cycle gene expression data analysis. Int. J. Approx. Reason. 2008, 47, 70–84. [Google Scholar] [CrossRef]
- Amato, R.; Ciaramella, A.; Deniskina, N.; Del Mondo, C.; di Bernardo, D.; Donalek, C.; Longo, G.; Mangano, G.; Miele, G.; Raiconi, G.; et al. A multi-step approach to time series analysis and gene expression clustering. Bioinformatics 2006, 22, 589–596. [Google Scholar] [CrossRef] [PubMed]
- Shyu, C.R.; Brodley, C.E.; Kak, A.C.; Kosaka, A.; Aisen, A.M.; Broderick, L.S. ASSERT: A Physician-in-the-Loop Content-Based Retrieval System for HRCT Image Databases. Comput. Vis. Image Underst. 1999, 75, 111–132. [Google Scholar] [CrossRef]
- Schirner, G.; Erdogmus, D.; Chowdhury, K.; Padir, T. The future of human-in-the-loop cyber-physical systems. Computer 2013, 46, 36–45. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems (NIPS 2012); Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; NIPS: San Diego, CA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Mikolov, T.; Deoras, A.; Povey, D.; Burget, L.; Cernocky, J. Strategies for training large scale neural network language models. In Proceedings of the IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU 2011), Waikoloa, HI, USA, 11–15 December 2011; pp. 196–201. [Google Scholar] [CrossRef]
- Helmstaedter, M.; Briggman, K.L.; Turaga, S.C.; Jain, V.; Seung, H.S.; Denk, W. Connectomic reconstruction of the inner plexiform layer in the mouse retina. Nature 2013, 500, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Leung, M.K.; Xiong, H.Y.; Lee, L.J.; Frey, B.J. Deep learning of the tissue-regulated splicing code. Bioinformatics 2014, 30, i121–i129. [Google Scholar] [CrossRef] [PubMed]
- Bar, Y.; Diamant, I.; Wolf, L.; Greenspan, H. Deep learning with non-medical training used for chest pathology identification. In Proceedings of the Medical Imaging 2015: Computer-Aided Diagnosis, Orlando, FL, USA, 21–26 February 2015. [Google Scholar] [CrossRef]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional Neural Networks for Medical Image Analysis: Full Training or Fine Tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Havaei, M.; Guizard, N.; Larochelle, H.; Jodoin, P.M. Deep learning trends for focal brain pathology segmentation in MRI. In Machine Learning for Health Informatics; Holzinger, A., Ed.; Springer: Cham, Switzerland, 2016; pp. 125–148. [Google Scholar] [CrossRef]
- Carrasquilla, J.; Melko, R.G. Machine learning phases of matter. Nat. Phys. 2017, 13, 431–434. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; Dieleman, S.; Grewe, D.; Nham, J.; Kalchbrenner, N.; Sutskever, I.; Lillicrap, T.; Leach, M.; Kavukcuoglu, K.; Graepel, T.; Hassabis, D. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G.; Gaissmaier, W. Heuristic Decision Making. Annu. Rev. Psychol. 2011, 62, 451–482. [Google Scholar] [CrossRef] [PubMed]
- Marewski, J.N.; Gigerenzer, G. Heuristic decision making in medicine. Dialogues Clin. Neurosci. 2012, 14, 77–89. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Wang, H.; Yeung, D.-Y. Bayesian deep learning: A framework and some existing methods. IEEE Trans Knowl. Data Eng. 2016, 28, 3395–3408. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- McCloskey, M.; Cohen, N.J. Catastrophic interference in connectionist networks: The sequential learning problem. In The Psychology of Learning and Motivation; Bower, G.H., Ed.; Academic Press: San Diego, CA, USA, 1989; Volume 24, pp. 106–165. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Mirza, M.; Xiao, D.; Courville, A.; Bengio, Y. An empirical investigation of catastrophic forgeting in gradient-based neural networks. arXiv, 2015; arXiv:1312.6211. [Google Scholar]
- Lee, J.; Kim, H.; Lee, J.; Yoon, S. Intrinsic Geometric Information Transfer Learning on Multiple Graph-Structured Datasets. arXiv, 2016; arXiv:1611.04687. [Google Scholar]
- Henaff, M.; Bruna, J.; LeCun, Y. Deep convolutional networks on graph-structured data. arXiv, 2015; arXiv:1506.05163. [Google Scholar]
- Tsymbal, A.; Zillner, S.; Huber, M. Ontology—Supported Machine Learning and Decision Support in Biomedicine. In Data Integration in the Life Sciences; Cohen-Boulakia, S., Tannen, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4544, pp. 156–171. [Google Scholar] [CrossRef]
- Holzinger, A.; Jurisica, I. Knowledge Discovery and Data Mining in Biomedical Informatics: The future is in Integrative, Interactive Machine Learning Solutions. In Lecture Notes in Computer Science LNCS 8401; Holzinger, A., Jurisica, I., Eds.; Springer: Burlin/Heidelberg, Germany, 2014; pp. 1–18. [Google Scholar] [CrossRef]
- Balcan, N.; Blum, A.; Mansour, Y. Exploiting Ontology Structures and Unlabeled Data for Learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1112–1120. [Google Scholar]
- Carlson, A.; Betteridge, J.; Kisiel, B.; Settles, B.; Hruschka, E.R., Jr.; Mitchell, T.M. Toward an Architecture for Never-Ending Language Learning (NELL). In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence (AAAI-10), Atlanta, GA, USA, 11–15 July 2010. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- Manning, C.D.; Schuetze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Frank, M.C.; Goodman, N.D.; Tenenbaum, J.B. Using speakers’ referential intentions to model early cross-situational word learning. Psychol. Sci. 2009, 20, 578–585. [Google Scholar] [CrossRef] [PubMed]
- Goodman, N.D.; Frank, M.C. Pragmatic language interpretation as probabilistic inference. Trends Cogn. Sci. 2016, 20, 818–829. [Google Scholar] [CrossRef] [PubMed]
- Rong, X. Word2vec parameter learning explained. arXiv, 2014; arXiv:1411.2738. [Google Scholar]
- Goldberg, Y.; Levy, O. word2vec Explained: deriving Mikolov et al.’s negative-sampling word-embedding method. arXiv, 2014; arXiv:1402.3722. [Google Scholar]
- Wallach, H.M. Topic modeling: Beyond bag-of-words. In Proceedings of the 23rd International Conference on Machine Learning (ICML), Pittsburgh, PA, USA, 25–29 June 2006; pp. 977–984. [Google Scholar]
- Weinberger, K.; Dasgupta, A.; Langford, J.; Smola, A.; Attenberg, J. Feature hashing for large scale multitask learning. In Proceedings of the 26th Annual International Conference on Machine Learning (ICML 2009), Montreal, QC, Canada, 14–18 June 2009; Bottou, L., Littman, M., Eds.; ACM: New York, NY, USA, 2009; pp. 1113–1120. [Google Scholar]
- Guyon, I.; Boser, B.; Vapnik, V. Automatic capacity tuning of very large VC-dimension classifiers. In Proceedings of the 7th Advances in Neural Information Processing Systems Conference (NIPS 1993), Denver, CO, USA; Cowan, J., Tesauro, G., Alspector, J., Eds.; NIPS: San Diego, CA, USA, 1993; Volume 7, pp. 147–155. [Google Scholar]
- Leskovec, J.; Chakrabarti, D.; Kleinberg, J.; Faloutsos, C.; Ghahramani, Z. Kronecker graphs: An approach to modeling networks. J. Mach. Learn. Res. 2010, 11, 985–1042. [Google Scholar] [CrossRef]
- Leskovec, J.; Sosic, R. SNAP: A general-purpose network analysis and graph-mining library. ACM Trans. Intell. Syst. Technol. 2016, 8, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Wood, F.; Meent, J.W.; Mansinghka, V. A new approach to probabilistic programming inference. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics (AISTATS) 2014, Reykjavik, Iceland, 22–25 April 2014; pp. 1024–1032. [Google Scholar]
- Malle, B.; Kieseberg, P.; Weippl, E.; Holzinger, A. The right to be forgotten: Towards Machine Learning on perturbed knowledge bases. In Springer Lecture Notes in Computer Science LNCS 9817; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 2016; pp. 251–266. [Google Scholar] [CrossRef]
- Goedertier, S.; Martens, D.; Vanthienen, J.; Baesens, B. Robust process discovery with artificial negative events. J. Mach. Learn. Res. 2009, 10, 1305–1340. [Google Scholar] [CrossRef]
- Doucet, A.; De Freitas, N.; Gordon, N. An introduction to sequential Monte Carlo methods. In Sequential Monte Carlo Methods in Practice; Springer: Heidelberg/Berlin, Germany, 2001; pp. 3–14. [Google Scholar] [CrossRef]
- Konecný, J.; McMahan, H.B.; Ramage, D.; Richtárik, P. Federated Optimization: Distributed Machine Learning for On-Device Intelligence. arXiv, 2016; arXiv:1610.02527v1. [Google Scholar]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Federated Learning on User-Held Data. arXiv, 2016; arXiv:1611.04482. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar]
- Leskovec, J.; Singh, A.; Kleinberg, J. Patterns of influence in a recommendation network. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Heidelberg/Berlin, Germany, 2006; pp. 380–389. [Google Scholar] [CrossRef]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef]
- Baxter, J. A model of inductive bias learning. J. Artif. Intell. Res. 2000, 12, 149–198. [Google Scholar] [CrossRef]
- Evgeniou, T.; Pontil, M. Regularized multi-task learning. In Proceedings of the Tenth ACM SIGKDD International Conference On Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 109–117. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Schoelkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar]
- Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Parameswaran, S.; Weinberger, K.Q. Large margin multi-task metric learning. In Advances in Neural Information Processing Systems 23 (NIPS 2010); Lafferty, J., Williams, C., Shawe-Taylor, J., Zemel, R., Culotta, A., Eds.; NIPS: San Diego, CA, USA, 2010; pp. 1867–1875. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; Hassabis, D.; Clopath, C.; Kumaran, D.; Hadsell, R.; et al. Overcoming catastrophic forgetting in neural networks. arXiv, 2016; arXiv:1612.00796. [Google Scholar]
- Pan, S.J.; Yang, Q.A. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer learning for reinforcement learning domains: A survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Sycara, K.P. Multiagent systems. AI Mag. 1998, 19, 79. [Google Scholar]
- Lynch, N.A. Distributed Algorithms; Morgan Kaufmann: San Francisco, CA, USA, 1996. [Google Scholar]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Swain, P.H. Consensus theoretic classification methods. IEEE Trans. Syst. Man Cybern. 1992, 22, 688–704. [Google Scholar] [CrossRef]
- Weller, S.C.; Mann, N.C. Assessing rater performance without a gold standard using consensus theory. Med. Decis. Mak. 1997, 17, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Roche, B.; Guegan, J.F.; Bousquet, F. Multi-agent systems in epidemiology: A first step for computational biology in the study of vector-borne disease transmission. BMC Bioinform. 2008, 9, 435. [Google Scholar] [CrossRef] [PubMed]
- Kok, J.R.; Vlassis, N. Collaborative multiagent reinforcement learning by payoff propagation. J. Mach. Learn. Res. 2006, 7, 1789–1828. [Google Scholar]
- Robert, S.; Büttner, S.; Röcker, C.; Holzinger, A. Reasoning Under Uncertainty: Towards Collaborative Interactive Machine Learning. In Machine Learning for Health Informatics: State-of-the-Art and Future Challenges; Holzinger, A., Ed.; Springer: Cham, Switzerland, 2016; pp. 357–376. [Google Scholar] [CrossRef]
- Holzinger, A. Successful Management of Research and Development; BoD: Norderstedt, Germany, 2011; p. 112. [Google Scholar]
- Holzinger, A. Machine Learning for Health Informatics. In Machine Learning for Health Informatics: State-of-the-Art and Future Challenges, Lecture Notes in Artificial Intelligence LNAI 9605; Holzinger, A., Ed.; Springer: Cham, Switzerland, 2016; pp. 1–24. [Google Scholar] [CrossRef]
- Theodoridis, S.; Slavakis, K.; Yamada, I. Adaptive Learning in a World of Projections. IEEE Signal Process. Mag. 2011, 28, 97–123. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Wu, W.; Nagarajan, S.; Chen, Z. Bayesian Machine Learning. IEEE Signal Process. Mag. 2016, 33, 14–36. [Google Scholar] [CrossRef]
- Russell, S.; Dietterich, T.; Horvitz, E.; Selman, B.; Rossi, F.; Hassabis, D.; Legg, S.; Suleyman, M.; George, D.; Phoenix, S. Letter to the Editor: Research Priorities for Robust and Beneficial Artificial Intelligence: An Open Letter. Available online: https://www.bibsonomy.org/bibtex/2185f9c84cb3aef91e7bb82eeb4728ce0/dblp (accessed on 25 June 2017).
- Anderson, M.; Anderson, S.L. Machine ethics: Creating an ethical intelligent agent. AI Mag. 2007, 28, 15–25. [Google Scholar]
- Boella, G.; van der Torre, L.; Verhagen, H. Introduction to the special issue on normative multiagent systems. Auton. Agents Multi-Agent Syst. 2008, 17, 1–10. [Google Scholar] [CrossRef]
- Cervantes, J.A.; Rodriguez, L.F.; Lopez, S.; Ramos, F.; Robles, F. Autonomous Agents and Ethical Decision-Making. Cogn. Comput. 2016, 8, 278–296. [Google Scholar] [CrossRef]
- Deng, B. The Robot’s dilemma. Nature 2015, 523, 24–26. [Google Scholar] [CrossRef] [PubMed]
- Thimbleby, H. Explaining code for publication. Softw. Pract. Exp. 2003, 33, 975–1001. [Google Scholar] [CrossRef]
- Sonnenburg, S.; Braun, M.L.; Ong, C.S.; Bengio, S.; Bottou, L.; Holmes, G.; LeCun, Y.; Muller, K.R.; Pereira, F.; Rasmussen, C.E.; et al. The need for open source software in machine learning. J. Mach. Learn. Res. 2007, 8, 2443–2466. [Google Scholar]
- Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine Learning: An Artificial Intelligence Approach; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Holzinger, A. On Knowledge Discovery and Interactive Intelligent Visualization of Biomedical Data—Challenges in Human–Computer Interaction & Biomedical Informatics. In Proceedings of the DATA 2012, International Conference on Data Technologies and Applications, Rome, Italy, 25–27 July 2012; pp. 5–16. [Google Scholar]
- Holzinger, A. Human—Computer Interaction and Knowledge Discovery (HCI-KDD): What is the benefit of bringing those two fields to work together? In Multidisciplinary Research and Practice for Information Systems, Springer Lecture Notes in Computer Science LNCS 8127; Cuzzocrea, A., Kittl, C., Simos, D.E., Weippl, E., Xu, L., Eds.; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 2013; pp. 319–328. [Google Scholar] [CrossRef]
- Holzinger, A. Trends in Interactive Knowledge Discovery for Personalized Medicine: Cognitive Science meets Machine Learning. IEEE Intell. Inform. Bull. 2014, 15, 6–14. [Google Scholar]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.A.; Hudspeth, A. Principles of Neural Science, 5th ed.; McGraw-Hill: New York, NY, USA, 2012; p. 1760. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holzinger, A. Introduction to MAchine Learning & Knowledge Extraction (MAKE). Mach. Learn. Knowl. Extr. 2019, 1, 1-20. https://doi.org/10.3390/make1010001
Holzinger A. Introduction to MAchine Learning & Knowledge Extraction (MAKE). Machine Learning and Knowledge Extraction. 2019; 1(1):1-20. https://doi.org/10.3390/make1010001
Chicago/Turabian StyleHolzinger, Andreas. 2019. "Introduction to MAchine Learning & Knowledge Extraction (MAKE)" Machine Learning and Knowledge Extraction 1, no. 1: 1-20. https://doi.org/10.3390/make1010001
APA StyleHolzinger, A. (2019). Introduction to MAchine Learning & Knowledge Extraction (MAKE). Machine Learning and Knowledge Extraction, 1(1), 1-20. https://doi.org/10.3390/make1010001