Study on the Mechanical Properties and Fracture Mechanisms of Anchor Cable Specimen Materials
Abstract
1. Introduction
2. Experimental Program
2.1. Specimen Configuration
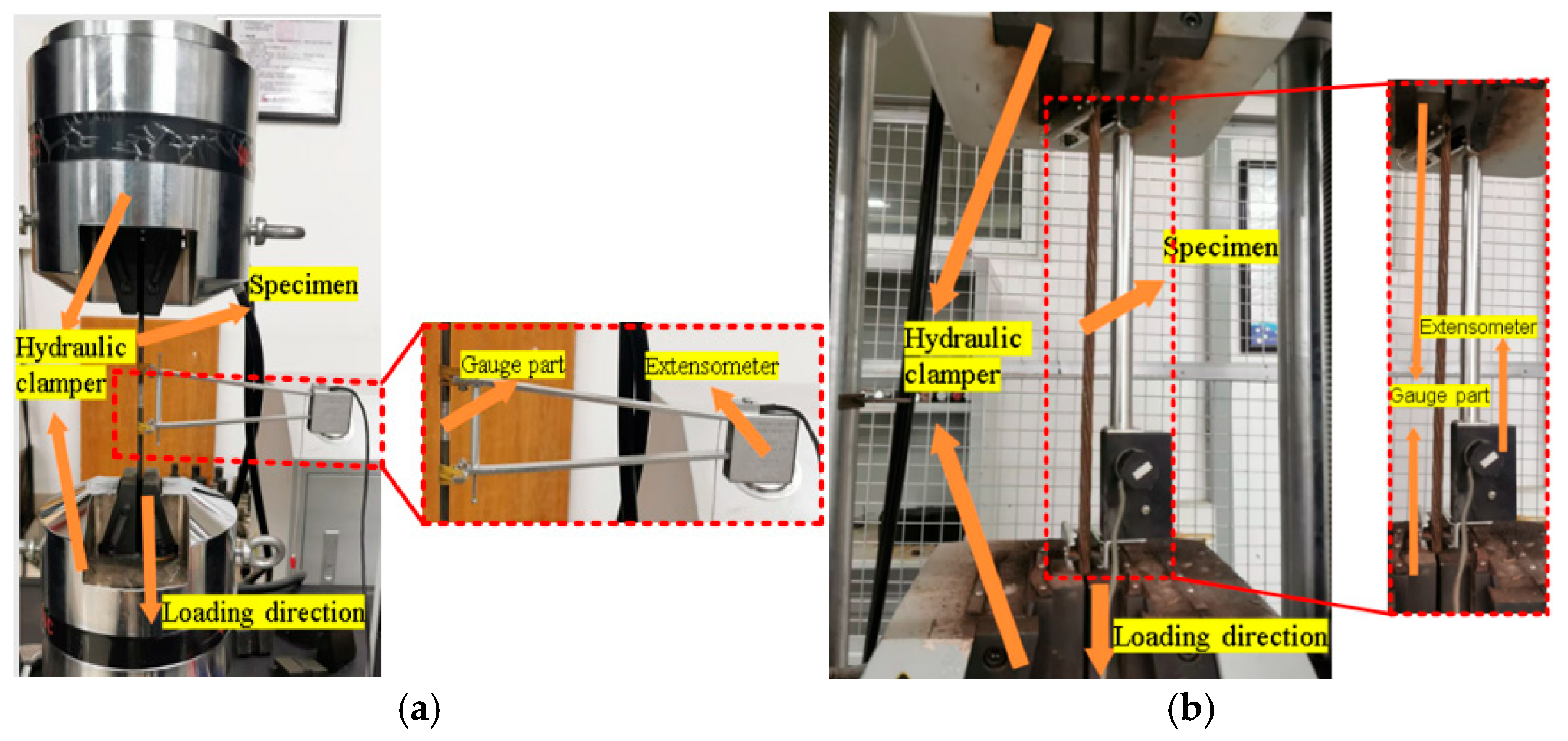
2.2. Tensile Specimen Test Set-Up and Results
2.3. Anchor Cable Specimen Test Set-Up and Results
3. Finite Element (FE) Simulation
3.1. FE Model
3.2. True Stress–Strain Relationship Model
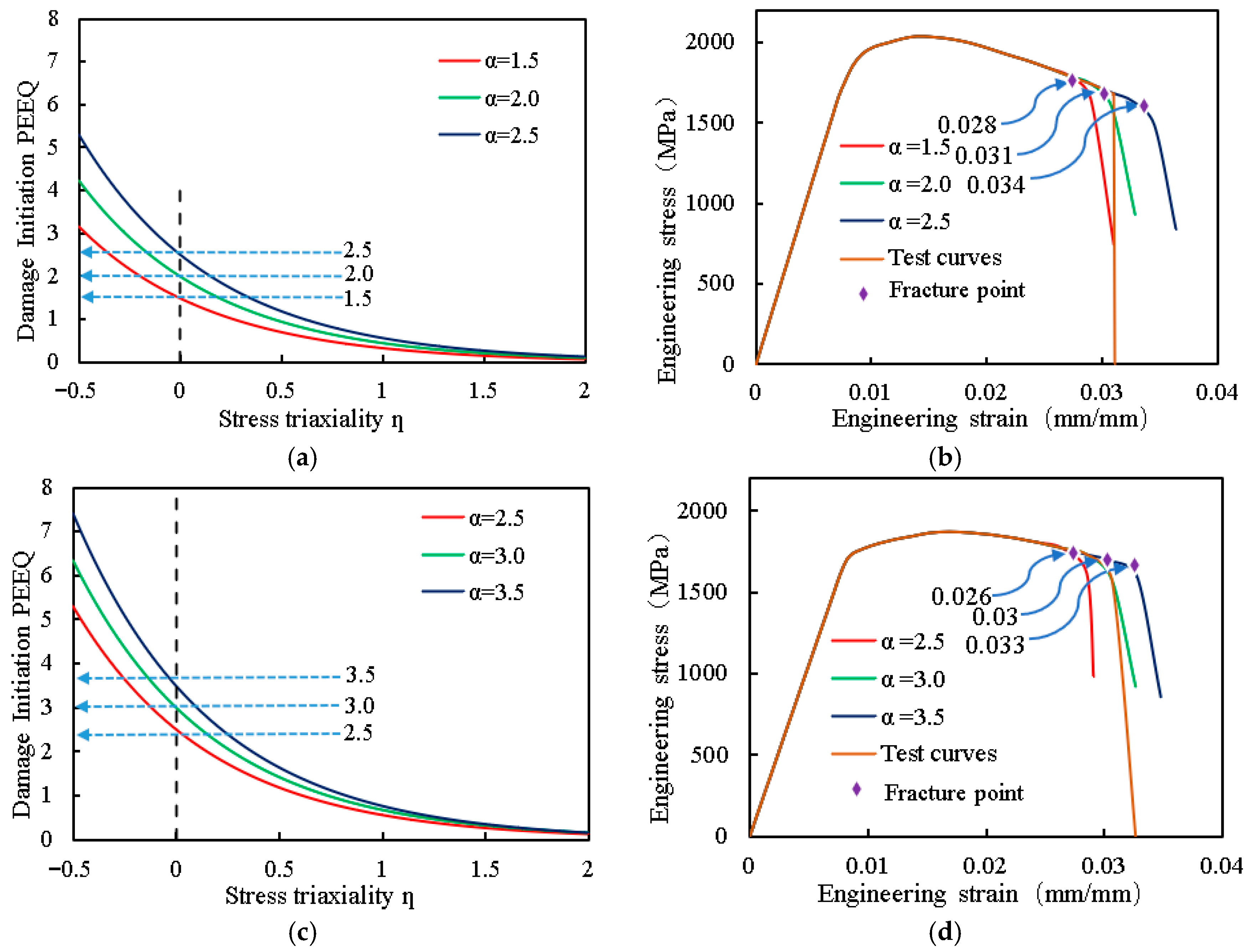
3.3. Fitting of True Stress–Strain Relationship
3.4. Fracture Model
3.5. Anchor Cable Specimen and Fracture Model
4. Tensile Fracture Mechanism of Anchor Cable Specimen
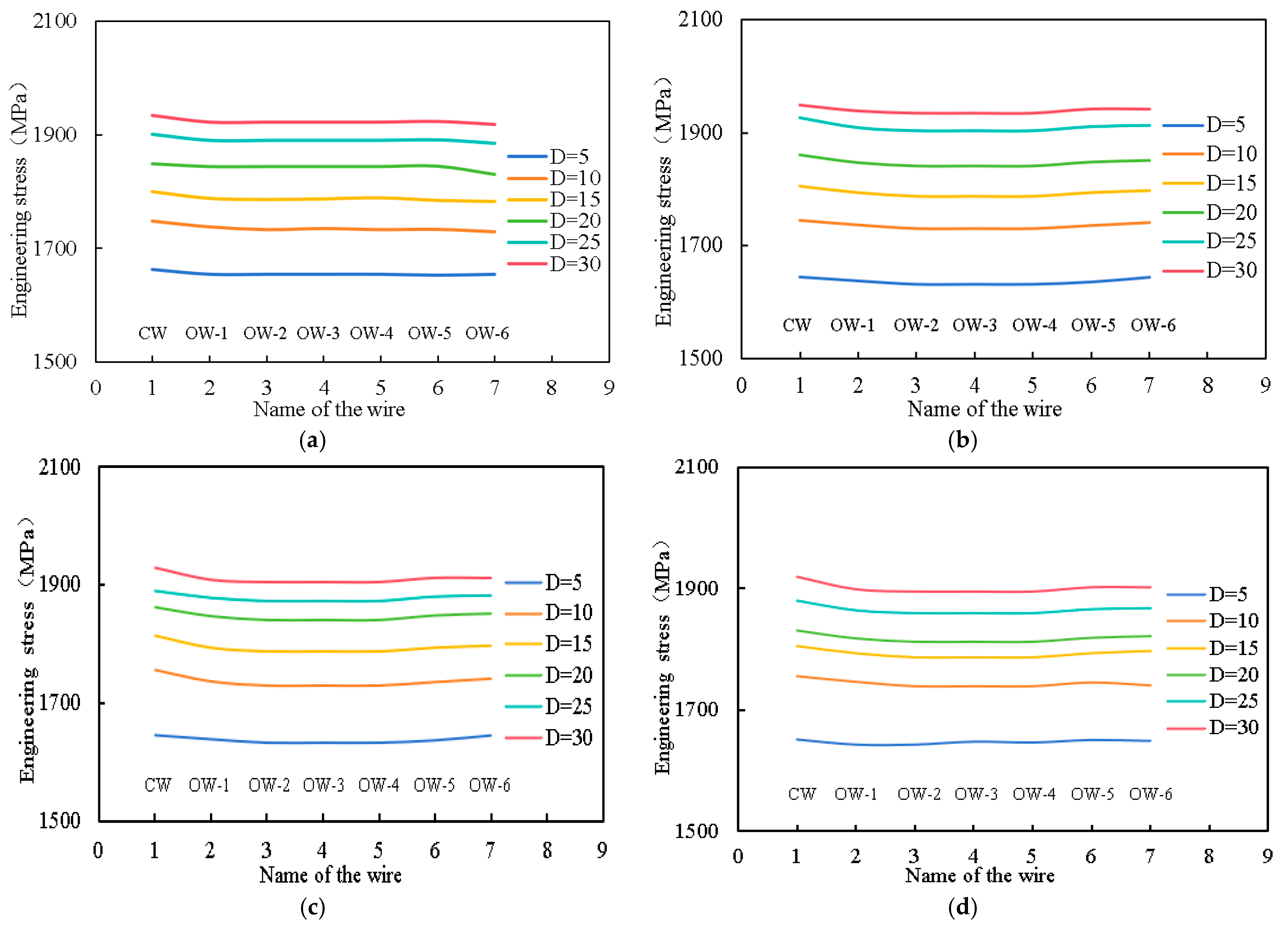
4.1. Analysis of Stress Distribution of Monofilament in Anchor Cable Specimen
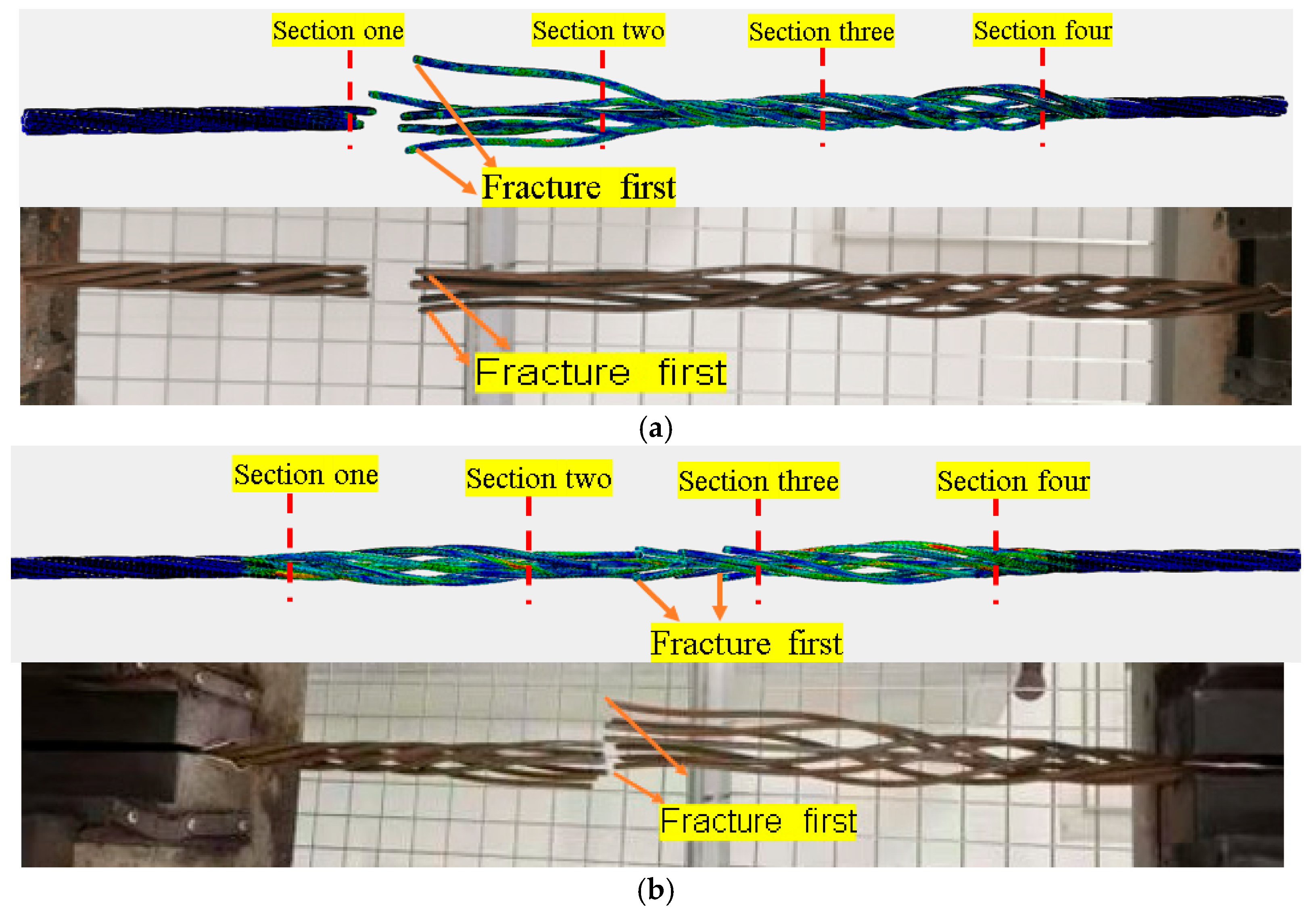
4.2. Analysis of Stress Characteristics of Anchor Cable Specimen Under Fracture
5. Conclusions
- (1)
- Investigation of the long-term durability and corrosion effects on the fracture behavior of anchor cables under combined mechanical and environmental loading
- (2)
- Extension of the current model to include cyclic loading and fatigue failure analysis for a more comprehensive understanding of anchor cable performance in real-world applications
- (3)
- Exploration of the influence of different wire arrangements and cable geometries on stress distribution and fracture mechanisms
- (4)
- Validation of the proposed Ling and R-T models under multi-axial stress states and complex boundary conditions to enhance their generalizability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bo, M.; Qian, Y.; Wen, H.J.; Liu, S. Stability control of deep-buried roadways using large deformation and increasing resistance anchor cables. J. Cent. South Univ. 2024, 31, 558–575. [Google Scholar]
- Cui, Z.; Tian, W.; Liu, K.; Guo, D. Seasonal frozen soil area frame beam anchor rod slope support structure frost heave mechanical characteristics simplified calculation model. Environ. Earth Sci. 2024, 83, 425. [Google Scholar] [CrossRef]
- Xing, T.; Liu, H.; Zheng, J.; Yu, X.; Li, Y.; Peng, H. Study on the Effect of Anchor Cable Prestress Loss on Foundation Stability. Appl. Sci. 2024, 14, 4908. [Google Scholar] [CrossRef]
- Yang, F.; Veljkovic, M.; Liu, Y. Ductile damage model calibration for high-strength structural steels. Constr. Build. Mater. 2020, 263, 120632. [Google Scholar] [CrossRef]
- Xue, S.; Shen, R.; Xue, H.; Zhu, X. Failure analysis of high-strength steel wire under random corrosion. Structures 2021, 33, 720–727. [Google Scholar] [CrossRef]
- Abreu, D.M.; Iordachescu, M.; Valiente, A. Influence of transversal loading on tensile and fatigue behaviour of high-strength lean duplex stainless steel wires. Eng. Fail. Anal. 2019, 102, 417–424. [Google Scholar] [CrossRef]
- Gao, X.; Jia, J.; Bao, X.; Mei, G.; Zhang, L.; Tu, B. Investigation of dynamic responses of slopes in various anchor cable failure modes. Soil Dyn. Earthq. Eng. 2025, 188, 109077. [Google Scholar] [CrossRef]
- Zhao, C. Non-concrete breakout failure modes of concrete mechanical anchors in tension a literature review. Constr. Build. Mater. 2023, 366, 130222. [Google Scholar]
- Feng, C.; Liu, S.W.; Fu, M.X.; Lyu, Q.; He, D.; He, Y. Study on the shear failure mechanism of the free section of prestressed anchor cables. Chin. J. Rock Mech. Eng. 2024, 43, 1468–1479. [Google Scholar]
- Shi, M.F. Study on Fatigue Performance and Failure Mechanism of Prestressed Steel Strand Reinforced RC Beams Under Different Parameters. Master’s Thesis, Huaqiao University, Xiamen, China, 2019. [Google Scholar]
- Zhang, F.; Zhao, G.-H.; Wu, Y.-F.; Zhang, Y. Effect of strand debonding on the shear strength of existing pretensioned PC hollow slab. Eng. Struct. 2023, 291, 116417. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile Deformation. AIME Trans. 1945, 162, 268–290. [Google Scholar]
- Voce, E. The Relationship Between Stress and Strain for Homogeneous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin, Germany, 1909. [Google Scholar]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Ling, Y. Uniaxial true stress-strain after necking. AMPJ. Technol. 1996, 5, 37–48. [Google Scholar]
- Wang, F.; Liu, G.; Shen, D.; Guo, N.; Guo, F.; Zhang, Z.; Sun, W.; Tang, B. Extended GTN-Thomason Model for Modeling Ductile Fracture of Fe-Cr-Mo-Mn Steel at a Wide Range of Stress States and Temperatures. J. Mater. Eng. Perform. 2025, 1–27. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr-Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Lou, Y.; Chen, L.; Clausmeyer, T.; Tekkaya, A.E.; Yoon, J.W. Modeling of ductile fracture from shear to balanced biaxial tension for sheet metals. Int. J. Solids Struct. 2017, 112, 169–184. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Extension of a shear-controlled ductile fracture model considering the stress triaxiality and the Lode parameter. Int. J. Solids Struct. 2013, 50, 447–455. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation. J. Mater. Process. Technol. 2013, 213, 1284–1302. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W.; Huh, H. Modeling of shear ductile fracture considering a changeable cut-off value for stress triaxiality. Int. J. Plast. 2014, 54, 56–80. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W.; Huh, H.; Chao, Q.; Song, J.-H. Correlation of the maximum shear stress with micro-mechanisms of ductile fracture for metals with high strength-to-weight ratio. Int. J. Mech. Sci. 2018, 146–147, 583–601. [Google Scholar] [CrossRef]
- Gu, G.; Mohr, D. Anisotropic Hosford-Coulomb fracture initiation model: Theory and application. Eng. Fract. Mech. 2015, 147, 480–497. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford-Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Huang, F. Extension of a shear-controlled ductile fracture criterion by considering the necking coalescence of voids. Int. J. Solids Struct. 2022, 236–237, 111324. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields*. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Ho, H.C.; Chung, K.F.; Xiao, T.Y.; Yam, M.C.H.; Nethercot, D.A. Non-linear necking behaviour of S275 to S960 structural steels under monotonic tension. Eng. Struct. 2022, 261, 114263. [Google Scholar] [CrossRef]
- Microcomputer-Controlled Electro-Hydraulic Servo Universal Testing Machine; Shijin Group Co., Ltd.: Jinan, China, 2006.
- GB/T228.1-2015; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standardization Administration of China: Beijing, China.
- Anon. Abaqus Analysis User’s Guide, Version 2020; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2020.
- Anon. Abaqus Analysis User’s Guide, Version 6.13; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2013.
- Zhang, Y.; Liu, Y.; Yang, F.; Zhou, Q.; Chen, A. Plasticity and ductile fracture of high-strength bolt materials under monotonic tension. J. Constr. Steel Res. 2024, 214, 108475. [Google Scholar] [CrossRef]
- Kanvinde, A.M.; Deierlein, G.G. The void growth model and the stress modified critical strain model to predict ductile fracture in structural steels. J. Struct. Eng. 2006, 132, 1907–1918. [Google Scholar] [CrossRef]
- Kanvinde, A.M.; Deierlein, G.G. Finite-element simulation of ductile fracture in reduced section pull-plates using micromechanics-based fracture models. J. Struct. Eng. 2007, 133, 656–664. [Google Scholar] [CrossRef]
- Jeon, C.-H.; Lee, J.-B.; Lon, S.; Shim, C.-S. Equivalent material model of corroded prestressing steel strand. J. Mater. Res. Technol. 2019, 8, 2450–2460. [Google Scholar] [CrossRef]
- Tan, D.; Luo, Y.; Tao, Y.; Peng, Y.; Luo, H.; Ji, B. Research on Broken Wire Based on a Fine Finite Element Model of Steel Strands. Materials 2025, 18, 3148. [Google Scholar] [CrossRef]
- Orhan, Y.; Marios, T.; Huanxin, Y.; Afshan, S. Comparative study on fracture characteristics of carbon and stainless steel bolt material. J. Constr. Steel Res. 2023, 210, 108102. [Google Scholar] [CrossRef]
- Wu, P.; Kardani, A.; Liu, M.; Lin, Z.; Bagherifard, S. Exploring the bonding mechanism in cold spray deposition of engineered graphene nanoplates-Ni nanocomposite powder. Compos. Part A Appl. Sci. Manuf. 2025, 191, 108741. [Google Scholar] [CrossRef]












| Specimens | Nominal Diameter (mm) | Measured Diameter (mm) | Machining Diameter (mm) | Specimens | Nominal Diameter (mm) | Measured Diameter (mm) | Machining Diameter (mm) |
|---|---|---|---|---|---|---|---|
| a-12.7-T1 | 4.30 | 4.28 | 3.73 | b-15.2-T1 | 5.20 | 5.22 | 4.70 |
| a-12.7-T2 | 4.30 | 4.31 | 3.66 | b-15.2-T2 | 5.20 | 5.21 | 4.65 |
| a-12.7-T3 | 4.30 | 4.30 | 3.71 | b-15.2-T3 | 5.20 | 5.18 | 4.69 |
| Mean | 4.30 | 4.30 | 3.70 | Mean | 5.20 | 5.20 | 4.68 |
| A-12.7-T1 | 12.70 | 12.69 | - | B-15.2-T1 | 15.20 | 15.22 | - |
| A-12.7-T2 | 12.70 | 12.74 | - | B-15.2-T2 | 15.20 | 15.23 | - |
| A-12.7-T3 | 12.70 | 12.70 | - | B-15.2-T3 | 15.20 | 15.21 | - |
| Mean | 12.70 | 12.71 | - | Mean | 15.20 | 15.22 | - |
| Specimens | E (GPa) | fu (MPa) | fy (MPa) | fy/fu | εf (mm/mm) | Elongation δ% |
|---|---|---|---|---|---|---|
| a-12.7-T1 | 194.51 | 1741.04 | 1990.42 | 1.09 | 0.035 | 2.02 |
| a-12.7-T2 | 190.23 | 1693.61 | 1949.15 | 1.09 | 0.032 | 2.01 |
| a-12.7-T3 | 189.41 | 1752.48 | 1990.40 | 1.08 | 0.031 | 2.15 |
| Average | 191.28 | 1729.04 | 1976.66 | 1.09 | 0.033 | 2.06 |
| b-15.2-T1 | 201.73 | 1777.14 | 1982.03 | 1.11 | 0.031 | 1.72 |
| b-15.2-T2 | 199.27 | 1765.27 | 1937.95 | 1.08 | 0.032 | 1.51 |
| b-15.2-T3 | 202.38 | 1743.04 | 1942.15 | 1.11 | 0.030 | 1.63 |
| Average | 201.13 | 1767.40 | 1954.04 | 1.10 | 0.031 | 1.63 |
| Specimens | Ultimate Load Fu (kN) | Limit Displacement ΔX (mm) |
|---|---|---|
| A-12.7-T1 | 196.68 | 34.54 |
| A-12.7-T2 | 195.47 | 35.27 |
| A-12.7-T3 | 194.96 | 35.49 |
| Average | 195.70 | 35.07 |
| B-15.2-T1 | 268.58 | 31.84 |
| B-15.2-T2 | 269.65 | 31.62 |
| B-15.2-T3 | 268.74 | 32.65 |
| Average | 268.99 | 32.04 |
| Tensile Specimen A | Tensile Specimen B | ||||
|---|---|---|---|---|---|
| Model | Sd | Cc | Model | Sd | Cc |
| Ling | 2.6718 | 0.9996 | Ling | 7.2019 | 0.9846 |
| Swift+Voce | 2.7132 | 0.9987 | Swift+Voce | 7.2414 | 0.9836 |
| Voce | 25.0749 | 0.8097 | Voce | 22.6861 | 0.8456 |
| Ludwik | 42.0252 | 0.7099 | Ludwik | 44.3114 | 0.8773 |
| Hollomon | 13.5702 | 0.9174 | Hollomon | 18.7326 | 0.8404 |
| Swift | 24.4332 | 0.8560 | Swift | 22.2154 | 0.8400 |
| Ul | Fd | Aul | Afd | Ul FEA/EXP | Fd FEA/EXP | |
|---|---|---|---|---|---|---|
| Anchor cable specimen A | 194.60 | 34.09 | - | - | 0.9943 | 0.972 |
| 194.89 | 35.28 | 195.70 | 35.07 | 0.9958 | 1.006 | |
| 195.78 | 36.33 | - | - | 1.0001 | 1.0359 | |
| Average | 195.09 | 35.50 | 195.70 | 35.07 | 0.9967 | 1.0046 |
| 266.74 | 32.07 | - | - | 0.9916 | 1.0009 | |
| Anchor cable specimen B | 267.26 | 33.13 | 268.99 | 32.04 | 0.9936 | 1.034 |
| 267.79 | 34.11 | - | - | 0.9955 | 1.0646 | |
| Average | 267.26 | 33.10 | 268.99 | 32.04 | 0.9936 | 1.0332 |
| Type A Anchor Cable Specimen | Type B Anchor Cable Specimen | ||||||
|---|---|---|---|---|---|---|---|
| σmax | σAvg | X | σmax | σAvg | X | ||
| CW | 2123 | 2052 | 1.034659 | CW | 1969 | 1933 | 1.018624 |
| OW-1 | 2138 | 1997 | 1.070606 | OW-1 | 1986 | 1909 | 1.040335 |
| OW-2 | 2134 | 2010 | 1.061692 | OW-2 | 1981 | 1896 | 1.044831 |
| OW-3 | 2131 | 2007 | 1.061784 | OW-3 | 1984 | 1905 | 1.044147 |
| OW-4 | 2132 | 2015 | 1.058065 | OW-4 | 1986 | 1910 | 1.039791 |
| OW-5 | 2135 | 2009 | 1.062718 | OW-5 | 1987 | 1892 | 1.050211 |
| OW-6 | 2130 | 2008 | 1.060757 | OW-6 | 1982 | 1894 | 1.046463 |
| Type A Anchor Cable Specimen | Type B Anchor Cable Specimen | ||
|---|---|---|---|
| Damage Initiation PEEQ | Damage Initiation PEEQ | ||
| CW | 0.783 | CW | 1.095 |
| OW-1 | 1.191 | OW-1 | 1.787 |
| OW-2 | 1.174 | OW-2 | 1.699 |
| OW-3 | 1.082 | OW-3 | 1.414 |
| OW-4 | 1.042 | OW-4 | 1.544 |
| OW-5 | 1.146 | OW-5 | 1.631 |
| OW-6 | 1.139 | OW-6 | 1.569 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Fan, G.; Zhang, K.; Zhang, Y.; Lian, J.; Huang, W.; Shi, S.; Zhang, M. Study on the Mechanical Properties and Fracture Mechanisms of Anchor Cable Specimen Materials. J. Compos. Sci. 2025, 9, 508. https://doi.org/10.3390/jcs9090508
Wang C, Fan G, Zhang K, Zhang Y, Lian J, Huang W, Shi S, Zhang M. Study on the Mechanical Properties and Fracture Mechanisms of Anchor Cable Specimen Materials. Journal of Composites Science. 2025; 9(9):508. https://doi.org/10.3390/jcs9090508
Chicago/Turabian StyleWang, Chenfei, Guangming Fan, Kai Zhang, Yajun Zhang, Junyin Lian, Wenkai Huang, Shuqin Shi, and Mincheng Zhang. 2025. "Study on the Mechanical Properties and Fracture Mechanisms of Anchor Cable Specimen Materials" Journal of Composites Science 9, no. 9: 508. https://doi.org/10.3390/jcs9090508
APA StyleWang, C., Fan, G., Zhang, K., Zhang, Y., Lian, J., Huang, W., Shi, S., & Zhang, M. (2025). Study on the Mechanical Properties and Fracture Mechanisms of Anchor Cable Specimen Materials. Journal of Composites Science, 9(9), 508. https://doi.org/10.3390/jcs9090508






