Experimental Investigation on Heat Generation of Tread Rubber Materials Under Tensile-Compression Cyclic Conditions

Abstract

Aiming at the heat generation behavior of rubber products such as tires under complex loads, the thermal behavior of tread rubber materials under tensile and compressive loads is investigated by using a torsional fatigue testing machine to comparatively analyze the temperature difference between the inside and outside of the rubber cylinders and the heating history under different torsion angles and rotational speeds. Results demonstrate that during the initial rotation phase under cyclic loading, the external surface temperature of the rubber material exceeds internal measurements. However, with the continuation of cyclic loading, the internal temperature progressively escalates beyond surface temperatures. Furthermore, the temperature rise exhibited significant correlations with both imposed torsional angles and operational rotational speeds. This study provides valuable insights into heat generation patterns of rubber materials under complex working conditions.

1. Introduction

Rubber composites are extensively utilized in diverse applications such as tires, dampers, and seals due to their exceptional elasticity and damping characteristics [1,2]. Due to the viscoelasticity of rubber composite materials, under cyclic loading conditions, a portion of the dissipated energy is converted into heat within the material [3,4]. Fundamentally, heat accumulation emerges as a direct consequence of such energy dissipation. However, the inherent low thermal conductivity of rubber composites impedes efficient heat dissipation, leading to progressive temperature elevation until thermal equilibrium with the external environment is achieved. This temperature rise critically compromises the mechanical integrity of rubber products, potentially degrading sealing performance and posing safety risks such as tire blowouts [5]. Furthermore, sustained heat accumulation accelerates material aging processes, ultimately reducing service life and exacerbating wear in rubber components like tires [6,7].

Investigating the heat generation mechanisms in rubber materials remains crucial and has attracted sustained attention within the research community. Studies indicate that the heat build-up in rubber composites is strongly correlated with loading frequency and strain amplitude [8,9,10,11]. Extensive efforts have been devoted to mitigating temperature rise through strategies such as optimizing filler types, refining processing techniques, and enhancing interfacial modifications [12,13,14,15]. Nevertheless, current research on hysteretic heat generation predominantly focuses on uniaxial tensile or compressive loading under simplified conditions [16]. For instance, Weng et al. [17] explored the heat buildup behavior of boron carbide (B₄C)-filled rubber composites via cyclic loading tests on cylindrical specimens. Zhan et al. [18] investigated the influence of cross-linking density on heat generation under uniaxial loading. Luo [19] and Li [20] analyzed temperature evolution during uniaxial compression using dynamic mechanical analysis (DMA). Keizo Akutagawa et al. [21] proposed novel interpretations of heat generation mechanisms in rubber under uniaxial tension. Liu et al. [22] investigated the temperature rise and fatigue crack growth in rubber materials through experiments and simulations, highlighting the influence of load waveform. Wu et al. [23] investigated the heat generation characteristics of rubber dumbbell-shaped specimens under uniaxial tension at varying strain levels through combined experimental and simulation approaches. Notably, the operational conditions of tires and analogous rubber components involve multiaxial loading, high-frequency excitation, and large-strain deformation, which cannot be adequately represented by simplified uniaxial tests. Andréas Hottin et al. [24] systematically characterized heat generation in natural rubber (NR) under multiaxial mechanical loads. O. Peter et al. [25] developed an innovative fatigue-heating apparatus to quantify internal and surface temperature variations in cylindrical rubber specimens under diverse bending angles and rotational speeds, complemented by finite element simulations. Kratina et al. [26] investigated the effect of cross-linked structures on rubber self-heating accumulation under multiaxial mechanical loading using a torsional fatigue testing machine.

Focusing on the complex operational conditions encountered by tires, this study utilizes a torsional fatigue testing machine to investigate the heat generation behavior of tread rubber materials under tensile-compression cyclic loading. The methodology commenced with a comprehensive characterization of the mechanical properties of the rubber material across varied temperature ranges. Subsequently, nine operating conditions were designed to systematically analyze the internal and external temperature evolution under different strain amplitudes (corresponding to bending angles) and loading frequencies (corresponding to rotational speeds). This comprehensive study provides fundamental insights into the heat generation behavior of tire rubber materials under dynamic usage conditions.

2. Materials and Methods

2.1. Materials

The rubber material employed in this study, specifically designed for tire tread applications, is supplied by Hangzhou Zhongce Rubber Co., Ltd. (Hangzhou, China). The tread rubber composition comprises 100 phr of natural rubber, 30 phr of carbon black, 25 phr of silica, 4 phr of silane coupling agent, 2 phr of petroleum resin, along with appropriate amounts of vulcanizing agent, antioxidant, and activator. The optimal vulcanization parameters (30 min at 150 °C) are determined using a rubber process analyzer (RPA S5, NORKA Instruments Co., Ltd., Shanghai, China). Specimen fabrication is conducted via a plate vulcanizing press (Jiangdu Changlong Testing Machinery Factory, Yangzhou, China) under a working pressure of 15 MPa, and the preparation process is shown in Figure 1. Cylindrical rubber specimens (Figure 2a) with a total length of 100 mm and diameter of 20 mm are fabricated, featuring 8 mm and 5 mm diameter holes at one end for thermocouple placement. Dumbbell-shaped specimens (Figure 2b) are die-cut from vulcanized rubber sheets prepared under identical curing conditions (150 °C, 30 min). All dimensional tolerances adhere to ASTM D412 standards for elastomeric material testing.

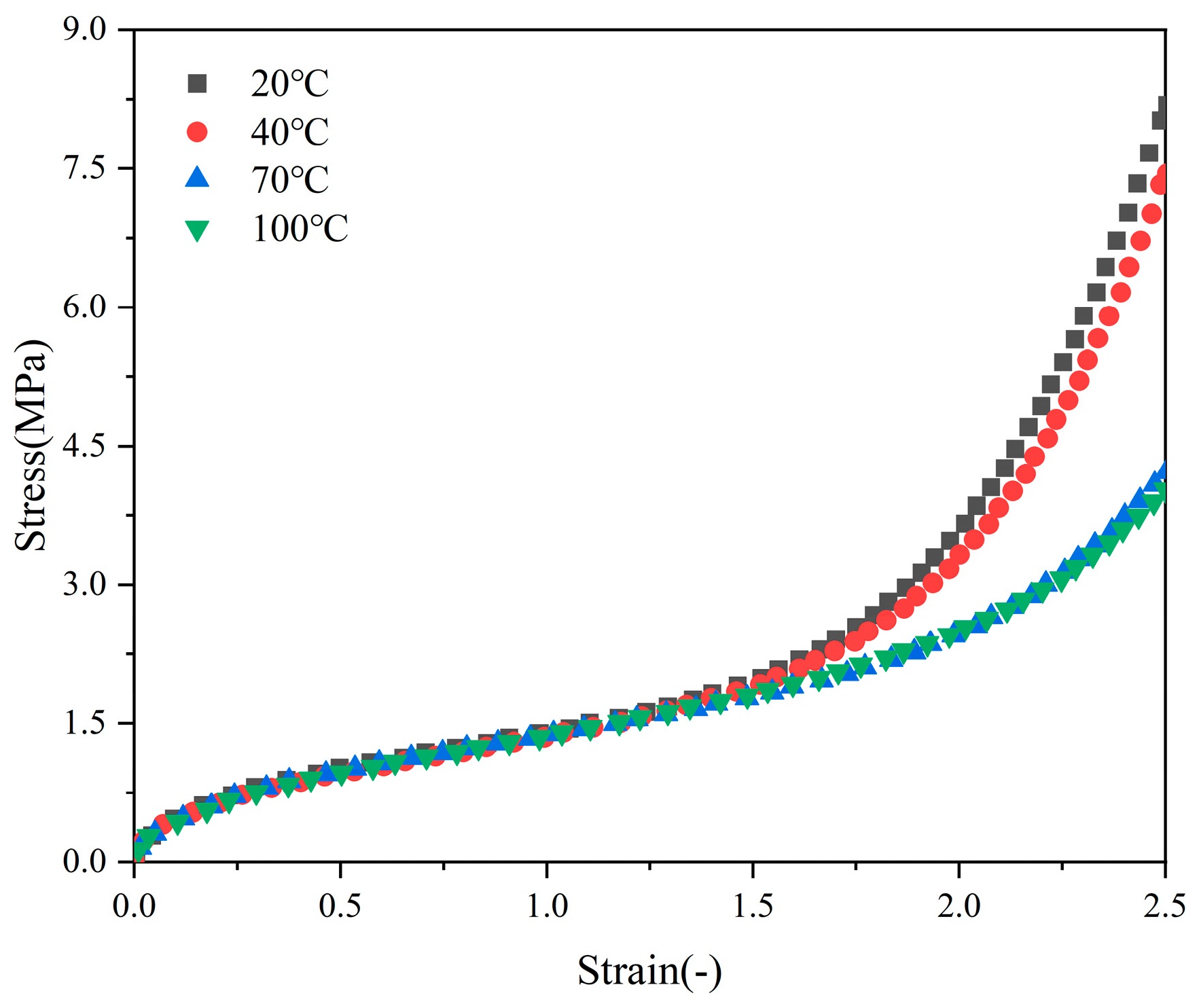
2.2. Tensile Test

The stress–strain behavior of rubber materials exhibits temperature-dependent characteristics. To investigate the thermomechanical response, uniaxial tensile tests are conducted on rubber specimens under varying temperature conditions using a high–low temperature tensile testing machine (Fule Technology (Shanghai) Co., Ltd., Shanghai, China), which has a tensile machine measurement accuracy of ±0.01%. Prior to the formal testing, three pre-stretching cycles are performed on dumbbell-shaped specimens to eliminate the Mullins effect. Subsequent tensile experiments are then carried out on tread rubber compounds at different temperatures. The experimental protocol strictly adheres to ISO 37:2005 standards, maintaining a constant speed of 500 mm/min [27]. Temperature conditions are controlled in accordance with ISO 23529:2004 specifications, with the test sequence conducted at 20, 40, 70, and 100 °C, respectively [28]. The strain range for all tests is maintained between 0% and 250% to ensure material response characterization within the elastic deformation regime.

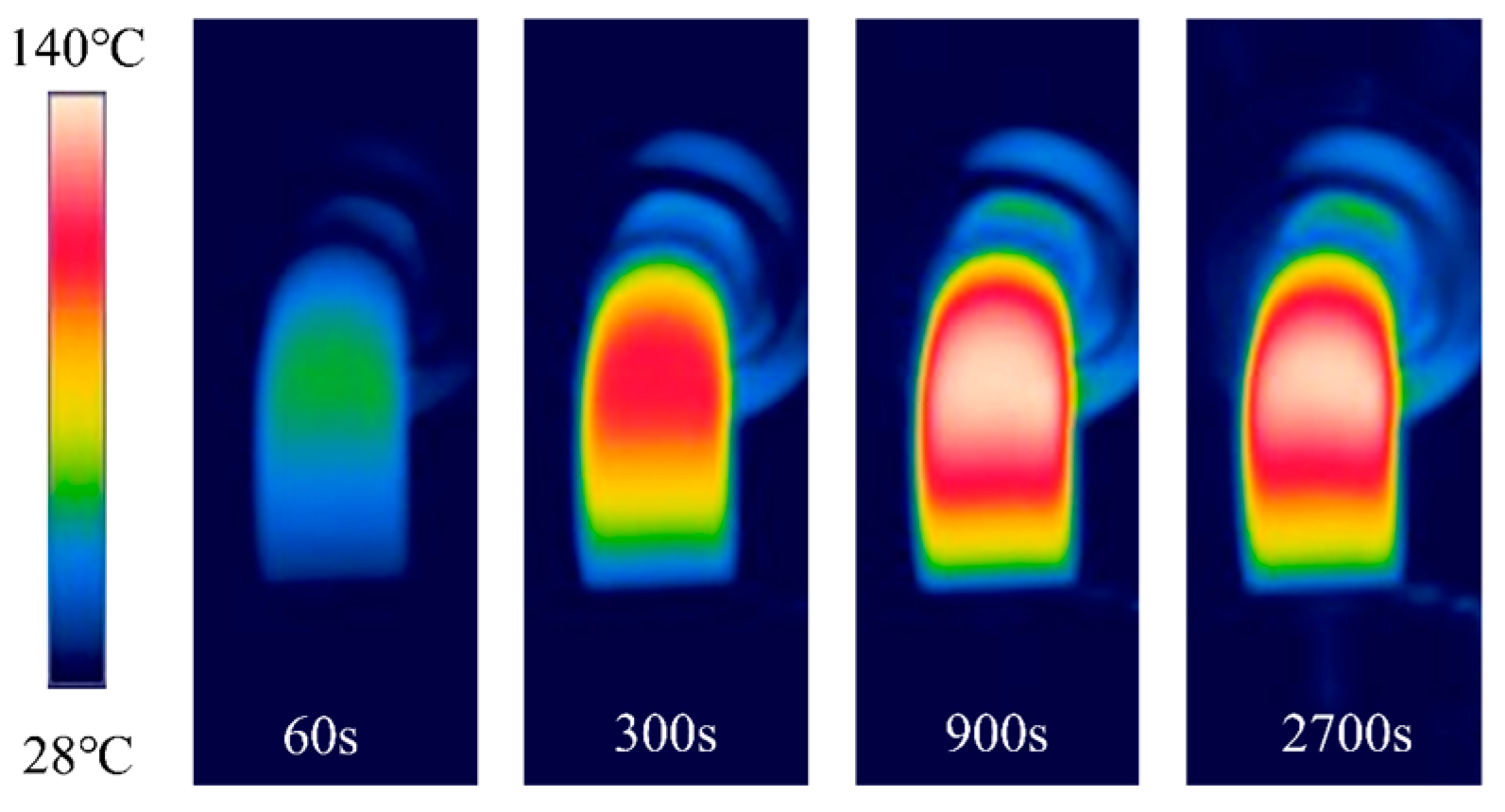
2.3. Heat Build-Up Test

A torsional fatigue testing apparatus (Coesfeld, Germany) is employed to investigate the heat generation behavior of rubber materials under cyclic deformation, as shown in Figure 3. This system enables precise control of bending angles (0–45°) and rotational speeds (0–1700 rpm), facilitating systematic analysis of thermomechanical coupling in rubber specimens. All tests are performed at an ambient temperature of 28 °C and an average humidity of 55%. The experimental procedure comprises three stages: (1) Specimen Installation: Cylindrical rubber specimens are securely clamped at both ends using customized mechanical fixtures, ensuring a uniform effective gripping length of 20 mm. To monitor internal temperature variations, a flexible temperature sensor with high sensitivity and flexibility is inserted into an axial hole within the specimen, with a sampling frequency of 1 Hz. A FLIR E4 WiFi infrared thermal camera, positioned perpendicularly to the specimen, records real-time surface temperature field distributions at a sampling frequency of 15 fps. According to the technical parameters provided by the thermal imaging company, at an ambient temperature of 10–35 °C, for test targets with temperatures above 0 °C, the temperature measurement accuracy of this type of thermal imager is ±2 °C. This configuration permits simultaneous acquisition of internal and external temperature data. (2) Angle Presetting: The displacement of the fixtures is accurately regulated via a programmable control system to impose a predefined bending angle on the specimen. This bending configuration induces tensile strain on one side and compressive strain on the opposite side of the specimen. (3) Cyclic Loading Initiation: The motors on both ends of the equipment rotate at preset speeds in the directions indicated in Figure 3, driving the fixture to cyclically twist the specimen. The superimposed rotational motion generates alternating tensile-compressive strains, replicating the complex dynamic stress conditions encountered by rubber materials in practical applications. Experimental data, including temperature profiles from thermocouples and infrared thermography, are collected throughout the tests. Each testing condition is repeated three times to ensure reproducibility. This methodology enables comprehensive characterization of hysteretic heat generation in rubber materials under controlled complex loading conditions.

3. Results and Discussion

3.1. Process of Temperature Rise

The general temperature variation pattern of a rubber cylinder was obtained using a torsional fatigue testing apparatus. Figure 4 shows the temperature rise characteristics under 45° bending and 1500 rpm rotational speed, where the red curve represents the temperature at the internal central point and the black curve denotes the temperature at the external midpoint. The figure reveals two distinct stages in temperature evolution: During the initial stage, the external surface temperature significantly exceeds the internal temperature, with a steeper temperature rise slope observed externally. Both internal and external temperature rise rates progressively decrease over time, as evidenced by diminishing curve slopes. In the second stage, as rotation continues, the external temperature rise rate decreases more rapidly, leading to thermal equivalence between internal and external surface temperatures at a specific timepoint. Subsequently, the internal temperature continues to rise and surpasses the external surface temperature. With continued rotation, both internal and external temperatures gradually stabilize and enter a steady-state phase.

The observed two-stage phenomenon can be attributed to the following mechanisms: During the initial rotation phase, the maximum stress and strain occur on the outer surface of the rubber cylinder specimen, generating the greatest heat per unit time. This results in a sharp external temperature rise. Combined with Figure 5, the stress–strain curves of rubber material under varying temperatures demonstrate a typical S-shaped pattern within 250% strain. Below 150% strain, temperature shows minimal influence on stress–strain behavior. However, within the 150–200% strain range, specimens tested above 70 °C exhibit significant softening. This indicates that temperature elevation alters the material’s mechanical properties, reducing stress levels and consequently decreasing heat generation, which contributes to the declining temperature rise rate. As rotation persists, partial heat dissipates through air convection while the remaining heat moves toward cooler internal regions. Due to rubber’s low thermal conductivity, heat accumulates internally. Continuous internal heat accumulation eventually causes the internal temperature to exceed external surface temperatures. After a certain period, thermal equilibrium is achieved between internal and external regions, leading to temperature stabilization.

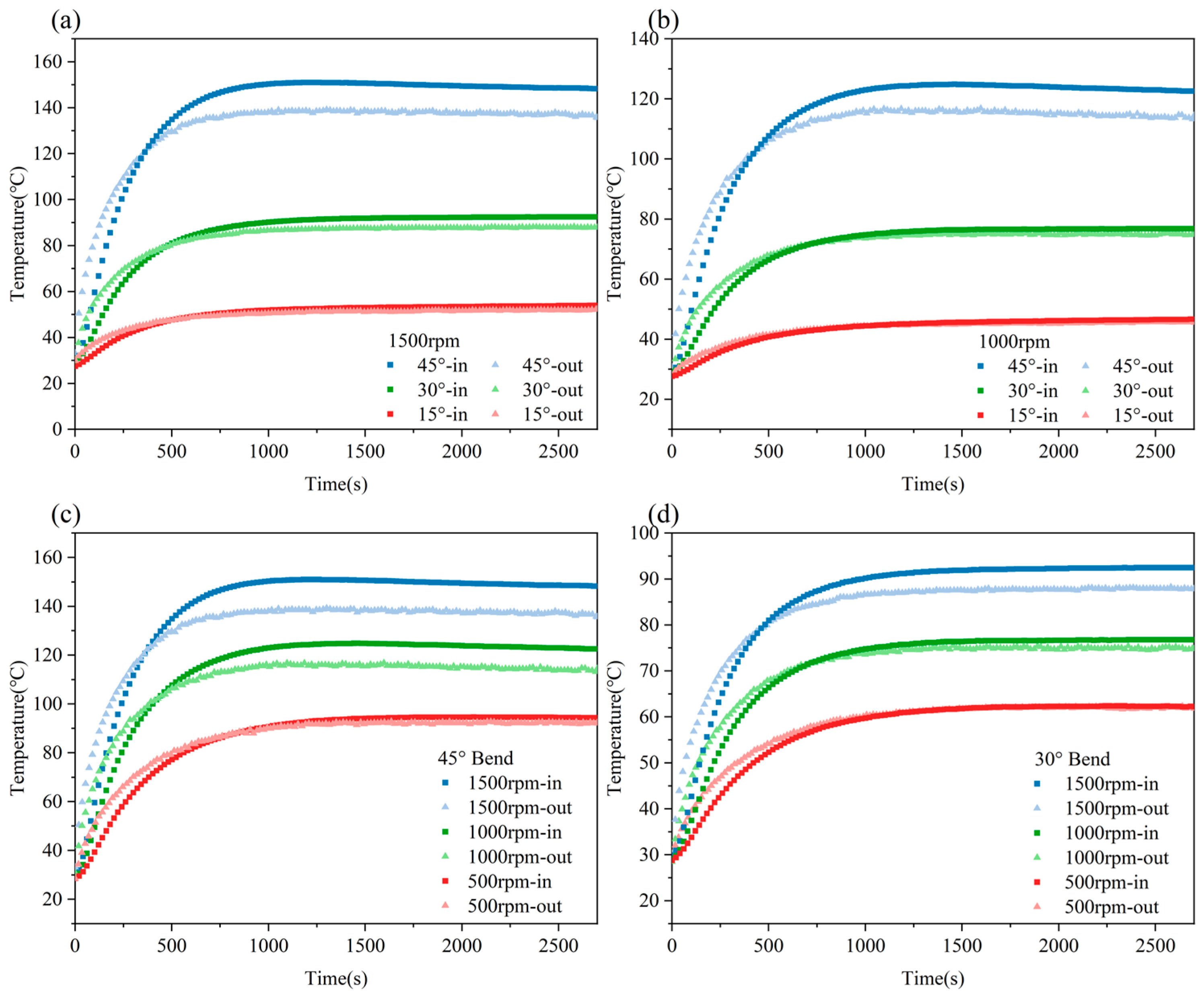
3.2. Effect of Different Operating Conditions on Temperature Rise

Experimental investigations are conducted at an ambient temperature (28 °C) with three bending angles (15°, 30°, and 45°) and rotational speeds (500, 1000, and 1500 rpm) to systematically analyze heat generation in tread rubber under tension-compression loading. Three repeated tests are performed for each operational condition. Internal temperature variations are continuously recorded via embedded thermocouples, while surface temperature profiles are simultaneously monitored using an infrared thermal imager.

Figure 6 illustrates the evolution of external surface temperature fields under 45° bending deformation at a rotational speed of 1500 rpm. The temperature contour maps reveal that during the initial phase, the maximum temperature occurs in the central region of the rubber cylinder, which corresponds to the area of maximum strain under bending deformation. According to the hysteretic heating principle, this region demonstrates the highest heat generation rate. Conversely, the minimum temperatures are observed near both ends adjacent to the metal fixtures, where reduced strain levels result in diminished heat generation per unit time, coupled with enhanced heat dissipation through direct contact with metallic components. As rotation progresses, heat continuously transfers to surrounding regions, evidenced by temperature elevation in peripheral areas around the central zone. Notably, the highest temperature remains concentrated in the central region throughout the process. After 900 s, the temperature distribution exhibits minimal variation, indicating attainment of thermal equilibrium.

Figure 7a,b display the internal and external temperature evolution of rubber specimens under three bending angles at 1500 rpm and 1000 rpm over 2700 s. The two aforementioned distinct temperature rise stages were observed under all conditions. Increasing the bending angle appeared to accelerate the thermal equivalence time between internal and external temperatures while elevating the corresponding equilibrium temperature. At 1500 rpm, thermal equivalence times for 15°, 30°, and 45° bending angles were measured at 472.47 s, 455.47 s, and 361.15 s, with equilibrium temperatures of 42.26 °C, 79.21 °C, and 120.71 °C, respectively. During initial rotation, maximum stress and strain occurred on the specimen’s outer surface, generating the highest heat per unit time under larger bending angles. This explains why steeper initial temperature rise slopes and higher equilibrium temperatures at equivalence points are observed with increased bending angles. Moreover, both the temperatures during the stable phase and the internal–external temperature differences of the rubber cylinder significantly increase with larger bending angles. This phenomenon arises because greater bending angles induce amplified stress and strain in the rubber material, resulting in enhanced heat generation per unit time. Consequently, these cumulative thermal effects drive the observed elevation in equilibrium temperatures.

It is noteworthy that under 45° bending deformation at 1500 rpm, both internal and external temperatures gradually decline after 1250 s, following their peak values. This phenomenon is likely attributed to the relaxation effect induced in the tread rubber specimen under prolonged high-frequency tensile-compressive cyclic loading. Prolonged exposure to high-frequency cyclic loading triggers stress relaxation in the rubber material, leading to reduced tensile-compressive stresses and consequently diminished heat generation per unit time. These combined effects ultimately result in the observed gradual temperature reduction.

Figure 7c,d present the internal and external temperature evolution of rubber cylinders under three rotational speeds (500 rpm, 1000 rpm, and 1500 rpm) to investigate the effect of loading frequency on heat generation. The results demonstrate that both the initial temperature rise rates and equilibrium temperatures exhibit a progressive increase with rotational speed. The analysis of internal and external temperatures during the steady-state phase (2700 s) under each experimental condition is presented in Figure 8. The internal temperature of the rubber cylindrical specimen consistently remains higher than the external temperature throughout the stabilization period. Both increased bending angle and rotational speed enhance thermal accumulation during the steady-state phase, leading to elevated temperatures in both internal and external regions. Particularly under conditions of higher rotational speeds and larger bending angles, greater temperature differentials are observed between the specimen’s interior and exterior regions, with the internal temperature being significantly higher than the external temperature. For instance, under 30° bending, the temperature difference increases from 0.19 °C (62.45 °C internal vs. 62.26 °C external) at 500 rpm to 3.69 °C at 1500 rpm.

This behavior arises from two competing mechanisms: (1) Increased rotational speed amplifies heat generation per unit time, accelerating temperature elevation; and (2) Enhanced convective heat transfer at higher rotational speeds intensifies surface cooling, thereby enlarging the internal–external temperature gradient. Figure 9 illustrates the external surface temperature distributions at 2700 s for 45° and 30° bending under different rotational speeds. The maximum temperatures are consistently concentrated in the central region of the cylinder under all testing conditions, with minimum temperatures observed near the metal fixtures at both ends. The temperature distribution demonstrates symmetrical patterns along the longitudinal axis of the rubber cylinder.

4. Conclusions

This study targets the tensile-compression cyclic loading conditions faced by rubber tires in practical applications and investigates the hysteretic heating behavior of rubber materials under varying bending angles and rotational speeds using a torsional fatigue testing apparatus. Experimental results reveal that the temperature evolution of the rubber cylinder can be categorized into two distinct phases: an initial phase with external temperatures surpassing internal temperatures, followed by a steady-state phase characterized by internal temperature dominance. During the initial phase, the temperature rise rates of both internal and external regions augment progressively with increased bending angles and rotational speeds. The temperature at which internal and external temperatures equilibrate increases with higher rotational speeds and bending angles, while the time required to reach this equilibrium decreases correspondingly, where the thermal equivalent time for 15° and 45° bending angles at 1500 rpm is 472.47 s and 361.15 s, respectively, and the equilibrium temperatures are 42.26 °C and 120.71 °C. During the steady-state phase, as rotational speed and bending angle increase, both internal and external temperatures rise, with a significant increase in the temperature difference between the inner and outer parts. At a 30° bending angle, this temperature difference measures 0.19 °C at 500 rpm and rises to 3.69 °C at 1500 rpm. This experiment focuses on the hysteretic heating behavior and evolutionary patterns of tire rubber materials under dynamic loading, which holds significance for gaining a deeper understanding of temperature rise effects during tire operation.