Abstract
Flexural testing provides a rapid and straightforward assessment of fiber-reinforced composites’ performance. In many high-strength composites, flexural strength is higher than compressive strength. A finite-element model was developed to better understand this improvement in load-bearing capability and to predict the flexural strength of three different carbon-fiber-reinforced polymer composite systems. The model is validated against publicly available experimental data and verified using theory. Different failure criteria are evaluated with respect to their ability to predict the strength of composites under flexural loading. The Tsai–Wu criterion best explains the experimental data. An expansion in compressive stress limit for all three systems was observed and is explained by the compression from the loading roller and Poisson’s effects.
1. Introduction
With the desire for high strength-to-weight ratio materials in aerospace, automotive, medical, and energy sectors, carbon-fiber-reinforced polymer composites (CFRP) have been attracting growing attention as a lightweight and strong material. Extensive composite material characterization ensures safety compliance and provides critical design data in the listed industries. Modeling the elastic behavior of orthotropic materials with transverse isotropy usually requires the characterization of five independent elastic constants, namely, and (or v23), which represent Young’s modulus in the fiber direction, Young’s modulus perpendicular to the fiber direction, the in-plane shear modulus, the in-plane Poisson’s ratio, the out-of-plane shear modulus, and the out-of-plane Poisson’s ratio, respectively [1]. However, there are few significant mathematical relations for material strength resulting in numerous resource-intensive destructive tests, often providing single failure mode results. Accordingly, it is advantageous to study composite behavior under combined loading, and their dominating failure modes.
A relatively inexpensive and straightforward test for composites is the ASTM D7264, utilized for obtaining flexural properties of polymer-reinforced composites. Though seldom used for design, flexural tests are often used for quality control in composites. Flexural testing requires a simple rectangular sample and uses a three-point bending setup to measure the flexural response of specimens. The dominating flexural failure modes are compression at the top ply (either fiber microbuckling or ply-level buckling) and tension at the bottom-most ply [2]. The flexural strength of different CFRP systems often surpasses their compressive strength (). Flexural strength lies between the fiber direction compressive and tensile strengths in the CFRP systems investigated here [3,4,5].
Through finite-element analysis (FEA), this study investigates stress interactions occurring in unidirectional, 20 ply CFRP samples loaded through a three-point flexural test, and predicts the flexural strength of each system with reasonable accuracy. Three CFRP systems of interest are investigated where their flexural strengths vary from their compressive strength, an average of the tensile and comprehensive strengths, to their tensile strength. Different failure criteria were evaluated with respect to their ability to predict the flexural strength of the three CFRP systems.
2. Materials and Methods
2.1. ASTM D7264
The evaluated test in this study is Procedure A (3-point bending) of ASTM D7264—Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials [2]. A diagram of the test is shown below in Figure 1. ASTM-recommended dimensions were utilized as shown in Table 1 below.

Figure 1.
Three-point bending test diagram.

Table 1.
ASTM D7264 parameters used in finite-element model.
The width and the loading/support rollers are not pictured. The resulting span-to-thickness ratio was 32:1, limiting out-of-plane shear deformations such as those experienced by short-beam test ASTM D2344. In the 3-point configuration, the expected failure was directly under the loading nose, as buckling (compression) or through the laminate cracking, originating due to tensile cracking at the bottom-most ply [2].
The chosen stacking sequence was to maintain the neutral (bending) axis at the center of the laminate and allow for the application of homogeneous beam theory to estimate flexural strength. Twenty plies were chosen to maintain an averaged ply thickness of 0.2 mm across systems, maintaining 4 mm overall thickness.
2.2. CFRP Systems
Three CFRPs were chosen on the basis of their flexural strength characteristics. Though thermoset composites still dominate the aerospace industry, there has been a recent push to incorporate thermoplastics in the industry [6]. Thermoplastic composites offer superior operational temperatures, weldability, and recyclability in comparison with thermoset composites [6,7]. Toray T700/TC1225 LM-PAEK exhibits flexural strength close to its compressive strength in the fiber direction [3]. Solvay APC-2 PEEK exhibits flexural strength near its tensile strength in the fiber direction [4]. Hexcel’s AS4—8552 epoxy exhibits flexural strength approximately halfway between its tensile and compressive strengths [5]. PEEK and LM-PAEK are thermoplastic-based systems, and 8552 is a thermosetting matrix. Toray and Hexcel material properties were obtained from the Wichita State NIAR database [8]. Table 2 summarizes their strength and strain values. Comprehensive test data are publicly available for the above systems (room temperature and dry conditions) [3,4,5].

Table 2.
Strengths and strains of three selected CFRP systems.
All three systems are present in the aerospace industry to varying degrees, contributing to primary and secondary aircraft structures such as fuselage panels and aircraft pressure bulkheads [4,9,10].
2.3. Failure Criteria
Different failure criteria were chosen to interface with the FEA to study the failure mechanisms observed in the tests. These criteria can be divided into three categories: noninteractive (limit theories), partially interactive, and fully interactive theories. These theories, their respective equations or criterion, and their categories are listed in Table 3.

Table 3.
Failure criteria chosen for analysis in this work [1,11].
Limit theories have no explicit interaction between stresses or strains, i.e., failure is predicted when a principal stress or strain reaches its limit. These criteria are expected to have the largest error in predicting flexural strength. Partially interactive criteria consider stress interactions, but have different criteria of failure. For example, Hashin–Rotem have failure coefficients for fiber failure, matrix failure, and delamination. Whichever coefficient is the largest of the three is considered to be the failure mode. Lastly, fully interactive criteria allow for stress interactions in 3D loading. A single failure coefficient is calculated from coupling terms and stresses, and no specific failure mode is predicted [1,12].
These criteria are selected because of their widely available documentation and ease of implementation in ANSYS ACP. The criteria mentioned above are also included in ACP for failure analysis. The inverse reserve factor is often used in place of the Tsai–Wu/Tsai–Hill criterion coefficient, as its calculation is identical when using the respective failure theories [12].
2.4. Prediction of Flexural Strength
To compute nominal flexural strength on the basis of maximal normal stress on either the top or bottom of a specimen, the following equation from the ASTM D7264 standard is employed:
where P is the load, L is the span length, b is the beam width, and h is the beam height. This relationship is valid when failure occurs in a brittle manner, the laminate acts as a homogeneous beam, and with a maximal fiber strain of 2% [2]. Here, P is directly calculated using finite-element analysis (ANSYS), while the other parameters are as explained in Section 2.1. Analysis employed a nonlinear elastic model with large deformations resulting in a maximal strain of under 1.5%, as no progressive damage was considered. Equation (1) was utilized to predict the flexural strength for the FEA.
2.5. Finite-Element Model
2.5.1. Geometry
A quarter symmetry model of the specimen is considered. In this model, thickness remained the same, while width and length were divided in half. Similarly, rollers were cut in half about the width. The rollers were also modeled to consider the effects of contact stresses under the loading nose. The symmetry allows for reducing the computational cost in the quarter-model geometry (Figure 2).
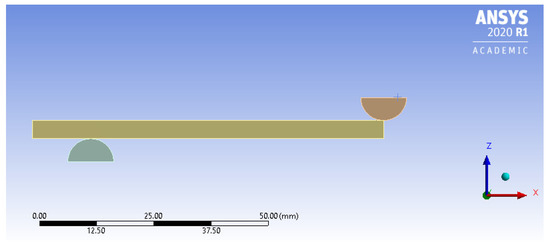
Figure 2.
Quarter symmetry model geometry.
2.5.2. Domain Discretization (Meshing)
The pre-ACP mesh consists of two separate meshes, the sample mesh and the roller mesh. The sample must be imported as a surface mesh because of ACP requirements. Two-dimensional (2D) Quad4 and Tri3 elements are utilized for the surface mesh, with finer mesh near the loading (0.5 mm element size) and coarser away from the loading (1 mm element size), resulting in a mesh of 748 elements and 846 nodes. With ACP preprocessing, the sizes are maintained, but elements become Hex8 and Wed6 elements. More elements and nodes are used to capture the stress interactions with reasonable accuracy near the loading nose where failure is expected. To improve contacts between the rollers and the sample, equal-size elements are applied to both (i.e., support roller has a 1 mm element size, and loading has a 0.5 mm size). Figure 3 shows the resultant mesh with the rollers having Hex8 solid elements.
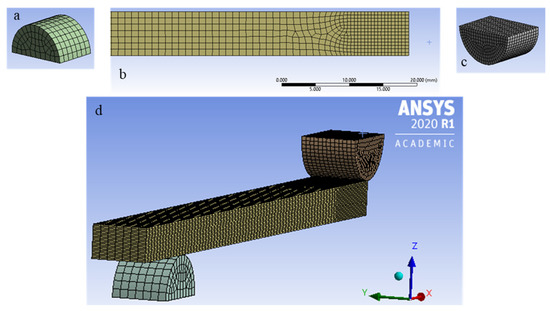
Figure 3.
FEA mesh of (a) support roller, (b) sample, and (c) loading roller; (d) complete mesh with sample and rollers.
Additional preprocessing was performed in ANSYS ACP. A solid mesh was generated utilizing the surface mesh for element sizing. There were 20 elements through the model’s thickness, one per ply, resulting in 14,960 elements and 17,766 nodes in the quarter symmetry model. The complete mesh is shown in Figure 3.
2.5.3. Boundary Conditions and Contact Settings
Contacts were formulated between the sample and roller supports. Additionally, the sample surface was split to limit the contact region accessible to the loading roller, improving computational efficiency, as shown in Figure 4. A frictionless contact was assigned at the support roller, while a no separation contact was assigned to the loading roller. Both utilized a friction coefficient of 0, but the frictionless support was considered to be nonlinear, as it allows for complete separation between the solids to occur. Some slipping can occur while the sample is loaded. However, there must be no separation between the roller and sample on the loading nose for a valid test. The assigned boundary conditions are as shown in Figure 4.
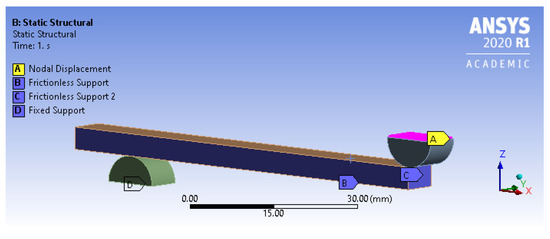
Figure 4.
Contact boundary conditions that were assigned in the model.
The symmetry condition imposes the need for frictionless supports at the “cut” surfaces. Frictionless support constraints motion normal to the plane while allowing for motion in the two other principal directions (e.g., at the surface located in the XZ plane, movement in the Y, and rotations about X and Z are constrained). A fixed support was applied at the bottom of the support roller constraining all degrees of freedom at the roller. Lastly, direct nodal displacement was applied at the top of the loading roller. Similar to the fixed support, all degrees of freedom for the roller were constrained with the addition of an imposed nodal displacement in the negative Z direction. The value for this displacement is dynamically changed, such that the sample is loaded just until failure.
With the above boundary conditions and contacts, the model was constrained in certain degrees of freedom, allowing for the proper capture of the physics involved in the 3-point flexural (bending) test.
2.5.4. Solver and Postprocessing
The mechanical APDL solver was used in this study. An iterative solver was chosen given the nonlinearity caused by the contact settings. Large deformations were not considered in the calculation of strains (e.g., infinite small strain tensor), and linear-elastic material property (Hooke’s Law) was employed. This was assumed because high-strength CFRP systems show brittle failure [13]. The model, due to the static structural formulation, only considered first-ply failure (FPF); progressive damage was not considered. It was expected that predicted strengths would be underestimated but still be within reasonable accuracy of reported experimental results. The failure was considered to be brittle due to low ultimate strains, corroborated by reported data [3,4,5].
Postprocessing was performed by both ANSYS Mechanical and ACP Post to estimate stresses across the thickness at the failure point and a point further away from loading. The latter point was used to obtain appropriate transverse shear stresses, as such stresses are irregular near loading, likely due to crushing effects [14].
2.6. Model Verification with Shear Stresses in Beam Bending
The model was verified by observing trends (e.g., compressive stress at the top ply, tensile stress at the bottom ply, as discussed in ASTM D7264) and employing analytical formulas in beam bending in the small strain regime. Beam theory predicts a shear profile as shown in Equation (2), for a point loaded beam with simple supports [15]:
where V, b, h, and y, are the shear force, beam width, beam height, and the distance from the neutral plane, respectively.
Using Bernoulli–Euler beam theory, the theoretical and numerical results were directly compared. Figure 5 shows good agreement between the FEA and the Bernoulli–Euler estimation. This agreement verifies the simulation. The slight difference can be attributed to the effect of shear deformations neglected in Bernoulli–Euler theory [16].
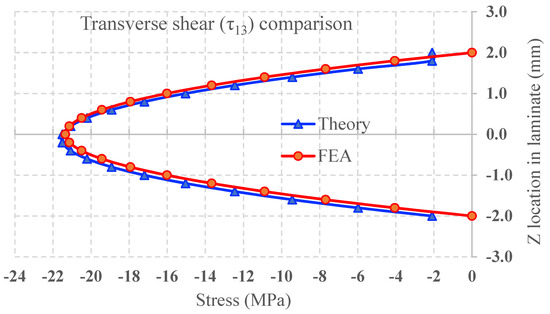
Figure 5.
Comparison of FEA-obtained shear to Bernoulli–Euler beam theory.
3. Results
Experimental and FEA strengths for three systems are summarized in Table 4. The FEA results were compared with experimental values obtained from datasheets for tensile, compressive, and flexural strengths. The Tsai–Wu failure criterion was utilized to determine stress at the onset of flexural failure. As mentioned earlier, all numerically obtained strengths were conservative due to nonprogressive damage analysis. The flexural specimen likely did not completely fail even if the Tsai–Wu index reached a value of 1 for a single finite element.

Table 4.
Summarized results for three chosen CFRP systems [3,4,5]. Values in red indicate nearest proximity from flexural strength to either tensile or compressive strength of the material in the fiber direction.
Tsai–Wu failure indices through the thickness the three systems are plotted in Figure 6. Failure occurs for a Tsai–Wu index above 1. An interesting finding was the failure of the Hexcel system in tension at the bottom ply, as opposed to the compressive failure experienced by the other two CFRPs.
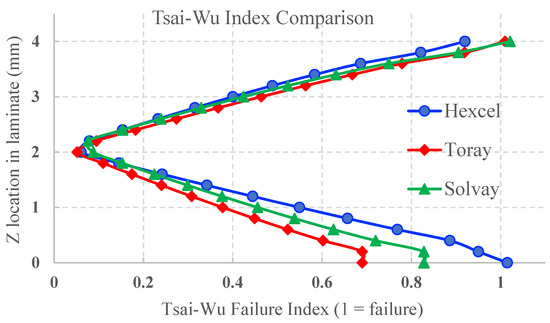
Figure 6.
Plotted Tsai–Wu indices across thickness for three systems.
Stresses across the thickness near the loading location are plotted and shown in Figure 7. Only stresses for the Toray system were plotted, as all analyzed systems showed similar trends. Shear stresses and were not plotted, as their values were near zero throughout the thickness, having negligible contribution to laminate failure.
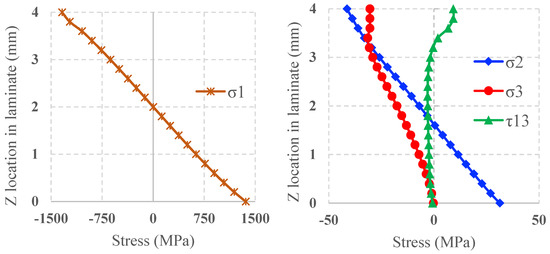
Figure 7.
Normal and shear stresses across flexural specimen thickness.
4. Discussion
A key trend in all three systems was that their flexural strength was between their tensile and compressive strengths. This implies that flexural failure occurs because of combined modes instead of a single failure mode. Table 5 summarizes the maximal FEA compressive stresses at the top ply under the loading nose, compared with the reported limits, i.e., compressive strengths.

Table 5.
FEA compressive stresses and compressive strengths for studied composite systems [3,4,5].
The Tsai–Wu criterion showed the closest results to experimental data. With compressive interactions occurring at the top ply between and due to Poisson’s effect, the effective stress limit was expanded [1]. Terms from the Tsai–Wu failure criterion are further explored in Table 6 for each analyzed system. Terms in bold font are those contributing to the enhanced load-bearing capacity of the samples.

Table 6.
Tsai–Wu index components for three analyzed systems. Bold terms contribute to the enhanced load-bearing capacity of the systems.
The Hexcel system, which fails in a tensile combined mode, had the highest reported compressive strength across the considered composite systems. Daniel and Ishai showed that, for similar stress interactions in combined loading, compressive load-bearing capabilities are much better than the tensile capabilities for a similar AS4 system, which could explain the tensile failure obtained by the FEA with the Hexcel AS4 system [1].
Lastly, the flexural finite-element model underpredicted flexural strength across all systems. This could be due to static structural analysis and no progressive damage being considered. The model effectively predicts a first ply failure (FPF), while an ultimate ply failure (UPF) prediction would likely return more accurate results. Nonetheless, the FPF returned values with reasonable accuracy at a lower computational cost to a UPF model.
Error in the prediction of failure consistently increases as flexural strength approaches its tensile strength. This could stem from an increased need for a UPF model, as brittleness could be less pronounced from a tensile failure due to crack propagation. As the system progresses through cracking, large rotations may occur, which in turn can induce significant membrane resultant forces. Equation (1) may not be a valued estimation in such a case, and a more complex theory of beams would be needed (e.g., geometrically exact beam theory) [17]. Lastly, both Hexcel and Solvay systems did not have centralized test data containing all strengths necessary for utilizing the Tsai–Wu criterion and reported flexural strength. Though the resin contents were nearly identical, a possible source of error stems from using mixed test data.
Though the Tsai–Wu failure criterion was chosen due to its fully interactive nature, other failure criteria were also explored. Numerical trends were similar for all systems, and thus only the data for the Toray system are summarized in Table 7. The Tsai–Wu index is provided, and safety factors for other criteria and their respective predicted flexural strength are included.

Table 7.
Summary of results from different failure criteria—Toray system.
The Tsai–Wu failure criterion predicted the strength most accurately from all failure criteria. Hoffman also predicted good results since it is fully interactive, with minor differences from the Tsai–Wu criterion. Partially interactive criterion Hashin had among the lowest predicted accuracy values, likely because of its lack of interaction between the fiber and transverse direction stresses. Noninteractive criteria (max stress, max strain) also underpredicted the flexural strength. Max strain exhibited marginally better performance, as its formulation allows for some Poisson effects in combined loading.
Tsai–Wu and Hoffman predicted failure at the bottom for the Hexcel system, while the other systems predicted a compressive failure occurring in the top ply. This likely stemmed from the lack of interaction and combined loading strength expansion.
5. Conclusions
Different failure criteria were evaluated for their ability to accurately predict failure stemming from combined stresses in a flexural test finite-element model. The model reasonably predicted flexural strength values for three different CFRP systems with different characteristics: one with flexural strength close to its tensile strength, another one with flexural strength close to its compressive strength, and the last one with flexural strength between its tensile and compressive strengths. There was an apparent discrepancy in the maximal compressive stress experienced by the three systems and their respective compressive strengths. This difference is explained by Poisson’s effect, causing stress in the in-plane transverse direction. The Tsai–Wu criterion requires many coupling terms. Therefore, comprehensive test data are necessary to interface with the model, including out-of-plane strengths. Such tests can be challenging and costly to perform. Some strength estimations are available, though they introduce additional errors [1] (pp. 116,120–122). The FEM consistently underpredicted strength due to modeling the first ply failure instead of the ultimate ply failure. As progressive damage is not considered, strengths are underestimated for systems that have extensive crack propagation before failure.
Author Contributions
Conceptualization, M.T.; methodology, M.T., S.A.; formal analysis, T.d.S.B.; writing—original draft preparation, T.d.S.B.; writing—review and editing, S.A., M.T.; funding acquisition, M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Air Force Office of Scientific Research (AFOSR) under award no. FA9550-21-1-0066.
Data Availability Statement
Data will be available upon request.
Acknowledgments
The authors are grateful for the support by the Air Force Office of Scientific Research (AFOSR), under award no. FA9550-21-1-0066.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials, 2nd ed; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- ASTM D7264/D7264M-07; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2015.
- Lian, E.; Lovingfoss, R.; Tanoto, V. Medium Toughness PAEK thermoplastics Toray TC1225 (LM PAEK) T700GC 12K T1E Unidirectional Tape Qualification Material Property Data Report. Natl. Inst. Aviat. Res. 2021. Available online: https://www.wichita.edu/industry_and_defense/NIAR/Documents/TorayTC1225UnitapeCAM-RP-2019-036RevA5.10.2021MPDRFinal.pdf (accessed on 15 September 2021).
- N.A. Solvay. APC-2 PEEK Datasheet. 2017. Available online: https://www.solvay.com/en/product/apc-2peeks2 (accessed on 10 February 2021).
- Marlett, K.; Ng, Y.; Tomblin, J.; By, A.; Hooper, E. Hexcel 8552 AS4 Unidirectional Material Property Data Report. Natl. Inst. Aviat. Res. 2011. Available online: https://www.wichita.edu/industry_and_defense/NIAR/Research/hexcel-8552/AS4-Unitape-2.pdf (accessed on 10 February 2021).
- Favaloro, M. Thermoplastic Composites in Aerospace—The Future Looks Bright | CompositesWorld. Available online: https://www.compositesworld.com/articles/thermoplastic-composites-in-aerospace-past-present-and-future (accessed on 29 April 2021).
- Offringa, A.R. Thermoplastic composites—Rapid processing applications. Compos. Part A Appl. Sci. Manuf. 1996, 27 Pt A, 329–336. [Google Scholar] [CrossRef]
- National Institute for Aviation Research. Available online: https://www.wichita.edu/research/NIAR/ (accessed on 1 May 2021).
- Gardiner, G. Integrating Antennas into Composite Aerostructures. 2021. Available online: https://www.compositesworld.com/articles/integrating-antennas-into-composite-aerostructures (accessed on 1 May 2021).
- Francis, S. Thermoplastic Composites: Poised to Step Forward. 2019. Available online: https://www.compositesworld.com/articles/thermoplastic-composites-poised-to-step-forward (accessed on 1 May 2021).
- Schellekens, J.C.J.; de Borst, R. The use of the Hoffman yield criterion in finite element analysis of anisotropic composites. Comput. Struct. 1990, 37, 1087–1096. [Google Scholar] [CrossRef]
- N.A. ANSYS Inc. Failure Criteria for Reinforced Materials—ACP Documentation. 2021. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v221/en/acp_ug/acp_failure_analysis.html (accessed on 15 September 2021).
- Sung, M.; Jang, J.; Tran, V.L.; Hong, S.T.; Yu, W.R. Increased breaking strain of carbon fiber-reinforced plastic and steel hybrid laminate composites. Compos. Struct. 2020, 235, 111768. [Google Scholar] [CrossRef]
- Fam, A.; Sharaf, T. Flexural performance of sandwich panels comprising polyurethane core and GFRP skins and ribs of various configurations. Compos. Struct. 2010, 92, 2927–2935. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 11th ed.; McGraw-Hill Education: New York, NY, USA, 2020; p. 119. [Google Scholar]
- Sancaktar, E. Mechanics of solids and structures. ASME Int. Mech. Eng. Congr. Expo. Proc. 2019, 10 Pt A, 53–90. [Google Scholar]
- Pai, P.F. Geometrically exact beam theory without Euler angles. Int. J. Solids Struct. 2011, 48, 3075–3090. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).