FEM-Validated Optimal Design of Laminate Process Parameters Based on Improved Genetic Algorithm
Abstract
:1. Introduction
2. Mathematical Model of Laminate and the IGA
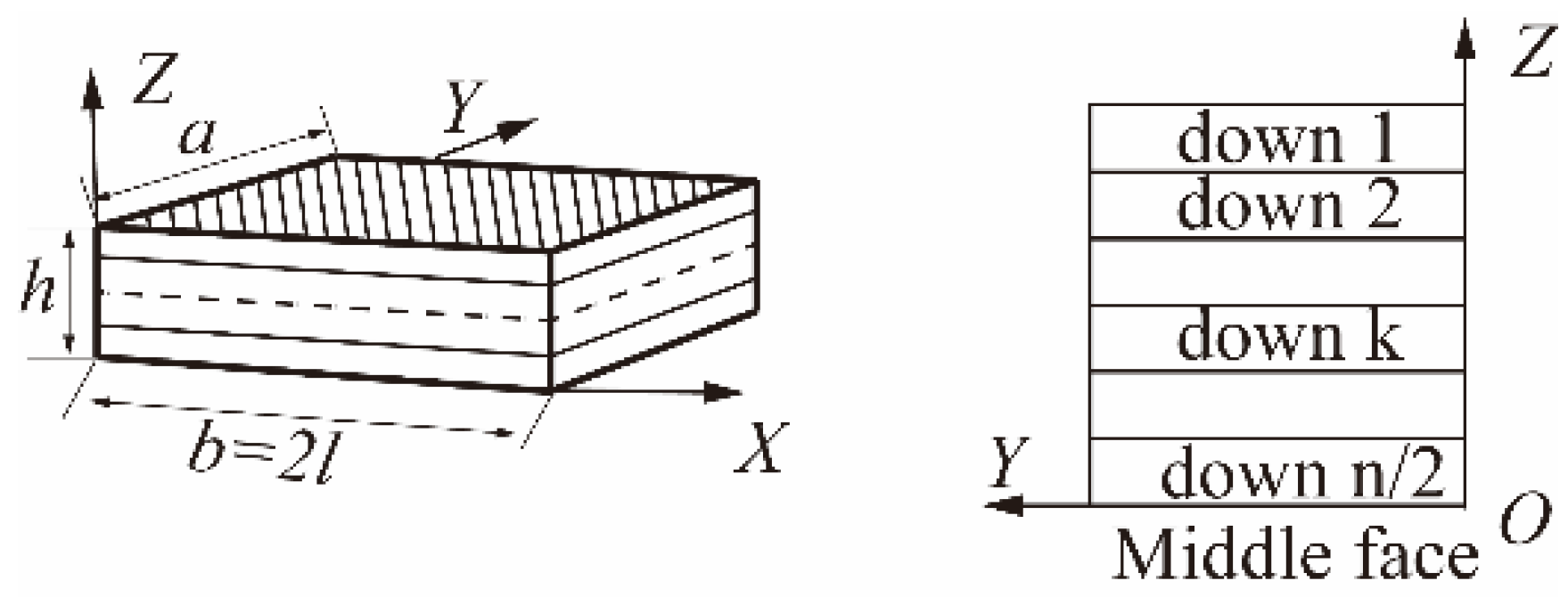
2.1. On- and off-Axis Stress Conversion of Laminates
- The layers of the laminate need to be firmly bonded so that the deformation between the layers is consistent, and relative slippage between the layers can be avoided;
- Laminates are thin plates with an invariable thickness, and their strength in the thickness direction is relatively small to negligible in respect to that in other directions;
- The bending deformation of the laminate needs to be in a small deflection range, and the straight line perpendicular to the midplane must be maintained before and after the bending deformation while the length of the straight line remains unchanged (viz. );
- It is considered that each monolayer of the laminate is in a plane stress state, that is, the theory of plane stress is suitable for the analysis of the laminate structure of thin planes, curved surfaces, or shells.
2.2. Failure Criterion for Laminates
- The absolute value of Equation (12) is relatively not very large, and it is a negative value, which is reasonable;
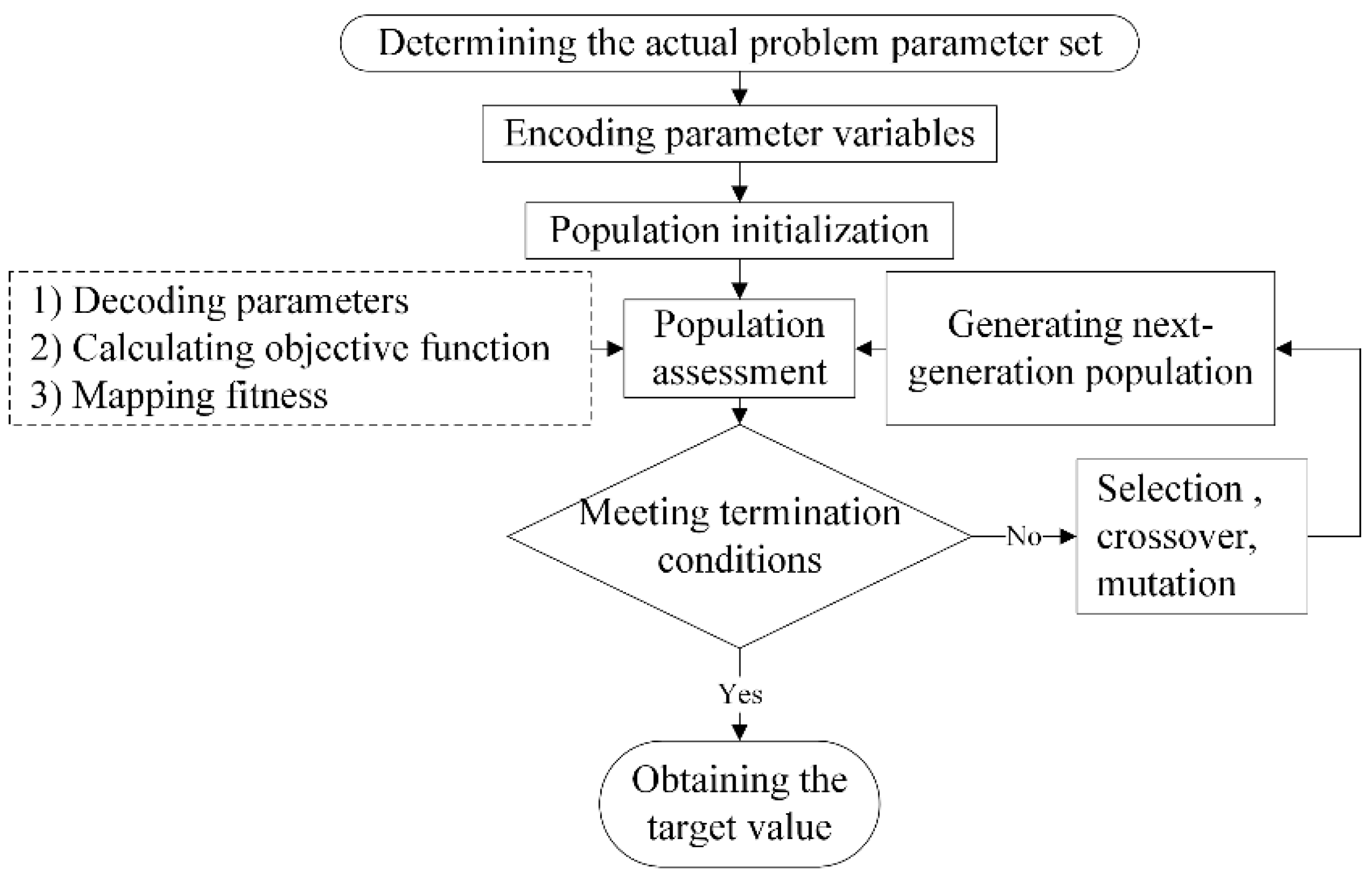
2.3. Genetic Algorithm and Its Improvement
3. IGA Applied to Composite Laminate Design
3.1. Ply Design Requirements for Laminates
- Standard laid layers should be adopted, which is supposed to include four angle values of 0°, ±45°, and 90°, respectively;
- Adjacent 4 monolayers cannot be formed at the same laying angle so as to prevent the substrate from cracking, and simultaneously a full 90° ply should be avoided;
- The proportion of 0° laid layers is between 20% and 40%, ±45° layers between 40% and 60%, and 90° layers must be between 10% and 30%.
3.2. Genetic Algorithm Coding
3.3. Fitness Function
3.4. Relevant Parameters Selection
4. A Case Study
4.1. Relevant Parameters Selection
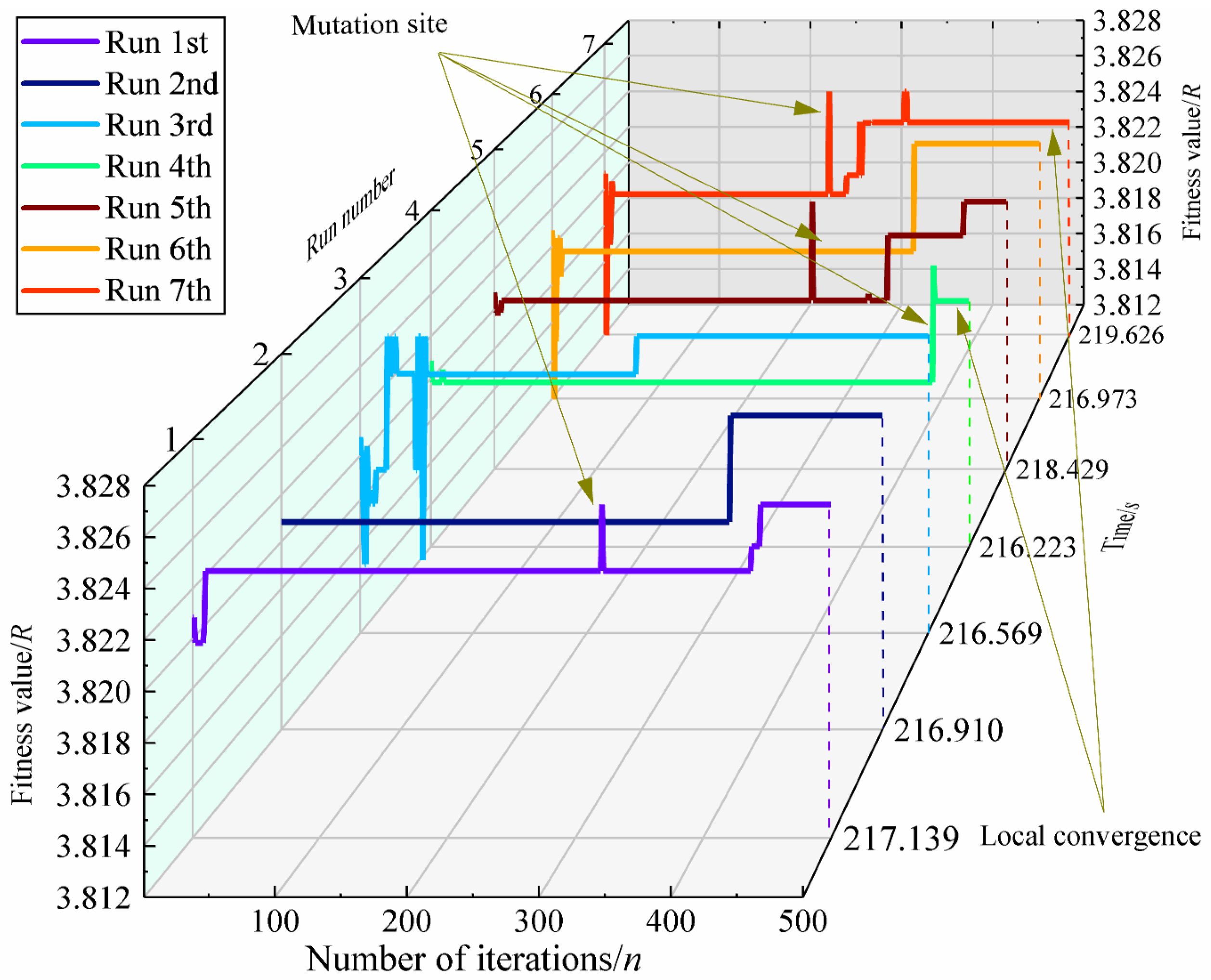
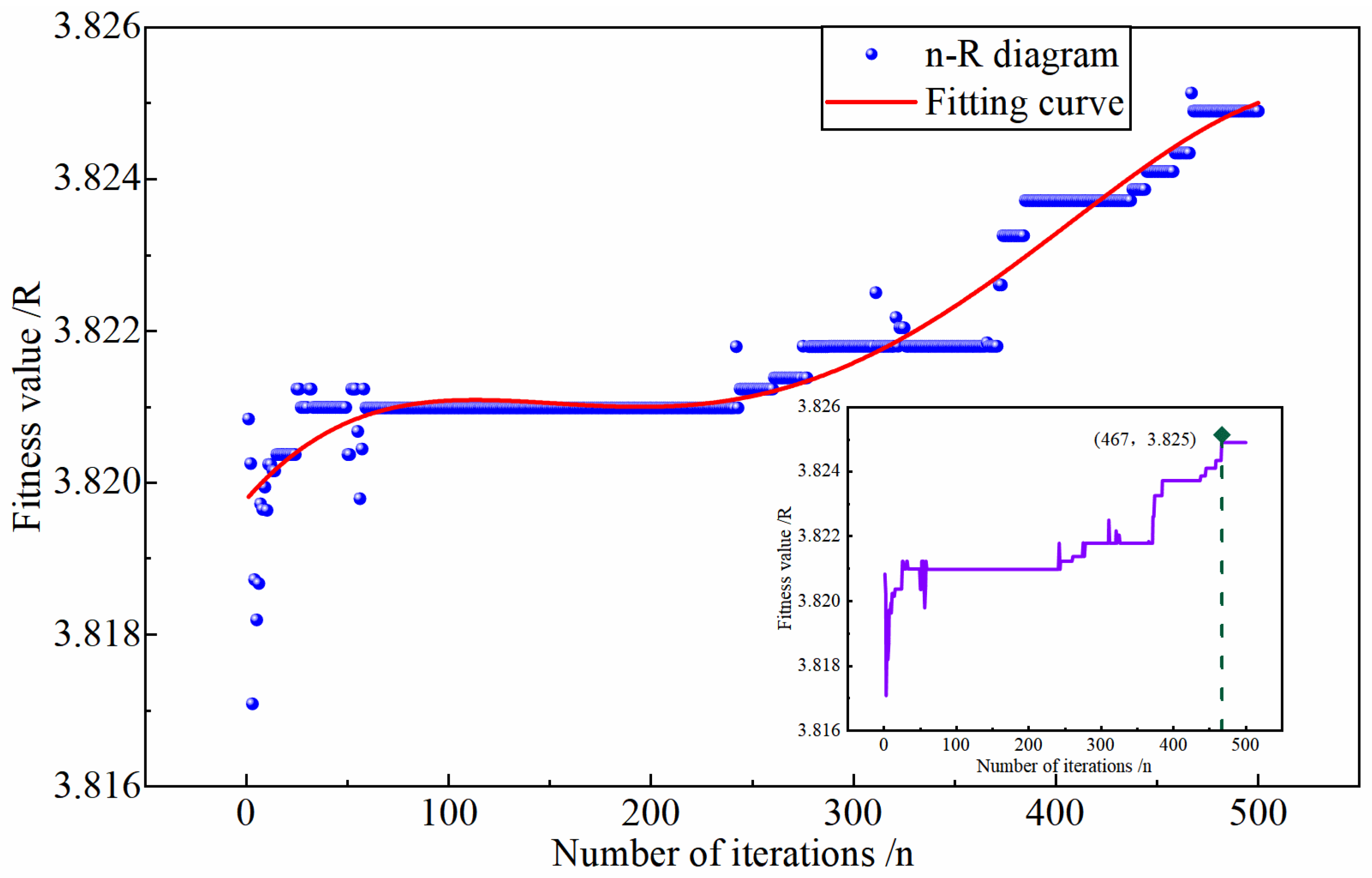
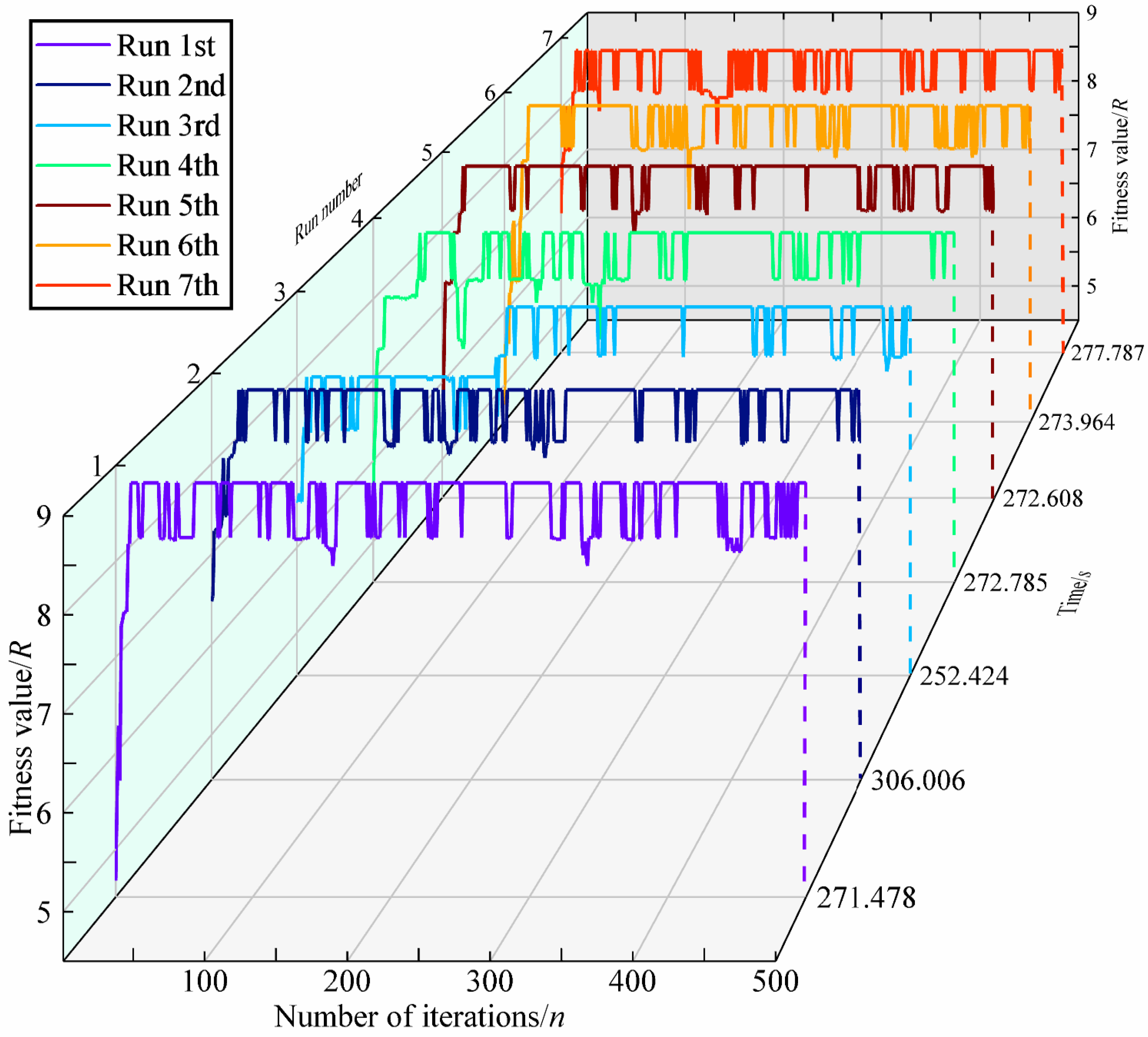
4.2. Results Discussion
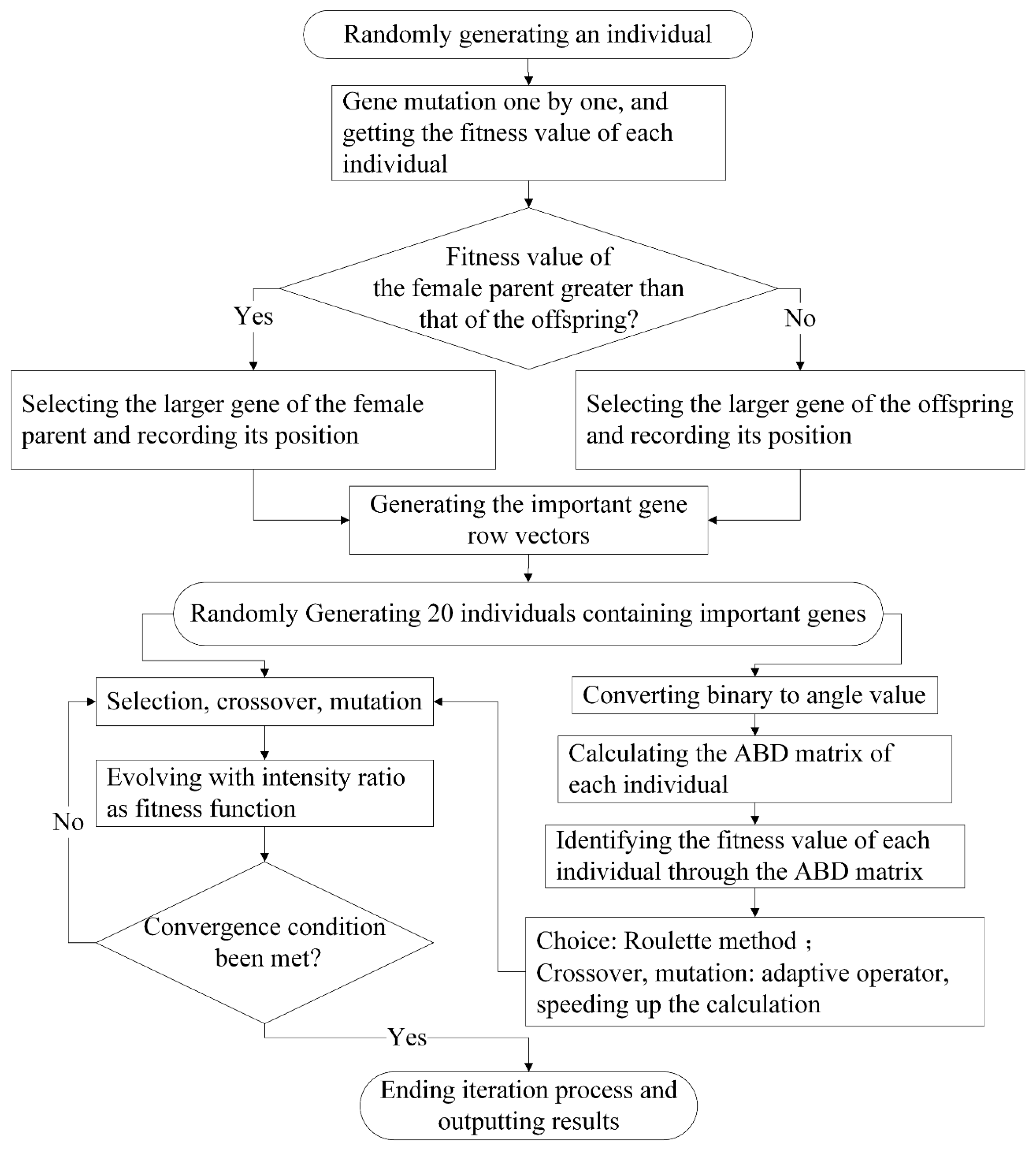
- Due to the existence of “gene mutation”, the IGA algorithm identifies the optimal strength ratio, but due to the existence of local convergence, it is necessary to rely on “gene mutation” to find the optimal strength ratio. Hence, “gene mutation” cannot be removed in actual operation. At the same time, in order to avoid contingency, it is necessary to run multiple times to ensure the unity of the results, thereby preventing local convergence produced by a single run. The GA algorithm has an “unreasonable” maximum strength ratio in the 149th generation, and this reversely indicates the occurrence of the “premature” phenomenon.
- The average running time of the IGA algorithm is 217.41 s, while the traditional genetic algorithm is 275.293 s. It is obvious that the IGA algorithm has a certain improvement in its iterative operation efficiency, with an increase of 21.03%.
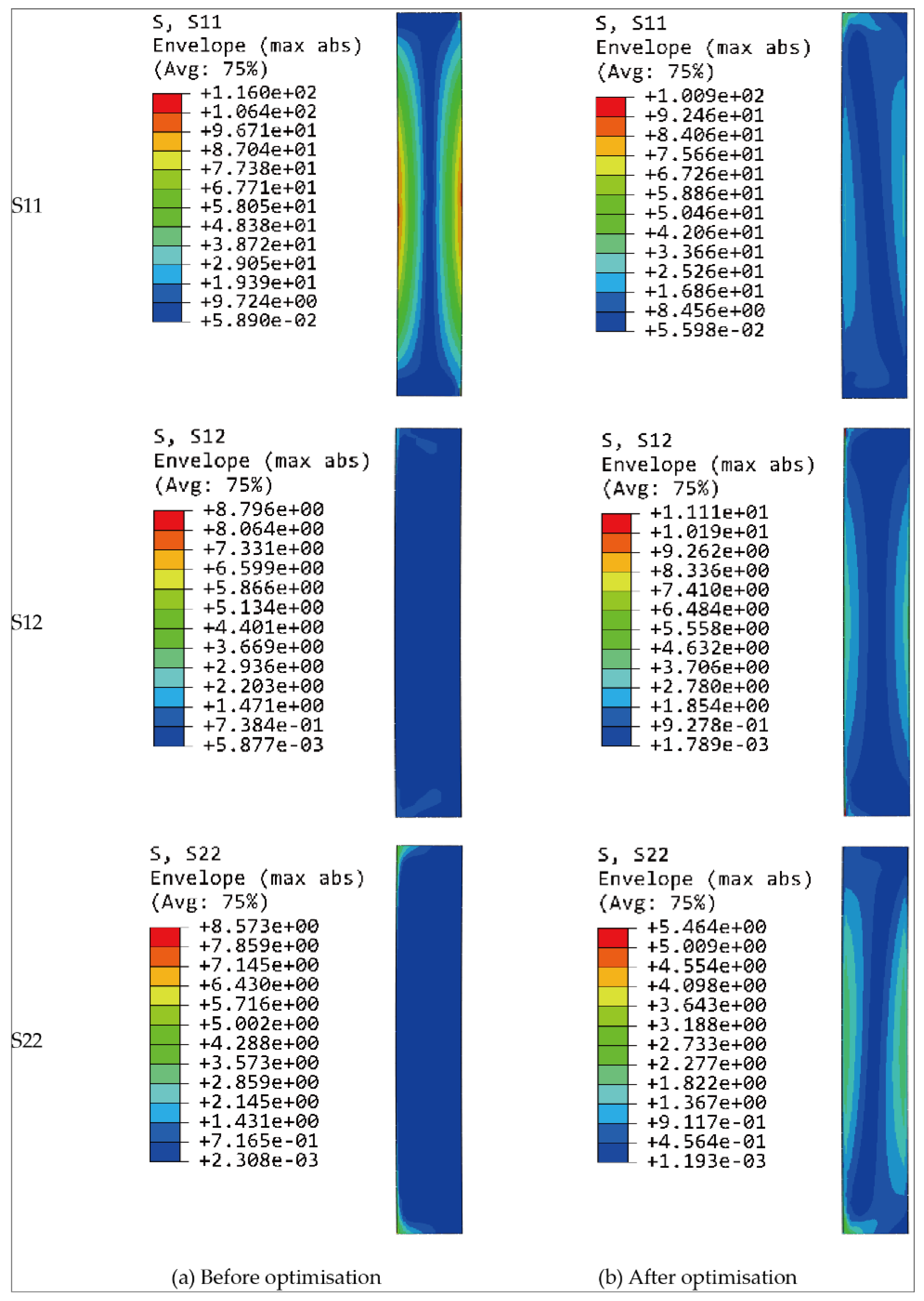
5. FEM Validation
6. Conclusions
- Based on the genetic algorithm, this paper optimised the layering angle of laminate, and adopted the identification of important genes to determine the important genes and their positions and reduced the query range so that the calculation cost in terms of time was reduced by 21.03%.
- In the process of genetic evolution, the operation “gene mutations” is essential and indispensable, and it proves that the “gene mutation” has the potential to facilitate the identification of global optimal solutions.
- Through the development of MATLAB script, it found the important genes were the first and fifth genes. The optimisation results show that the improved strength ratio is 3.825, and the optimal laying angle is sequentially [−45°/+45°/−45°/ 45°/0°/90°/0°/0°/90°]s.
- The stresses before and after the optimisation were 116.0 MPa and 100.9 MPa, respectively, with a decrease of 13.02%. This comparison validates the IGA and the optimal results can provide a reference for engineering design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| off-axis modulus of row i and column j | |
| the fitted value | |
| the stress of kth layer along x direction | |
| the stress of kth layer along y direction | |
| the shear stress of kth layer in x–y plane | |
| in-plane flexibility matrix | |
| polynomial coefficients, i = 0……4 | |
| in-plane stiffness of row i and column j in matrix | |
| coupling flexibility matrix | |
| coupling stiffness of row i and column j in matrix | |
| bending flexibility matrix | |
| bending stiffness of row i and column j in matrix | |
| , | strength parameter, i, j = 1, 2, 6 respresnting x, y, and x–y direction, respectively |
| the average value of the initial data | |
| mean fitness values of individuals in each generation | |
| the i-th initial data | |
| maximum fitness in each generation of individuals | |
| minimum fitness value in each generation of individuals | |
| fitness function | |
| flexibility matrix | |
| flexibility coefficients | |
| flexibility coefficients | |
| flexibility coefficients | |
| flexibility coefficient of row i and column j in matrix | |
| individual space | |
| longitudinal compressive strength | |
| longitudinal tensile strength | |
| transverse compressive strength | |
| transverse tensile strength | |
| number of same layering angles for four consecutive layers | |
| number of layers that do not meet the ratio requirement | |
| the kth gene | |
| crossover probability | |
| mutation probability | |
| the shear strain of middle plane in x–y plane | |
| the shear strain of kth layer in x–y plane | |
| the strain of middle plane along x-direction | |
| the strain of kth layer along x-direction | |
| the strain of middle plane along y-direction | |
| the strain of kth layer along y-direction | |
| the stress of kth layer along fibre direction | |
| the stress of kth layer along the vertical fiber direction | |
| the shear stress of layer in-plane | |
| the shear stress of kth layer in-plane | |
| a | width of laminate |
| b | length of laminate |
| E1 | longitudinal modulus of elasticity |
| E2 | transverse modulus of elasticity |
| G12 | shear modulus of elasticity in the plane of the lamina |
| h | thickness of laminates |
| k | kth layers |
| Mx | the bending moment of x-direction |
| Mxy | the torque of x–y plane |
| My | the bending moment of y-direction |
| n | total number of layers |
| Nx | the force of x-direction |
| Nxy | the shear force of x–y plane |
| Ny | the force of y-direction |
| Q | shear stress |
| q | uniform loading pressure |
| R | the ratio of a certain component of the ultimate stress to the corresponding component of loading stress. |
| S | the shear strength in x–y plane |
| T | the indicator to evaluate the degree of fitting |
| x | the fiber direction |
| y | the vertical fiber direction |
| Zk | the z coordinate of kth layer |
| Zk−1 | the z coordinate of k − 1th layer |
| μ1 | poisson’s ratio in the x-direction |
| ρ | density |
| φ | stress function |
| genetic operator evaluates parameters | |
| half-length of laminate | |
| an infinitesimal value |
Appendix A
- Balance equation (ignoring body stress)
- Geometric compatibility equations
- Physical equations
- Substituting (A3) into (A6) and then into (A4), it can obtain the equation below,
- 1.
- When the upper and lower boundaries y = ±h/2, (this holds for any x), through the above equation, the relational expressions of can be derived.
- 2.
- With the boundary of , the shear force ,
- 3.
- Since the at the x-axis direction is zero; the moment is also zero. Hence, it gives
References
- Riccio, A.; Palumbo, C.; Acanfora, V.; Sellitto, A.; Russo, A. Influence of Failure Criteria and Intralaminar Damage Progression Numerical Models on the Prediction of the Mechanical Behavior of Composite Laminates. J. Compos. Sci. 2021, 5, 310. [Google Scholar] [CrossRef]
- Hu, R.-X.; Zhou, J.Y. Optimal Design of Automobile Battery Shell Made of Carbon Fiber Reinforced Composites. Mach. Des. Manuf. 2017, 12, 229–233. [Google Scholar]
- Wallentowitz, H. Innovation in Automotive Engineering:A look into the future. J. Automot. Saf. Energy 2013, 4, 95–108. [Google Scholar]
- Feng, Z.; Yi, G.; Li, P.; Li, H.; Yu, D. Review of parallel genetic algorithm. Comput. Appl. Softw. 2018, 35, 1–7+80. [Google Scholar]
- Wang, H.; Duan, Y.; Dilimulati, A.; Zhang, X. Design Optimization of CFRP Stacking Sequence Using a Multi-Island Genetic Algorithms under Low-velocity Impact Loads. J. Wuhan Univ. Technol. 2017, 32, 720–725. [Google Scholar] [CrossRef]
- Chen, Y.T.; Xiang, S.; Zhao, W.P. Fiber Orientation Angle Optimization for Minimum Stress of Laminated Composite Plates. Appl. Mech. Mater. 2015, 709, 135–138. [Google Scholar] [CrossRef]
- Xiu, Y.S.; Cui, D.G. Ply optimization design for stability of composite laminates. Eng. Mech. 2005, 6, 212–216. [Google Scholar]
- Feng, X.B.; Huang, H.; Wang, W.; Zhang, H.D. Strength optimization of laminate based on the genetic algorithm. Fiber Reinf. Plast. Compos. 2012, 3, 7–13. [Google Scholar]
- Jin, D.; Liu, Z.; Fan, Z. Ply optimization of composite laminate with ply drop based on genetic algorithm. Acta Mater. Compos. Sin. 2015, 32, 236–242. [Google Scholar]
- Park, J.H.; Hwang, J.H.; Lee, C.S.; Hwang, W. Stacking sequence design of composite laminates for maximum strength using genetic algorithms. Compos. Struct. 2001, 52, 217–231. [Google Scholar] [CrossRef]
- Wang, P.Y.; Chen, Z.; Geng, X.L.; Yue, Z.F. Stacking Sequence Optimization of Composite Laminates Based on a Modified Adaptive Genetic Algorithm. Sci. Technol. Eng. 2018, 18, 336–340. [Google Scholar]
- Yang, Y.; Dai, W.; Nian, C. Optimum design of composite laminates based on adaptive genetic algorithms. Mach. Build. Autom. 2020, 49, 22–25. [Google Scholar]
- Hwang, S.F.; Hsu, Y.C.; Chen, Y. A genetic algorithm for the optimization of fiber angles in composite laminates. J. Mech. Sci. Technol. 2014, 28, 3163–3169. [Google Scholar] [CrossRef]
- Krishan, K.C. Composite Materials; Science and Engineering: London, UK, 2012. [Google Scholar]
- Tsai, S.W.; Hahn, T.H. Introduction to Composite Materials. In Fibrous and Textile Materials for Composite Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Adelman, M. Evaluation of the Tensor Polynomial and Hoffman Strength Theories for Composite Materials. J. Compos. Mater. 1977, 11, 366–377. [Google Scholar]
- Wang, Z. Composite Material Mechanics and Composite Material Structure Mechanics; Machinery Industry Press: Xi’an, China, 1991. [Google Scholar]
- Wang, Y. Mechanics and Structural Design of Composite Materials; East China University of Science and Technology Press: Shanghai, China, 2012. [Google Scholar]
- Dassault. Isight 5.9 User’s Guide; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2014. [Google Scholar]
- Zhang, W. Mathematical Fundamentals of Genetic Algorithms; Xi’an Jiaotong University Press: Xi’an, China, 2000. [Google Scholar]
- Yi, X.; Du, S. Handbook for Composite Materials; Chemical Industry Press: Beijing, China, 2009. [Google Scholar]
- Lei, Y.; Zhang, S. MATLAB Genetic Algorithm Toolbox and Application; Xidian University Press: Xi’an, China, 2014. [Google Scholar]
- Lu, Z.; Zhang, E.Y.; Liu, B. Ply optimization of composite laminate based on improved adaptive genetic algorithm. Fiber Reinf. Plast. Compos. 2016, 2, 53–56. [Google Scholar]
- Chen, L.; Zhao, X. Mechanical analysis of simply supported beam based on classical laminated plate theory. Mech. Eng. 2019, 41, 152–156. [Google Scholar]
- Fan, Z. Prediction and Analysis of Mechanical Properties of Carbon Fibre Reinforced Composite Laminates; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]



| E1/Gpa | E2/Gpa | XT/MPa | XC/MPa | G12/Gpa | YT/MPa | YC/MPa | S/MPa | μ1 | ρ/(kg/m3) |
|---|---|---|---|---|---|---|---|---|---|
| 144 | 9.3 | 1633 | 1021 | 4.68 | 53.8 | 232 | 90 | 0.312 | 1610 |
| Population Size | Maximum Number of Iterations | ||
|---|---|---|---|
| 0.95 | 0.005 | 20 | 500 |
| Earliest Number of Iterations | Converging Globally? | Strength Ratio/R |
|---|---|---|
| 321 | Y | 3.825 |
| 374 | Y | |
| 52 | Y | |
| 467 | N | |
| 311 | Y | |
| 372 | Y | |
| 242 | N |
| Strength Ratio/R | Layup Scheme/° | |
|---|---|---|
| Before optimisation | 2.57 | [0/+45/90/−45/0/+45/−45/90/−45]S * |
| After optimisation | 3.825 | [−45/+45/−45/+45/0/90/0/0/90]S * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, X.; Shen, Z.; Liu, H.; Xv, H.; Xia, X.; Chen, S. FEM-Validated Optimal Design of Laminate Process Parameters Based on Improved Genetic Algorithm. J. Compos. Sci. 2022, 6, 21. https://doi.org/10.3390/jcs6010021
Mou X, Shen Z, Liu H, Xv H, Xia X, Chen S. FEM-Validated Optimal Design of Laminate Process Parameters Based on Improved Genetic Algorithm. Journal of Composites Science. 2022; 6(1):21. https://doi.org/10.3390/jcs6010021
Chicago/Turabian StyleMou, Xing, Zhiqiang Shen, Honghao Liu, Hui Xv, Xianzhao Xia, and Shijun Chen. 2022. "FEM-Validated Optimal Design of Laminate Process Parameters Based on Improved Genetic Algorithm" Journal of Composites Science 6, no. 1: 21. https://doi.org/10.3390/jcs6010021
APA StyleMou, X., Shen, Z., Liu, H., Xv, H., Xia, X., & Chen, S. (2022). FEM-Validated Optimal Design of Laminate Process Parameters Based on Improved Genetic Algorithm. Journal of Composites Science, 6(1), 21. https://doi.org/10.3390/jcs6010021






