Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials
Abstract
:1. Introduction
2. Materials and Methods
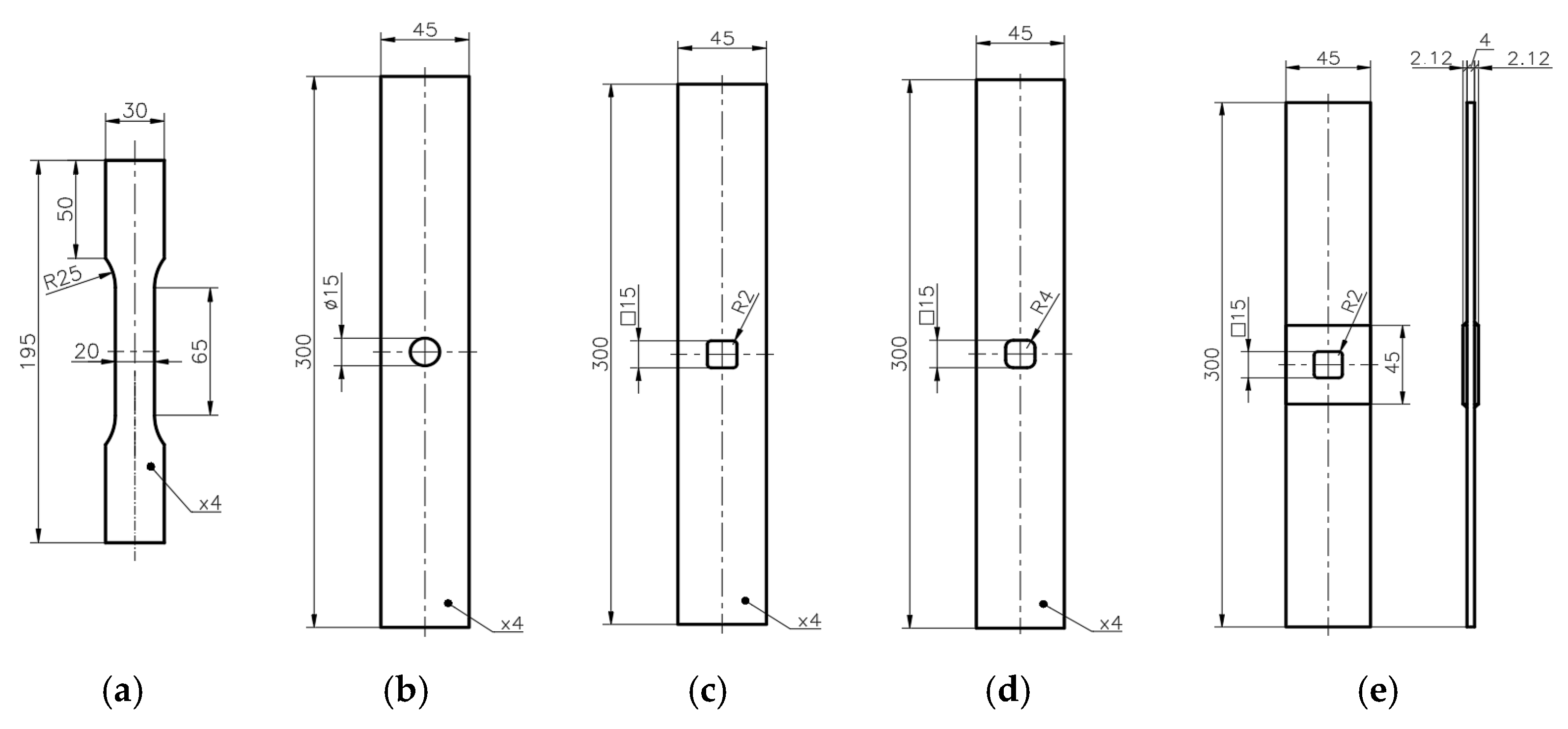
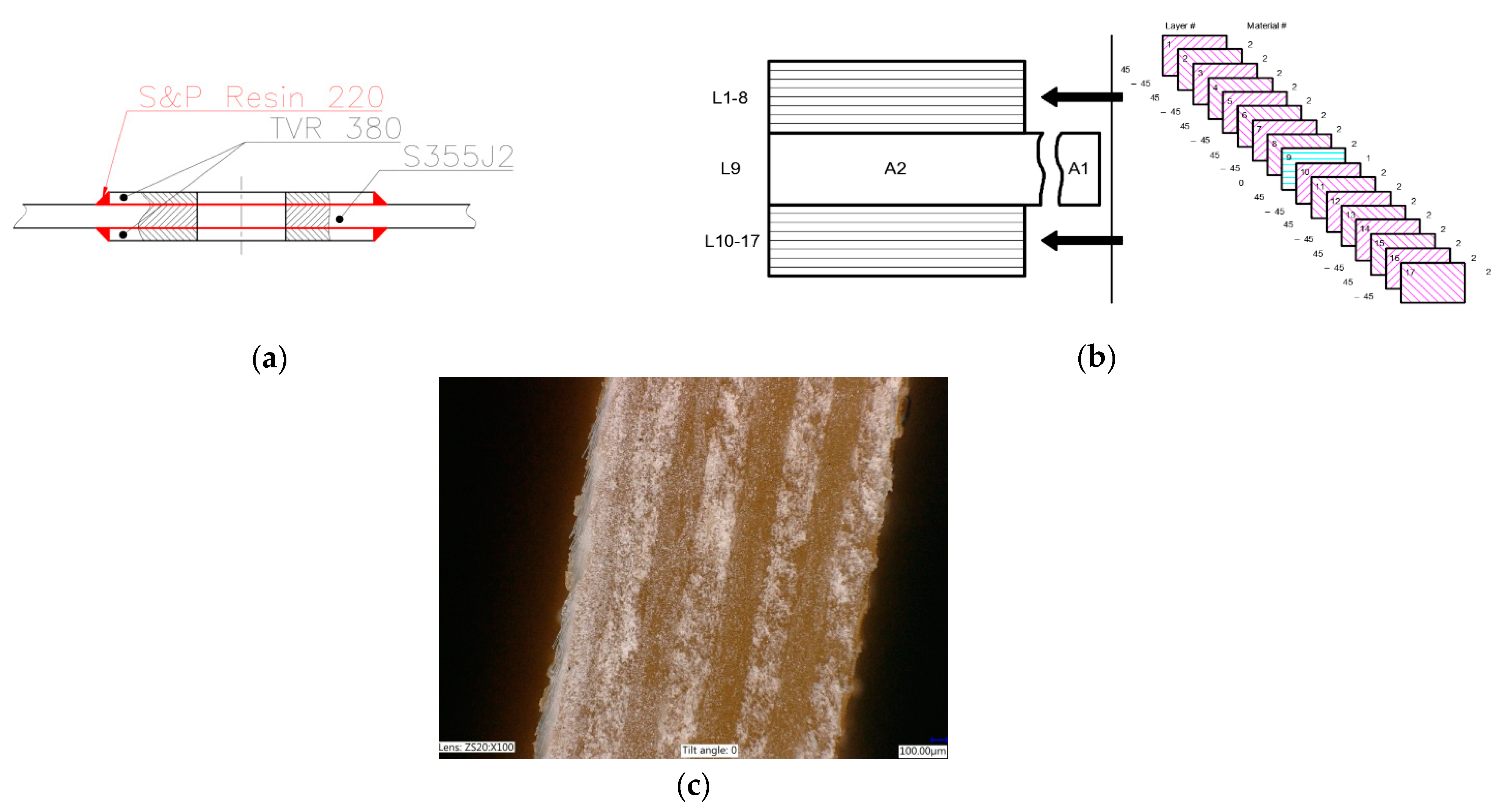
Materials and Samples
3. Experimental Tests
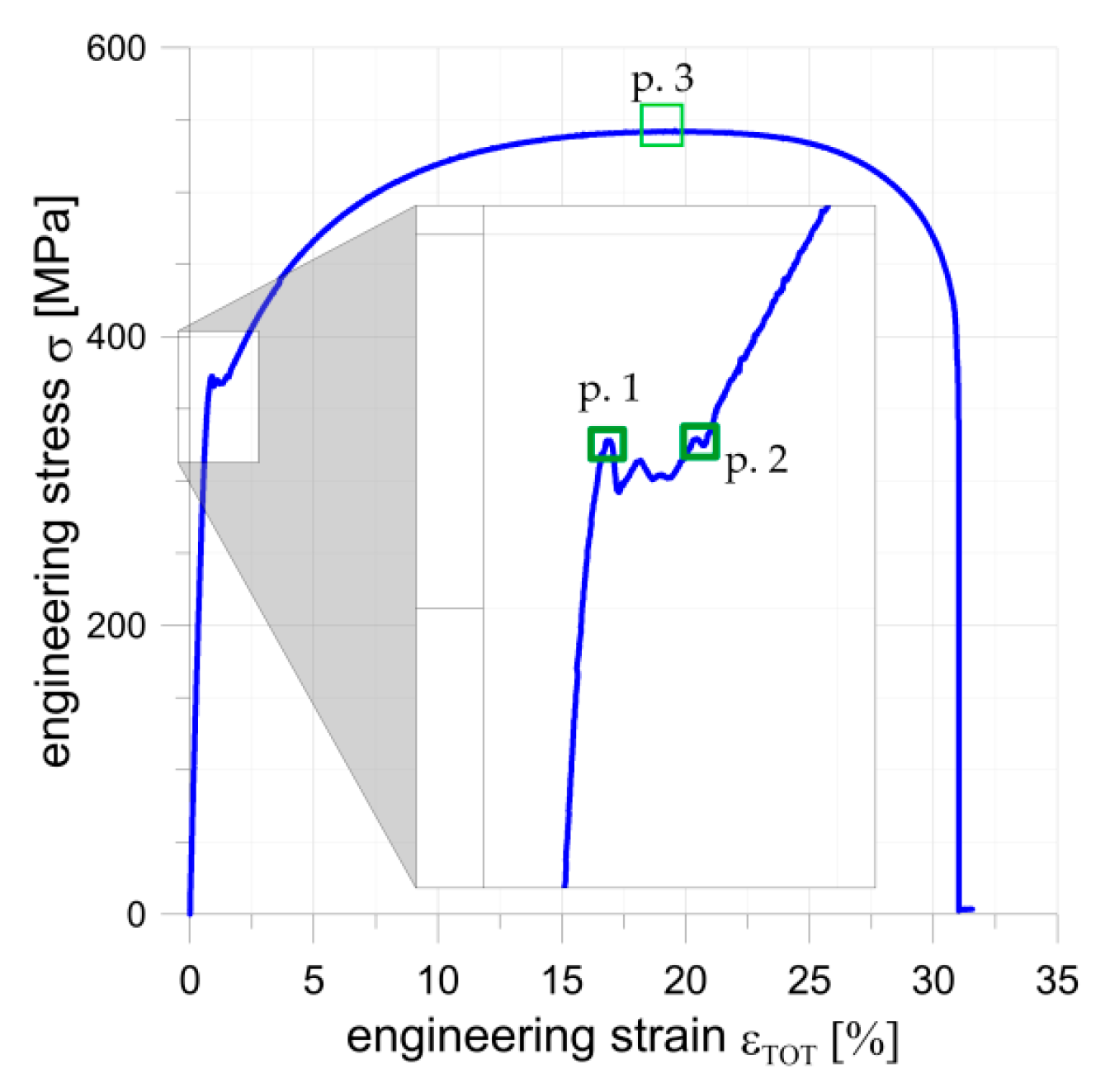
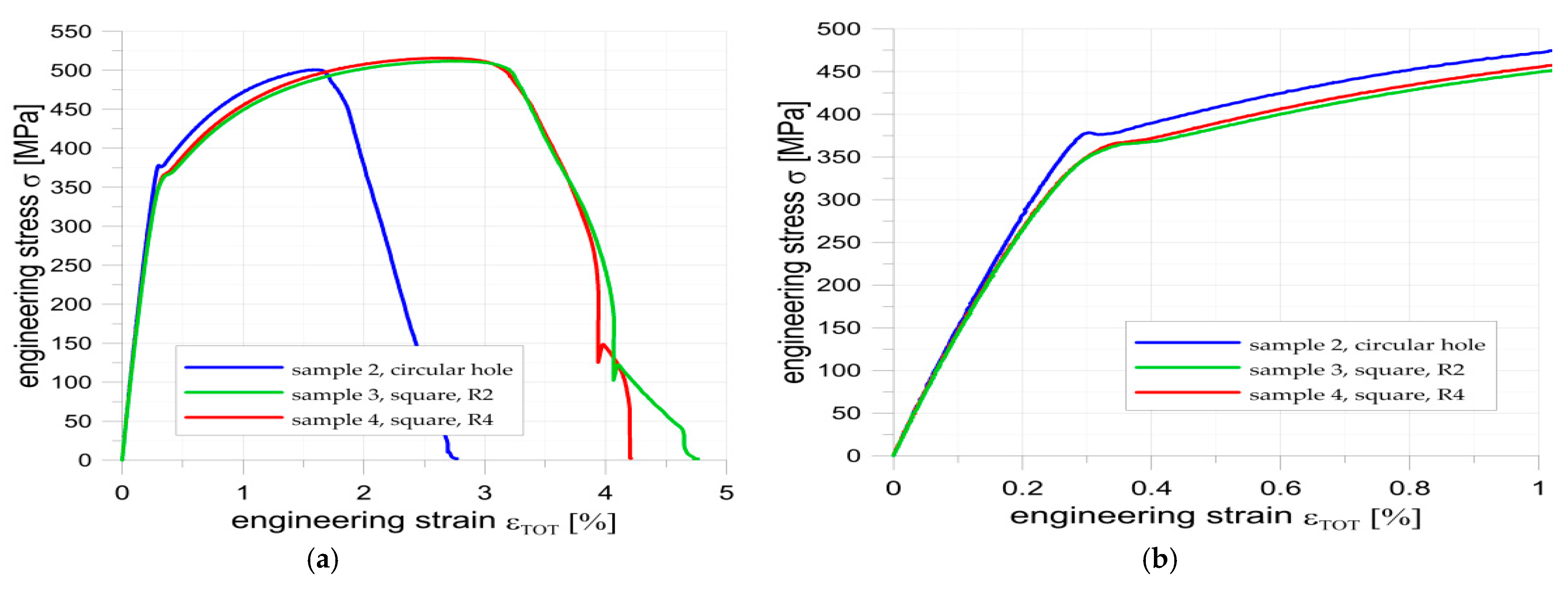
3.1. Stress–Strain Behavior of S355J2+N
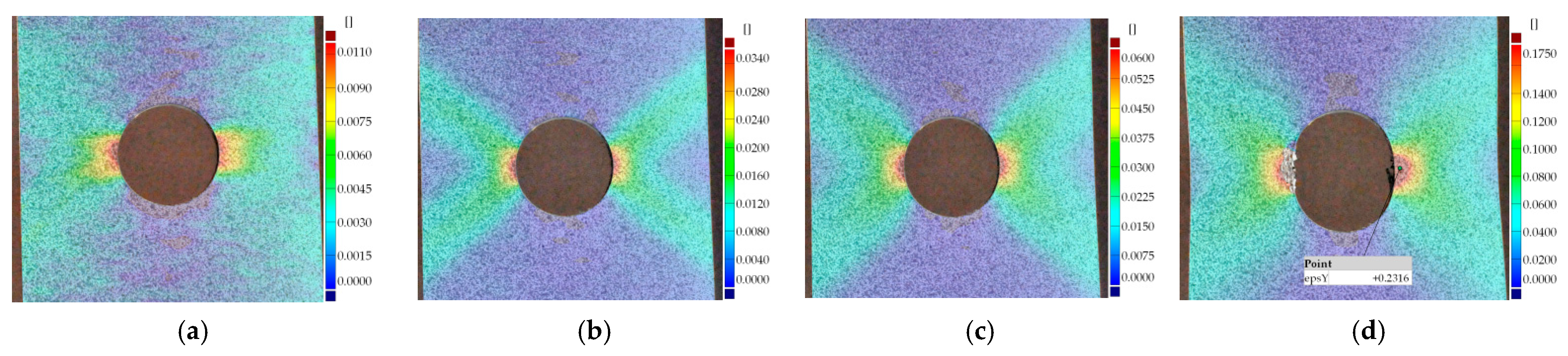
3.2. Unreinforced Metal Samples with Holes
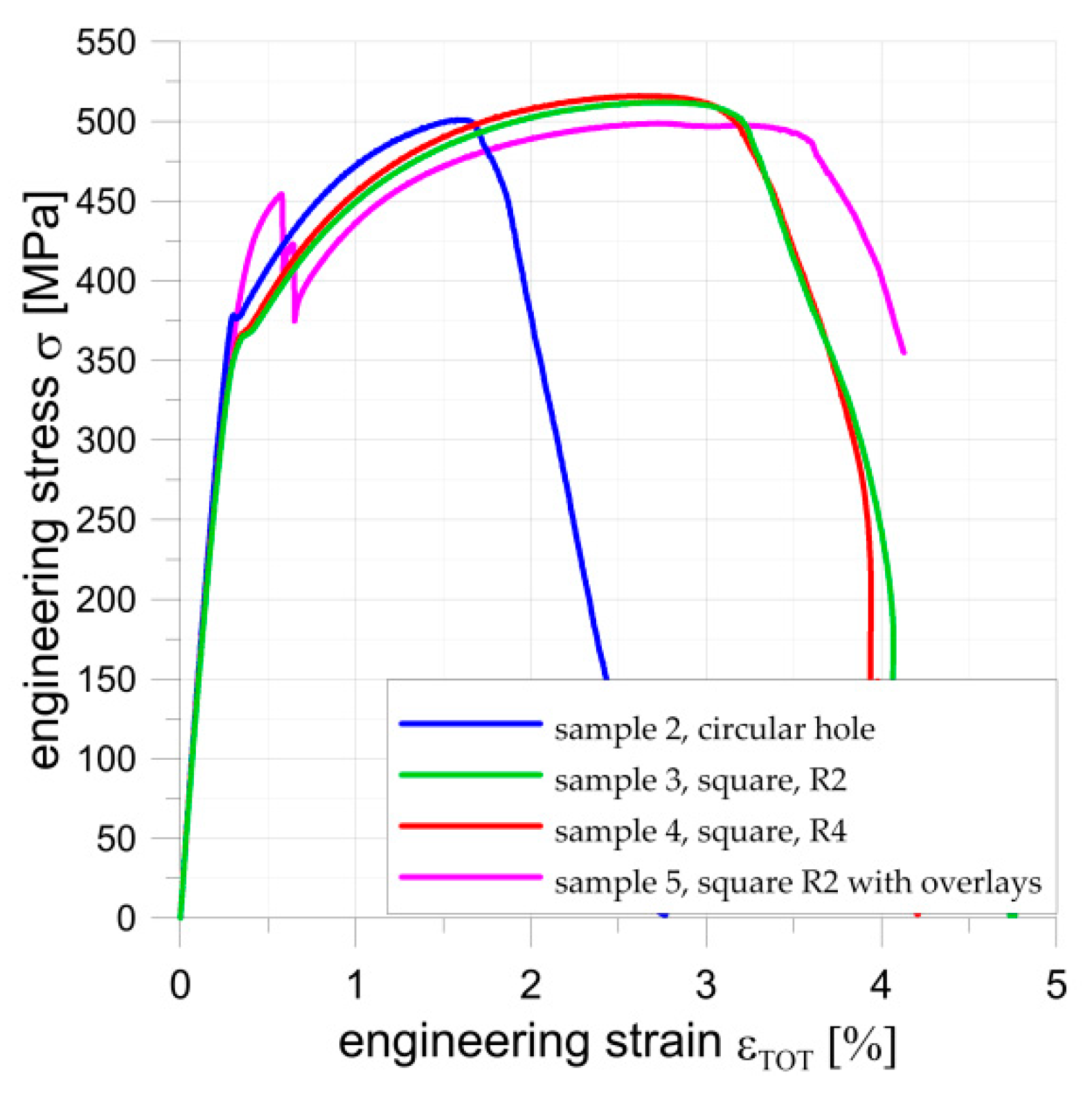
3.3. Metal Samples with Holes Reinforced by Composite Materials
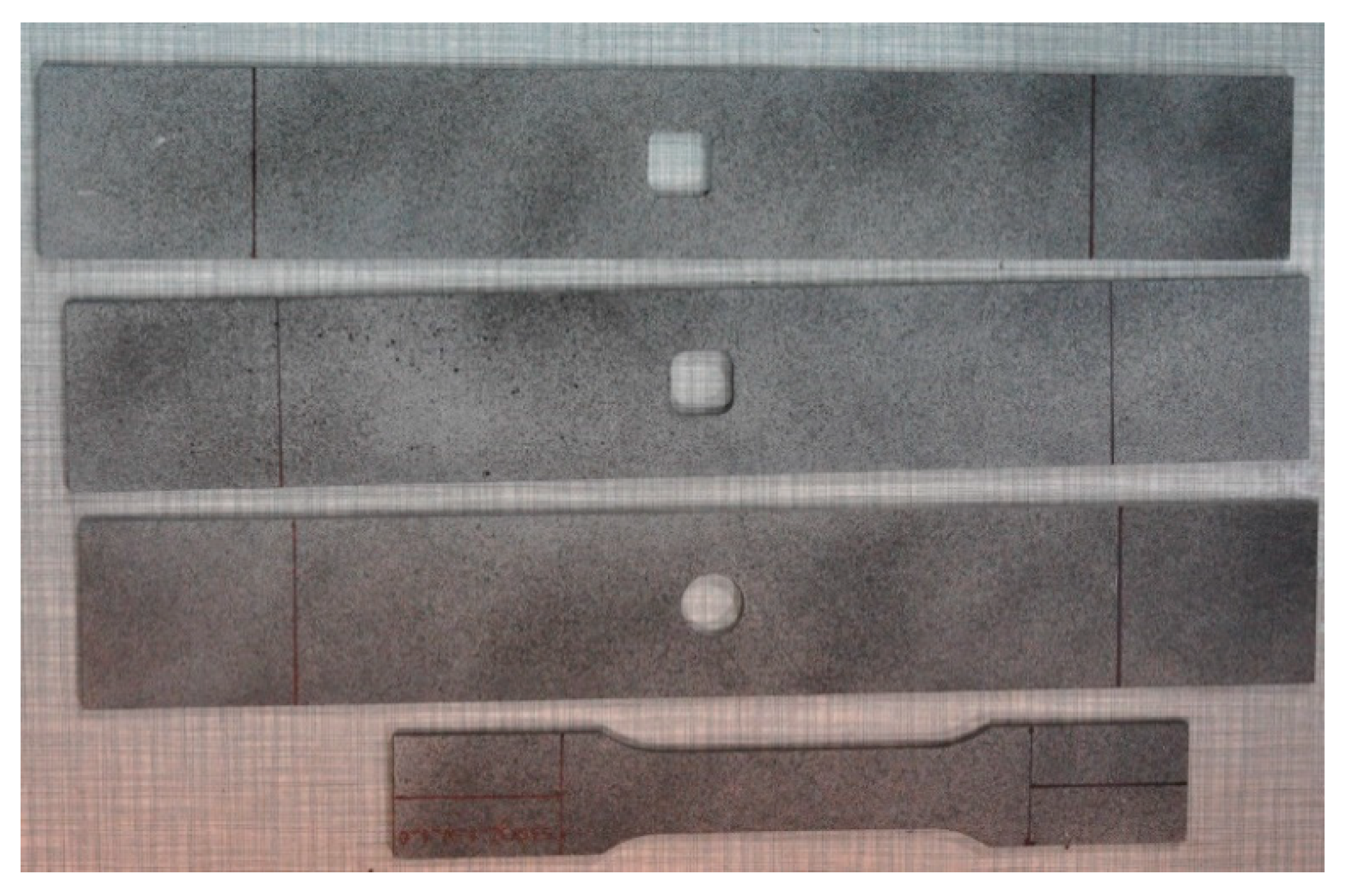
- The metal part—four points (not visible in presented attached Figures, but can be assessed in the example of the plate without reinforcements—Figure 11);
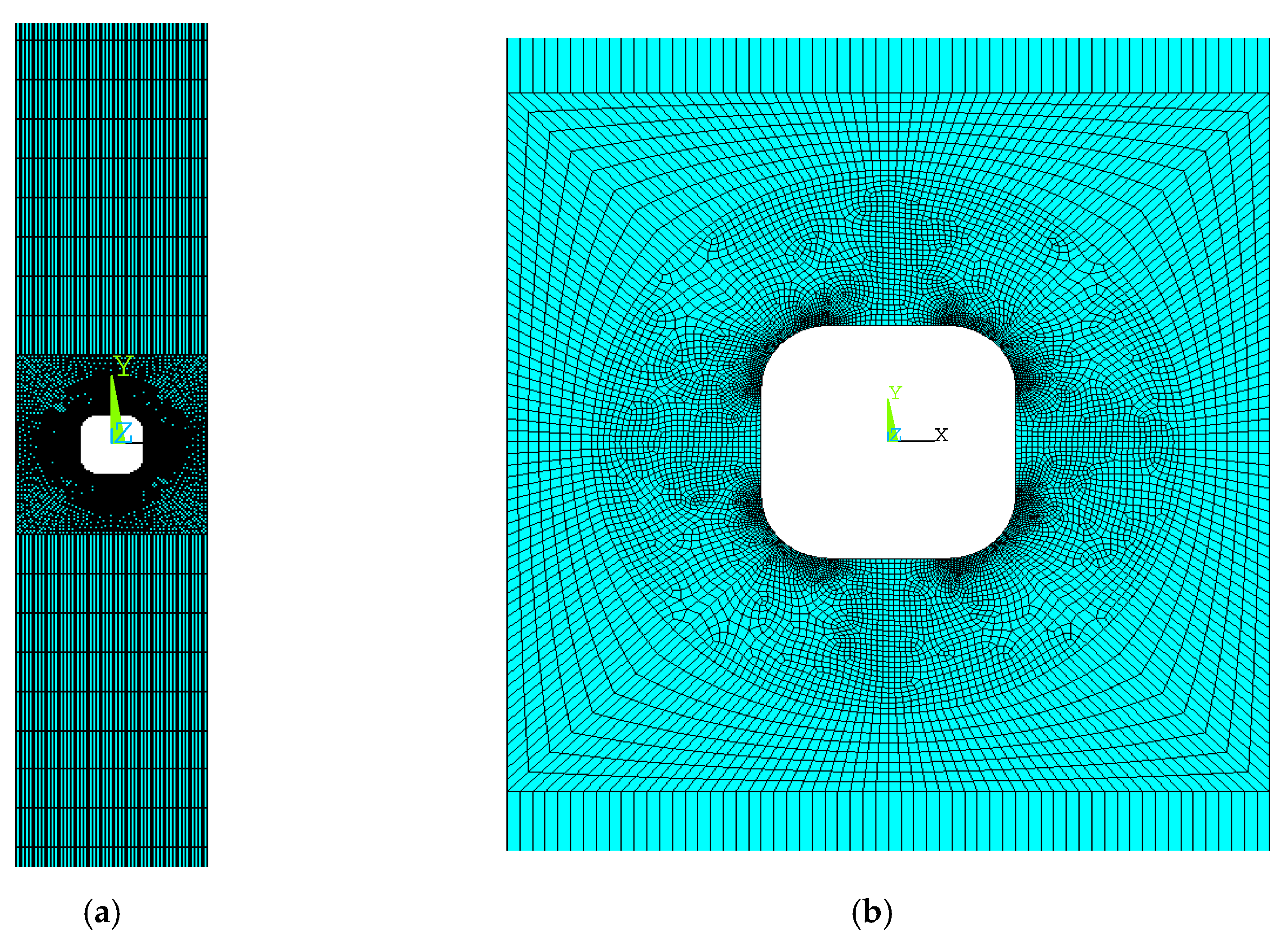
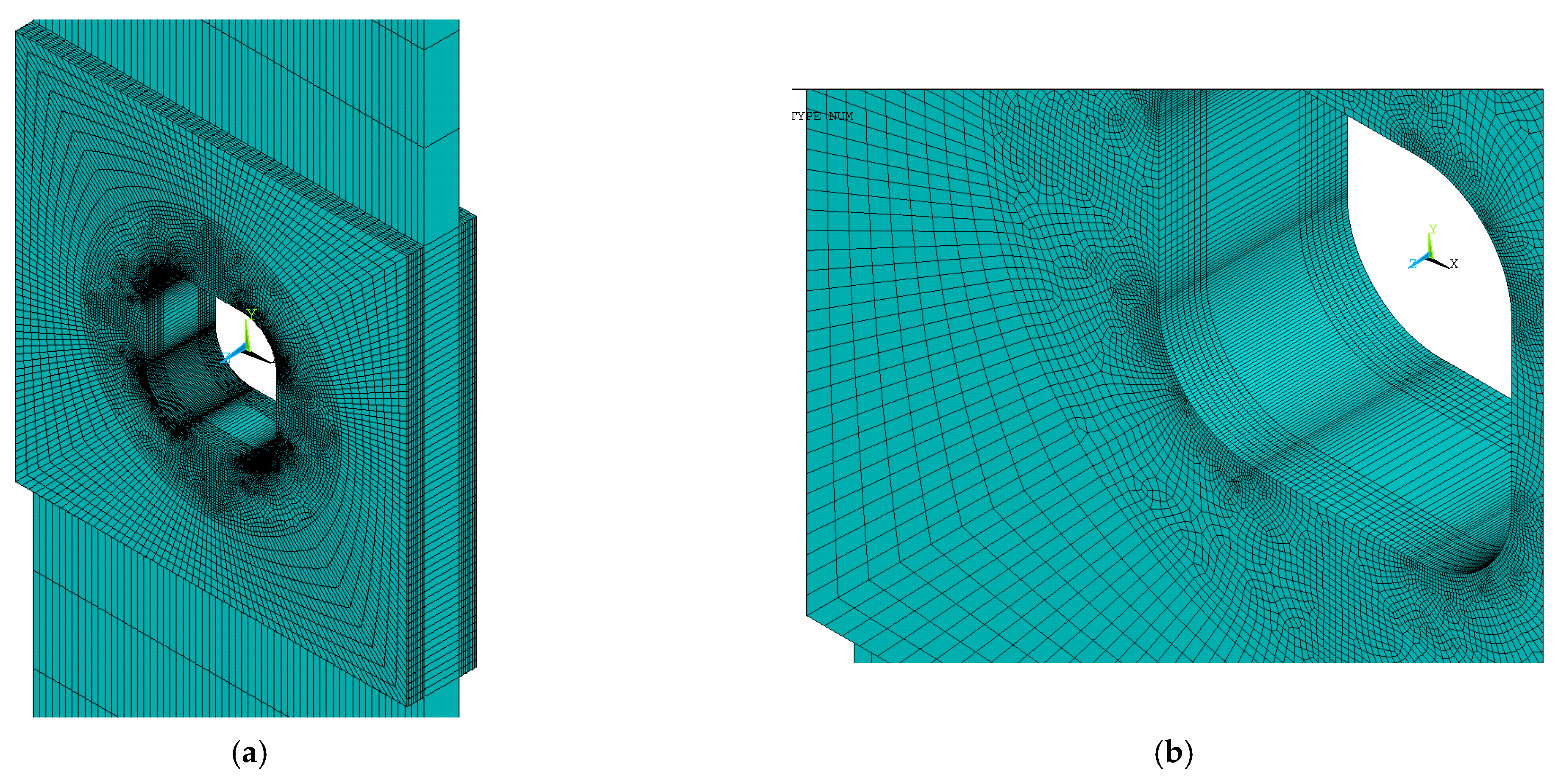
4. Finite Element Analyses
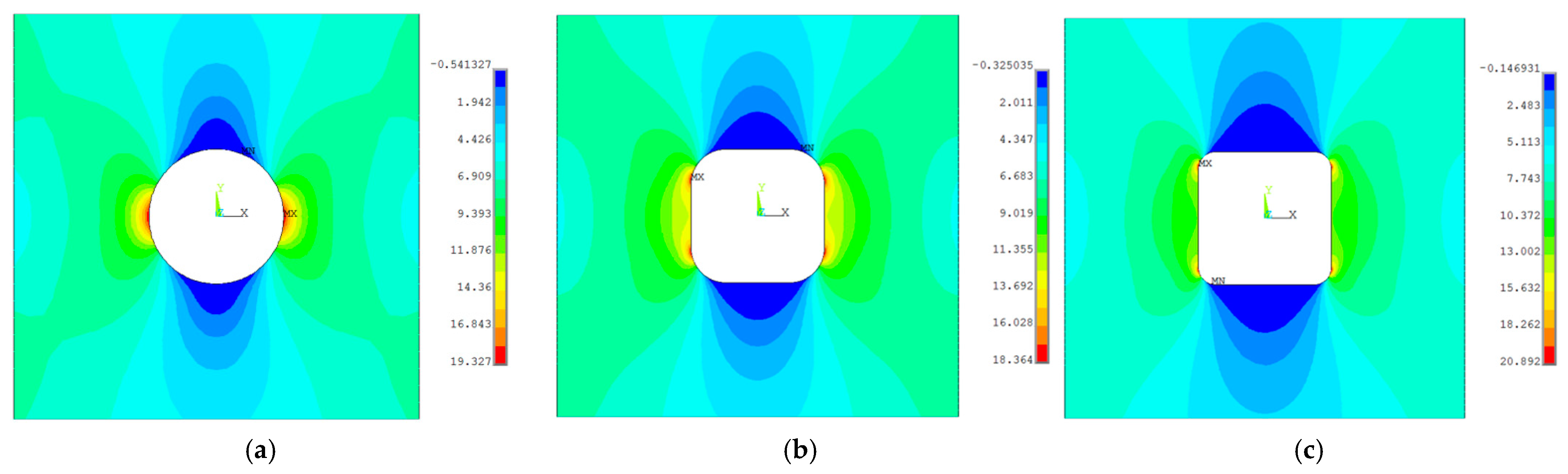
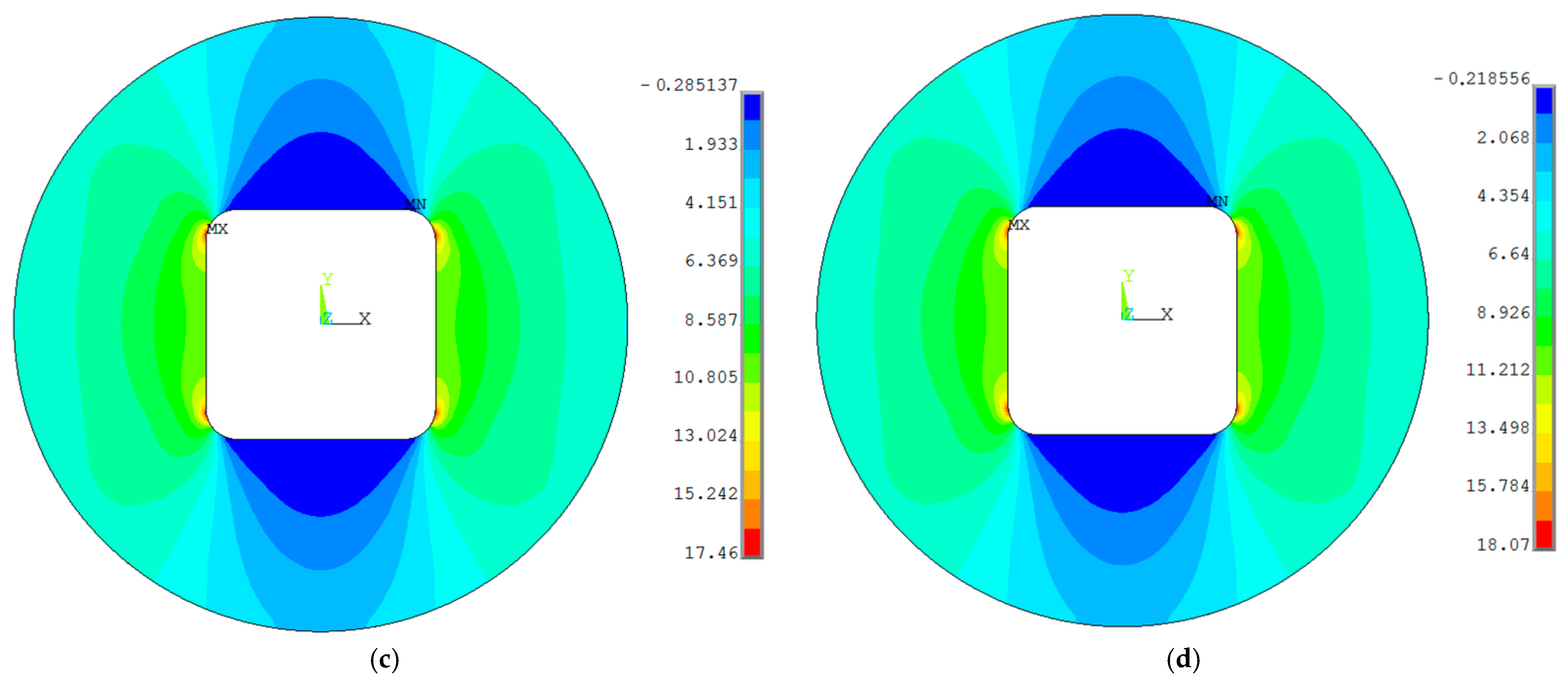
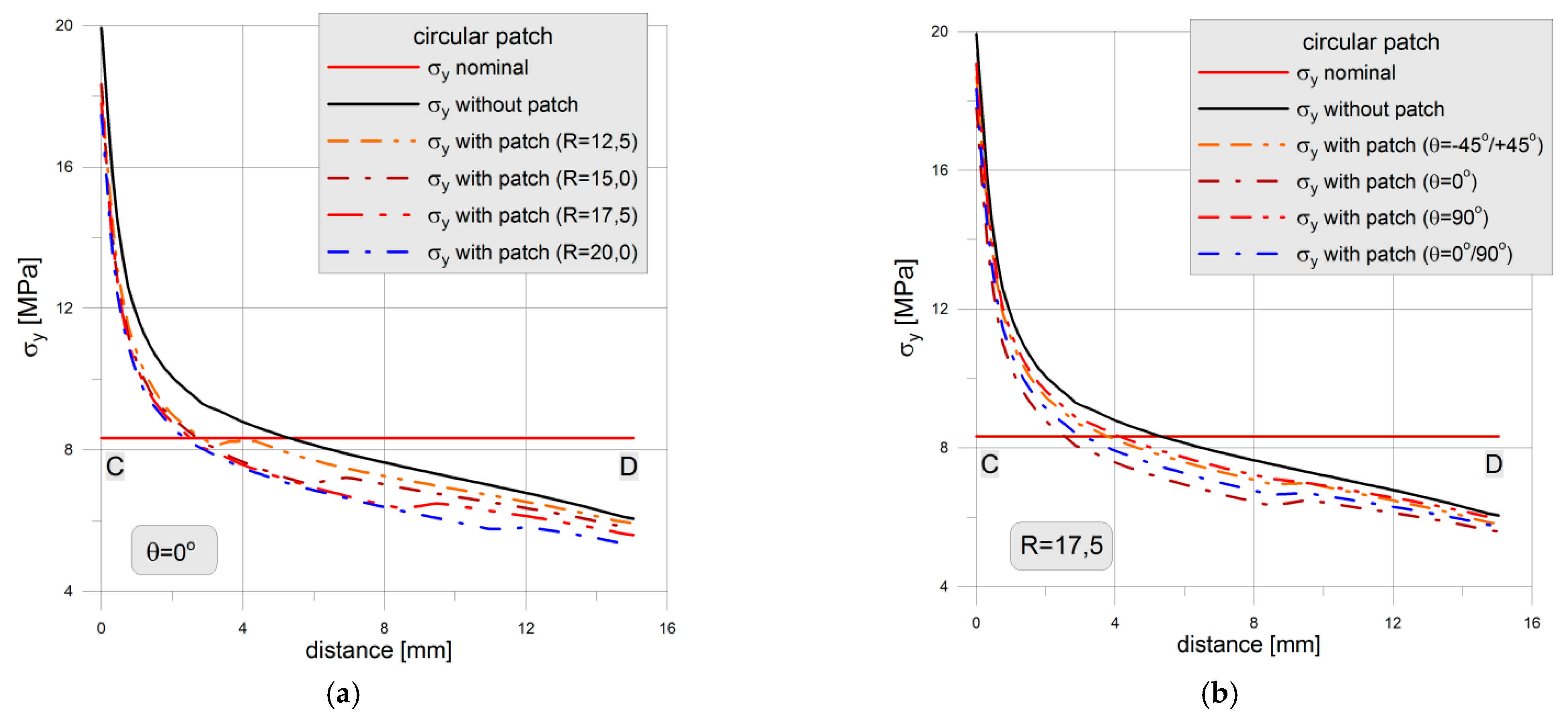
4.1. Circular Patch
4.2. Square Patch
5. Discussion
6. Conclusions
- the good agreement between the DIC results with the FEM results has confirmed the usefulness of the DIC tool and GOM software in the non-destructive analysis of structural elements;
- the effectiveness of the composite overlay application has been confirmed by the reduction of the stress concentration factor in the notch area. In the investigated example, the application of the square composite overlay increased the structure strength even by 25%;
- the stress concentration reduction is the function of the fiber orientation and is the highest in the case of fibers set in parallel to the applied loading;
- the bigger size of the overlay patch the bigger reduction of the stress concentration is observed.
Author Contributions
Funding
Conflicts of Interest
References
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Application of DIC Method in the Analysis of Stress Concentration and Plastic Zone Development Problems. Materials 2020, 13, 3460. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.T.; Li, Q.H.; Xu, S.L.; Li, C.F. Development of reinforced ultra-high toughness cementitious composite permanent formwork: Experimental study and Digital Image Correlation analysis. Compos. Struct. 2017, 180, 892–903. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M.; Romanowicz, P.; Stawiarski, A. Fatigue-Damage Evolution of Notched Composite Multilayered Structures under Tensile Loads. J. Compos. Sci. 2018, 2, 27. [Google Scholar] [CrossRef] [Green Version]
- Muc, A.; Romanowicz, P. Effect of notch on static and fatigue performance of multilayered composite structures under tensile loads. Compos. Struct. 2017, 178, 27–36. [Google Scholar] [CrossRef]
- Kirsch, E.G. Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre. Z. Ver. Dtsch. Ing. 1898, 42, 797–807. [Google Scholar]
- Kolosov, G.V. Application of Complex Diagrams and the Theory of Functions of a Complex Variable to the Theory of Elasticity; ONTI: Moscow, Russia; Leningrad, Russia, 1935; 224p. (In Russian) [Google Scholar]
- Inglis, C.E. Stress in a plane due to the presence of cracks and sharp corners. Trans. Inst. Naval. Archit. 1913, 55, 219–241. [Google Scholar]
- Neuber, H. Kerbspannungslehre: Grundlagen für genaue Festigkeitsberechnung mit Berücksichtigung von Konstruktionsform und Werkstoff, 4th ed.; Springer: Berlin, Germany, 2001. [Google Scholar] [CrossRef]
- Savin, G.N. Stress Distribution around Holes (Translated from Russian) NASA Technical Translation NASA TT F-607; NASA: Washington, DC, USA, 1970; 300p. Available online: https://archive.org/details/nasa_techdoc_19710000647/page/n1/mode/2up (accessed on 18 May 2020).
- Mushkelishvilli, N. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Howland, R.C.J. On the stresses in the neighborhood of a circular hole in a strip under tension. Philos. Trans. R. Soc. (Lond.) Ser. A 1930, 229, 49–86. [Google Scholar]
- Lekhnitskiy, S.G. Theory of Elasticity of an Anisotropic Body; Mir Publishers: Moscow, Russia, 1981; 431p, Available online: https://www.twirpx.com/file/762362 (accessed on 18 May 2021).
- Tan, S.C. Finite-width correction factors for anisotropic plate containing a central opening. J. Compos. Mater. 1988, 22, 1080–1097. [Google Scholar] [CrossRef]
- Rezaeepazhand, J.; Jafari, M. Stress concentration in metallic plates with special shaped cutout. Int. J. Mech. Sci. 2010, 52, 96–102. [Google Scholar] [CrossRef]
- Tanaka, K.; Nakai, Y. Prediction of fatigue threshold of notched components. Trans. ASME 1984, 106, 192–199. [Google Scholar] [CrossRef]
- Smith, R.A.; Miller, K.J. Prediction of Fatigue Regimes in Notched Components. Int. J. Mech. Sci. 1978, 20, 201–206. [Google Scholar] [CrossRef]
- Heywood, R.B. Designing by Photoelasticity; Chapman and Hall, Ltd.: London, UK, 1952. [Google Scholar]
- Frocht, M.M. Photoelasticity; John Wiley & Sons: New York, NY, USA, 1957. [Google Scholar]
- Sobey, A.J. ARC reports and memoranda No. 3407. H.M. In Stress-Concentration Factors for Rounded Rectangular Holes in Infinite Sheets; Stationery Office: London, UK, 1963. [Google Scholar]
- Mitchell, M.R. Fundamentals of modern fatigue analysis for design. In ASM Handbook, Volume 19: Fatigue and Fracture; Lampman, S.R., Ed.; ASM International: Material Park, OH, USA, 1996; pp. 227–249. [Google Scholar]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Savruk, M.P.; Kazberuk, A. Stress Concentration at Notches; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pedersen, P. On optimal shapes in materials and structures. Struct. Multidisc. Optim. 2000, 19, 169–182. [Google Scholar] [CrossRef]
- Szybiński, B.; Wróblewski, A. Parametric optimization of stress relief groove shape in flat ends of boilers. J. Strain Anal. Eng. Des. 2012, 47, 55–63. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier-Butterworth-Heinemann: Burlington, MA, USA, 2006. [Google Scholar]
- European Committee for Standardization. European Standard, EN 13445-3, Unfired Pressure Vessels—Part 3: Design; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- Angus, C.C.; Lam, J.J.; Roger, C.; Michael, C.H.Y.; Gaylene, D.K. Repair of steel structures by bonded carbon fibre reinforced polymer patching: Experimental and numerical study of carbon fibre reinforced polymer—Steel double-lap joints under tensile loading. Can. J. Civ. Eng. 2007, 34, 1542–1553. [Google Scholar] [CrossRef]
- Łagoda, M.; Kowal, M. CFRP composite materials strengthening of flat steel elements to reduce the stresses in the steel. Struct. Environ. 2014, 6, 5–12. [Google Scholar]
- Wang, Z.Y.; Wang, Q.Y.; Li, L.; Zhang, N. Fatigue behaviour of CFRP strengthened open-hole steel plates. Thin-Walled Struct. 2017, 115, 176–187. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhang, T.; Li, X.; Wang, Q.Y.; Huang, W.; Shen, M. Characterization of the effect of CFRP reinforcement on the fatigue strength of aluminium alloy plates with fastener holes. Eng. Struct. 2018, 177, 739–752. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y.; Li, J.; Zhang, L.; Deng, J. Experimental study on tensile behaviour of steel plates with centre hole strengthened by CFRP plates under marine environment. Int. J. Adhes. Adhes. 2018, 84, 18–26. [Google Scholar] [CrossRef]
- Aljabar, N.J.; Zhao, X.L.; Al-Mahaidi, R.; Ghafoori, E.; Motavalli, M.; Koay, Y.C. Experimental investigation on the CFRP strengthening efficiency of steel plates with inclined cracks under fatigue loading. Eng. Struct. 2018, 172, 877–890. [Google Scholar] [CrossRef]
- Ye, H.; Shuai, C.; Zhang, X.; Xu, X.; Ummenhofer, T. Determination of S-N fatigue curves for damaged steel plates strengthened with prestressed CFRP plates under tension loading. Eng. Struct. 2018, 175, 669–677. [Google Scholar] [CrossRef]
- de Medeiros, R.; Borges, E.N.; Tita, V. Experimental analyses of metal-composite bonded joints: Damage identification. Appl. Adhes. Sci. 2014, 2, 13. [Google Scholar] [CrossRef] [Green Version]
- Szybiński, B.; Wygoda, M. Numerical investigations of stress concentration in reinforcement steel structure by composite overlays. J. KONES Powertrain Transp. 2019, 26, 4. [Google Scholar] [CrossRef]
- Rudawska, A. Comparison of the adhesive joints’ strength of the similar and dissimilar systems of metal alloy/polymer composite. Appl. Adhes. Sci. 2019, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Tsokanas, P.; Loutas, T.; Nijhuis, P. Interfacial Fracture Toughness Assessment of a New Titanium–CFRP Adhesive Joint: An Experimental Comparative Study. Metals 2020, 10, 699. [Google Scholar] [CrossRef]
- Derewońko, A. Failure simulation of metal-composite joints. Fibres Text. East. Eur. 2013, 5, 131–134. [Google Scholar]
- Yahya, N.A.; Hashim, S. Stress analysis of steel/carbon composite double lap shear joints under tensile loading. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 230, 88–104. [Google Scholar] [CrossRef]
- Ghoddous, B. Theoretical Analysis of Stress Distribution in Bonded Single Strap and Stiffened Joints. Lat. Am. J. Solids Struct. 2017, 14, 256–276. [Google Scholar] [CrossRef]
- da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology; Springer International Publishing: New York, NY, USA, 2018; pp. 689–723. [Google Scholar]
- Jeevi, G.; Nayak, S.K.; Kader, M.A. Review on adhesive joints and their application in hybrid structures. J. Adhes. Sci. Technol. 2019, 33, 1497–1520. [Google Scholar] [CrossRef]
- Banea, M.D.; da Silva, L.F.M. Adhesively bonded joints in composite materials: An overview. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2009, 223, 1–18. [Google Scholar] [CrossRef]
- Dobrzański, P.; Oleksiak, W. Design and analysis methods for composite bonded joints. Trans. Aerosp. Res. 2021, 1, 45–63. [Google Scholar] [CrossRef]
- Volkersen, O. Die niektraftverteilung in zugbeanspruchten mit konstanten laschenquerschritten. Luftfahrtforschung 1938, 15, 41–68. [Google Scholar]
- Goland, M.; Reissner, E. The stresses in cemented lap joints. J. Appl. Mech. 1944, 66, A17–A27. [Google Scholar] [CrossRef]
- Stukhlyak, P.D.; Mytnyk, M.M.; Orlov, V.O. Influence of boundary interlayers on properties of composite polymeric materials (a review). Mater. Sci. 2001, 37, 80–86. [Google Scholar] [CrossRef]
- Maruschak, P.O.; Panin, S.V.; Stachowicz, F.; Danyliuk, I.M.; Vlasov, I.V.; Bishchak, R.T. Structural levels of fatigue failure and damage estimation in 17Mn1Si steel on the basis of a multilevel approach of physical mesomechanics. Acta Mech. 2016, 227, 151–157. [Google Scholar] [CrossRef]
- Romanowicz, P. Experimental and numerical estimation of the damage level in multilayered composite plates. Mater. Werkst. 2018, 49, 591–605. [Google Scholar] [CrossRef]
- Carbas, R.J.C.; da Silva, L.F.M.; Madureira, M.L.; Critchlow, G.W. Modelling of Functionally Graded Adhesive Joints. J. Adhes. 2014, 90, 698–716. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Morton, J. An investigation into the stresses in double-lap adhesive joints with laminated composite adherends. Int. J. Solids Struct. 2010, 47, 3317–3325. [Google Scholar] [CrossRef] [Green Version]
- Barski, M.; Kędziora, P.; Muc, A.; Romanowicz, P. Structural Health Monitoring (SHM) methods in machine design and operation. Arch. Mech. Eng. 2014, 61, 653–677. [Google Scholar] [CrossRef]
- Salski, B.; Gwarek, W.; Korpas, P.; Reszewicz, S.; Chong, A.Y.B.; Theodorakeas, P.; Hatziioannidis, I.; Kappatos, V.; Selcuk, C.; Gan, T.H.; et al. Non-destructive testing of carbon-fibre-reinforced polymer materials with a radio-frequency inductive sensor. Compos. Struct. 2015, 122, 104–112. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 10025-2:2004 Hot Rolled Products of Structural Steels—Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Romanowicz, P.; Muc, A. Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests. Materials 2018, 11, 2180. [Google Scholar] [CrossRef] [Green Version]
- ASTM D 3039. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Ostapiuk, M.; Surowska, B. Comparative analysis of failure of Al/GFRP laminates after tensile strength test. Compos. Theory Pract. 2015, 15, 259–265. [Google Scholar]
- European Committee for Standardization. EN ISO 6892-1 Metallic Materials—Tensile Testing—Part. 1: Method of Test. at Room Temperature; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- GOM Software 2018 Hotfix 1. Available online: www.gom.com (accessed on 26 September 2018).
- Ansys Software. Available online: www.ansys.com (accessed on 30 March 2021).





















| Chemical Components of S355J2 Steel (in Weight %) | |||||||||
| Material | C | Si | Mn | P | S | Cu | Al | Cr | Fe |
| S355J2+N (tested material) | 0.19 | 0.20 | 0.99 | 0.012 | 0.01 | 0.03 | 0.04 | 0.02 | res. |
| S355J2, Standards [55], max % | 0.20–0.22 | 0.55 | 1.60 | 0.025 | 0.025 | 0.55 | - | - | res. |
| Mechanical Properties of S355J2 Steel | |||||||||
| Material (EN) | Material (AISI, ASTM) | Upper Yield Limit YeH | Tensile Strength Rm | ||||||
| S355J2 [55] | A765 | Min. 355 MPa | 470–630 MPa | ||||||
| Material | E1 [GPa] | E2, E3 [GPa] | G12, G13 [GPa] | G23 [GPa] | ν12,ν13 | ν23 | Tensile Strength (MPa) | ||
|---|---|---|---|---|---|---|---|---|---|
| [0°]8 | [90°]8 | [+45°/−45°]4 | |||||||
| HEXCEL TVR 380 M12/26%/R-glass/epoxy | 46.43 | 14.92 | 5.23 | 9.15 | 0.269 | 0.3 | 1601 SD 1:59.2 | 68.7 SD:6.7 | 141.8 SD:8.4 |
| No. of Sample | Geometry | Hole Type | Material | Remarks |
|---|---|---|---|---|
| 1 | Figure 2a | - | S355J2+N | - |
| 2 | Figure 2b | Circular φ15 mm | S355J2+N | - |
| 3 | Figure 2c | square 15 × 15 mm | S355J2+N | corner fillet radii 2 mm |
| 4 | Figure 2d | square 15 × 15 mm | S355J2+N | corner fillet radii 4 mm |
| 5 | Figure 2e | square 15 × 15 mm | S355J2+N/TVR 380 θ = [+45°/−45°]4 | corner fillet radii 2 mm |
| Cut-out | Kt | C0 | C1 | C2 | C3 | f1 | f2 | f3 | KtINF | CW | Remarks |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Circular (sample 2) | 2.314 | 2.000 | 0.284 | −0.600 | 1.320 | 1 − d/W = 0.667 | 1 − d/W | 1 − d/W | 2.314 | 1 | D = 15 mm W = 45 mm |
| Rectangular R2 1 (sample 3) | 2.479 | 8.842 | −13.676 | 12.847 | −4.518 | b/a = 1 | b/a | b/a | 3.495 | 0.709 | R/b = 2/15 b/W = 1/3 |
| Rectangular R4 1 (sample 4) | 2.084 | 7.641 | −13.202 | 13.808 | −5.309 | b/a = 1 | b/a | b/a | 2.939 | 0.709 | R/b = 4/15 b/W = 1/3 |
| Overlay Data In (mm) | Kt (−) | 1 | θ |
|---|---|---|---|
| No Overlay | |||
| - | 2.508 | 0.301 | - |
| Circular Patch | |||
| Rov = 12.5 | 2.262 | 0.262 | [−45°/45°]4 |
| Rov = 15.0 | 2.289 | 0.260 | [−45°/45°]4 |
| Rov = 17.5 | 2.242 | 0.253 | [−45°/45°]4 |
| Rov = 20.0 | 2.231 | 0.250 | [−45°/45°]4 |
| Rov = 12.5 | 2.195 | 0.357 | [0°]8 |
| Rov = 15.0 | 2.201 | 0.359 | [0°]8 |
| Rov = 17.5 | 2.135 | 0.342 | [0°]8 |
| Rov = 20.0 | 2.096 | 0.452 | [0°]8 |
| Rov = 12.5 | 2.305 | 0.152 | [90°]8 |
| Rov = 15.0 | 2.334 | 0.154 | [90°]8 |
| Rov = 17.5 | 2.288 | 0.151 | [90°]8 |
| Rov = 20.0 | 2.270 | 0.149 | [90°]8 |
| Rov = 12.5 | 2.243 | 0.484 | [90°/0°]4 |
| Rov = 15.0 | 2.258 | 0.488 | [90°/0°]4 |
| Rov = 17.5 | 2.200 | 0.473 | [90°/0°]4 |
| Rov = 20.0 | 2.169 | 0.465 | [90°/0°]4 |
| Rectangular Patch | |||
| Size (45 × 45) | 2.183 | 2.044 | [−45°/45°]4 |
| Size (45 × 45) | 2.014 | 3.628 | [0°]8 |
| Size (45 × 45) | 2.228 | 1.222 | [90°]8 |
| Size (45 × 45) | 2.104 | 3.761 | [90°/0°]4 |
| Patch Type | Overlay Fiber Orientation θ with Respect to Tension Direction | |||
|---|---|---|---|---|
| [−45°/45°]4 | [0°]8 | [90°]8 | [90°/0°]4 | |
| Circular, Rov = 20, R2 | 10.7 | 15.7 | 9.5 | 13.5 |
| Square 45 × 45, R2 | 13.5 | 20.4 | 11.1 | 16.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials. J. Compos. Sci. 2021, 5, 134. https://doi.org/10.3390/jcs5050134
Romanowicz PJ, Szybiński B, Wygoda M. Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials. Journal of Composites Science. 2021; 5(5):134. https://doi.org/10.3390/jcs5050134
Chicago/Turabian StyleRomanowicz, Paweł J., Bogdan Szybiński, and Mateusz Wygoda. 2021. "Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials" Journal of Composites Science 5, no. 5: 134. https://doi.org/10.3390/jcs5050134
APA StyleRomanowicz, P. J., Szybiński, B., & Wygoda, M. (2021). Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials. Journal of Composites Science, 5(5), 134. https://doi.org/10.3390/jcs5050134






