Four Point Flexural Response of Acrylonitrile–Butadiene–Styrene
Abstract
1. Introduction
2. Materials and Methods
3. Numerical Modeling
3.1. The Utilized Test Data for ABS in SAMP-1
3.2. Damage Modeling
3.2.1. GISSMO Damage Model
3.2.2. DIEM Damage Model
3.2.3. Damage model of SAMP-1
3.2.4. Failure Modeling by EPFAIL and DEPRPT Parameters in SAMP-1 Material Law
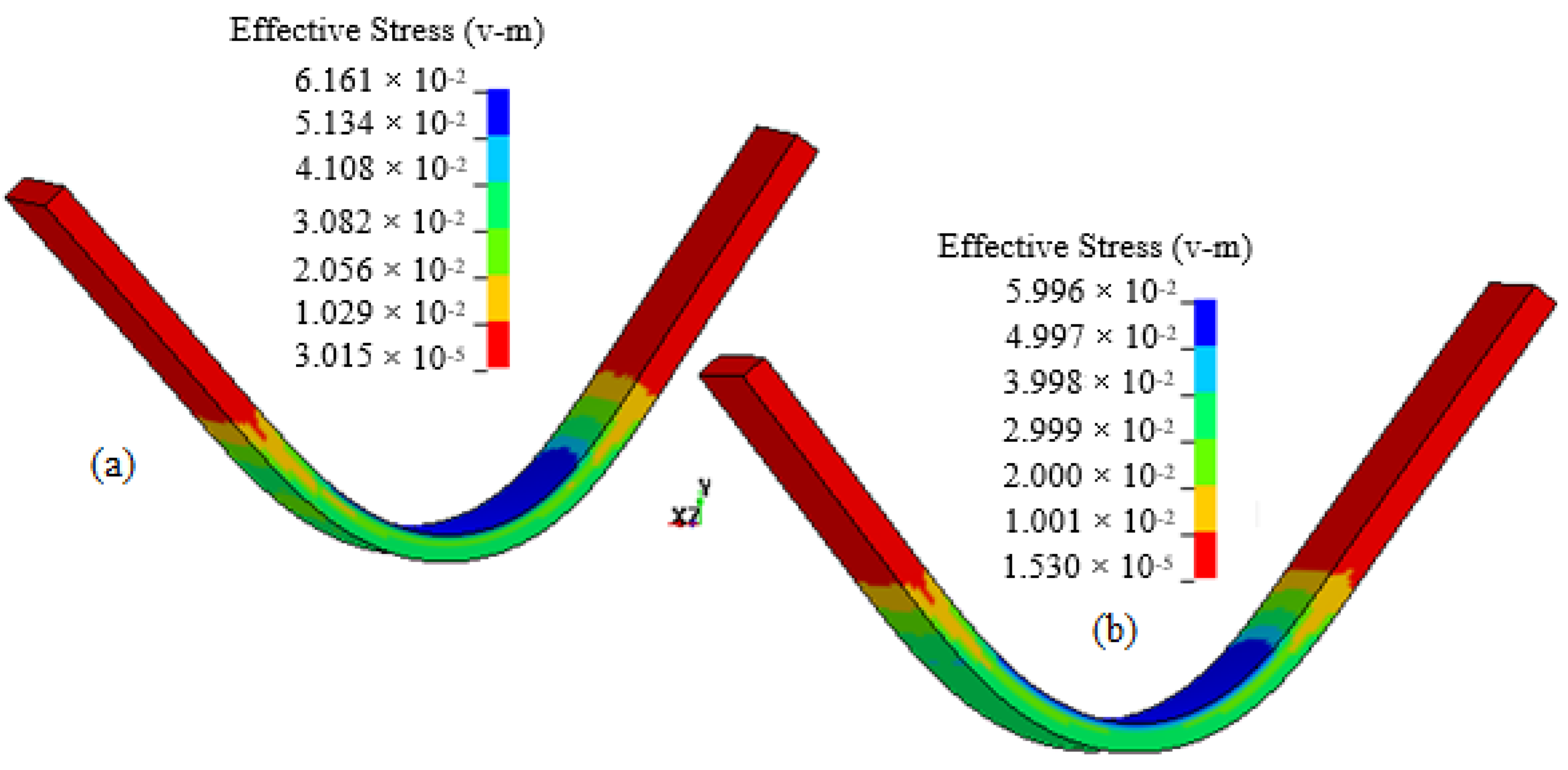
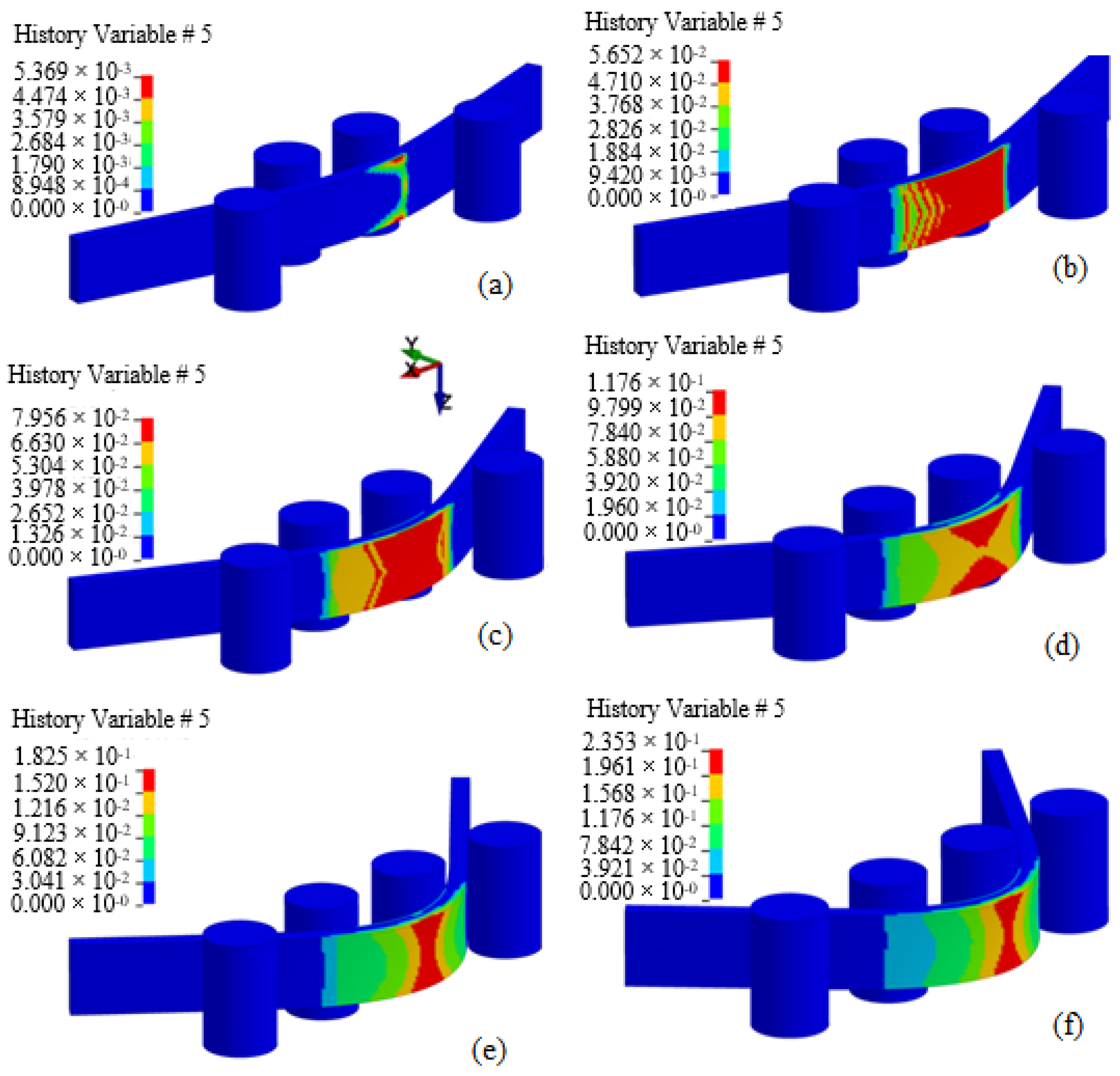
4. Results and Discussions
5. Parametric Simulations
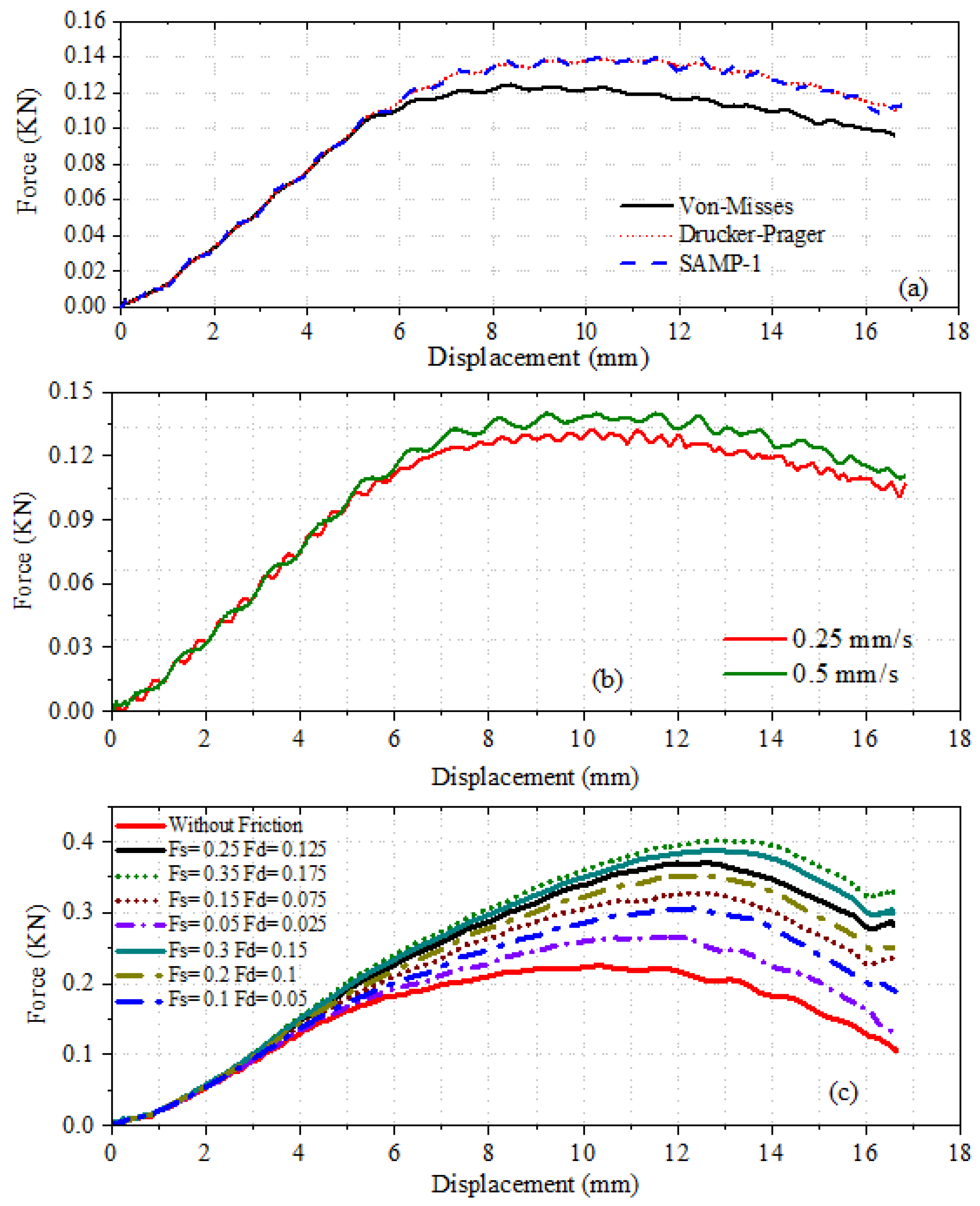
5.1. Yield Surfaces
5.2. Loading Rates
5.3. Contact Friction
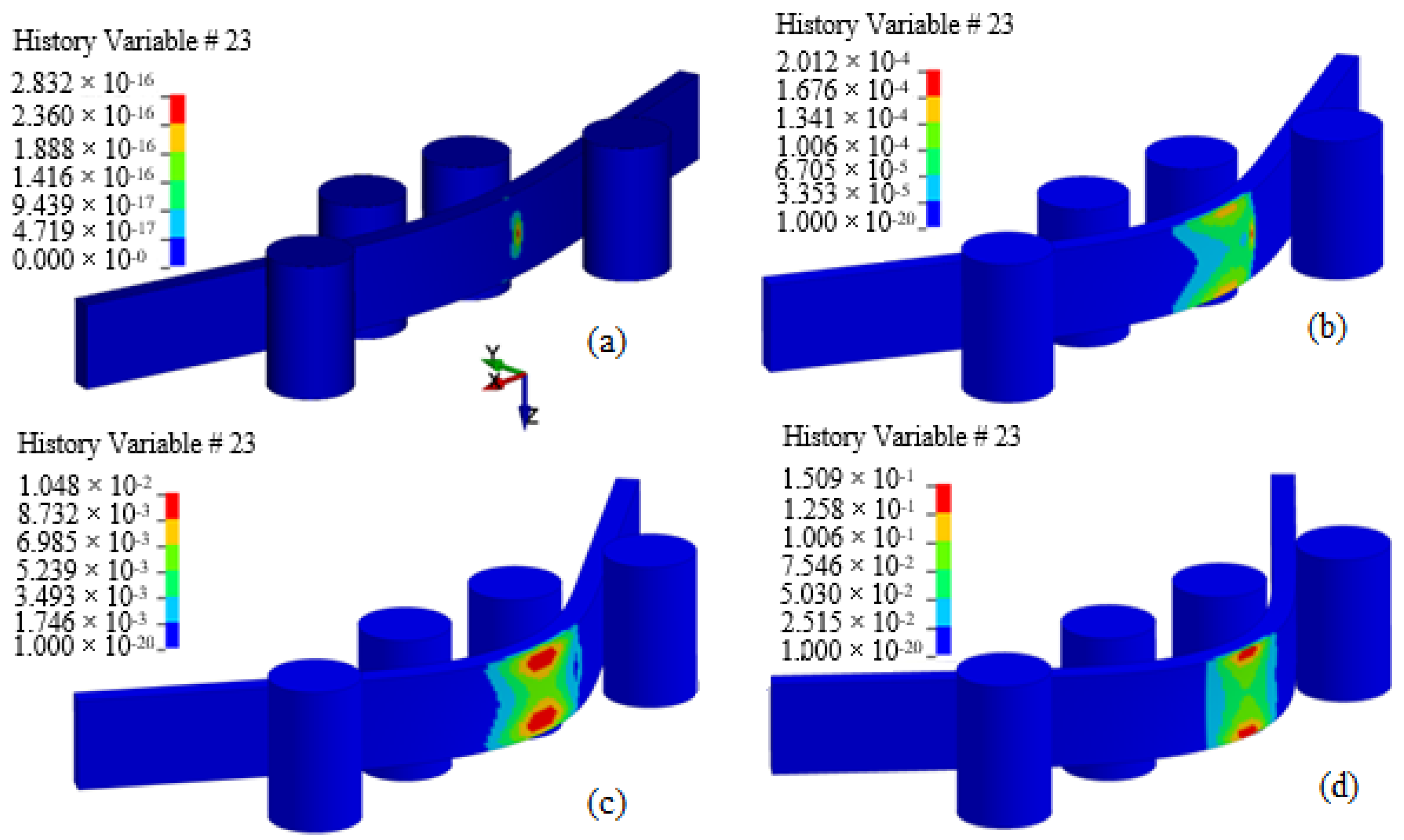
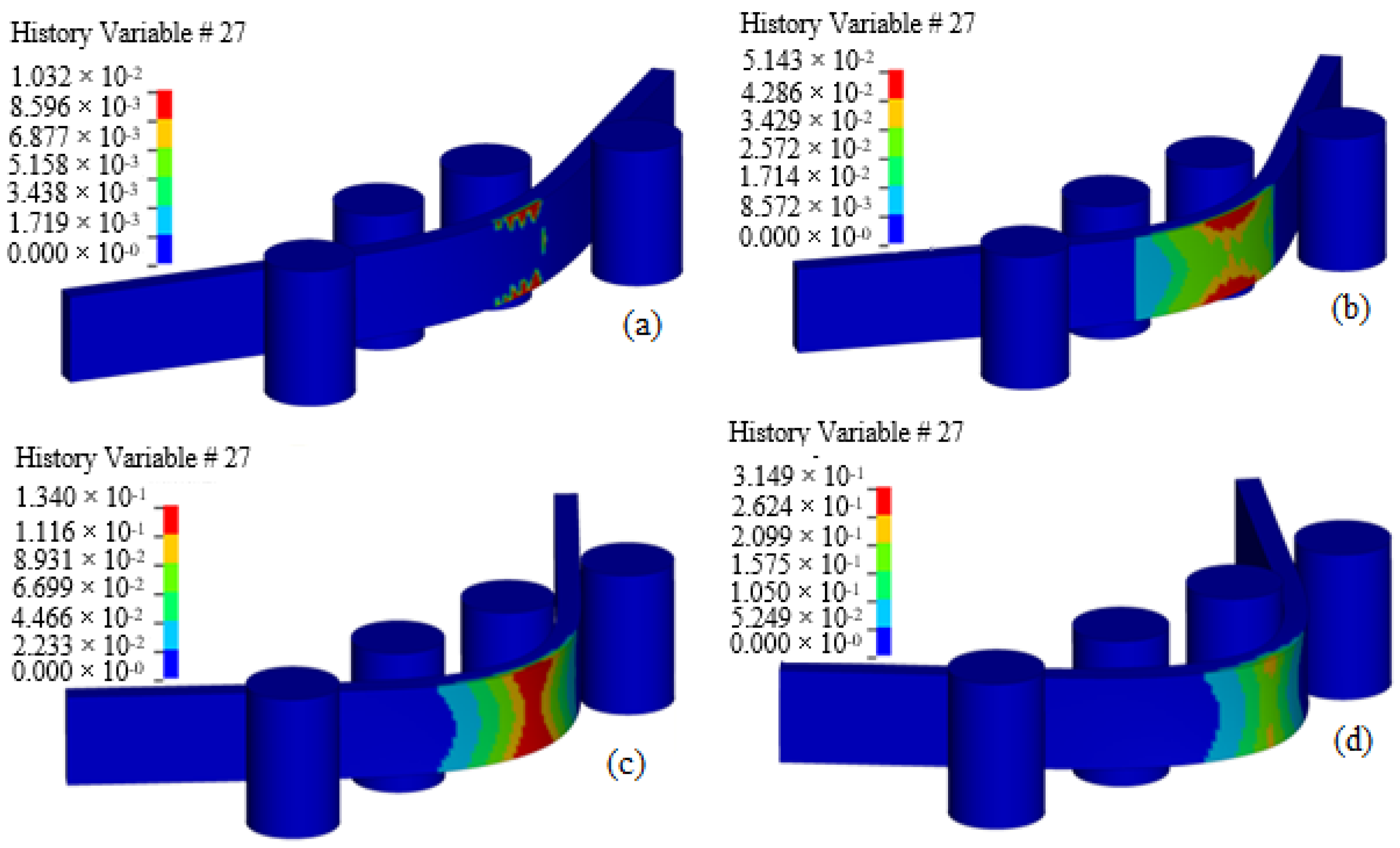
5.4. Damage Modeling
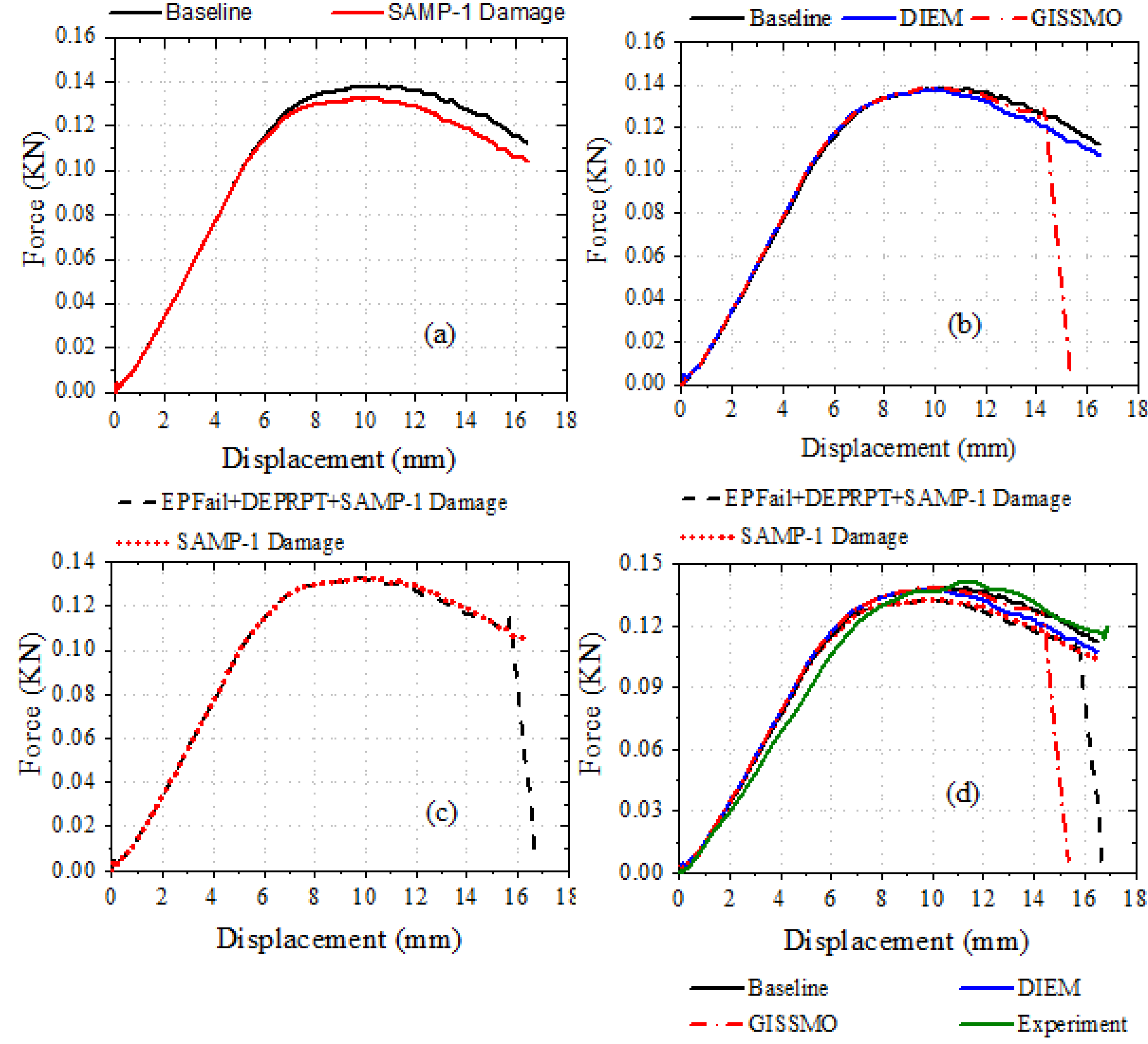
5.4.1. SAMP-1 Damage Formulation
5.4.2. GISSMO and DIEM Damage Formulation
5.4.3. Material failure modeling with EPFAIL and DEPRPT parameters
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mulliken, A.D. Mechanics of Amorphous Polymers and Polymer Nanocomposites during High Rate Deformation; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Rösler, J.; Harders, H.; Bäker, M. Mechanical Behaviour of Engineering Materials: Metals, Ceramics, Polymers, and Composites; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Dean, G.; Wright, L. An evaluation of the use of finite element analysis for predicting the deformation of plastics under impact loading. Polym. Test. 2003, 22, 625–631. [Google Scholar] [CrossRef]
- Altenbach, H.; Tushtev, K. A new static failure criterion for isotropic polymers. Mech. Compos. Mater. 2001, 37, 475–482. [Google Scholar] [CrossRef]
- Galeski, A. Strength and toughness of crystalline polymer systems. Prog. Polym. Sci. 2003, 28, 1643–1699. [Google Scholar] [CrossRef]
- Rabinowitz, S.; Ward, I.; Parry, J. The effect of hydrostatic pressure on the shear yield behaviour of polymers. J. Mater. Sci. 1970, 5, 29–39. [Google Scholar] [CrossRef]
- Ognedal, A.S. Large-Deformation Behaviour of Thermoplastics at Various Stress States: An Experimental and Numerical Study. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Qi, H.; Boyce, M. Stress–strain behavior of thermoplastic polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Boyce, M.C.; Parks, D.M.; Argon, A.S. Large inelastic deformation of glassy polymers. part I: Rate dependent constitutive model. Mech. Mater. 1988, 7, 15–33. [Google Scholar] [CrossRef]
- Argon, A.S. A theory for the low-temperature plastic deformation of glassy polymers. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1973, 28, 839–865. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Spathis, G. Theory for the plastic deformation of glassy polymers. J. Mater. Sci. 1997, 32, 1943–1950. [Google Scholar] [CrossRef]
- Roetling, J.A. Yield stress behaviour of polymethylmethacrylate. Polymer 1965, 6, 311–317. [Google Scholar] [CrossRef]
- Bauwens, J.C.; Bauwens-Crowet, C.; Homès, G. Tensile yield-stress behavior of poly(vinyl chloride) and polycarbonate in the glass transition region. J. Polym. Sci. Part A-2 Polym. Phys. 1969, 7, 1745–1754. [Google Scholar] [CrossRef]
- Bowden, P.B.; Raha, S. A molecular model for yield and flow in amorphous glassy polymers making use of a dislocation analogue. Philos. Mag. 1974, 29, 149–166. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. Evolution of plastic anisotropy in amorphous polymers during finite straining. Int. J. Plast. 1993, 9, 697–720. [Google Scholar] [CrossRef]
- Raghava, R.; Caddell, R.M.; Yeh, G.S. The macroscopic yield behaviour of polymers. J. Mater. Sci. 1973, 8, 225–232. [Google Scholar] [CrossRef]
- Caddell, R.M.; Raghava, R.S.; Atkins, A.G. Pressure dependent yield criteria for polymers. Mater. Sci. Eng. 1974, 13, 113–120. [Google Scholar] [CrossRef]
- Whitney, W.; Andrews, R.D. Yielding of glassy polymers: Volume effects. J. Polym. Sci. Part C: Polym. Symp. 1967, 16, 2981–2990. [Google Scholar] [CrossRef]
- Mulliken, A.; Boyce, M. Mechanics of the rate-dependent elastic–plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Bowden, P.; Jukes, J. The plastic flow of isotropic polymers. J. Mater. Sci. 1972, 7, 52–63. [Google Scholar] [CrossRef]
- Ratai, A.; Kolling, S.; Haufe, A.; Feucht, M.; Bois, P.D. Validation and Verification of Plastics under Multiaxial Loading. In Proceedings of the 7th GERMAN LS-DYNA Forum, Bamberg, Germany, 30 September 2008. [Google Scholar]
- Kolling, S.; Haufe, A.; Feucht, M.; Bois, P.D. A Constitutive Formulation for Polymers Subjected to High Strain Rates. In Proceedings of the 9th International LS-DYNA User Conference, Dearborn, MI, USA, 1–6 June 2008. [Google Scholar]
- Vitali, M.N.-M. Characterization of Polyolefins for Design under Impact: From True Stress/Local Strain Measurements to the FE Simulation with LS-Dyna Mat. SAMP-1. In Proceedings of 7th German LSDYNA Forum, Bamberg, Germany, 30 September 2008. [Google Scholar]
- Daiyan, H.; Andreassen, E.; Grytten, F.; Osnes, H.; Gaarder, R.H. Shear testing of polypropylene materials analysed by digital image correlation and numerical simulations. Exp. Mech. 2012, 52, 1355–1369. [Google Scholar] [CrossRef]
- Standard, A.S.T.M. Standard Test Method for Tensile Properties of Plastics; ASTM International: Designation: West Conshohocken, PA, USA, 2014; Volume D638, pp. 1–14. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). Livermore Software Technology Corporation, LS DYNA Version 971, Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2017; Volume II Material Models. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). Livermore Software Technology Corporation, LS DYNA Version 971, Theory Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2017. [Google Scholar]
- Lemaitre, J. A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
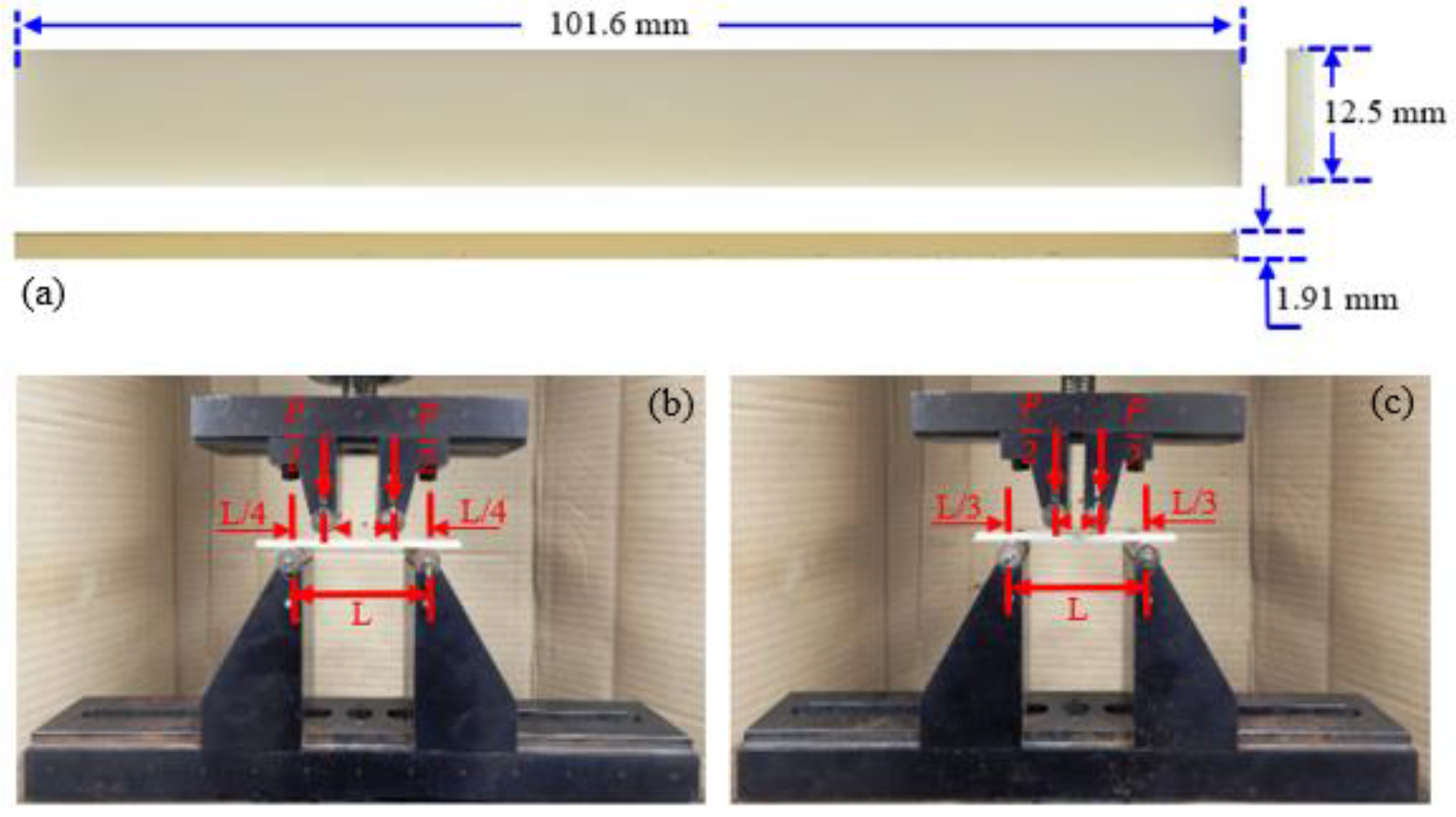
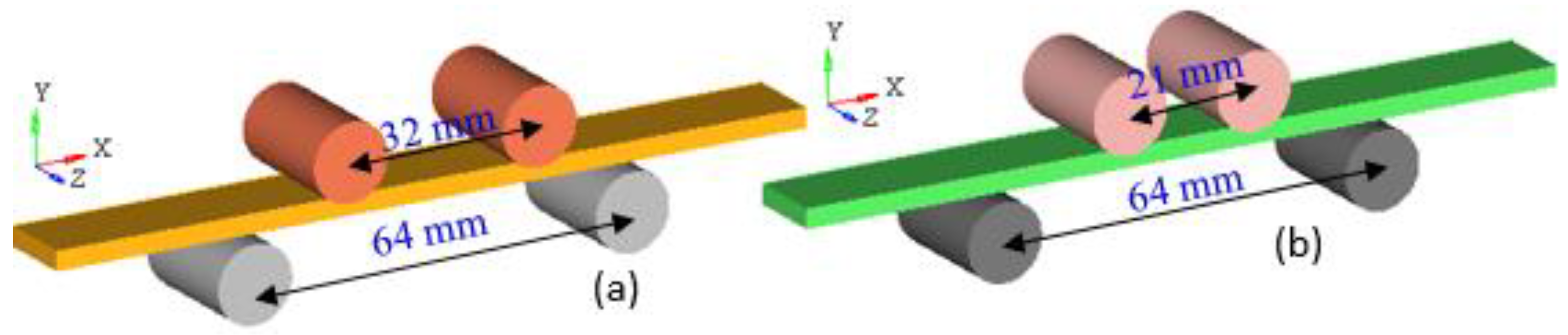

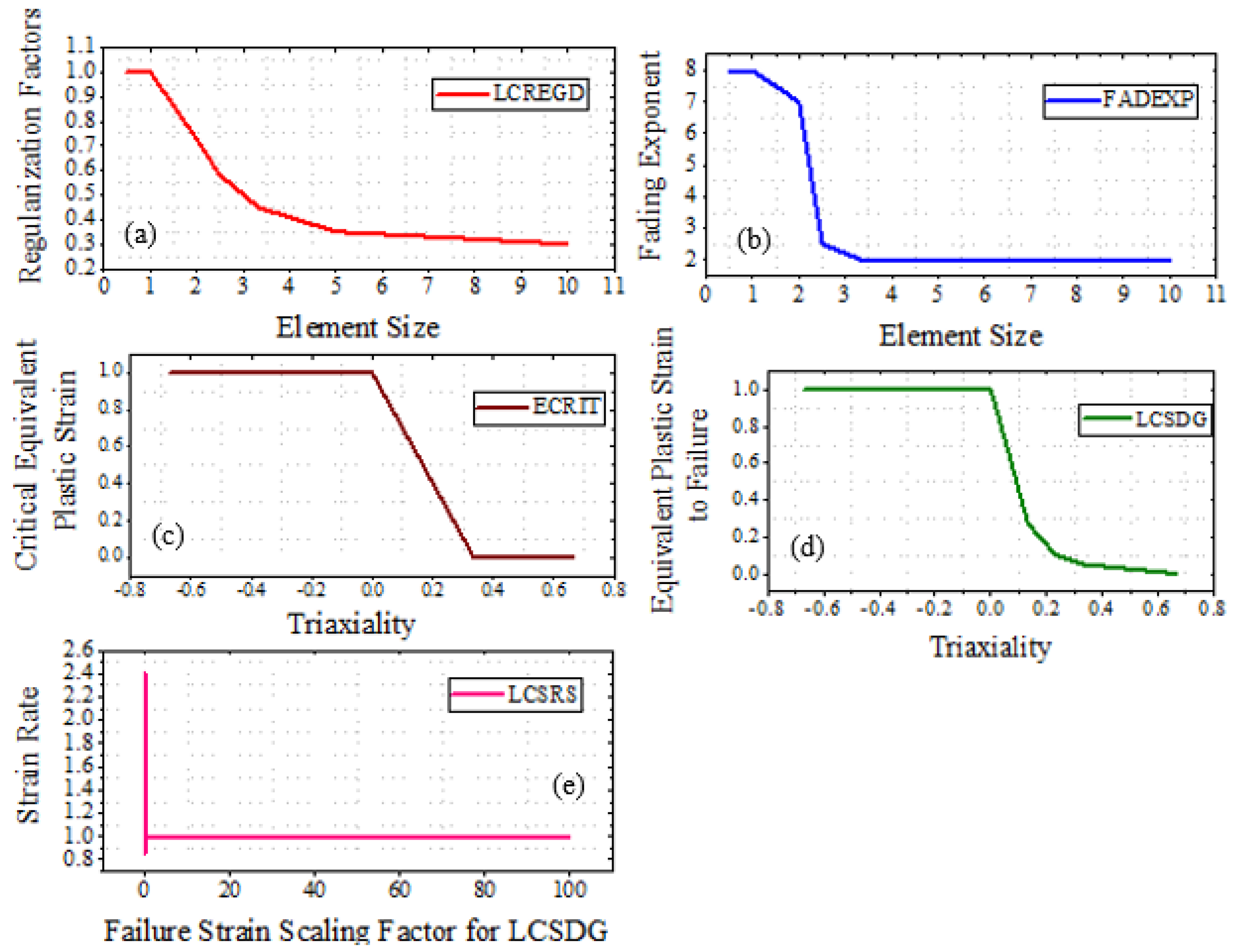
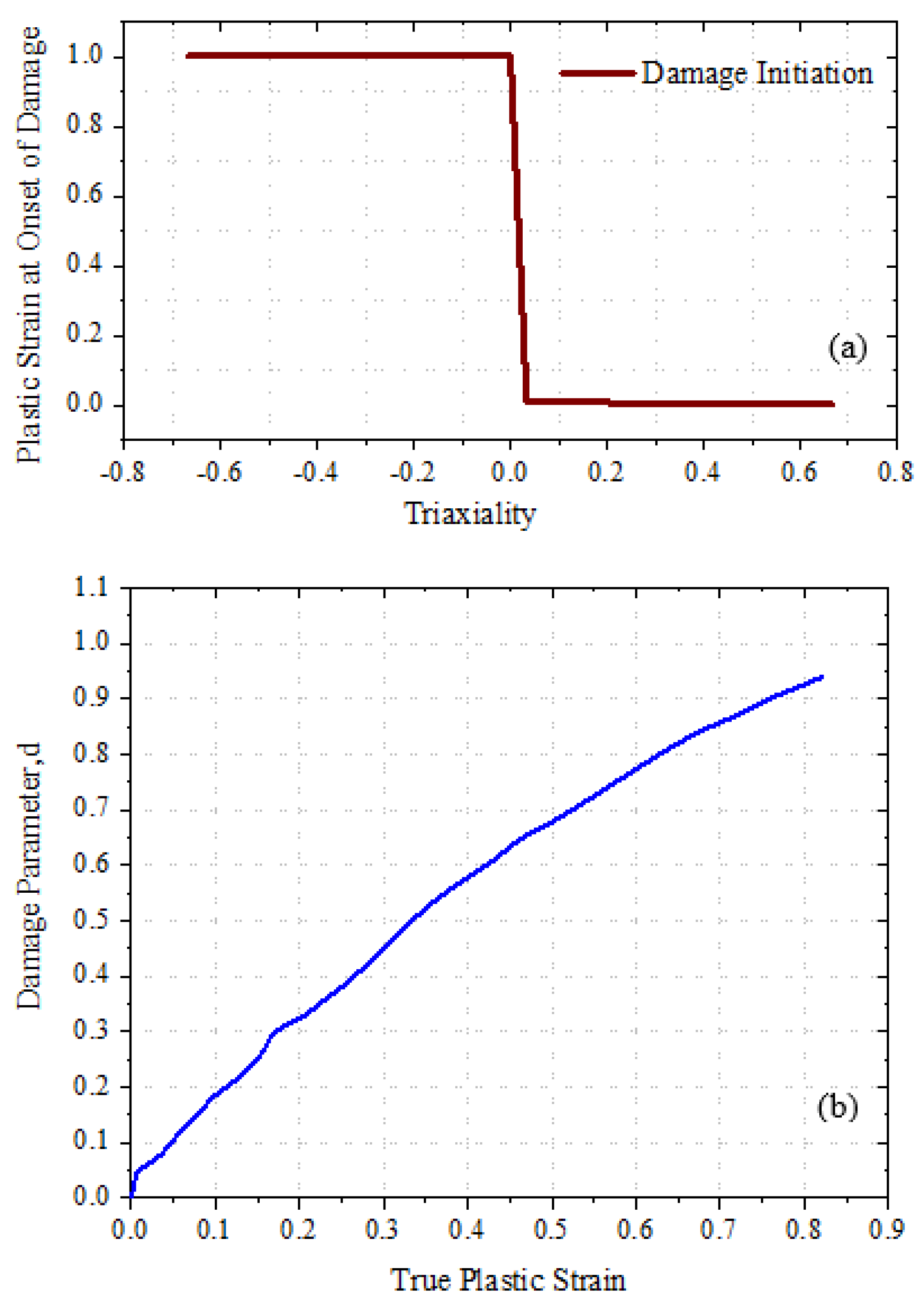
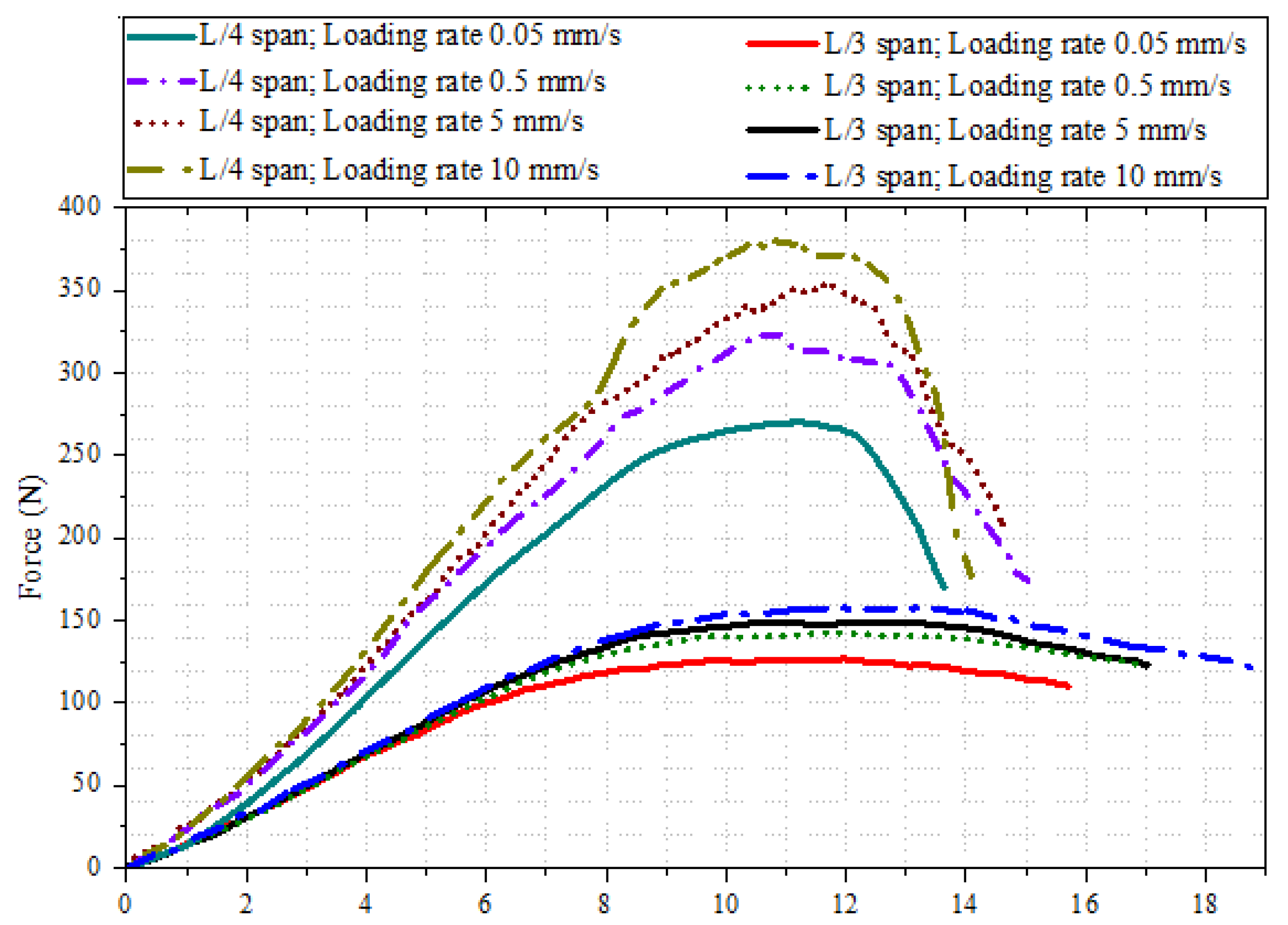
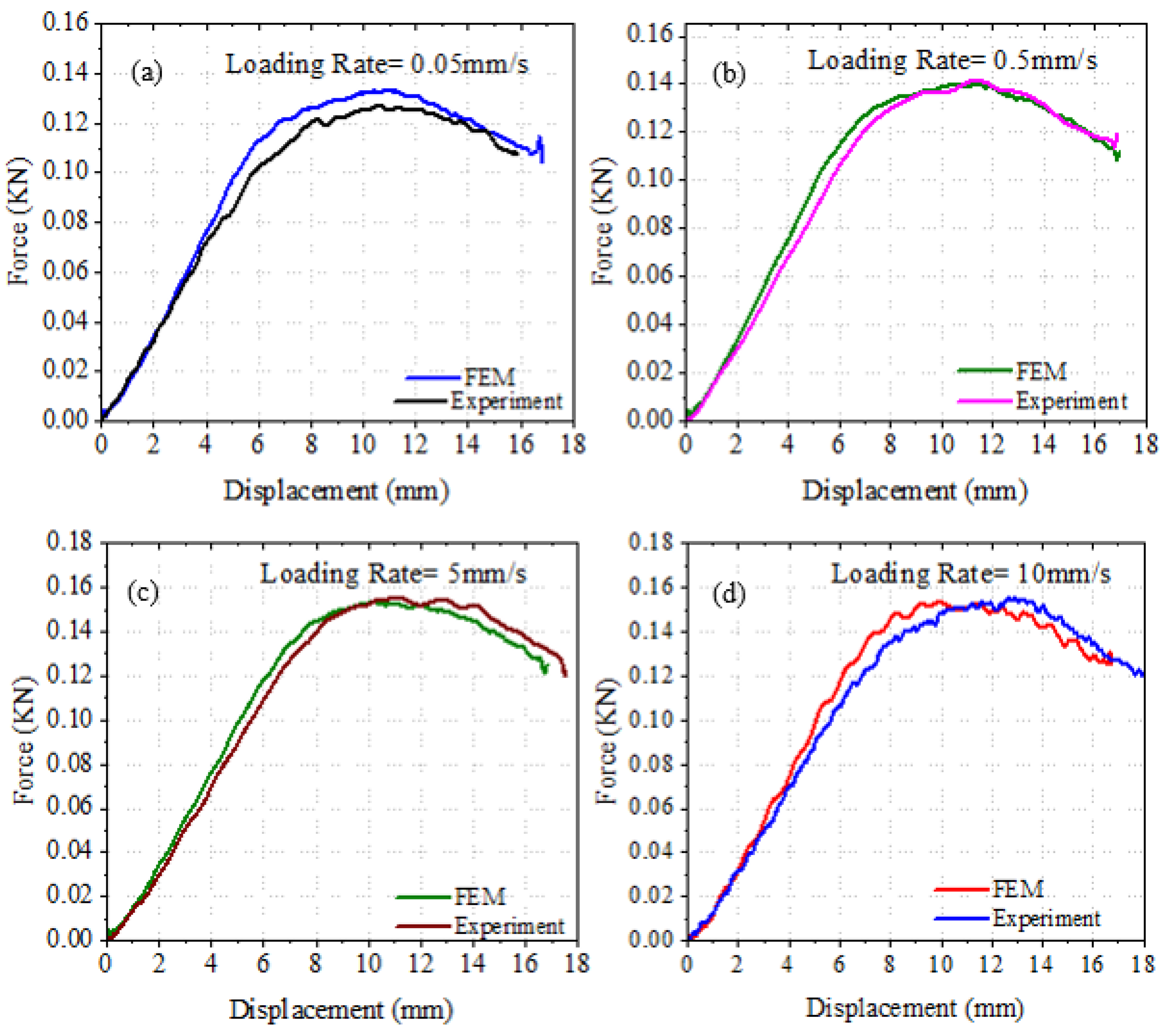
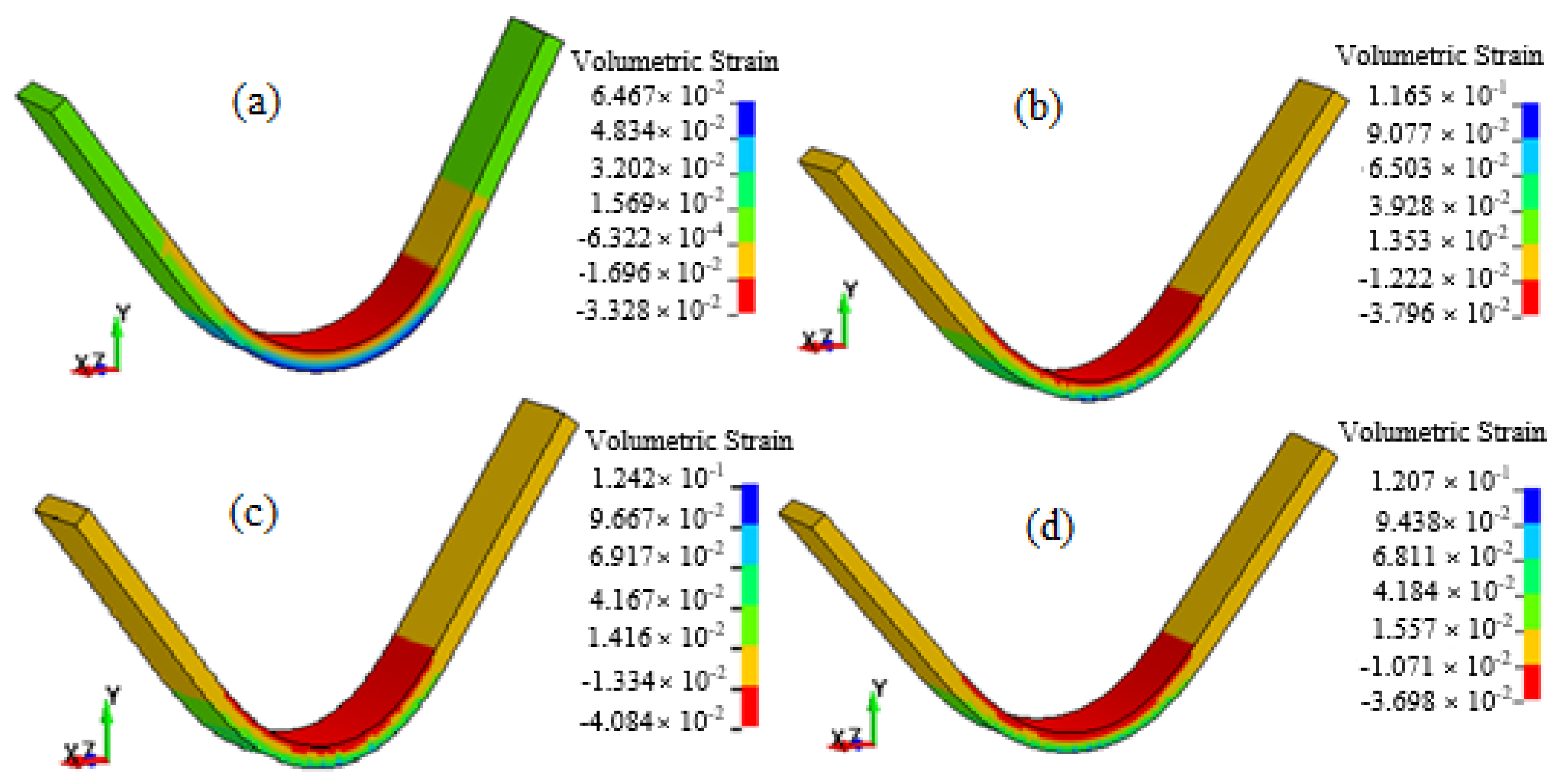
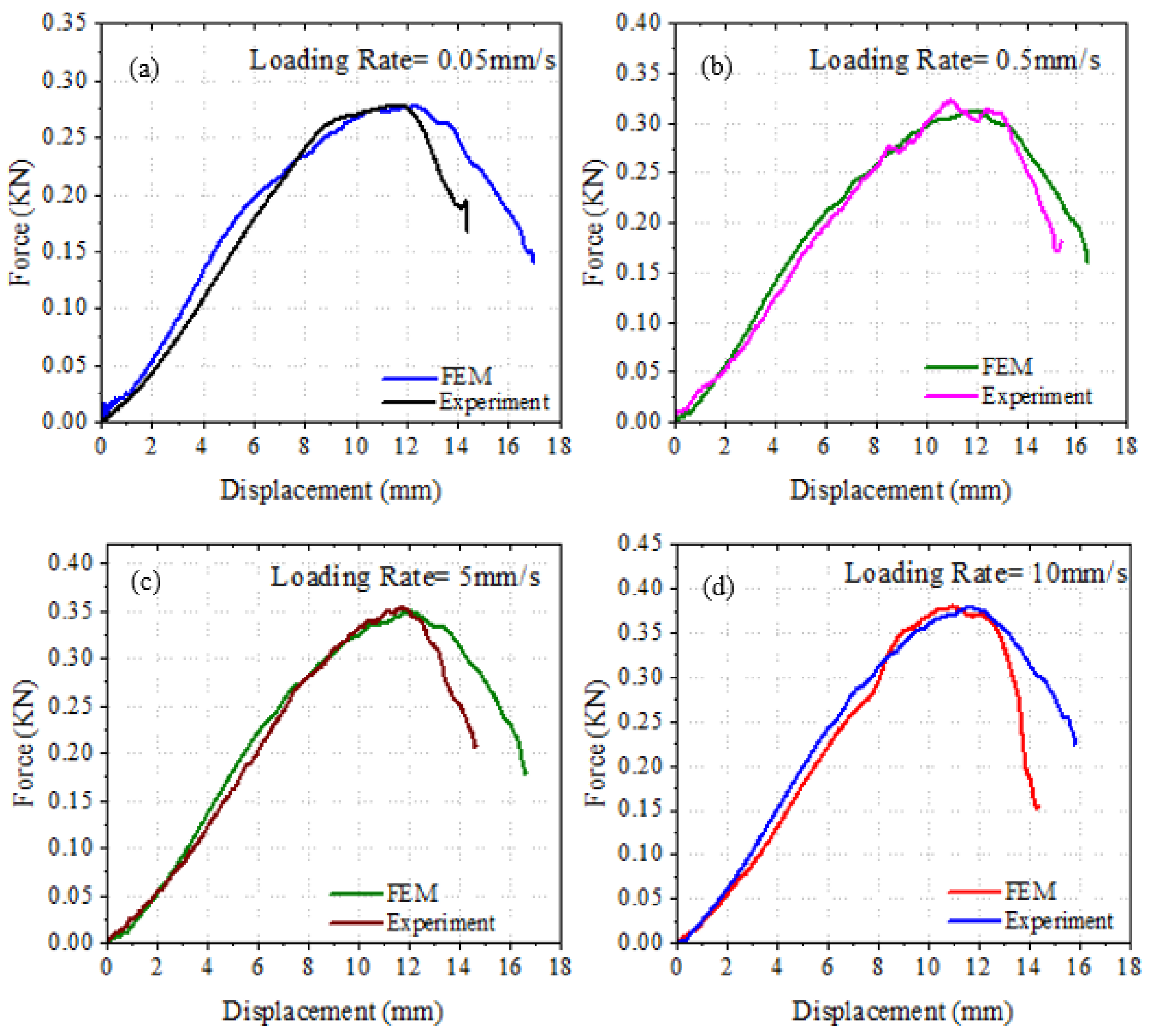


| Strain Rate (1/s) | True Tensile Elastic Modulus (GPa) |
|---|---|
| 0.001 | 1.826 |
| 0.02 | 1.938 |
| 0.1 | 2.026 |
| 0.2 | 2.070 |
| Bulk Modulus (GPa) | Tensile Modulus (GPa) | Poisson’s Ratio | Density (tonne/mm3) |
|---|---|---|---|
| 3.59 | 1.9735 | 0.38 | 1024 × 10−12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhaliwal, G.S.; Dundar, M.A. Four Point Flexural Response of Acrylonitrile–Butadiene–Styrene. J. Compos. Sci. 2020, 4, 63. https://doi.org/10.3390/jcs4020063
Dhaliwal GS, Dundar MA. Four Point Flexural Response of Acrylonitrile–Butadiene–Styrene. Journal of Composites Science. 2020; 4(2):63. https://doi.org/10.3390/jcs4020063
Chicago/Turabian StyleDhaliwal, Gurpinder S., and Mehmet Akif Dundar. 2020. "Four Point Flexural Response of Acrylonitrile–Butadiene–Styrene" Journal of Composites Science 4, no. 2: 63. https://doi.org/10.3390/jcs4020063
APA StyleDhaliwal, G. S., & Dundar, M. A. (2020). Four Point Flexural Response of Acrylonitrile–Butadiene–Styrene. Journal of Composites Science, 4(2), 63. https://doi.org/10.3390/jcs4020063




