Mechanical Properties of Nacre-Like Composites: A Bottom-Up Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Organic Matrix
2.2. Aragonite
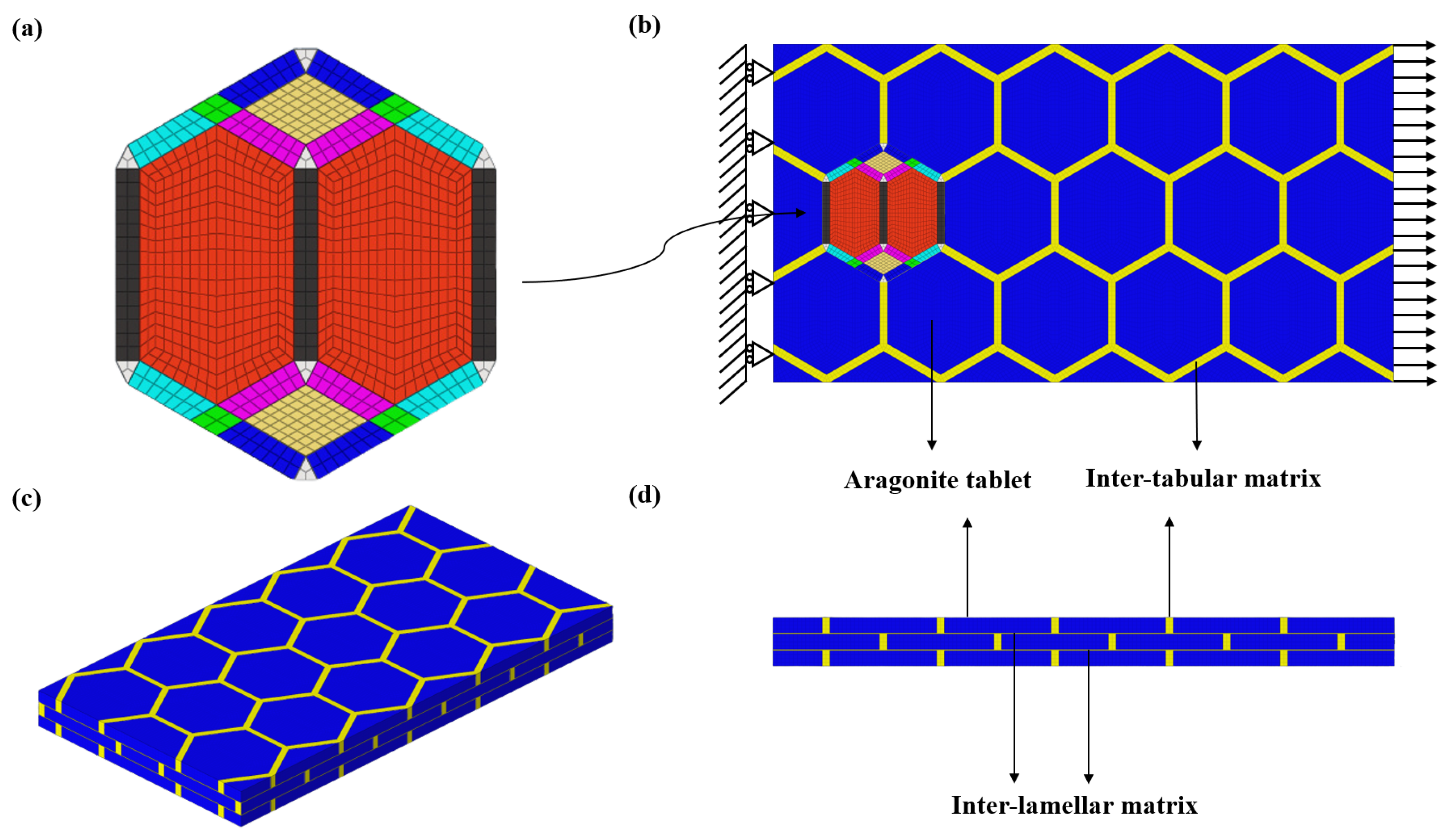
2.3. Construction of 3D FE Model
3. Results and Discussion
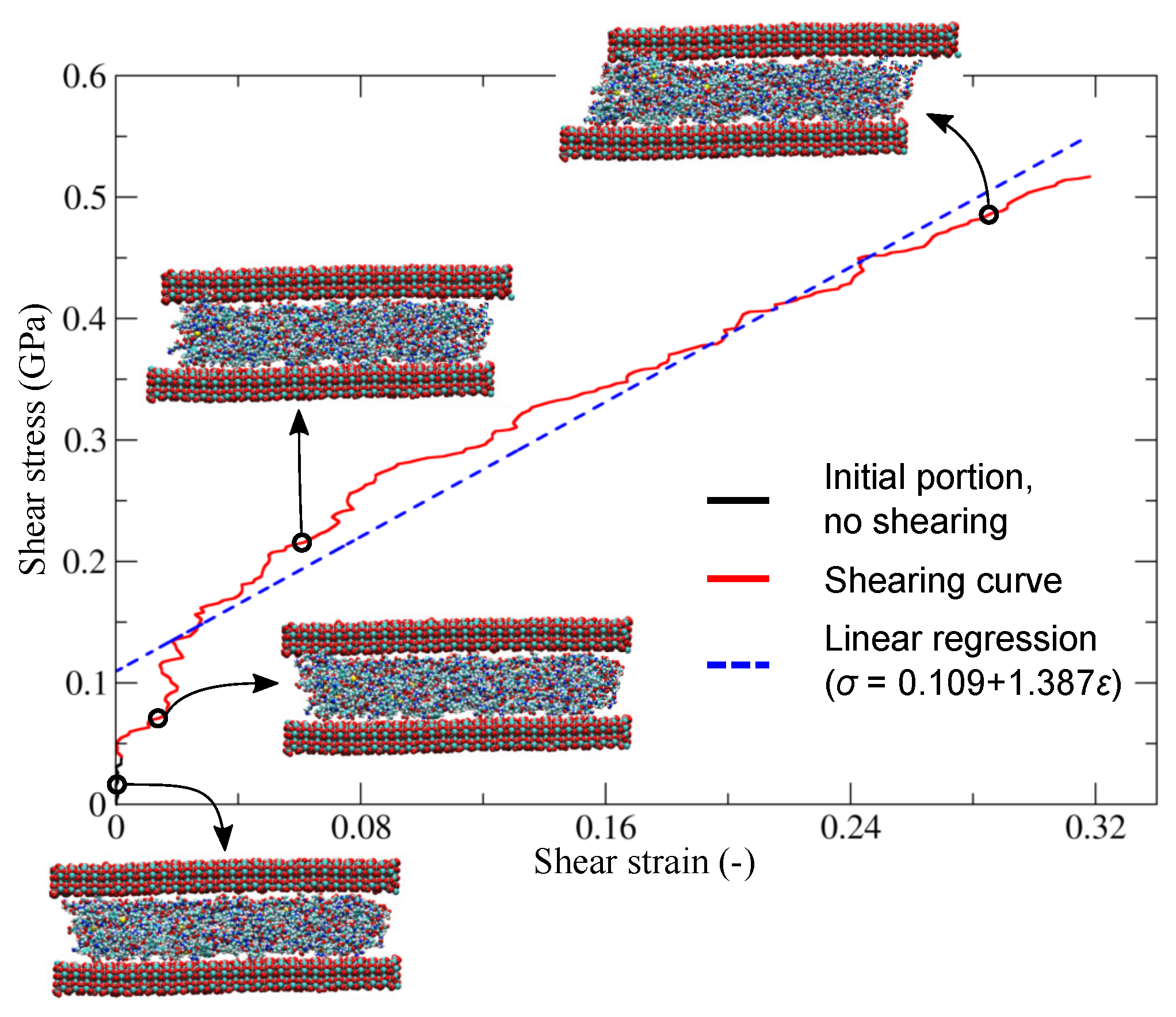
3.1. Shear Modulus of Organic Matrix
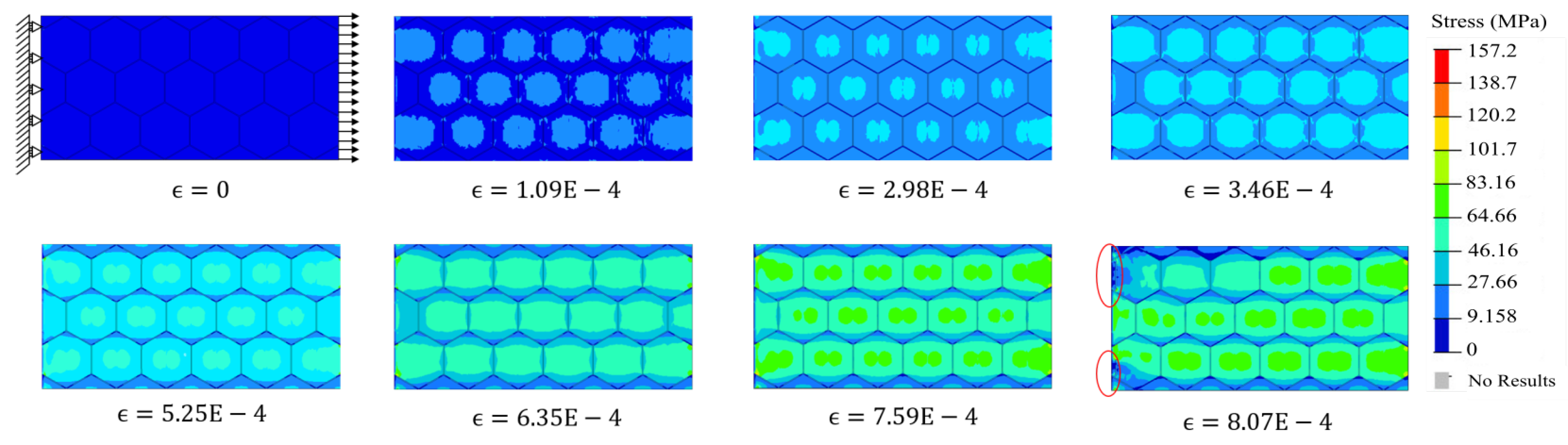
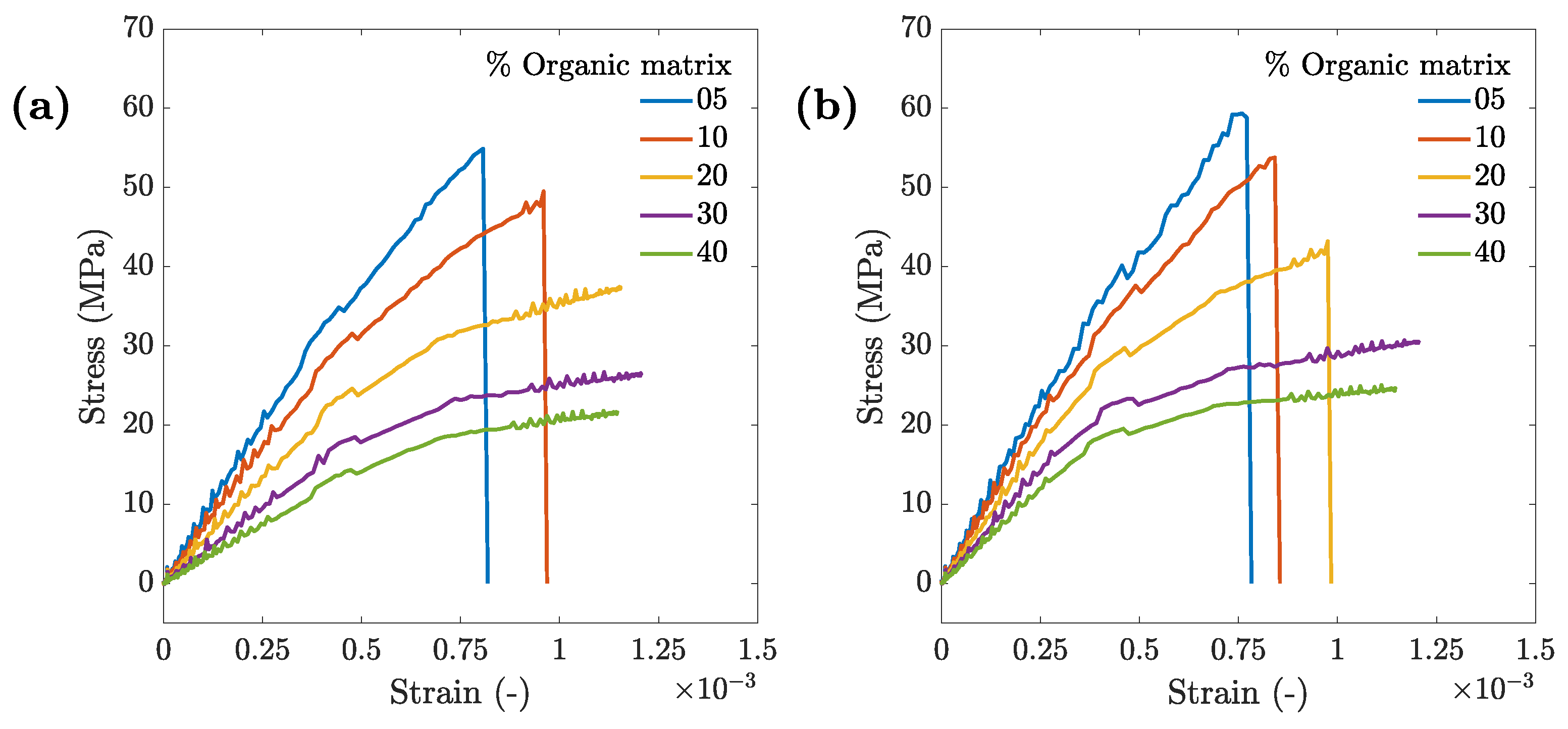
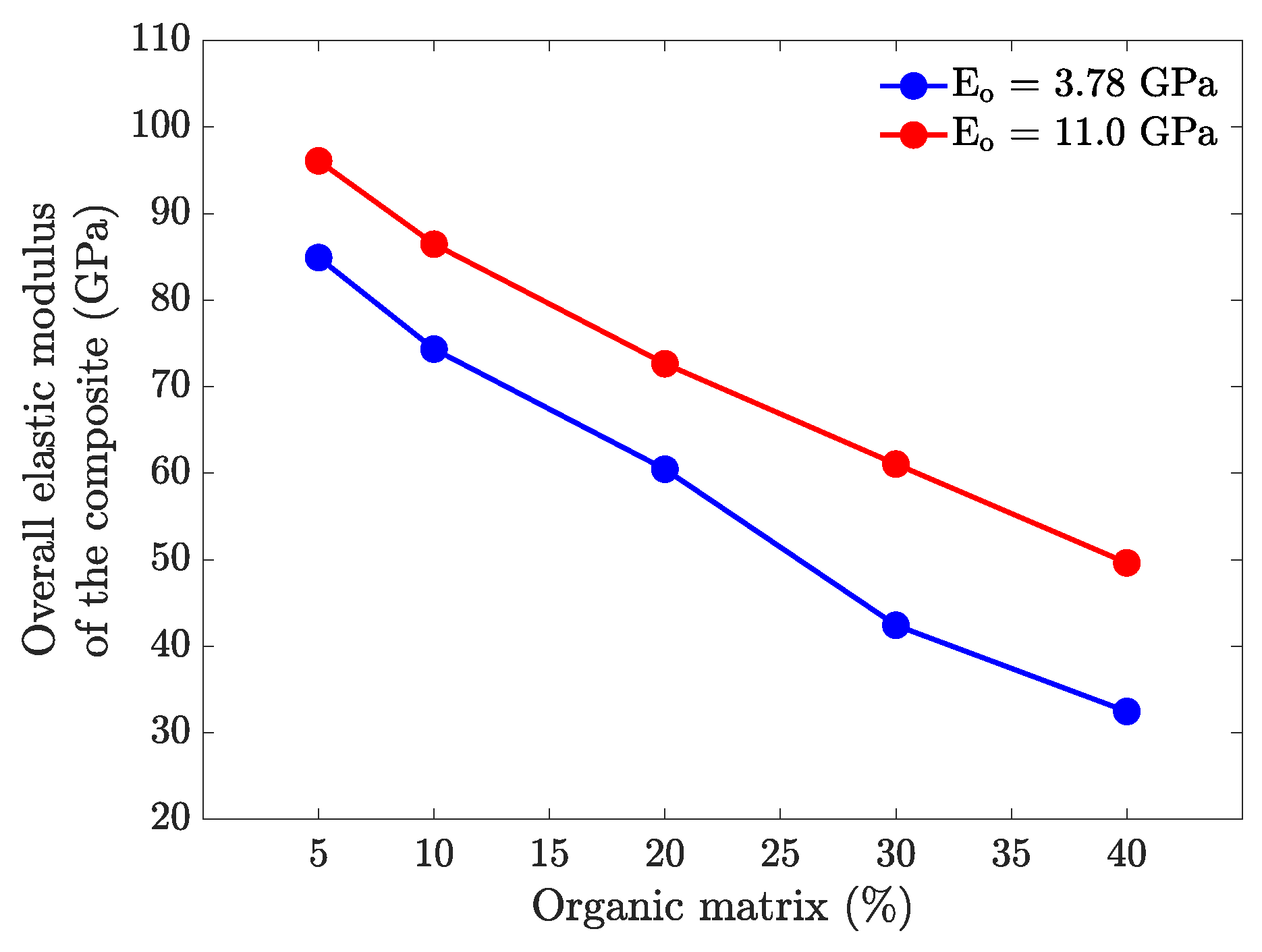
3.2. Stress–Strain Response of the 3D FE Nacre Models
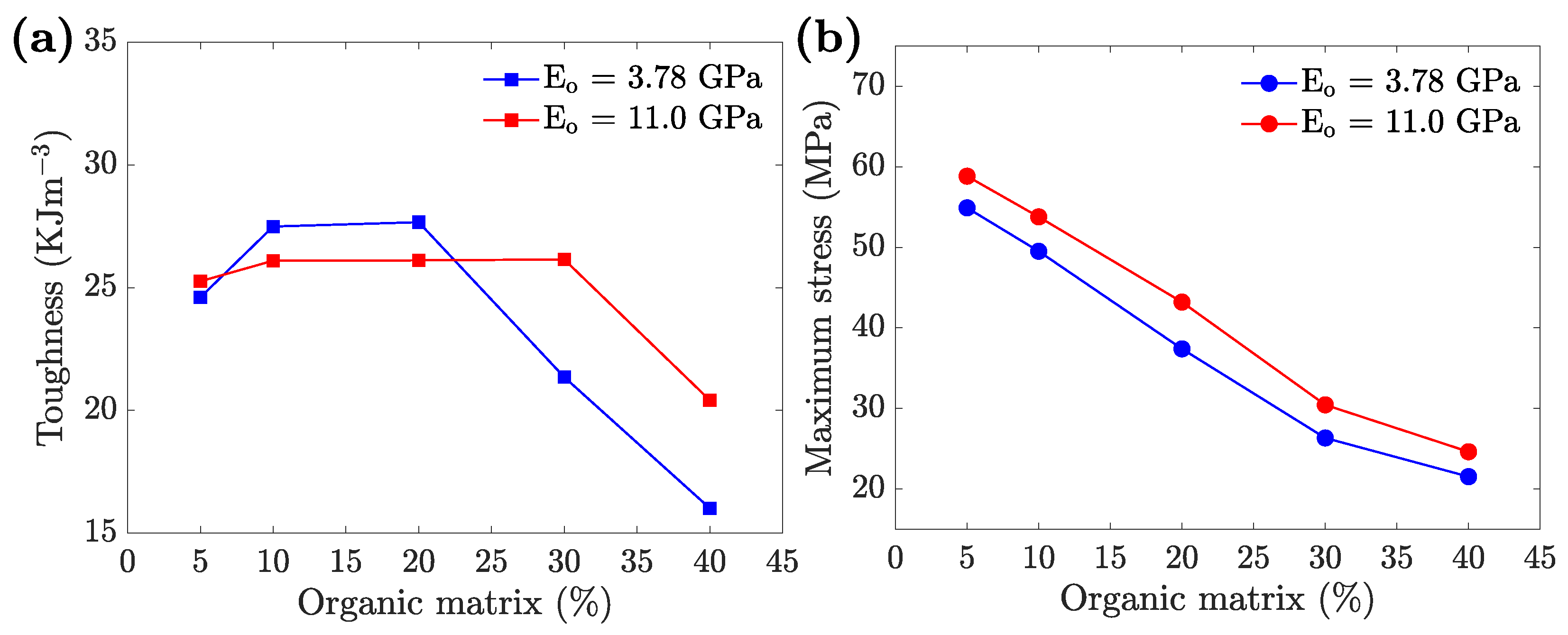
3.3. Toughness–Strength Trade-Off
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jackson, A.P.; Vincent, J.F.V.; Turner, R.M. The Mechanical Design of Nacre. Proc. R. Soc. Lond. B Biol. Sci. 1988, 234, 415–440. [Google Scholar]
- Sun, J.; Bhushan, B. Hierarchical structure and mechanical properties of nacre: a review. RSC Adv. 2012, 2, 7617–7632. [Google Scholar] [CrossRef]
- Finnemore, A.; Cunha, P.; Shean, T.; Vignolini, S.; Guldin, S.; Oyen, M.; Steiner, U. Biomimetic layer-by-layer assembly of artificial nacre. Nat. Commun. 2012, 3, 966. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Chen, Y. Molecular origin of the sawtooth behavior and the toughness of nacre. Mater. Sci. Eng. C 2012, 32, 1542–1547. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, S.; Xiong, L.; Hong, Y.; Chen, Y. Nanoscale toughening mechanism of nacre tablet. J. Mech. Behav. Biomed. Mater. 2016, 53, 200–209. [Google Scholar] [CrossRef]
- Barthelat, F.; Li, C.M.; Comi, C.; Espinosa, H.D. Mechanical properties of nacre constituents and their impact on mechanical performance. J. Mater. Res. 2006, 21, 1977–1986. [Google Scholar] [CrossRef]
- Patil, S.P.; Heider, Y.; Hernandez Padilla, C.A.; Cruz-Chú, E.R.; Markert, B. A comparative molecular dynamics-phase-field modeling approach to brittle fracture. Comput. Methods Appl. Mech. Eng. 2016, 312, 117–129. [Google Scholar] [CrossRef]
- Cruz-Chu, E.R.; Xiao, S.; Patil, S.P.; Gkagkas, K.; Gräter, F. Organic Filling Mitigates Flaw-Sensitivity of Nanoscale Aragonite. ACS Biomater. Sci. Eng. 2017, 3, 260–268. [Google Scholar] [CrossRef]
- Padilla, C.H.; Patil, S.; Heider, Y.; Markert, B. 3D modelling of brittle fracture using a joint all-atom and phase-field approach. GAMM-Mitteilungen 2017, 40, 91–101. [Google Scholar] [CrossRef]
- Patil, S.P.; Heider, Y. A Review on Brittle Fracture Nanomechanics by All-Atom Simulations. Nanomaterials 2019, 9, 1050. [Google Scholar] [CrossRef]
- Barthelat, F.; Espinosa, H.D. An Experimental Investigation of Deformation and Fracture of Nacre-Mother of Pearl. Exp. Mech. 2007, 47, 311–324. [Google Scholar] [CrossRef]
- Barthelat, F. Nacre from mollusk shells: a model for high-performance structural materials. Bioinspir. Biomim. 2010, 5, 035001. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.Y.; Lin, A.Y.M.; Lin, Y.S.; Seki, Y.; Stokes, A.G.; Peyras, J.; Olevsky, E.A.; Meyers, M.A.; McKittrick, J. Structure and mechanical properties of selected biological materials. J. Mech. Behav. Biomed. Mater. 2008, 1, 208–226. [Google Scholar] [CrossRef]
- Katti, K.S.; Katti, D.R.; Mohanty, B. Biomimetic Lessons Learnt from Nacre. Biomim. Learn. Nat. 2010, 1, 193. [Google Scholar]
- Zhang, B.; Wustman, B.A.; Morse, D.; Evans, J.S. Model peptide studies of sequence regions in the elastomeric biomineralization protein, Lustrin A. I. The C-domain consensus-PG-, -NVNCT-motif. Biopolymers 2002, 63, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Meyers, M.A.; Lin, A.Y.M.; Chen, P.Y.; Muyco, J. Mechanical strength of abalone nacre: Role of the soft organic layer. J. Mech. Behav. Biomed. Mater. 2008, 1, 76–85. [Google Scholar] [CrossRef]
- Meyers, M.; Lim, C.; Li, A.; Nizam, B.H.; Tan, E.; Seki, Y.; McKittrick, J. The role of organic intertile layer in abalone nacre. Mater. Sci. Eng. C 2009, 29, 2398–2410. [Google Scholar] [CrossRef]
- Currey, J.D.; Zioupos, P.; Peter, D.; Casinos, A. Mechanical properties of nacre and highly mineralized bone. Proc. R. Soc. Lond. B Biol. Sci. 2001, 268, 107–111. [Google Scholar] [CrossRef]
- Ghosh, P.; Katti, D.R.; Katti, K.S. Mineral Proximity Influences Mechanical Response of Proteins in Biological Mineral-Protein Hybrid Systems. Biomacromolecules 2007, 8, 851–856. [Google Scholar] [CrossRef]
- Mann, K.; Siedler, F.; Treccani, L.; Heinemann, F.; Fritz, M. Perlinhibin, a cysteine-, histidine-, and arginine-rich miniprotein from abalone (Haliotis laevigata) nacre, inhibits in vitro calcium carbonate crystallization. Biophys. J. 2007, 93, 1246–1254. [Google Scholar] [CrossRef]
- Treccani, L.; Mann, K.; Heinemann, F.; Fritz, M. Perlwapin, an abalone nacre protein with three four-disulfide core (whey acidic protein) domains, inhibits the growth of calcium carbonate crystals. Biophys. J. 2006, 91, 2601–2608. [Google Scholar] [CrossRef] [PubMed]
- Weiss, I.M.; Göhring, W.; Fritz, M.; Mann, K. Perlustrin, a Haliotis laevigata (Abalone) Nacre Protein, Is Homologous to the Insulin-like Growth Factor Binding Protein N-Terminal Module of Vertebrates. Biochem. Biophys. Res. Commun. 2001, 285, 244–249. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.L.; Schäffer, T.E.; Viani, M.; Thompson, J.B.; Frederick, N.A.; Kindt, J.; Belcher, A.; Stucky, G.D.; Morse, D.E.; Hansma, P.K. Molecular mechanistic origin of the toughness of natural adhesives, fibres and composites. Nature 1999, 399, 761–763. [Google Scholar] [CrossRef]
- Shen, X.; Belcher, A.M.; Hansma, P.K.; Stucky, G.D.; Morse, D.E. Molecular cloning and characterization of lustrin A, a matrix protein from shell and pearl nacre of Haliotis rufescens. J. Biol. Chem. 1997, 272, 32472–32481. [Google Scholar] [CrossRef] [PubMed]
- Weiss, I.M.; Kaufmann, S.; Mann, K.; Fritz, M. Purification and characterization of perlucin and perlustrin, two new proteins from the shell of the mollusc Haliotis laevigata. Biochem. Biophys. Res. Commun. 2000, 267, 17–21. [Google Scholar] [CrossRef]
- Mann, K.; Weiss, I.M.; André, S.; Gabius, H.J.; Fritz, M. The amino-acid sequence of the abalone (Haliotis laevigata) nacre protein perlucin. Detection of a functional C-type lectin domain with galactose/mannose specificity. Eur. J. Biochem. 2000, 267, 5257–5264. [Google Scholar] [CrossRef]
- Ghosh, P.; Katti, D.R.; Katti, K.S. Mineral and Protein-Bound Water and Latching Action Control Mechanical Behavior at Protein-Mineral Interfaces in Biological Nanocomposites. J. Nanomater. 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Xu, Z.H.; Yang, Y.; Huang, Z.; Li, X. Elastic modulus of biopolymer matrix in nacre measured using coupled atomic force microscopy bending and inverse finite element techniques. Mater. Sci. Eng. C 2011, 31, 1852–1856. [Google Scholar] [CrossRef]
- Currey, J. Mechanical properties of mother of pearl in tension. Proc. R. Soc. Lond. B Biol. Sci. 1977, 196, 443–463. [Google Scholar]
- Vincent, J.F.; Currey, J.D. The Mechanical Properties of Biological Materials: Symposia of the Society for Experimental Biology, Number XXXIV [edited by JFV Vincent and JD Currey].; Cambridge University Press for the Society for Experimental Biology: Cambridge, UK, 1980. [Google Scholar]
- Weiner, S.; Traub, W.; Parker, S. Macromolecules in mollusc shells and their functions in biomineralization. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1984, 304, 425–434. [Google Scholar]
- Katti, D.; Katti, K.; Sopp, J.; Sarikaya, M. 3D finite element modeling of mechanical response in nacre-based hybrid nanocomposites. Comput. Theor. Polym. Sci. 2001, 11, 397–404. [Google Scholar] [CrossRef]
- Katti, K.S.; Katti, D.R.; Pradhan, S.M.; Bhosle, A. Platelet interlocks are the key to toughness and strength in nacre. J. Mater. Res. 2005, 20, 1097–1100. [Google Scholar] [CrossRef]
- Lin, A.Y.M.; Meyers, M.A. Interfacial shear strength in abalone nacre. J. Mech. Behav. Biomed. Mater. 2009, 2, 607–612. [Google Scholar] [CrossRef] [PubMed]
- Katti, D.R.; Katti, K.S. Modeling microarchitecture and mechanical behavior of nacre using 3D finite element techniques Part I Elastic properties. J. Mater. Sci. 2001, 36, 1411–1417. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Meille, S.; Van de Moortèle, B.; Stevenson, A.; Deville, S. Strong, Tough and Stiff Bioinspired Ceramics from Brittle Constituents. Nat. Mater. 2014, 13, 508–514. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Nalla, R.; Tomsia, A. Freezing as a Path to Build Complex Composites. Science 2006, 311, 515–518. [Google Scholar] [CrossRef]
- Corni, I.; Harvey, T.J.; Wharton, J.A.; Stokes, K.R.; Walsh, F.C.; Wood, R.J.K. A review of experimental techniques to produce a nacre-like structure. Bioinspir. Biomim. 2012, 7, 031001. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, L. Nacre-Inspired Structural Composites: Performance-Enhancement Strategy and Perspective. Adv. Mater. 2017, 29, 1702903. [Google Scholar] [CrossRef]
- Radi, K.; Jauffrès, D.; Deville, S.; Martin, C.L. Elasticity and fracture of brick and mortar materials using discrete element simulations. J. Mech. Phys. Solids 2019, 126, 101–116. [Google Scholar] [CrossRef]
- Zentz, F.; Bédouet, L.; Almeida, M.J.; Milet, C.; Lopez, E.; Giraud, M. Characterization and quantification of chitosan extracted from nacre of the abalone Haliotis tuberculata and the oyster Pinctada maxima. Mar. Biotechnol. 2001, 3, 36–44. [Google Scholar] [CrossRef]
- Walters, D.A.; Smith, B.L.; Belcher, A.M.; Paloczi, G.T.; Stucky, G.D.; Morse, D.E.; Hansma, P.K. Modification of calcite crystal growth by abalone shell proteins: an atomic force microscope study. Biophys. J. 1997, 72, 1425–1433. [Google Scholar] [CrossRef]
- Schäffer, T.E.; Ionescu-Zanetti, C.; Proksch, R.; Fritz, M.; Walters, D.A.; Almqvist, N.; Zaremba, C.M.; Belcher, A.M.; Smith, B.L.; Stucky, G.D.; et al. Does Abalone Nacre Form by Heteroepitaxial Nucleation or by Growth through Mineral Bridges? Chem. Mater. 1997, 9, 1731–1740. [Google Scholar] [CrossRef]
- Falini, G.; Albeck, S.; Weiner, S.; Addadi, L. Control of Aragonite or Calcite Polymorphism by Mollusk Shell Macromolecules. Science 1996, 271, 67–69. [Google Scholar] [CrossRef]
- Levi, Y.; Albeck, S.; Brack, A.; Weiner, S.; Addadi, L. Control Over Aragonite Crystal Nucleation and Growth: An In Vitro Study of Biomineralization. Chem. Eur. J. 1998, 4, 389–396. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Liu, L.G.; Chen, C.C.; Lin, C.C.; Yang, Y.J. Elasticity of single-crystal aragonite by Brillouin spectroscopy. Phys. Chem. Miner. 2005, 32, 97–102. [Google Scholar] [CrossRef]
- Levy, M.; Bass, H.; Keppens, V. Handbook of Elastic Properties of Solids, Liquids, and Gases; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Barthelat, F.; Espinosa, H.D. Elastic Properties of Nacre Aragonite Tablets. In Proceedings of the SEM Annual Conference and Exposition on Experimental and Applied Mechanics, Charlotte, NC, USA, 2–4 June 2003. [Google Scholar]
- Livermore Software Technology Corporation. LS-DYNA Keyword Users Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2010. [Google Scholar]
- Livermore Software Technology Corporation. Ls-Pre/Post; Livermore Software Technology Corporation: Livermore, CA, USA, 2011. [Google Scholar]
- Patil, S.P.; Markert, B.; Gräter, F. Rate-dependent behavior of the amorphous phase of spider dragline silk. Biophys. J. 2014, 106, 2511–2518. [Google Scholar] [CrossRef]
- Patil, S.P.; Xiao, S.; Gkagkas, K.; Markert, B.; Gräter, F. Viscous friction between crystalline and amorphous phase of dragline silk. PLoS ONE 2014, 9, e104832. [Google Scholar] [CrossRef] [PubMed]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, M.; Patil, S.P.; Markert, B. Mechanical Properties of Nacre-Like Composites: A Bottom-Up Approach. J. Compos. Sci. 2020, 4, 35. https://doi.org/10.3390/jcs4020035
Raj M, Patil SP, Markert B. Mechanical Properties of Nacre-Like Composites: A Bottom-Up Approach. Journal of Composites Science. 2020; 4(2):35. https://doi.org/10.3390/jcs4020035
Chicago/Turabian StyleRaj, Mayank, Sandeep P. Patil, and Bernd Markert. 2020. "Mechanical Properties of Nacre-Like Composites: A Bottom-Up Approach" Journal of Composites Science 4, no. 2: 35. https://doi.org/10.3390/jcs4020035
APA StyleRaj, M., Patil, S. P., & Markert, B. (2020). Mechanical Properties of Nacre-Like Composites: A Bottom-Up Approach. Journal of Composites Science, 4(2), 35. https://doi.org/10.3390/jcs4020035







