Progress in Experimental and Theoretical Evaluation Methods for Textile Permeability
Abstract
:1. Introduction
1.1. Problem Statement
- The drawing of the part
- The viscosity of the resin
- The permeability tensor
1.2. State of Art on Reviews
1.3. Article Structure
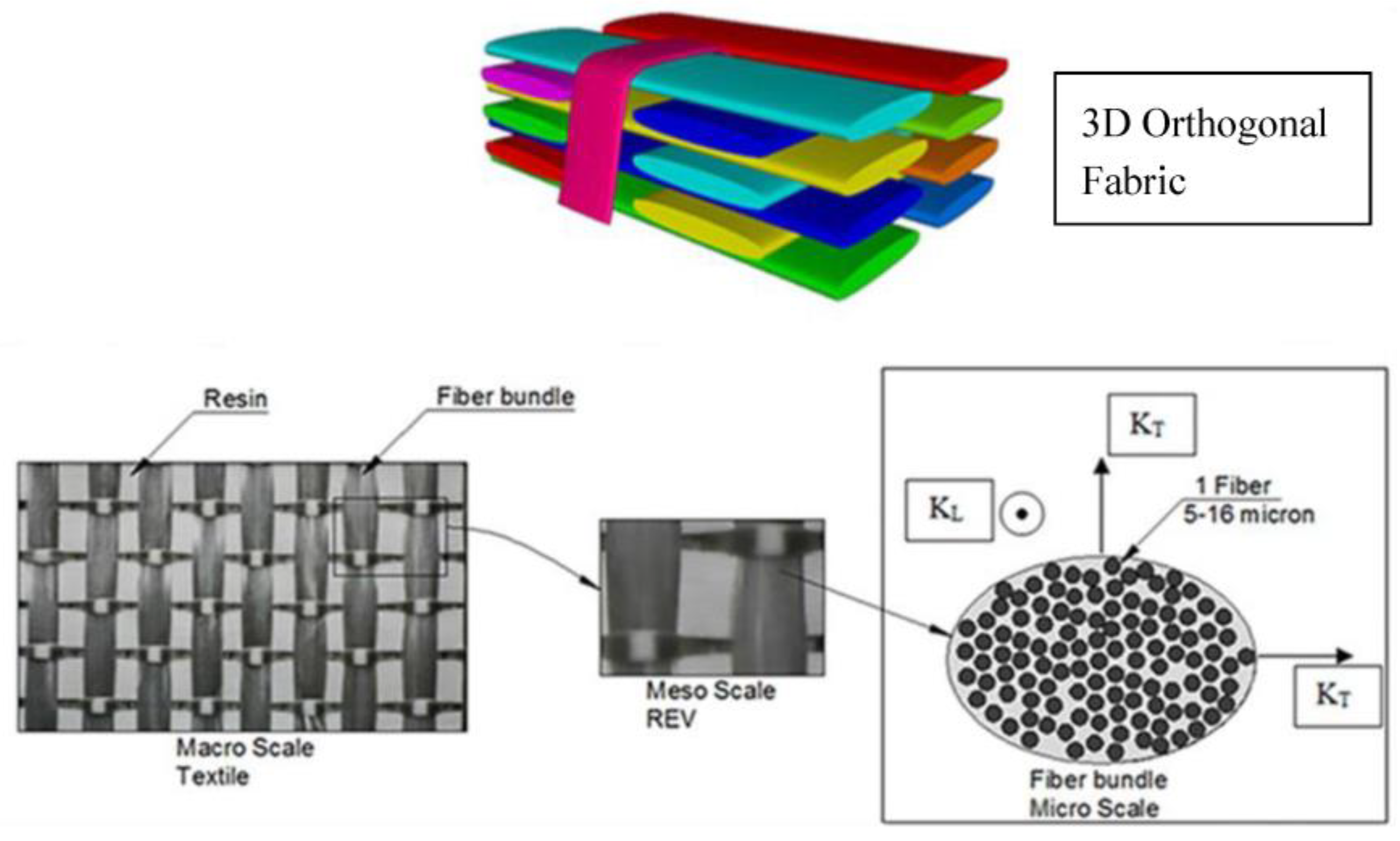
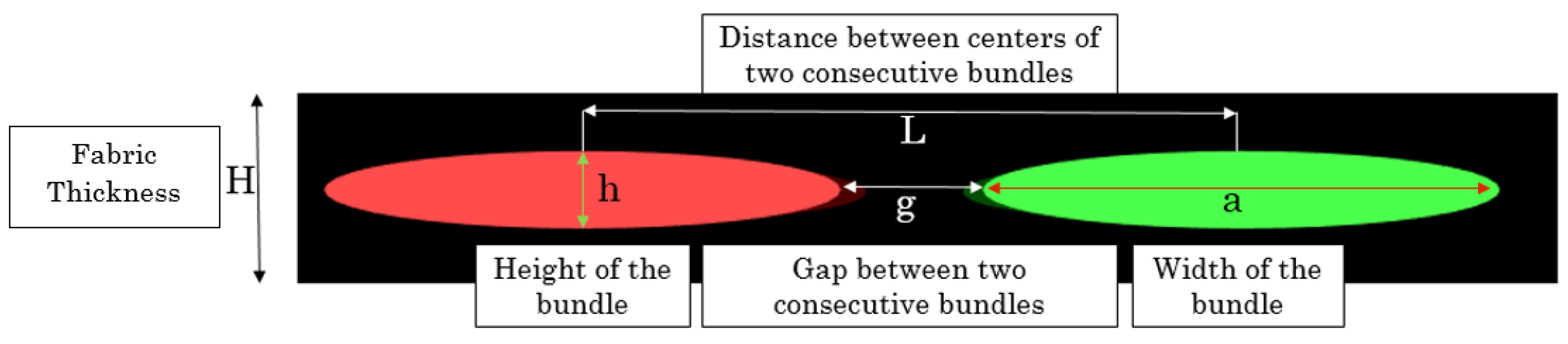
2. Fiber Bundle Permeability: Analytical Modeling
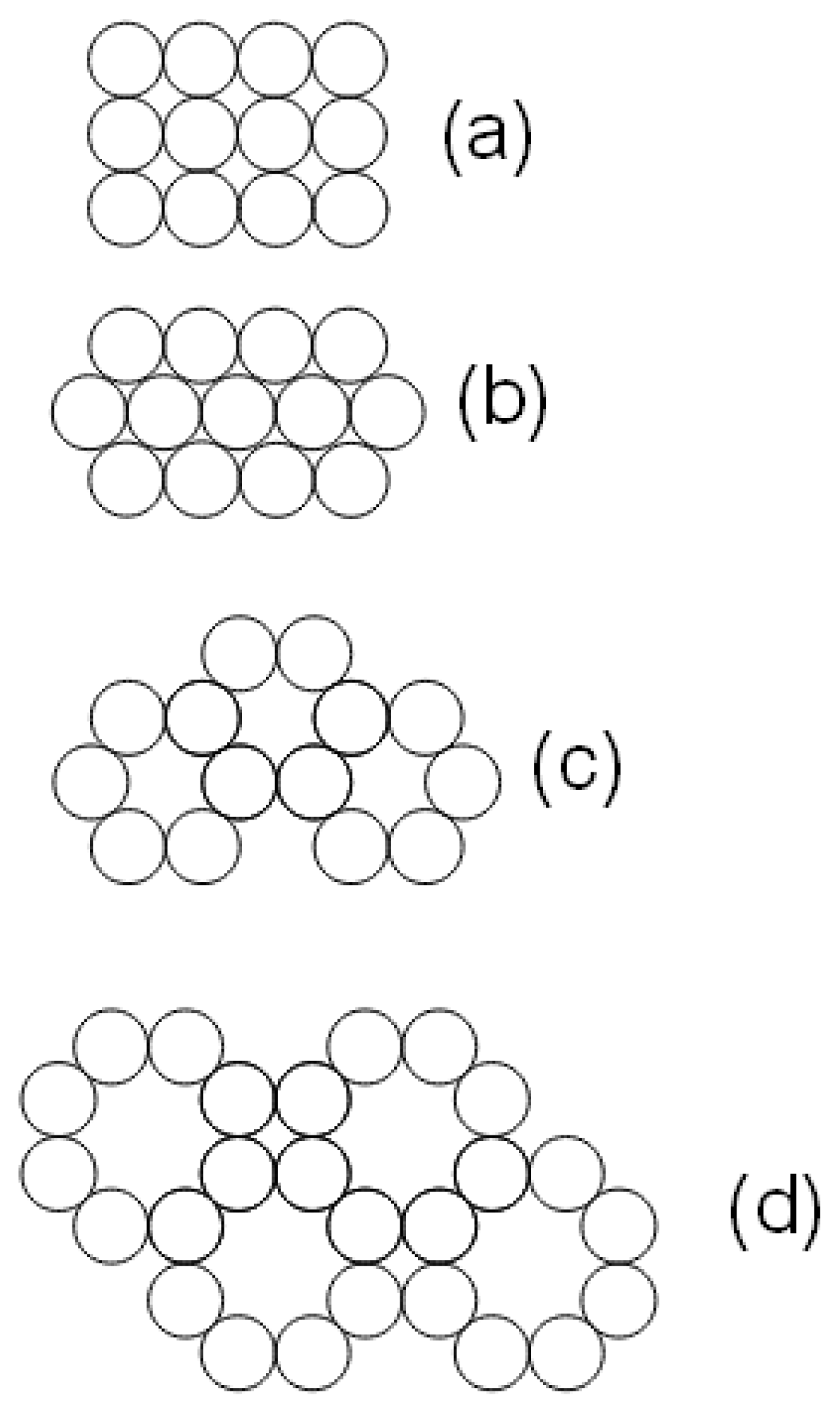
2.1. Review of Fiber Bundle Permeability Analytical Models
- lubrication theory,
- capillary model,
- analytic cell calculation,
- mixed models based on previous approaches.
2.2. Fiber Bundle Permeability: A Comparative Study
3. Experimental Measurements
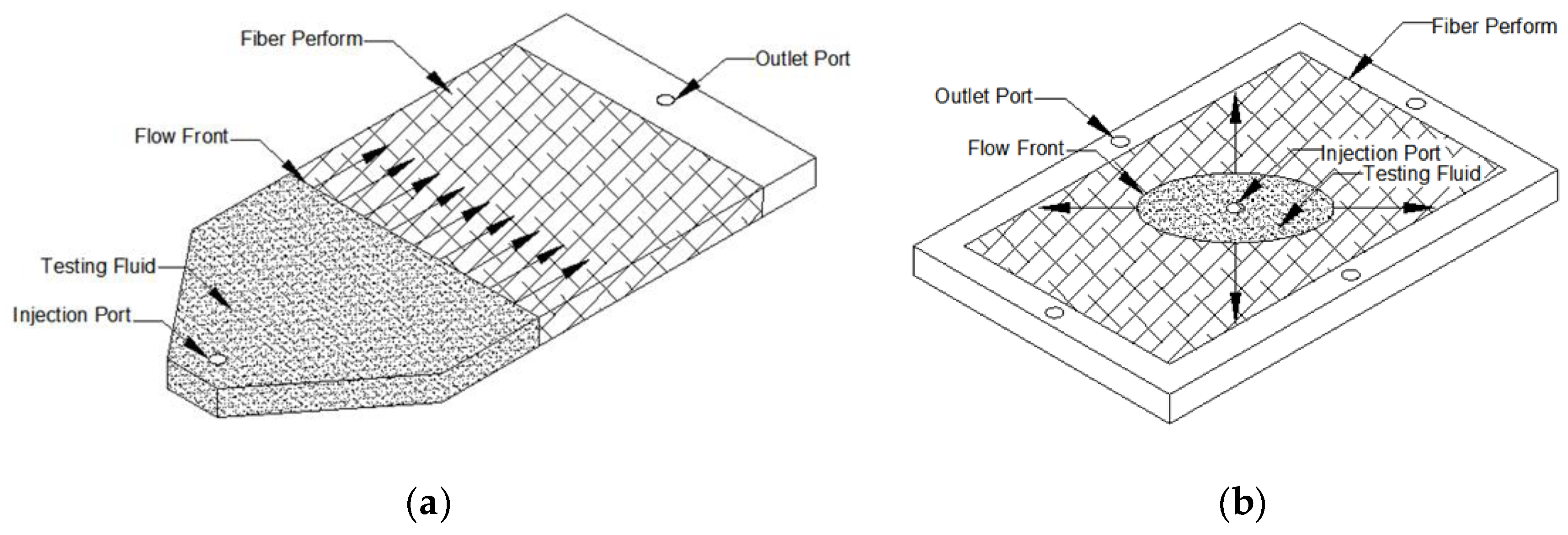
- radial or longitudinal, depending on the position of the inlet gate, see Figure 5 for the in-plane permeability;
- saturated or unsaturated, depending on whether the preform is saturated with resin or dry when measuring permeability;
- constant pressure at the inlet or constant velocity during the injection;
- type of injected fluid; and
- measuring device.
3.1. Review on Measuring in-Plane Permeability
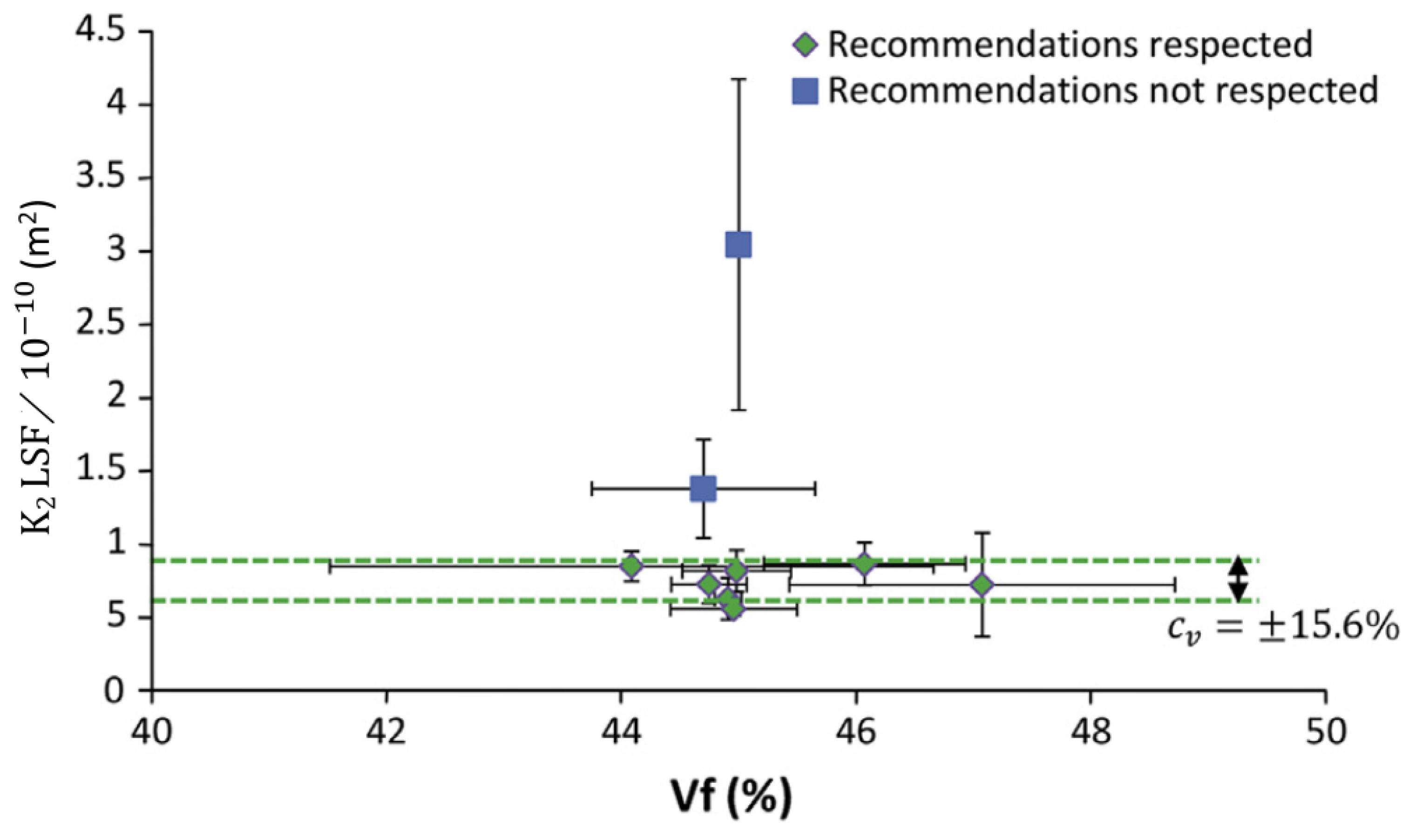
3.1.1. Benchmark Exercise
3.1.2. Conclusions
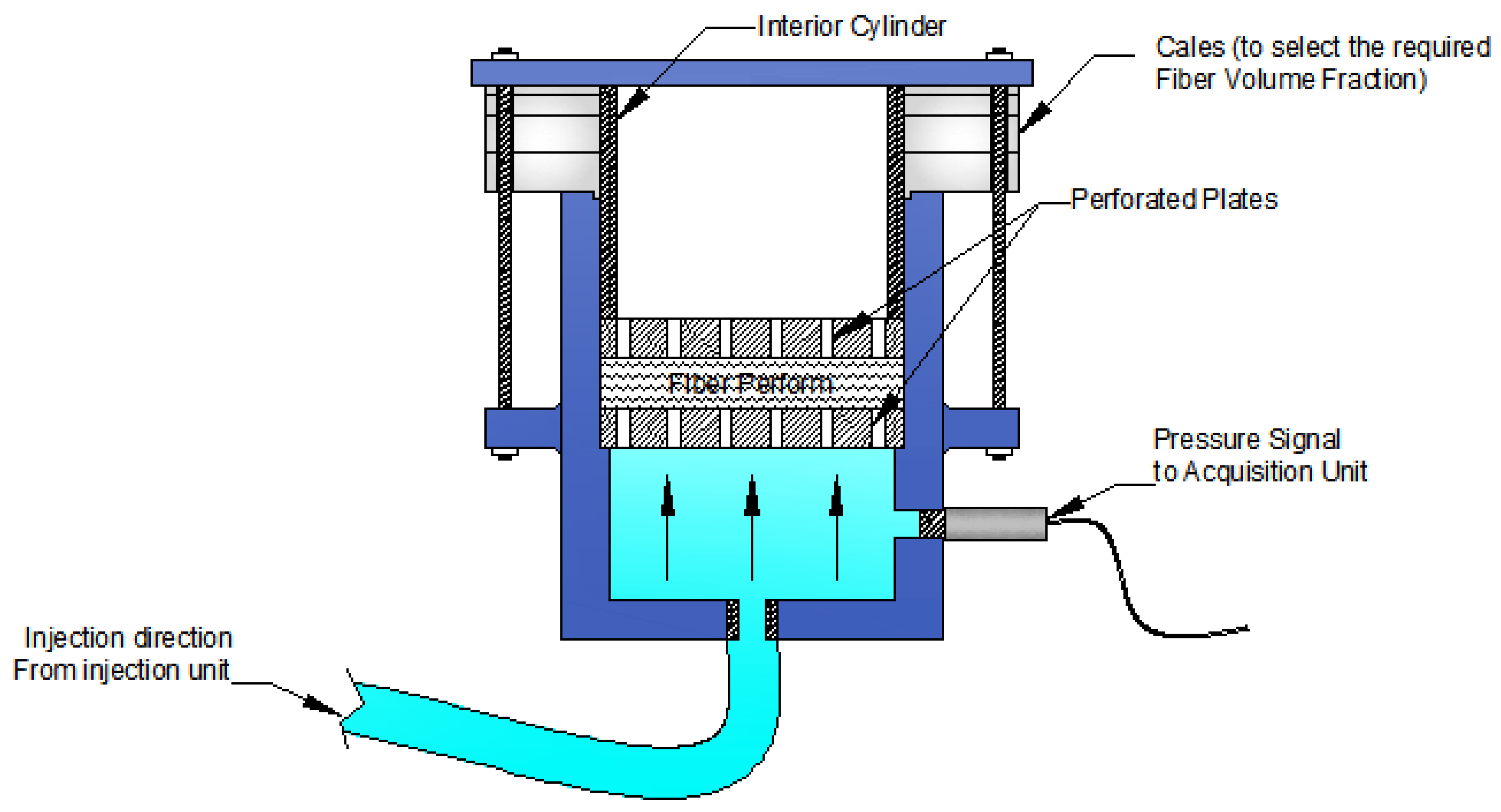
3.2. Review on Measuring through-Thickness Permeability
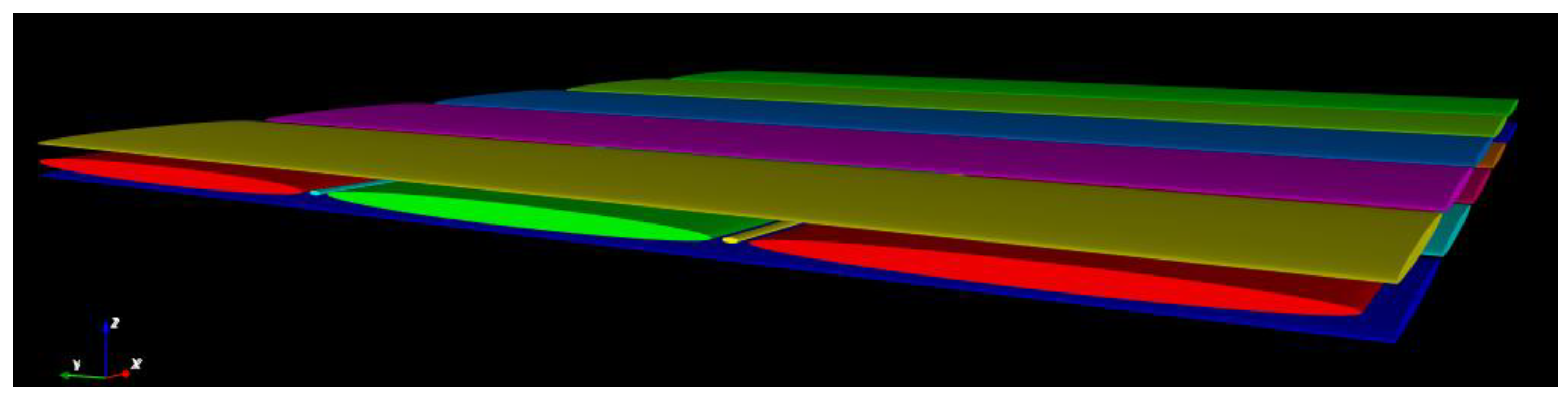
4. Fabric Permeability Prediction: Analytical Models
4.1. Review of Fabric Permeability Prediction: Analytical Models
4.2. Developed Analytical Model
4.3. Conclusion on Predicting Fabric Permeability
- They are applicable for a certain type of architecture;
- they are valid on a selected fiber volume fraction; and
- some are semi-empirical models and are expressed as a function of geometrical parameters.
5. Fabric Permeability Prediction: Numerical Simulations
5.1. Review of Fabric Permeability Prediction: Numerical Simulations
5.2. Advance in Numerical Methodology
- Static mode;
- single porous medium; and
- meshing is done in the mesopores region.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| ε | Porosity |
| εeff | Effective porosity |
| Vfy | Intra yarn fiber volume fraction |
| Vf | Fiber volume fraction |
| Vf0 | Vf for non-compacted fabrics |
| Vfi | Vf for compacted fabrics |
| Q | Resin flow |
| H | Fabric thickness |
| H0 | Fabric thickness prior to compaction |
| K0° | Macroscopic permeability warp direction |
| K90° | Macroscopic permeability weft direction |
| KL | Microscopic longitudinal permeability |
| KT | Microscopic transversal permeability |
| Hi | Fabric thickness on Vfi |
| hw | Warp yarn thickness |
| ρs | Surface density of the fabric |
| Ρ | Material density |
| hf | Weft yarn thickness |
Appendix A. Unidirectional Permeability Predicting Models
| Fiber Arrangement | c | ||
|---|---|---|---|
| Quadratic | 57 | ||
| Hexagonal | 53 |
References
- Hu, J.; Liu, Y.L.; Shao, Y. Study on void formation in multi-layer woven fabrics. Compos. Part A Appl. Sci. Manuf. 2004, 35, 595–603. [Google Scholar]
- Mayer, C.; Wang, X.; Neitzel, M. Macro-and micro-impregnation phenomena in continuous manufacturing of fabric reinforced thermoplastic composites. Composites Part A 1998, 29, 783–793. [Google Scholar] [CrossRef]
- Shih, C.H.; Lee, L.J. Analysis of void removal in liquid composite molding using microflow models. Polym. Compos. 2002, 23, 120–131. [Google Scholar] [CrossRef]
- Lundstrom, T.; Gebart, B.; Lundemo, C. Void formation in RTM. J. Reinf. Plast. Compos. 1993, 12, 1339–1349. [Google Scholar] [CrossRef]
- Sadiq, T.; Advani, S.; Parnas, R. Experimental investigation of transverse flow through aligned cylinders. Int. J. Multiph. Flow 1995, 21, 755–774. [Google Scholar] [CrossRef]
- Available online: www.esi-group.com (accessed on 8 July 2019).
- Available online: https://www.ccm.udel.edu/software/lims-software/ (accessed on 8 July 2019).
- Available online: https://www.innovmetric.com/en/products/polyworks-inspector (accessed on 8 July 2019).
- Karaki, M. Permeability Modeling of Engineering Textiles Used in Composite Materials; Université de Technologie de Troyes: Troyes, France, 2017. [Google Scholar]
- Babadagli, T.; Al-Salmi, S. A review of permeability-prediction methods for carbonate reservoirs using well-log data. SPE Reservoir Eval. Eng. 2004, 7, 75–88. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 2017, 177, 436–457. [Google Scholar] [CrossRef]
- Renard, P.; De Marsily, G. Calculating equivalent permeability: A review. Adv. Water Res. 1997, 20, 253–278. [Google Scholar] [CrossRef]
- Patiño, I.; Vargas, C.; Vanegas, J. Methods for permeability measurements of fibrous reinforced preforms. Revista Facultad de Ingeniería Universidad de Antioquia 2014, 72, 186–2002. [Google Scholar]
- Chen, X.; Papathanasiou, T. Micro-scale modeling of axial flow through unidirectional disordered fiber arrays. Compos. Sci. Technol. 2007, 67, 1286–1293. [Google Scholar] [CrossRef]
- Drummond, J.; Tahir, M. Laminar viscous flow through regular arrays of parallel solid cylinders. Int. J. Multiph. Flow 1984, 10, 515–540. [Google Scholar] [CrossRef]
- Choi, M.A.; Lee, M.H.; Chang, J.; Lee, S.J. Permeability modeling of fibrous media in composite processing. J. Non-Newtonian Fluid Mech. 1998, 79, 585–598. [Google Scholar] [CrossRef]
- Gebart, B. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Berdichevsky, A.L.; Cai, Z. Preform permeability predictions by self-consistent method and finite element simulation. Polym. Compos. 1993, 14, 132–143. [Google Scholar] [CrossRef]
- Cai, Z.; Berdichevsky, A. An improved self-consistent method for estimating the permeability of a fiber assembly. Polym. Compos. 1993, 14, 314–323. [Google Scholar] [CrossRef]
- Tamayol, A.; Bahrami, M. Analytical determination of viscous permeability of fibrous porous media. Int. J. Heat Mass Transf. 2009, 52, 2407–2414. [Google Scholar] [CrossRef]
- Wang, J.F.; Hwang, W.R. Permeability prediction of fibrous porous media in a bi-periodic domain. J. Compos. Mater. 2008, 42, 909–929. [Google Scholar] [CrossRef]
- Bruschke, M.; Advani, S. Flow of generalized Newtonian fluids across a periodic array of cylinders. J. Rheol. 1993, 37, 479–498. [Google Scholar] [CrossRef]
- Carman, P. The determination of the specific surface of powders. J. Soc. Chem. Ind. Trans. 1938, 57, 225. [Google Scholar]
- Sullivan, R. Specific surface measurements on compact bundles of parallel fibers. Appl. Phys. 1942, 13, 725–730. [Google Scholar] [CrossRef]
- Kuwabara, S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. J. Phys. Soc. Jpn. 1959, 14, 527–532. [Google Scholar] [CrossRef]
- Happel, J. Viscous flow relative to arrays of cylinders. AIChE J. 1959, 5, 174–177. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Noordhoff International Publishing: Leyden, the Netherlands, 1973. [Google Scholar]
- Sangani, A.; Acrivos, A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiph. Flow 1982, 8, 193–206. [Google Scholar] [CrossRef]
- Sahraoui, M.; Kaviany, M. Slip and no-slip velocity boundary conditions at interface of porous, plain media. J. Heat Mass Transf. 1992, 35, 927–943. [Google Scholar] [CrossRef] [Green Version]
- Gutowski, T.; Cai, Z.; Bauer, S.; Boucher, D.; Kingery, J.; Wineman, S. Consolidation experiments for laminate composites. J. Compos. Mater. 1987, 21, 650–669. [Google Scholar] [CrossRef]
- Phelan, F.R.; Wise, G. Analysis of transverse flow in aligned fibrous porous media. Compos. Part A Appl. Sci. Manuf. 1996, 27, 25–34. [Google Scholar] [CrossRef]
- Lee, S.; Yang, J. Modeling of Darcy-Forchheimer drag for fluid flow across a bank of circular cylinders. J. Heat Mass Transf. 1997, 40, 3149–3155. [Google Scholar] [CrossRef]
- Van der Westhuizen, J.; Du Plessis, J.P. An attempt to quantify fibre bed permeability utilizing the phase average Navier-Stokes equation. Compos. Part A Appl. Sci. Manuf. 1996, 27, 263–269. [Google Scholar] [CrossRef]
- Tamayol, A.; Bahrami, M. Transverse permeability of fibrous porous media. Phys. Rev. E 2011, 83, 046314. [Google Scholar] [CrossRef] [Green Version]
- Karaki, M.; Hallal, A.; Younes, R.; Trochu, F.; Lafon, P.; Hayek, A.; Kobeissy, A.; Fayad, A. A comparative analytical, numerical and experimental analysis of the microscopic permeability of fiber bundles in composite materials. Int. J. Compos. Mater. 2017, 7, 82–102. [Google Scholar]
- Dave, R.; Kardos, J.; Duduković, M. A model for resin flow during composite processing part 2: Numerical analysis for unidirectional graphite/epoxy laminates. Polym. Compos. 1987, 8, 123–132. [Google Scholar] [CrossRef]
- Naik, N.; Sirisha, M.; Inani, A. Permeability characterization of polymer matrix composites by RTM/VARTM. Prog. Aerosp. Sci. 2014, 65, 22–40. [Google Scholar] [CrossRef]
- Shojaei, A.; Trochu, F.; Ghaffarian, S.; Karimian, S.; Lessard, L. An experimental study of saturated and unsaturated permeabilities in resin transfer molding based on unidirectional flow measurements. J. Reinf. Plast. Compos. 2004, 23, 1515–1536. [Google Scholar] [CrossRef]
- Hoes, K.; Dinescu, D.; Sol, H.; Vanheule, M.; Parnas, R.S.; Luo, Y.; Verpoest, I. New set-up for measurement of permeability properties of fibrous reinforcements for RTM. Compos. Part A Appl. Sci. Manuf. 2002, 33, 959–969. [Google Scholar] [CrossRef]
- Song, Y.-S.; Youn, J.-R. Asymptotic expansion homogenization of permeability tensor for plain woven fabrics. Compos. Part A Appl. Sci. Manuf. 2006, 37, 2080–2087. [Google Scholar] [CrossRef]
- Comas-Cardona, S.; Binetruy, C.; Krawczak, P. Unidirectional compression of fibre reinforcements. Part 2: A continuous permeability tensor measurement. Compos. Sci. Technol. 2007, 67, 638–645. [Google Scholar] [CrossRef]
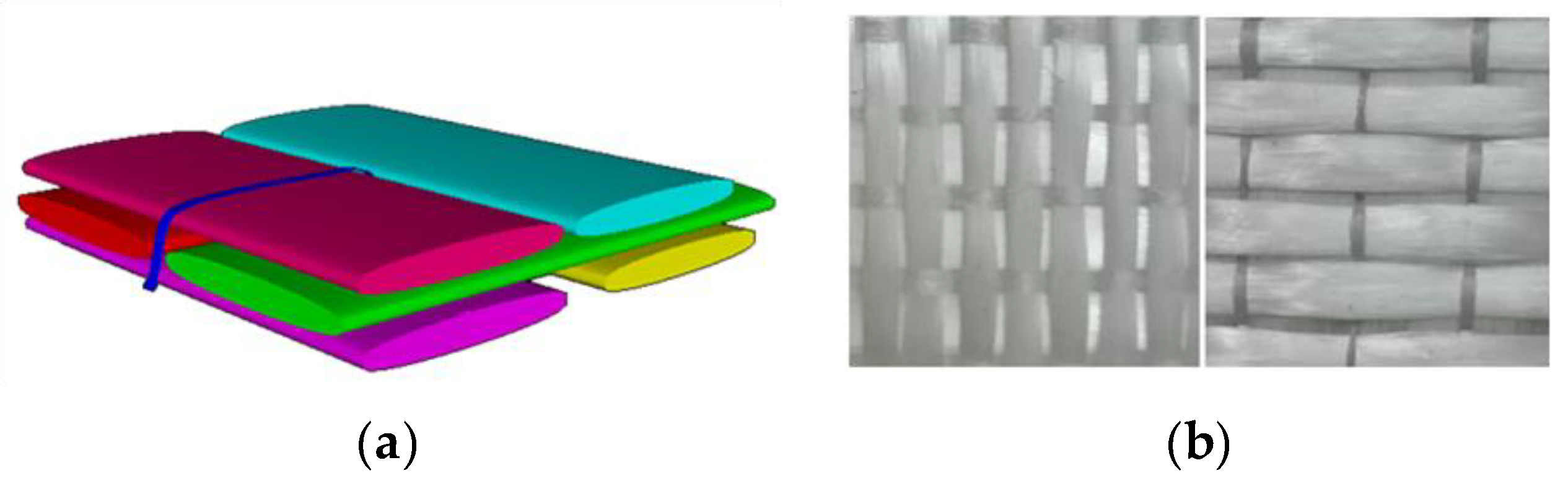
- Endruweit, A.; Long, A. Analysis of compressibility and permeability of selected 3D woven reinforcements. J. Compos. Mater. 2010, 44, 2833–2862. [Google Scholar] [CrossRef]
- Liu, Q.; Parnas, R.S.; Giffard, H.S. New set-up for in-plane permeability measurement. Compos. Part A Appl. Sci. Manuf. 2007, 38, 954–962. [Google Scholar] [CrossRef]
- Arbter, R.; Beraud, J.; Binetruy, C.; Bizet, L.; Bréard, J.; Comas-Cardona, S.; Demaria, C.; Endruweit, A.; Ermanni, P.; Gommer, F. Experimental determination of the permeability of textiles: A benchmark exercise. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1157–1168. [Google Scholar] [CrossRef]
- Vernet, N.; Ruiz, E.; Advani, S.; Alms, J.; Aubert, M.; Barburski, M.; Barari, B.; Beraud, J.; Berg, D.; Correia, N. Experimental determination of the permeability of engineering textiles: Benchmark II. Compos. Part A Appl. Sci. Manuf. 2014, 61, 172–184. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.K.; Song, Y.S.; Kang, T.J.; Chung, K.; Youn, J.R. Permeability measurement of a circular braided preform for resin transfer molding. Fibers Polym. 2003, 4, 135–144. [Google Scholar] [CrossRef]
- Chae, H.S.; Song, Y.S.; Youn, J.R. Transverse permeability measurement of a circular braided preform in liquid composite molding. Korea-Aust. Rheol. J. 2007, 19, 17–25. [Google Scholar]
- Trevino, L.; Rupel, K.; Young, W.; Liou, M.J.; Lee, L.J. Analysis of resin injection molding in molds with preplaced fiber mats. I: Permeability and compressibility measurements. Polym. Compos. 1991, 12, 20–29. [Google Scholar] [CrossRef]
- Weitzenböck, J.; Shenoi, R.; Wilson, P. Measurement of three-dimensional permeability. Compos. Part A Appl. Sci. Manuf. 1998, 29, 159–169. [Google Scholar] [CrossRef]
- Wu, X.; Li, J.; Shenoi, R. A new method to determine fiber transverse permeability. J. Compos. Mater. 2007, 41, 747–756. [Google Scholar] [CrossRef]
- Nedanov, P.B.; Advani, S.G. A method to determine 3D permeability of fibrous reinforcements. J. Compos. Mater. 2002, 36, 241–254. [Google Scholar] [CrossRef]
- Elbouazzaoui, O.; Drapier, S.; Henrat, P. An experimental assessment of the saturated transverse permeability of non-crimped new concept (NC2) multiaxial fabrics. J. Compos. Mater. 2005, 39, 1169–1193. [Google Scholar] [CrossRef]
- Drapier, S.; Pagot, A.; Vautrin, A.; Henrat, P. Influence of the stitching density on the transverse permeability of non-crimped new concept (NC2) multiaxial reinforcements: Measurements and predictions. Compos. Sci. Technol. 2002, 62, 1979–1991. [Google Scholar] [CrossRef]
- Ouagne, P.; Bréard, J. Continuous transverse permeability of fibrous media. Composites Part A 2010, 41, 22–28. [Google Scholar] [CrossRef] [Green Version]
- Scholz, S.; Gillespie, J.W.; Heider, D. Measurement of transverse permeability using gaseous and liquid flow. Composites Part A 2007, 38, 2034–2040. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Shih, C.H.; Lee, L.J. Effect of fiber architecture on permeability in liquid composite molding. Polym. Compos. 1998, 19, 626–639. [Google Scholar] [CrossRef]
- Šimáček, P.; Advani, S.G. Permeability model for a woven fabric. Polym. Compos. 1996, 17, 887–899. [Google Scholar] [CrossRef]
- Skartsis, L.; Khomami, B.; Kardos, J. Resin flow through fiber beds during composite manufacturing processes. Part II: Numerical and experimental studies of Newtonian flow through ideal and actual fiber beds. Polym. Eng. Sci. 1992, 32, 231–239. [Google Scholar] [CrossRef]
- Yu, B.; James Lee, L. A simplified in-plane permeability model for textile fabrics. Polym. Compos. 2000, 21, 660–685. [Google Scholar] [CrossRef]
- Yu, B.; Lee, L.J.; Cao, H. A fractal in-plane permeability model for fabrics. Polym. Compos. 2002, 23, 201–221. [Google Scholar] [CrossRef]
- Dong, S.; He, H.; Jia, Y.; Wang, C.; Jiao, X. A new structure-related model to predict the permeability of non-crimp fabric preform. J. Compos. Mater. 2013, 47, 3053–3063. [Google Scholar] [CrossRef]
- Nordlund, M.; Lundström, T.; Frishfelds, V.; Jakovics, A. Permeability network model for non-crimp fabrics. Composites Part A 2006, 37, 826–835. [Google Scholar] [CrossRef]
- Chen, Z.-R.; Ye, L.; Lu, M. Permeability predictions for woven fabric preforms. J. Compos. Mater. 2009. [Google Scholar] [CrossRef]
- Adams, K.L.; Miller, B.; Rebenfeld, L. Forced in-plane flow of an epoxy resin in fibrous networks. Polym. Eng. Sci. 1986, 26, 1434–1441. [Google Scholar] [CrossRef]
- Bahrami, M.; Yovanovich, M.M.; Culham, J.R. A novel solution for pressure drop in singly connected microchannels of arbitrary cross-section. Int. J. Heat Mass Transfer 2007, 50, 2492–2502. [Google Scholar] [CrossRef]
- Nordlund, M.; Lundstrom, T.S. Numerical study of the local permeability of noncrimp fabrics. J. Compos. Mater. 2005, 39, 929–947. [Google Scholar] [CrossRef]
- Shou, D.; Ye, L.; Tang, Y.; Fan, J.; Ding, F. Transverse permeability determination of dual-scale fibrous materials. Int. J. Heat Mass Transfer 2013, 58, 532–539. [Google Scholar] [CrossRef]
- Papathanasiou, T. Flow across structured fiber bundles: A dimensionless correlation. Int. J. Multiph. Flow 2001, 27, 1451–1461. [Google Scholar] [CrossRef]
- Vernet, N.; Trochu, F. Permeability analytical modeling of 3d interlock fabrics. In Proceedings of the 19th International Conference on Composite Materials, Montreal, QC, Canada, 28 July–2 August 2013. [Google Scholar]
- Vernet, N.; Trochu, F. Analysis of mesoscopic pore size in 3D-interlock fabrics and validation of a predictive permeability model. J. Reinf. Plast. Compos. 2016, 35, 471–486. [Google Scholar] [CrossRef]
- Karaki, M.; Hallal, A.; Younes, R.; Trochu, F.; Lafon, P. In-plane permeability prediction model for non-crimp and 3D orthogonal fabrics. J. Text. Inst. 2018, 109, 1110–1126. [Google Scholar] [CrossRef]
- Fournier, R. Optimisation et modélisation du procédé RTM. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2003. [Google Scholar]
- Hoareau, C. Injection sur Renfort: Etude du Remplissage de Moule et Détermination Théorique de la Perméabilité des Tissus. Ph.D. Thesis, Ecole nationale supérieure des Mines de Paris, Paris, France, 1994. [Google Scholar]
- Laine, B. Influence des Déformations d’un Renfort Fibreux sur sa Perméabilité: Modélisations et Expériences. Ph.D. Thesis, Arts et Métiers ParisTech, Paris, France, 2008. [Google Scholar]
- Laine, B.; Beauchêne, P.; Boisse, P.; Hivet, G.; Lomov, S.V.; Hirsekorn, M.; Badel, P. Permeability of woven fabrics: Analytical and numerical predictions. In Proceedings of the FPCM-10, 10th International Conference on Flow Processes in Composite Materials, Monte Verità/Ascona, Switzerland, 12–15 July 2010. [Google Scholar]
- Loix, F.; Badel, P.; Orgéas, L.; Geindreau, C.; Boisse, P. Woven fabric permeability: From textile deformation to fluid flow mesoscale simulations. Compos. Sci. Technol. 2008, 68, 1624–1630. [Google Scholar] [CrossRef]
- Ngo, N.; Tamma, K. Microscale permeability predictions of porous fibrous media. Int. J. Heat Mass Transfer 2001, 44, 3135–3145. [Google Scholar] [CrossRef]
- Takano, N.; Zako, M.; Okazaki, T.; Terada, K. Microstructure-based evaluation of the influence of woven architecture on permeability by asymptotic homogenization theory. Compos. Sci. Technol. 2002, 62, 1347–1356. [Google Scholar] [CrossRef]
- Spaid, M.A.; Phelan, F.R. Modeling void formation dynamics in fibrous porous media with the lattice Boltzmann method. Composites Part A 1998, 29, 749–755. [Google Scholar] [CrossRef]
- Martys, N.S.; Chen, H. Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method. Phys. Rev. E 1996, 53, 743. [Google Scholar] [CrossRef]
- Dunkers, J.P.; Phelan, F.R.; Flynn, K.M.; Sanders, D.P.; Parnas, R.S. Permeability Prediction from Non-Destructive Imaging of Composite Microstructure. In Proceedings of the 59th Society of Plastics Engineers Annual Conference, Dallas, TX, USA, 1 May 2001. [Google Scholar]
- Chen, H.; Gould, H.; Tobochnik, J. Discrete Boltzmann systems and fluid flows. Comput. Phys. 1993, 7, 632–637. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941. [Google Scholar] [CrossRef]
- Spaid, M.A.; Phelan Jr, F.R. Lattice Boltzmann methods for modeling microscale flow in fibrous porous media. Phys. Fluids 1997, 9, 2468–2474. [Google Scholar] [CrossRef]
- Irayani, Z.; Fauzi, U.; Viridi, S.; Latief, F. Calculation of anisotropy permeability from 3D tomographic images using renormalization group approaches and lattice Boltzmann method. J. Pet. Explor. Prod. Technol. 2018, 9, 889–897. [Google Scholar] [CrossRef] [Green Version]
- Auzerais, F.; Dunsmuir, J.; Ferreol, B.; Martys, N.; Olson, J.; Ramakrishnan, T.; Rothman, D.; Schwartz, L. Transport in sandstone: A study based on three dimensional microtomography. Geophys. Res. Lett. 1996, 23, 705–708. [Google Scholar] [CrossRef]
- Sethian, J.A. Level set methods and fast marching methods. J. Comput. Inf. Technol. 2003, 11, 1–2. [Google Scholar]
- Verleye, B.; Croce, R.; Griebel, M.; Klitz, M.; Lomov, S.V.; Morren, G.; Sol, H.; Verpoest, I.; Roose, D. Permeability of textile reinforcements: Simulation, influence of shear and validation. Compos. Sci. Technol. 2008, 68, 2804–2810. [Google Scholar] [CrossRef]
- Verleye, B.; Klitz, M.; Croce, R.; Roose, D.; Lomov, S.V.; Verpoest, I. Computation of permeability of textile reinforcements. In Proceedings of the 17th IMACS World Congres, CD-edition, Paris, France, 11–15 July 2005. [Google Scholar]
- Trochu, F.; Gauvin, R. Limitations of a boundary-fitted finite difference method for the simulation of the resin transfer molding process. J. Reinf. Plast. Compos. 1992, 11, 772–786. [Google Scholar] [CrossRef]
- Hori, M. Bounds for effective material properties of statistically nonhomogeneous solid. Struct. Engrg. Earthq. Engrg 1993, 11, 131s–140s. [Google Scholar]
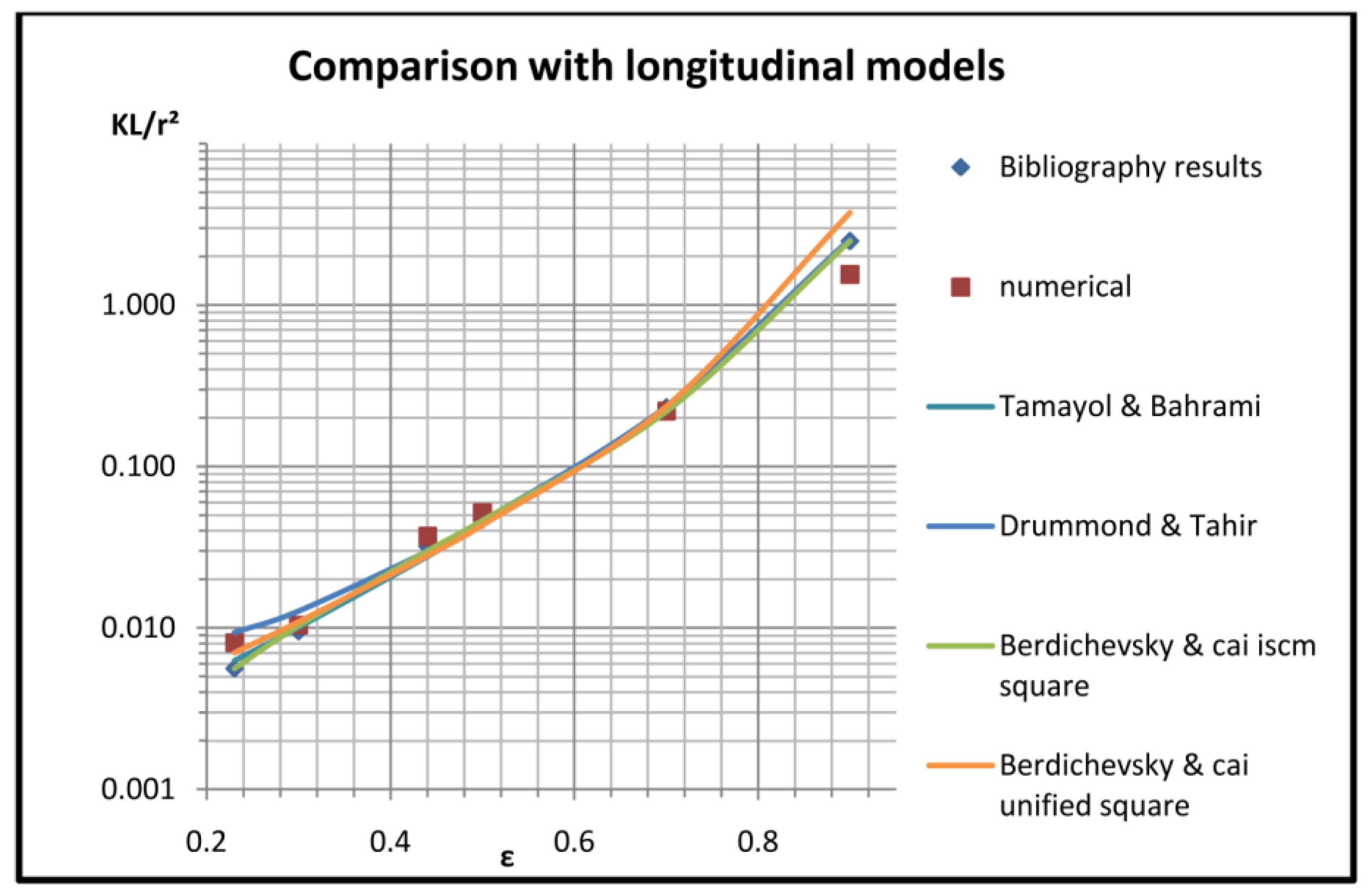
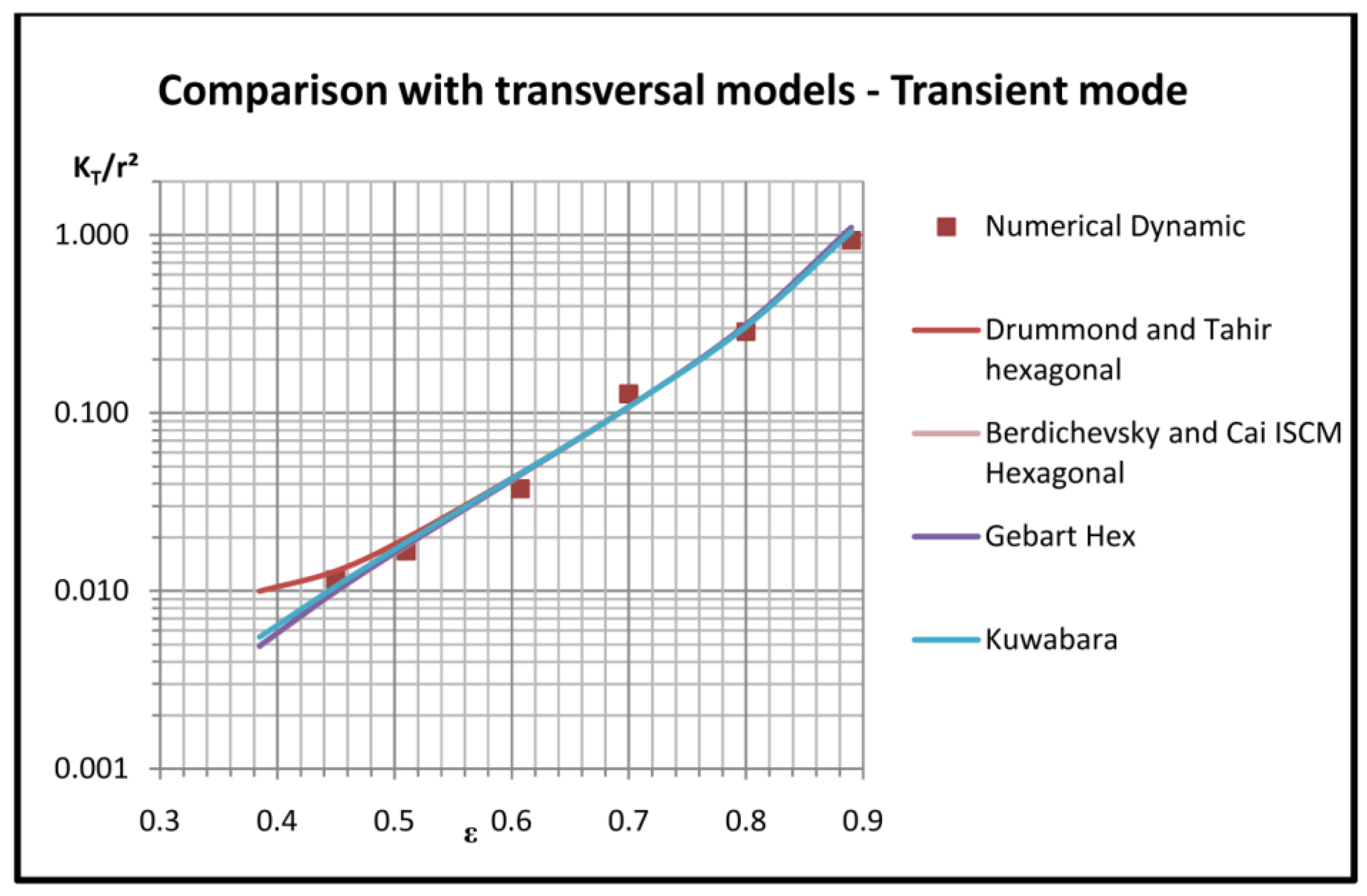




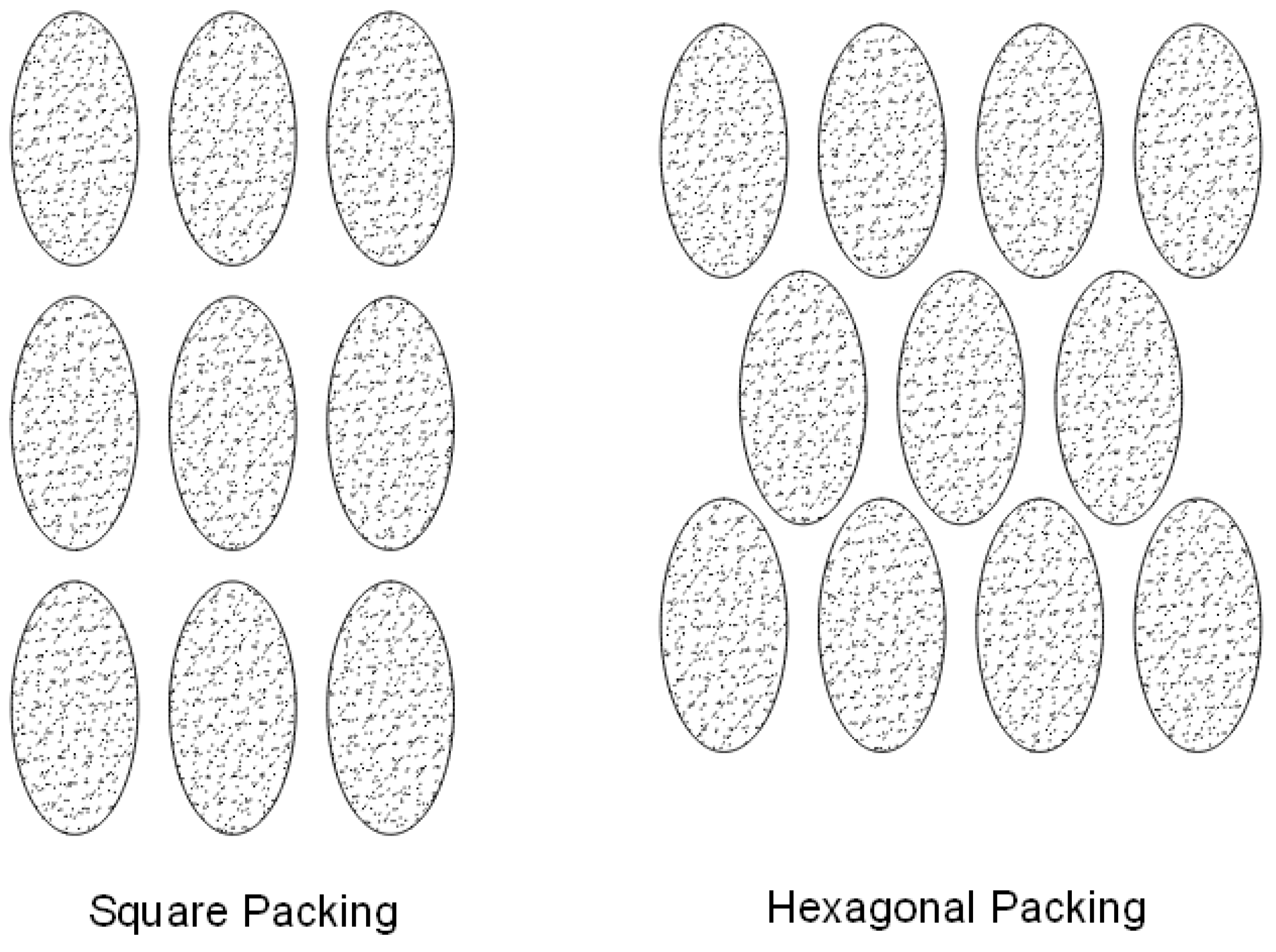
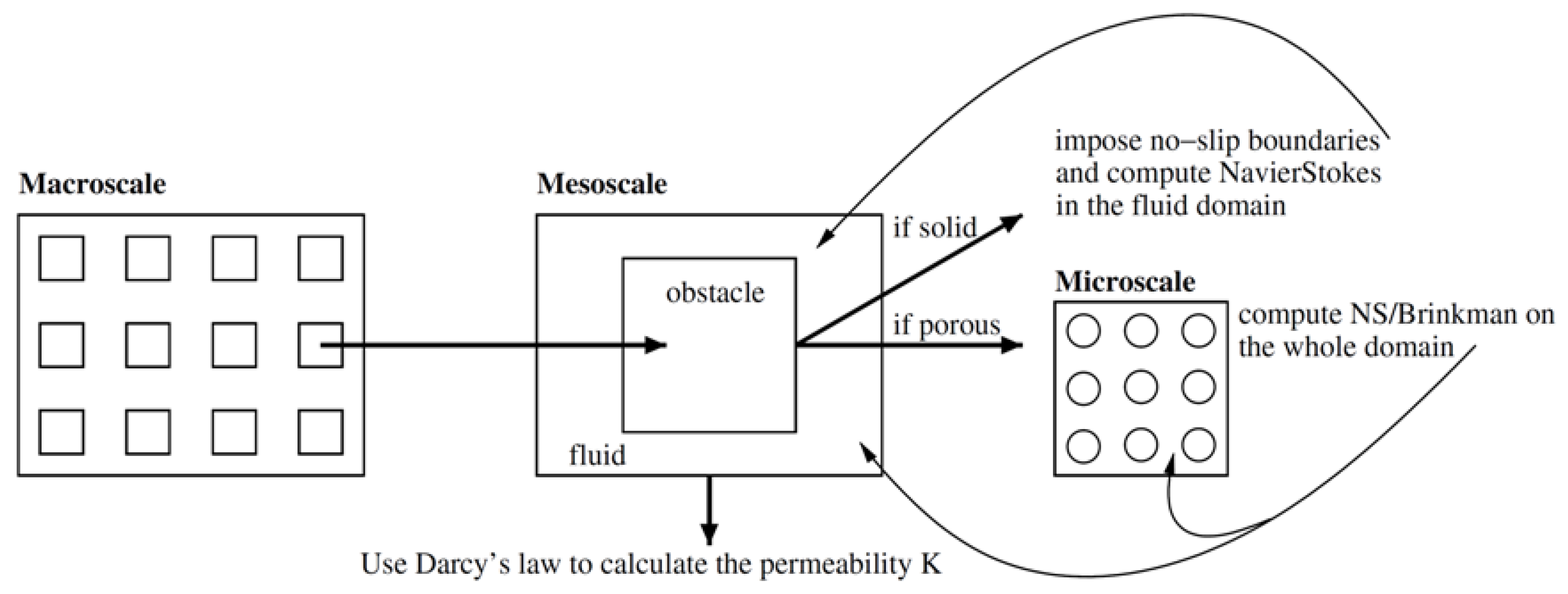
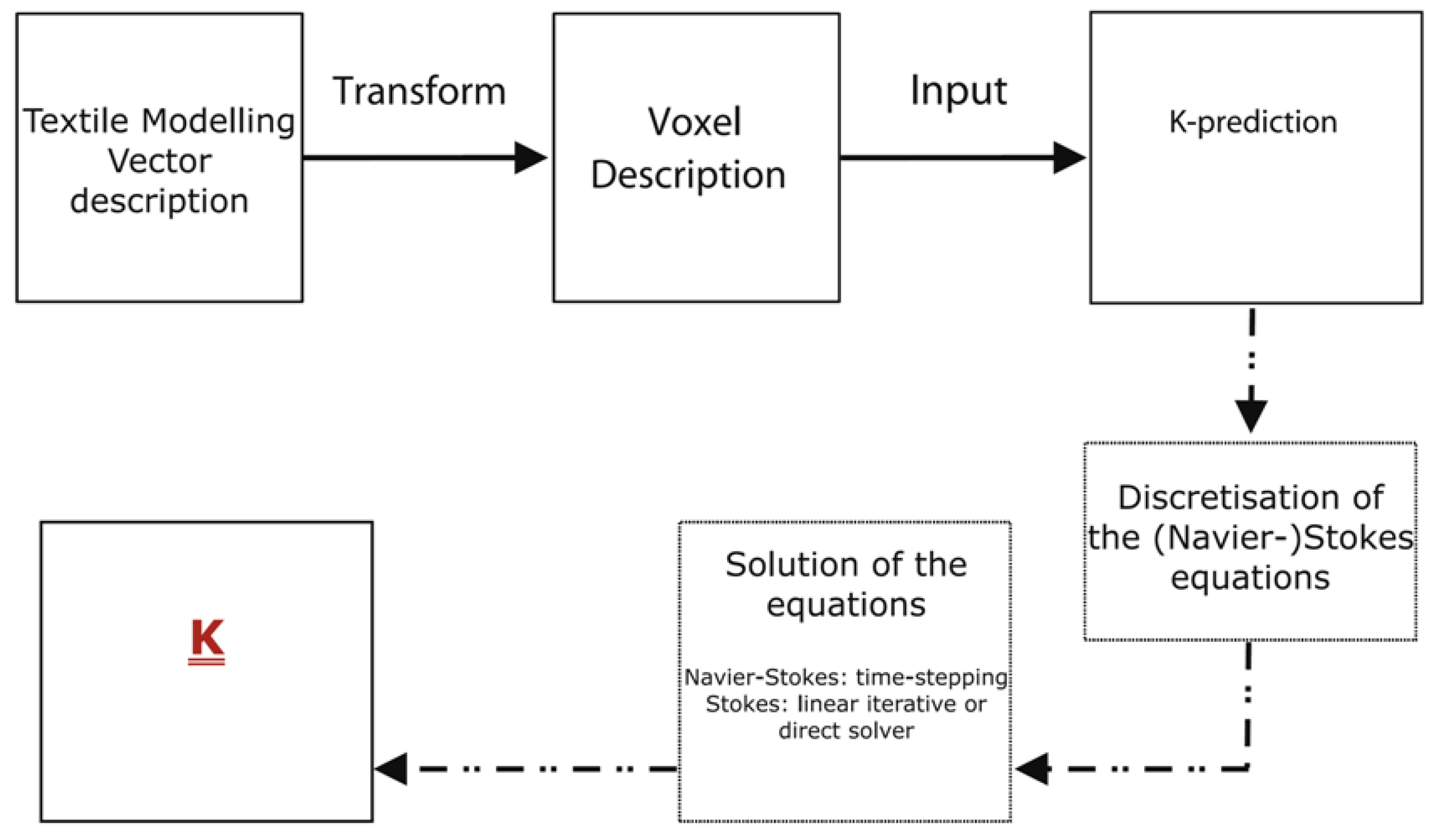
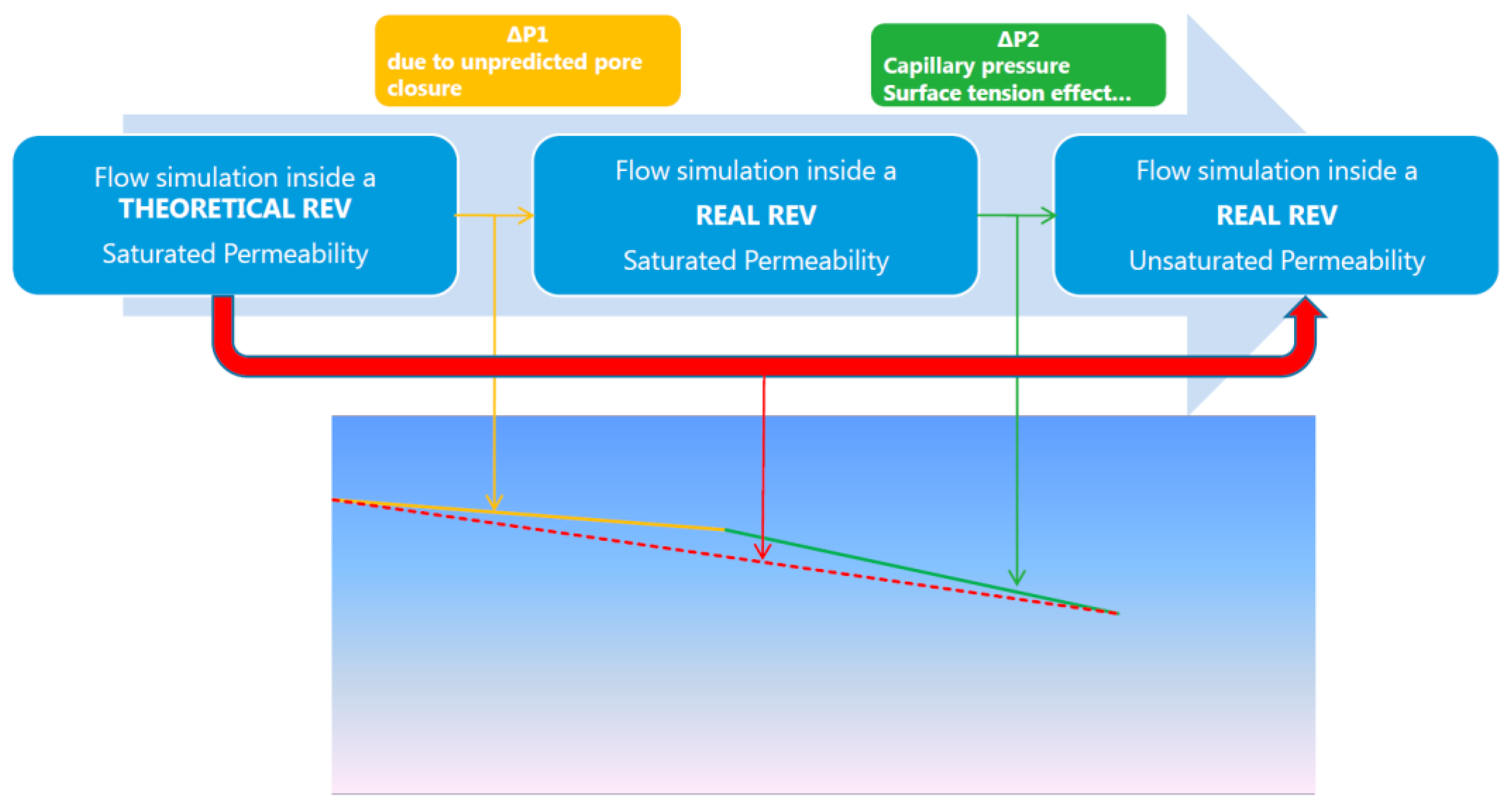



| Model Name/(ε = 0.5) | KL/r2 | KT/r2 |
|---|---|---|
| Kuwabara [33] | 0.0342 | 0.017 |
| Gutowski (for Va = 0.83) [34] | - | 0.0131 |
| Gutowski (for Va = 0.78) [34] | 0.1786 | 0.0086 |
| Gebart (Square) [27] | 0.0702 | 0.0129 |
| Gebart (Hexagonal) [27] | 0.0755 | 0.0164 |
| Berdichevsky and Cai ISCM (Square) [29] | 0.0464 | 0.0097 |
| Berdichevsky and Cai ISCM (Hexagonal) [29] | 0.0354 | 0.0116 |
| Tamayol and Bahrami (Square) [35] | - | 0.0117 |
| Scattering | 67.7% | 217.6% |
| ε | KT/r2 | Reference | Difference % |
|---|---|---|---|
| 0.4345 | 0.007912 | Coulaud | 55% |
| 0.4345 | 0.005076 | Lee and yang | |
| 0.5 | 0.0488 | Sangani and Yao | 300% |
| 0.5 | 0.012 | Sadiq et Al | |
| 0.7 | 0.1292 | Kirsch and Fuchs | 240% |
| 0.7 | 0.24 | Sangani and Yao |
| Reference | Geometry | ε = 0.3 | ε = 0.7 | ε = 0.3 | ε = 0.7 | ||
|---|---|---|---|---|---|---|---|
| KT/r2 | Average | Scatter | Average | Scatter | |||
| Dave et al. [36] | - | 1.25 × 103 | 8.66 × 101 | 1.04 × 103 | 75.85% | 1.86 × 101 | 130.59% |
| Gutowski [30] | Square Packing | 1.92 × 104 | 8.65 × 102 | ||||
| Gutowski [30] | Hex. Packing | 1.31 × 103 | 1.23 × 101 | ||||
| Berd. and Cai [19] | - | 2.57 × 103 | 1.54 × 101 | ||||
| Berd.and Cai [19] | Hex. Packing | 1.62 × 103 | 1.08 × 101 | ||||
| Berd. and Cai [19] | Square Packing | 3.32 × 104 | 1.02 × 101 | ||||
| Wang et al. [21] | Square Packing | 4.26 × 104 | 1.10 × 101 | ||||
| Choi et al. [16] | Hex. Packing | 1.57 × 103 | 9.84 × 102 | ||||
| Choi et al. [16] | Square Packing | 8.18 × 105 | 2.44 × 102 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaki, M.; Younes, R.; Trochu, F.; Lafon, P. Progress in Experimental and Theoretical Evaluation Methods for Textile Permeability. J. Compos. Sci. 2019, 3, 73. https://doi.org/10.3390/jcs3030073
Karaki M, Younes R, Trochu F, Lafon P. Progress in Experimental and Theoretical Evaluation Methods for Textile Permeability. Journal of Composites Science. 2019; 3(3):73. https://doi.org/10.3390/jcs3030073
Chicago/Turabian StyleKaraki, Mohamad, Rafic Younes, Francois Trochu, and Pascal Lafon. 2019. "Progress in Experimental and Theoretical Evaluation Methods for Textile Permeability" Journal of Composites Science 3, no. 3: 73. https://doi.org/10.3390/jcs3030073





