How the Mix Factors Affect the Dynamic Modulus of Hot-Mix Asphalt
Abstract
:1. Introduction
2. Materials
- The letter ‘S’ means the NMAS of 0.75 in. (19 mm).
- The letter ‘SX’ means the NMAS of 0.5 in. (12.5 mm).
- The numbers in the parenthesis such as 75 and 100 are the numbers of gyrations used in the mix design.
- The first numbers in the PG binder such as 58 and 64, are the average seven-day maximum pavement temperature (°C)
- The second numbers in the PG binder such as −22 or −28 are the minimum pavement design temperature likely to be experienced (°C).
3. Dynamic Modulus (E*) Testing
4. Analysis of the Effects of Mix Factors on the Dynamic Modulus
- = dynamic modulus
- ωr = reduced frequency, Hz
- Max = limiting maximum modulus, ksi
- Min = limiting minimum modulus, ksi
- β and γ = fitting parameters
- ωr = reduced frequency at the reference temperature
- ω = loading frequency at the test temperature
- Tr = reference temperature, K
- T = test temperature, K
- ∆Ea = activation energy (treated as a fitting parameter)
- a(T) = shift factor at temperature T
- limiting maximum dynamic modulus, psi
- VMA = voids in mineral aggregates, %
- VFA = voids filled with asphalt, %
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Christensen, D.W.; Pellinen, T.K.; Bonaquist, R.F. Hirsch Model for Estimating the Modulus of Asphalt Concrete. J. Assoc. Asph. Paving Technol. 2003, 72, 97–121. [Google Scholar]
- Mohammad, L.N.; Wu, Z.; Myers, L.; Cooper, S.; Abadie, C. A Practical Look at Simple Performance Tests: Louisiana’s Experience. J. Assoc. Asph. Paving Technol. 2005, 74, 557–600. [Google Scholar]
- Ceylan, H.; Schwartz, C.; Kim, S.; Gopalakrishnan, K. Accuracy of Predictive Models for Dynamic Modulus of Hot-Mix Asphalt. J. Mater. Civ. Eng. 2009, 21, 286–293. [Google Scholar] [CrossRef] [Green Version]
- Birgisson, B.; Sholar, G.; Roque, R. Evaluation of Predicted Dynamic Modulus for Florida Mixtures. In Proceedings of the 84th Annual Meeting of the Transportation Research Board, Paper No. 05-1309, Washington, DC, USA, 9–13 January 2005. [Google Scholar]
- Sakhaeifar, M.; Kim, Y.; Kabir, P. New predictive models for the dynamic modulus of hot mix asphalt. Constr. Build. Mater. 2015, 76, 221–231. [Google Scholar] [CrossRef]
- Kim, Y.R.; King, M.; Momen, M. Typical Dynamic Moduli Values of Hot Mix Asphalt in North Carolina and Their Prediction. In Proceedings of the 84th Annual Meeting of the Transportation Research Board, Paper No. 05-2568, Washington, DC, USA, 9–13 January 2005. [Google Scholar]
- Hu, H.; Shen, S. An Investigation of Dynamic Modulus and Flow Number Properties of Asphalt Mixtures in Washington State; Final Report, No. 709867, USDOT; Office of the Secretary of Transportation: Washington, DC, USA, 2012.
- Clyne, T.R.; Li, X.; Marasteanu, M.O.; Skok, E.L. Dynamic and Resilient Modulus of Mn/DOT Asphalt Mixtures; Report No. MN/ RC-2003-09; Minnesota Department of Transportation: St. Paul, MN, USA, 2003.
- Tran, N.H.; Hall, K.D. Evaluating the Predictive Equation in Determining Dynamic Moduli of Typical Asphalt Mixtures Used in Arkansas. J. Assoc. Asph. Paving Technol. 2005, 74, 1–17. [Google Scholar]
- Rahman, A.; Islam, M.R.; Tarefder, R.A. Modifying the Viscosity Based Witczak Model and Developing Phase Angle Predictive Model for New Mexico’s Superpave Mixes. In Proceedings of the Transportation Research Board (TRB) 95th Annual Meeting, Arehington, DC, USA, 10–14 January 2016. Paper ID. 16-3180. [Google Scholar]
- Robinette, C.; Williams, R.C. The Effects of the Testing History and Preparation Method on the Superpave Simple Performance Test. J. Assoc. Asph. Paving Technol. 2006, 75, 297–317. [Google Scholar]
- Tandon, V.; Bai, X.; Nazarian, S. Impact of Specimen Geometry on Dynamic Modulus Measurement Test Setup. J. Mater. Civ. Eng. 2006, 18, 477–484. [Google Scholar] [CrossRef]
- Shah, A.; McDaniel, R.; Gallivan, V. Evaluation of Mixtures using Dynamic Modulus Tester: Results and Practical Considerations. J. Assoc. Asph. Paving Technol. 2005, 74, 1–21. [Google Scholar]
- AASHTO TP 62. Standard Method of Test for Determining Dynamic Modulus of Hot Mix Asphalt (HMA); American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2007; pp. 1–21. [Google Scholar]
- Bodley, T.; Andriescu, A.; Hesp, S.; Tam, K. Comparison between Binder and Hot Mix Asphalt Properties and Early Top-Down Wheel Path Cracking in a Northern Ontario Pavement Trial. J. Assoc. Asph. Paving Technol. 2007, 76, 345. [Google Scholar]
| Mix ID | NMAS, in. (mm) | Binder | Number of Gyrations |
|---|---|---|---|
| S(100) PG 64-22 | 0.75 (19) | PG 64-22 | 100 |
| S(100) PG 76-28 | 0.75 (19) | PG 76-28 | 100 |
| SMA PG 76-28 | 0.50 (12.5) | PG 76-28 | 100 |
| SX(75) PG 58-28 | 0.50 (12.5) | PG 58-28 | 75 |
| SX(75) PG 58-34 | 0.50 (12.5) | PG 58-34 | 75 |
| SX(75) PG 64-22 | 0.50 (12.5) | PG 64-22 | 75 |
| SX(75) PG 64-28 | 0.50 (12.5) | PG 64-28 | 75 |
| SX(100) PG 58-28 | 0.50 (12.5) | PG 58-28 | 100 |
| SX(100) PG 64-22 | 0.50 (12.5) | PG 64-22 | 100 |
| SX(100) PG 64-28 | 0.50 (12.5) | PG 64-28 | 100 |
| SX(100) PG 76-28 | 0.50 (12.5) | PG 76-28 | 100 |
| Mix Type | Property | Comments |
|---|---|---|
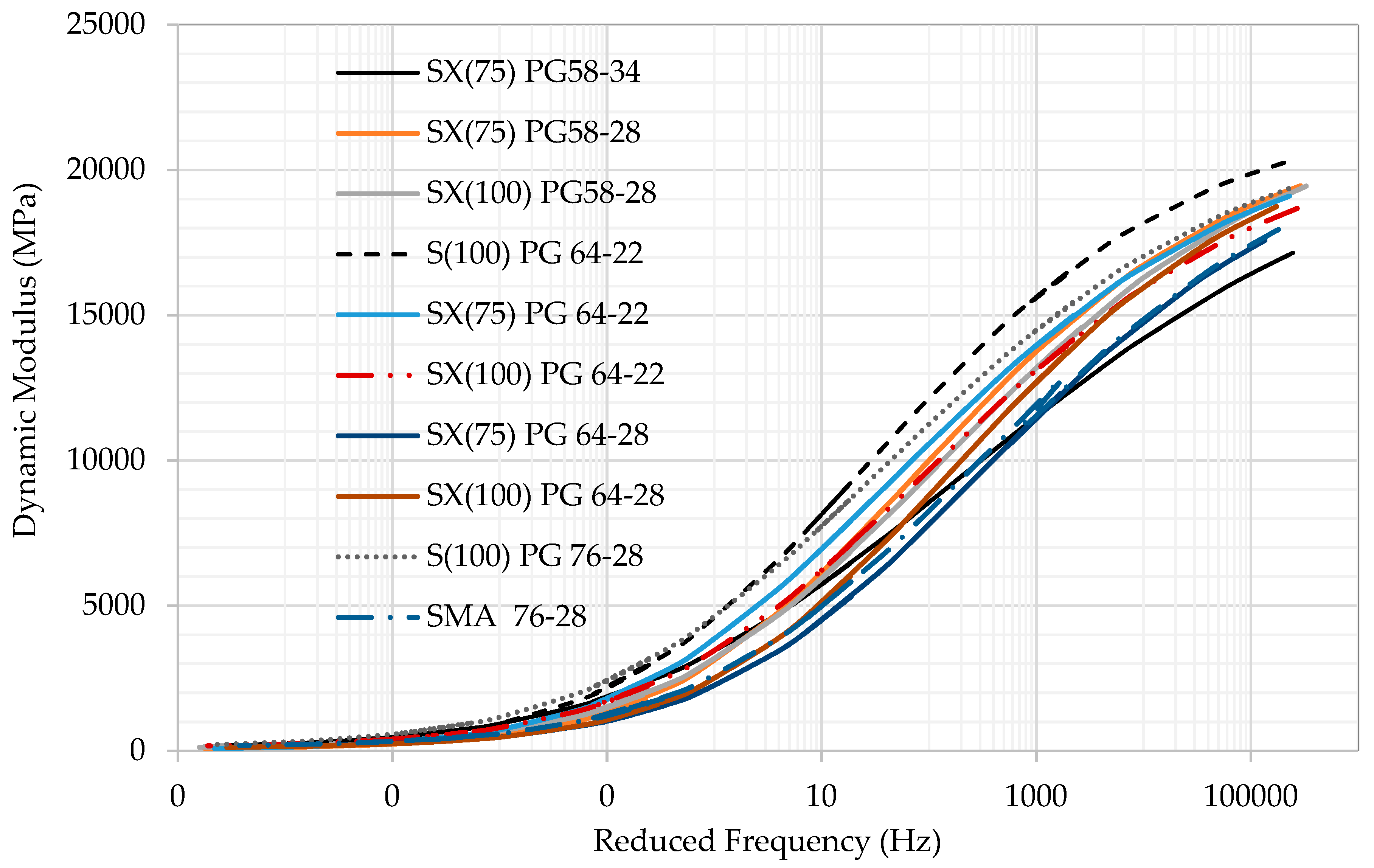
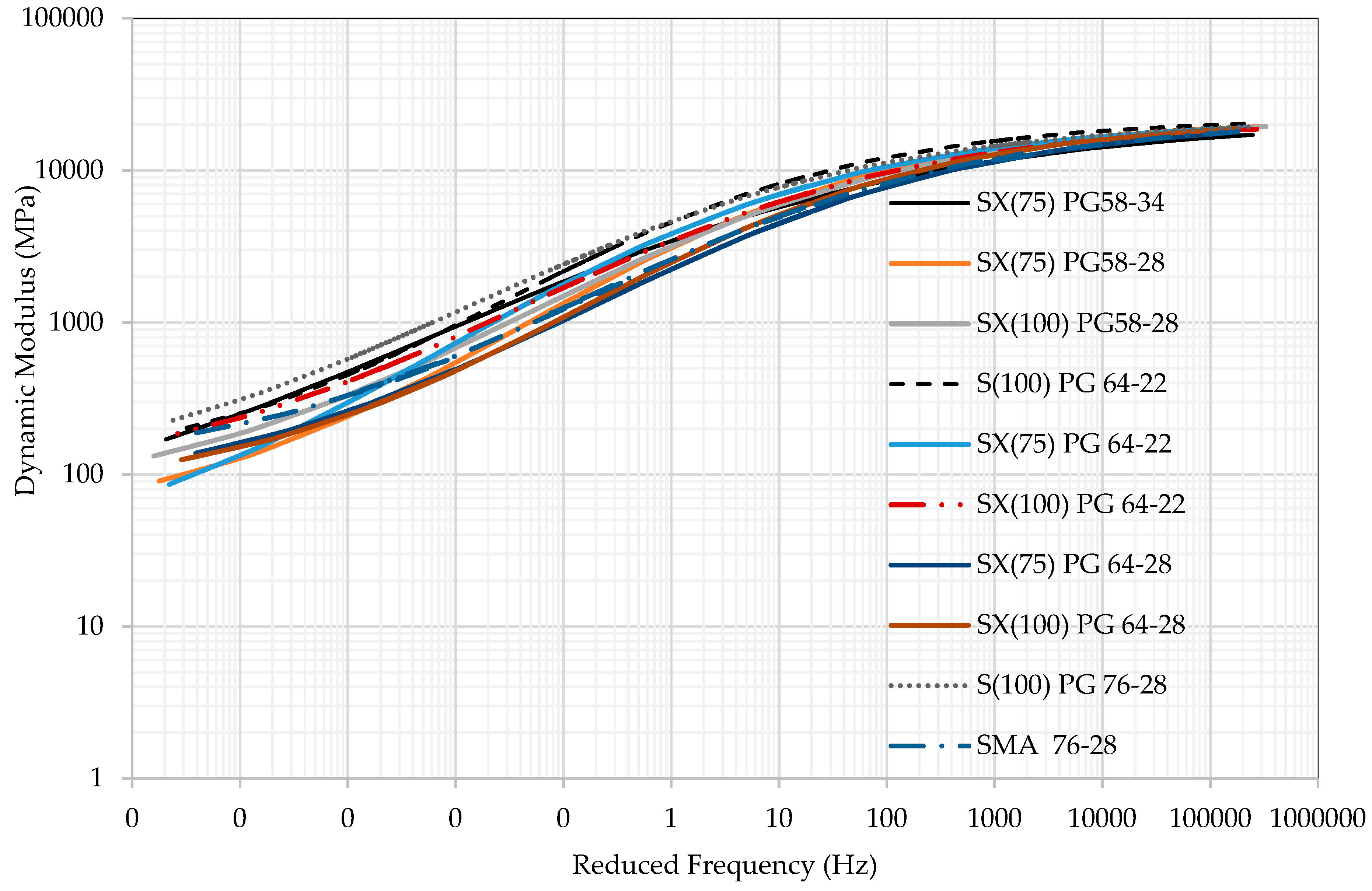
| S(100) PG 76-28 | Highest at high temperature | Best mix for rutting |
| SX(75) PG 64-28 | Lowest at high temperature | Worst for rutting |
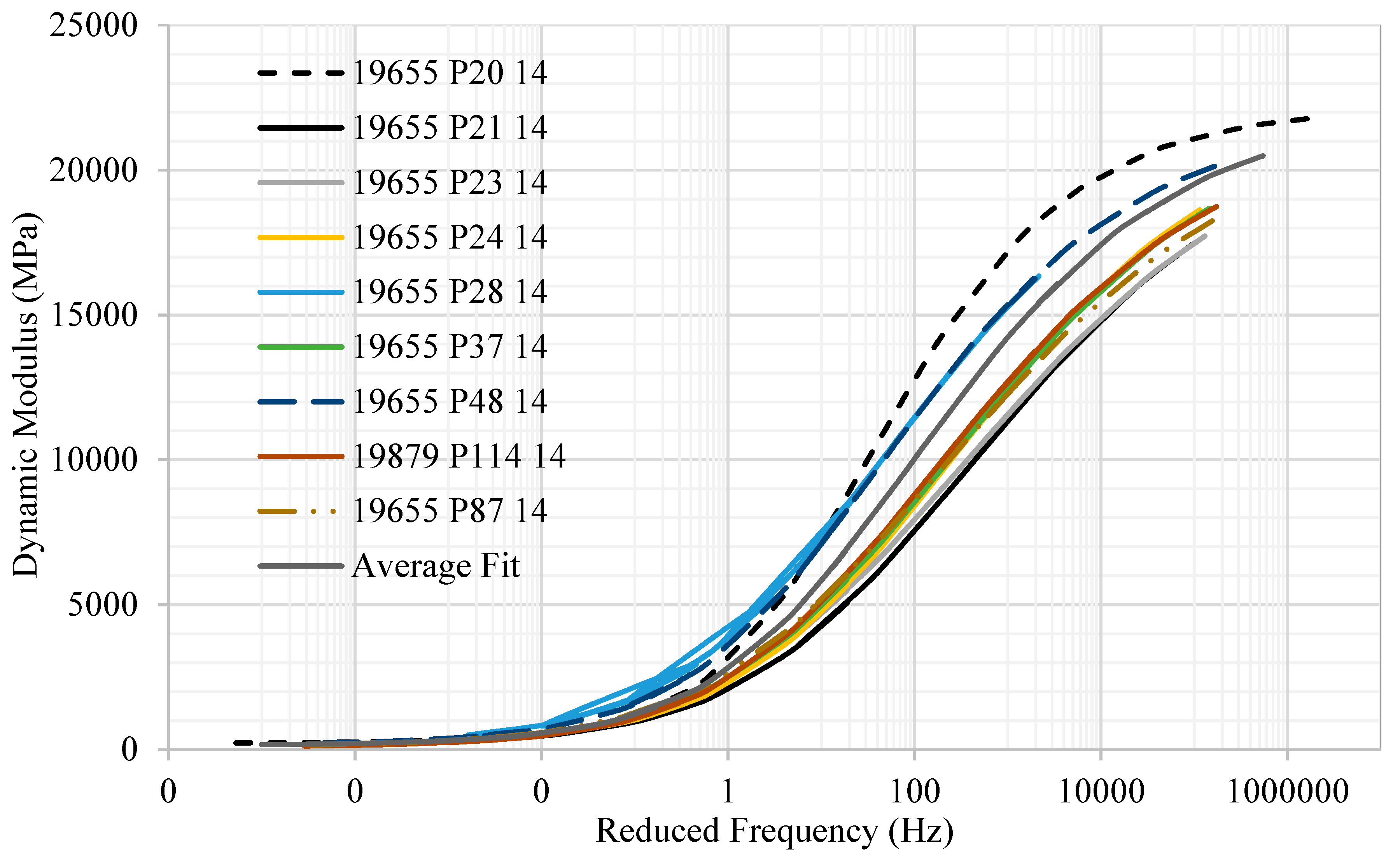
| Specimen No. | Vbe (%) | Va (%) | VMA (%) | VFA (%) | AC (%) |
|---|---|---|---|---|---|
| 19655 P20 14 | 10.59 | 6.06 | 17.0 | 64.0 | 5.58 |
| 19655 P21 14 | 10.85 | 6.06 | 17.1 | 63.5 | 5.80 |
| 19655 P23 14 | 10.56 | 6.06 | 16.7 | 65.1 | 5.70 |
| 19655 P24 14 | 10.97 | 6.06 | 16.0 | 64.2 | 5.78 |
| 19655 P28 14 | 10.71 | 6.06 | 16.1 | 63.0 | 5.61 |
| 19655 P37 14 | 10.48 | 6.06 | 15.8 | 62.4 | 5.65 |
| 19655 P48 14 | 13.18 | 6.60 | 17.4 | 62.0 | 5.50 |
| 19655 P87 14 | 13.18 | 6.30 | 17.1 | 63.2 | 5.50 |
| 19879 P114 14 | 10.05 | 6.90 | 17.5 | 63.5 | 4.90 |
| Mix ID | Vbe (%) | Va (%) | VMA (%) | VFA (%) | AC (%) |
|---|---|---|---|---|---|
| S(100) PG 64-22 | Decreases | Increases | Decreases | Increases | Decreases |
| S(100) PG 76-28 | -- | Increases | Decreases | Decreases | -- |
| SMA PG 76-28 | Decreases | Increases | Increases | Increases | Increases |
| SX(75) PG 58-28 | Increases | Decreases | Decreases | Increases | Increases |
| SX(75) PG 58-34 | NA | NA | NA | NA | NA |
| SX(75) PG 64-22 | Increases | Decreases | Increases | Decreases | Increases |
| SX(75) PG 64-28 | Increases | Decreases | -- | Increases | -- |
| SX(100) PG 58-28 | NA | NA | NA | NA | NA |
| SX(100) PG 64-22 | Increases | Increases | Decreases | Decreases | Decreases |
| SX(100) PG 64-28 | Increases | Increases | Decreases | Decreases | Decreases |
| SX(100) PG 76-28 | Decreases | Increases | Decreases | Increases | Decreases |
| Summary | 5 Increases 3 Decreases 1 Insensitive | 6 Increases 3 Decreases | 2 Increases 6 Decreases 1 Insensitive | 5 Increases 4 Decreases | 3 Increases 4 Decreases 2 Insensitive |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.R.; Kalevela, S.A.; Mendel, G. How the Mix Factors Affect the Dynamic Modulus of Hot-Mix Asphalt. J. Compos. Sci. 2019, 3, 72. https://doi.org/10.3390/jcs3030072
Islam MR, Kalevela SA, Mendel G. How the Mix Factors Affect the Dynamic Modulus of Hot-Mix Asphalt. Journal of Composites Science. 2019; 3(3):72. https://doi.org/10.3390/jcs3030072
Chicago/Turabian StyleIslam, Md Rashadul, Sylvester A. Kalevela, and Guy Mendel. 2019. "How the Mix Factors Affect the Dynamic Modulus of Hot-Mix Asphalt" Journal of Composites Science 3, no. 3: 72. https://doi.org/10.3390/jcs3030072





