Abstract
Lattice cell structures (LCS) are being investigated for applications in sandwich composites. To obtain an optimized design, finite element analysis (FEA) -based computational approach can be used for detailed analyses of such structures, sometime at full scale. However, developing a large-scale model for a lattice-based structure is computationally expensive. If an equivalent solid FEA model can be developed using the equivalent solid mechanical properties of a lattice structure, the computational time will be greatly reduced. The main idea of this research is to develop a material model which is equivalent to the mechanical response of a lattice structure. In this study, the mechanical behavior of a body centered cubic (BCC) configuration under compression and within elastic limit is considered. First, the FEA approach and theoretical calculations are used on a single unit cell BCC for several cases (different strut diameters and cell sizes) to predict equivalent solid properties. The results are then used to develop a neural network (NN) model so that the equivalent solid properties of a BCC lattice of any configuration can be predicted. The input data of NN are bulk material properties and output data are equivalent solid mechanical properties. Two separate FEA models are then developed for samples under compression: one with 5 × 5 × 4 cell BCC and one completely solid with equivalent solid properties obtained from NN. In addition, 5 × 5 × 4 cell BCC LCS specimens are fabricated on a Fused Deposition Modeling uPrint SEplus 3D printer using Acrylonitrile Butadiene Styrene (ABS) and tested under compression. Experimental load-displacement behavior and the results obtained from both the FEA models are in good agreement within the elastic limit.
1. Introduction
Lattice cell structures (LCS) are a kind of engineered structure having periodic cell made of struts at different orientations. Due to the advent of new additive manufacturing (AM) technologies, applications of LCS are currently being explored in several industries including gas storage, filtering, thermal science, and aerospace [1,2,3,4]. AM can be used to fabricate application specific LCS with greater complexity as the AM is a flexible manufacturing technique that involves layer-by-layer processing. To obtain an optimized LCS design for any particular application, finite element analysis (FEA) tools are usually used to model and numerically analyze many lattice configurations. Additionally, the optimized design may require further investigation using the FEA modeling approach at full scale. To have precision results, the FEA involves a massive number of degrees of freedom to resolve for each strut in structures, which increases the computational time extremely [5]. For example, a body centered cubic BCC unit cell with a strut diameter of 0.7 mm and dimensions of 5 mm × 5 mm × 5 mm in x, y, and z direction respectively under tension has been simulated using finite element analysis with a computational time of 10 h [5]. To reduce computational time, it is beneficial to develop a solid FEA model with a fewer number of degrees of freedom that represents the complex LCS. In that case, it is necessary to develop material model that can be used for the equivalent solid FEA that represents the LCS. The main idea of an equivalent mechanical properties is to replace and represent the lattice structure model with an equivalent compact solid material.
To obtain the equivalent mechanical properties for a wide range of strut and cell sizes, and materials used, artificial neural networks (ANN) can be used to develop an input-output algorithm where the input would be cell and strut characteristics and the mechanical properties of raw material and the output would be equivalent solid mechanical properties. ANN is being used as a computational approach that learns to simulate and solve the engineering problems [6]. ANN predicts a desired property based on previous learning cycles or training. The artificial neural networks were applied to engineering problems including structure optimization problems, material analysis problems, thermophysical properties of manufactured materials, prediction of crack geometry, the behavior of fracture toughness, and prediction of the deformation of a linear elastic beam [5,7,8,9,10,11,12]. Neurons or nodes are the basic processing elements of neural networks. In the mathematical model of the neuron, the connection weights in matrix form represent the effects of the synapses that modulate the effect of the connected input signals and the nonlinear property showed by neurons is represented by a transfer function. One of the most important steps to building the structure of neural networks is selecting the best dataset to use for training a network. In general, the datasets of the neural network are divided into three parts including training, validation, and testing datasets. The training dataset optimize the weights of interconnection between nodes so that the neural network will have capability to predict accurate results of output for a given set of inputs. To check the performance of the new data during the training, the data for validation is used. An important portion of developing neural network is the test set which is not used during training. So, the test set measures how well the network can recall what it has learnt.
In this research, the load-displacement and stress-strain results is first obtained from the FEA of BCC unit cell under compression and shear in all three orthogonal directions. The stress-strain plots are then used to calculate the equivalent mechanical properties such as elastic modulus (Ee), shear modulus (Ge), and Poisson’s ratio (νe) for several strut diameter/cell sizes. These results are then used to develop a neural networks NN model so that the equivalent solid properties of a BCC lattice cell can be predicted for any combination of strut diameters and cell sizes. The bulk material properties along with the cell configurations are used in the input dataset of NN and the equivalent solid mechanical properties are obtained from the output dataset.
2. Methodology Strategy
The main idea of this research is to replace and depict the BCC lattice structure with an equivalent elastic material model. The equivalent material model is a solid material model and does not contain any struts, which is equivalent to the mechanical response of a lattice structure. A methodology is developed to create correlation between a conventional BCC lattice structure and an equivalent solid model. It may be mentioned here that the BCC lattice unit cell, having the same dimension in all three directions with uniform strut diameter, have three orthogonal planes of material symmetry. The mechanical properties of the unit cell are same in all three orthogonal directions and hence can be considered as quasi-isotropic whose shear modulus is not a function of elastic modulus and Poisson’s ratio. This homogenization technique is valid for a structure which is composed of at least three by three by three cells so that the boundary conditions of the equivalent solid structures do not affect the mechanical response [13]. The equivalent elastic mechanical properties considered here are elasticity (Ee) and shear moduli (Ge) and Poisson’s ratio (νe).
In reference [14], Ashby showed that the mechanical properties of lattice structures depend on three factors: its material, lattice shape of the cell (pattern), and aspect ratio. These factors influence the load-displacement of a lattice structure. Therefore, in this research the finite element analysis and theoretical approaches on BCC lattice with various relative densities of several cases (different strut diameters and cell sizes), and Acrylonitrile Butadiene Styrene (ABS) as model material, provide the ability to determine a correlation between these configurations and their load-displacement of a lattice structure.
The general methodology strategy is schematically illustrated in Figure 1 in which the BCC unit cell is used as a basic model for predicting the mechanical responses of the larger lattice structure. The following is the solution process flow of this work:
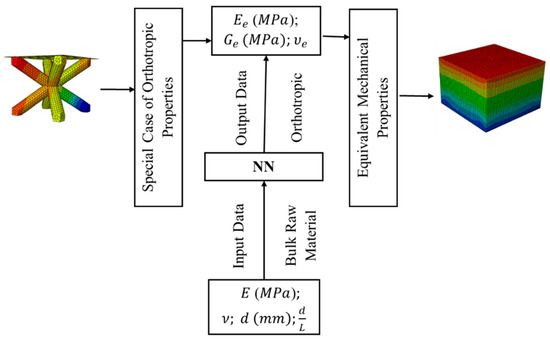
Figure 1.
A methodology strategy from finite element analysis (FEA) model to neural networks (NN) model to Equivalent solid model.
a. First, sixteen models of BCC unit cell are simulated using FEA with a considerable number of elements to calculate the elastic modulus and Poisson’s ratio for different strut diameters and cell sizes.
b. Second, sixteen models are simulated using FEA to predict the shear modulus. So, the total number will be thirty-two models. Figure 2 shows one case of various unit cell diameter for BCC configuration with cell size of 5 mm.
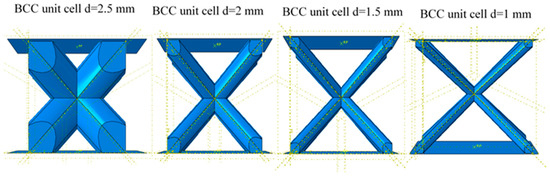
Figure 2.
Various unit cell diameter for body centered cubic (BCC) configuration at 5 mm.
c. Ten of the sixteen equivalent mechanical property and design parameter data sets are used to train a NN to predict the equivalent properties for any cell size and material with significantly less time than a full finite element. The six remaining data sets that are not included in the training data are used as testing of the NN predictions.
d. A representative solid FEA is developed with equivalent properties to compare its load-displacement behavior with that from FEA of BCC lattice structure.
e. The BCC lattice used in step (d) is 3D printed and tested under compression to compare its load-displacement behavior with that obtained from both solid and lattice models obtained in part (d).
3. Finite Element Modeling of Unit Cell
3.1. Material and Physical Parameters
In this step, the FEA software Abaqus Explicit 2017 [15] was used to model the compression and shear test of a BCC unit cell configuration (Figure 3a) for different strut diameters and cell sizes within the elastic limit to predict equivalent solid properties of the lattice structure. The BCC configuration has a quasi-isotropic material behavior, which has three independent parameters constants which include equivalent elastic modulus () Poisson’s ratio = , and Shear modulus (. Acrylonitrile Butadiene Styrene (ABS) is considered as model material. In the scope of the parametric study, the strut diameters are 1.0, 1.5, 2, and 2.5 mm, the dimensions of a single unit cell sizes are 2.5 × 2.5 × 2.5, 5 × 5× 5, 7.5 × 7.5 × 7.5, and 10 × 10 × 10 mm, and aspect ratios (diameter truss/ unit cell length) are 0.1, 0.1333, 0.15, 0.2, 0.25, 0.2666, 0.3, 0.3333, 0.4, 0.5, 0.6, 0.8, and 1. The design space domain of this parametric has covered the engineering application of this study. Typically, this will be perfect to select dataset of training the intelligent NN model in surrounding these parameters. Fidelity and stability of the neural network model depend on the selected data of training.
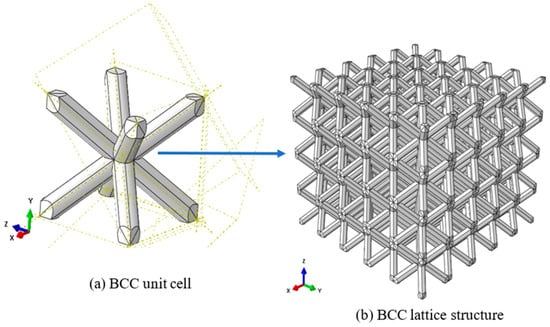
Figure 3.
Micromechanics technique design (a) BCC unit cell (b) BCC lattice structure.
3.2. Design and Mesh Generation
The BCC unit cell and lattice structures are designed and meshed using the micromechanics software Abaqus 6.17. The main reason to use micromechanics technique instead of SolidWorks® software is because it has more flexibility in selecting element types during mesh generation for a lattice structure. Most of the models are developed using Hexahedral mesh generation because of geometric complicacy imposed by branching and embedded structures. Although tetrahedral mesh generation can be easily automated, it gives inaccurate results as compared with hexahedral elements [16]. BCC unit cell and comprehensive configuration of cell connection of the lattice structure designed by using Micromechanics in Abaqus 2017 is illustrated in Figure 3.
Using the Micromechanics technique in Abaqus, Hexahedral mesh (element type C3D8R) is used for all models to generate the mesh. To accomplish FEA with high performance, both mesh sensitivity analysis and type of mesh generation are adopted. Because meshing is very significant to obtain precision results, in this research, mesh sensitivity was performed by observing the stiffness () versus the total number of the element. Figure 4 shows the mesh sensitivity of one case BCC unit cell (5 × 5 × 5) mm with d = 1 mm, this curve illustrated the mesh convergence when the mesh size decreases from 1.1 (coarse) to 0.25 (fine) and the percentage variation of stiffness is within 2%. Following the same procedure, the mesh sensitivity analysis is performed for all cell sizes and strut diameters of BCC unit cell.
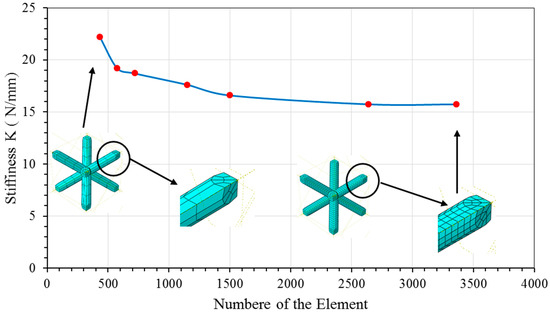
Figure 4.
Mesh Sensitivity of BCC unit cell (5 × 5 × 5) mm and d = 1 mm for mesh size from 1.1 (Coarse) to 0.25 (Fine) mm.
3.3. Applied Load and Boundary Conditions
In order to capture the behavior of the entire lattice structure based on the analysis of the BCC unit cell, it is important to select appropriate boundary conditions. For shear modulus simulation, the model is placed between two plates, thereby the upper and lower faces are clamped to those plates. Shear displacement is applied parallel to the upper face while the lower face or the base of the model is kept fixed. Loading and boundary conditions for the shear model is shown in Figure 5a. For both elastic modulus and Poisson’s ratio, symmetric boundary conditions are used on the top and bottom surfaces. In other words, all the translational and rotational degrees of freedom on the upper and lower struts are except one strut is fixed to avoid rigid body motion. Furthermore, the boundary conditions are not applied on the fronts and sides of the cellular structure. In the same manner, an applied displacement on the upper faces moves towards the bottom of the model. Loading and boundary conditions for the compression model is shown in Figure 5b. Moreover, the displacement loading for both the shear and compression models are applied by using the dynamic explicit FEA model on ABAQUS 2017 (Providence, RI, USA).
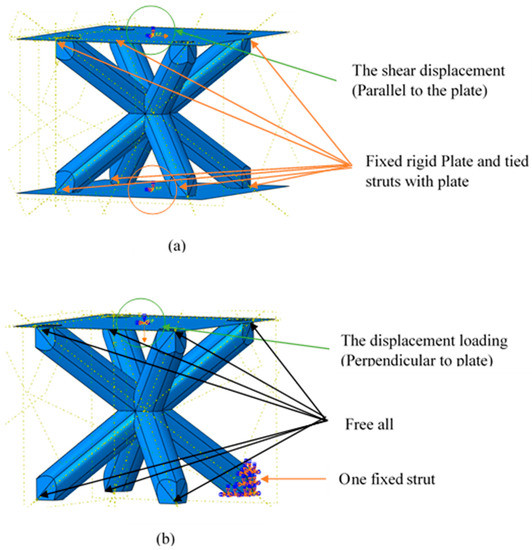
Figure 5.
Boundary conditions of BCC unit cell for FEA model (a) Boundary condition for Shear modulus (b) Boundary condition for Elastic modulus and Poisson’s ratio.
3.4. Material Properties
The raw material that is used for all finite element simulations is Acrylonitrile Butadiene Styrene (ABS) supplied by Stratasys. The bulk material properties of ABS used in the FEA simulations of lattice unit cell (Figure 5) are given in Table 1. The data in Table 1 was previously measured from the standard compression (ASTM D695, ISO 604) and tension test (ASTM D882) by this group [17]. The compression and tension specimens were fabricated using a Stratasys uPrint SEplus 3D printer. The default temperature settings used for the model material were as follows. The printer head temperature of 300 °C and the chamber temperature of 77 °C were maintained. Layer thickness was set to 0.254 mm. The models were printed using the Stratasys standard sparse high-density fill patterns where the linear scan pattern is used to create fully dense solid structure.

Table 1.
Material properties of Acrylonitrile Butadiene Styrene (ABS) material [17].
3.5. Data Collection
Both the shear and compression FEA models are run and stress-strain curves are plotted. Load is obtained from the reaction force as displacement is applied on the top plate. Stress is calculated by dividing load with area of a unit cell face L2. Strain is calculated from applied displacement divided by cell height L. Slopes of the stress-strain plots from the compression and shear models are elasticity modulus Ee and shear modulus Ge of the equivalent solid model, respectively. In addition, transverse displacement vs. longitudinal displacement is plotted from the compression model and Poisson’s ratio (νe) is obtained from the slope of the curve. Variation of elasticity modulus Ee, Poisson’s ratio νe, and shear modulus Ge, are shown in Figure 6, Figure 7 and Figure 8, respective, by solid line.
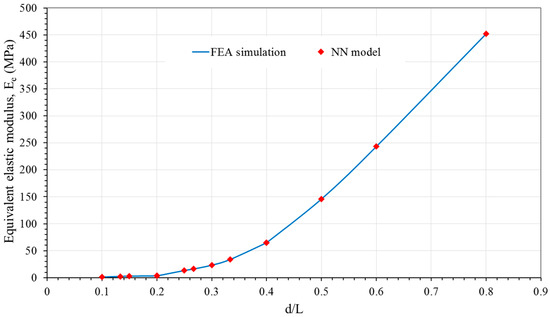
Figure 6.
Comparison of equivalent elastic moduli from FEA simulation and NN model for BCC pattern.
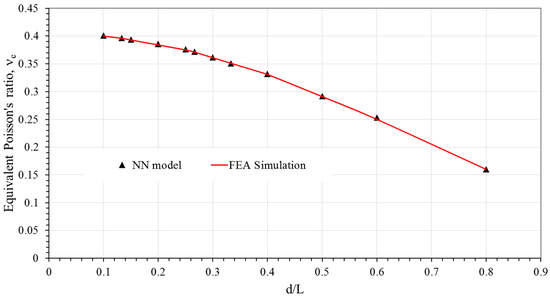
Figure 7.
Comparison of equivalent Poisson’s ratio from FEA simulation and NN model for BCC pattern.
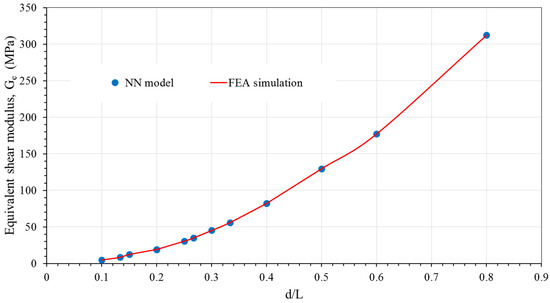
Figure 8.
Comparison of equivalent shear moduli from FEA simulation and NN model for BCC pattern.
4. Neural Network for Equivalent Material Model
In this research the surrogate intelligence model is used to predict the equivalent mechanical properties of the lattice structure using FEA results. MATLAB software (R2017, The Mathworks, Inc., Natick, MA, USA) is used to model the neural network prediction. This technique is used to investigate the equivalent mechanical properties of the lattice structures. Ten of the sixteen datasets are first used in training to develop the neural network (NN) model. To demonstrate the success of the neural NN in predicting accurate equivalent mechanical properties, some of the ten and the remaining six data sets are used for testing.
4.1. The NN Model Used
The design of the NN model used in this study is illustrated in Figure 9. The number of hidden layers and nodes in each hidden layer of the structural NN model are not achieved directly. No rules can be employed to estimate the exact number of hidden layer and nodes. So, the number of hidden layers and nodes are affected essentially by the network application. Many approximation problems can be solved sufficiently by using a single hidden layer. However, using two hidden layers makes it easier to solve complicated problems [18]. One of the significant rules that is used to select the number of nodes, the maximum error between the actual value (Target) and both training patterns and testing patterns (output NN) should be small as possible. In addition, the number of iteration (Epochs) should be as less as possible too. As a result, performing of the neural network model with the number nodes in one hidden layer and two hidden layers, the idea is modeling with one and two hidden layer arrangement with an increase in the number of nodes in each layer.
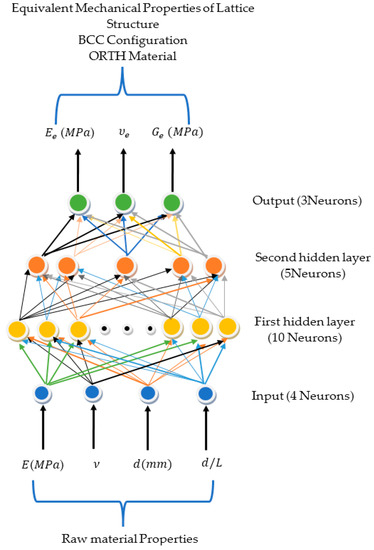
Figure 9.
The structure of the NN model for BCC configuration.
Table 2 illustrates various significant algorithms that are used to test the NN [19]. The factors that dictate which algorithm is the best for a given problem are the intricacy of the problem, the number of data training set, the size of the matrix weights and biases, the maximum error between the actual data and prediction of NN, and the capability of NN to predict the pattern (regression approximate).

Table 2.
Various algorithms for NN model.
In this research, all the algorithms given in Table 2 are tested. Comparing different algorithms, the Resilient Backpropagation (trainrp) algorithm gives the best performance as the mean square error (MSE) is the least at a particular number of epochs (number of iteration), as shown in Figure 10. It is clear from Figure 10 that minimum number of epoch is 100 gives accurate results or least MSE
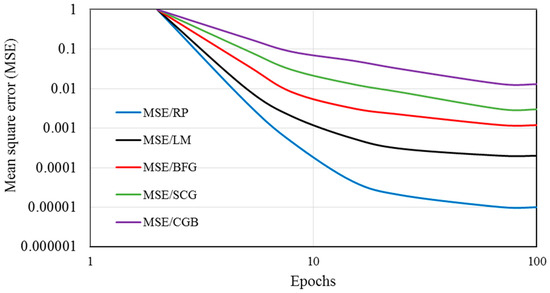
Figure 10.
Convergence of NN results for train sets based on different algorithms.
4.2. Training and Testing Patterns Used
One of the most sensitive elements in building a neural network model is dataset selection. The dataset that produces the neural network is divided into two subsets: a training data and a testing data. Both stability and precision of the neural network model depend on the training phase. In this research, the training data consists of orthotropic material training data sets explained next.
The parameters represented by the input (training data) vector elements of raw material include elastic modulus (), Poisson’s ratio , strut diameters (), and relative dimension . So, the total number of training input isotropic material will be four parameters. The training output parameters are equivalent properties of BCC lattice unit cell from FEA, which include equivalent elastic modulus in x, y, and z direction, Poisson’s ratio , and shear modulus . The quasi-isotropic data that are used to train the NN as training data are illustrated in Table 3, Table 4 and Table 5, and Figure 9.

Table 3.
Input/Output parameters for training and testing of BCC configuration.

Table 4.
Input training data with E = 861 MPa, and ν = 0.35.

Table 5.
Output training data for BCC configuration.
To demonstrate the accurate prediction of the equivalent mechanical properties from NN, testing patterns that include remaining six data sets are not included in above tables.
5. Experimental Procedure
To validate the BCC unit cell FEA and NN results, 25 mm × 25 mm × 20 mm LCS was 3D printed and tested under compression. The dimensions of a single unit cell are 5 mm × 5 mm × 5 mm with strut diameter of 1 mm. The model was first designed using the CAD software Solidworks (Figure 11a) and was saved in .STL format. The .STL file was then processed with the 3D printer software Stratasys Catalyst. A fused deposition modeling (FDM) based 3D printer, Stratasys uPrint SE plus [20] was used to print the samples using default settings including 0.254 mm layer thickness and high sparse density. The material used to fabricate the specimens was an ivory-colored production-grade thermoplastic polymer ABSplus-P430. Three specimens were fabricated for the same model and the support material was removed from the printed samples using Stratasys cleaning apparatus, SCA, 1200HT parts [21]. The completed final sample for testing is shown in Figure 11b.
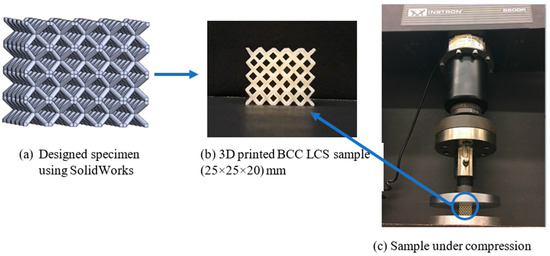
Figure 11.
Experimental procedures, (a) sample design in SolidWorks; (b) sample fabrication using 3D printing; and (c) compression test.
The compression test was conducted on the fabricated samples using a universal testing machine, Instron 5500R [22]. The load-displacement data was collected using Bluehill2®, i.e., software connected with the testing machine, and were plotted in Excel.
6. Finite Element Modeling of LCS and Equivalent Solid
Figure 12 shows the optimized discretized models of a 25 mm × 25 mm × 20 mm LCS with 5 mm × 5 mm × 5 mm unit cell having strut diameter of 1 mm (Figure 12a) and a 25 mm × 25 mm × 20 mm solid (Figure 12b). Both the LCS in Figure 12a and the equivalent solid in Figure 12b are modeled with hexagonal elements. After mesh sensitivity analysis, the number of elements for LCS is 339,360 whereas the number of elements for the equivalent solid model is about 100,000 (Figure 4). It is mentioned here that the minimum number of elements for the same lattice structure of dimension 25 mm × 25 mm × 20 mm modeled using tetrahedral elements in reference [16] was about 500,000 elements. Furthermore, the time needed to create the mesh and seed part for LCS about three hours without running the simulation of FEA model while that for an equivalent solid model is seconds.
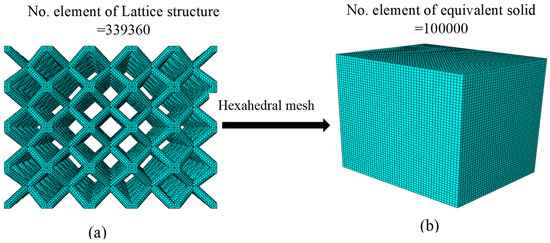
Figure 12.
Full-FEA simulation for (a) LCS; and (b) the equivalent solid.
The bulk material properties used for the LCS model are shown previously in Table 1. For the equivalent solid model, the equivalent properties obtained from the unit cell FEA (Section 3) and shown in Table 4 and Table 5 (data number 3) are used. To mimic the experimental boundary conditions, all degrees of freedom of the top and bottom faces are constrained by tying them to perfect rigid plates. A displacement load is applied in the downward direction. After the models are run, the reaction force on the bottom fixed are considered as load and the load-displacement curves for both the LCS and equivalent solid model are shown in Figure 13.
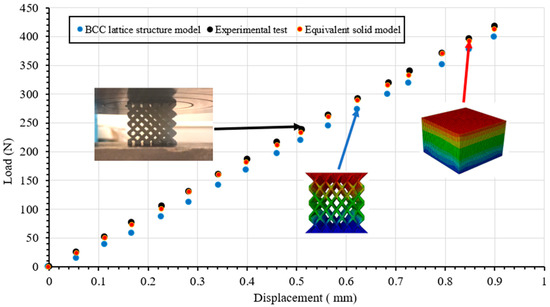
Figure 13.
Comparison of the FEA simulation of LCS, experiment test and equivalent solid model results.
7. Results and Discussion
As the equivalent mechanical properties are obtained after training of NN using the outcomes of unit cell FEA models, the results of the NN model are supposed to approach that of FEA. Figure 6, Figure 7 and Figure 8 show elasticity modulus Ee, Poisson’s ratio νe, and shear modulus Ge, respectively. The figures include both the lattice cell FEA results (indicated by solid lines) and the NN output or random tasting data (indicated by discrete points). It is clear that the random tasting NN data are in satisfactory agreement with the FEA results for all cases. Furthermore, it is clear from Figure 6 that the elastic modulus of BCC configuration increases when the aspect ratio d/L. Figure 7 illustrated the NN for randomly choosing of the test for Poisson’s ratio that matched well with FEA results (solid). It is observed that the Poisson’s ratio decreases with an increase in aspect ratio. Finally, Figure 8 shows the intelligent model NN for a random testing data of Shear modulus at different d/L ratio are in good agreement with the FEA simulation (solid curves). Like elastic modulus, the shear modulus also increases when the aspect ratio increases. In all cases, the NN model is examined with 1 and 2 hidden layers with an increase in the number of nodes in each layer. The sensitivity of the neural network prediction increases for two hidden layers or more as a number of nodes for each layer increases. The outcomes demonstrate that the two hidden layer network accomplishes significantly better than the one hidden layer network. The optimum number of nodes in two hidden layers for NN that gives minimum mean square error (MSE) is 10:5 (10 nodes for the first hidden layer and 5 for the second hidden layer). As mentioned before that the complicacy of the problem lead to increase the number of nodes in each layer network. Studying various algorithms, the Resilient Backpropagation (trainrp) algorithm gives the best implementation as goal met MSE between the output of NN and the FEA results at least number of iterations. It is clear from statistical outcomes (R = 0.999) that the proposed neural network model accurately learned to map the relationship between the equivalent mechanical properties for quasi-isotropic material of BCC unit cell and varying parameters.
To validate the development of equivalent solid model methodology, two separate FEA models are developed for samples under compression: one with 5 × 5 × 4 cell BCC and one completely solid with equivalent solid with equivalent solid properties that are then compared with experimental results. The load-displacement plots obtained from the LCS FEA (blue solid circles), equivalent solid FEA (red solid circles) and experimental compression test of 3D printed LCS (black solid circles) are together shown in Figure 13. A good correlation among FEA simulation of LCS and the equivalent solid model, and experimental data is observed. It is thus concluded that the material model developed in this study for BCC LCS is acceptable. Thus, the equivalent solid FEA of a large-scale model for a lattice-based structure is able to capture the mechanical response of a lattice structure. It may be mentioned that the computation time for the equivalent solid model is about 8 min compared with the FEA simulation time of the LCS, which is 48 h. The higher computation time for the FEA of LCS is due to the complexity of the cellular configuration and is in agreement with previous study [17].
8. Conclusions
In this study, a NN algorithm is developed to determine the equivalent material properties of equivalent orthotropic material with the help of the FEA of BCC unit cells. The NN is observed to be able to predict the equivalent solid properties of BCC lattice considerably well. Therefore, the neural network model of BCC configurations is very precise, swift and practical for use as compared to numerical FEA models. By using the equivalent material properties from NN, a larger and more complicated BCC LCS with any arbitrary cell size, strut diameter, and type of material can be computationally investigated using FEA with considerably less computational time. It was demonstrated that the computational time and analysis speed of lattice structure could be reduced from several hours to a few minutes.
Author Contributions
Conceptualization, T.A.A. and A.M.; Methodology, T.A.A. and A.M.; Software, T.A.A.; Validation, T.A.A. and A.M.; Investigation, T.A.A. and A.M.; Resources, A.M.; Data Curation, T.A.A.; Writing-Original Draft Preparation, T.A.A.; Writing-Review & Editing, A.M.; Supervision, A.M.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bible, M.; Sefa, M.; Fedchak, J.A.; Scherschligt, J.; Natarajan, B.; Ahmed, Z. 3D-Printed Acrylonitrile Butadiene Styrene-Metal Organic Framework Composite Materials and Their Gas Storage Properties. 3D Print. Add. Manuf. 2018, 5. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M. Lattice Structures and Functionally Graded Applications in Additive Manufacturing of Orthopedic Implants. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Alsalla, H.; Hao, L.; Smith, C. Fracture toughness and tensile strength of 316L stainless steel cellular lattice structures manufactured using the selective laser melting technique. Mater. Sci. Eng. 2016, 669, 1–6. [Google Scholar] [CrossRef]
- Wilmoth, N. Determining the Mechanical Properties of Lattice Block Structures; NASA Technical Report Server; NASA: Washington, DC, USA, 2013.
- Koeppe, A.; Padilla, C.A.H.; Voshage, M.; Schleifenbaum, J.H.; Markert, B. Efficient numerical modeling of 3D-printed lattice-cell structures using neural networks. Manuf. Lett. 2018, 15, 147–150. [Google Scholar] [CrossRef]
- Flood, I. Towards Next Generation Artificial Neural Networks and Their Application to Civil Engineering. Adv. Eng. Inform. 2008, 22, 4–14. [Google Scholar] [CrossRef]
- Villarrubia, G.; Paz, J.F.D.; Chamoso, P.; Prieta, F.D.L. Artificial Neural Networks used in Optimization Problems. Neurocomputing 2017, 272, 10–16. [Google Scholar] [CrossRef]
- Arslan, M.A.; Hajela, P. Counterpropagation Neural Networks in Decomposition Based Optimal Design. Comput. Struct. 1997, 65, 641–650. [Google Scholar] [CrossRef]
- Bagheripoor, M.; Bisadi, H. Application of artificial neural networks for the prediction of roll force and roll torque in hot strip rolling process. Appl. Math. Model. 2013, 37, 4593–4607. [Google Scholar] [CrossRef]
- Kutuk, M.A.; Atmaca, N.; Guzelbey, l.H. Explicit Formulation of SIF using Neural Networks for Opening Mode of Fracture. Eng. Struct. 2007, 29, 2080–2086. [Google Scholar] [CrossRef]
- Haque, M.E.; Sudhakar, K.V. ANN back-propagation prediction model for fracture toughness in microalloy steel. Int. J.Fatigue 2002, 24, 1003–1010. [Google Scholar] [CrossRef]
- Koeppe, A.; Bamer, F.; Markert, B. Model reduction and submodelling using neural networks. Proc. Appl. Math. Mech. 2016, 16, 537–538. [Google Scholar] [CrossRef]
- Abdulhadi, H.S.; Mian, A. Effect of Strut Length and Orientation on the Elastic Mechanical Response of Modified BCC Lattice Structures. Part L J. Mater. Des. Appl. 2019, in press. [Google Scholar]
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Abaqus CAE User’s Guide; DS Simulia Abaqus: Providence, RI, USA, 2017.
- Tadepalli, S.C.; Erdemir, A.; Cavanagh, P.R. Comparison of hexahedral and tetrahedral elements in finite element analysis of the foot and footwear. J. Biomech. 2011, 44, 2337–2343. [Google Scholar] [CrossRef] [PubMed]
- Al Rifaie, M.J. Resilience and Toughness Behavior of 3D-Printed Polymer Lattice Structures: Testing and Modeling. Master’s Thesis, Wright State Univerity, Dayton, OH, USA, 2017. [Google Scholar]
- Lu, W. Neural Network Model for Distortional Buckling Behaviour of Cold-Formed Steel Compression Members. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2000. [Google Scholar]
- MATLAB Decumentation. The Langusge of Technical Computing (R2017); MathWorks Inc.: Natick, MA, USA, 2017. [Google Scholar]
- “Stratasys,” uPrint SE Plus, 2017. Available online: http://www.stratasys.com/3d-printers/idea-series/uprint-se-plus (accessed on 1 November 2018).
- “Support Removal,” Phoenix Analysis & Design Technologies, 09 September 2015. Available online: www.SupportRemoval.com (accessed on 26 March 2019).
- “INSTRON,” Instron Series 5500. Available online: https://www.instron.us/en-us/products/testing-accessories/digital/digital-controller/5500-series (accessed on 27 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).