Optimization of Fiber Orientation Model Parameters in the Presence of Flow-Fiber Coupling
Abstract
1. Introduction
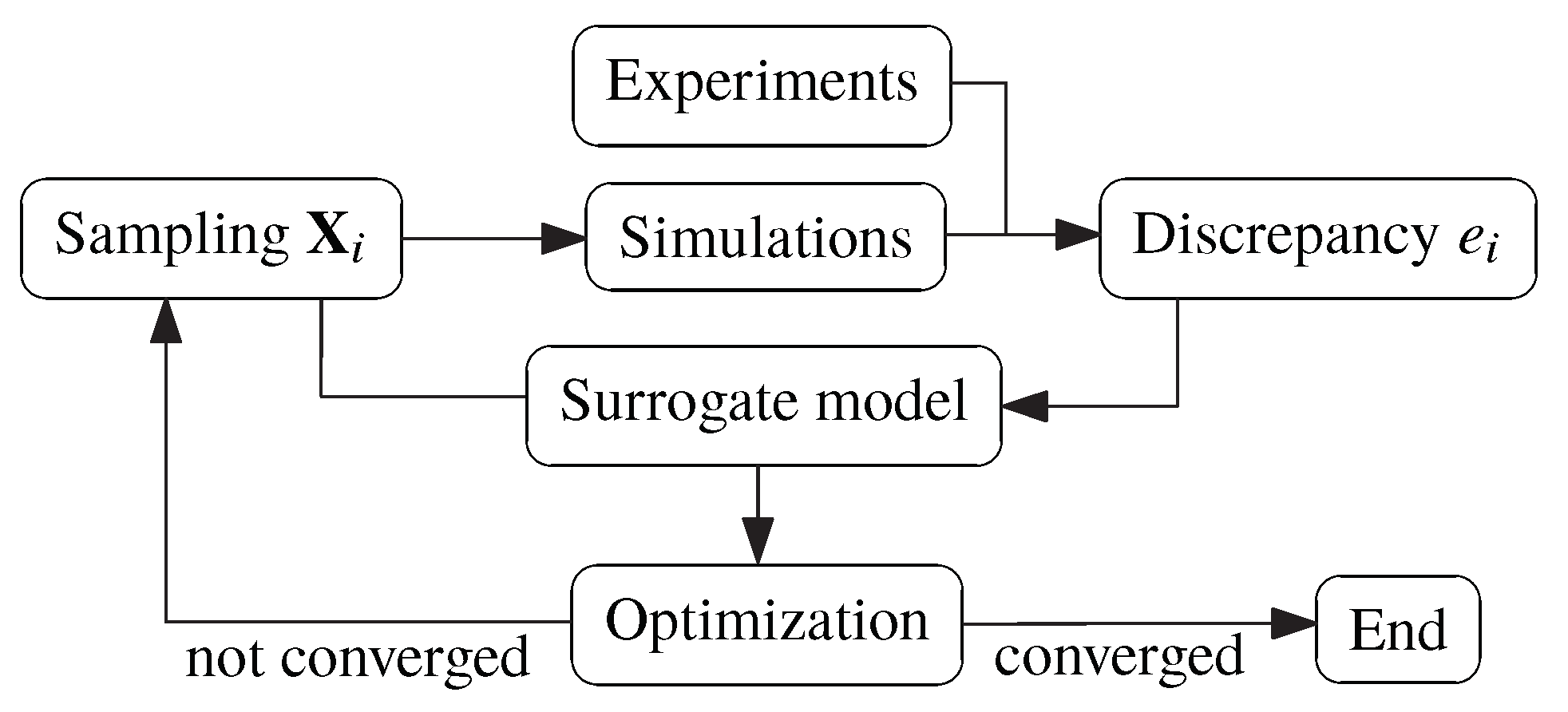
2. Optimization of Fiber Orientation Model Parameters via Surrogate Modeling
2.1. Fiber Orientation Predictions in the Presence of Flow-Fiber Coupling
2.2. Discrepancy Measure between Simulation and Experiment
2.3. Metamodeling and Adaptive Global Optimization
3. Application on a Center-Gated Disk Problem
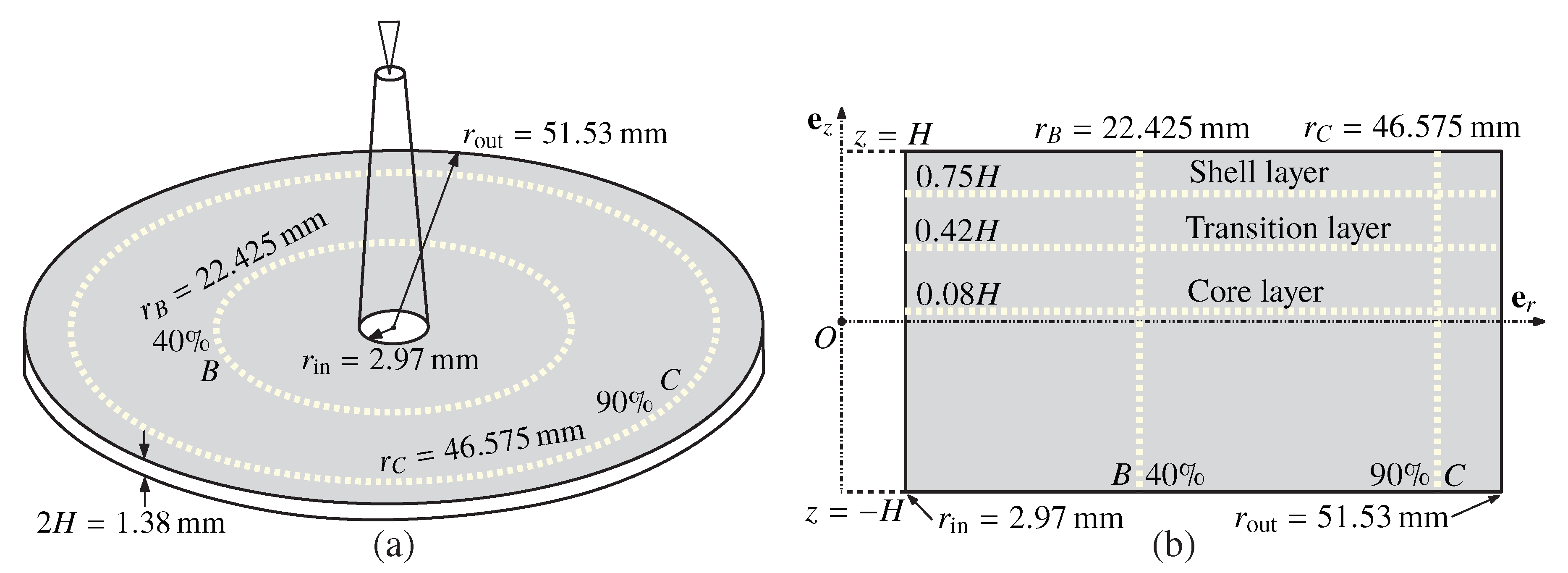
3.1. Problem Statement
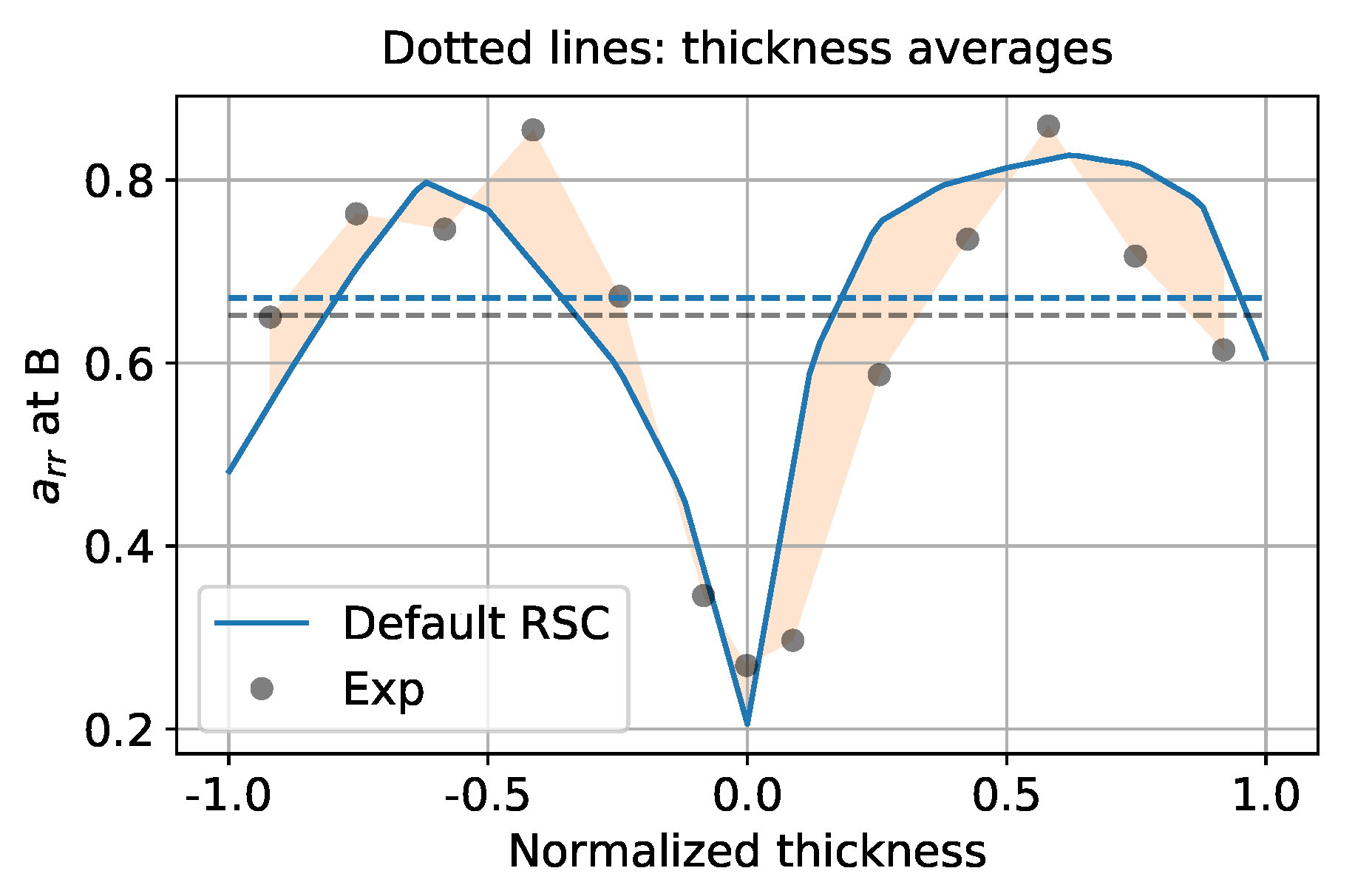
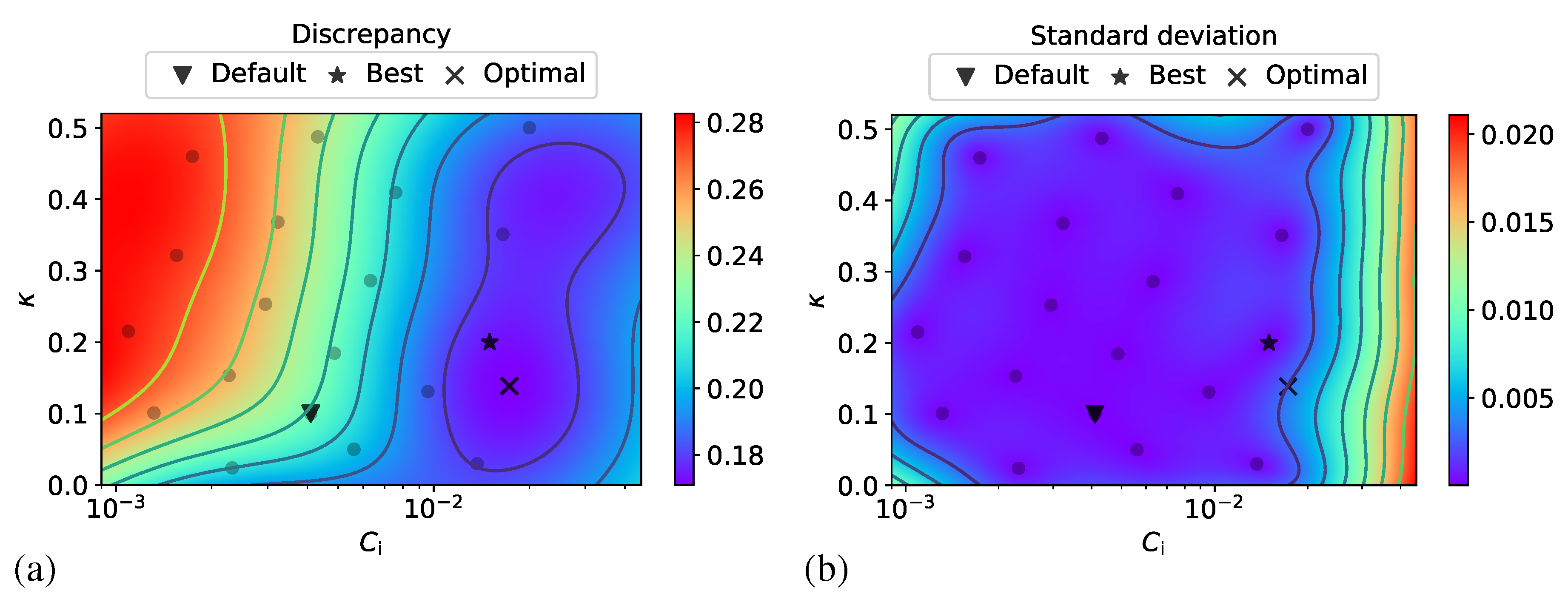
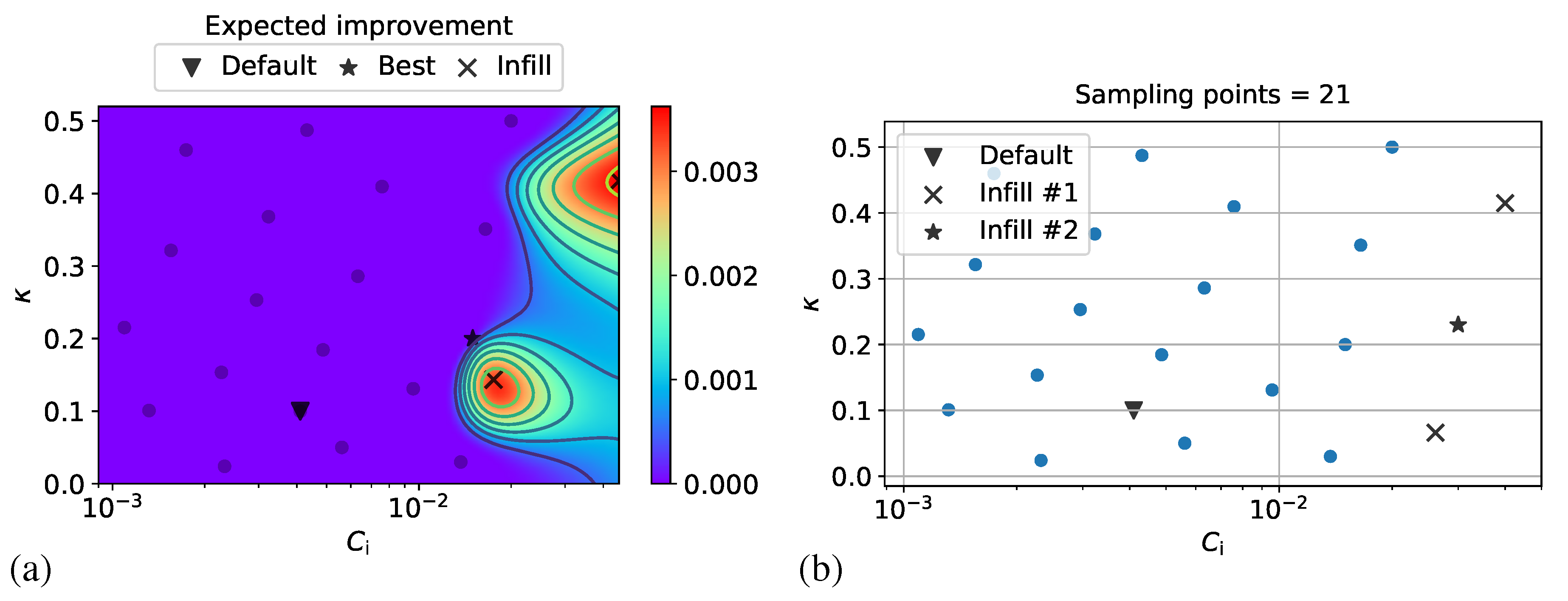
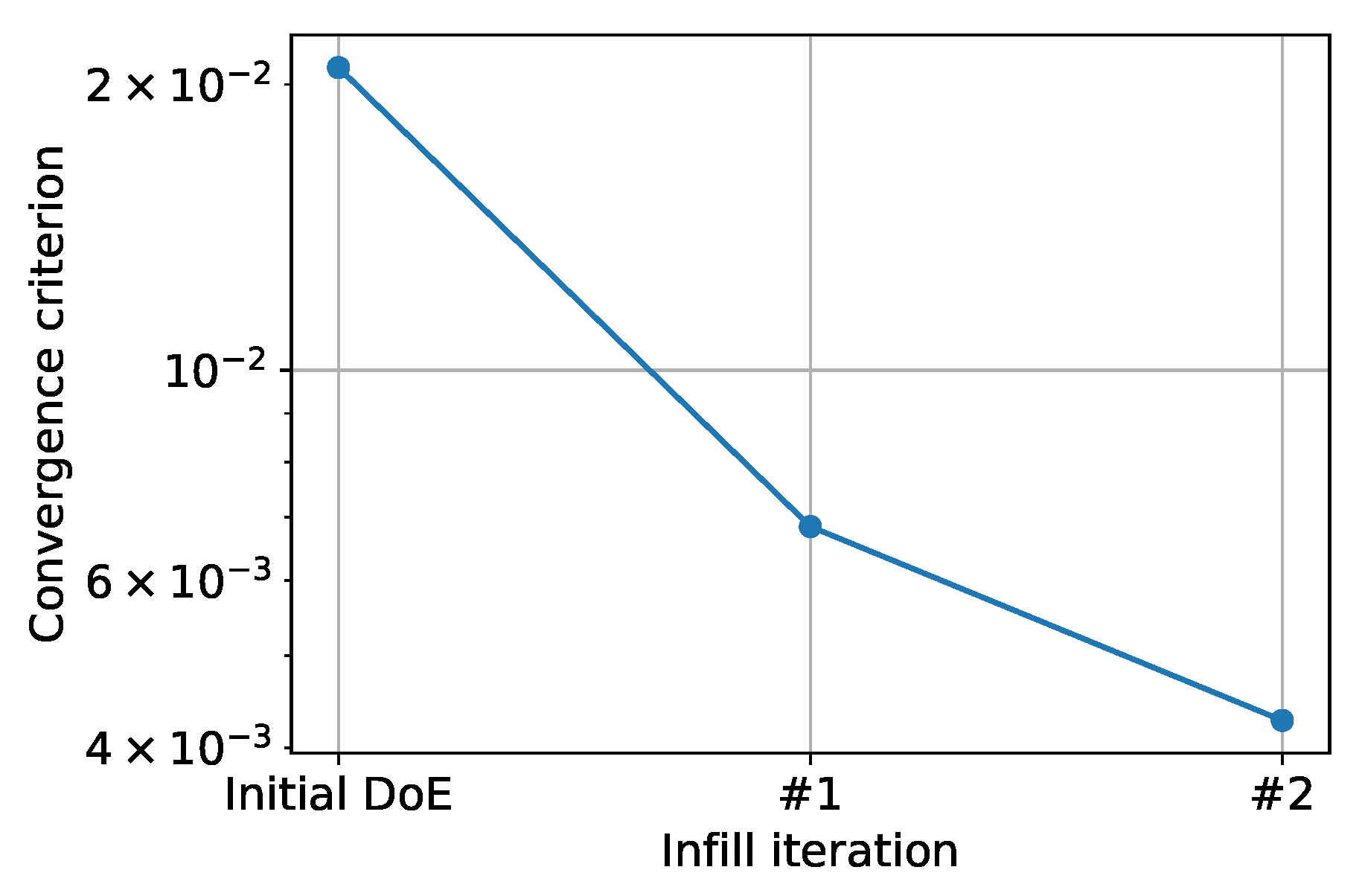
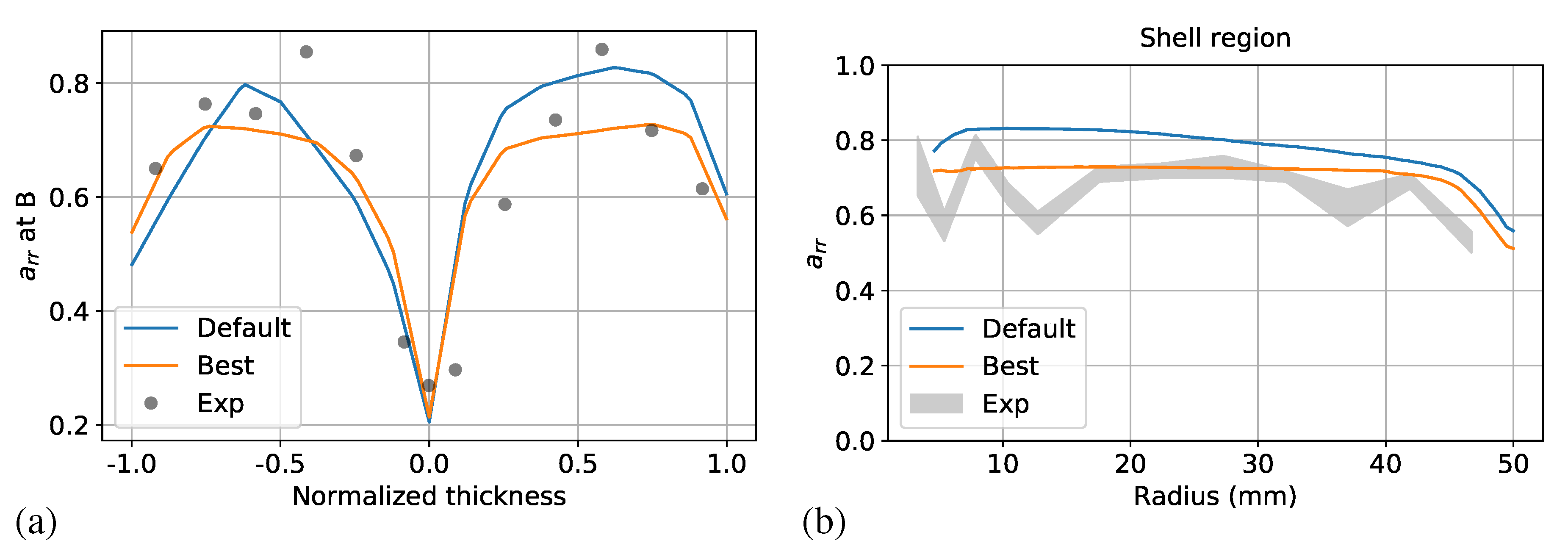
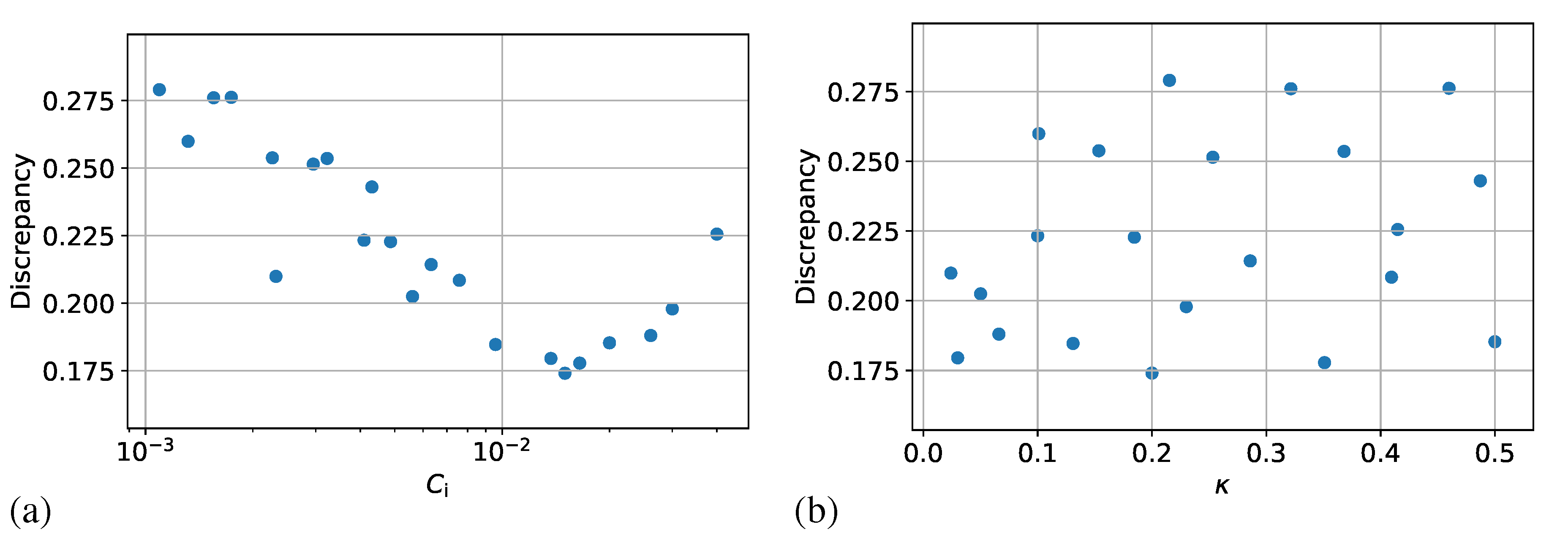
3.2. Adaptive Optimization Iterations
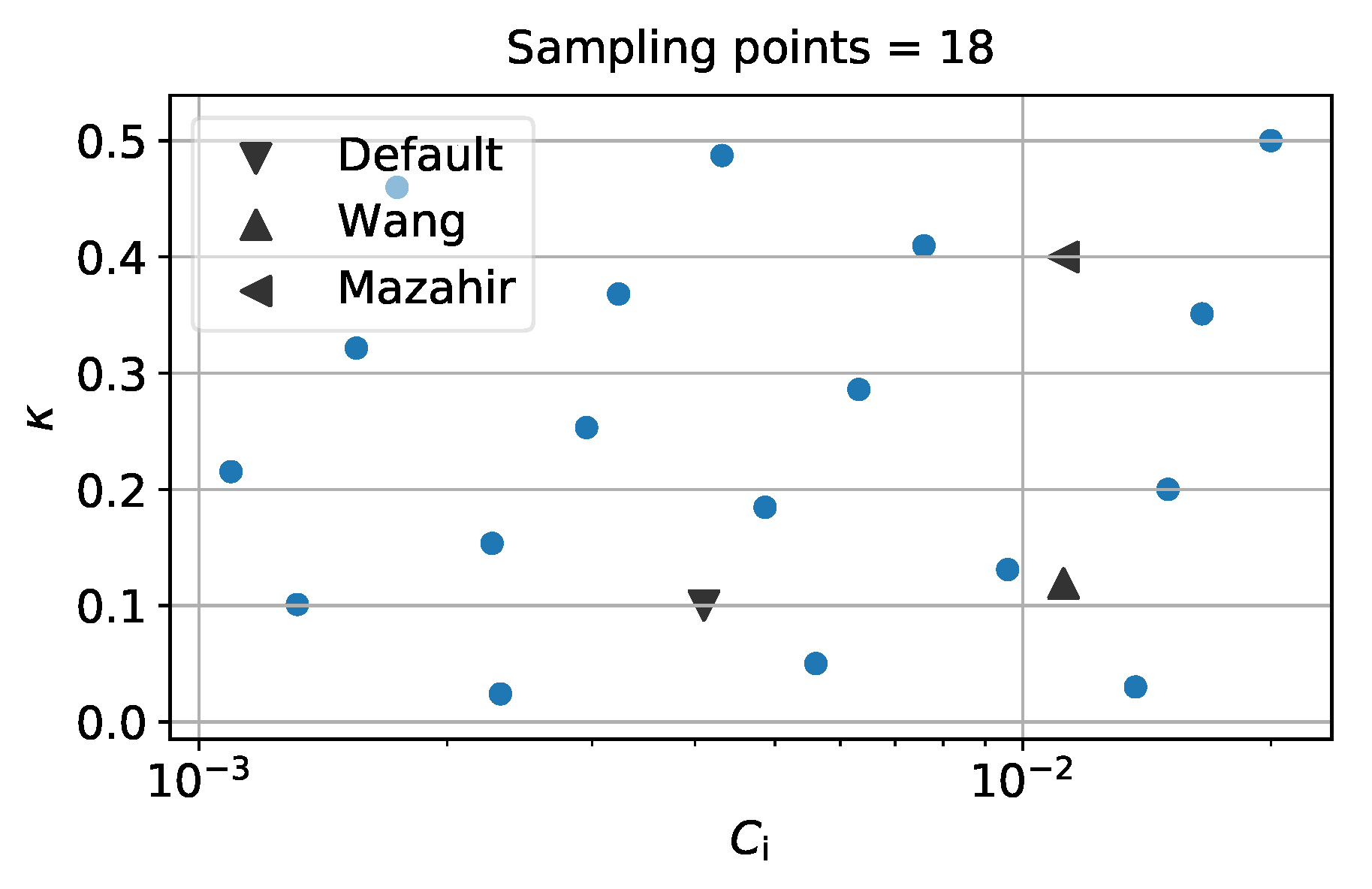
- For the interaction coefficient , the initial sampling interval is used. This interval covers in particular the default value automatically proposed by Moldflow, as well as the value previously found by fitting against their rheological measurements [9,11]. The empirical equation of Phan-Thien et al. [7] also provides an estimation of at a given fiber aspect ratio and concentration fraction. Its predicted value also falls in the proposed interval.
- Concerning the reduction factor , the interval is chosen. The lower bound is chosen so that the RSC orientation model is well-posed and does not predict a zero fiber orientation evolution rate (see Equation (1)). The upper bound is selected to include the default value and the previous ones and given by Wang et al. [9] and Mazahir et al. [11].
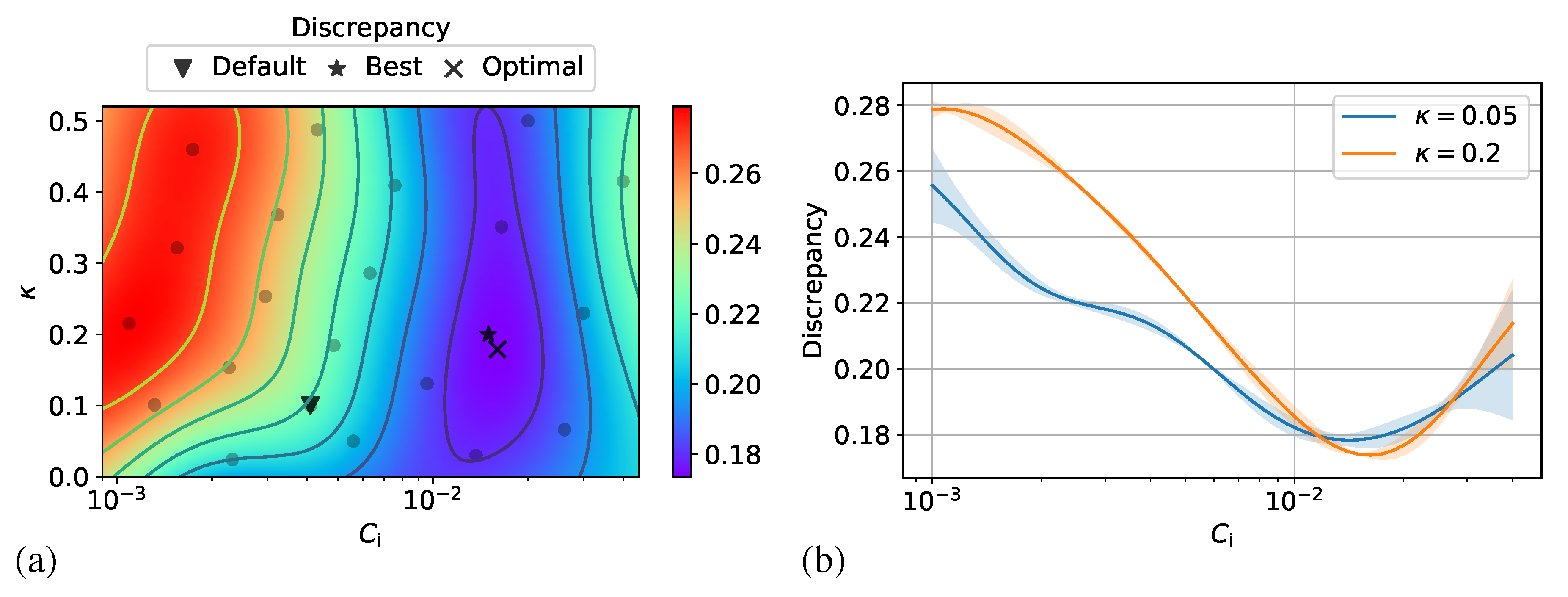
3.3. Effect of the RSC Model Parameters Based on Uncoupled Simulations
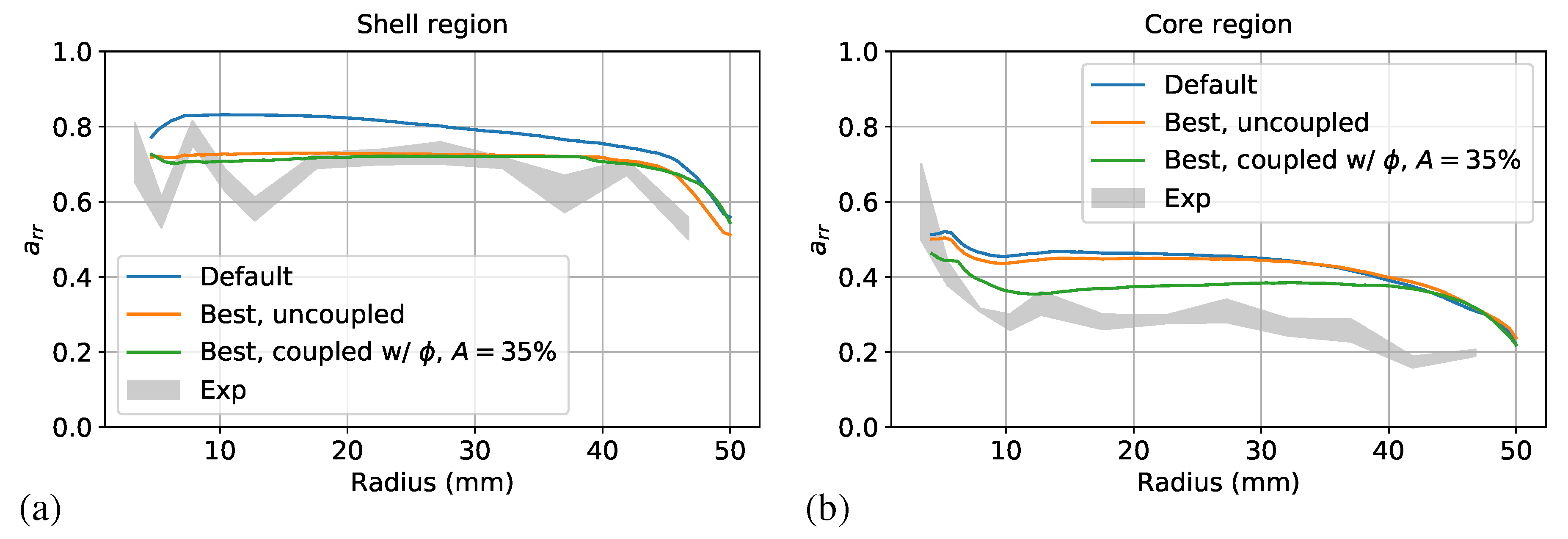
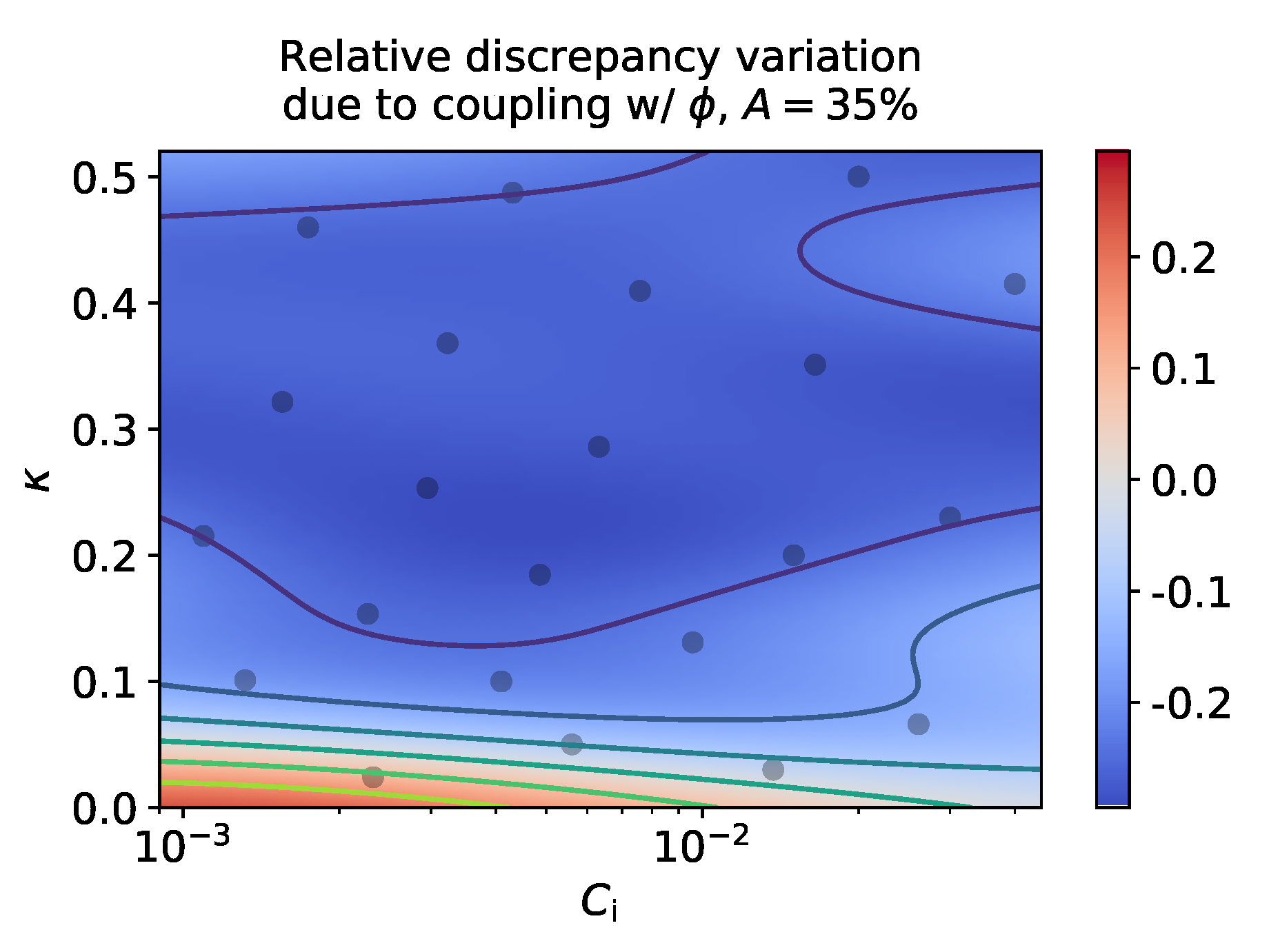
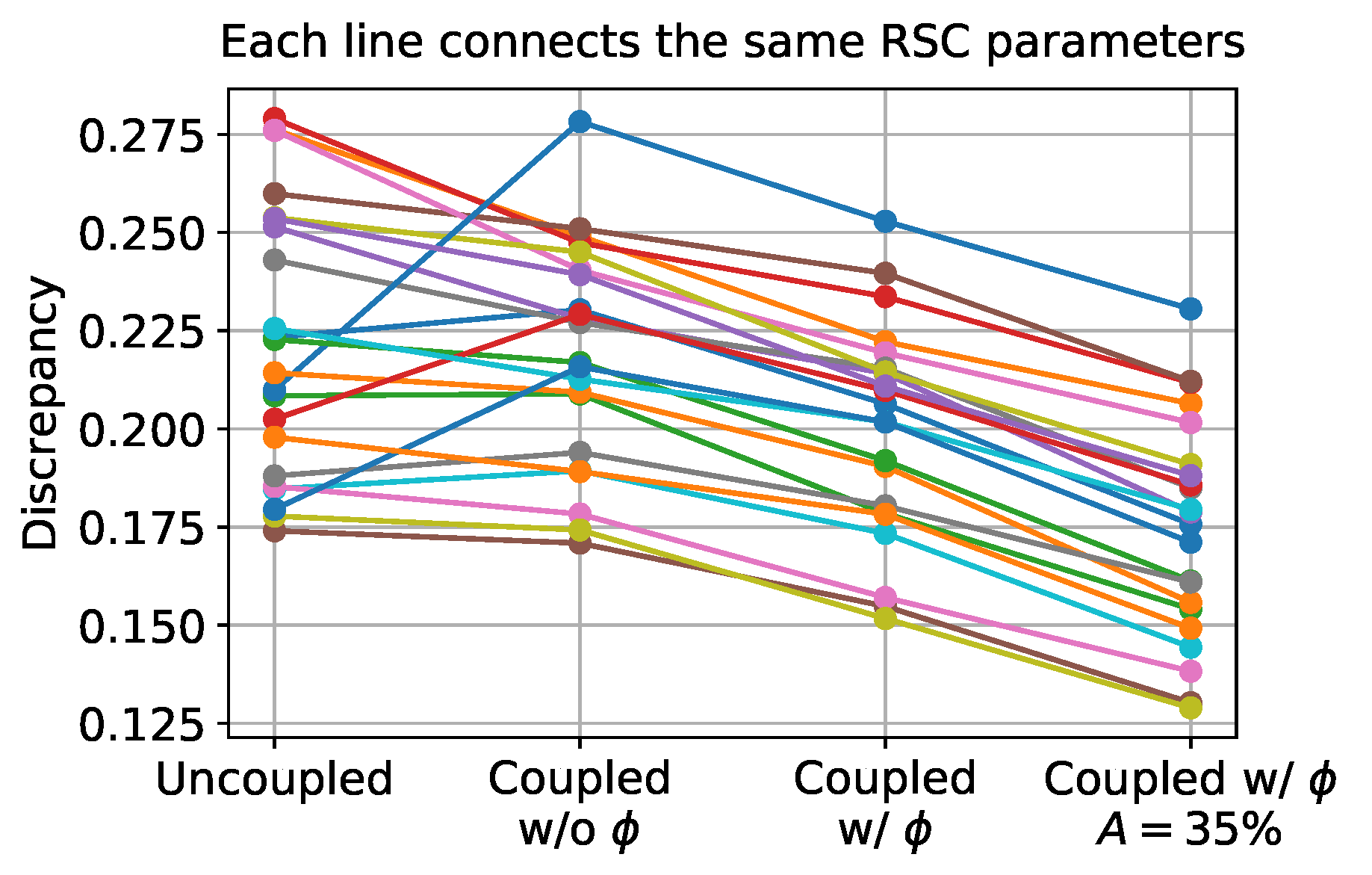
3.4. Effect of Flow-Fiber Coupling During Optimization
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RSC | Reduction Strain Closure model |
| Coupled w/o | Flow-fiber coupled simulations with nominal fiber concentration |
| Coupled w/ | Flow-fiber coupled simulations with non-uniform fiber concentration |
References
- Papathanasiou, T.D. Flow-induced alignment in injection molding of fiber-reinforced polymer composites. In Flow-Induced Alignment in Composite Materials; Papthanasiou, T.D., Guell, D.C., Eds.; Woodhead Publishing: Cambridge, UK, 1997. [Google Scholar]
- Gupta, M.; Wang, K.K. Fiber orientation and mechanical properties of short-fiber-reinforced injection-molded composites: Simulated and experimental results. Polym. Compos. 1993, 14, 367–382. [Google Scholar] [CrossRef]
- Arif, M.F.; Saintier, N.; Meraghni, F.; Fitoussi, J.; Chemisky, Y.; Robert, G. Multiscale fatigue damage characterization in short glass fiber reinforced polyamide-66. Compos. Part B Eng. 2014, 61, 55–65. [Google Scholar] [CrossRef]
- Rolland, H.; Saintier, N.; Robert, G. Damage mechanisms in short glass fibre reinforced thermoplastic during in situ microtomography tensile tests. Compos. Part B Eng. 2016, 90, 365–377. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L., III. Orientation behavior of fibers in concentrated suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L., III. The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Fan, X.J.; Tanner, R.I.; Zheng, R. Folgar-Tucker constant for a fibre suspension in a Newtonian fluid. J. Non-Newton. Fluid Mech. 2002, 103, 251–260. [Google Scholar] [CrossRef]
- Sepehr, M.; Ausias, G.; Carreau, P.J. Rheological properties of short fiber filled polypropylene in transient shear flow. J. Non-Newton. Fluid Mech. 2004, 123, 19–32. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker , C.L., III. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Eberle, A.P.R.; Baird, D.G.; Wapperom, P.; Vélez-García, G.M. Using transient shear rheology to determine material parameters in fiber suspension theory. J. Rheol. 2009, 53, 685–705. [Google Scholar] [CrossRef]
- Mazahir, S.M.; Vélez-García, G.M.; Wapperom, P.; Baird, D. Evolution of fibre orientation in radial direction in a center-gated disk: Experiments and simulation. Compos. Part A Appl. Sci. Manuf. 2013, 51, 108–117. [Google Scholar] [CrossRef]
- Perumal, V.; Gupta, R.K.; Bhattacharya, S.N.; Costa, F.S. Fiber orientation prediction in Nylon-6 glass fiber composites using transient rheology and 3-dimensional X-ray computed tomography. Polym. Compos. 2018. [Google Scholar] [CrossRef]
- Lambert, G.; Wapperom, P.; Baird, D. Obtaining short-fiber orientation model parameters using non-lubricated squeeze flow. Phys. Fluids 2017, 29, 121608. [Google Scholar] [CrossRef]
- Bay, R.S.; Tucker, C.L., III. Fiber orientation in simple injection moldings. Part II: Experimental results. Polym. Compos. 1992, 13, 332–341. [Google Scholar] [CrossRef]
- Vélez-García, G.M.; Mazahir, S.M.; Wapperom, P.; Baird, D.G. Simulation of Injection Molding Using a Model with Delayed Fiber Orientation. Int. Polym. Process. 2011, 26, 331–339. [Google Scholar] [CrossRef]
- Caton-Rose, P.; Hine, P.; Costa, F.; Jin, X.; Wang, J.; Parveen, B. Measurement and prediction of short glass fibre orientation in injection moulding composites. In Proceedings of the 15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Meyer, K.J.; Hofmann, J.T.; Baird, D.G. Prediction of short glass fiber orientation in the filling of an end-gated plaque. Compos. Part A Appl. Sci. Manuf. 2014, 62, 77–86. [Google Scholar] [CrossRef]
- van Haag, J.; Bontenackels, C.; Hopmann, C. Fiber orientation prediction of long fiber-reinforced thermoplastics: Optimization of model parameters. In Proceedings of the SPE ANTEC Conference, Orlando, FL, USA, 23–25 March 2015. [Google Scholar]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Improved fiber orientation predictions for injection molded fiber composites. Compos. Part A Appl. Sci. Manuf. 2017, 99, 65–75. [Google Scholar] [CrossRef]
- Kleindel, S.; Salaberger, D.; Eder, R.; Schretter, H.; Hochenauer, C. Prediction and Validation of Short Fiber Orientation in a Complex Injection Molded Part with Chunky Geometry. Int. Polym. Process. 2015, 30, 366–380. [Google Scholar] [CrossRef]
- Li, T.; Luyé, J.F. Flow-fiber coupled viscosity in injection molding simulations of short fiber reinforced thermoplastics. Int. Polym. Process. 2018. Available online: https://hal.archives-ouvertes.fr/hal-01683052 (accessed on 18 December 2018).
- Li, T.; Luyé, J.F. Flow-fiber coupled injection molding simulations with non-uniform fiber concentration effects. 2018, in press. [Google Scholar]
- Wang, J.; Cook, P.; Bakharev, A.; Costa, F.; Astbury, D. Prediction of fiber orientation in injection-molded parts using three-dimensional simulations. AIP Conf. Proc. 2016, 1713, 40007. [Google Scholar] [CrossRef]
- Forrester, A.; Keane, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Autodesk. Autodesk Moldflow 2019 Technology Preview: What Is New; Autodesk Australia Pty Ltd.: Kilsyth, VIC, Australia, 2018. [Google Scholar]
- Tucker, C.L., III. Flow regimes for fiber suspensions in narrow gaps. J. Non-Newton. Fluid Mech. 1991, 39, 239–268. [Google Scholar] [CrossRef]
- Costa, F.; Cook, P.; Pickett, D. A Framework for Viscosity Model Research in Injection Molding Simulation, Including Pressure and Fiber Orientation Dependence. In Proceedings of the SPE ANTEC Conference, Orlando, FL, USA, 23–25 March 2015. [Google Scholar]
- Goris, S.; Osswald, T.A. Process-induced fiber matrix separation in long fiber-reinforced thermoplastics. Compos. Part A Appl. Sci. Manuf. 2018, 105, 321–333. [Google Scholar] [CrossRef]
- Morris, J.F. A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 2009, 48, 909–923. [Google Scholar] [CrossRef]
- Costa, F. Autodesk Moldflow Insight: Solver Enhancements and Research Directions. In Proceedings of the Benelux Autodesk Moldflow User Meeting, Eindhoven, The Netherlands, 24 June 2016. [Google Scholar]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Predictions of fiber concentration in injection molding simulation of fiber-reinforced composites. J. Thermoplast. Compos. Mater. 2017. [Google Scholar] [CrossRef]
- VerWeyst, B.E.; Tucker, C.L., III; Foss, P.H.; O’Gara, J.F. Fiber Orientation In 3-d Injection Molded Features: Prediction and Experiment. Int. Polym. Process. 1999, 14, 409–420. [Google Scholar] [CrossRef]
- Vélez-García, G.M.; Wapperom, P.; Baird, D.G.; Aning, A.O.; Kunc, V. Unambiguous orientation in short fiber composites over small sampling area in a center-gated disk. Compos. Part A Appl. Sci. Manuf. 2012, 43, 104–113. [Google Scholar] [CrossRef]
- Autodesk. Autodesk Moldflow Insight 2017 R2: Fiber orientation Accuracy Validation Report; Autodesk Australia Pty Ltd.: Kilsyth, VIC, Australia, 2016. [Google Scholar]
- Jones, D.R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Morris, M.D.; Mitchell, T.J. Exploratory designs for computational experiments. J. Stat. Plan. Inference 1995, 43, 381–402. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Vu, K.K.; d’Ambrosio, C.; Hamadi, Y.; Liberti, L. Surrogate-based methods for black-box optimization. Int. Trans. Oper. Res. 2016, 24, 393–424. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X. Surrogate-based process optimization for reducing warpage in injection molding. J. Mater. Process. Technol. 2009, 209, 1302–1309. [Google Scholar] [CrossRef]
- Ginsbourger, D.; Riche, R.L.; Carraro, L. Kriging Is Well-Suited to Parallelize Optimization. In Computational Intelligence in Expensive Optimization Problems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 131–162. [Google Scholar]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: http://www.scipy.org/ (accessed on 18 December 2018).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]

| Using (2) | Using (3) | |
|---|---|---|
| Discrepancy | 12% | 2.9% |
| RSC Parameters | Discrepancy | |
|---|---|---|
| Default | 0.223 | |
| Best | 0.174 | |
| Optimal | 0.174 |
| Optimal Parameters | Discrepancy | Compared to “Default” | |
|---|---|---|---|
| Uncoupled | 0.174 | −22% | |
| Coupled w/o | 0.170 | −24% | |
| Coupled w/ | 0.149 | −33% | |
| Coupled w/, | 0.127 | −43% |
| Interaction Coefficient | Reduction Factor | Flow-Fiber Coupling |
|---|---|---|
| 78% | 0% | 22% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Luyé, J.-F. Optimization of Fiber Orientation Model Parameters in the Presence of Flow-Fiber Coupling. J. Compos. Sci. 2018, 2, 73. https://doi.org/10.3390/jcs2040073
Li T, Luyé J-F. Optimization of Fiber Orientation Model Parameters in the Presence of Flow-Fiber Coupling. Journal of Composites Science. 2018; 2(4):73. https://doi.org/10.3390/jcs2040073
Chicago/Turabian StyleLi, Tianyi, and Jean-François Luyé. 2018. "Optimization of Fiber Orientation Model Parameters in the Presence of Flow-Fiber Coupling" Journal of Composites Science 2, no. 4: 73. https://doi.org/10.3390/jcs2040073
APA StyleLi, T., & Luyé, J.-F. (2018). Optimization of Fiber Orientation Model Parameters in the Presence of Flow-Fiber Coupling. Journal of Composites Science, 2(4), 73. https://doi.org/10.3390/jcs2040073





