Biomechanical Modeling of Wounded Skin
Abstract
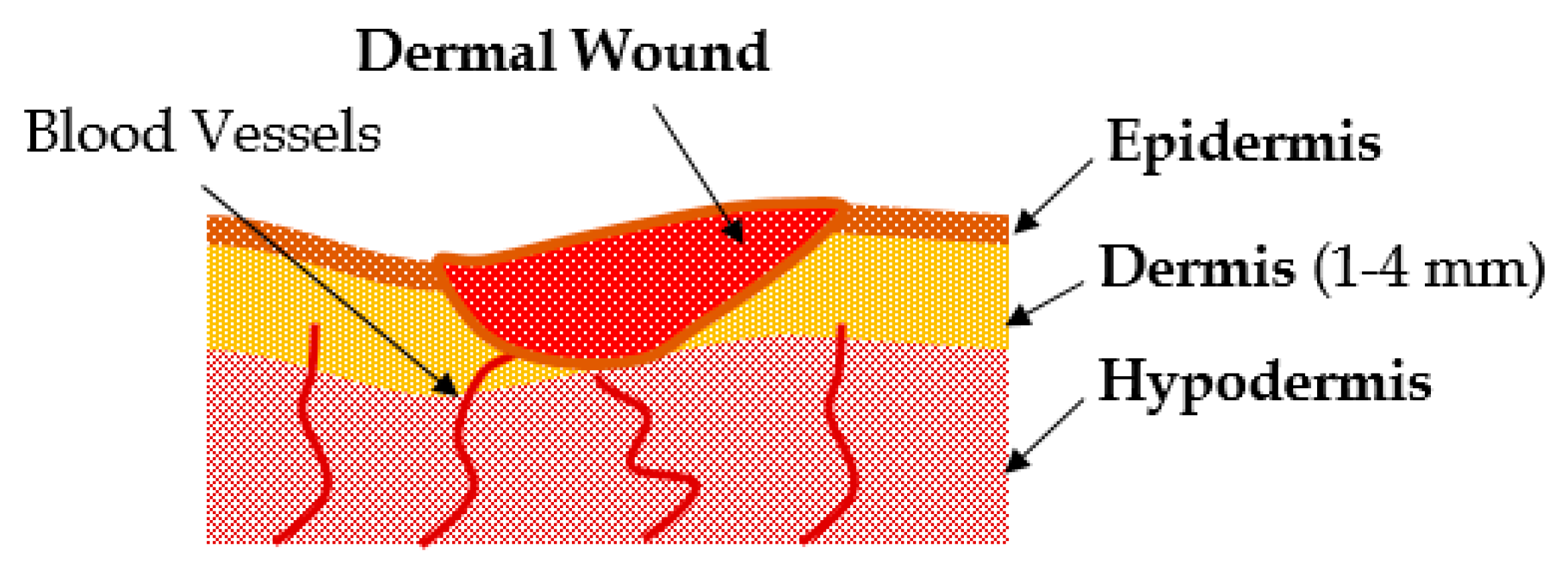
1. Introduction
2. Materials and Methods
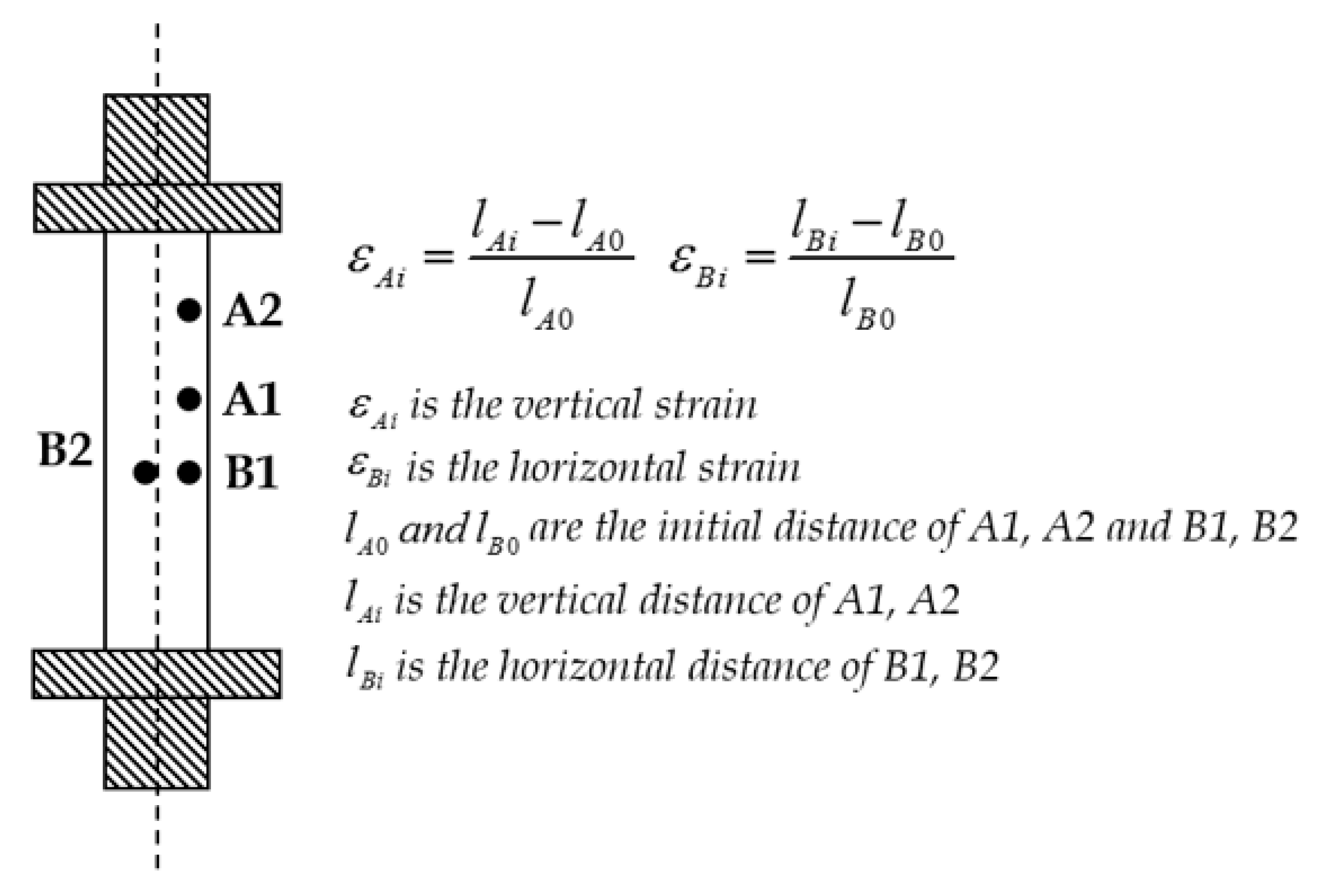
2.1. Test Specimen Fabrication and Digital Image Correlation (DIC) Framework
2.2. Mechanical Tensile Testing
2.3. Finite Element Modeling
2.4. Nonlinear Material Modeling
3. Results and Discussion
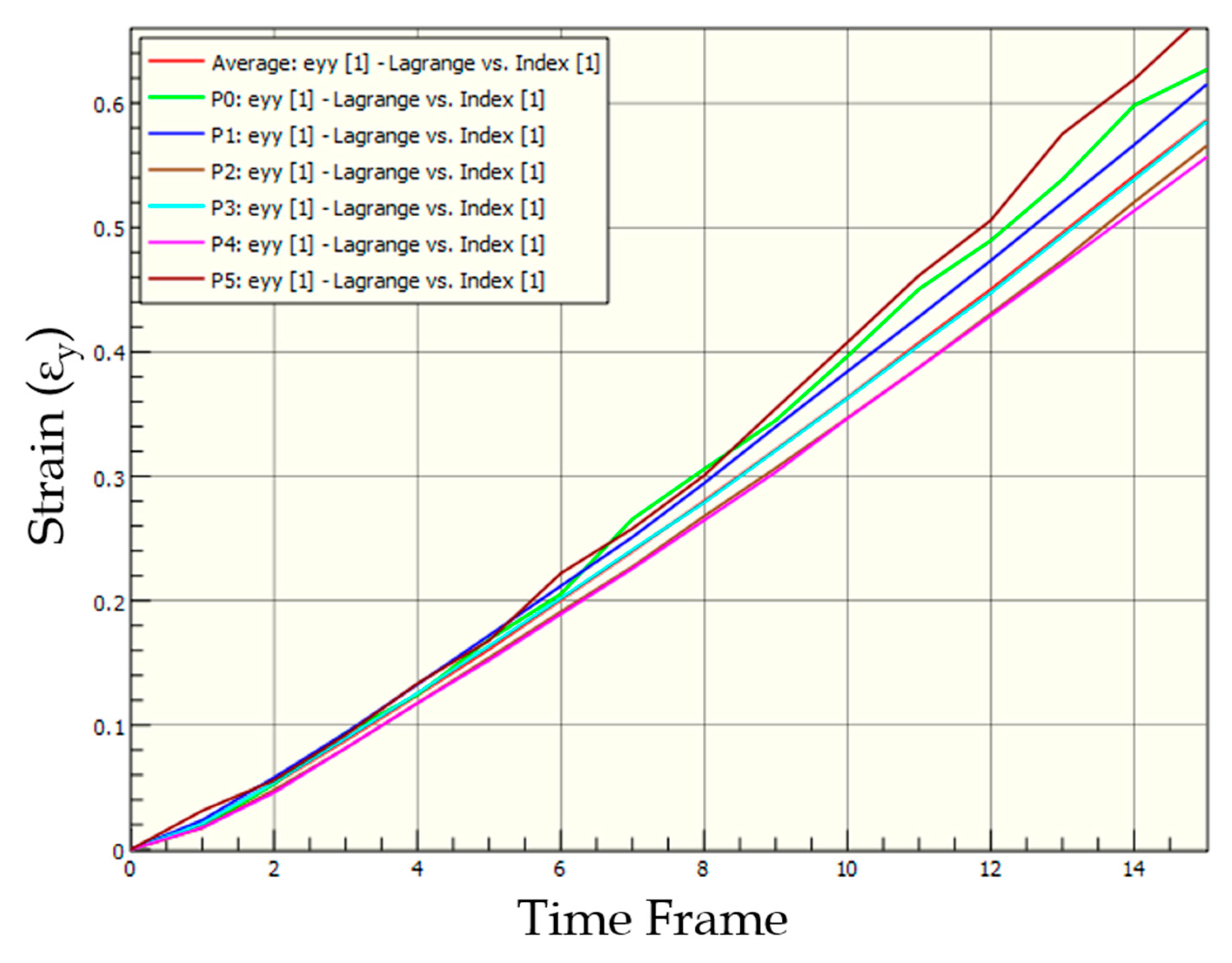
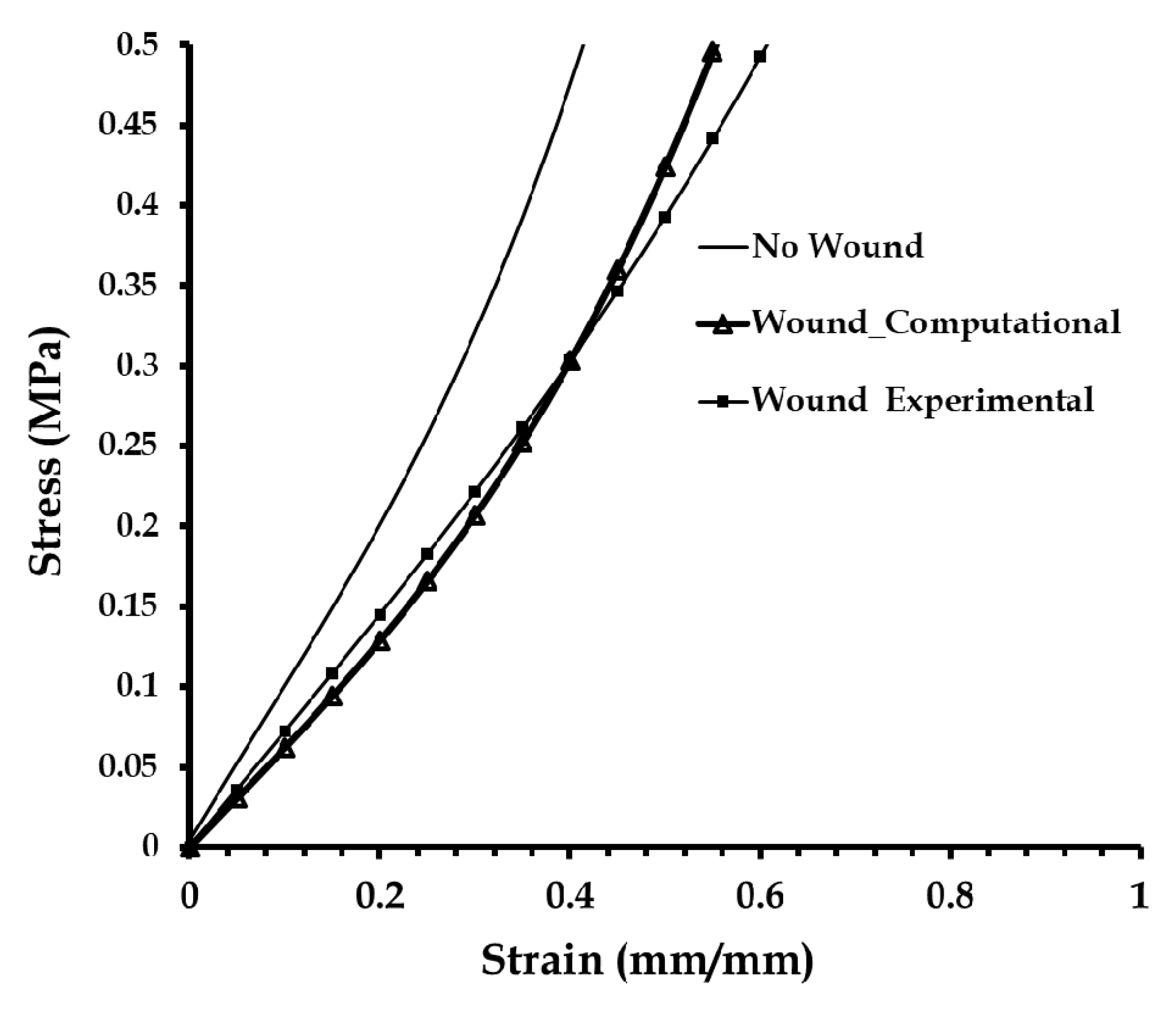
3.1. Strain in Skin Phantom without Wound
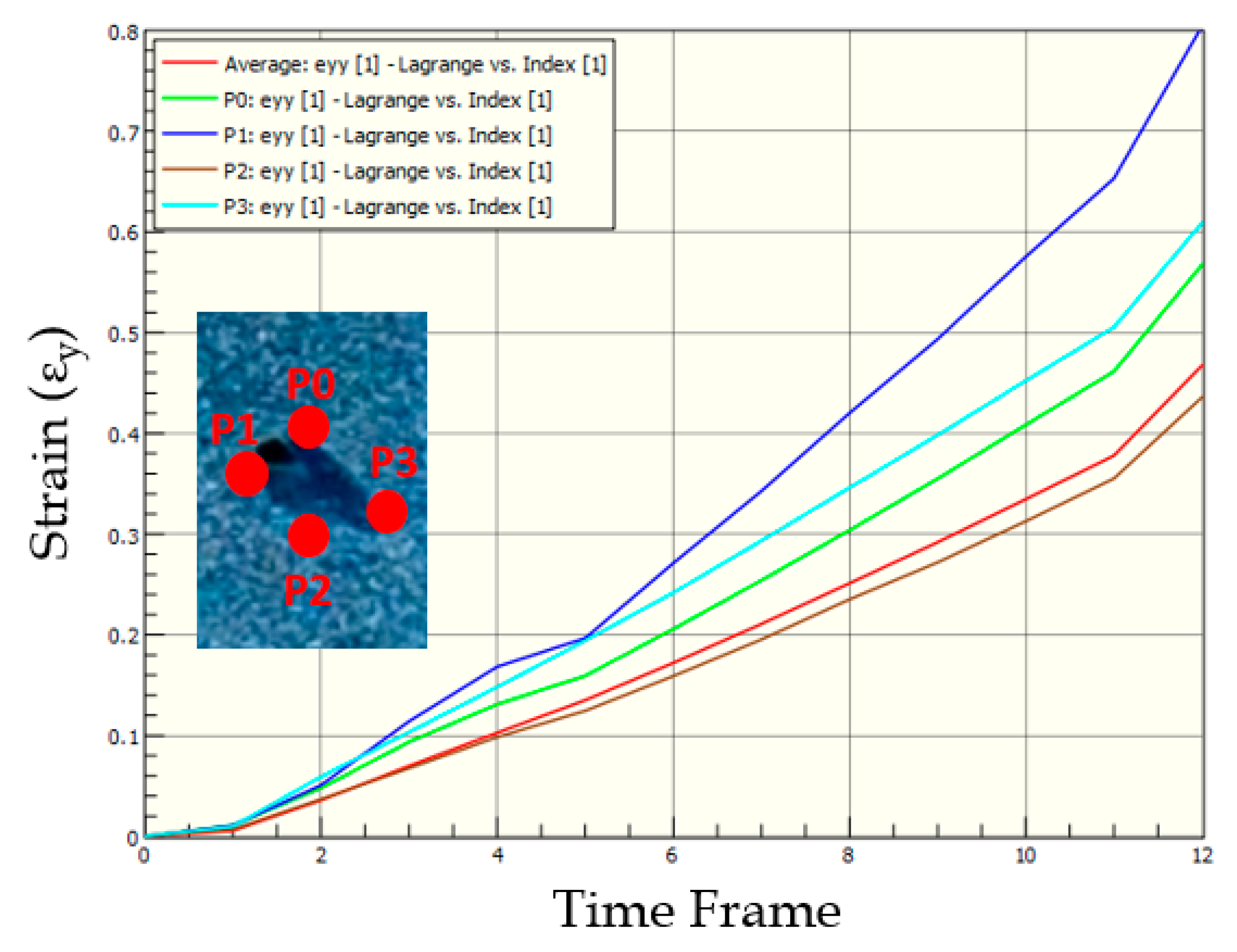
3.2. Strains in Skin Phantom with Symmetric-Short Wound
3.3. Strains in Skin Phantom with Symmetric-Long Wound
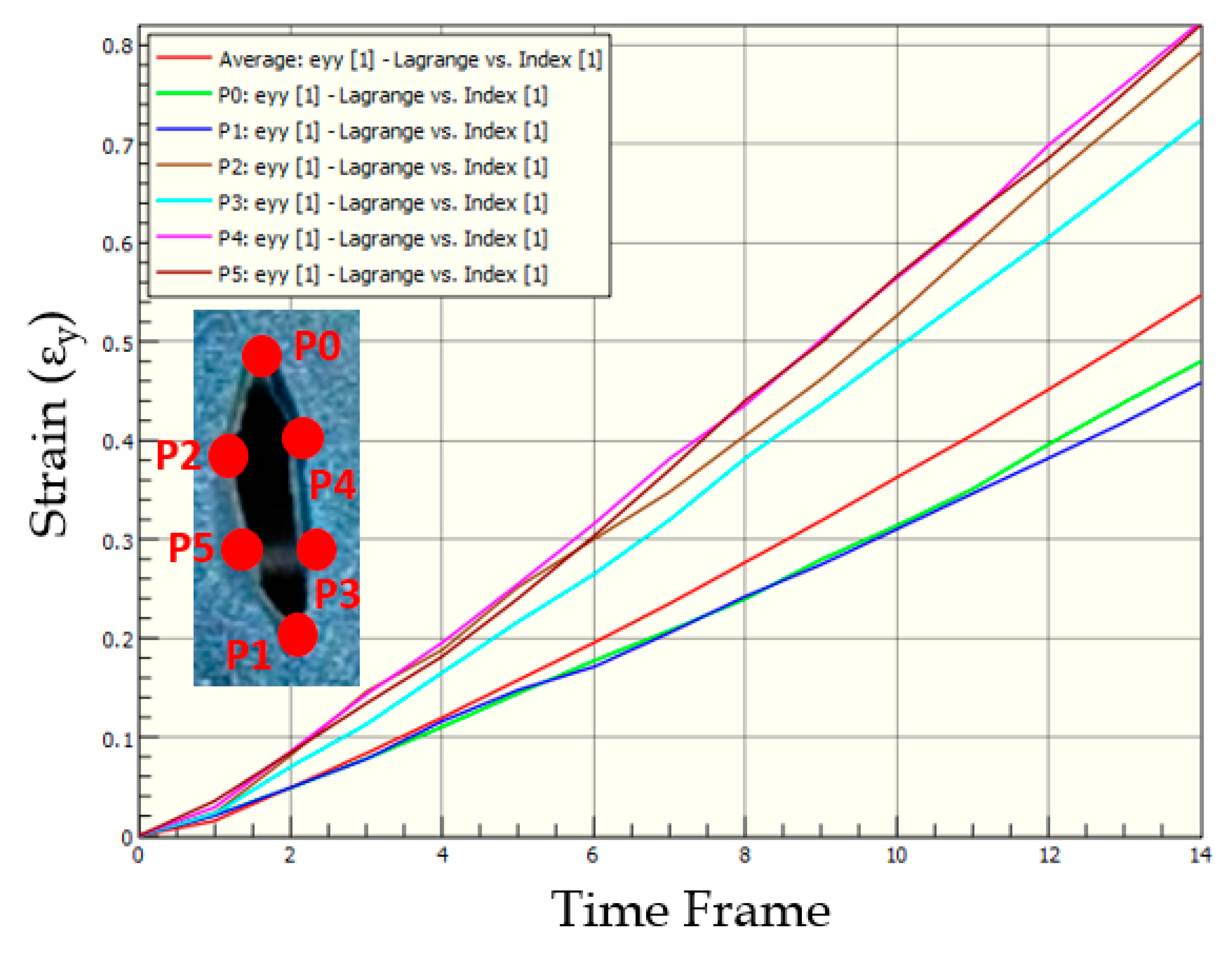
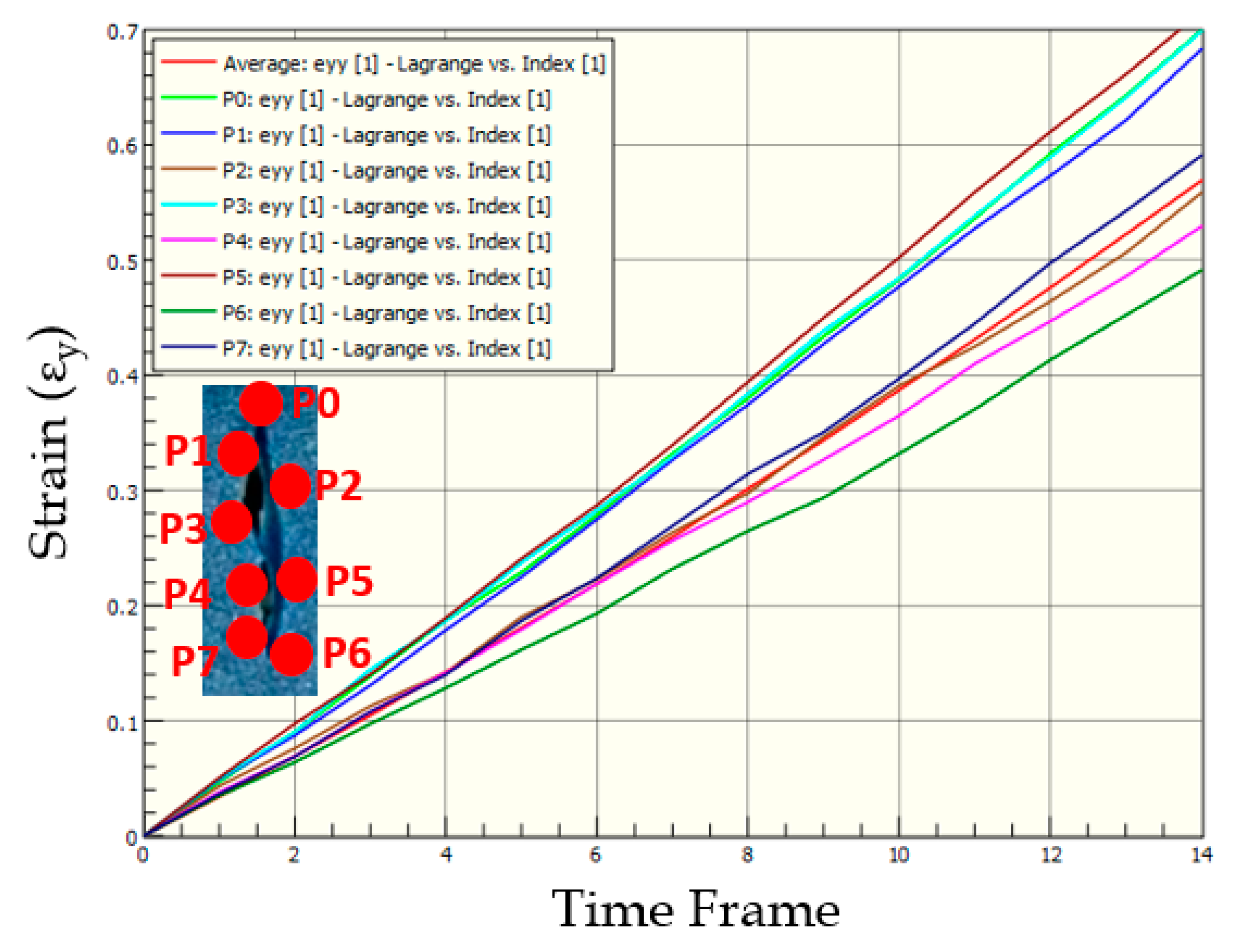
3.4. Strains in Skin Phantom with Asymmetric-Wide Wound
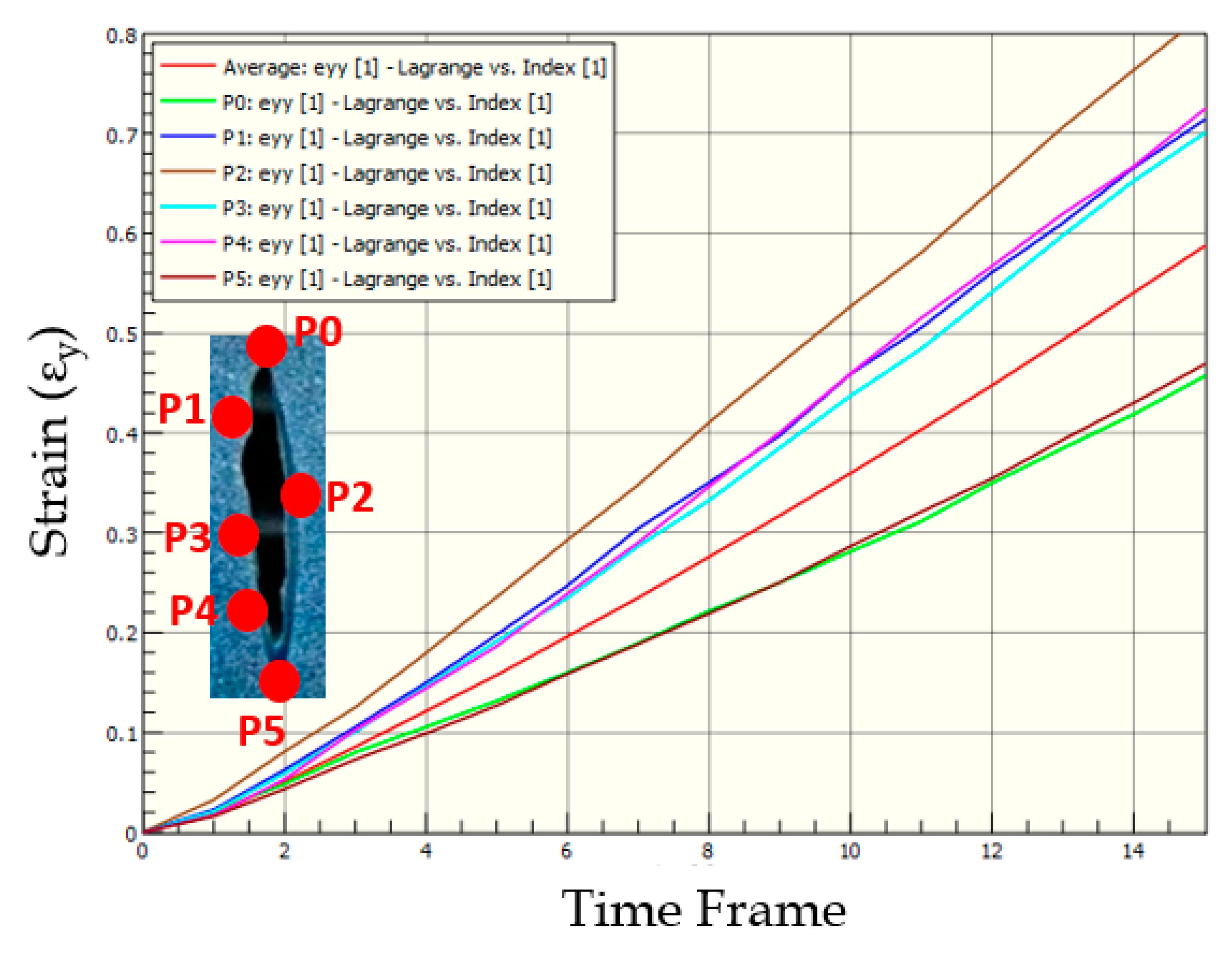
3.5. Strains in Skin Phantom with Asymmetric-Thin Wound
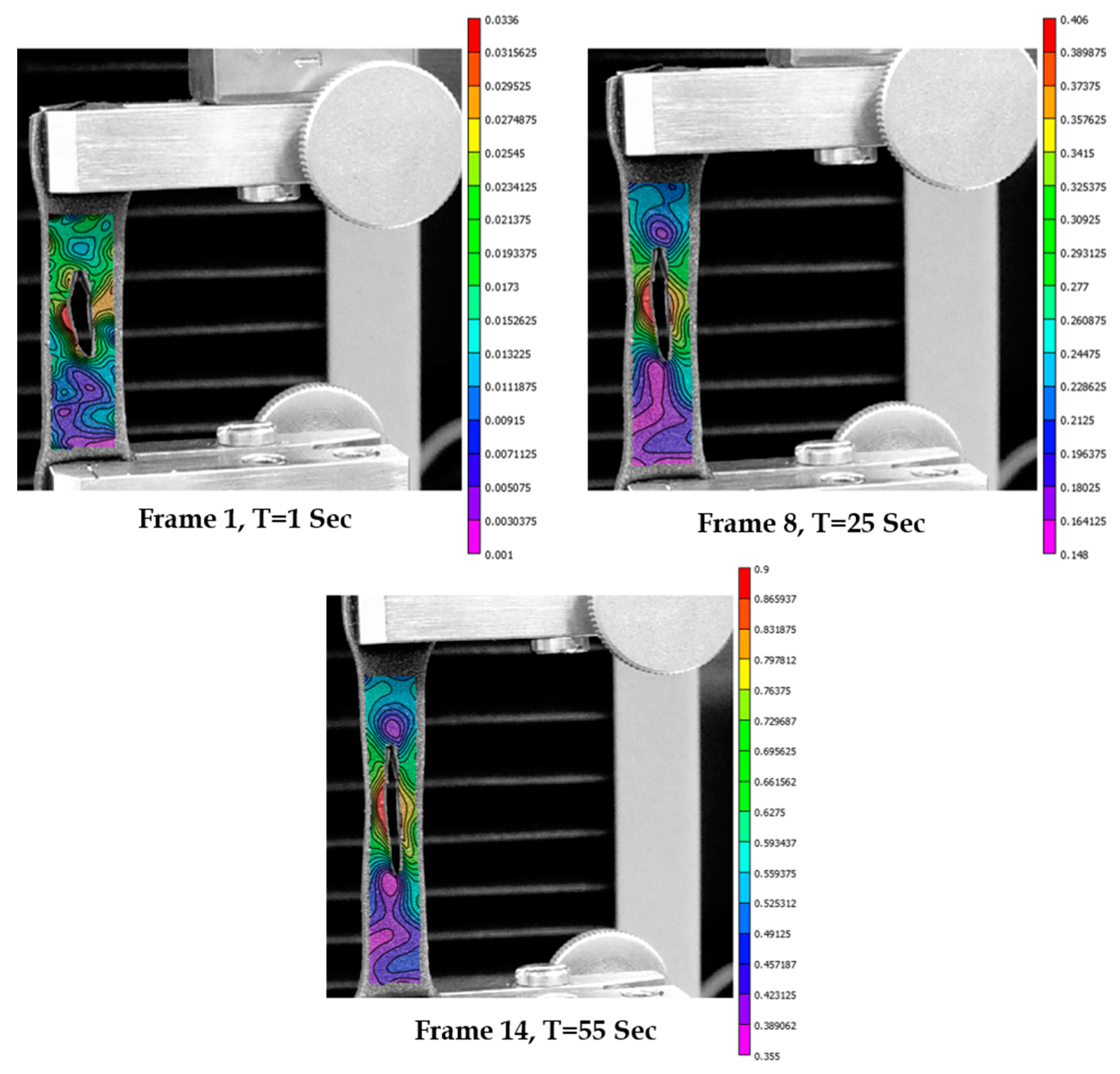
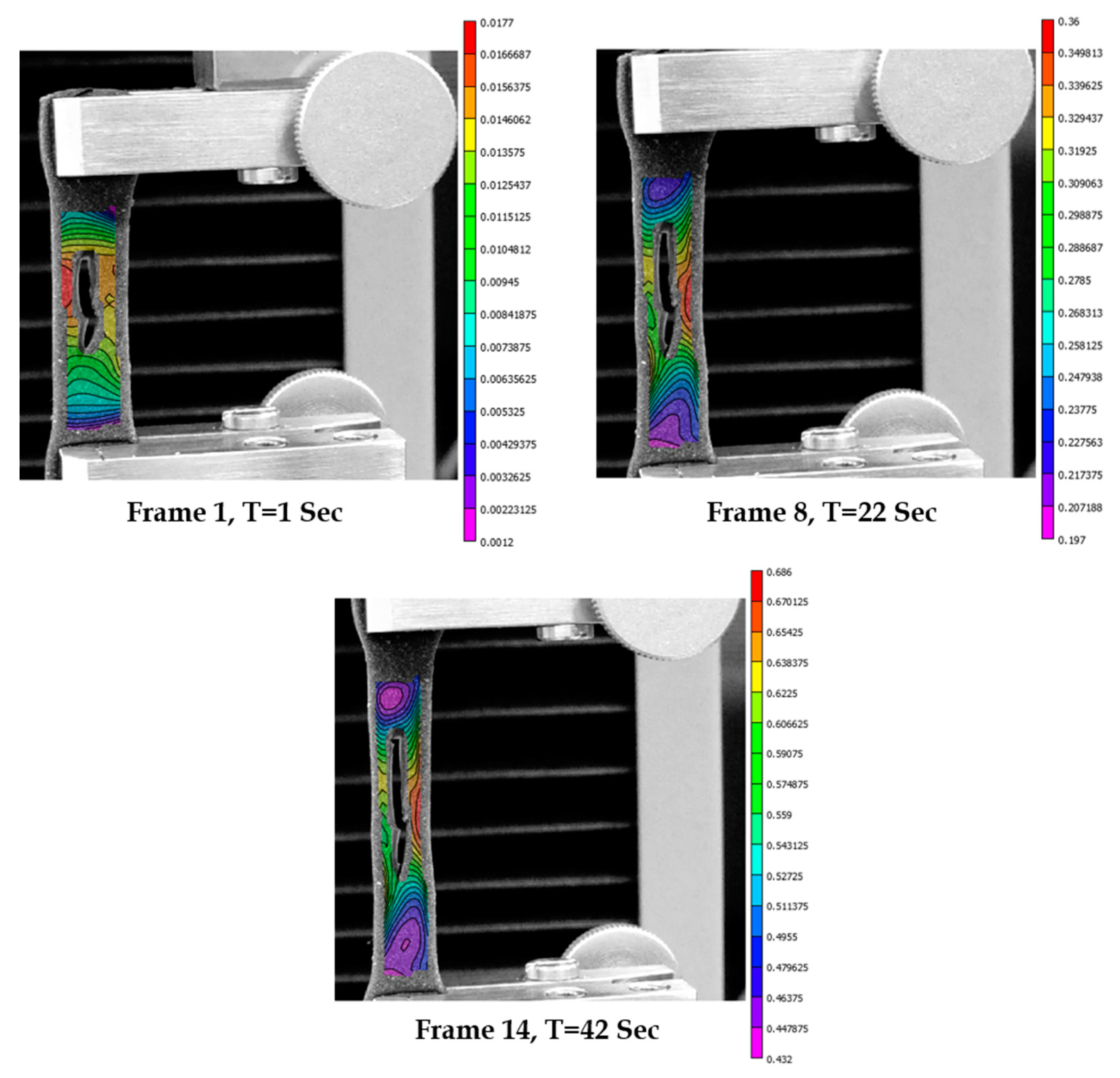
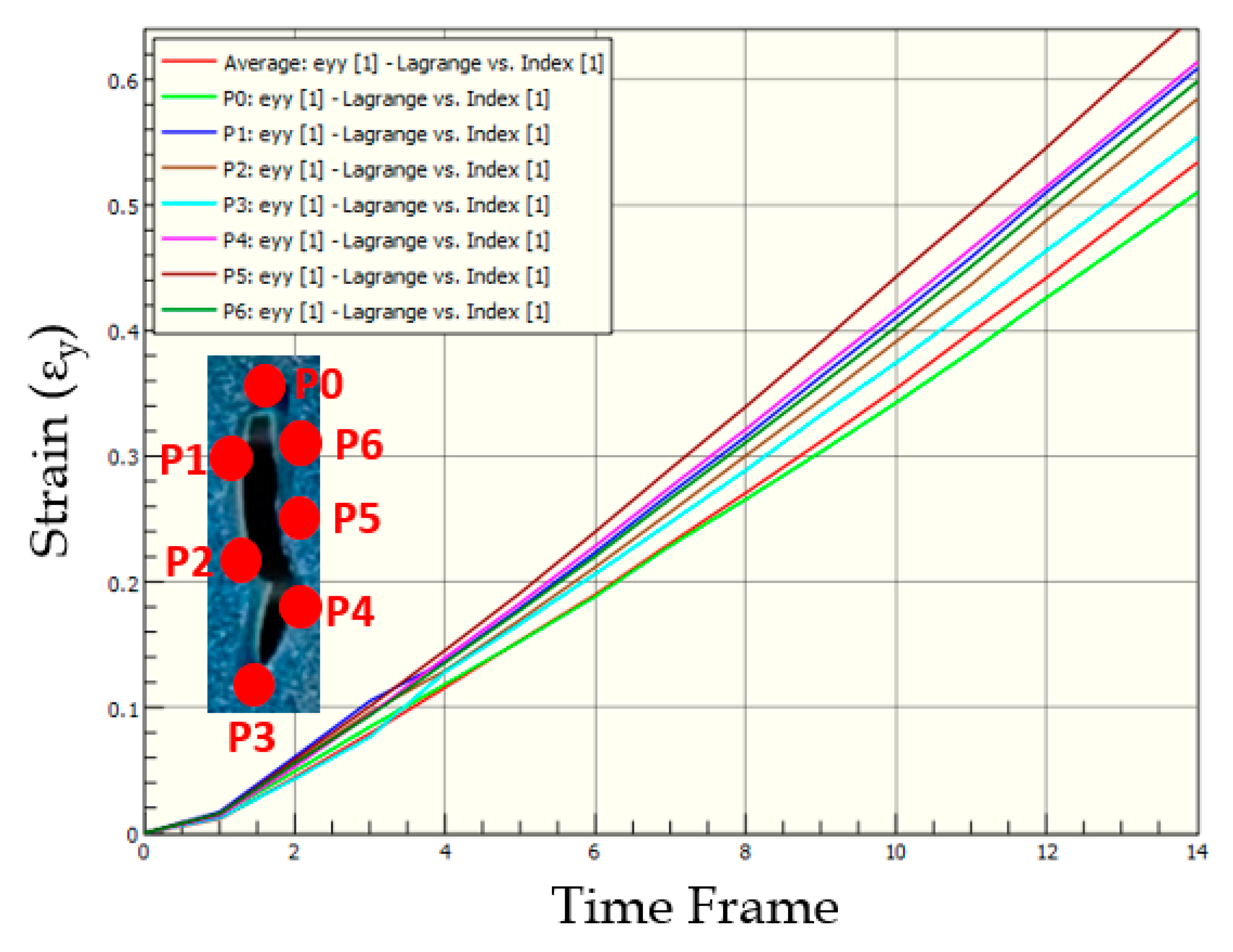
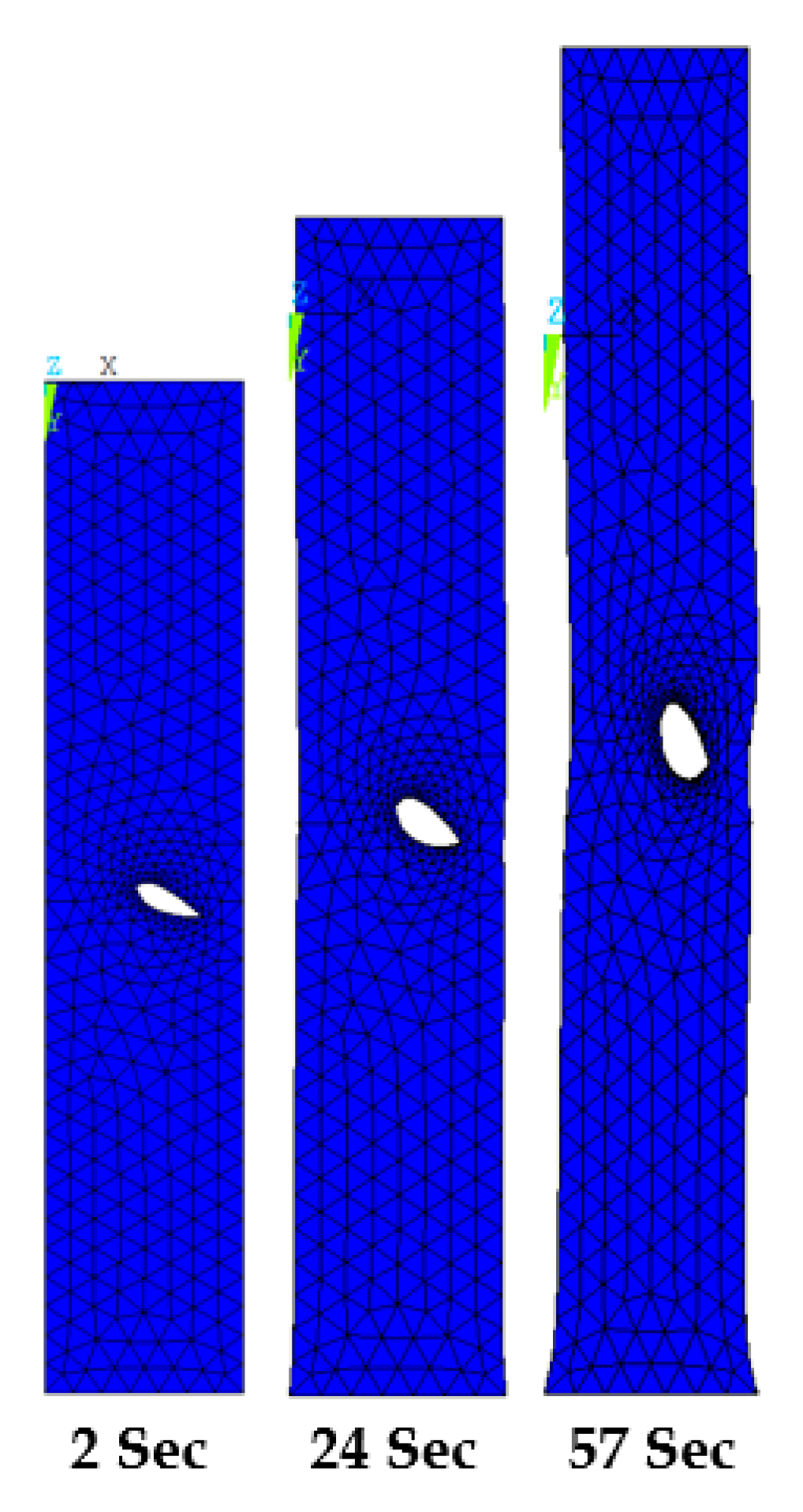
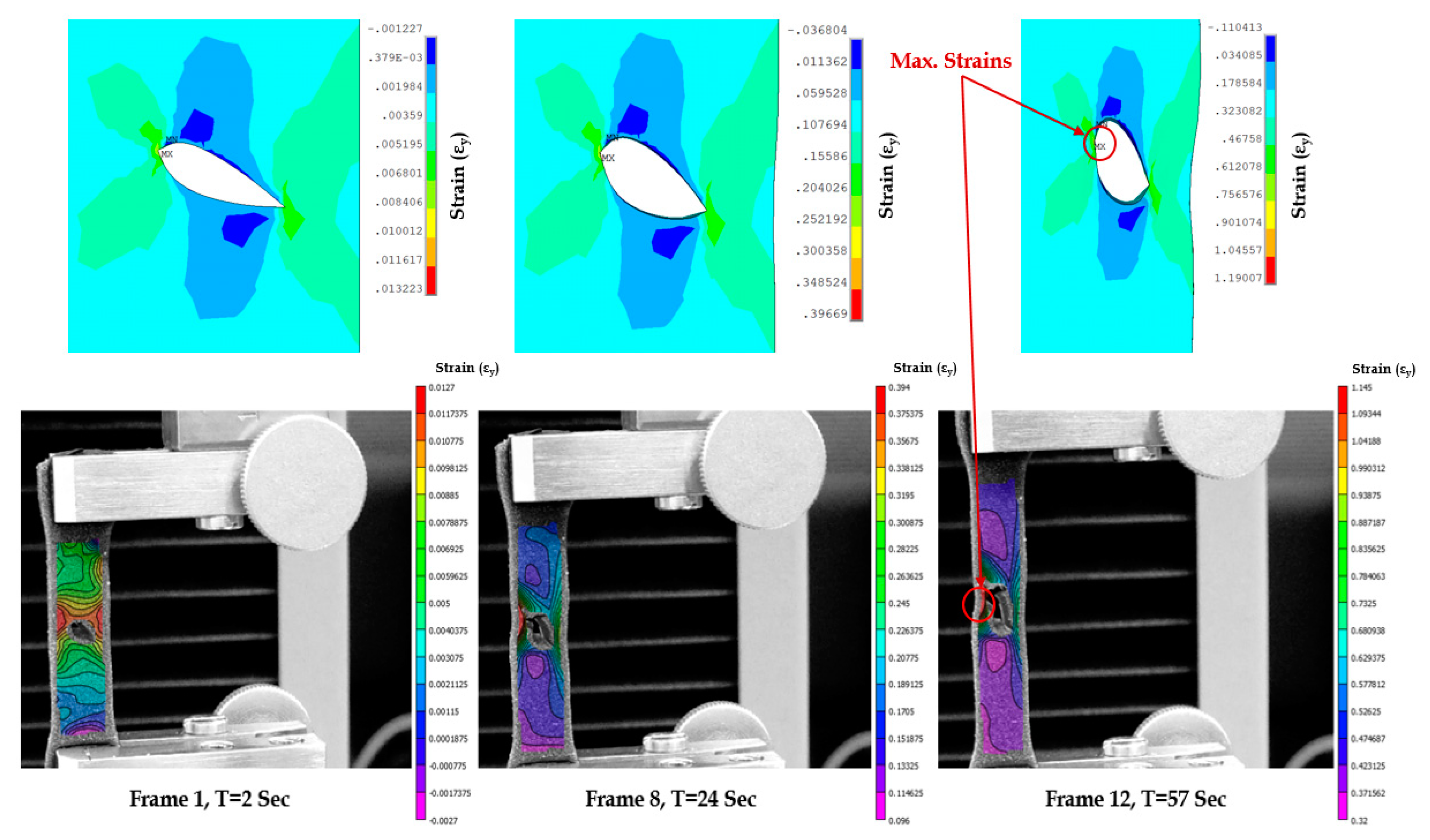
3.6. Strains in Skin Phantom with Transverse Wound
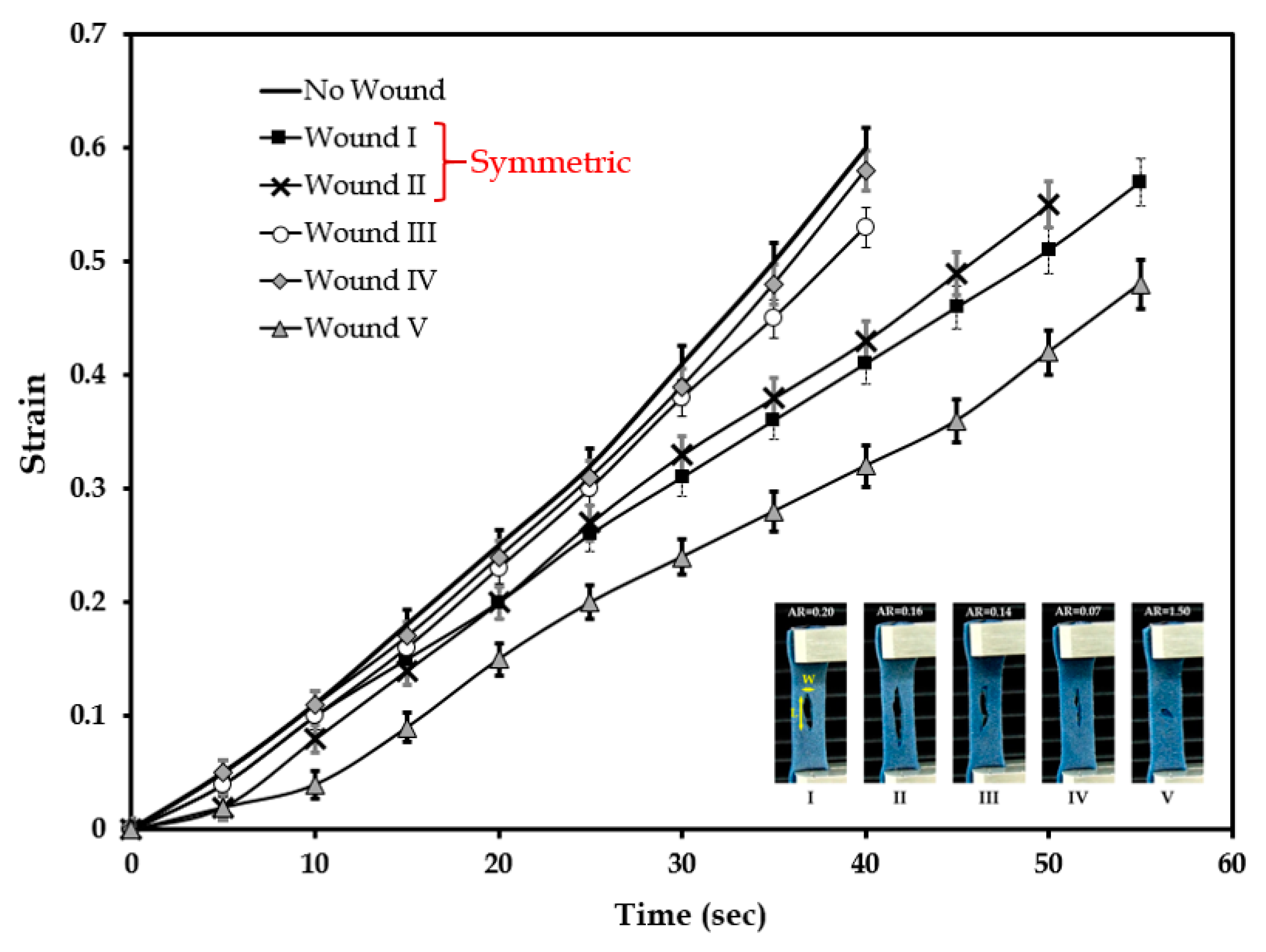
3.7. Comparison of Strains in Skin Phantoms across Wound Geometries
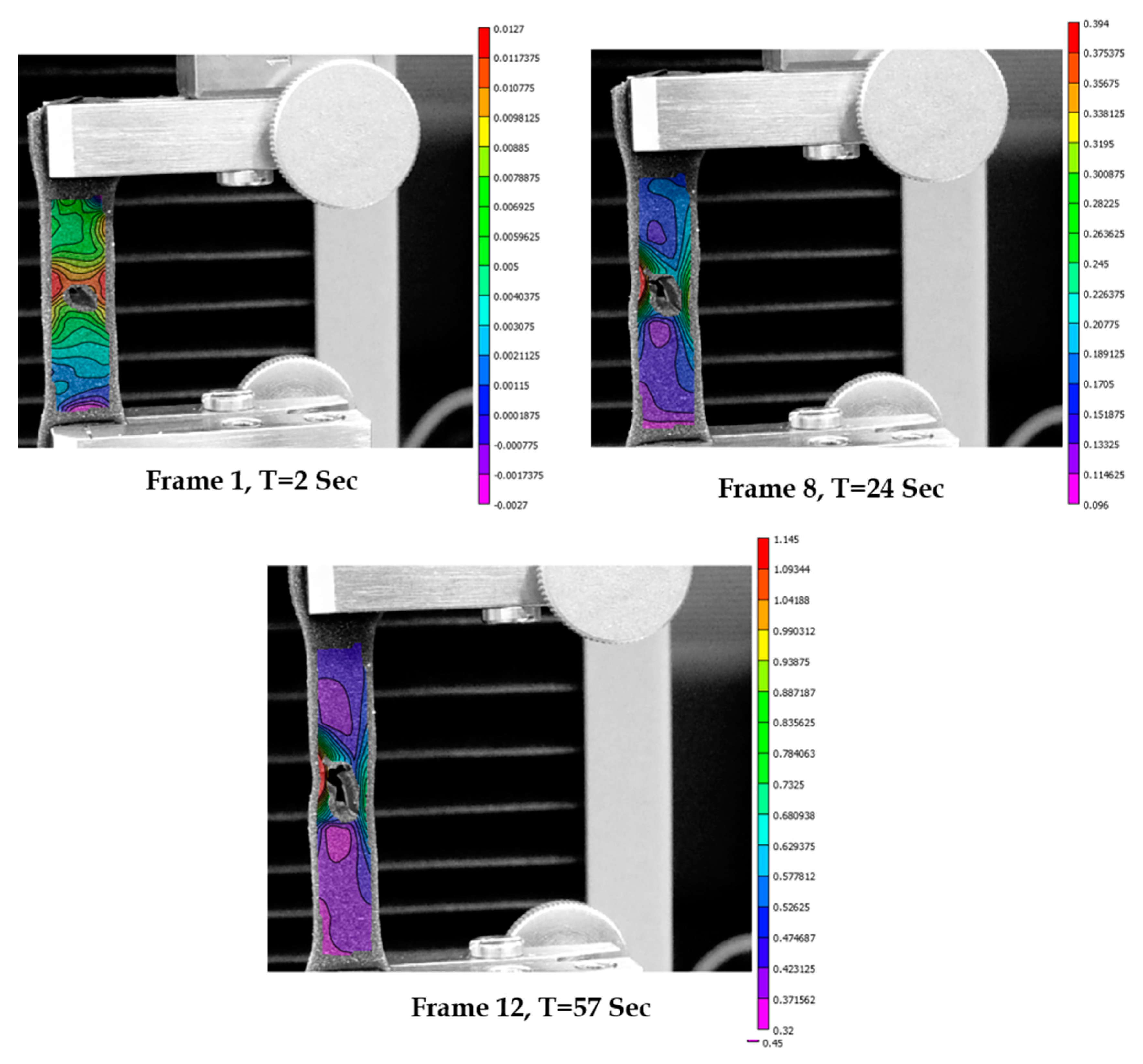
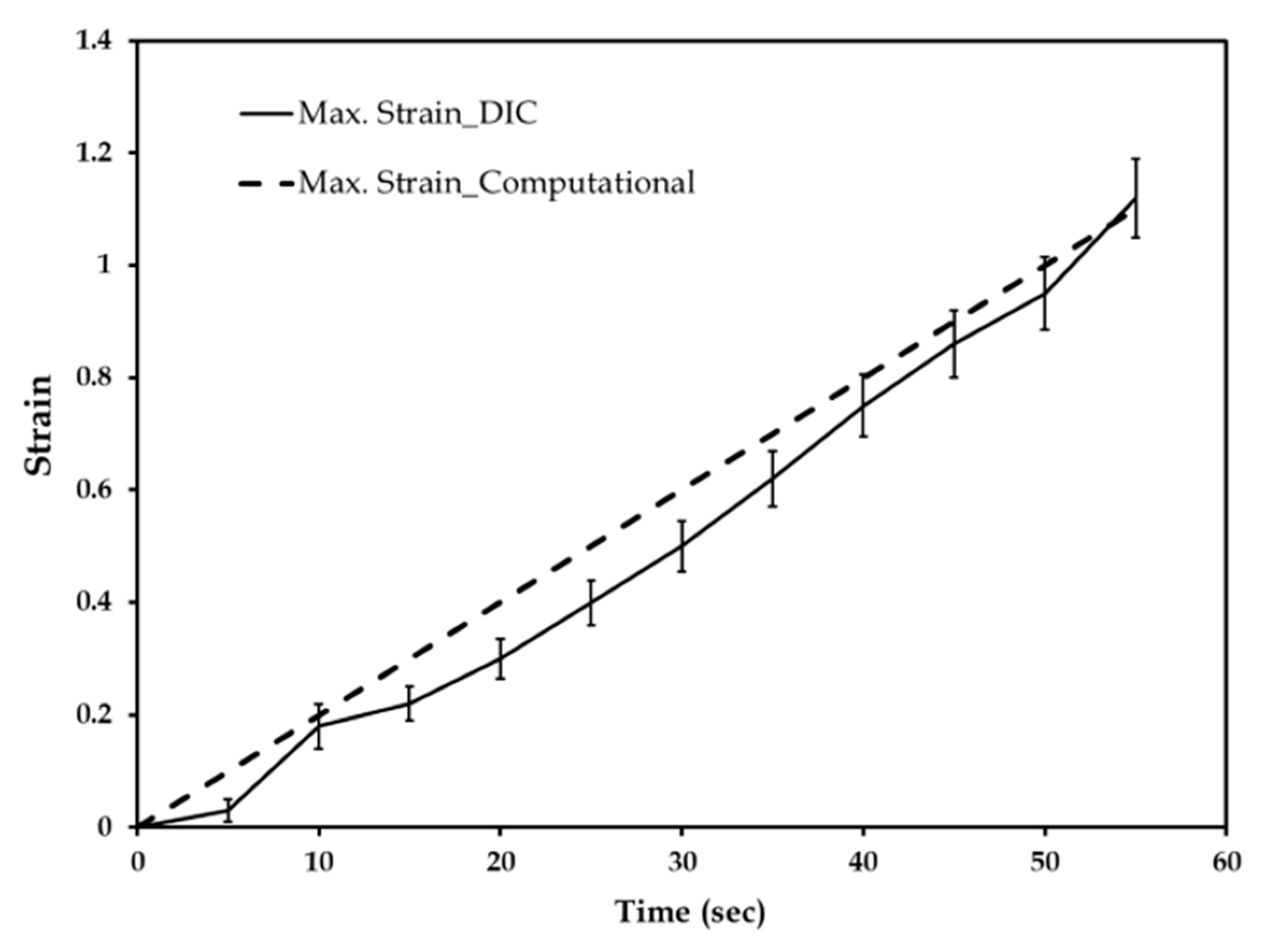
3.8. Computational Modeling of Stress and Strain on Transverse Wound
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stillman, R.M.; Bella, F.J.; Seligman, S.J. Skin wound closure: The effect of various wound closure methods on susceptibility to infection. Arch. Surg. 1980, 115, 674–675. [Google Scholar] [CrossRef] [PubMed]
- Broughton, G., 2nd; Janis, J.E.; Attinger, C.E. The basic science of wound healing. Plast. Reconstruct. Surg. 2006, 117, 12S–34S. [Google Scholar] [CrossRef] [PubMed]
- Reiley, C.E.; Lin, H.C.; Varadarajan, B.; Vagvolgyi, B.; Khudanpur, S.; Yuh, D.; Hager, G. Automatic recognition of surgical motions using statistical modeling for capturing variability. Stud. Health Technol. Informat. 2008, 132, 396–401. [Google Scholar]
- Chanda, A.; Ruchti, T.; Unnikrishnan, V. Computational modeling of wound suture: A review. IEEE Rev. Biomed. Eng. 2018, 11, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Danielson, D.; Natarajan, S. Tension field theory and the stress in stretched skin. J. Biomech. 1975, 8, 135–142. [Google Scholar] [CrossRef]
- Larrabee, W.F.; Galt, J. A finite element model of skin deformation. III. The finite element model. Laryngoscope 1986, 96, 413–419. [Google Scholar] [CrossRef] [PubMed]
- Cavicchi, A.; Gambarotta, L.; Massabò, R. Computational modeling of reconstructive surgery: The effects of the natural tension on skin wrinkling. Finite Elem. Anal. Des. 2009, 45, 519–529. [Google Scholar] [CrossRef]
- Flynn, C.; McCormack, B.A. Finite element modelling of forearm skin wrinkling. Skin Res. Technol. 2008, 14, 261–269. [Google Scholar] [CrossRef]
- Flynn, C. Finite element models of wound closure. J. Tissue Viabil. 2010, 19, 137–149. [Google Scholar] [CrossRef]
- Capek, L.; Jacquet, E.; Dzan, L.; Simunek, A. The analysis of forces needed for the suturing of elliptical skin wounds. Med. Biol. Eng. Comput. 2012, 50, 193–198. [Google Scholar] [CrossRef]
- Feng, A.L.; Clark, J.H.; Agrawal, N.; Moussa, W.; Richmon, J.D. Neck incision planning for total laryngectomy: A finite element analysis. J. Biomech. 2015, 48, 4149–4154. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V. A Realistic 3D Computational Model of the Closure of Skin Wound with Interrupted Sutures. J. Mech. Med. Biol. 2016, 17, 1750025. [Google Scholar] [CrossRef]
- Chanda, A.; Flynn, Z.; Unnikrishnan, V. Biofidelic Vaginal Tissue Surrogate. U.S. Provisional Patent No. 62/263942, 7 July 2015. [Google Scholar]
- Melis, P.; Noorlander, M.L.; Bos, K.E. Tension Decrease during Skin Stretching in Undermined versus Not Undermined Skin: An Experimental Study in Piglets. Plast. Reconstr. Surg. 2001, 107, 1201–1205. [Google Scholar] [CrossRef] [PubMed]
- Frick, T.; Marucci, D.; Cartmill, J.; Martin, C.; Walsh, W. Resistance forces acting on suture needles. J. Biomech. 2001, 34, 1335–1340. [Google Scholar] [CrossRef]
- Cacou, C.; Muir, I. Effects of plane mechanical forces in wound healing in humans. J. R. Coll. Surg. Edinb. 1995, 40, 38–41. [Google Scholar]
- Cacou, C.; Anderson, J.; Muir, I.F. Measurements of closing force of surgical wounds and relation to the appearance of resultant scars. Med. Biol. Eng. Comput. 1994, 32, 638–642. [Google Scholar] [CrossRef]
- Corr, D.T.; Hart, D.A. Biomechanics of scar tissue and uninjured skin. Adv. Wound Care 2013, 2, 37–43. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V. Human tissue simulants for study of traumatic brain injury (TBI). In Proceedings of the American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA, USA, 19–22 September 2016. [Google Scholar]
- Chanda, A.; Flynn, Z.; Unnikrishnan, V. Biomechanical characterization of normal and prolapsed vaginal tissue surrogates. J. Mech. Med. Biol. 2018, 18, 1750100. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z.; Lackey, K. Experimental study on tissue phantoms to understand the effect of injury and suturing on human skin mechanical properties. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 80–91. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V. Customized Insoles for Diabetic and Pressure Ulcers. Google Patents US20180008000A1, 1 January 2018. [Google Scholar]
- Chanda, A.; Graeter, R. Human Skin-Like Composite Materials for Blast Induced Injury Mitigation. J. Compos. Sci. 2018, 2, 44. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Roy, S.; Richter, H.E. Computational modeling of the female pelvic support structures and organs to understand the mechanism of pelvic organ prolapse: A review. Appl. Mech. Rev. 2015, 67, 040801. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Richter, H.E.; Lockhart, M.E. Computational Modeling of Anterior and Posterior Pelvic Organ Prolapse (POP). In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z. Biofidelic Skin Simulant. U.S. Patents US20170011657A1, 12 Jaunary 2017. [Google Scholar]
- Chanda, A.; Callaway, C.; Clifton, C.; Unnikrishnan, V. Biofidelic Human Brain Tissue Surrogates; Taylor & Francis: New York, NY, USA, 2016. [Google Scholar]
- Chanda, A.; Unnikrishnan, V.; Lackey, K. Biofidelic Conductive Synthetic Skin Composites. In Proceedings of the American Society for Composites—Thirty-second Technical Conference, West Lafayette, IN, USA, 23–25 October 2017. [Google Scholar]
- Chanda, A.; Curry, K. Patient-Specific Biofidelic Human Coronary Artery Surrogates. J. Mech. Med. Biol. 2018, 18. [Google Scholar] [CrossRef]
- Chanda, A.; Callaway, C. Tissue Anisotropy Modeling Using Soft Composite Materials. Appl. Bion. Biomech. 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A. Biofidelic Soft Composites–Experimental and Computational Modeling; University of Alabama Libraries: Tuscaloosa, AL, USA, 2017. [Google Scholar]
- Xu, H. Application of Visual Imaging Correlation-2D to Strain Measurement. Master’s Thesis, Rochester Institute for Technology, Rochester, NY, USA, 27 July 2014. [Google Scholar]
- Abanto-Bueno, J.; Lambros, J. Investigation of crack growth in functionally graded materials using digital image correlation. Eng. Fracture Mech. 2002, 69, 1695–1711. [Google Scholar] [CrossRef]
- Annaidh, A.N.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Groves, R.B.; Coulman, S.A.; Birchall, J.C.; Evans, S.L. An anisotropic, hyperelastic model for skin: Experimental measurements, finite element modelling and identification of parameters for human and murine skin. J. Mech. Behav. Biomed. Mater. 2013, 18, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Payne, T.; Mitchell, S.; Bibb, R.; Waters, M. Initial validation of a relaxed human soft tissue simulant for sports impact surrogates. Procedia Eng. 2014, 72, 533–538. [Google Scholar] [CrossRef]
- Payne, T.; Mitchell, S.; Bibb, R.; Waters, M. The evaluation of new multi-material human soft tissue simulants for sports impact surrogates. J. Mech. Behav. Biomed. Mater. 2015, 41, 336–356. [Google Scholar] [CrossRef]
- Annaidh, A.N.; Destrade, M.; Ottenio, M.; Bruyere, K.; Gilchrist, M.D. Strain rate effects on the failure characteristics of excised human skin. J. Mech. Behav. Biomed. Mater. 2015, 41, 241–250. [Google Scholar]
- Wang, E.; Nelson, T.; Rauch, R. Back to elements-tetrahedra vs. hexahedra. In Proceedings of the 2004 International ANSYS Conference, Pittsburg, PA, USA, 24–26 May 2004. [Google Scholar]
- Chanda, A.; Graeter, R.; Unnikrishnan, V. Effect of blasts on subject-specific computational models of skin and bone sections at various locations on the human body. AIMS Mater. Sci 2015, 2, 425–447. [Google Scholar] [CrossRef]
- Martins, P.; Natal Jorge, R.; Ferreira, A. A Comparative Study of Several Material Models for Prediction of Hyperelastic Properties: Application to Silicone-Rubber and Soft Tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]
- Chanda, A.; Callaway, C. Computational modeling of blast induced whole-body injury: A review. J. Med. Eng. Technol. 2018, 42, 88–104. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Meyer, I.; Richter, H.E.; Lockhart, M.E.; Moraes, F.R.; Unnikrishnan, V. Vaginal changes due to varying degrees of rectocele prolapse: A computational study. J. Biomech. Eng. 2017, 139, 101001. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V. Effect of bladder and rectal loads on the vaginal canal and levator ani in varying pelvic floor conditions. Mech. Adv. Mater. Struct. 2017, 25, 1214–1223. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Richter, H.E.; Lockhart, M.E. A biofidelic computational model of the female pelvic system to understand effect of bladder fill and progressive vaginal tissue stiffening due to prolapse on anterior vaginal wall. Int. J. Numer. Methods Biomed. Eng. 2016, 32. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z. Biofidelic Human Skin Simulant. U.S. Patent 15/204353, 7 July 2015. [Google Scholar]
- Ghoneim, H.; Chanda, A. Pumping potential of a left-ventricle-like flexiblematrix-composite structure. In Proceedings of the 19th international conference on composite materials (ICCM19), Montreal, QC, Canada, 28 July–2 August 2013; pp. 7457–7462. [Google Scholar]
- Gonzalez, L.Y.S.; Botero, M.G.; Betancur, M. Hyperelastic Material Modeling; Technical Report; Departamento de Ingenieria Mecanica, Universidad EAFIT: Medellın, Colombia, 2005. [Google Scholar]
- Holzapfel, G.A. Nonlinear Solid Mechanics; Wiley: Chichester, UK, 2000; Volume 24. [Google Scholar]







| Veronda-Westmann Model | (MPa) | (MPa) |
|---|---|---|
| Biofidelic Human Skin Phantom | 0.737 | 0.338 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanda, A.; Upchurch, W. Biomechanical Modeling of Wounded Skin. J. Compos. Sci. 2018, 2, 69. https://doi.org/10.3390/jcs2040069
Chanda A, Upchurch W. Biomechanical Modeling of Wounded Skin. Journal of Composites Science. 2018; 2(4):69. https://doi.org/10.3390/jcs2040069
Chicago/Turabian StyleChanda, Arnab, and Weston Upchurch. 2018. "Biomechanical Modeling of Wounded Skin" Journal of Composites Science 2, no. 4: 69. https://doi.org/10.3390/jcs2040069
APA StyleChanda, A., & Upchurch, W. (2018). Biomechanical Modeling of Wounded Skin. Journal of Composites Science, 2(4), 69. https://doi.org/10.3390/jcs2040069




