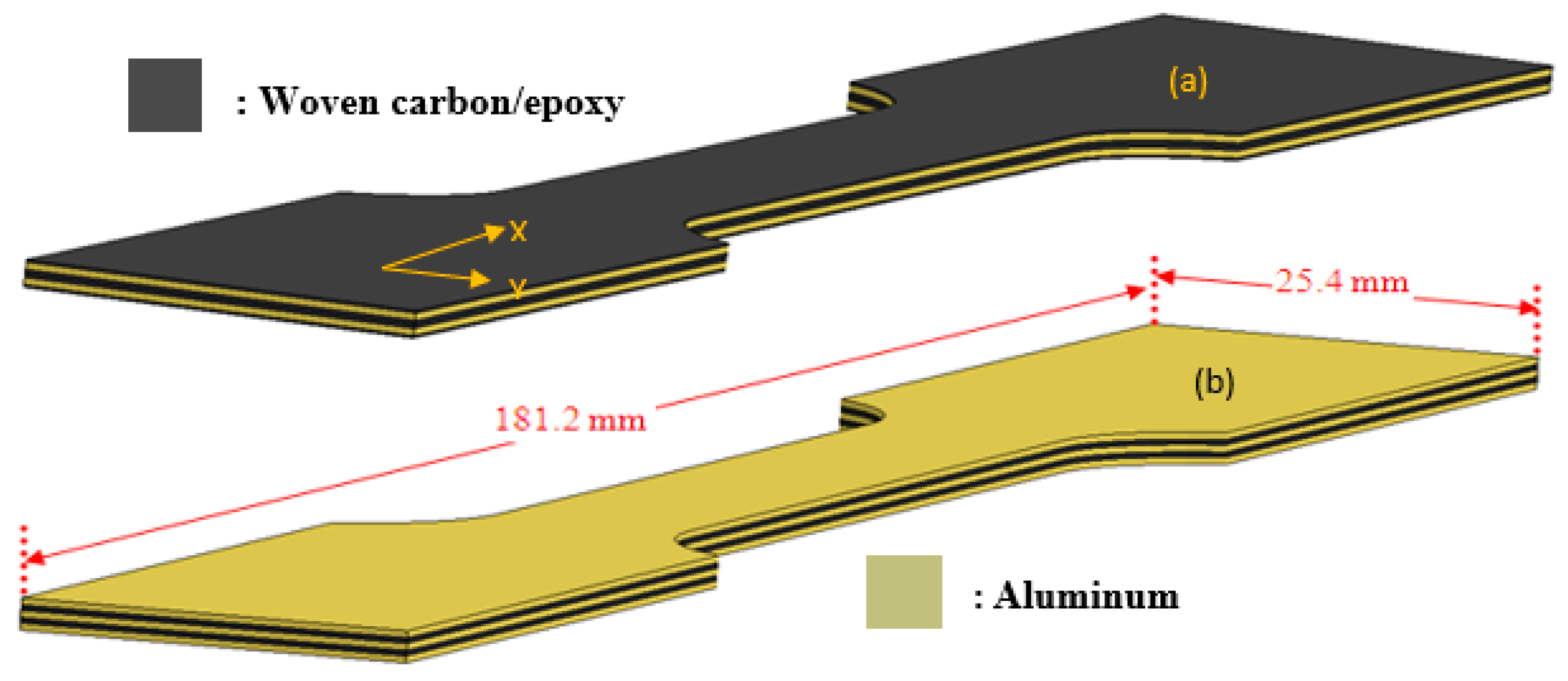
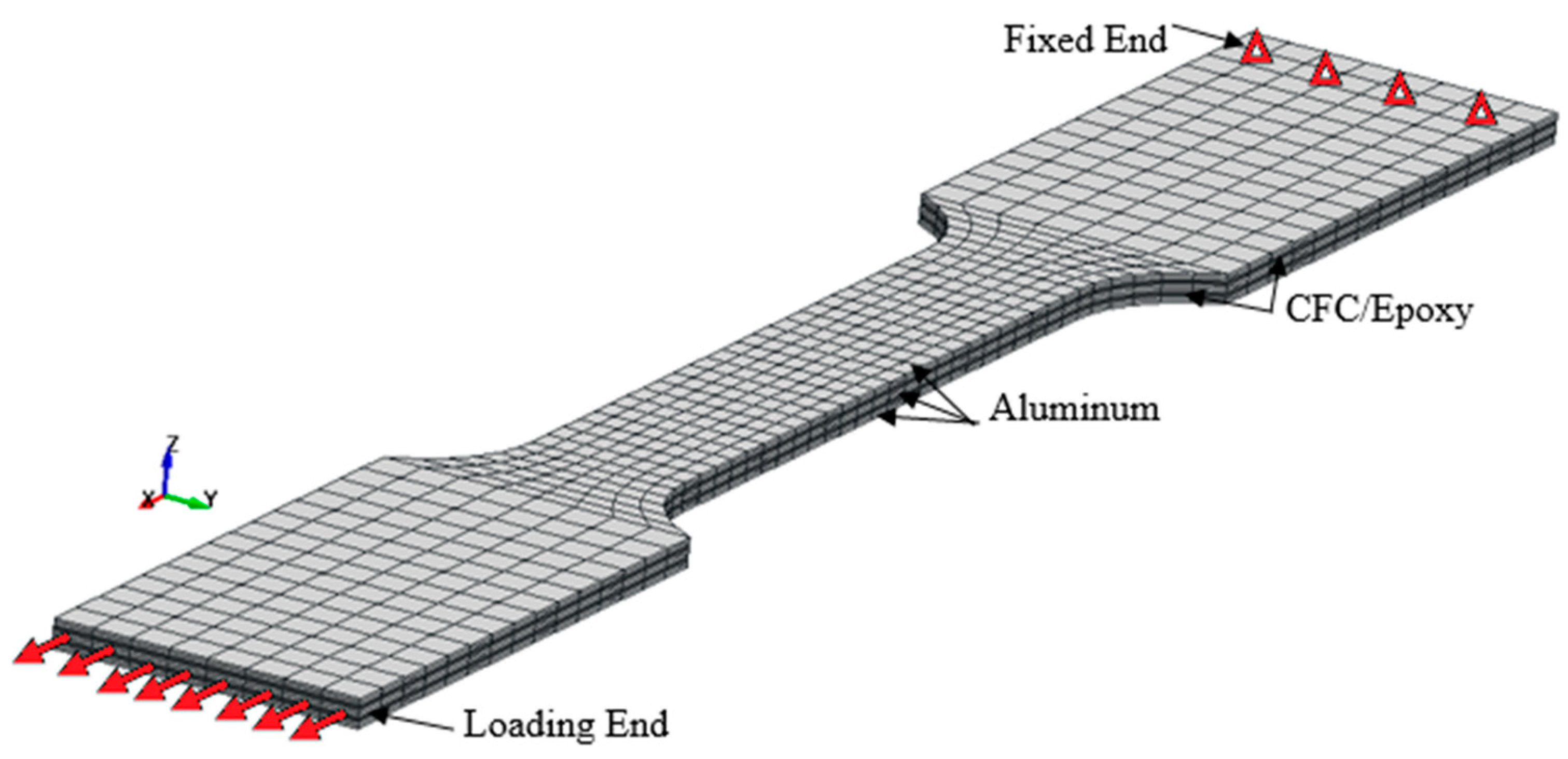
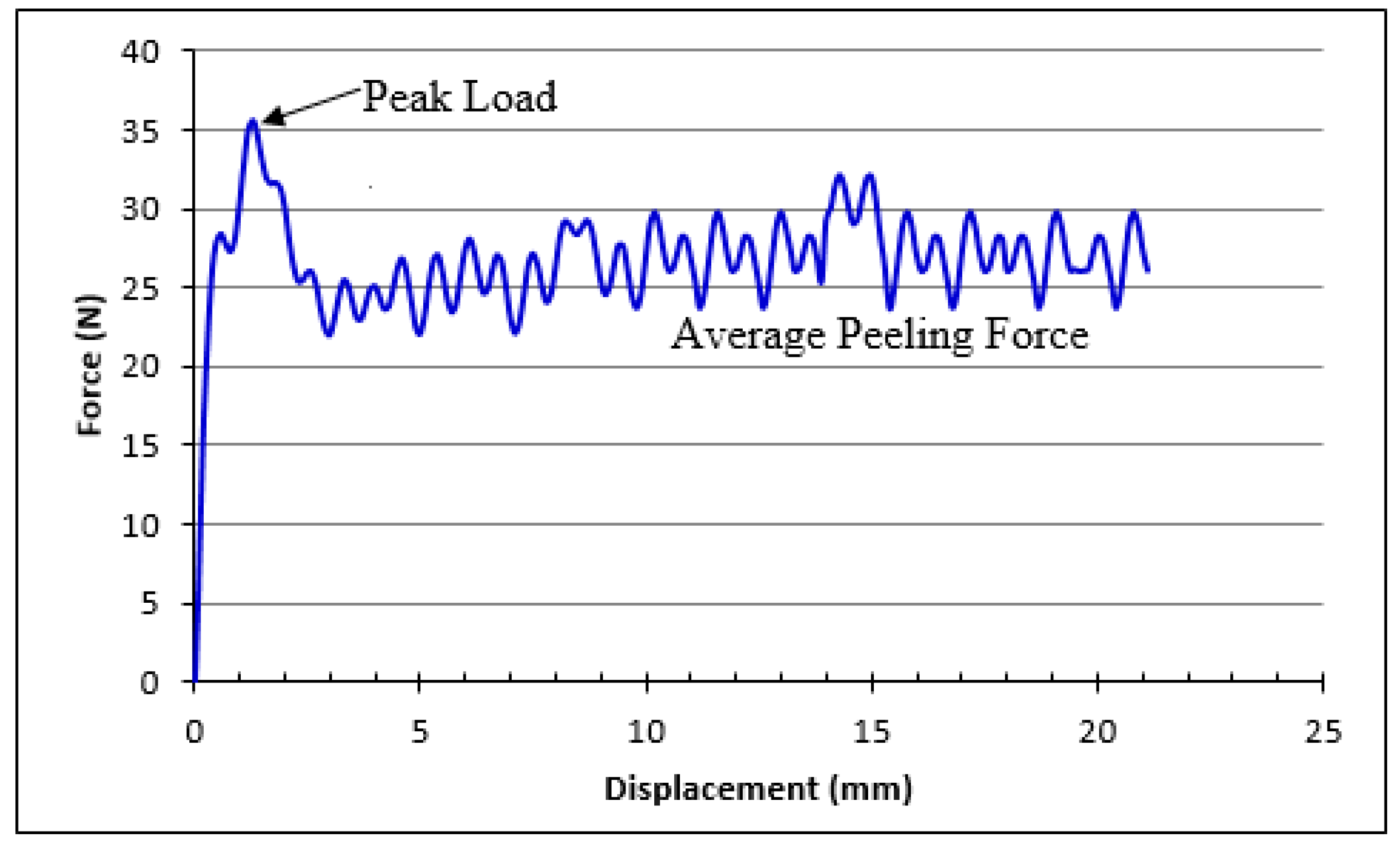
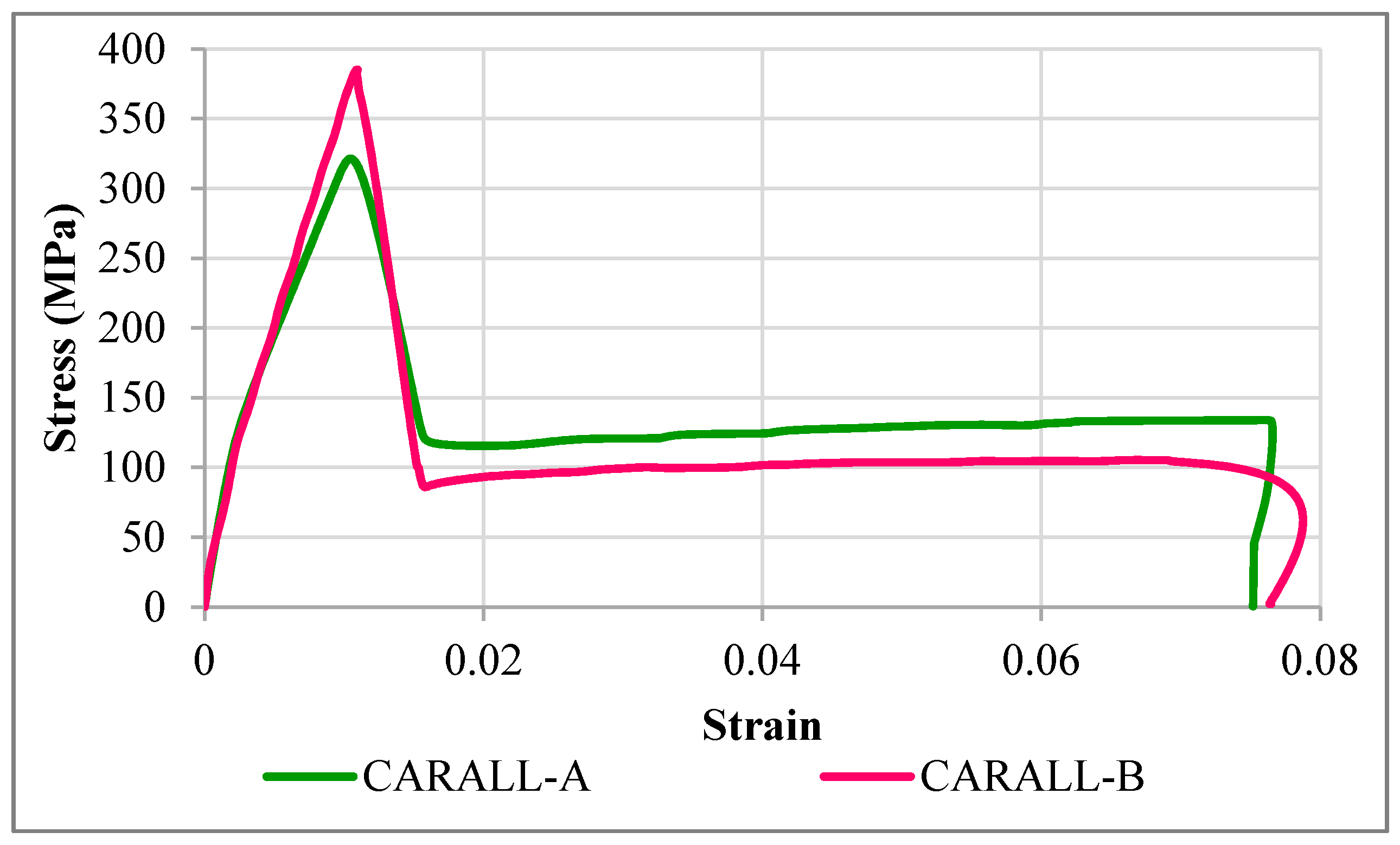
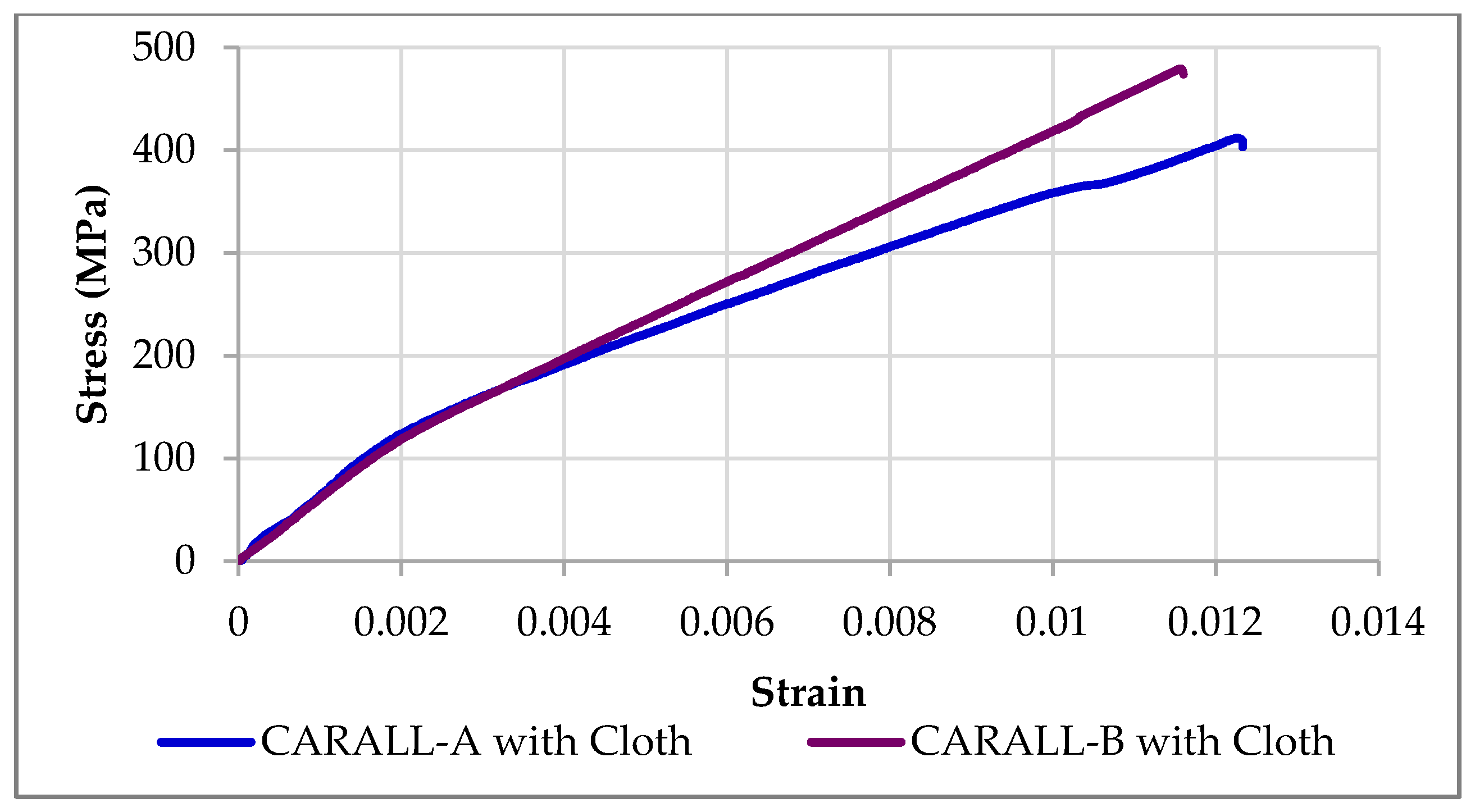
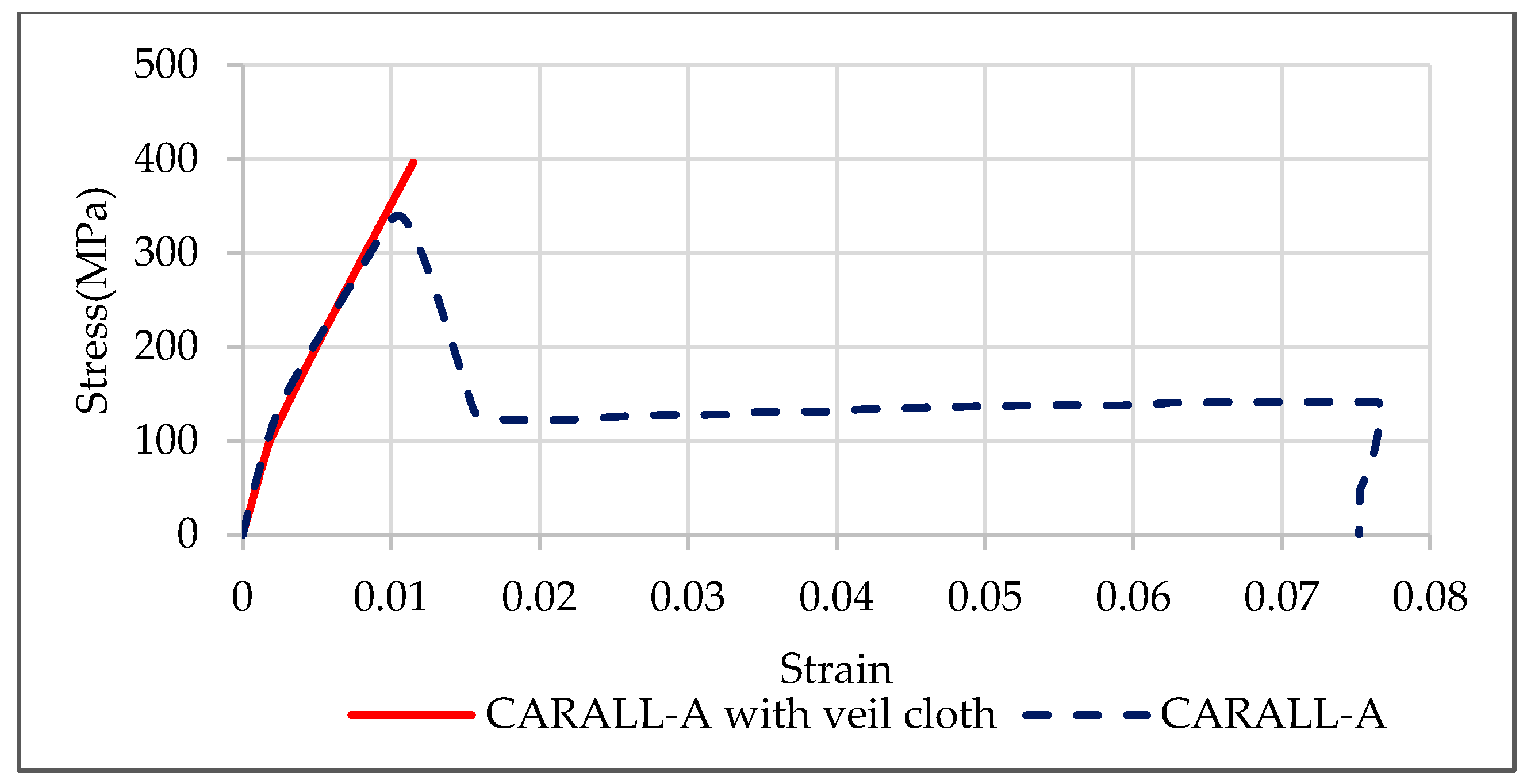
4.1. Thermal Residual Stresses
Fiber metal laminates are lightweight materials, consisting of very thin layers of metallic sheets interspersed with layers of fiber reinforced adhesives. The engineering aim behind the design of fiber metal laminates is to combine the best properties of metals and fiber-reinforced composites. Different materials can be used to create such hybrid material systems. However, any arbitrary combinations of materials would result in poor structural quality due to the existence of difficulties, such as very high residual thermal stresses during the fabrication process, galvanic corrosion, etc., during the manufacturing of these mixed materials. Residual stresses are developed in fiber metal laminates (FML) during the autoclave curing process due to a mismatch between the coefficients of thermal expansion of fiber layers and metal layers. Several other parameters, such as thermal contraction, which arises during the post-fabrication cooling process, laminate layup, volumetric shrinkage of resin, the morphology of fibers, mold material, thermal gradient during cooling, etc., contribute to the development of these residual stresses. The undesirable effects of residual stresses are distortions of the finished components when cooled and removed from molds (dimensional stability), failure in the manufactured products (e.g., matrix cracking, interfacial failure, ply failure), etc. Such stresses can subsequently reduce the design life and durability of fiber metal laminates. Therefore, the prediction and measurement of residual stresses is important to achieve the durable performance of fiber metal laminates. Therefore, the prediction of these residual stresses was done in the above stated two FML configurations before predicting their mechanical behavior.
4.5. Composite (CFRP) Material Model
The tensile behavior of the woven carbon fiber/epoxy layers was modeled using Chang-Chang [
48] damage initiation criteria inbuilt in the enhanced composite damage (Mat_054) material model of LS-DYNA. According to this failure criterion, damage in composite laminate occurs when one of the following failure equations is equal to or greater than zero. Fiber tension, fiber compression, matrix tension, and matrix compression are the four failure modes considered in the Chang-Chang failure criteria [
48]. The failure equations are represented separately as follows:
Tensile failure, fiber direction:
Upon failure E1 = E2 = G12 = ν12 = ν21 = 0.
Compressive failure, fiber direction:
Upon failure: E1 = ν12 = ν21 = 0.
Tensile failure, matrix direction:
Upon failure: E2 = G12 = ν21 = 0.
Compressive failure, matrix direction:
Upon failure: E2 = G12 = ν12 = ν21 = 0.
Where, σ1 is the nominal stress in the lamina in the fiber direction; σ2 is the nominal stress in the lamina in the matrix direction; τ12 is the nominal shear stress in the plane of the lamina; XT is the tensile strength of the fibers; XC is the compressive strength of the fibers; YT is the tensile strength in the transverse direction of the fibers; YC is the compressive strength in the transverse direction of the fibers; S is the shear strength; and Ψ is the shear stress correction parameter in the tensile failure mode. The value of Ψ equal to zero was considered in the finite element analysis performed in this research study.
The fibers in the weft direction were also considered in the failure of the individual ply by setting up the two-way fiber flag equal to 1. When the two-way fiber flag is set equal to 1, then the failure criteria for tensile and compressive fiber failure in the local X direction are unchanged. For the local y-direction, the same failure criteria as for the x-direction fibers are used.
Tension, y direction
Compressive, y direction
Matrix failure criterion
When one of the above conditions is exceeded in a ply within the element, the specified elastic properties for that ply are set to zero. The mechanism by which MAT54 applies this elastic property reduction, however, only prevents the failed ply from carrying increased stress rather than reducing the stress to zero or a near zero value. The equations used by MAT54 to determine 1- and 2-direction element stress in the ith time step provides insight into this mechanism.
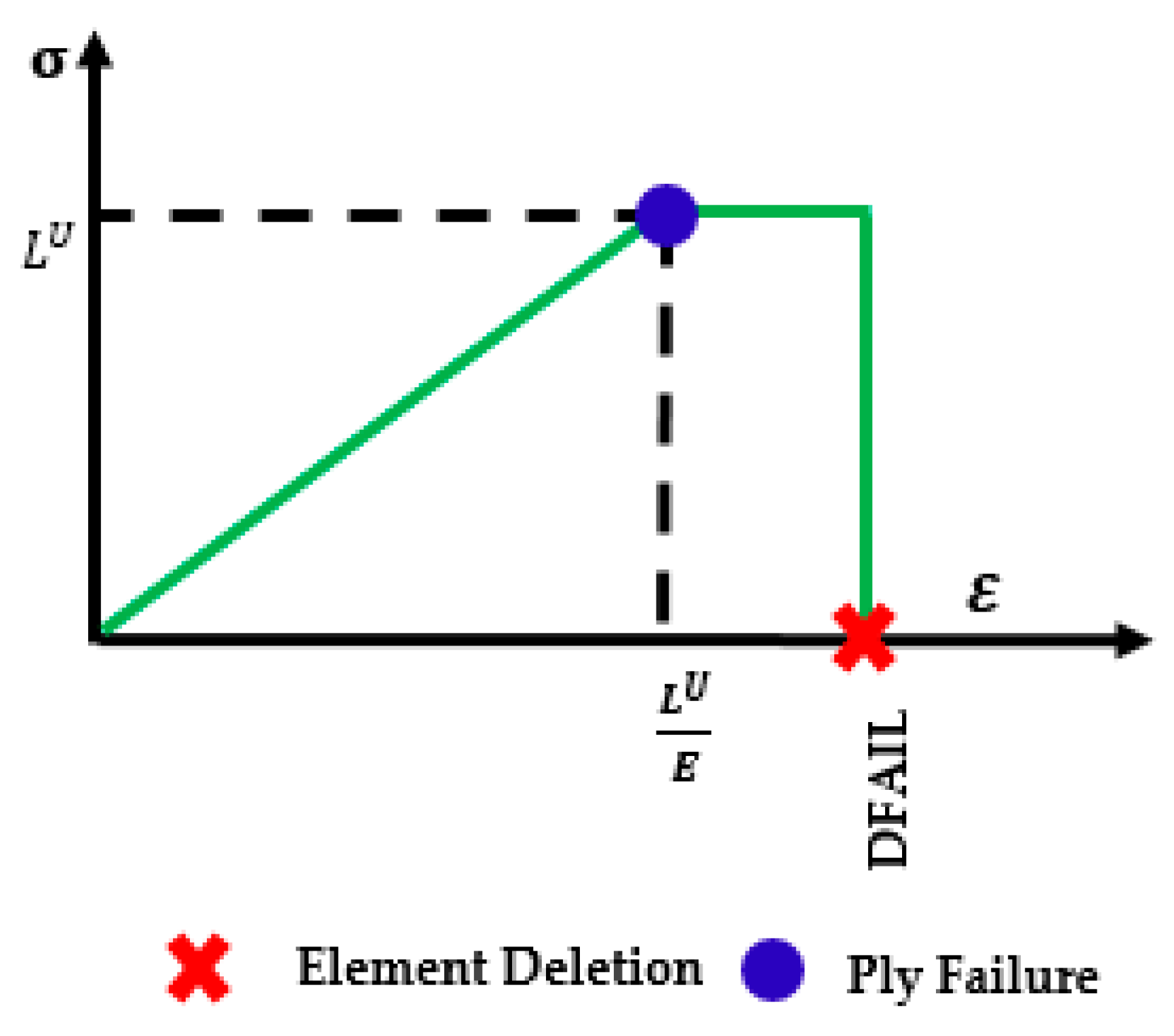
When ply failure occurs in the
ith time step, constitutive properties in the stiffness matrix, C, go to zero, but the stress from the
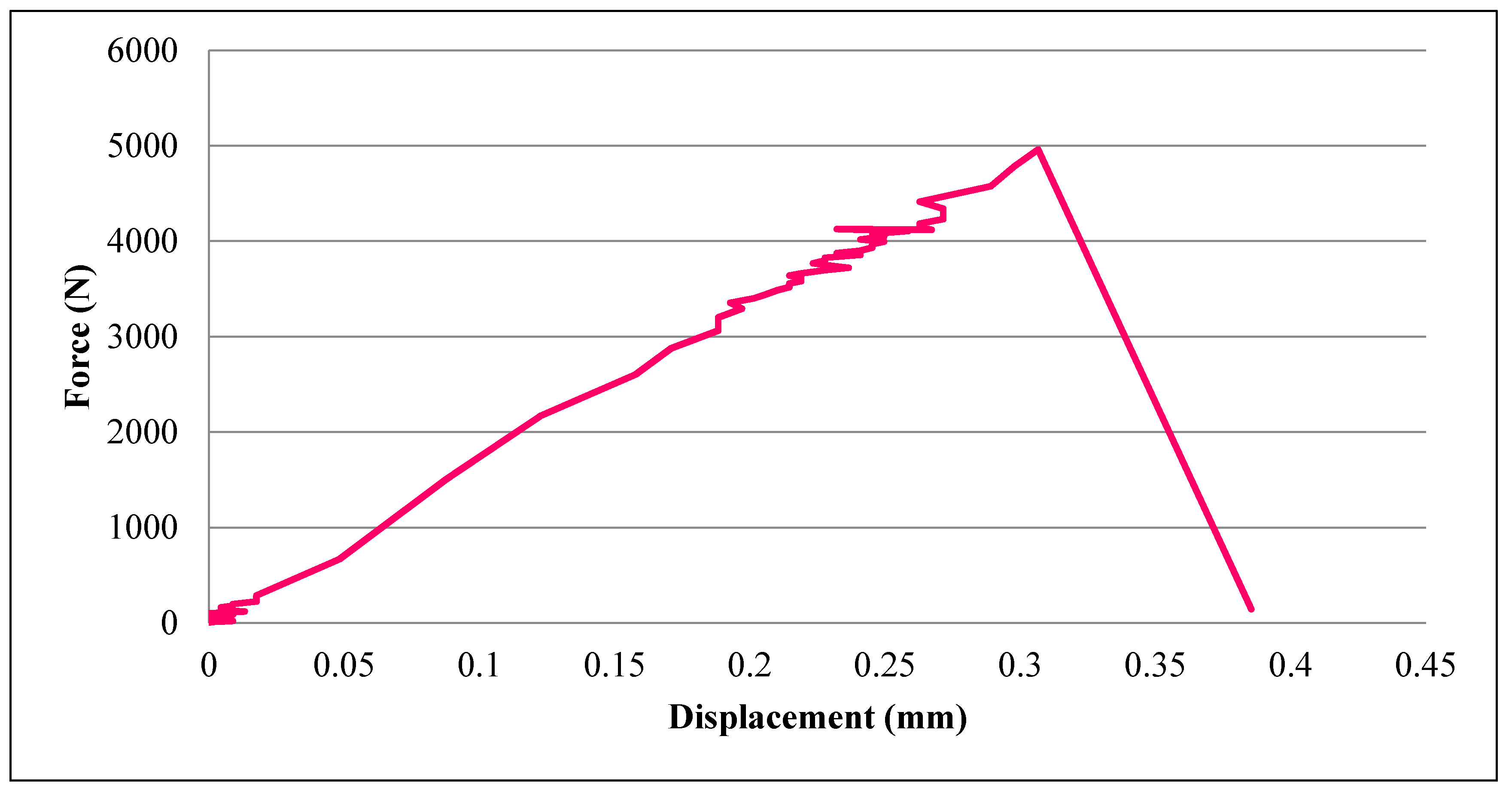
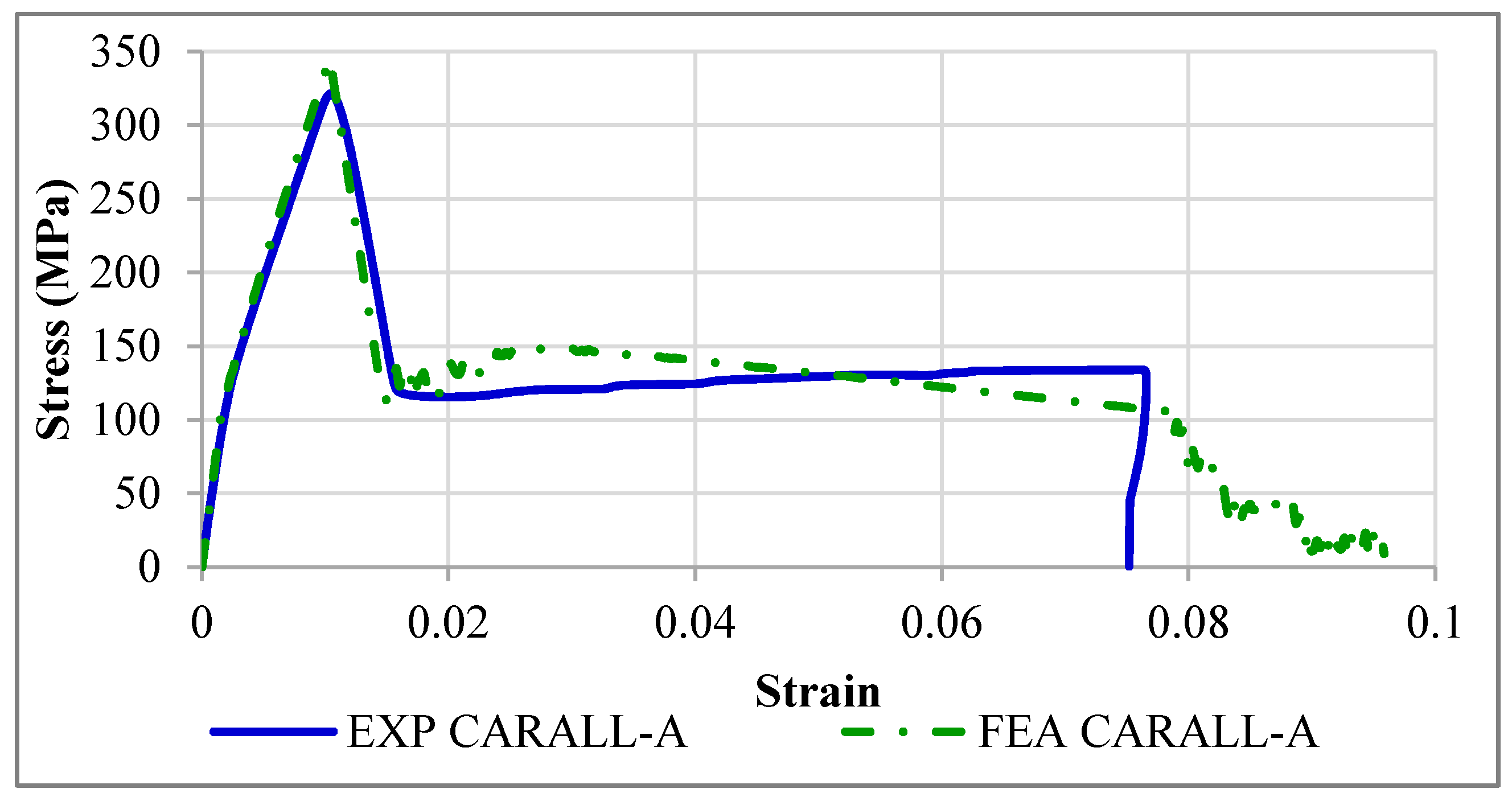
ith−1 time step is non-zero. The ply stresses of a failed ply are unchanged from the stress state just prior to failure. This produces a constant stress state in the ply stress-strain curve following failure. The resulting plastic behavior, shown in
Figure 14, only occurs when the strength is reached before the failure strain. MAT54 applies property degradation following failure in this way rather than degrading properties in the elastic equations.
The MAT54’s FBRT and YCFAC strength reduction parameters are used to degrade the pristine fiber strengths of a ply if compressive matrix failure takes place. This strength reduction simulates damage done to the fibers from the failed matrix. This strength degradation is applied using the following equations:
The FBRT parameter defines the percentage of the pristine fiber strength that is left following failure, therefore, its value may only be in the range [0, 1]. The YCFAC parameter uses the pristine matrix strength, YC, to determine the damaged compressive fiber strength, which means that the upper limit of YCFAC is XC/YC. The input value for the two parameters, FBRT and YCFAC, cannot be measured experimentally and must be determined by trial and error. The failure equations described in Equations (2)–(8) provide the maximum stress limit of a ply, and the damage mechanisms described in Equations (9)–(11) reduce the stress limit by a specified value given specific loading conditions. None of these mechanisms, however, causes the ply stress to go to zero, as would be expected of a failed ply. Instead, five critical strain values reduce the ply stresses to zero.
These are the strain to failure values in the positive fiber direction (tension), DFAILT; in the negative fiber direction (compression), DFAILC; in the matrix direction, DFAILM; in shear, DFAILS; and a non-physical failure strain parameter called EFS. It is important to note that in the matrix direction, there is only one failure strain value, which is used for both tension and compression. When the two-way fiber flag is considered to model woven fabrics, then the DFAILT and DFAILC parameters are taken as the fiber tensile failure strain and fiber compressive failure strain in both local x and y directions. Four of the failure strains can be measured through coupon-level tests, but if they are not known, LS-DYNA gives the user the option to employ a generic failure strain parameter, EFS (effective failure strain). The EFS immediately reduces the ply stresses to zero when the strain in any direction exceeds EFS, which is given by:
A critical EFS value can be calculated for any simulation by determining 1-, 2-, and 12-strains at element failure, and using them in Equation (12). EFS values below the critical EFS will cause premature element deletion. The default value for EFS is zero, which is interpreted by MAT54 to be numerically infinite. An element is deleted once all of the plies in that element have zero stress. In this study, failure strains for CFRP layers were not used.
4.6. Aluminum Material Model
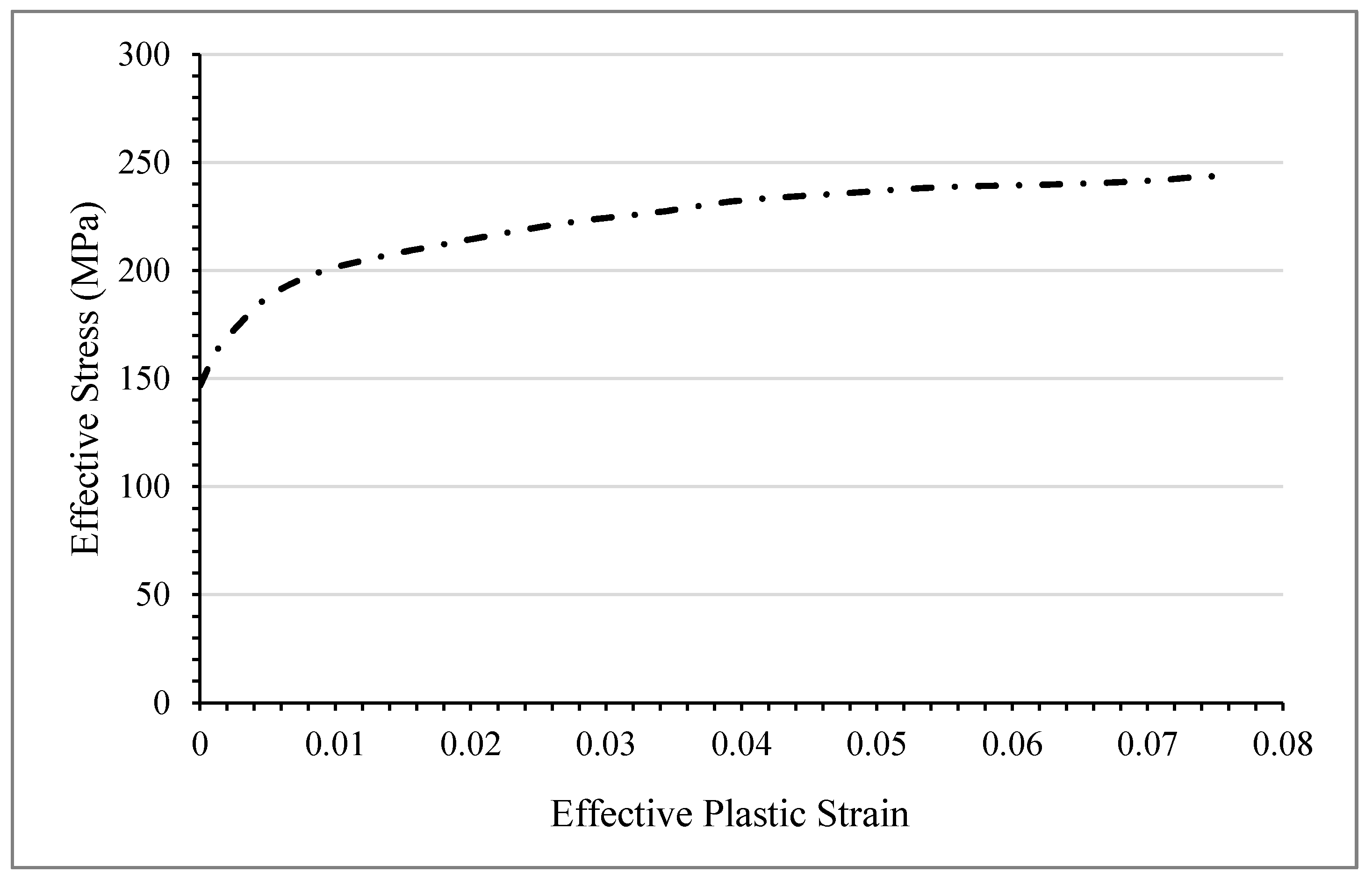
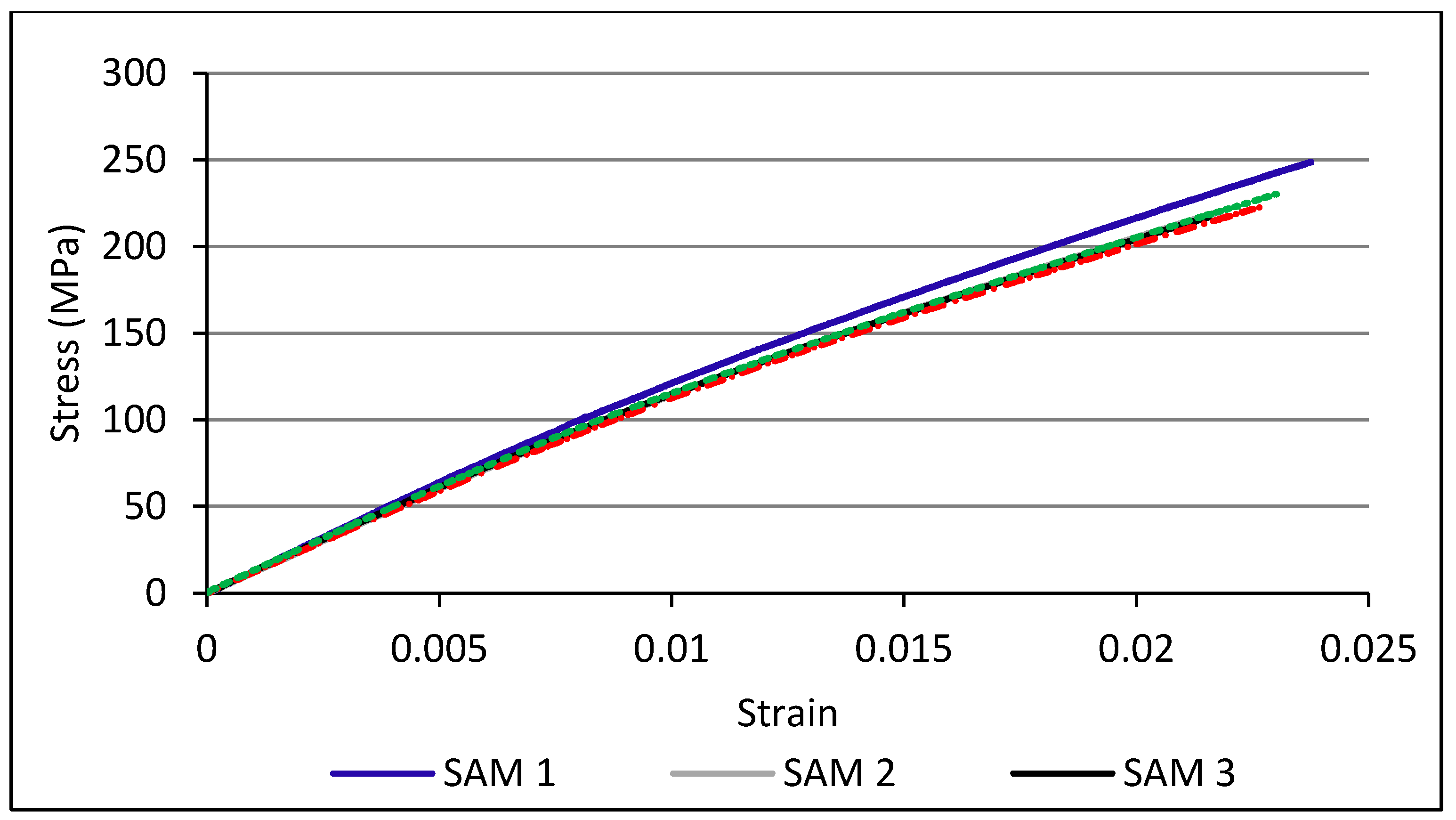
The piecewise linear plasticity material model (Mat_024) was utilized to model the elastoplastic behavior of aluminum layers by defining the effective stress-effective plastic strain curve obtained from experimental data. The failure of aluminum layers was modeled in this study by defining a plastic failure strain in the constitutive model card of LS-DYNA. The effective stress-effective plastic strain curve used as input to the piecewise linear plasticity material model is shown in
Figure 15. The material properties’ parameters of aluminum and carbon fiber/epoxy used for predicting the tensile behavior of FMLs are presented in
Table 2 and
Table 3. The mechanical properties of 5052-H32 aluminum alloy shown in
Table 2 were evaluated experimentally with the tensile test performed in the lab and cross-checked with the values given in reference [
49].
In this material model, the plasticity treatment includes the strain rate and yield function, which is defined as:
where:
In this material model, the hardening function,
, can be defined in tabular form or specified in linear form as
. The effective plastic strain is defined as
and
denotes the initial yield strength. The plastic strain rate,
is the difference between the total and elastic strain rates. The strain rate effects can be added in this model by using the Cowper-Symonds model. The yield stress is scaled in this model with the factor,
, where C and p are the user defined input constants. The complete mathematical equations for the piecewise linear plasticity material model can be found in the LS-DYNA theory manual [
50]. However, we have not used any strain rate and hardening effects in our analysis. The implementation of the piecewise linear plasticity model is done in LS-DYNA by updating the deviatoric stresses elastically, checking the yield function, and the deviatoric stresses are accepted if the yield function is satisfied. The incremental plastic strain is computed if the yield function is not satisfied.
where G and E
p are the shear modulus and actual plastic hardening modulus, respectively. The trial deviatoric stress,
, state is then scaled back as:
4.7. Delamination Failure Model
Interlaminar delamination between the carbon fiber/epoxy (CFRP) and aluminum interfaces was modeled by employing cohesive tiebreak algorithms available in LS-DYNA [
51]. The transmission of both compressive and tensile forces is allowed in these penalty-based contact algorithms, which are used to model the connection between surfaces. The tie-break contact algorithms prevent the separation of the slave node from the master segment before failure of a connection, and after the failure, the contact behaves like a surface to surface contact with thickness offsets due to the removal of tensile coupling. Depending upon the nature of the connection, an optional failure criterion can be defined in all tie-break contacts. In this study, to simulate interlaminar debonding, the CONTACT AUTOMATIC SURFACE TO SURFACE TIEBREAK—DYCOSS Option 7 was chosen [
52,
53,
54]. The cohesive contact criteria in this tiebreak contact algorithm are based on the bilinear constitutive traction-separation law. The linear elastic/linear softening model for mode 1 crack opening is shown in
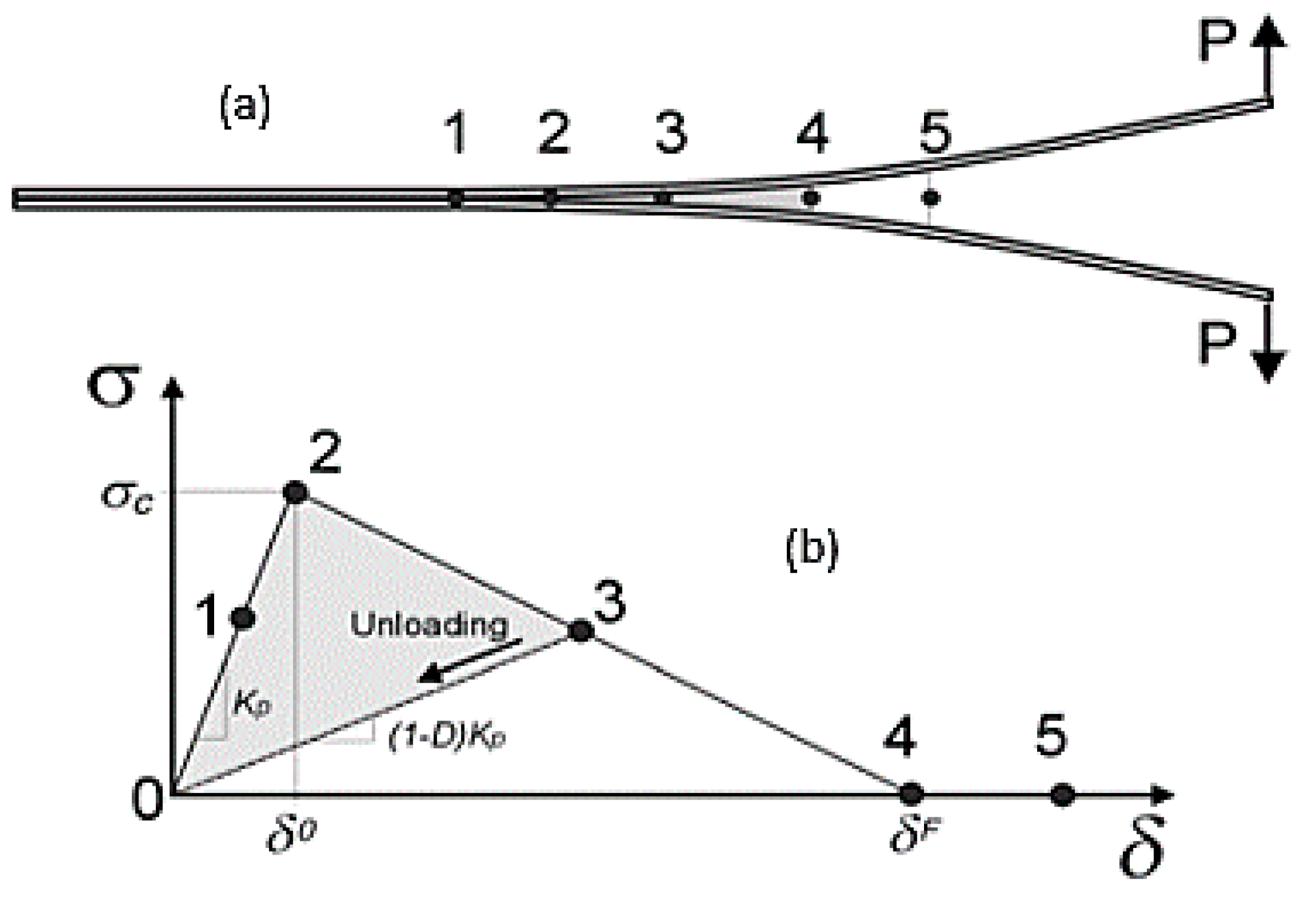
Figure 16. The stress-strain assumption with key points and the corresponding points with delamination progression are shown in
Figure 16a,b. As point 1 is in elastic part of the material response, no material damage had occurred at this point and the unloading would follow the elastic line. The onset of damage is represented by point 2, and material softening (damage growth) starts at the point. When the loading had progressed to point 3, the material has suffered some damage, but the plies have not separated yet (damage parameter (α) is greater than zero, but less than 1). The unloading is assumed to follow the start line from point 3 to 0 if it occurs at point 3. Non-recoverable energy dissipated to partial damage of bonding is represented by the shaded area in
Figure 16b. The plies have separated permanently at point 4 as the damage parameter (α) had reached unity. Fracture energy (G) required to delaminate two plies is represented by the total area of the triangle (0-2-4). The input parameter in LS-DYNA has energy/area as units.
In the DYCOSS discrete crack model, the interface forces in the uncracked state (point 1) are calculated from the relative displacements assuming linear elastic behavior.
where
and
are the stresses in mode I and mode II,
and
are secant stiffness terms for mode I and mode II, and
and
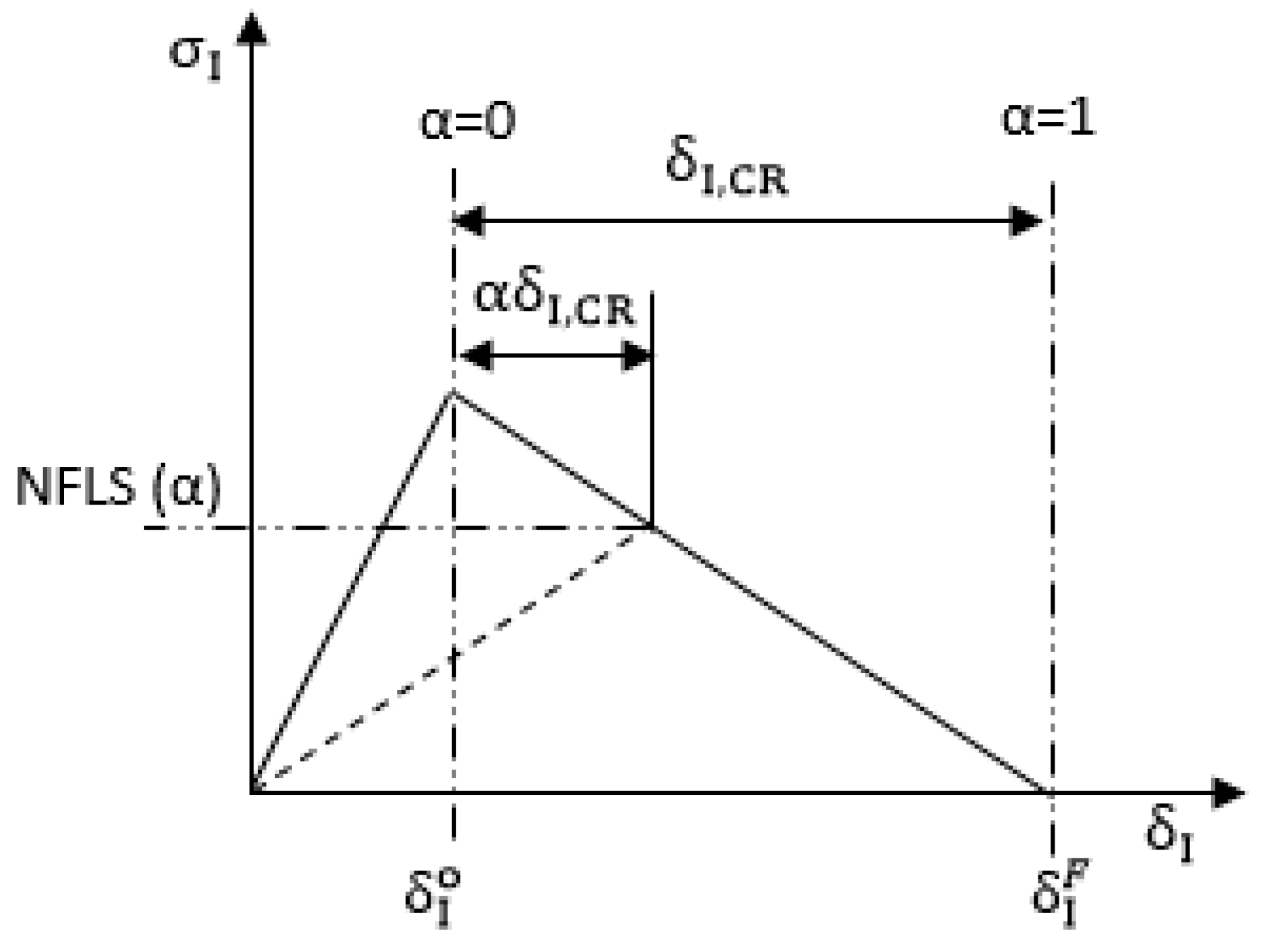
are the displacements for mode I and mode II. The allowable shear stresses may increase under increasing normal stress for heavy woven fabrics laminate. The relation for the crack initiation, in this case, is developed by extending the Hashin criterion with a friction angle (Φ) given as:
where NFLS is normal failure stress, SFLS is the shear failure stress, and Φ is the friction angle in degrees. When the loading is beyond the crack initiation point, the degradation of material is described by considering two damage variables,
and D
II.
where 1-D is the stress reduction factor. The value of D ranges from 0 to 1. Damage evolution in mode I depends on displacement,
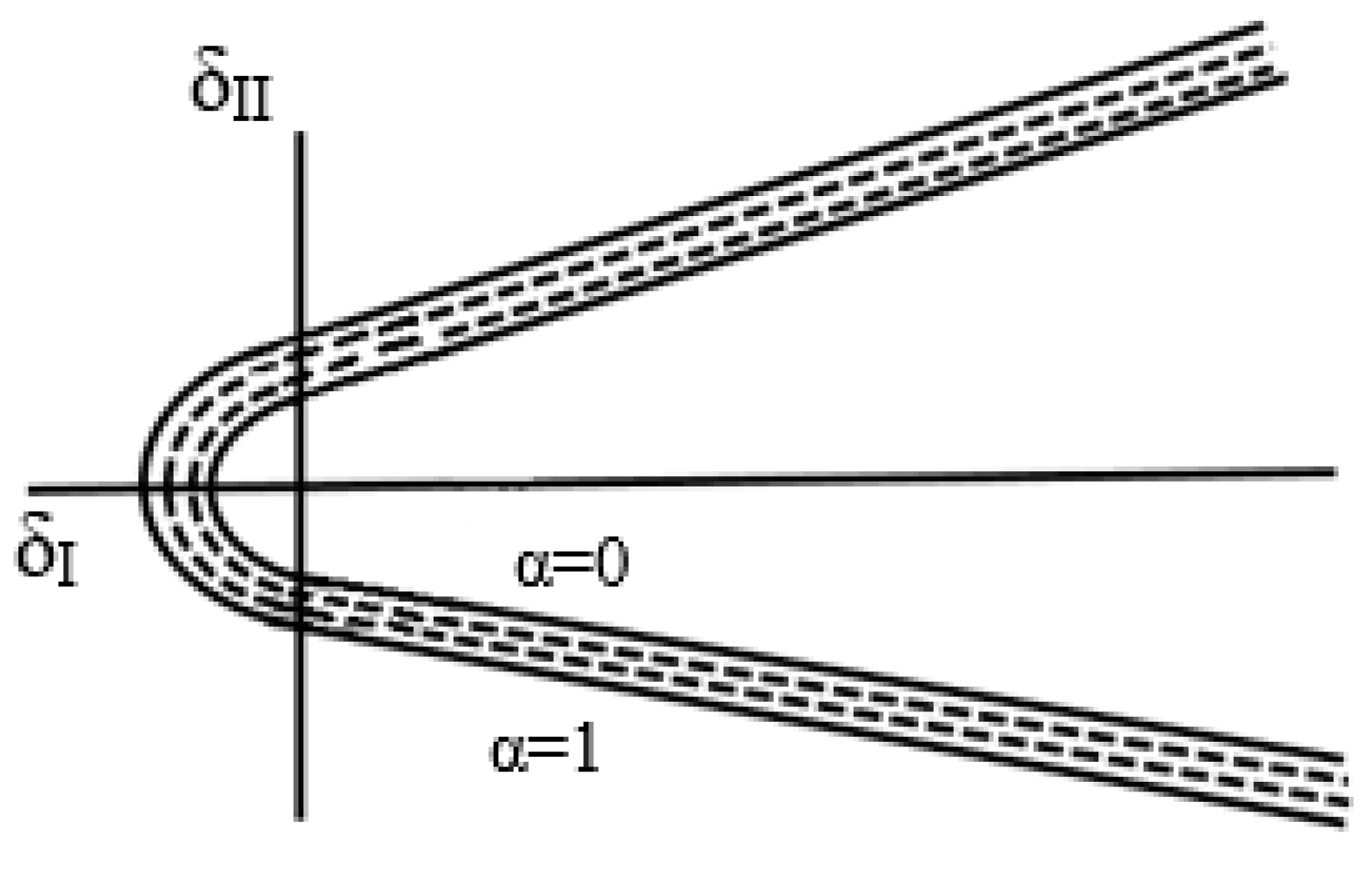
, only. The concept of friction angle is extended in the damage growth process for compressive normal displacements resulting in iso-lines, α, in
planes, as shown in
Figure 17.
The relation for crack propagation in terms of the internal parameter, α, is given as:
The interface stresses are expressed in terms of interface displacements as:
The initial and final displacement for mode I and mode II are given as:
Substituting Equations (19) and (20) into (18), we get:
The above equation is a nonlinear equation between α and known interface displacements. Linearizing it with respect to α gives:
After α is calculated, the secant terms are obtained as:
The damage matrix is given as:
The interface stresses for the crack development state are given by:
The complete mathematical equations for the DYCOSS discrete crack model can be found in Lemmen and Meijer’s technical paper [
56]. In this study, the mode II failure condition was considered dominant for modeling interlaminar delamination crack growth in an area located locally underneath the loading pin. Therefore, only shear failure strength (SFLS) = 15 MPa and shear energy release rate (ERATES) = 0.23 MPa·mm was used as input to the delamination model. Due to the lack of available data, the mode II energy release rate value was assumed.