Simulating Mold Filling in Compression Resin Transfer Molding (CRTM) Using a Three-Dimensional Finite-Volume Formulation

Abstract

Light-weight structural components are increasingly made of continuous fiber reinforced plastics (CoFRP), but their mass production is still very expensive. Because of its high automation potential, especially the Compression Resin Transfer Molding (CRTM) process gains more and more attention. Numerical mold filling simulations help to optimize this process and can avoid expensive experimental studies. Here, we present a new method to simulate mold filling in CRTM using a full three-dimensional finite-volume (FV) method. In comparison to known finite-element (FE) methods, it contains a compressible two-phase/Volume-of-Fluid description of the air- and resin-phase. This approach is combined with a moving mesh to account for the change of cavity height during the process, which results in a change of fiber volume fractions and thus permeabilities. We verify the method by comparison to analytic solutions of the Darcy equation and to solutions of state-of-the-art mold filling simulation software. The presented method enables CRTM mold filling simulation of complex parts, which is shown in two application examples. Furthermore, this shows the potential of using FV-based tools to simulate mold filling in RTM process variants containing non-constant cavity geometries.

1. Introduction

Recently, the use of continuous fiber reinforced plastics (CoFRP) is significantly increasing in the aerospace and the automotive industry because of their excellent weight-specific mechanical properties. Especially in the automotive industry this leads to new research activities to optimize the manufacturing process regarding cost-efficient high quality components. In this context, Liquid Composite Molding (LCM) processes as the Resin Transfer Molding (RTM) offers good conditions for mass production of high performance composite structures because of its high automation potential [1,2,3]. In RTM the liquid resin is injected into a heated rigid mold containing a dry fibrous reinforcement. The reinforcement is infiltrated and the resin cures inside the heated cavity until finally the part can be demolded. To minimize the cycle-time and ensure a complete filling, the injection strategy and process parameters like resin mass flow or temperature have to be optimized. To avoid time-consuming and expensive experimental studies, numerical simulations of the mold filling are increasingly used [4,5,6,7,8,9].

Traditionally, the mold is fully closed when the injection of the resin starts, called Injection-RTM (IRTM). To shorten cycle times, more and more process variants like Compression-RTM (CRTM) are used. In this RTM variant, the mold is not fully closed when the resin is injected, which improves the infiltration behavior of the fibrous reinforcement. When the appropriate amount of resin is injected, the mold starts to close until the final part thickness is reached and the component is completely infiltrated. This two-step process can help to minimize cycle time or reduce cavity pressure [10]. However, modeling of this process is more complex as for the traditional RTM process, because it includes more process parameters and especially a changing cavity geometry during the process. First simulations of CRTM were conducted by Pham [11,12] modeling one-dimensional and two-dimensional resin flow in the cavity based on Darcy’s law and using a finite-element method. Shojaei [13] developed a three-dimensional finite-element/control volume method to simulate the resin flow of a CRTM process in thick components, where a through-thickness impregnation can not be neglected. Furthermore Simacek et al. [14] simulated CRTM also using a three-dimensional finite-element/control volume method focusing on the implementation of an open gap between the fibrous preform and the mold which is assumed to occur for wide mold openings. To the knowledge of the authors up to now is no three-dimensional two-phase CRTM simulation method available, which is based on a finite-volume formulation.

Magagnato et al. [7] developed a finite-volume based method to simulate mold filling of IRTM by modeling a two-phase flow through porous media considering local permeability, where the permeability tensor at each element is evaluated using local fiber orientations and fiber volume fractions. Additionally a compressible formulation of the air phase was implemented to predict the development, movement and dispersion of air bubbles, which is not possible with finite-element based commercial RTM mold filling simulation software.

A three-dimensional CRTM simulation is the basis for future RTM process simulation because it allows to simulate a more accurate mold filling for thick-walled parts, the simulation of resin flow around embedded foam cores and the simulation of advanced CRTM variants as for example pressure controlled processes [15]. In this work, we present a new possibility to simulate mold filling of CRTM based on a three-dimensional finite-volume discretization. The approach is implemented in the open-source toolbox OpenFOAM^®. To include the CRTM simulation method in this open-source framework enables to flexibly embed the simulations in a virtual process chain for CoFRP manufacturing, like developed by Kärger et al. [16].

We verify the CRTM simulation method by comparison to analytic solutions of the one-dimensional Darcy equation and to results using a state-of-the-art commercial RTM mold filling simulation software. Furthermore, we present the simulation results of one complex geometry and one sandwich geometry with an embedded rigid core material. The results shall emphasize the possibilities of this method to simulate the resin flow in CRTM for sandwich components including core materials, which is so far not possible by using state-of-the-art mold filling simulation software.

2. Basic Fluid Mechanic Equations for Mold Filling Simulations

On macro-scale, the mold filling process of RTM is regarded as a flow through anisotropic porous media and can be modeled by Darcy’s law [17]

$$\tilde{\mathbf{v}}=-\frac{\mathbf{K}}{\mu }·(\nabla p),$$

(1)

where $\tilde{\mathbf{v}}$ is the volume averaged velocity and $\nabla p$ is the pressure gradient in the cavity. Relevant material parameters are the dynamic resin viscosity $\mu$ and the permeability $\mathbf{K}$ of the fibrous preform, which is a second order tensor. It is important to mention that the permeability of a dry fabric strongly depends on fiber orientation and fiber volume fraction. Assuming the resin to be an incompressible fluid in the mold filling process, the equation of continuity yields

$$\nabla ·\tilde{\mathbf{v}}=0.$$

(2)

Combined with Darcy’s law (1) a second order partial differential equation is obtained

$$0=\nabla ·\left(-\frac{\mathbf{K}}{\mu }\nabla p\right).$$

(3)

This differential equation can be solved by a numerical method. Commercial software explicitly developed for the filling simulation of RTM is mostly based on Darcy’s law. To solve the Darcy equation and ensure mass conservation, which is crucial for CFD (computational fluid dynamics) simulations, often a finite-element method with non-conforming elements [6,18] is used like e.g., in PAM-RTM^® by ESI Group.

A more general formulation to simulate a two-phase fluid flow in porous media is based on the Navier-Stokes-equations for Newtonian fluids (assuming incompressibility), where the continuity equation

$$\nabla ·\mathbf{v}=0,$$

(4)

and the momentum equation

$$\rho \frac{\delta \mathbf{v}}{\delta t}+\nabla \left(\rho \mathbf{v}\mathbf{v}\right)=-\nabla p+\mu {\nabla }^2\mathbf{v}+\mathbf{S},$$

(5)

with the fluid velocity $\mathbf{v}$, the fluid density $\rho$ and the source term $\mathbf{S}$

$$\mathbf{S}=-\left(\frac{\mu }{\mathbf{K}}+\frac{1}{2}\rho \left|\mathbf{v}\right|F\right)\mathbf{v}.$$

(6)

This source term S is also known as the Darcy-Forchheimer term containing the Darcy term $\frac{\mu }{\mathbf{K}}$ and the Forchheimer term $\frac{1}{2}\rho \left|\mathbf{v}\right|F$ with the fluid density $\rho$ and the inertial resistance coefficient F. For small fluid velocities and high permeabilities all terms in Equation (5) except the pressure gradient $\nabla p$ and the Darcy term can be neglected, which again leads to the Darcy equation. The Navier-Stokes-equations can be numerically solved by the finite-volume (FV) method. This method uses the integral form of the differential equations in a control volume $V_p$ and the Gauss’ theorem to alter the volume integrals of the spatial derivatives to surface integrals of the element faces, which in total leads to several volume and surface integrals that have to be evaluated. The main source about the implementation of the FV method in OpenFOAM is the work of Jasak [19], where all equations are derived in detail. The discretisation of Equation (4) using Gauss’ theorem and assuming linearity yields

$${\int }_{V_p}\nabla ·\mathbf{v}dV=\sum _f\left({\int }_{f}dA·\mathbf{v}\right)=\sum _f{\mathbf{A}}_f·{\mathbf{v}}_f=0,$$

(7)

which is the sum of the fluxes ${\mathsf{\Phi }}_f$

$$\sum _f{\mathbf{A}}_f·{\mathbf{v}}_f=\sum _f{\mathsf{\Phi }}_f=0$$

(8)

through the element faces f with the face interpolated velocity ${\mathbf{v}}_f$ and the surface area vector ${\mathbf{A}}_f$ of the element face. As implemented in OpenFOAM, the fluxes are conservative to assure the important mass conservation of the fluid.

To discretize Equation (5), the equation is split into its individual terms, whereby two points need special attention. Firstly the non-linearity and secondly the pressure-velocity coupling. The non-linear convection term $\nabla \left(\rho \mathbf{v}\mathbf{v}\right)$ is linearized and discretized to

$$\nabla \left(\rho \mathbf{v}\mathbf{v}\right)=\sum _f{\rho }_f{\mathsf{\Phi }}_f{\mathbf{v}}_f=a_p·{\mathbf{v}}_p+\sum _n{a}_n·{\mathbf{v}}_n,$$

(9)

where ${\mathbf{v}}_p$ is the velocity at the cell center, ${\mathbf{v}}_n$ at the neighboring cell centers and $a_p$ and $a_n$ are functions of $\mathbf{v}$. The discretization of the diffusion term $\mu {\nabla }^2\mathbf{v}$ leads to

$${\int }_{V_p}\mu {\nabla }^2\mathbf{v}dV=\sum _f{\mu }_f{\mathbf{A}}_f\nabla {\mathbf{v}}_f=\sum _f{\mu }_f\nabla {\mathbf{v}}_f.$$

(10)

To calculate the face gradient $\nabla {\mathbf{v}}_f$, first the cell-centered gradients of the neighboring cells are calculated and subsequently interpolated to the face. When using non-orthogonal meshes (which is unfortunately usually the case), the face gradients are split into an orthogonal and a non-orthogonal part to ensure boundedness. All existing source terms $\mathbf{S}$ (which can be a function of $\mathbf{v}$ like the Darcy term) are first linearized

$$\mathbf{S}=Su+Sp·\mathbf{v},$$

(11)

where $Su$ and $Sp$ can be functions of $\mathbf{v}$. The volume integral is then calculated as

$${\int }_{V_p}\mathbf{S}dV=Su·V_p+Sp·V_p·{\mathbf{v}}_p.$$

(12)

The Darcy source term is already linear and, therefore, the linearization does not affect its implementation. Time integration is done using schemes as for example the implicit Crank–Nicholson or the Euler-Implicit method. The momentum Equation (5) with Equations (9), (10) and (12) implemented give the semi-discretized form of the momentum equation

$$a_p·{\mathbf{v}}_p=H\left(\mathbf{v}\right)-\nabla p.$$

(13)

where $H\left(\mathbf{v}\right)$ consists of all discretized terms except the pressure gradient. This equation is the basis for the pressure-velocity coupling, which is done by using the PISO (Pressure Implicit Split of Operators) algorithm proposed by Issa [20]. For further information about numerical fluid mechanics and the FV discretization, the book by Ferziger and Peric [21] is also recommended .

The two-phase flow (e.g., resin and air) is solved in one simulation domain by using a volume of fluid (VoF) scheme. Therefore, additionally the phase fraction equation

$$\frac{\delta \alpha }{\delta t}=\nabla \left(\alpha \mathbf{v}\right)$$

(14)

is solved, where $\alpha$ indicates to what extent an element is filled with the first phase (e.g., resin, $\alpha =1$) or with the second phase (e.g., air, $\alpha =0$). Firstly, this equation separates the two fluids and defines where the resin and air material parameters are used. Secondly, it allows to easily track the flow front in the simulation domain. In OpenFOAM, Equation (14) is solved using the implemented scheme MULES (Multidimensional Universal Limiter with Explicit Solution) which is commonly used for different types of multiphase flow [22]. The treatment as two-phase flow is one difference to the commercially used finite-element formulations , where the Darcy-equation is only solved in the filled domain. Solving all governing equations for both fluids enables to better predict the formulation, movement, compression and dispersion of entrapped air in the cavity as also stated in the introduction chapter. Furthermore, because of its CFD based approach, it is possible to combine porous regions with non-porous regions and therefore using OpenFOAM can have advantages, for example when modeling race-tracking [9].

3. Finite-Volume CRTM Mold Filling Simulation Method and Implementation to OpenFOAM

3.1. Treatment of the Mesh Deformation during the Compression Step

As introduced before, in a CRTM process the compression step starts after injection of the desired amount of resin. In this compression step, the volume of the cavity decreases and the resin is squeezed through the fabric until a full infiltration of the preform is reached. The decrease of cavity volume leads to higher fiber volume fractions and therefore smaller permeabilities. To simulate the filling step of CRTM, this compression step has to be modeled subsequently to the injection step. In the presented method, the compression step is modeled based on a deformation and compression of the simulation mesh in vertical direction. The cavity gap height is considered small, so that the assumption can be made that the fibrous preform always completely fills the cavity and no empty channels form on top of the preform. Figure 1 shows schematically the deformation of a two-dimensional mesh during the compression step of a CRTM simulation. The vertical movement must be distributed uniformly to all elements to ensure a constant element deformation over the mesh height, while the number and connectivity of the elements is not changing during the compression step.

To realize the movement, the capability of the existing RTM solver [7] is extended to the use of dynamic meshes with the available “dynamicMesh” library, that offers different types of mesh motion solvers. The uniform deformation over the mesh height is guaranteed by solving a Laplace equation with a uniform diffusivity coefficient for the movement of the mesh nodes.

The change in cavity height leads to an increasing fiber volume fraction $\phi$ during the compression which is indicated by the colors in Figure 1. The equal distribution of the movement of the upper wall to all elements allows to evaluate fiber volume fraction based on element volumes. Knowing the initial fiber volume fraction ${\phi }_0$ and the initial volume $V_0$ of an element, the actual fiber volume fraction ${\phi }_i$ (or porosity ${\varphi }_i$) at each time step i can be calculated by

$${\phi }_i=(1-{\varphi }_i)={\phi }_0·\frac{V_0}{V_i}.$$

(15)

This equation is valid for all geometrical types of elements like triangles or rectangles but also for three-dimensional element types like tetrahedrons or hexahedrons. Additionally it can be used for calculation of the fiber volume fraction of elements inside inclined walls and therefore can be fully used for three-dimensional simulations of CRTM. With the calculated fiber volume fraction and a given fiber orientation, the local permeability at each cell is evaluated at each time step using one of the above mentioned analytic (Gebart, Equations (18) and (19)) or experimental values and finally the continuity and momentum equations are solved on the deforming mesh.

3.2. Modeling of the Fluid Velocity

As in all simulations where the fibrous preform is homogenized to a porous medium, the solid fibers are not explicitly dissolved which leads to the difference in the real physical and the volume averaged fluid velocity as e.g., pointed out by Papathanasiou [23]. The Darcy equation is defined with the volume averaged velocity $\tilde{\mathbf{v}}$

$$\tilde{\mathbf{v}}=\varphi \mathbf{v},$$

(16)

which is related to the actual fluid velocity by the porosity $\varphi$. In the present simulations by the finite-volume method the face fluxes ${\mathsf{\Phi }}_f$ (Equation (8)) are artificially divided by the face porosity ${\varphi }_f$, which is interpolated from the adjacent element centers

$${\mathsf{\Phi }}_{f,\mathrm{porous}}=\frac{{\mathsf{\Phi }}_f}{{\varphi }_f},$$

(17)

which accelerates the fluid velocity and therefore the flow front velocity to account for the already occupied volume by the fibers. As can be seen from Equation (17), for a porosity of 1, the approach yields the original equation for the flux ${\mathsf{\Phi }}_f$.

4. Verification of the CRTM Mold Filling Simulation Method

To verify the simulation method, we perform a benchmark for Injection-RTM to show the capabilities of the method used on a constant cavity geometry. In a second verification step, we extend the benchmark to Compression-RTM boundary conditions. We compare all the simulation results to analytic solutions of the Darcy equation and furthermore to solutions using the commercial mold filling software PAM-RTM^® by ESI Group.

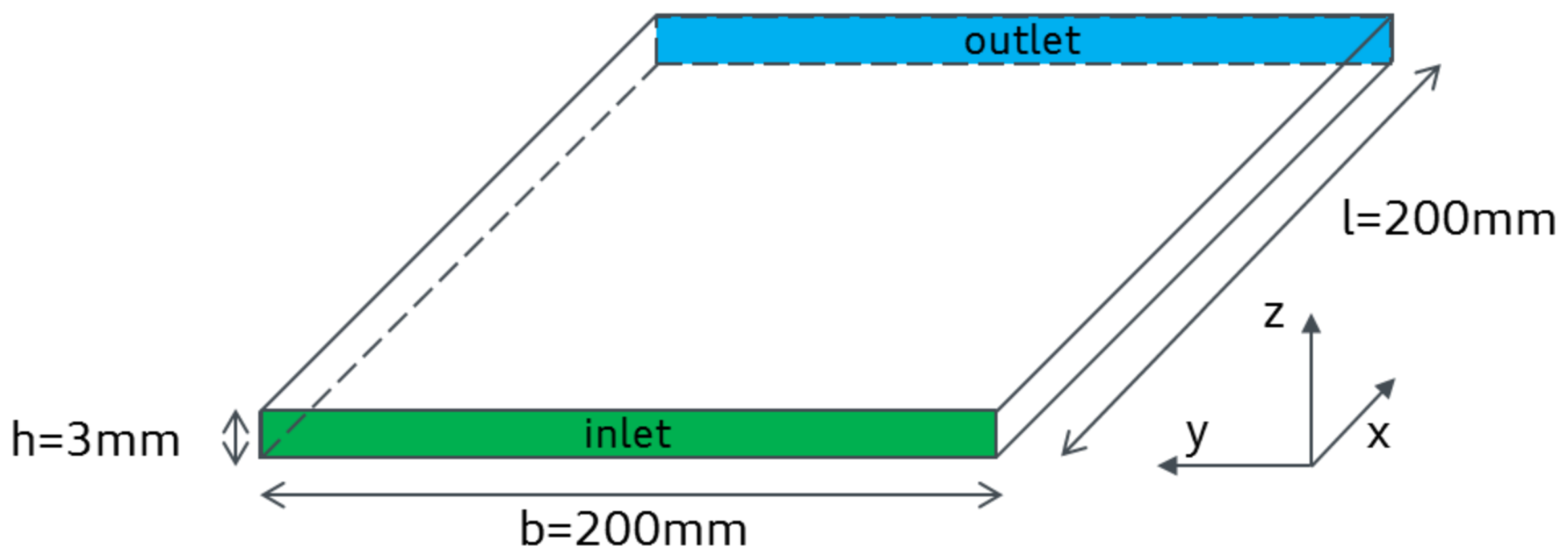
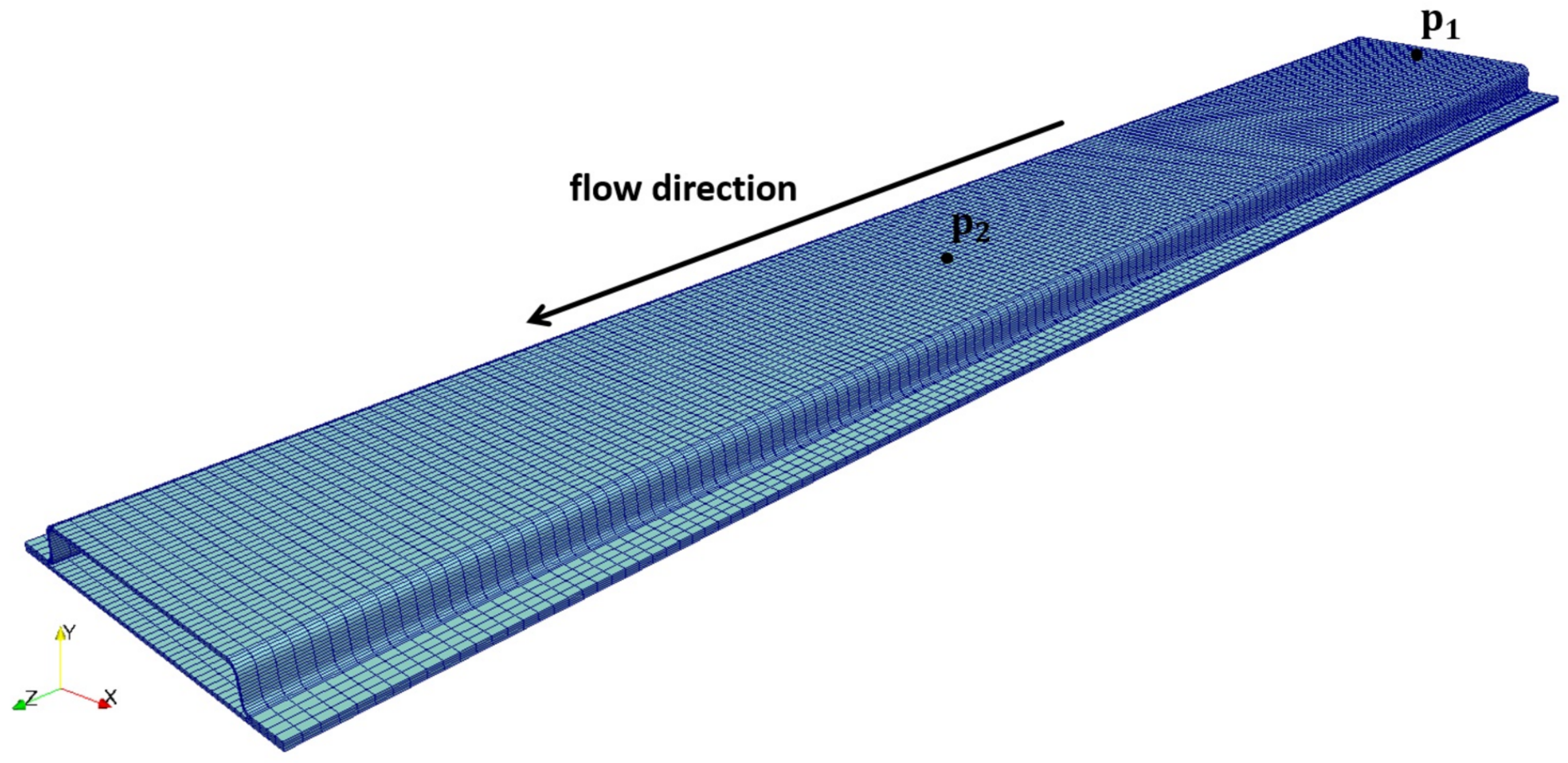
4.1. Simulation Model and Parameters

With the new CRTM simulation method, IRTM is simply be defined with a zero wall velocity at the upper part of the mold. Therefore, also IRTM can be simulated using the new solver.

A simple rectangular geometry of the size 200 mm × 200 mm × 3 mm is used as simulation domain (cf. Figure 2), which is meshed using hexahedrons and consists of 50 × 50 × 3 elements. The commercial software PAM-RTM^® only allows a two-dimensional CRTM simulation containing triangular elements. To compare the results to the finite-volume simulations, the triangular element size is chosen to have the same mean edge length in flow direction as the hexahedrons in the finite-volume simulation.

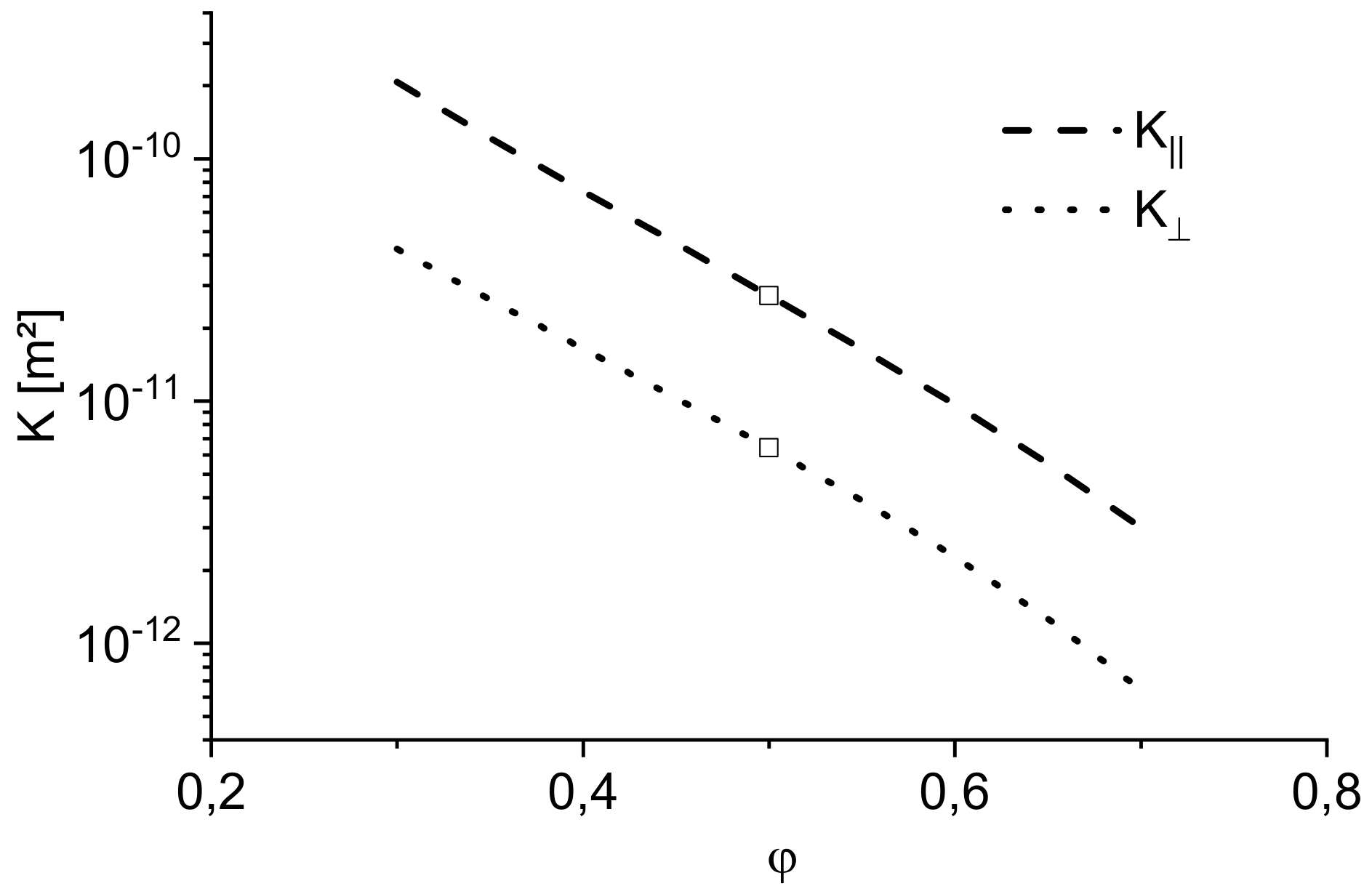
4.1.1. Material Parameters

The dependency of the permeability on fiber volume fraction is implemented based on the Gebart equations [24]

$$K_{\parallel }=A·\frac{{(1-\phi )}^3}{{\phi }^2}$$

(18)

$$K_{\perp }=B·{\left(\sqrt{\frac{{\phi }_{max}}{\phi }}-1\right)}^{5/2}$$

(19)

with the permeabilities $K_{\left|\right|}$ and $K_{\perp }$ for flow parallel and perpendicular to the fibers. In Equations (18) and (19), ${\phi }_{max}$ is the maximum fiber volume fraction for a quadratic or hexagonal fiber array, A and B are variables containing geometrical information of the fabric like effective fiber radius and fiber arrangement.

Permeability measurements of a non-crimp unidirectional reinforcement (Zoltek^TM, type: PX35UD0300) were carried out by process-oriented experiments using a unidirectional permeability test setup. In the experiments, the fibrous preform with a previously defined fiber volume fraction is placed in a rectangular plate mold made of stainless steel and a linear injection with constant pressure is performed. The advancement of the flow front is tracked with several pressure sensors that are integrated in flow direction into the mold. Details of the permeability measurements are explained in [25]. The results for the fiber-parallel and fiber-perpendicular permeabilities of a unidirectional carbon fiber preform at a fiber volume fraction of ${\phi }_{exp}=0.5$ are $K_{\perp ,exp}=6.40\times {10}^{-12}$ m${}^2$ and $K_{\parallel ,exp}=2.72\times {10}^{-11}$ m${}^2$, respectively. By applying these values to Equations (18) and (19) and assuming a hexagonal fiber arrangement with ${\phi }_{max}=90.69\%$, the values of A and B can be calculated, which allows for evaluating permeabilites for different fiber volume fractions. The resulting dependency of the permeability on fiber volume fraction and fiber orientation is shown in Figure 3. It should be stated here that this approach is not always valid for fibrous preforms because it is based on micro-scale assumptions; however, it is chosen to show the influence of an increasing fiber volume fraction on the permeability and thus on the resulting cavity pressure. It facilitates the calculation of the analytic solution of a one-dimensional Compression-RTM mold filling.

The initial fiber volume fraction is set to ${\phi }_{t=0s}=0.333$ and the fiber orientation is parallel to flow direction, so that $K_{\parallel }$ is used in the calculations. The dynamic viscosity of the resin is set to $\mu =0.113$ Pas.

4.1.2. Boundary Conditions

At the injection step, two cases are verified. First, a constant volume flow rate at the inlet of $q=4000$ mm³/s is applied. The injection time is 10 s which leads to a half filled cavity after the injection step. Second, a constant pressure of $3\times {10}^5$ Pa is set at the inlet until the cavity is half filled. In the compression step, the compression velocity is set to $v_{comp}=0.1$ mm/s so that the cavity is fully filled with a final height of $h_{t=20s}=2$ mm and a final fiber volume fraction of ${\phi }_{t=20s}=0.5$.

4.2. Analytic Solution

To verify the numerical simulations, we use an analytic solution of this filling process. The filling of a plate using a linear injection is a one-dimensional filling process (in x-direction), where the pressure distribution $p_{inj}(x,t)$ at the injection step and the pressure distribution $p_{comp}(x,t)$ at the compression step can be calculated with an analytic solution of the Darcy equation

$$p_{inj}(x,t)=\frac{v_x·\mu }{K_{\parallel }\left(h\left(t\right)\right)}·\left(X_f\left(t\right)-x\right)+p_0,$$

(20)

$$p_{comp}(x,t)=\frac{1}{2}\frac{v_{comp}}{h\left(t\right)}\frac{\mu }{K_{\parallel }\left(h\left(t\right)\right)}·\left(X_f{\left(t\right)}^2-x^2\right)+p_0,$$

(21)

with the injection velocity $v_x=q/\left(b·h\left(t\right)\right)$, the resin viscosity $\mu$, the permeability in x-direction $K_{\parallel }$ (which depends on the fiber volume fraction and therefore on the cavity height), the flow front position $X_f\left(t\right)$, the outlet pressure $p_0$, a constant compression velocity $v_{comp}$ and the cavity height $h\left(t\right)$. For a detailed derivation of these equations, see the Appendix A.

4.3. Simulation Results

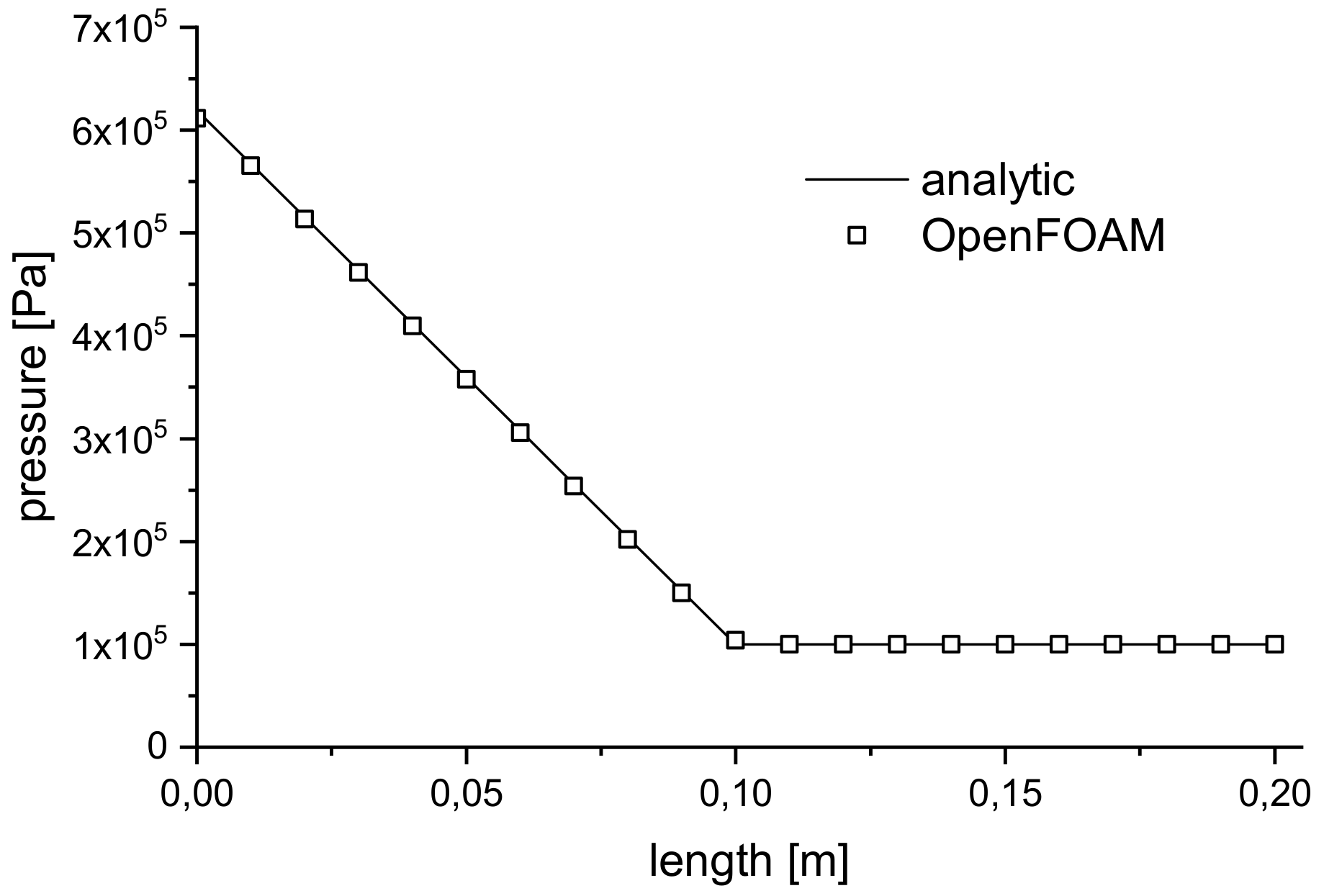
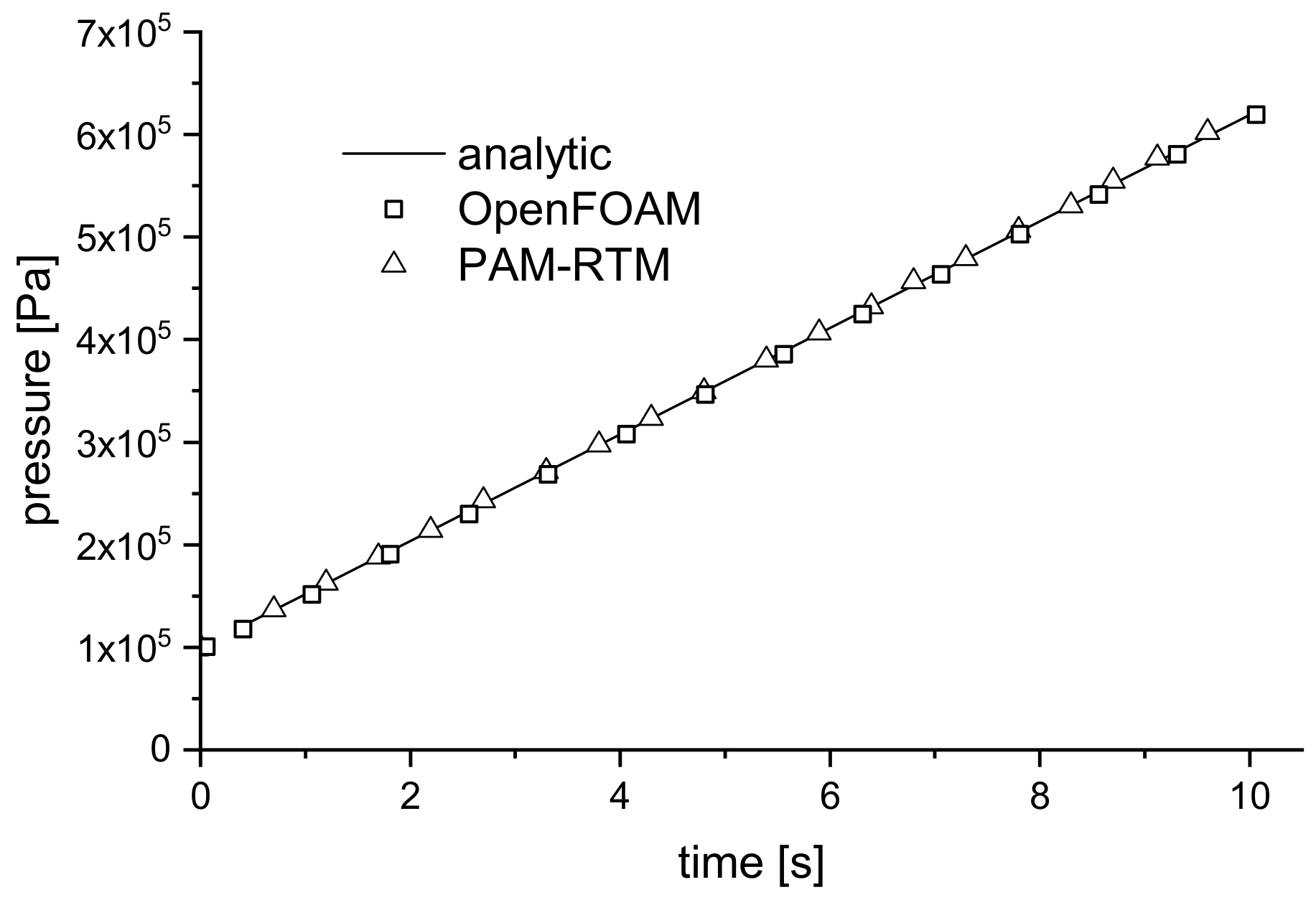
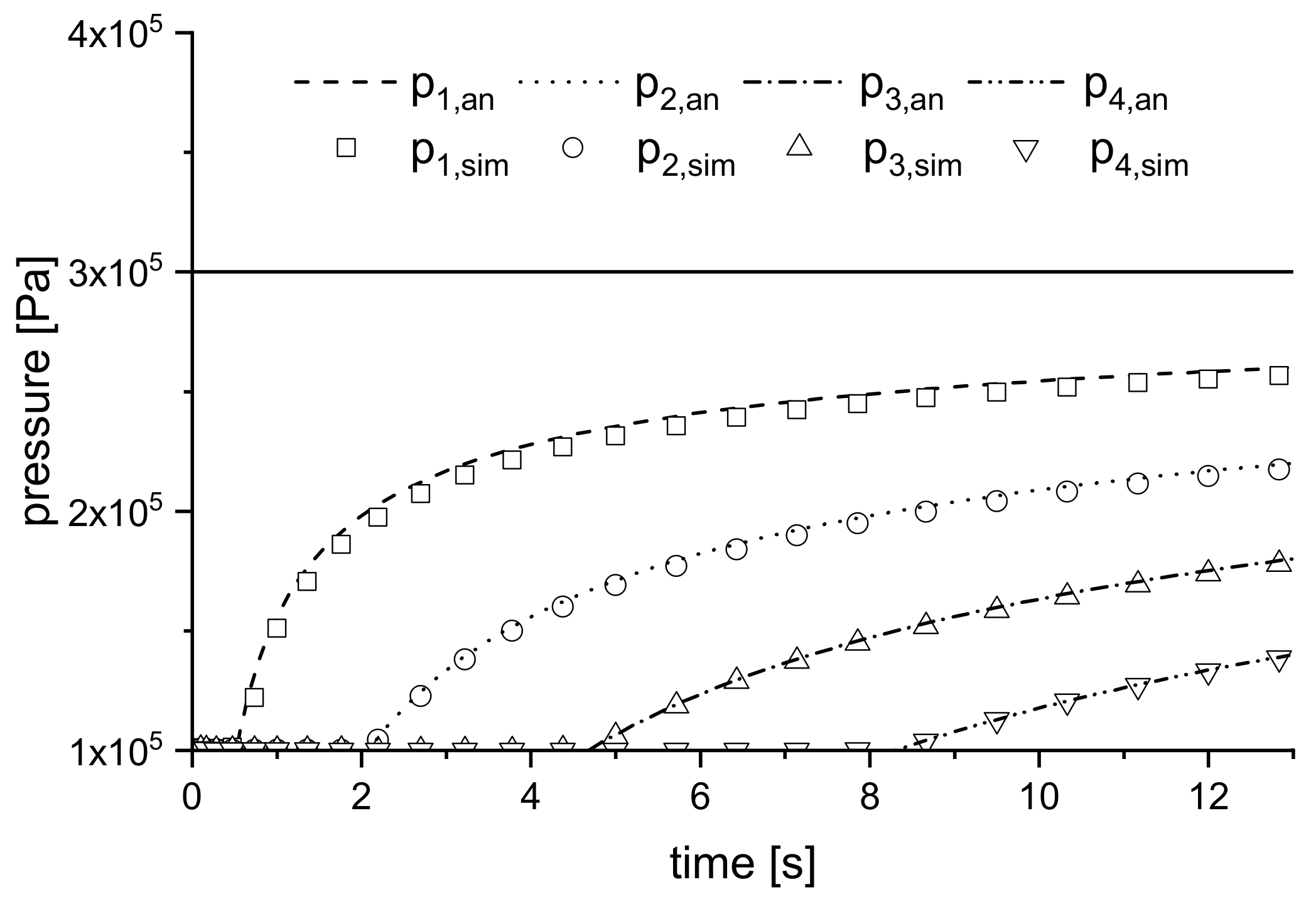
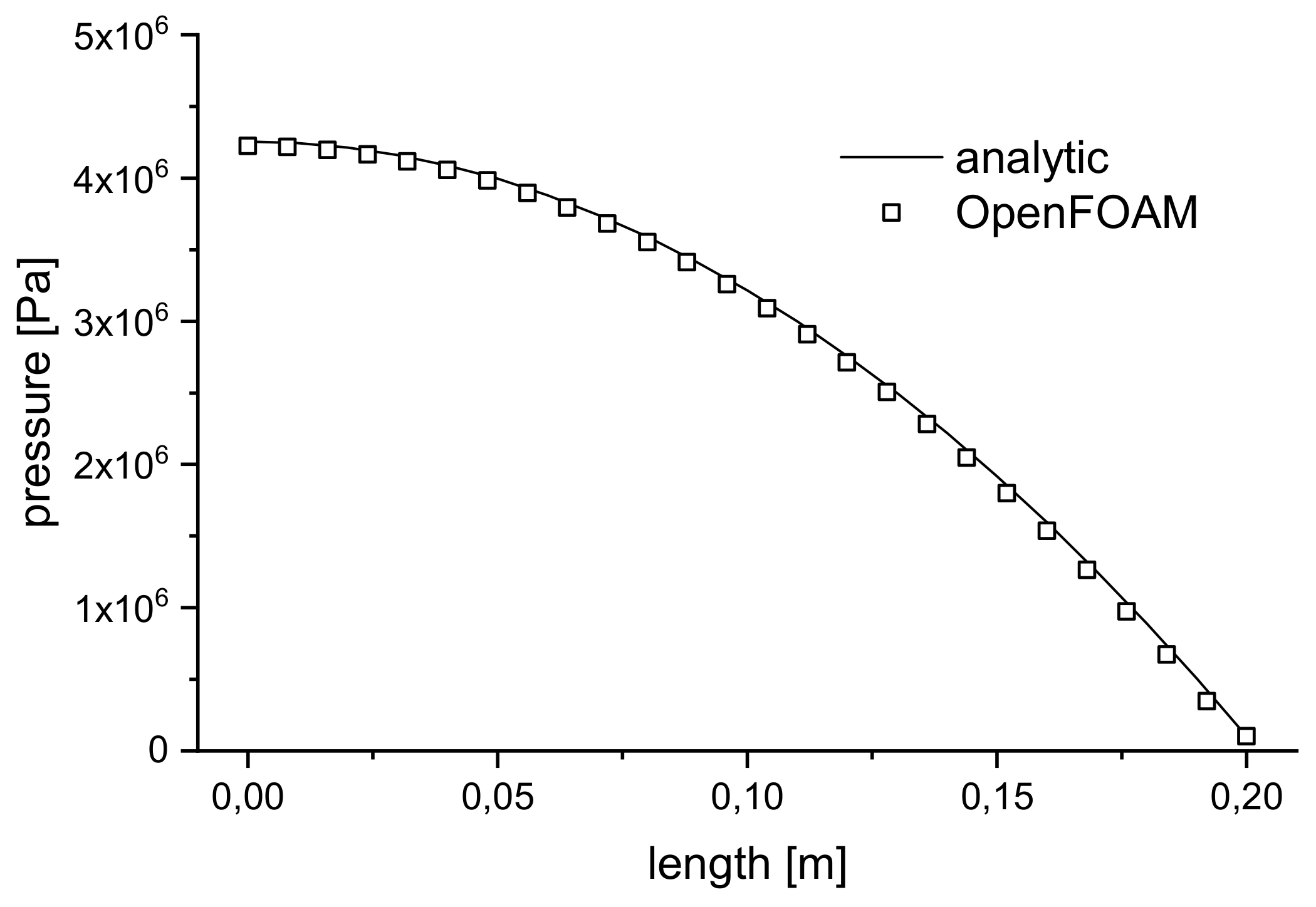
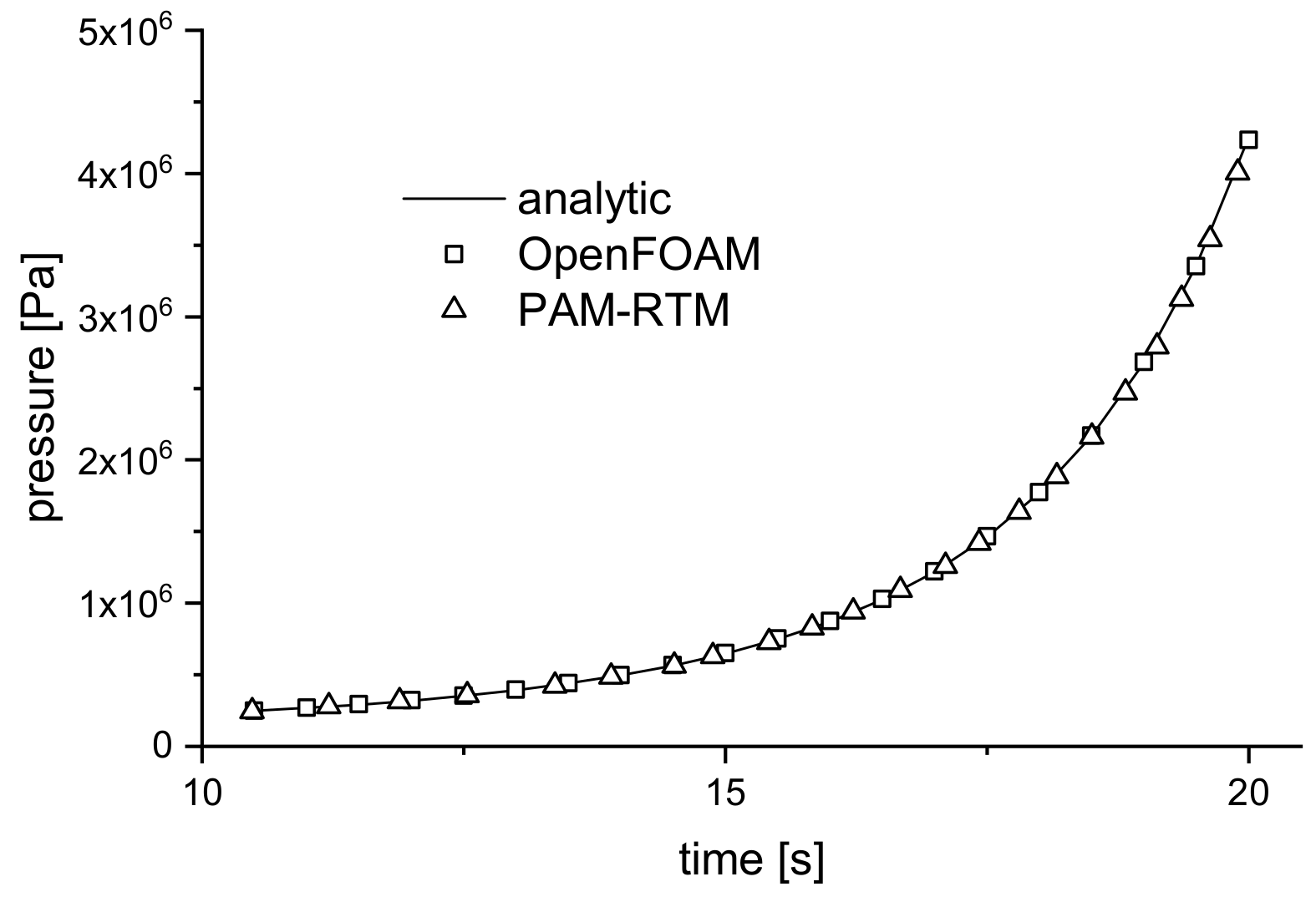
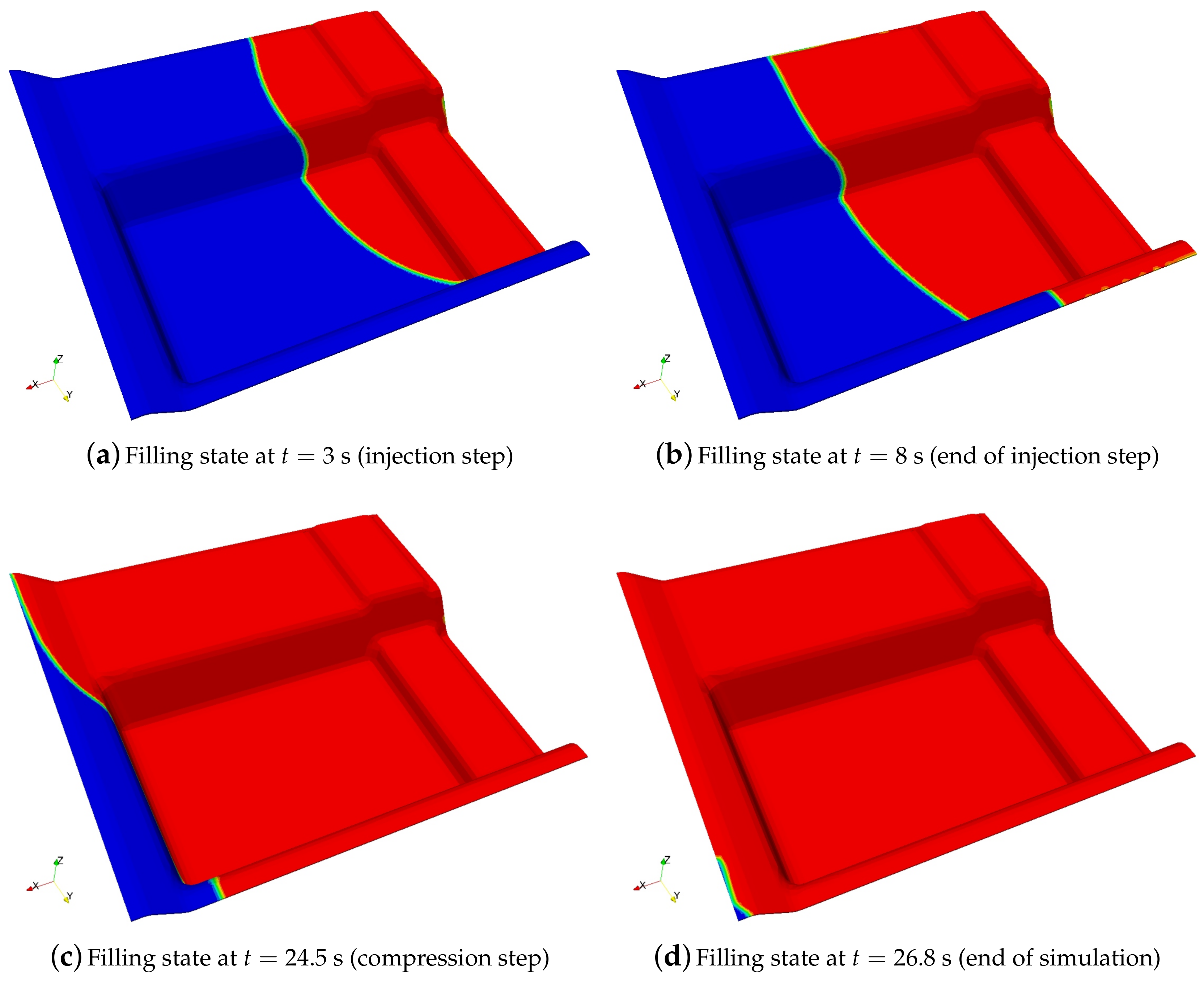
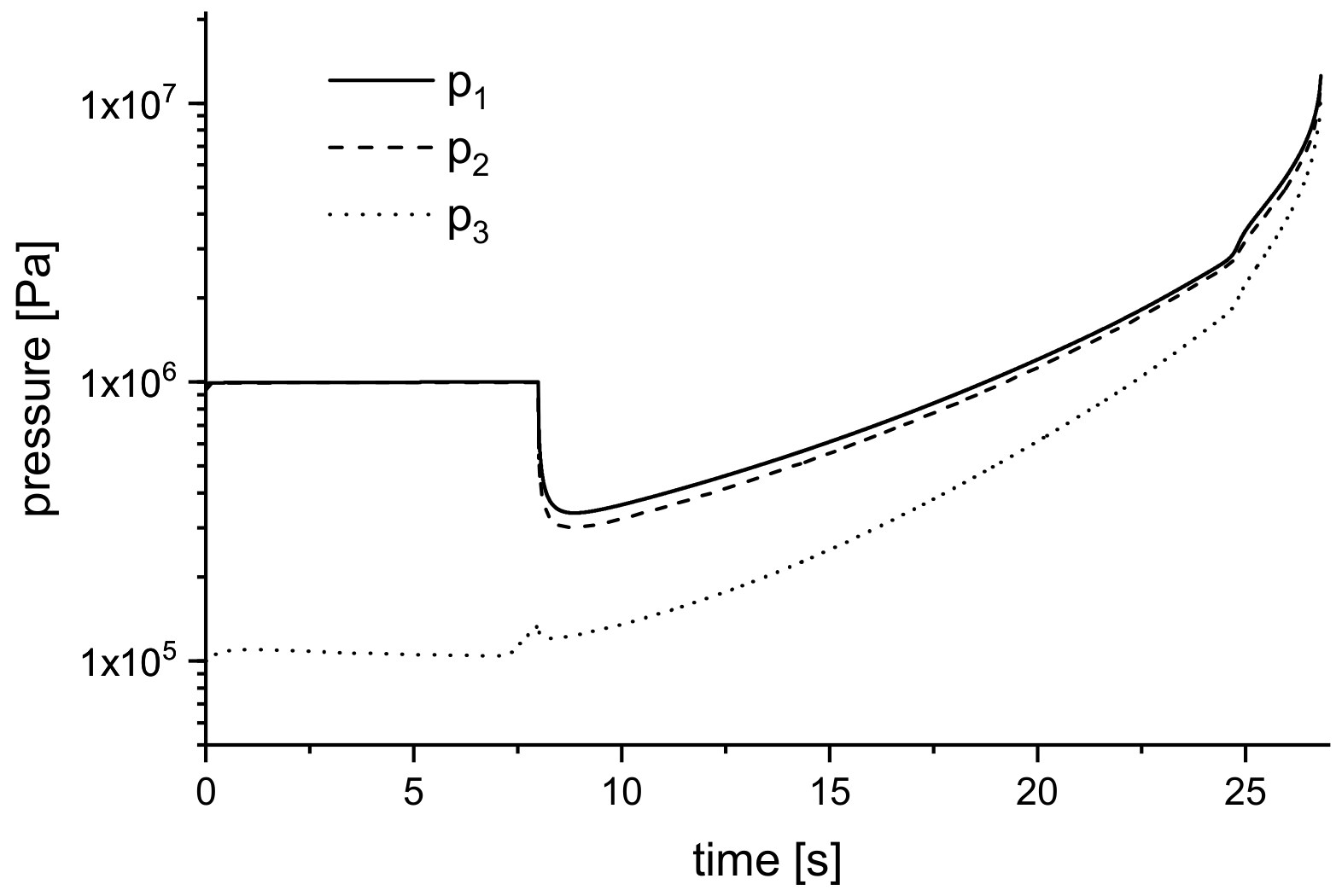
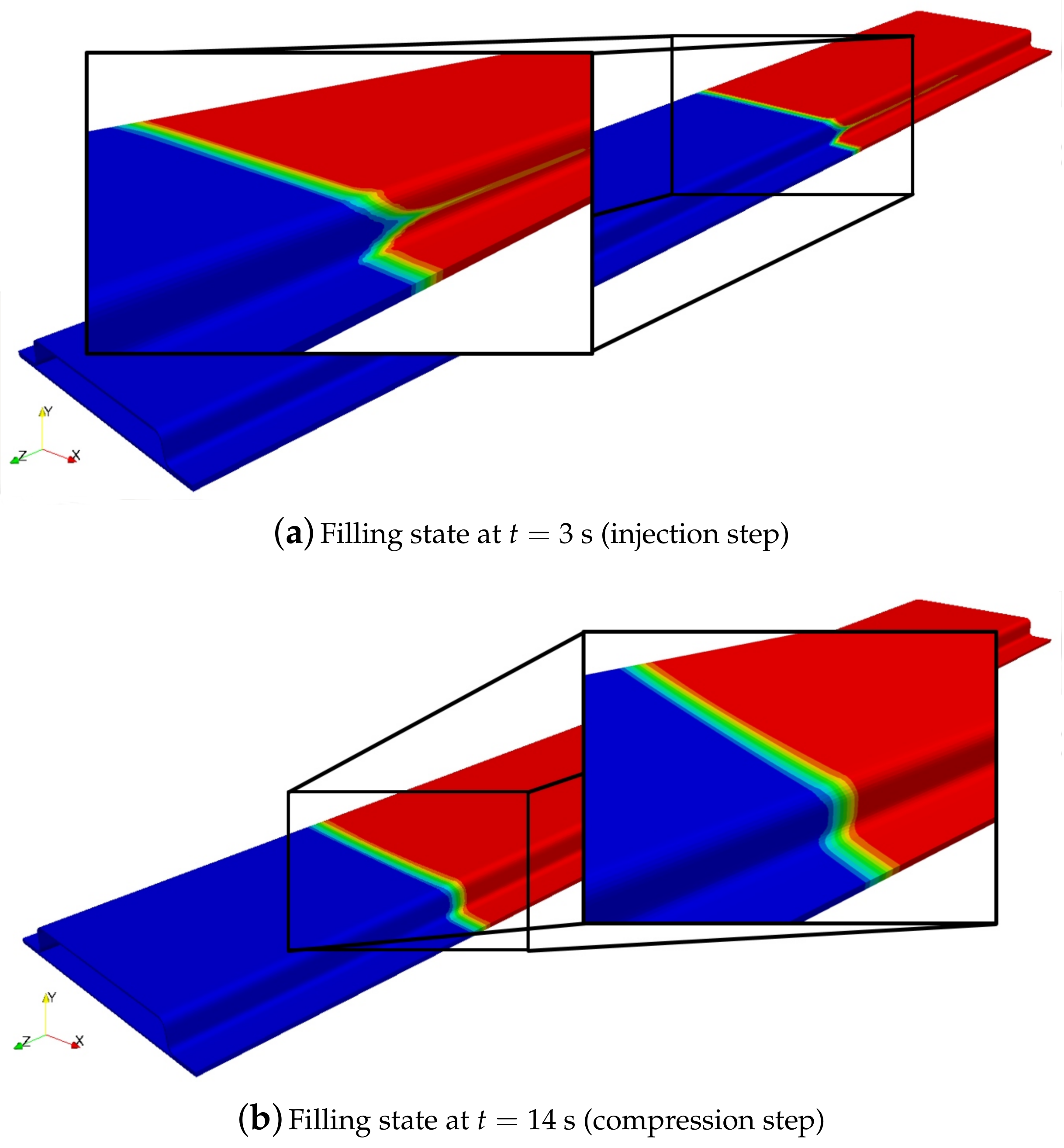
4.3.1. Results for Injection-RTM Boundary Conditions

First, the injection step of the process is calculated. To verify the solver, the pressure distribution of the simulation at the end of the injection is compared to the analytic 1D solution using Darcy’s law. The results are shown in Figure 4. The analytic solution and the simulation results agree perfectly and show a linearly increasing pressure distribution in the filled part between the flow front at $0.1$ m and the inlet, as expected from Equation (20).

Furthermore, the injection pressure at the inlet is evaluated. Figure 5 shows the solution of the OpenFOAM simulation in comparison with the numerical simulation using PAM-RTM^® and the analytic solution. The graphs show a linear increase of the injection pressure and all three graphs are indistinguishable.

Another relevant verification case is an injection using a constant inlet pressure boundary condition. Therefore, the simulated solutions using OpenFOAM and the analytically calculated solutions for this Injection-RTM setup are shown in Figure 6. The analytic filling time until a half-filled cavity is reached, is $12.98$ s. To show the pressure evolution in the cavity, the pressure is compared at four points in the cavity. Sensors $p_1$, $p_2$, $p_3$ and $p_4$ are located at a distance of $0.02$ m, $0.04$ m, $0.06$ m and $0.08$ m to the inlet, respectively. Again, the analytic solution matches almost exactly the simulated results.

4.3.2. Results for Compression-RTM Boundary Conditions

After the injection has stopped, the compression step starts with a constant compression velocity. The inlet is closed and set to a wall boundary condition, which leads to an immediate pressure drop at the beginning of the compression step. As for the injection step, again the pressure distribution at the end of the step is compared to the analytic solution, which is shown in Figure 7. As can be seen, the analytic pressure distribution as well as the simulation result show now a quadratic form (see Equation (21)).

Figure 8 shows the pressure development at the inlet position throughout the compression step. Again, the result of the OpenFOAM simulation agrees perfectly well with the analytic solution as well as with the solution of PAM-RTM^®.

Additionally, we performed a mesh study for the finite-volume simulation model which showed a fast convergence to the analytic solution with increasing element number in flow direction.

5. Application Examples of CRTM Mold Filling Simulations

To show the capabilities of the new three-dimensional finite-volume method, we present the simulation results of the filling of a complex geometry containing differently inclined walls and furthermore the filling of a sandwich part containing an embedded rigid core material.

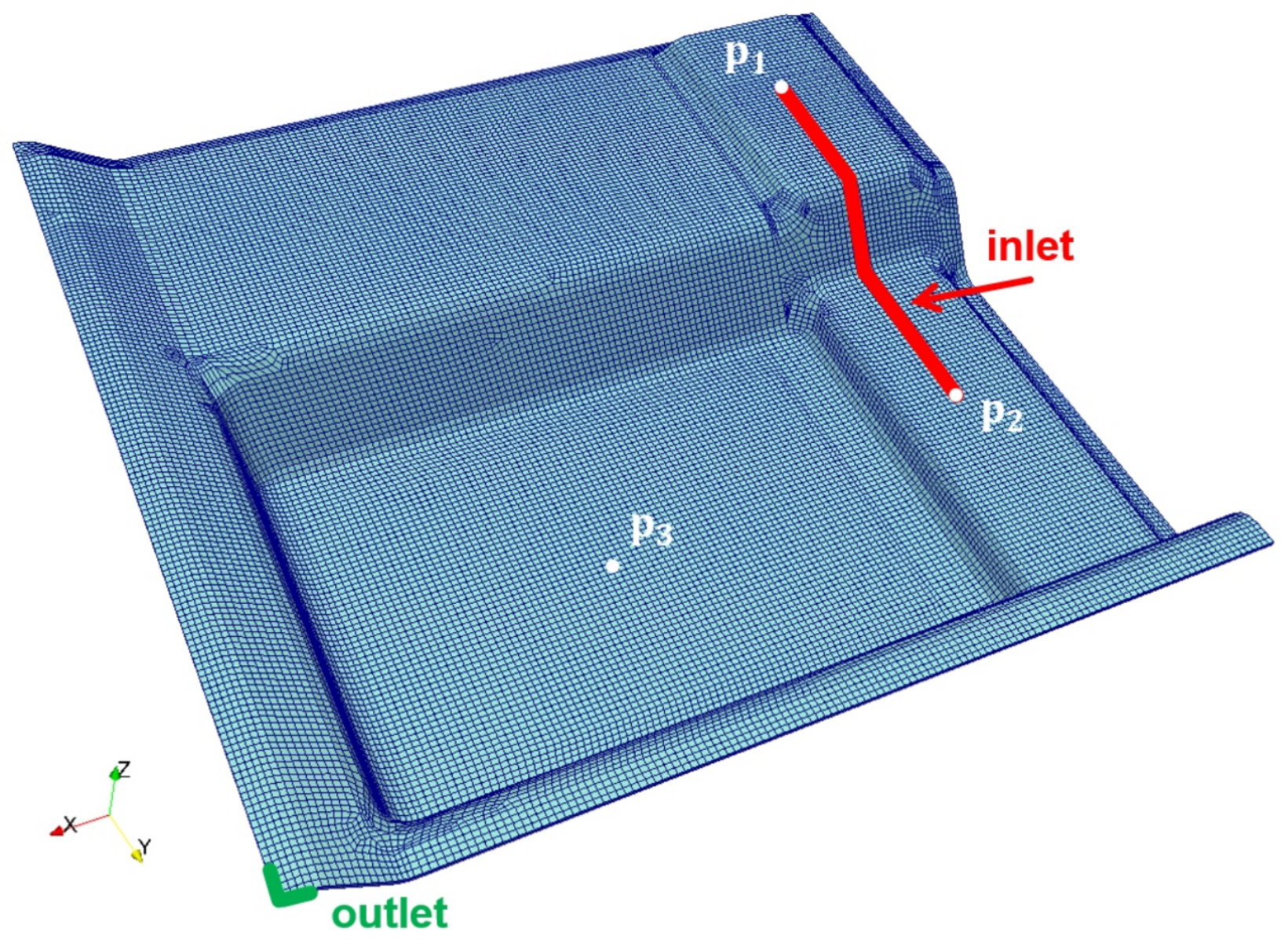
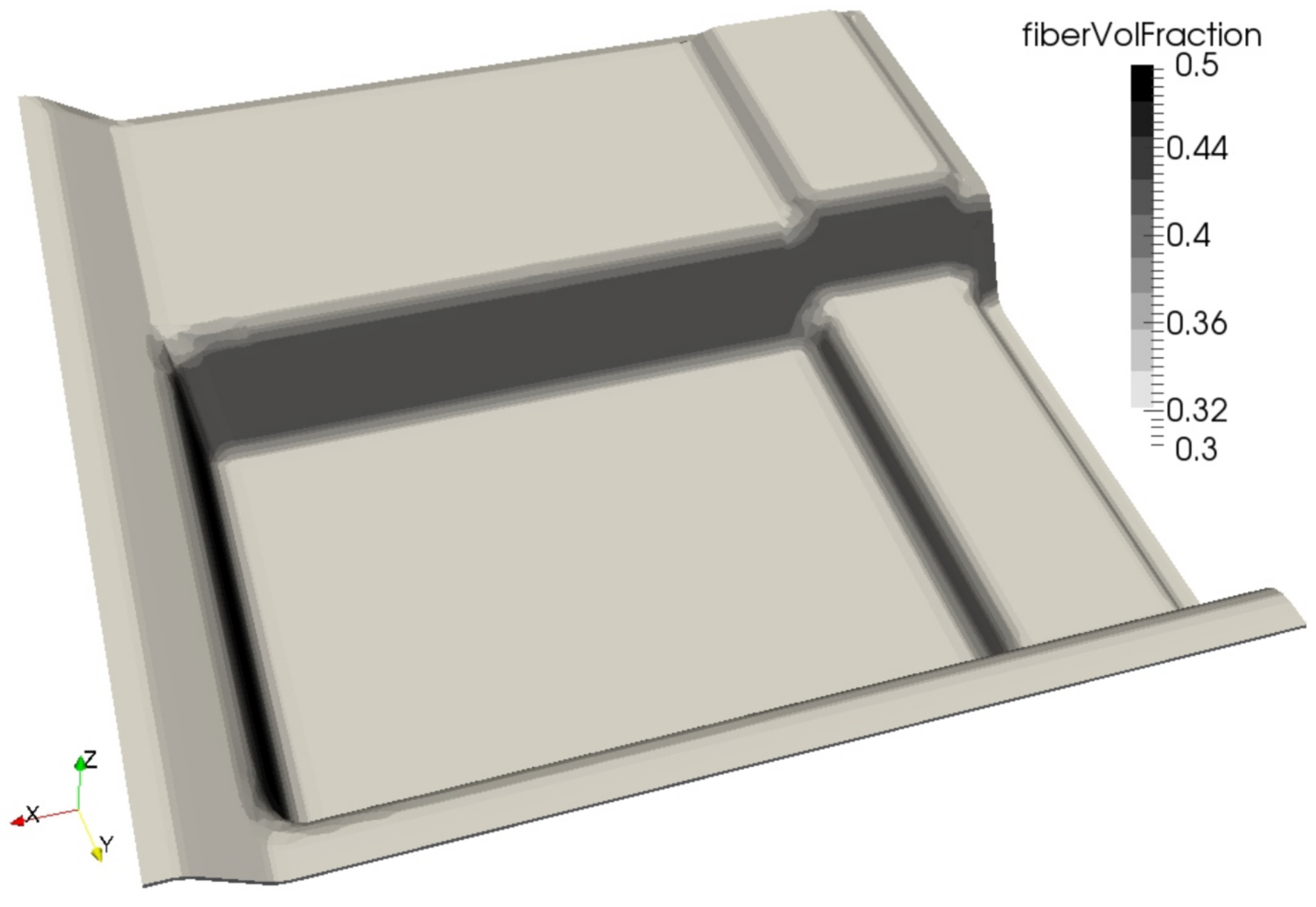
5.1. Application 1: Complex Geometry

Figure 9 shows the meshed geometry with inlet and outlet locations of the first application example. It consists of 52,250 hexahedrons and its overall size is approximately $0.7$ m × $0.7$ m. The average element size in-plane is 5 mm and two solid element layers are used. The permeability is again based on the experimental measurements (cf. Figure 3) and set to isotropic (based on $K_{\perp }$). Dynamic resin viscosity is set to $\mu =0.02$ Pas.

The final part thickness is 2 mm in the whole domain with a constant fiber volume fraction of $50\%$. The cavity opening at the beginning of the injection is 1 mm which leads to significantly lower fiber volume fractions at the beginning of the mold filling, especially in the horizontal parts of the cavity. Figure 10 shows the variation of the fiber volume fraction in the simulation domain. As can be seen, in the inclined walls, the fiber volume fraction is significantly higher than in the horizontal parts.

Ambient pressure at the outlet is set to $1\times {10}^5$ Pa and at the inlet a constant pressure of $10\times {10}^5$ Pa is set. After an injection time of 8 s, the calculated amount of resin is injected and the compression starts with a constant vertical velocity of $0.05$ mm/s. The pressure evolution is analyzed by introducing three pressure sensors into the part. Sensors $p_1$ and $p_2$ are located at the end of the linear inlet and sensor $p_3$ is located in the middle of the bottom horizontal part. Figure 11a shows the filling state at a process time of 3 s, shortly after the beginning of the injection. As can be seen, the high permeability caused by the low fiber volume fraction eases the resin flow in the horizontal parts. At the inclined walls, the fluid velocity is smaller and therefore the flow front lacks behind. The second Figure 11b shows the filling state at 8 s, so at the end of the injection, where the influence of the different permeabilities in horizontal and inclined parts is also still slightly visible. Figure 11c shows the filling state at 24.5 s of simulation time. The flow front is now very homogeneous in the whole part. Finally Figure 11d shows the filling state at the last time step of the simulation, where the part is fully filled and only at the outlet boundary a small area of air phase is still visible which is caused by the stop of the simulation at a filling grade of 99.9%. Total mold filling time is 26.8 s.

Comparing the pressure evolution of the three embedded sensors (Figure 12), the drop in cavity pressure at the change from injection to compression boundary conditions at 8 vs is obvious. Sensor 3 shows a small peak shortly before the change from compression to injection which is caused by the arriving resin front. It is also visible, that there is a sharp increase of the pressure at about 25 s, which indicates the flow front arriving the left back wall (shortly after the filling state visualized in Figure 11c), which changes the whole pressure field in the filled domain.

5.2. Application 2: Sandwich Part

The second example is a mold filling simulation of a sandwich part with a rigid core embedded between the fiber layers. This kind of simulation is not possible using a two-dimensional (or 2,5-dimensional) simulation with shell elements. The part has a length of 1.13 m and is 0.2 m wide. The final layer thickness above and under the core material is 1.35 mm each and the height of the core is 22 mm. An equal layer thickness for above and under the core material is assumed for all process steps, so that the rigid core material stays in the middle of the cavity. The resulting fiber volume fraction of the part at the end of the compression step is again set to 50%.

At the beginning of the simulation the mold opening of the cavity is set to 1.5 mm. The geometry with boundary conditions and the included two pressure sensors $p_1$ and $p_2$ is shown in Figure 13 and the resulting fiber volume fraction is shown in Figure 14. The fiber volume fraction at the inclined walls is still close to 50% whereas in the horizontal parts the fiber volume fraction is about 33%. The mesh contains of 39,300 hexahedrical elements. The element size in flow direction is 7.5 mm and two solid element layers at each side of the core are used, which leads to four element layers in the monolithic regions. At the injection step a constant inlet resin velocity of $0.1$ m/s is set. Permeability and viscosity are equal to the first application example.

As can be seen in Figure 15, there is a visible delay of the flow front in the sidewalls of the part during the injection step. This is because of the resulting lower permeability of the sidewalls than in the horizontal parts.

The pressure evolution of the embedded sensors (Figure 16) shows the characteristics of a uniform mold filling as in the plate geometry. A linear increase in pressure in the injection step is followed by a pressure drop and a non-linear increase in the compression step. The flow front reaches sensor $p_2$ after approximately 3.7 s and the total mold filling time is 17.6 s.

6. Summary and Conclusions

A three-dimensional formulation is necessary to enable a CRTM mold filling simulation for complex components and sandwich geometries with a core material embedded between the reinforcement layers. Here, we presented a mold filling simulation method based on a three-dimensional finite-volume formulation. This CRTM mold filling simulation method is implemented into the OpenFOAM framework. The verification of an unidirectional flow shows excellent agreement with analytic solutions and solutions of a commercial mold filling software. By directly adjusting the flux and therefore the fluid velocity with the porosity, the resin flow front propagation can be correctly simulated. The application examples show the possibility to simulate complex geometries using this method including differently inclined walls and a between the fiber layers embedded rigid core material.

This method is the first step towards mold filling simulations of many more process applications as for example CRTM with non-constant compression velocities or a modeling of articulated molds. Also pressure controlled CRTM process variants can be simulated by adjusting the boundary on the upper surface of the cavity to a formulation depending on local cavity pressure. Even a further development to simulate three-dimensional mold filling including the influence of deforming core materials is possible based on this method. All these future application examples show the capability of the presented mold filling simulation method. One major future improvement of this method has to be the implementation of an open gap above the preform, which can occur at great mold openings in the injection stage.