Manufacturing Design and Analysis of Bending Technology by the Variation of the Initial Technological Parameters
Abstract
1. Introduction
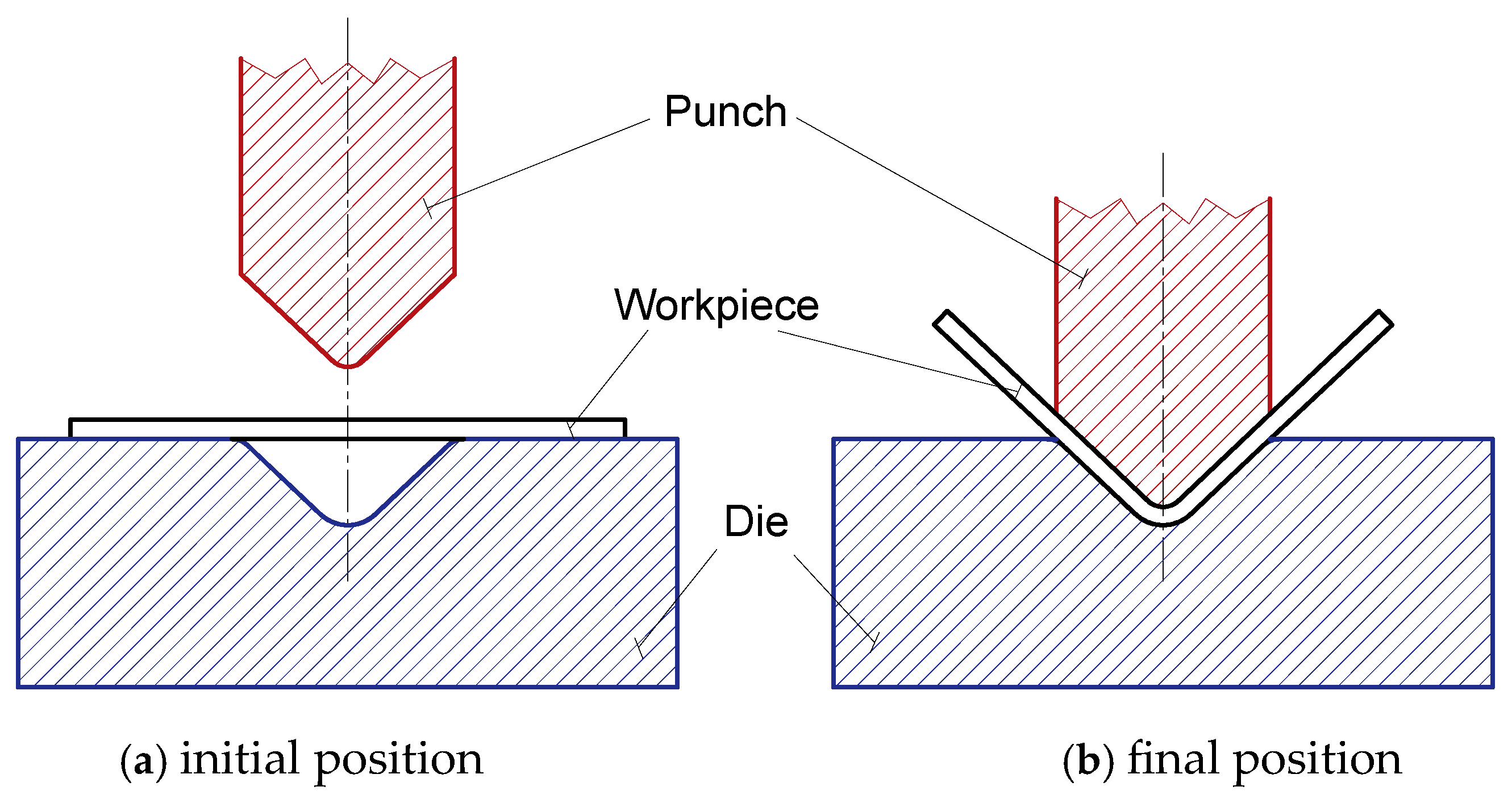
2. Materials and Methods
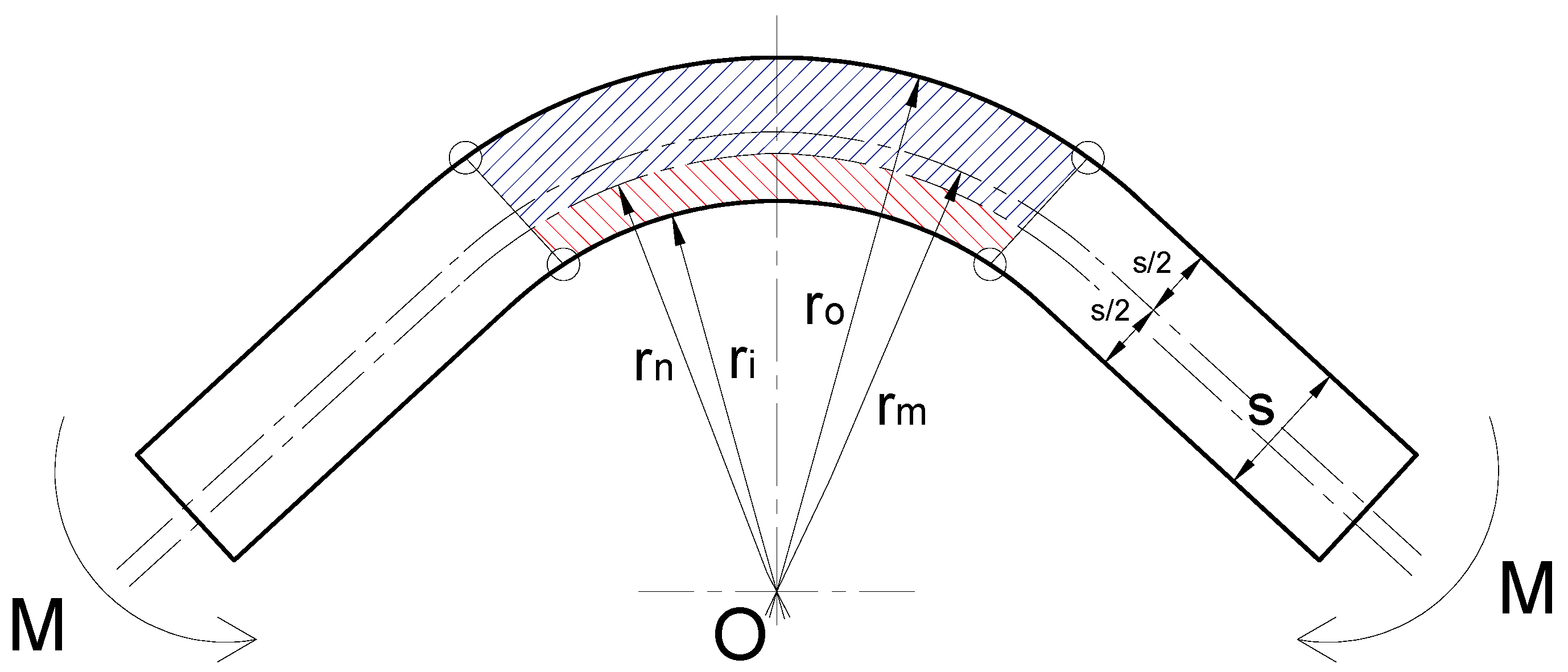
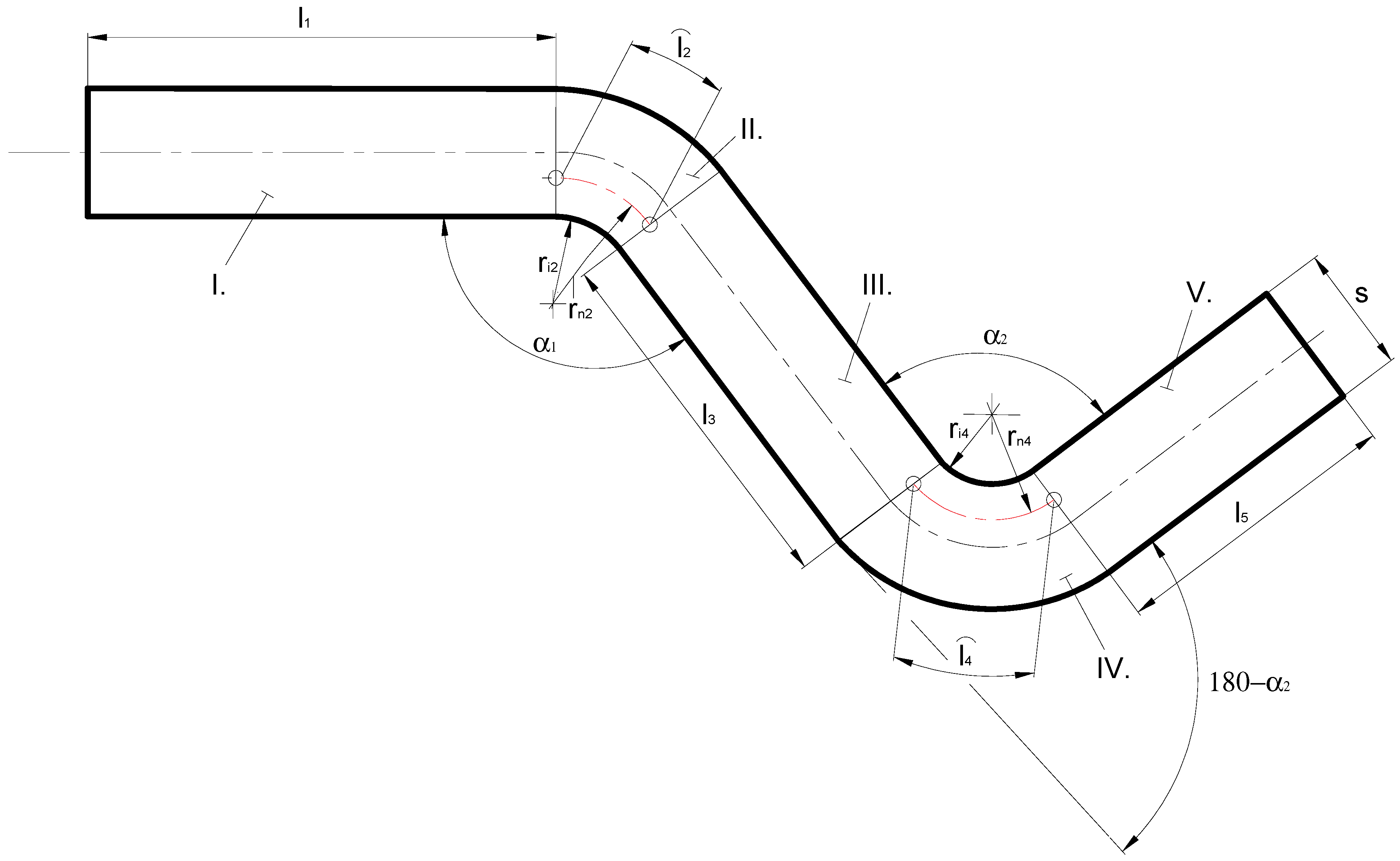
2.1. Determination of the Cover Length
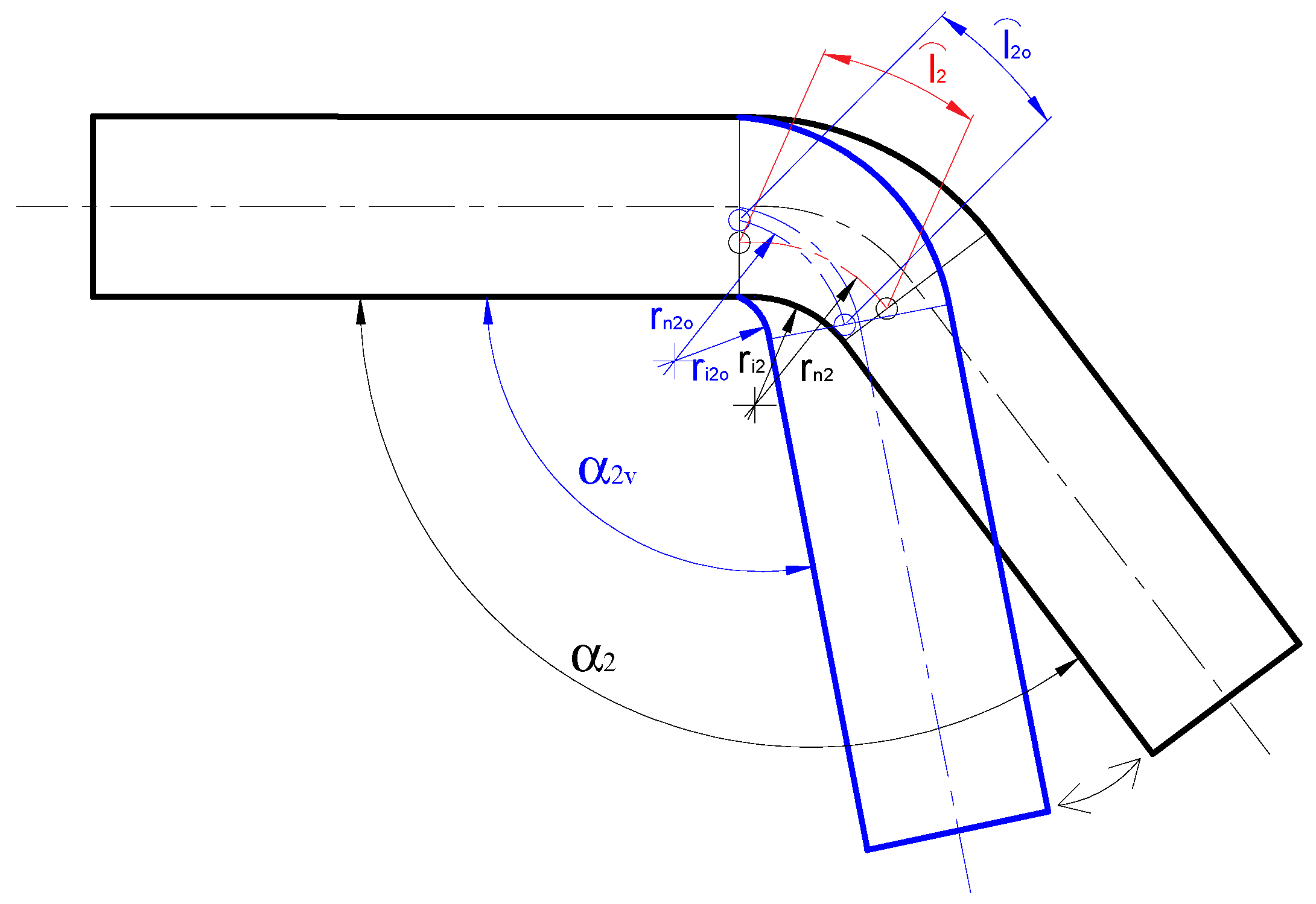
2.2. Springback Phenomenon
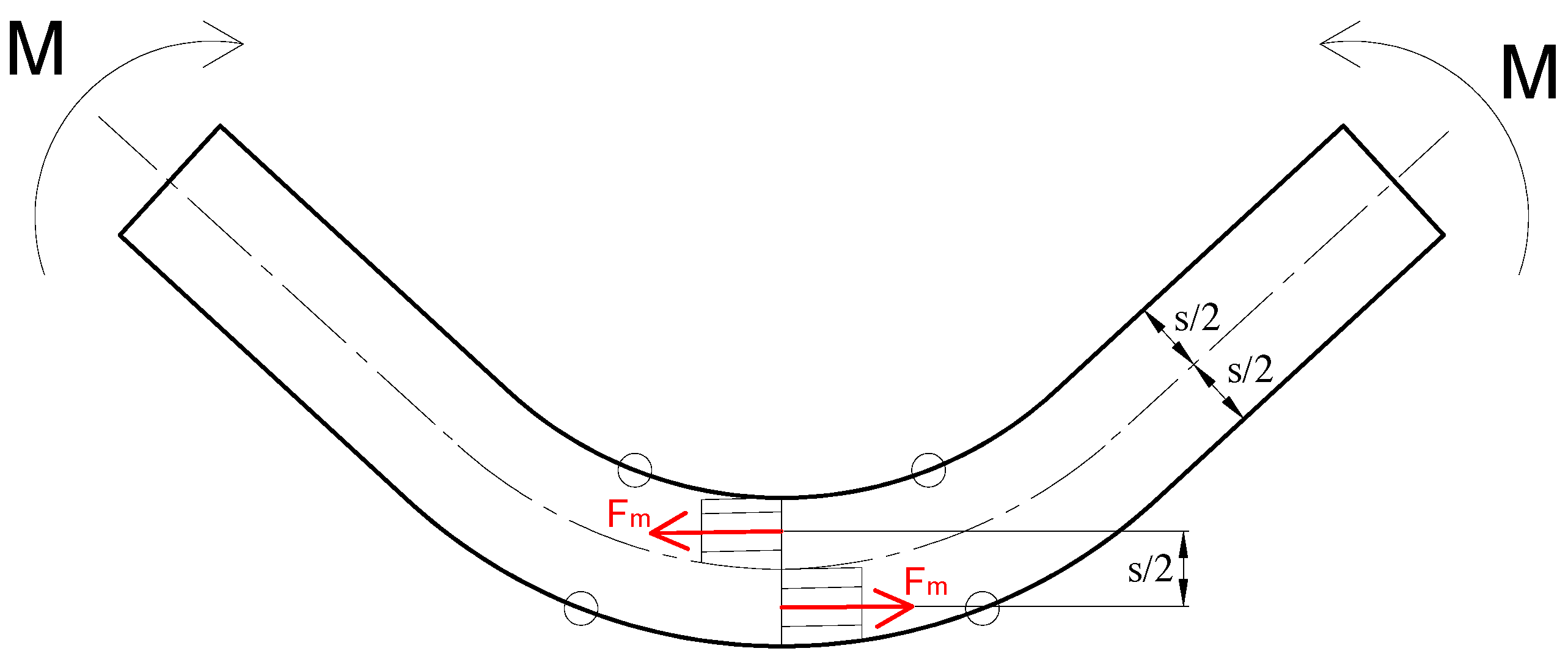
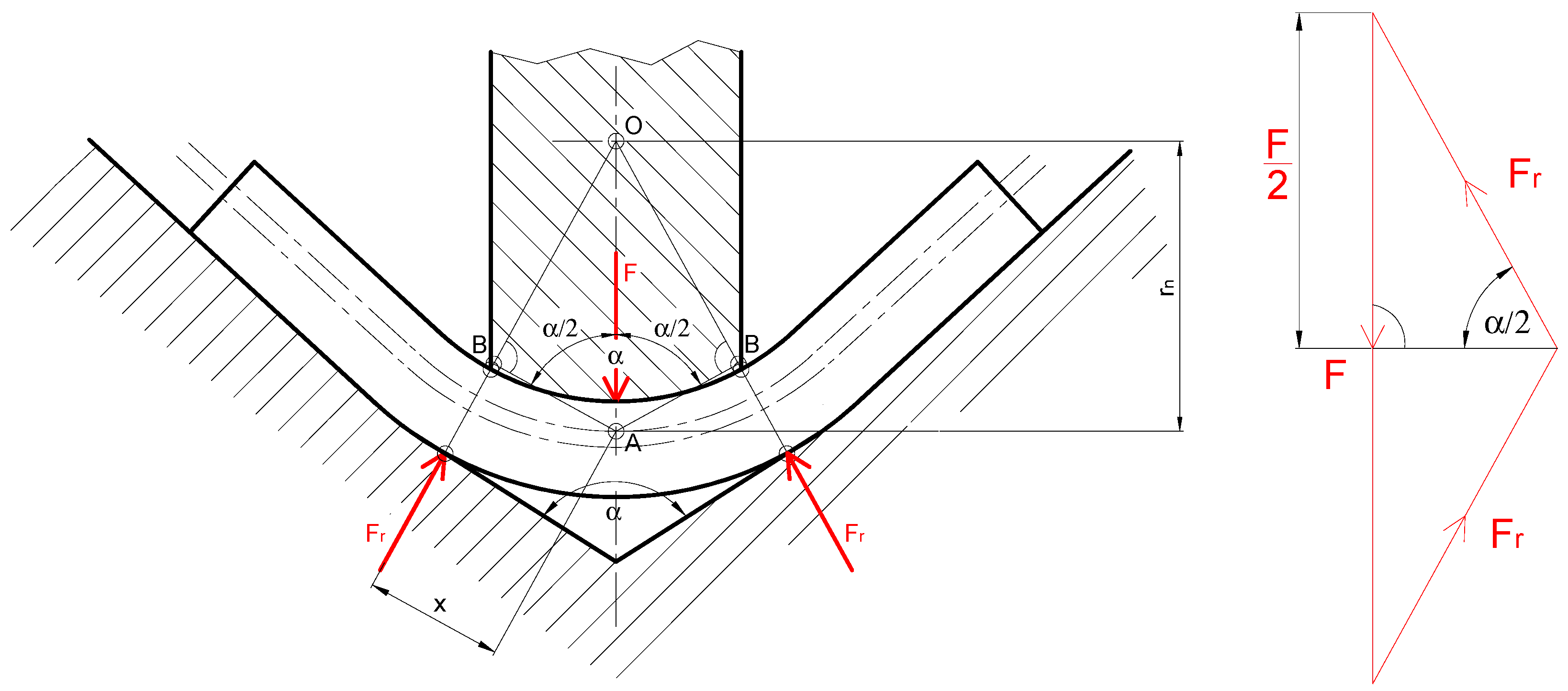
2.3. Determination of the Bending Force and Bending Torque
3. Results
3.1. Experiment I
3.2. Experiment II
3.3. Experiment III
3.4. Experiment IV
4. Discussion
- Finite Element Analysis (FEA) during the metal forming process can be conducted using either a static or dynamic approach. In the static method, the analysis assumes that the load is applied slowly and steadily, without considering inertial effects, which is suitable for processes where deformation occurs gradually. On the other hand, the dynamic method takes into account time-dependent factors, including inertia and impact forces, making it more appropriate for high-speed or sudden deformation processes. The choice between static and dynamic analysis depends on the specific characteristics of the forming operation being studied.
- Various types of bending tools can be designed and modeled depending on the specific requirements of the bending process. These tools can be tailored to different material properties, bending angles, and product geometries. Through computer-aided design (CAD) and simulation techniques, such as Finite Element Analysis (FEA), the performance of these tools can be evaluated and optimized before physical production. This allows for improved accuracy, reduced material waste, and enhanced process efficiency in practical applications.
- A wider range of materials can be analyzed to investigate how different technological parameters—such as bending speed, tool geometry, temperature, and material thickness—affect their behavior during the forming process. By conducting simulations or experiments on various materials, the influence of these parameters can be thoroughly examined. The results can then be compared to identify material-specific responses, optimize process conditions, and support the selection of the most suitable material for a given application. This comparative analysis contributes to a better understanding of material performance and process efficiency.
- The manufacturing design and detailed analysis of the individual components of the designed bending tool can also represent a valuable and promising research direction. This includes the geometric and material design of parts such as punches, dies, and supports, as well as their structural behavior under operational loads. By applying advanced modeling techniques, such as CAD and Finite Element Analysis (FEA), researchers can optimize the tool components for durability, precision, and performance. Additionally, studying the manufacturing processes used to produce these components—such as machining, heat treatment, or surface finishing—can further enhance the overall efficiency and quality of the bending tool system.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Name | Unit |
| arc length | [mm] | |
| b | sheet width | [mm] |
| F | the necessary bending force | [N] |
| Fm | internal force | [N] |
| Fr | the reaction force of the die | [N] |
| K | springback factor | |
| k, j | running index numbers | |
| kf | flow stress | [MPa] |
| L | cover length | [mm] |
| l | length of the linear section on the part | [mm] |
| M | bending torque | [Nm] |
| Mi | internal torque | [Nm] |
| Mo | external torque | [Nm] |
| O | bending center point | |
| ri | inner bending radius | [mm] |
| ri_v | modified inner bending radius | [mm] |
| rm | middle radius | [mm] |
| rn | neutral radius | [mm] |
| ro | outer bending radius | [mm] |
| s | sheet thickness | [mm] |
| x | the distance between the line of action of the reaction force of the die and the intersection point of the center line of the punch and the neutral strand | [mm] |
| α | bending angle | [°] |
| α_v | modified bending angle | [°] |
| β | β factor of the workpiece material | |
| ξ | bending factor |
References
- Skriba, Z. Fémek Képlékeny Alakítása, 3rd ed.; Tankönyvkiadó: Budapest, Hungary, 1966; p. 429. [Google Scholar]
- Gulyás, J.; Pintér, K.; Kiss, E.; Reisz, G.; Mecseki, I.; Tóth, L.; Voith, M. Képlékenyalakítás; Tankönyvkiadó: Budapest, Hungary, 1987; p. 691. ISBN 963 17 9492 X. [Google Scholar]
- Yang, H.; Li, H.; Zhang, Z.; Zhan, M.; Liu, J.; Li, G. Advances and Trends on Tube Bending Forming Technologies. Chin. J. Aeronaut. 2012, 25, 1–12. [Google Scholar] [CrossRef]
- Gantner, P.; Bauer, H.; Harrison, D.K.; De Silva Anjali, K.M. Free-Bending—A new bending technique in the hydroforming process chain. J. Mater. Process. Technol. 2005, 167, 302–308. [Google Scholar] [CrossRef]
- Gantner, P.; Harrison, D.K.; De Silva, A.K.M.; Bauer, H. New Bending Technologies for the Automobile Manufacturing Industry. In Proceedings of the 34th International MATADOR Conference, Manchester, UK, 7–9 July 2004; Hinduja, S., Ed.; Springer: London, UK, 2004. [Google Scholar] [CrossRef]
- El-Aty, A.A.; Guo, X.; Lee, M.-G.; Tao, J.; Hou, Y.; Hu, S.; Li, T.; Wu, C.; Yang, Q. A review on flexibility of free bending forming technology for manufacturing thin-walled complex-shaped metallic tubes. Int. J. Lightweight Mater. Manuf. 2023, 6, 165–188. [Google Scholar] [CrossRef]
- Liang, J.; Gao, S.; Teng, F.; Yu, P.; Song, X. Flexible 3D stretch-bending technology for aluminum profile. Int. J. Adv. Manuf. Technol. 2014, 71, 1939–1947. [Google Scholar] [CrossRef]
- Li, Y.; Han, X.; Liang, J.; Teng, F.; Liang, C. Effect of multi-point roller dies on the forming accuracy of profile in flexible 3D stretch bending technology. Int. J. Adv. Manuf. Technol. 2021, 112, 897–905. [Google Scholar] [CrossRef]
- Zaragoza, V.G.; Strano, M.; Iorio, L.; Monno, M. Sheet metal bending with flexible tools. Procedia Manuf. 2019, 29, 232–239. [Google Scholar] [CrossRef]
- Yang, J.-B.; Jeon, B.-H.; Oh, S.-I. The tube bending technology of a hydroforming process for an automotive part. J. Mater. Process. Technol. 2001, 111, 175–181. [Google Scholar] [CrossRef]
- Chen, H.; Wang, H.; Abd El-Aty, A.; Qin, Y.; Li, J.; Zhang, Y.; Li, T.; Guo, X. Impact of bending dies with different friction forms on forming force and quality of tubes manufactured by free bending technology. Chin. J. Aeronaut. 2021, 34, 253–264. [Google Scholar] [CrossRef]
- Welo, T.; Wideroe, F. Precision bending of high-quality components for volume applications. Trans. Nonferrous Met. Soc. China 2010, 20, 2100–2110. [Google Scholar] [CrossRef]
- Yang, S.; Li, Y.; Liang, J.; Wen, Y.; Liang, C.; Han, Q. Adaptive multi-point flexible-bending technology for improving the quality of profile using discrete dies driven by snake-shaped motion mechanism. J. Mater. Process. Technol. 2024, 325, 118297. [Google Scholar] [CrossRef]
- Stiller, T.; Kerschbaumer, R.C.; Waly, C.; Zink, B.; Slapnik, J.; Pinter, G. Investigating the influence of bending stiffness and processing parameters on single-leg bending geometries of additively manufactured composites. Results Eng. 2024, 24, 103276. [Google Scholar] [CrossRef]
- Karfidov, A.O.; Chichenev, N.A.; Vasil’ev, M.V.; Chicheneva, O.N. Production of arc sheet elements by stepped bending method. Izvestiya. Ferr. Metall. 2025, 68, 233–238. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Y.; Chen, W.; Yuan, C.; Wang, L. Advanced Bending and Forming Technologies for Bimetallic Composite Pipes. Materials 2025, 18, 111. [Google Scholar] [CrossRef] [PubMed]
- Ahemad, M.W.; Palani, I.A.; Joshi, S.S. Investigation on multiple bending using laser forming of mild steel plate and its bend angle prediction. J. Micromanuf. 2025. [Google Scholar] [CrossRef]
- Neuman, W.L. Social Research Methods: Qualitative and Quantitative Approaches, 7th ed.; Pearson Education Limited: Harlow, UK, 2014; ISBN 9781292020235. [Google Scholar]
- Patton, M.Q. Qualitative Research & Evaluation Methods, 3rd ed.; Sage Publications: Thousand Oaks, CA, USA, 2002; ISBN 9780761919711. [Google Scholar]
- Hunyady, G. (Ed.) Társadalomtudományi Kutatások Módszertana; Osiris Publisher: Budapest, Hungary, 2002; ISBN 963389429X. [Google Scholar]
- Creswell, J.W. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches, 4th ed.; SAGE Publications: Thousand Oaks, CA, USA, 2014; ISBN 9781452226101. [Google Scholar]
- Babbie, E. The Practice of Social Research, 12th ed.; Wadsworth Cengage Learning: Belmont, CA, USA, 2010; ISBN 9780495598411. [Google Scholar]
- Saunders, M.; Lewis, P.; Thornhill, A. Research Methods for Business Students, 7th ed.; Pearson Education Limited: Harlow, UK, 2016; ISBN 9781292016627. [Google Scholar]

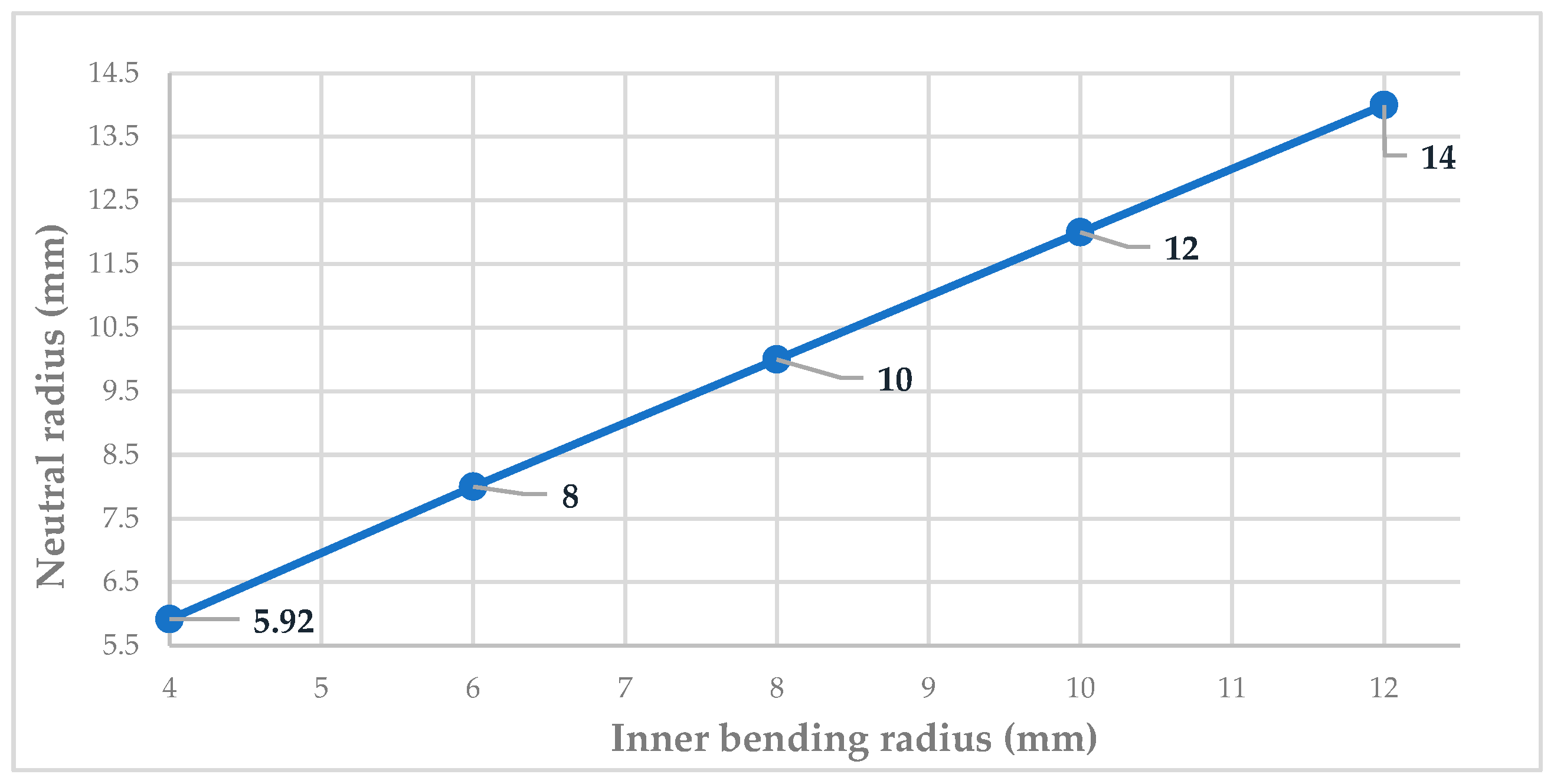


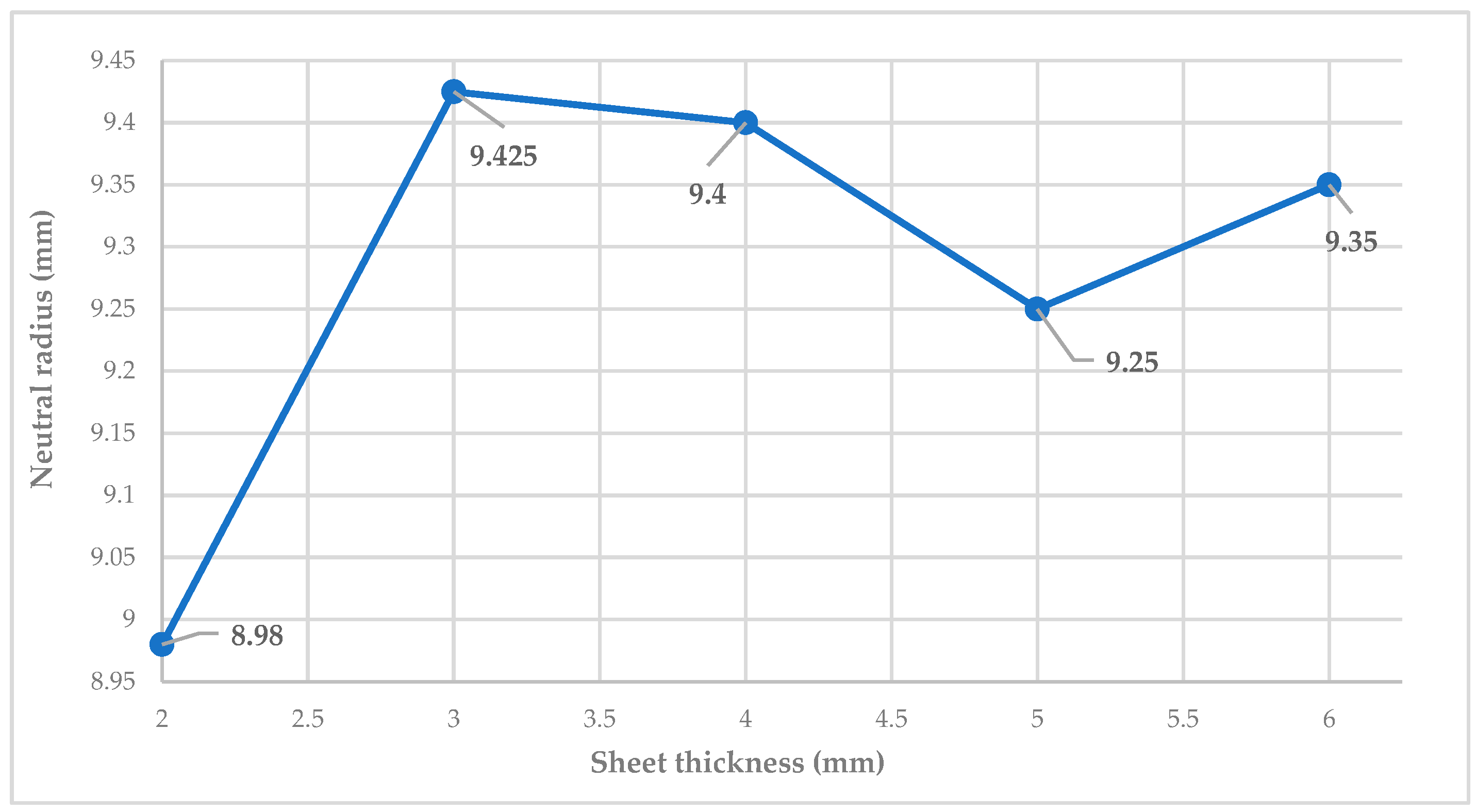
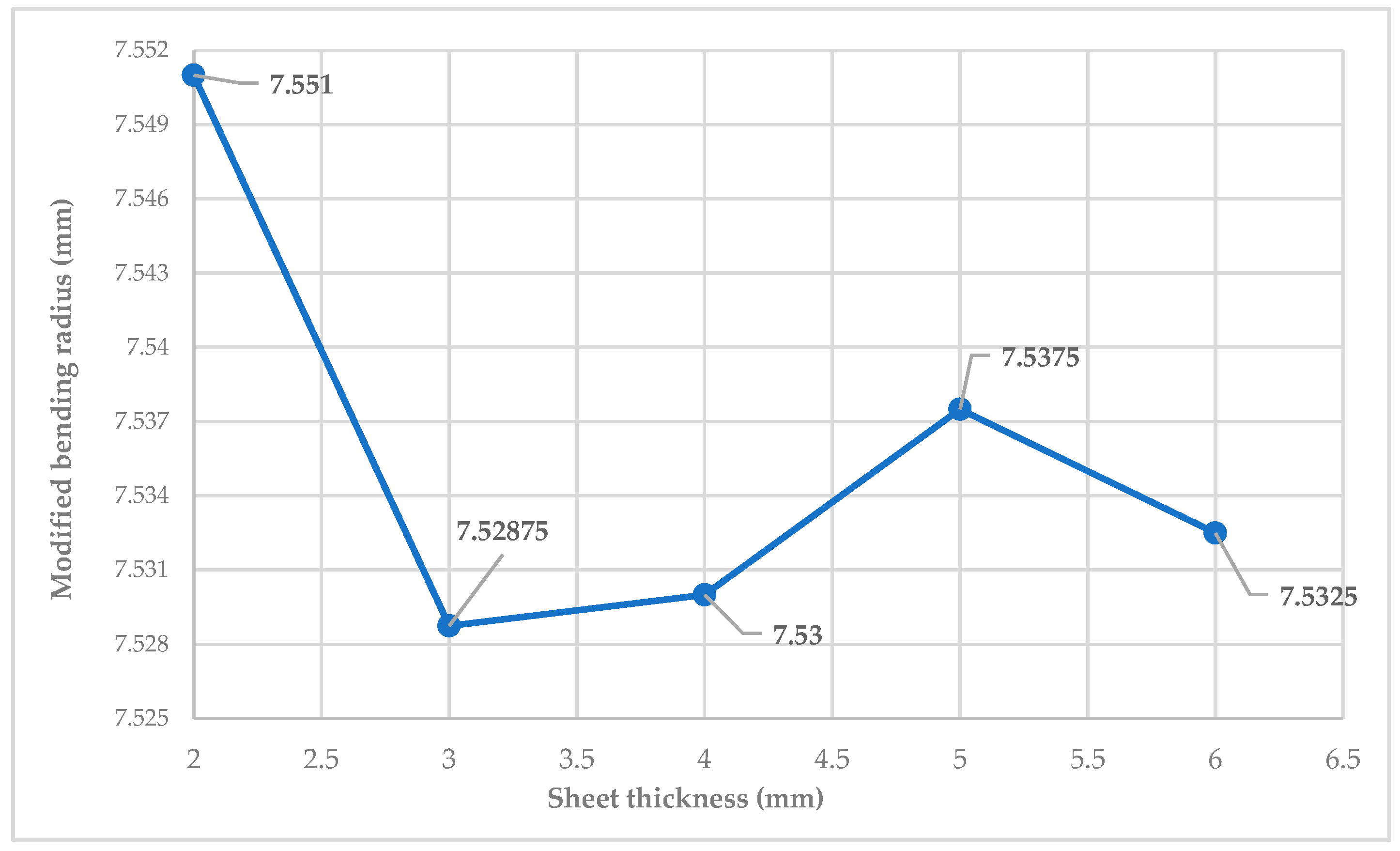
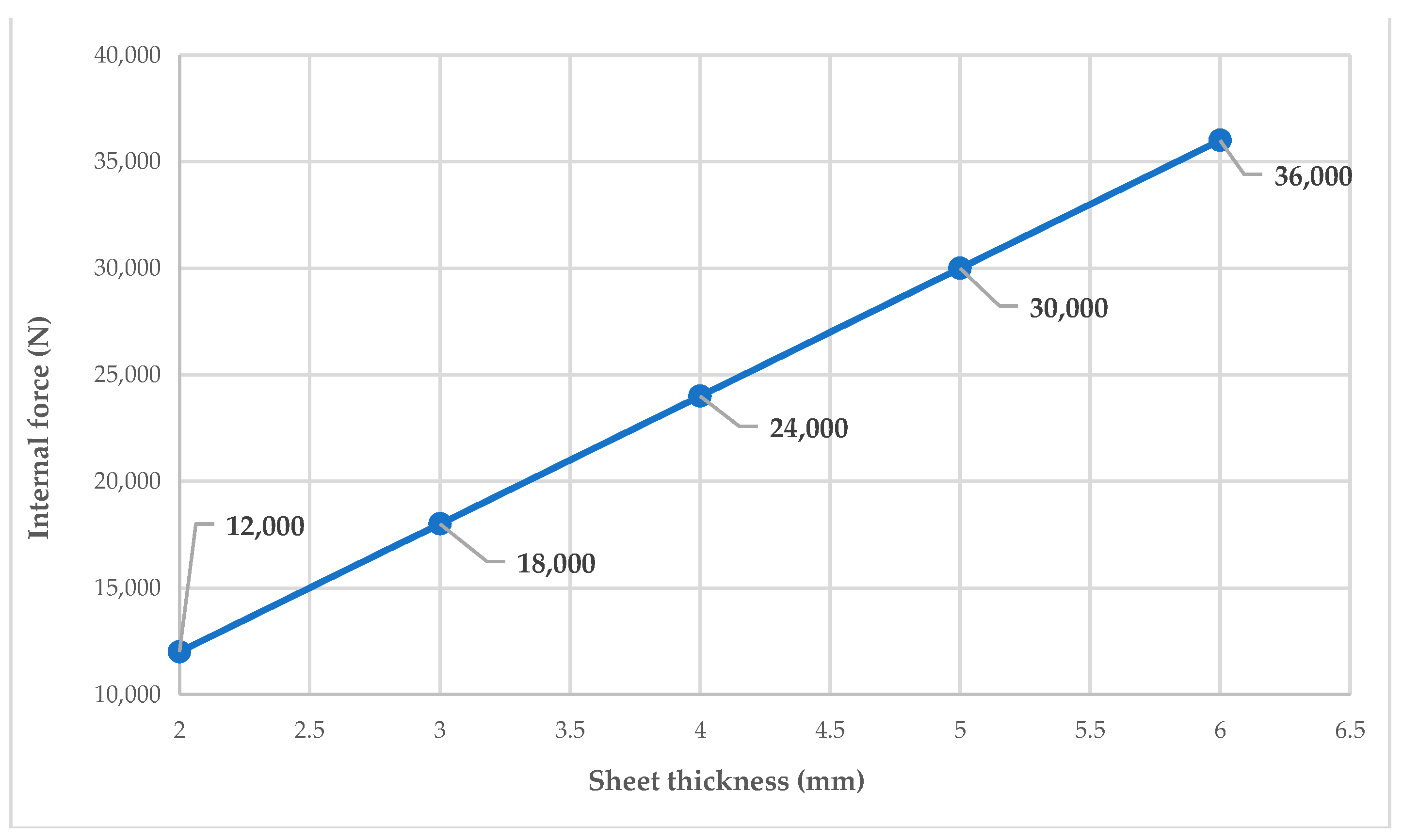
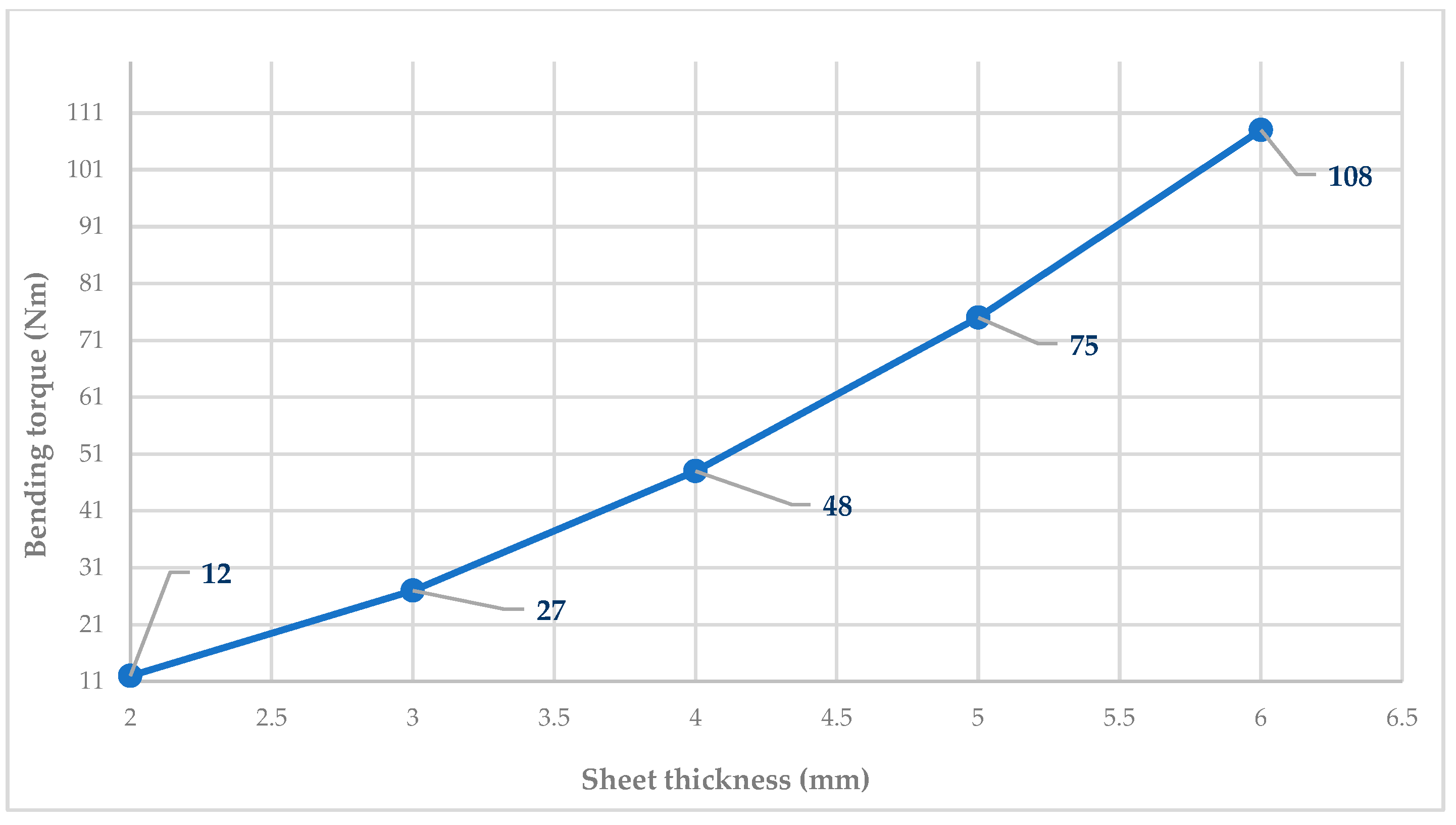
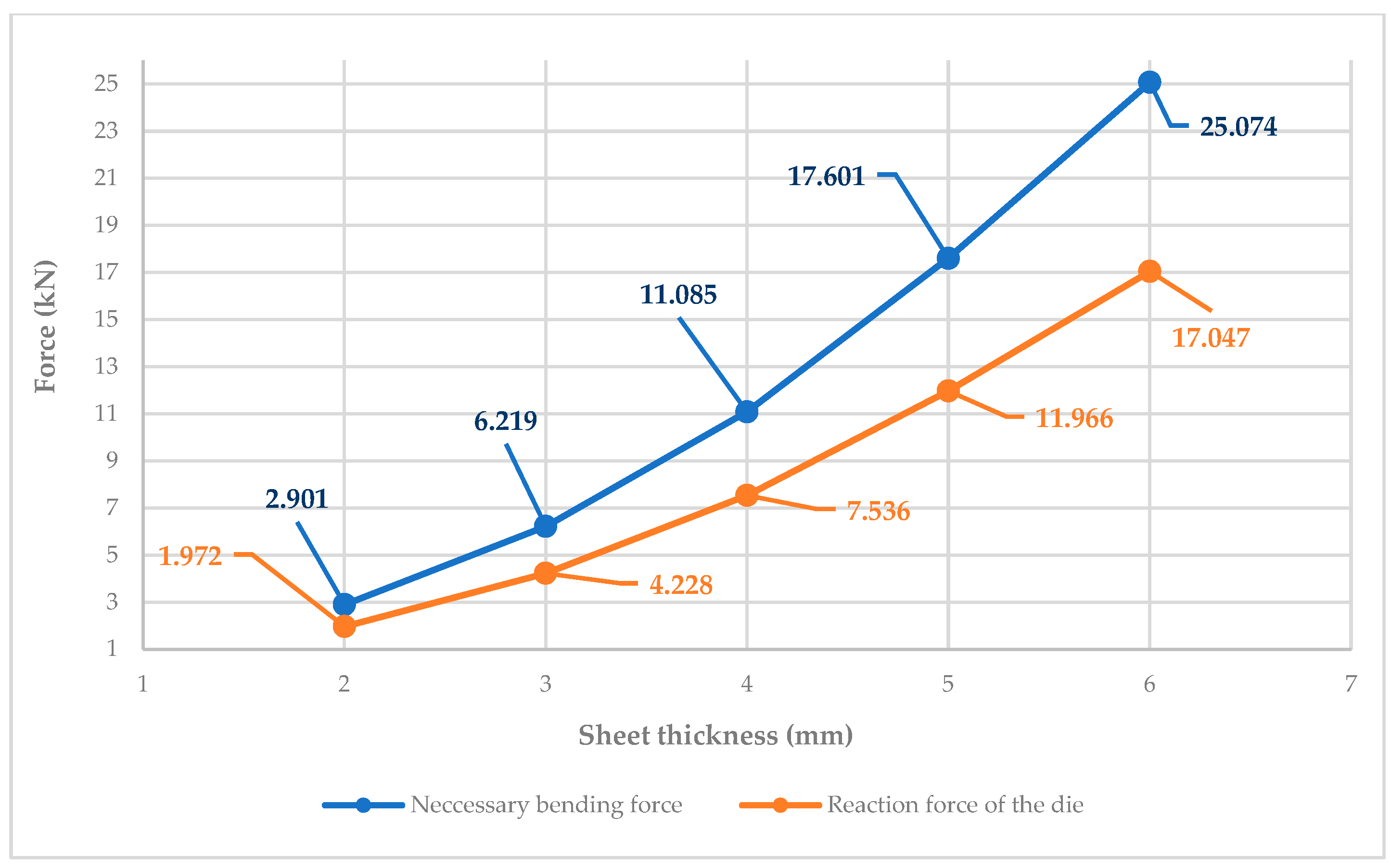


| Inner bending radius (ri) | 4 mm | 6 mm | 8 mm | 10 mm | 12 mm |
| Sheet thickness (s) | 4 mm | ||||
| Bending factor (ξ) | 0.96 | 1 | |||
| Bending angle (α) | 90° | ||||
| Springback factor (K) | 0.95 | ||||
| Modified bending angle (αm) | 94.737 | ||||
| Middle radius (rm) | 6 mm | 8 mm | 10 mm | 12 mm | 14 mm |
| Outer radius (ro) | 8 mm | 10 mm | 12 mm | 14 mm | 16 mm |
| Sheet width (b) | 30 mm | ||||
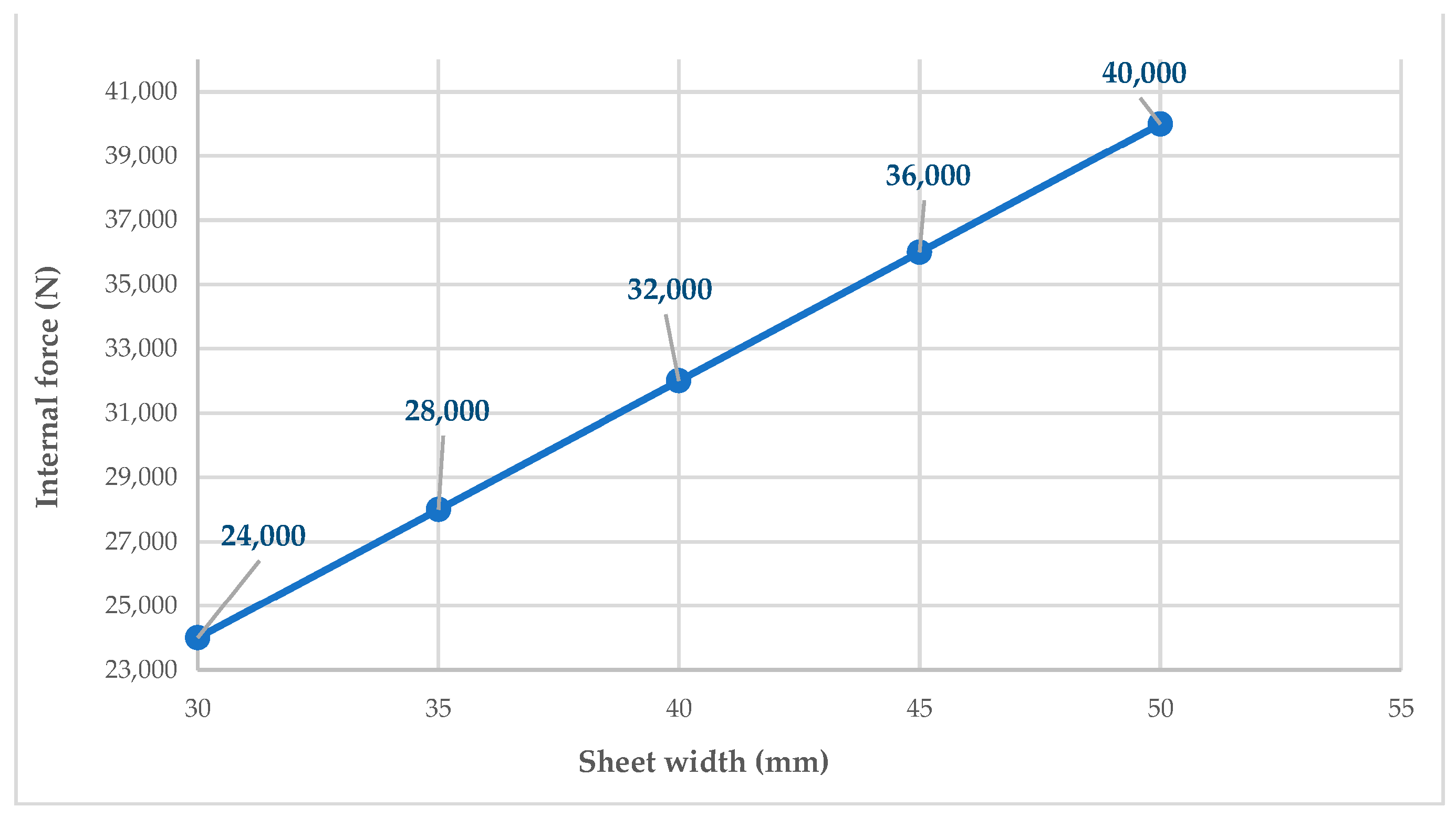
| Internal force (Fm) | 24 kN | ||||
| Bending torque (M) | 48 Nm | ||||
| Inner bending radius (ri) | 8 mm | ||||
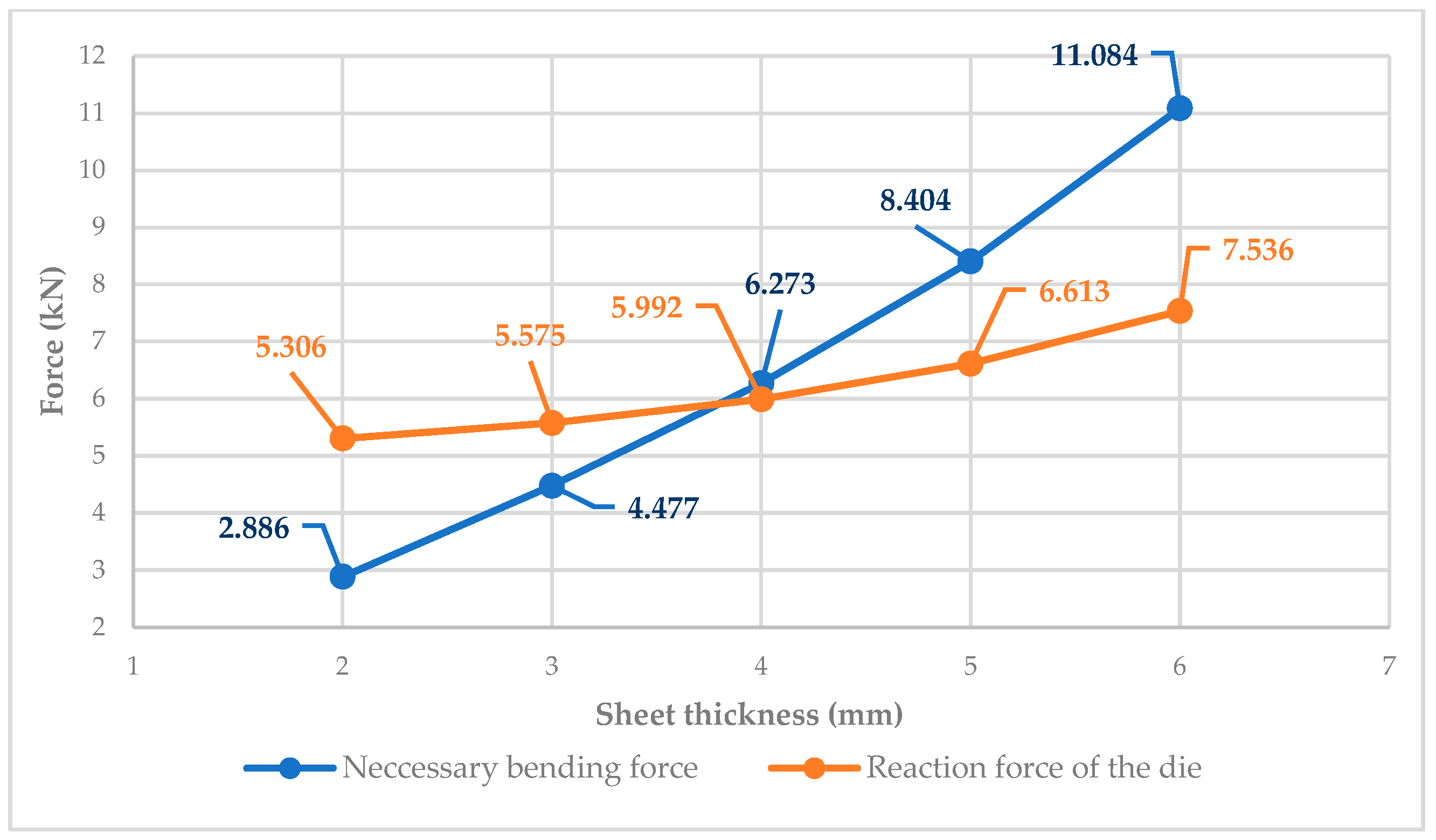
| Sheet thickness (s) | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm |
| Bending factor (ξ) | 0.98 | 0.94 | 0.7 | 0.5 | 0.45 |
| Bending angle (α) | 90° | ||||
| Springback factor (K) | 0.95 | ||||
| Modified bending angle (αm) | 94.737 | ||||
| Middle radius (rm) | 9 mm | 9.5 mm | 10 mm | 10.5 mm | 11 mm |
| Outer radius (ro) | 10 mm | 11 mm | 12 mm | 13 mm | 14 mm |
| Sheet width (b) | 30 mm | ||||
| Inner bending radius (ri) | 8 mm | ||||
| Sheet thickness (s) | 4 mm | ||||
| Bending factor (ξ) | 0.7 | ||||
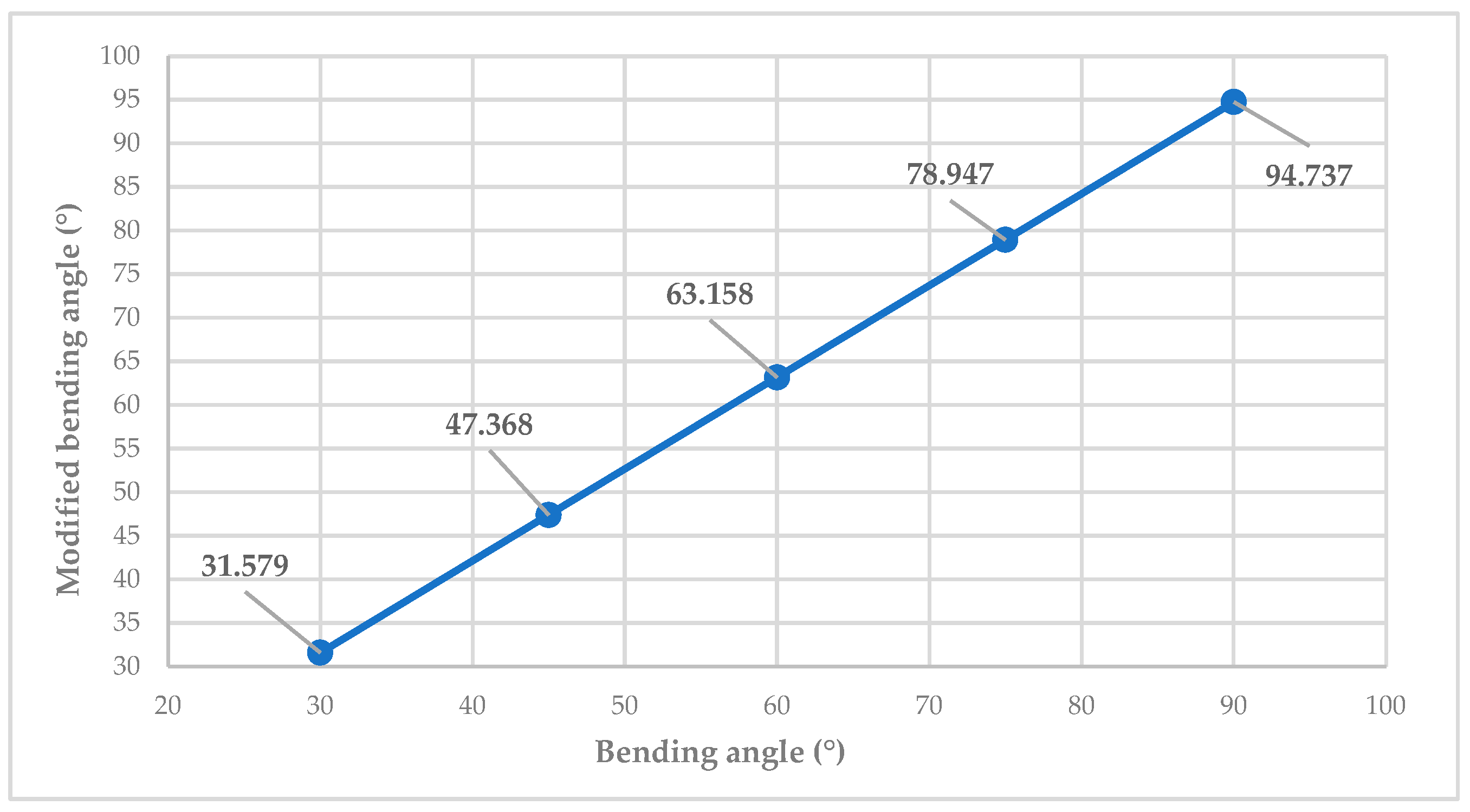
| Bending angle (α) | 30° | 45° | 60° | 75° | 90° |
| Springback factor (K) | 0.95 | ||||
| Middle radius (rm) | 10 mm | ||||
| Outer radius (ro) | 12 mm | ||||
| Modified bending angle (αm) | 7.53 mm | ||||
| Sheet width (b) | 30 mm | ||||
| Internal force (Fm) | 24 kN | ||||
| Bending torque (M) | 48 Nm | ||||
| Inner bending radius (ri) | 8 mm | ||||
| Sheet thickness (s) | 4 mm | ||||
| Bending factor (ξ) | 0.7 | ||||
| Bending angle (α) | 90° | ||||
| Springback factor (K) | 0.95 | ||||
| Middle radius (rm) | 10 mm | ||||
| Outer radius (ro) | 12 mm | ||||
| Modified bending angle (αm) | 7.53 mm | ||||
| Sheet width (b) | 30 mm | 35 mm | 40 mm | 45 mm | 50 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodzás, S.; Szanyi, G. Manufacturing Design and Analysis of Bending Technology by the Variation of the Initial Technological Parameters. J. Manuf. Mater. Process. 2025, 9, 272. https://doi.org/10.3390/jmmp9080272
Bodzás S, Szanyi G. Manufacturing Design and Analysis of Bending Technology by the Variation of the Initial Technological Parameters. Journal of Manufacturing and Materials Processing. 2025; 9(8):272. https://doi.org/10.3390/jmmp9080272
Chicago/Turabian StyleBodzás, Sándor, and Gyöngyi Szanyi. 2025. "Manufacturing Design and Analysis of Bending Technology by the Variation of the Initial Technological Parameters" Journal of Manufacturing and Materials Processing 9, no. 8: 272. https://doi.org/10.3390/jmmp9080272
APA StyleBodzás, S., & Szanyi, G. (2025). Manufacturing Design and Analysis of Bending Technology by the Variation of the Initial Technological Parameters. Journal of Manufacturing and Materials Processing, 9(8), 272. https://doi.org/10.3390/jmmp9080272






