Additively Produced Ti-6Al-4V Osteosynthesis Devices Meet the Requirements for Tensile Strength and Fatigue
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Element (FE) Modelling
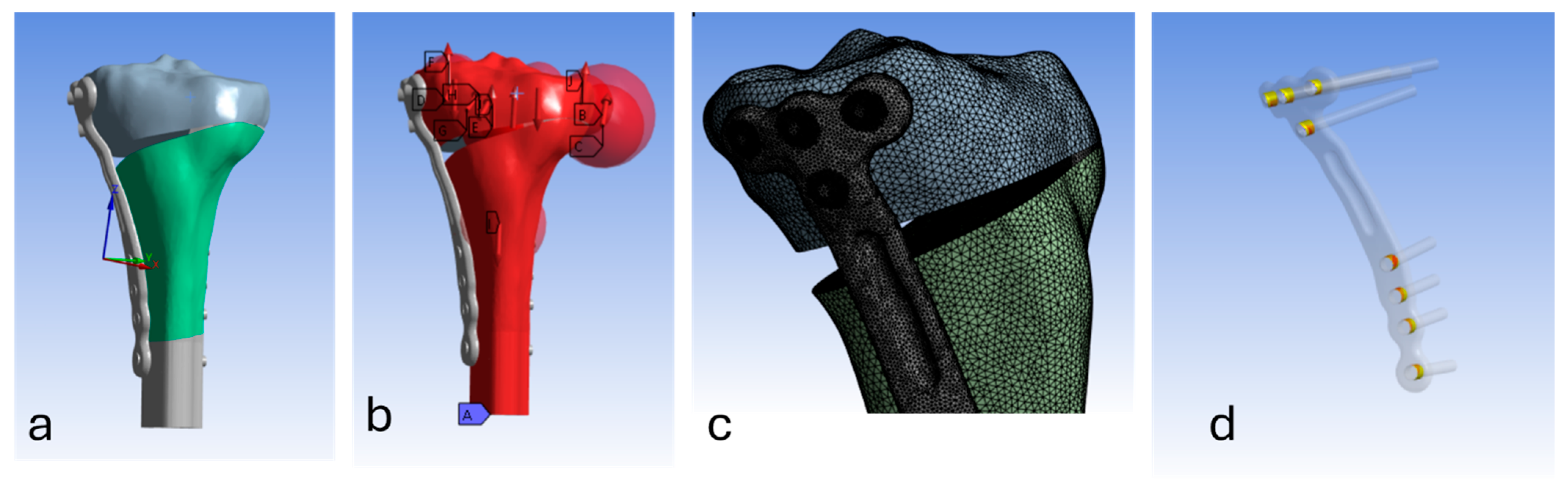
2.1.1. Geometries and Meshing
2.1.2. Material Properties
2.1.3. Contact Interactions
2.1.4. Loading & Boundary Conditions
2.1.5. Solver/Solution
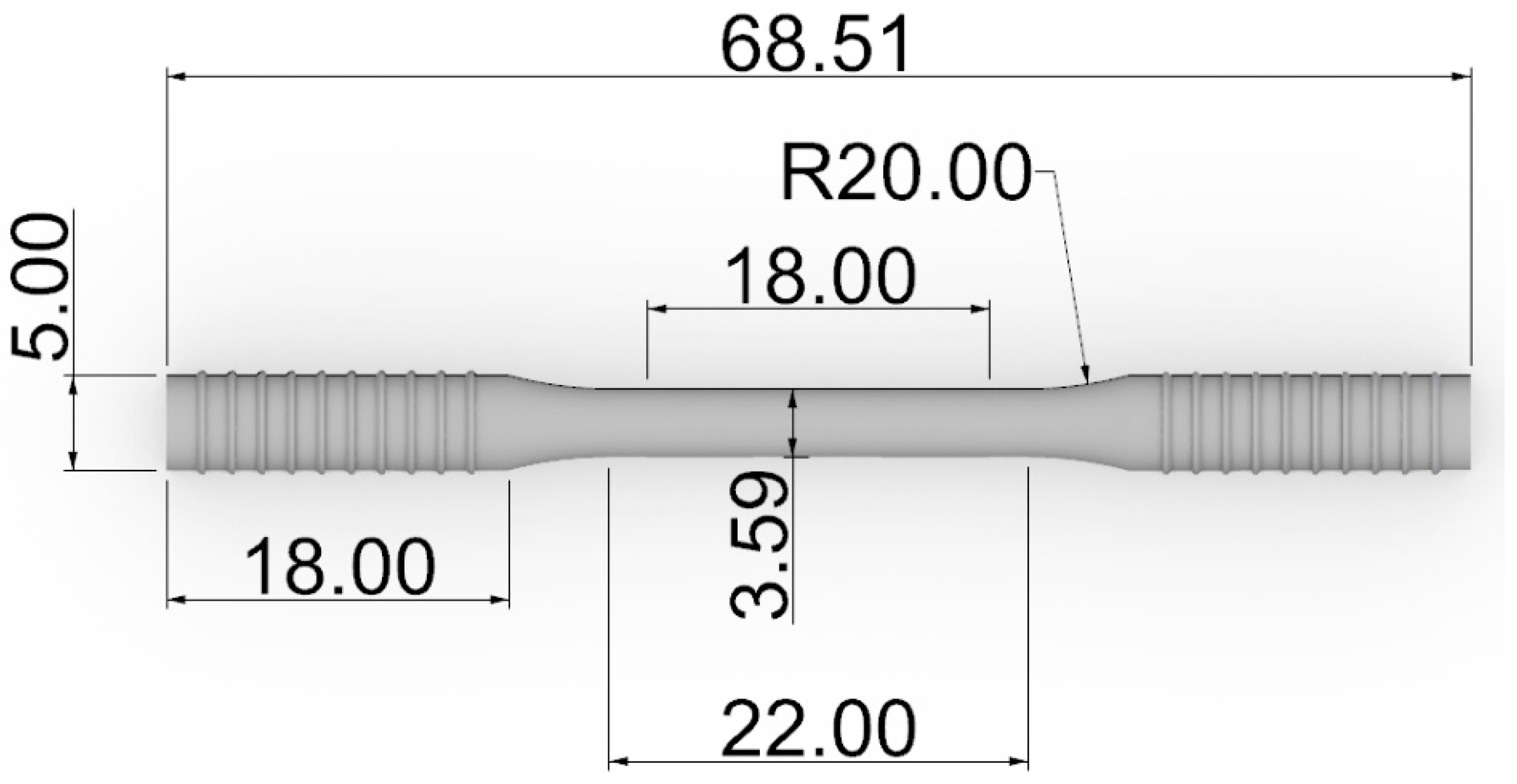
2.2. Production of Tensile Test Specimens
2.3. Tensile Testing
2.4. Fatigue Test Specimens
2.5. Fatigue Testing
2.6. Microscopy
2.7. Nano-Indentation
2.8. Scanning Electron Microscopy (SEM)
3. Results
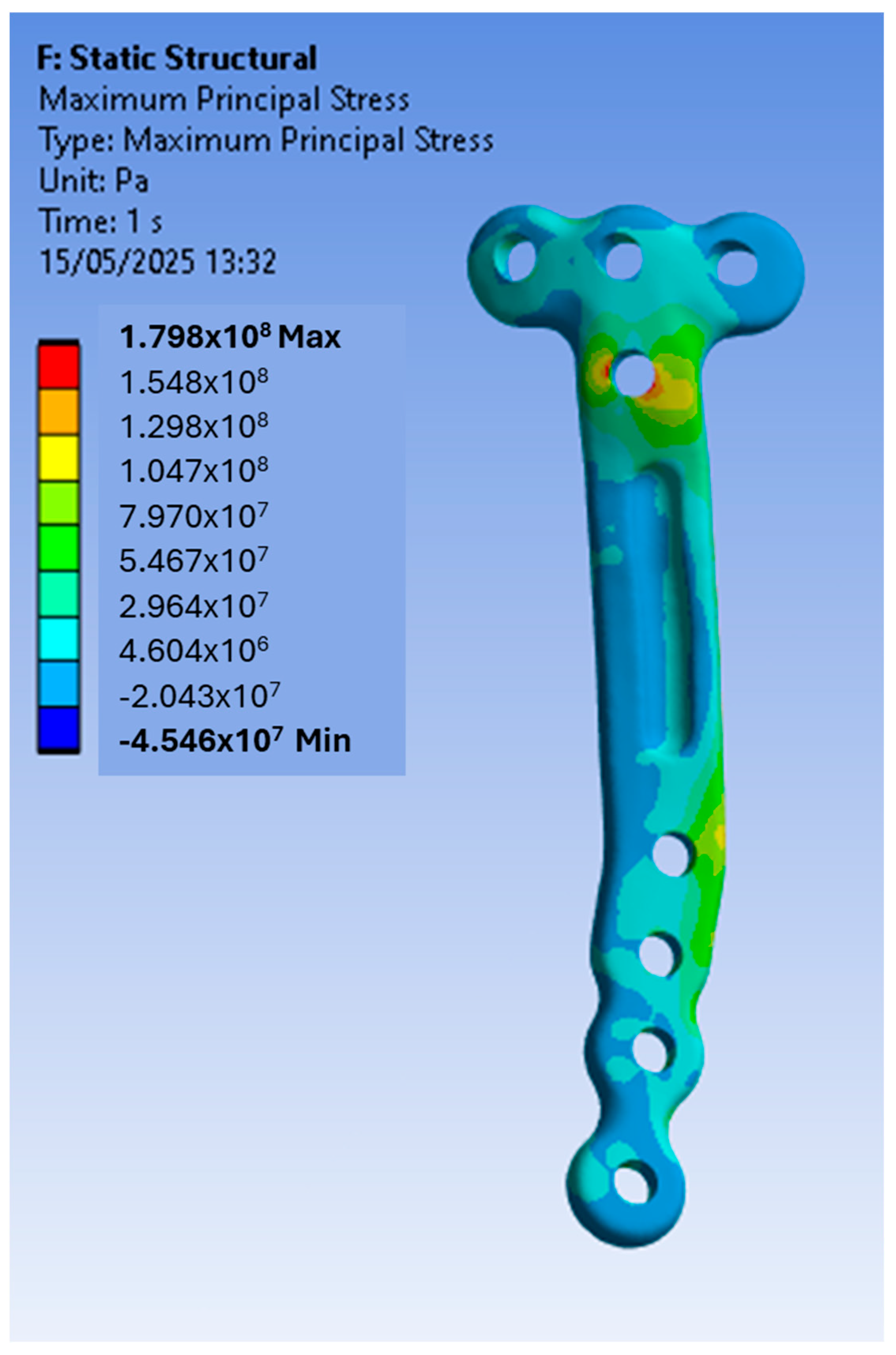
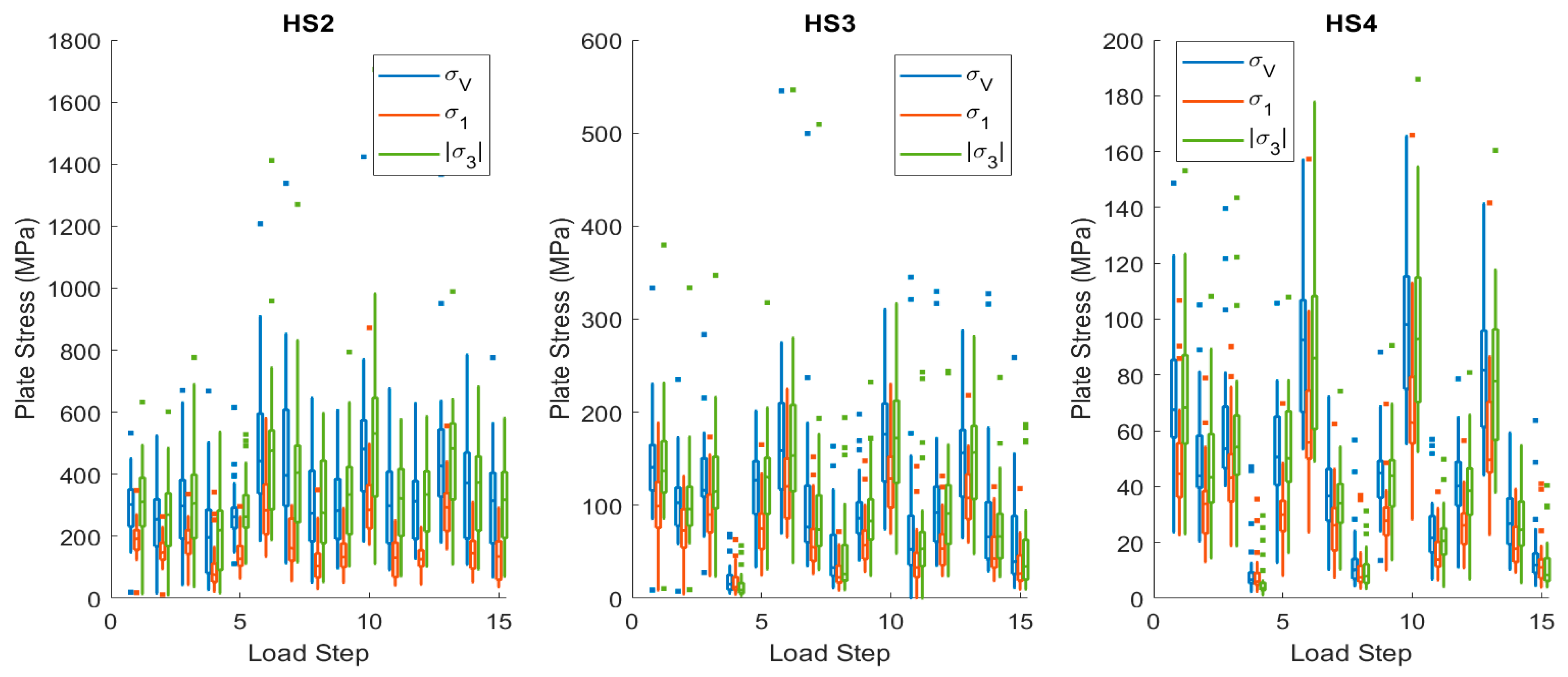
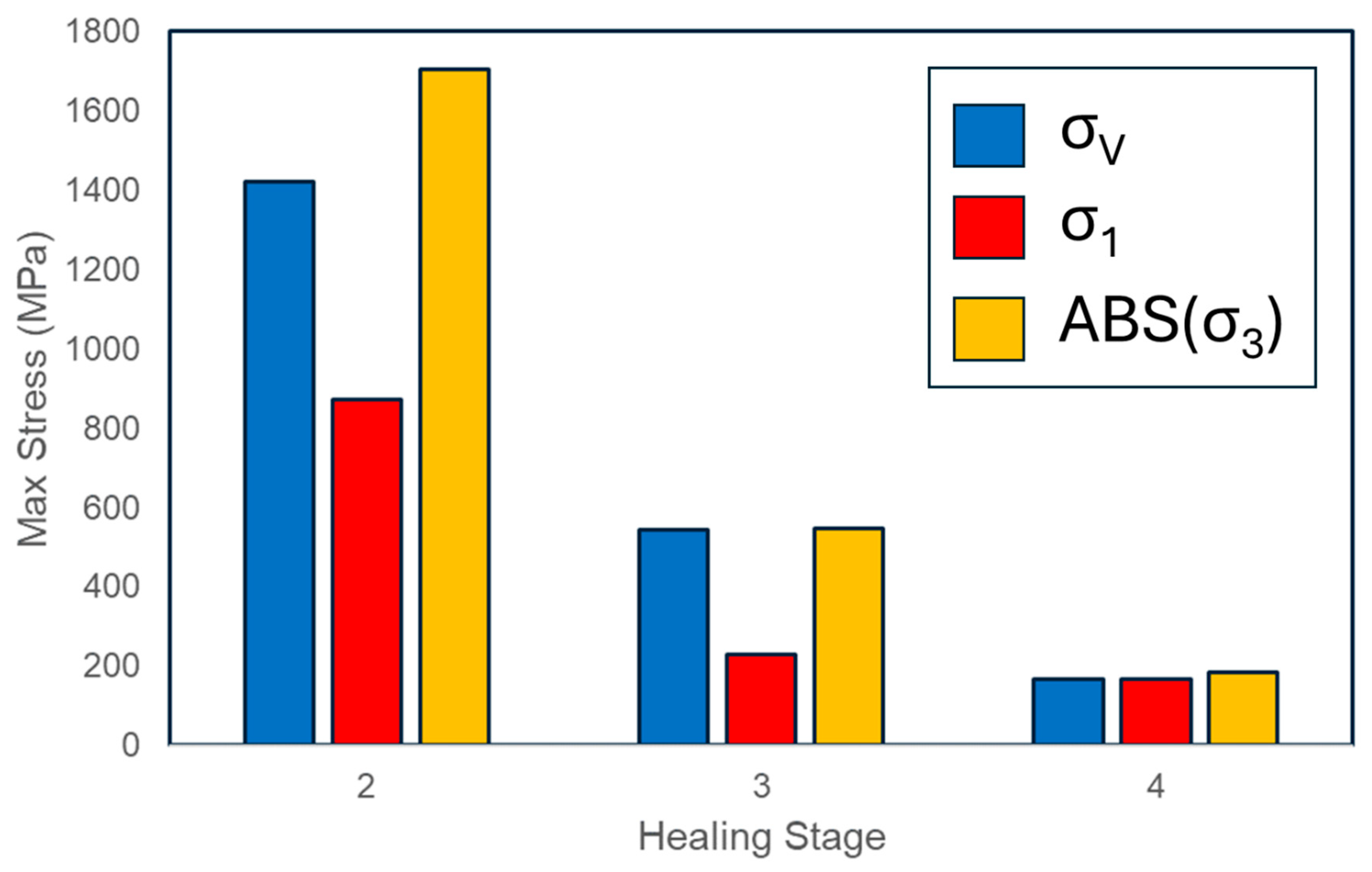
3.1. Finite Element Modelling
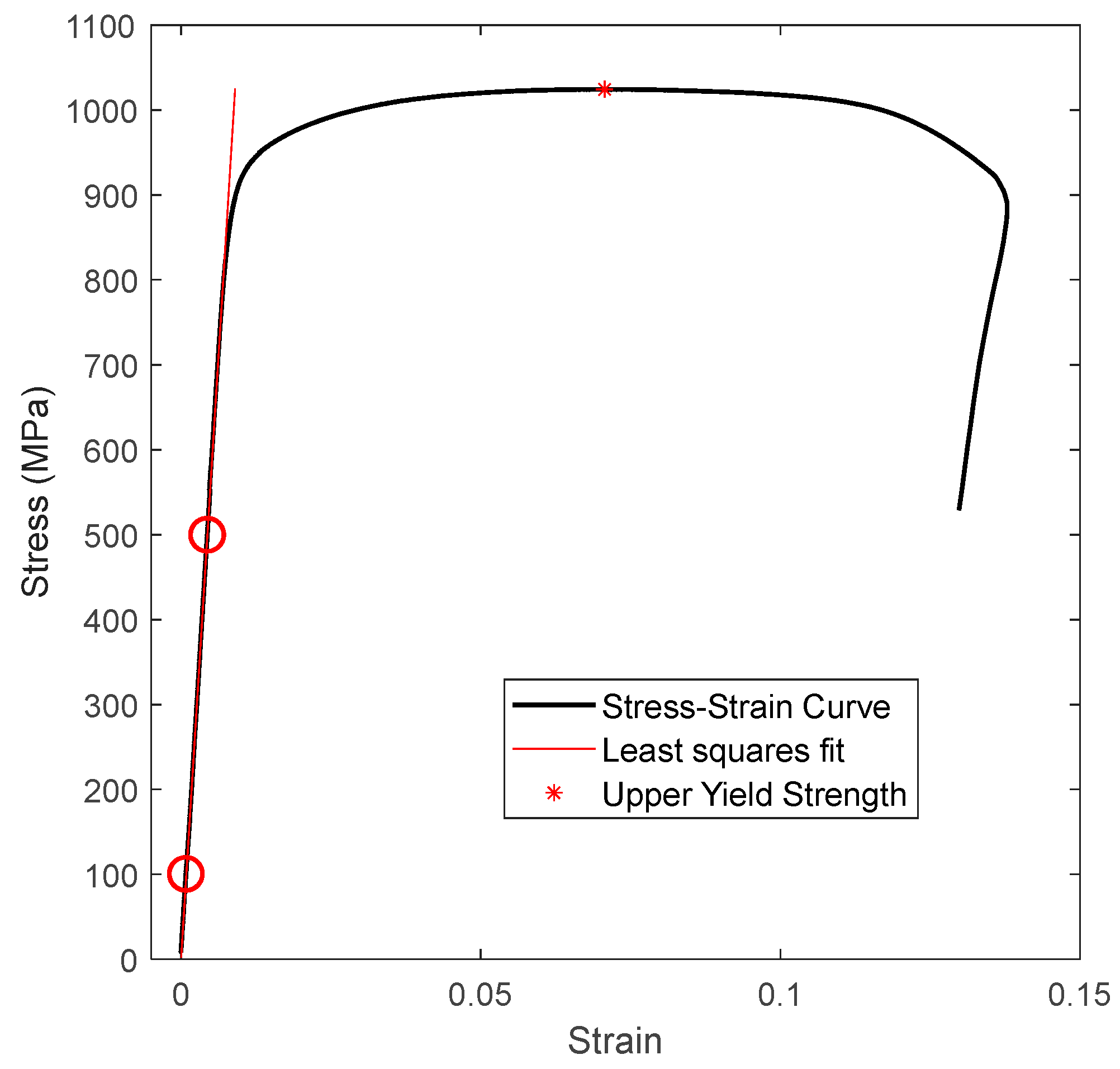
3.2. Tensile Tests
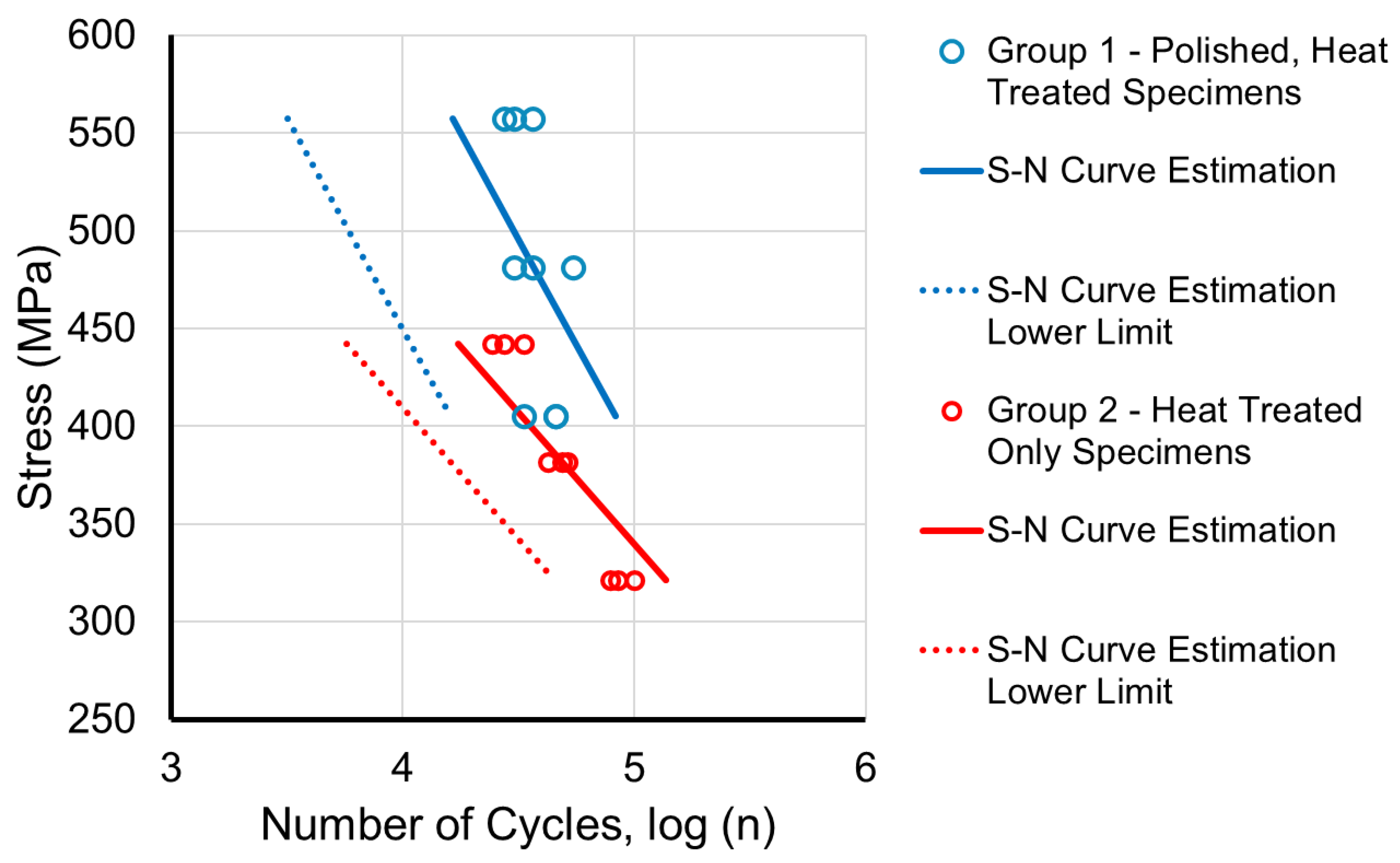
3.3. Fatigue Tests
3.4. Microstructural Analysis
3.5. Nano-Indentation
3.6. Scanning Electron Microscopy (SEM)
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Specimen | Pre Average Diameter (mm) | Post Average Diameter (mm) | Difference (mm) | Percentage Difference (%) |
|---|---|---|---|---|
| 1 | 3.46 | 3.28 | −0.17 | −5.01 |
| 2 | 3.47 | 3.25 | −0.22 | −6.35 |
| 3 | 3.45 | 3.27 | −0.18 | −5.31 |
| 4 | 3.50 | 3.35 | −0.15 | −4.29 |
| 5 | 3.46 | 3.31 | −0.15 | −4.43 |
| 6 | 3.46 | 3.27 | −0.19 | −5.49 |
| 7 | 3.46 | 3.25 | −0.21 | −6.17 |
| 8 | 3.44 | 3.24 | −0.20 | −5.72 |
| 9 | 3.45 | 3.30 | −0.14 | −4.16 |
| 10 | 3.45 | 3.31 | −0.14 | −4.06 |
| Average | 3.46 | 3.28 | −0.18 | −5.10 |
| Specimen | Peak Force (MPa) | Peak Stress (MPa) | Youngs Modulus, E (MPa) | Initial Gauge Length (mm) | Maximum Extension (mm) | Maximum Extension (%) |
|---|---|---|---|---|---|---|
| 1 | 9551 | 1015 | 112,679 | 19.90 | 2.74 | 13.78 |
| 2 | 9563 | 1011 | 107,801 | 20.50 | 2.92 | 14.23 |
| 3 | 9373 | 1003 | 110,616 | 21.49 | 3.09 | 14.38 |
| 4 | 9353 | 972 | 112,737 | 21.64 | 2.48 | 11.47 |
| 5 | 9382 | 998 | 111,863 | 20.91 | 2.76 | 13.20 |
| 6 | 9624 | 1024 | 111,321 | 21.50 | 2.54 | 11.80 |
| 7 | 9423 | 1002 | 108,416 | 20.75 | 3.20 | 15.41 |
| 8 | 9696 | 1043 | 113,196 | 21.02 | 3.04 | 14.47 |
| 9 | 9566 | 1023 | 110,096 | 20.87 | 3.00 | 14.38 |
| 10 | 9656 | 1033 | 112,079 | 21.55 | 2.94 | 13.66 |
| Mean | 9519 | 1012 | 111,080 | 21.01 | 2.87 | 13.68 |
| SD | 120 | 19 | 1746 | 0.52 | 0.22 | 1.16 |
| Number of Cycles to Failure | ||||||
|---|---|---|---|---|---|---|
| Repetition Number | ||||||
| Group | Stress (MPa) | 1 | 2 | 3 | Mean | SD |
| 1 | 557 | 27,351 | 36,468 | 30,390 | 31,403 | 4642 |
| 481 | 36,468 | 30,390 | 54,702 | 40,520 | 12,652 | |
| 405 | 45,585 | 45,585 | 33,429 | 41,533 | 7018 | |
| 2 | 442 | 33,429 | 27,351 | 24,312 | 28,364 | 4642 |
| 382 | 48,624 | 51,663 | 42,546 | 47,611 | 4642 | |
| 321 | 100,287 | 85,092 | 79,014 | 88,131 | 10,957 | |
References
- Auricchio, F.; Marconi, S. 3D printing: Clinical applications in orthopaedics and traumatology. EFORT Open Rev. 2016, 1, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Mulford, J.S.; Babazadeh, S.; Mackay, N. Three-dimensional printing in orthopaedic surgery: Review of current and future applications. ANZ J. Surg. 2016, 86, 648–653. [Google Scholar] [CrossRef] [PubMed]
- Mumith, A.; Thomas, M.; Shah, Z.; Coathup, M.; Blunn, G. Additive manufacturing: Current concepts, future trends. Bone Jt. J. 2018, 100-B, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S.; Shi, Q.; Van Dessel, J.; Gu, Y.; Sun, Y.; Yang, S.; Constantinus, P. Biomechanical validation of structural optimized patient-specific mandibular reconstruction plate orienting additive manufacturing. Comput. Methods Programs Biomed. 2022, 224, 107023. [Google Scholar] [CrossRef]
- Robinson, D.L.; Bucknill, A.; Ferragina, A.; Campbell, C.; Lee, P.V.S. Fixation of pelvic acetabular fractures using 3D-printed fracture plates: A cadaver study. J. Orthop. Surg. Res. 2023, 18, 360. [Google Scholar] [CrossRef]
- Sun, H.; Hu, C.; Zhou, C.; Wu, L.; Sun, J.; Zhou, X.; Xing, F.; Long, C.; Kong, Q.; Liang, J.; et al. 3D printing of calcium phosphate scaffolds with controlled release of antibacterial functions for jaw bone repair. Mater. Des. 2020, 189, 108540. [Google Scholar] [CrossRef]
- Wong, K.C.; Kumta, S.M.; Geel, N.V.; Demol, J. One-step reconstruction with a 3D-printed, biomechanically evaluated custom implant after complex pelvic tumor resection. Comput. Aided Surg. 2015, 20, 14–23. [Google Scholar] [CrossRef]
- Wong, K.C. 3D-printed patient-specific applications in orthopedics. Orthop. Res. Rev. 2016, 8, 57–66. [Google Scholar] [CrossRef]
- Perticarini, L.; Zanon, G.; Rossi, S.M.; Benazzo, F.M. Clinical and radiographic outcomes of a trabecular titanium acetabular component in hip arthroplasty: Results at minimum 5 years follow-up. BMC Musculoskelet. Disord. 2015, 16, 375. [Google Scholar] [CrossRef]
- De Meo, F.; Cacciola, G.; Bellotti, V.; Bruschetta, A.; Cavaliere, P. Trabecular Titanium acetabular cups in hip revision surgery: Mid-term clinical and radiological outcomes. Hip Int. 2018, 28, 61–65. [Google Scholar] [CrossRef]
- Faizan, A.; Bhowmik-Stoker, M.; Alipit, V.; Kirk, A.E.; Krebs, V.E.; Harwin, S.F.; Meneghini, R.M. Development and Verification of Novel Porous Titanium Metaphyseal Cones for Revision Total Knee Arthroplasty. J. Arthroplast. 2017, 32, 1946–1953. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Y.; Lu, M.; Wang, Y.; Gong, T.; Hu, X.; He, X.; Zhou, Y.; Min, L.; Tu, C. 3D-printed Personalized Porous Acetabular Component to Reconstruct Extensive Acetabular Bone Defects in Primary Hip Arthroplasty. Orthop. Surg. 2024, 16, 1642–1647. [Google Scholar] [CrossRef] [PubMed]
- Geetha, M.; Singh, A.K.; Asokamani, R.; Gogia, A.K. Ti based biomaterials, the ultimate choice for orthopaedic implants – A review. Progress. Mater. Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- ASTM F136-13; Standard Specification for Wrought Titanium-6Aluminum-4Vanadium ELI (Extra Low Interstitial) Alloy for Surgical Implant Applications (UNS R56401). ASTM International: West Conshohocken, PA, USA, 2013. [CrossRef]
- ASTM F3001-14; Standard Specification for Additive Manufacturing Titanium-6 Aluminum-4 Vanadium ELI (Extra Low Interstitial) with Powder Bed Fusion. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
- ISO 5832-3:2016; Implants for Surgery—Metallic Materials. Part 3: Wrought Titanium 6-aluminium 4-vanadium Alloy. ISO: Geneva, Switzerland, 2016.
- Hollander, D.A.; Wirtz, T.; von Walter, M.; Linker, R.; Schultheis, A.; Paar, O. Development of IndividualThree-Dimensional Bone Substitutes Using “Selective LaserMelting”. Eur. J. Trauma. 2003, 29, 228–234. [Google Scholar] [CrossRef]
- Haslauer, C.M.; Springer, J.C.; Harrysson, O.L.; Loboa, E.G.; Monteiro-Riviere, N.A.; Marcellin-Little, D.J. In vitro biocompatibility of titanium alloy discs made using direct metal fabrication. Med. Eng. Phys. 2010, 32, 645–652. [Google Scholar] [CrossRef]
- Sidambe, A.T. Biocompatibility of Advanced Manufactured Titanium Implants—A Review. Materials 2014, 7, 8168–8188. [Google Scholar] [CrossRef]
- Lin, X.; Xiao, X.; Wang, Y.; Gu, C.; Wang, C.; Chen, J.; Liu, H.; Luo, J.; Li, T.; Wang, D.; et al. Biocompatibility of Bespoke 3D-Printed Titanium Alloy Plates for Treating Acetabular Fractures. Biomed. Res. Int. 2018, 2018, 2053486. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Yang, Y.; Xie, D.; Li, L.; Mao, N.; Wang, C.; Tian, Z.; Jiang, Q.; Shen, L. Trabecular-like Ti-6Al-4V scaffolds for orthopedic: Fabrication by selective laser melting and in vitro biocompatibility. J. Mater. Sci. Technol. 2019, 35, 1284–1297. [Google Scholar] [CrossRef]
- Tuomi, J.T.; Björkstrand, R.V.; Pernu, M.L.; Salmi, M.V.J.; Huotilainen, E.I.; Wolff, J.E.H.; Vallittu, P.K.; Mäkitie, A.A. In vitro cytotoxicity and surface topography evaluation of additive manufacturing titanium implant materials. J. Mater. Sci. Mater. Med. 2017, 28, 53. [Google Scholar] [CrossRef]
- Jennison, T.; Brinsden, M. Fracture admission trends in England over a ten-year period. Ann. R. Coll. Surg. Engl. 2019, 101, 208–214. [Google Scholar] [CrossRef]
- Banerjee, S.; Kulesha, G.; Kester, M.; Mont, M.A. Emerging technologies in arthroplasty: Additive manufacturing. J. Knee Surg. 2014, 27, 185–191. [Google Scholar] [CrossRef]
- Chen, X.; Possel, J.K.; Wacongne, C.; van Ham, A.F.; Klink, P.C.; Roelfsema, P.R. 3D printing and modelling of customized implants and surgical guides for non-human primates. J. Neurosci. Methods 2017, 286, 38–55. [Google Scholar] [CrossRef]
- Bayliss, L.E.; Culliford, D.; Monk, A.P.; Glyn-Jones, S.; Prieto-Alhambra, D.; Judge, A.; Cooper, C.; Carr, A.J.; Arden, N.K.; Beard, D.J.; et al. The effect of patient age at intervention on risk of implant revision after total replacement of the hip or knee: A population-based cohort study. Lancet 2017, 389, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Wainwright, C.; Theis, J.C.; Garneti, N.; Melloh, M. Age at hip or knee joint replacement surgery predicts likelihood of revision surgery. J. Bone Jt. Surg. Br. 2011, 93, 1411–1415. [Google Scholar] [CrossRef] [PubMed]
- Murray, R.; Winkler, P.W.; Shaikh, H.S.; Musahl, V. High Tibial Osteotomy for Varus Deformity of the Knee. J. Am. Acad. Orthop. Surg. Glob. Res. Rev. 2021, 5, e1. [Google Scholar] [CrossRef]
- Bergmann, G.; Bender, A.; Dymke, J.; Duda, G.; Damm, P. Standardized Loads Acting in Hip Implants. PLoS ONE 2016, 11, e0155612. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, G.; Bender, A.; Graichen, F.; Dymke, J.; Rohlmann, A.; Trepczynski, A.; Heller, M.O.; Kutzner, I. Standardized loads acting in knee implants. PLoS ONE 2014, 9, e86035. [Google Scholar] [CrossRef]
- Schorler, H.; Capanni, F.; Gaashan, M.; Wendlandt, R.; Jurgens, C.; Schulz, A.P. Bone plates for osteosynthesis - a systematic review of test methods and parameters for biomechanical testing. Biomed. Tech. 2017, 62, 235–243. [Google Scholar] [CrossRef]
- MacLeod, A.R.; Pankaj, P. Pre-operative planning for fracture fixation using locking plates: Device configuration and other considerations. Injury 2018, 49 (Suppl. S1), S12–S18. [Google Scholar] [CrossRef]
- MacLeod, A.R.; Serrancoli, G.; Fregly, B.J.; Toms, A.D.; Gill, H.S. The effect of plate design, bridging span, and fracture healing on the performance of high tibial osteotomy plates: An experimental and finite element study. Bone Jt. Res. 2018, 7, 639–649. [Google Scholar] [CrossRef]
- Hu, Y.N.; Wu, S.C.; Withers, P.J.; Zhang, J.; Bao, H.Y.X.; Fu, Y.N.; Kang, G.Z. The effect of manufacturing defects on the fatigue life of selective laser melted Ti-6Al-4V structures. Mater. Des. 2020, 192, 108708. [Google Scholar] [CrossRef]
- Chen, G.; Schmutz, B.; Wullschleger, M.; Pearcy, M.J.; Schuetz, M.A. Computational investigations of mechanical failures of internal plate fixation. Proc. Inst. Mech. Eng. H. 2010, 224, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Nica, M.; Cretu, B.; Ene, D.; Antoniac, I.; Gheorghita, D.; Ene, R. Failure Analysis of Retrieved Osteosynthesis Implants. Materials 2020, 13, 1201. [Google Scholar] [CrossRef]
- MacLeod, A.; Peckham, N.; Serrancolí, G.; Rombach, I.; Hourigan, P.; Mandalia, V.I.; Toms, A.D.; Fregly, B.J.; Gill, H.S. Personalised high tibial osteotomy has mechanical safety equivalent to generic device in a case-control in silico clinical trial. Commun. Med. 2021, 1, 6. [Google Scholar] [CrossRef]
- Mohammed, M.M. Fundamental Drivers of Metal Fatigue Failure and Performance. Multidiscip. Mater. Chron. 2024, 1, 49–61. [Google Scholar] [CrossRef]
- Sabzevari, S.; Ebrahimpour, A.; Roudi, M.K.; Kachooei, A.R. High Tibial Osteotomy: A Systematic Review and Current Concept. Arch. Bone Jt. Surg. 2016, 4, 204–212. [Google Scholar]
- Taddei, F. Bonemat. Available online: https://bonemat.ior.it/en (accessed on 14 May 2025).
- Taddei, F.; Pancanti, A.; Viceconti, M. An improved method for the automatic mapping of computed tomography numbers onto finite element models. Med. Eng. Phys. 2004, 26, 61–69. [Google Scholar] [CrossRef] [PubMed]
- Isaksson, H.; Wilson, W.; van Donkelaar, C.C.; Huiskes, R.; Ito, K. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J. Biomech. 2006, 39, 1507–1516. [Google Scholar] [CrossRef]
- Steiner, M.; Claes, L.; Ignatius, A.; Niemeyer, F.; Simon, U.; Wehner, T. Prediction of fracture healing under axial loading, shear loading and bending is possible using distortional and dilatational strains as determining mechanical stimuli. J. R. Soc. Interface 2013, 10, 20130389. [Google Scholar] [CrossRef]
- MacLeod, A.R.; Pankaj, P.; Simpson, A.H. Does screw-bone interface modelling matter in finite element analyses? J. Biomech. 2012, 45, 1712–1716. [Google Scholar] [CrossRef]
- Serrancoli, G.; Kinney, A.L.; Fregly, B.J.; Font-Llagunes, J.M. Neuromusculoskeletal Model Calibration Significantly Affects Predicted Knee Contact Forces for Walking. J. Biomech. Eng. 2016, 138, 0810011. [Google Scholar] [CrossRef] [PubMed]
- Renishaw plc. Datasheet: Ti6Al4V ELI-0406 Powder for Additive Manufacturing; Renishaw plc: Wotton-under-Edge, UK, 2017. [Google Scholar]
- Xiao, Z.; Chen, C.; Zhu, H.; Hu, Z.; Nagarajan, B.; Guo, L.; Zeng, X. Study of residual stress in selective laser melting of Ti6Al4V. Mater. Des. 2020, 193, 108846. [Google Scholar] [CrossRef]
- ISO 6892-1:2019; Metallic materials—Tensile testing. Part 1: Method. of test at room temperature. ISO: Geneva, Switzerland, 2019.
- Guilherme, A.S.; Henriques, G.E.; Zavanelli, R.A.; Mesquita, M.F. Surface roughness and fatigue performance of commercially pure titanium and Ti-6Al-4V alloy after different polishing protocols. J. Prosthet. Dent. 2005, 93, 378–385. [Google Scholar] [CrossRef] [PubMed]
- ISO 12107:2012; Metallic materials—Fatigue testing. Statistical planning and analysis of data. ISO: Geneva, Switzerland, 2012.
- Vander Voort, G.F. Metallography: Principles and Practice; ASM International: Materials Park, OH, USA, 1984. [Google Scholar]
- Tong, J.; Bowen, C.R.; Persson, J.; Plummer, A. Mechanical properties of titanium-based Ti–6Al–4V alloys manufactured by powder bed additive manufacture. Mater. Sci. Technol. 2017, 33, 138–148. [Google Scholar] [CrossRef]
- Vrancken, B.; Thijs, L.; Kruth, J.-P.; Van Humbeeck, J. Heat treatment of Ti6Al4V produced by Selective Laser Melting: Microstructure and mechanical properties. J. Alloys Compd. 2012, 541, 177–185. [Google Scholar] [CrossRef]
- Titanium Metals Corporation. Datasheet: TIMETAL 6-4, 6-4 ELI & 6-4-.1R U Medium to High Strength General-Purpose Alloys; Titanium Metals Corporation: Warrensville Heights, OH, USA, 2000. [Google Scholar]
- Alcisto, J.; Enriquez, A.; Garcia, H.; Hinkson, S.; Steelman, T.; Silverman, E.; Valdovino, P.; Gigerenzer, H.; Foyos, J.; Ogren, J.; et al. Tensile Properties and Microstructures of Laser-Formed Ti-6Al-4V. J. Mater. Eng. Perform. 2011, 20, 203–212. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, X.; Chen, J.; Huang, W. Heat-treated microstructure and mechanical properties of laser solid forming Ti-6Al-4V alloy. Rare Met. 2009, 28, 537–544. [Google Scholar] [CrossRef]
- Kaletsch, A.; Qin, S.; Herzog, S.; Broeckmann, C. Influence of high initial porosity introduced by laser powder bed fusion on the fatigue strength of Inconel 718 after post-processing with hot isostatic pressing. Addit. Manuf. 2021, 47, 102331. [Google Scholar] [CrossRef]
- Pessard, E.; Lavialle, M.; Laheurte, P.; Didier, P.; Brochu, M. High-cycle fatigue behavior of a laser powder bed fusion additive manufactured Ti-6Al-4V titanium: Effect of pores and tested volume size. Int. J. Fatigue 2021, 149, 106206. [Google Scholar] [CrossRef]
- Du, C.; Zhao, Y.; Jiang, J.; Wang, Q.; Wang, H.; Li, N.; Sun, J. Pore defects in Laser Powder Bed Fusion: Formation mechanism, control method, and perspectives. J. Alloys Compd. 2023, 944, 169215. [Google Scholar] [CrossRef]
- Silva, M.; Shepherd, E.F.; Jackson, W.O.; Dorey, F.J.; Schmalzried, T.P. Average patient walking activity approaches 2 million cycles per year: Pedometers under-record walking activity. J. Arthroplast. 2002, 17, 693–697. [Google Scholar] [CrossRef] [PubMed]
- Ganse, B.; Yang, P.F.; Gardlo, J.; Gauger, P.; Kriechbaumer, A.; Pape, H.C.; Koy, T.; Muller, L.P.; Rittweger, J. Partial weight bearing of the tibia. Injury 2016, 47, 1777–1782. [Google Scholar] [CrossRef] [PubMed]
- Takahara, Y.; Furumatsu, T.; Nakashima, H.; Itani, S.; Nakamura, M.; Uchida, Y.; Kato, H.; Tsujimura, Y.; Iwasaki, Y.; Ochi, N. Time to Bone Union after Hybrid Closed-Wedge High Tibial Osteotomy. Acta Med. Okayama 2019, 73, 511–516. [Google Scholar] [CrossRef]
- Brinkman, J.M.; Luites, J.W.; Wymenga, A.B.; van Heerwaarden, R.J. Early full weight bearing is safe in open-wedge high tibial osteotomy. Acta Orthop. 2010, 81, 193–198. [Google Scholar] [CrossRef] [PubMed]

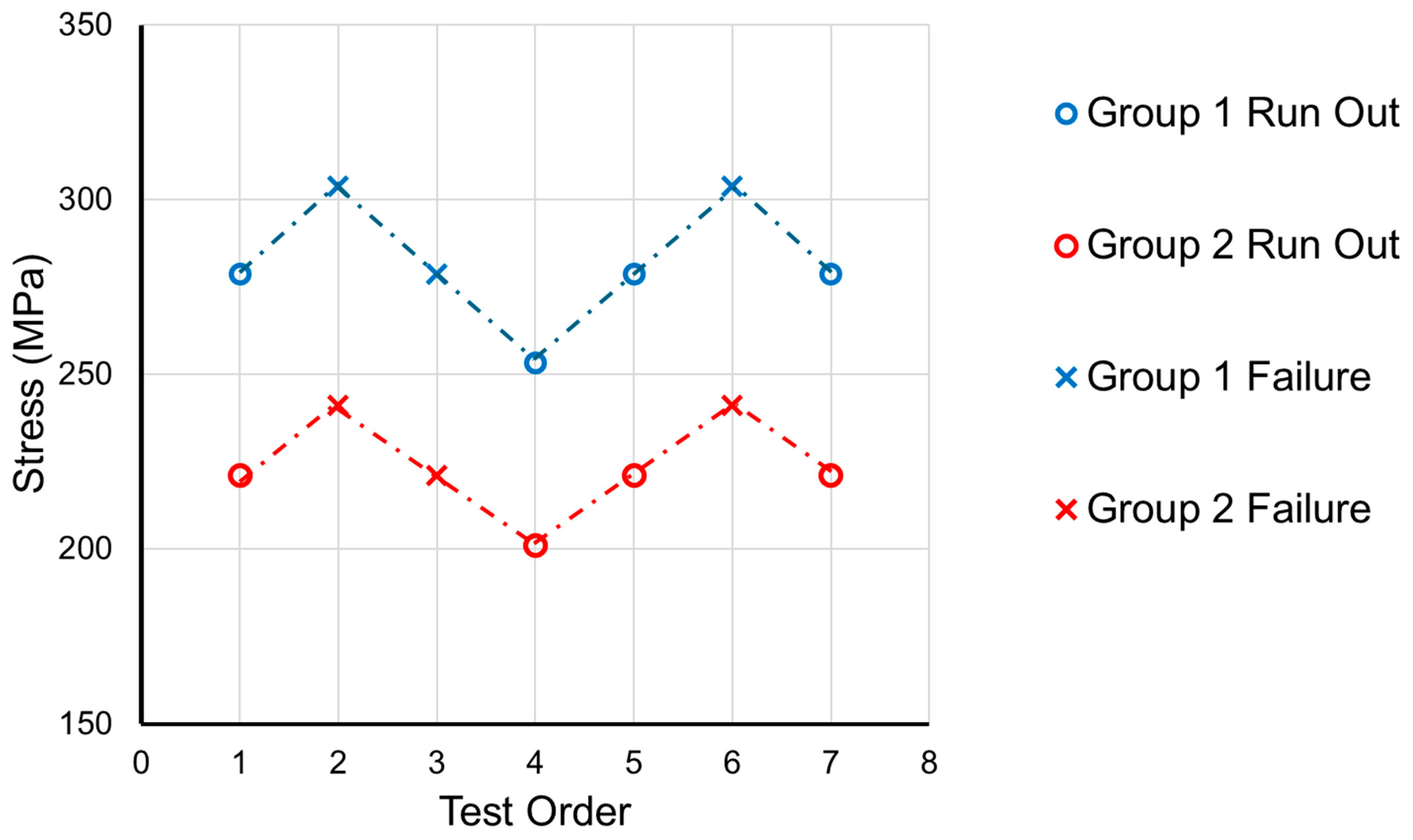



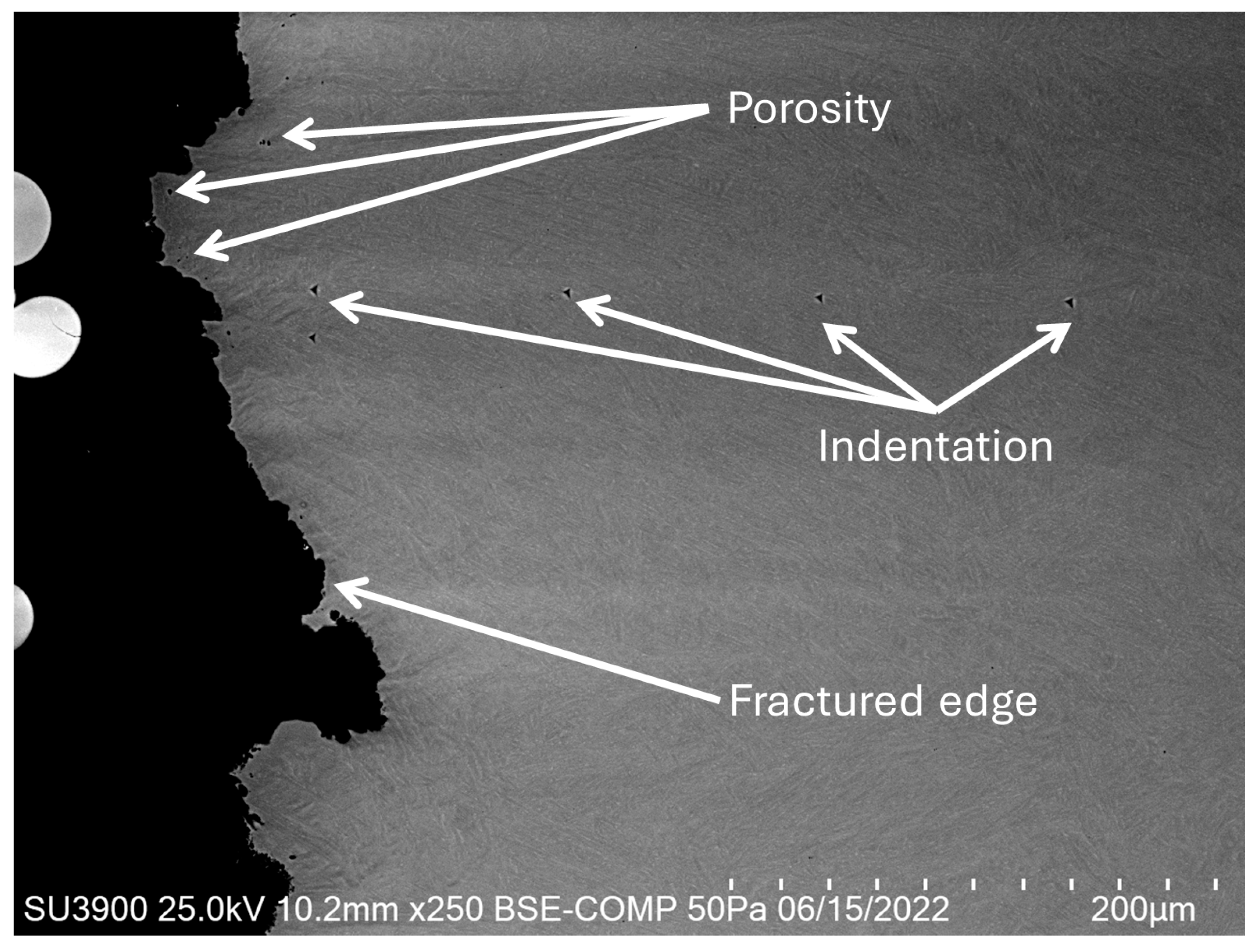
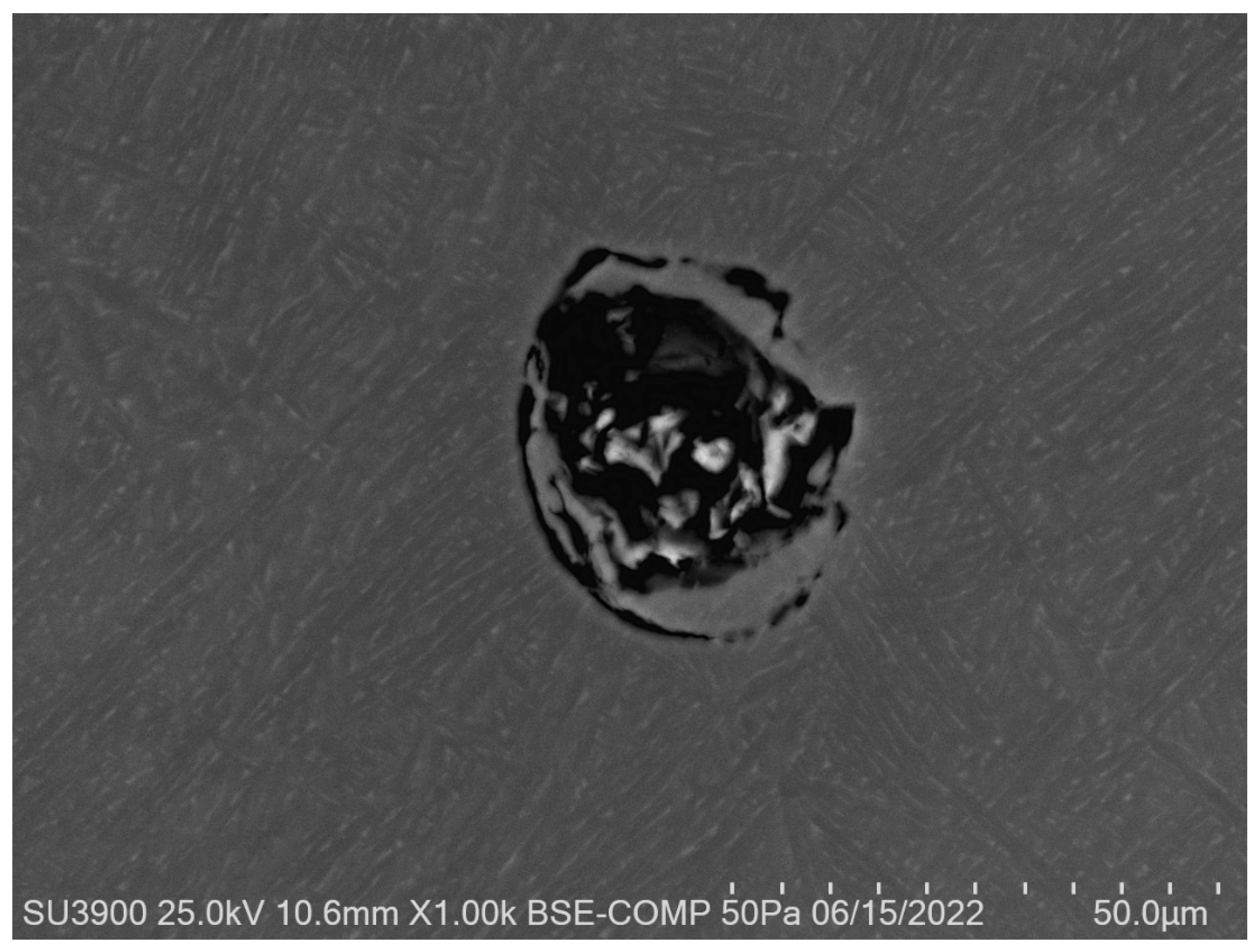

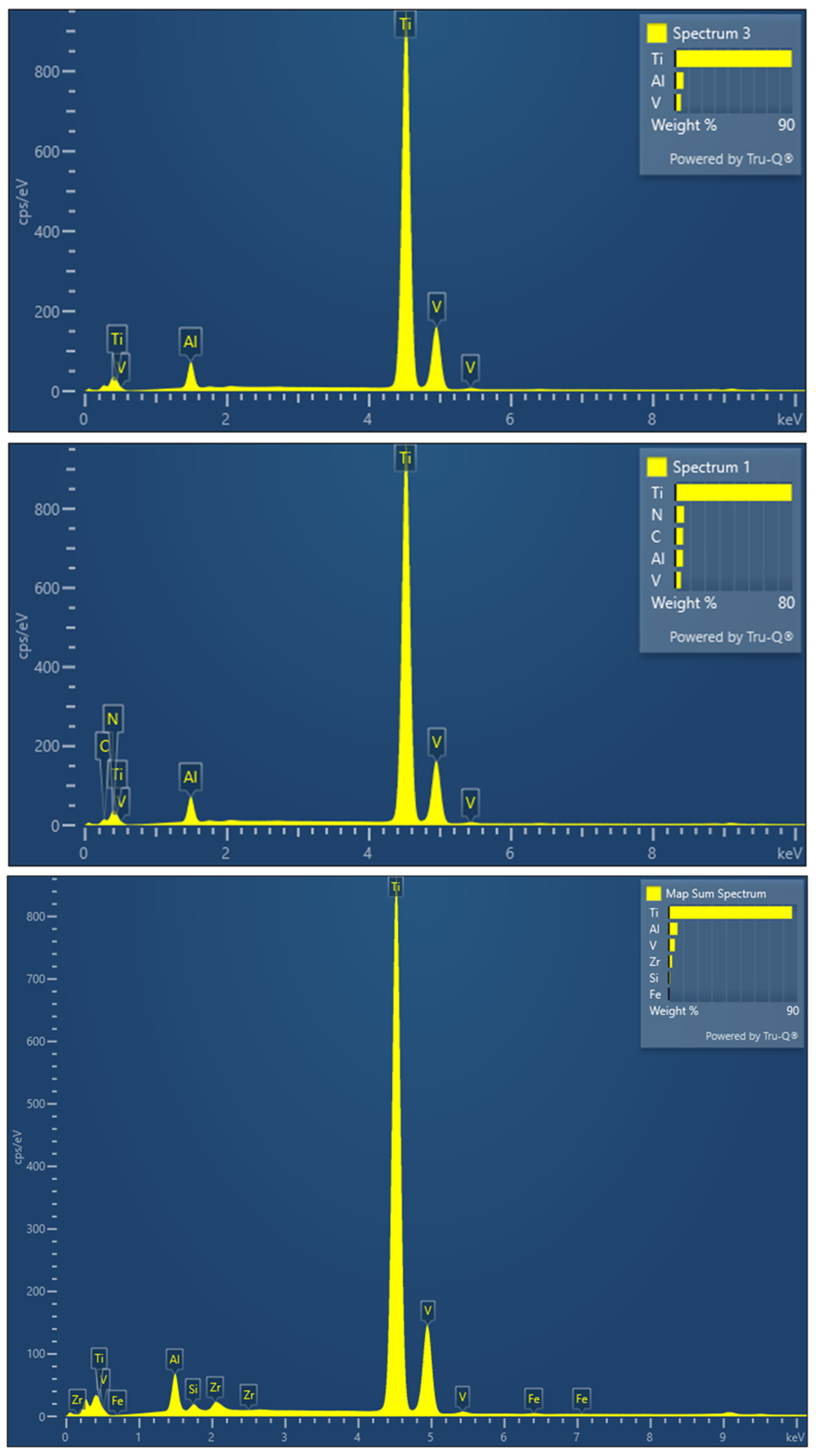
| Bending Moment (Nm) | Group 1 Bending Stress (MPa) | Group 2 Bending Stress (MPa) | Number of Repeats |
|---|---|---|---|
| 2.2 | 557.3 | 442.0 | 3 |
| 1.9 | 481.3 | 381.8 | 3 |
| 1.6 | 405.3 | 321.5 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacLeod, A.R.; Bishop, M.; Longo, A.C.; Shokrani, A.; Bowen, C.R.; Gill, H.S. Additively Produced Ti-6Al-4V Osteosynthesis Devices Meet the Requirements for Tensile Strength and Fatigue. J. Manuf. Mater. Process. 2025, 9, 227. https://doi.org/10.3390/jmmp9070227
MacLeod AR, Bishop M, Longo AC, Shokrani A, Bowen CR, Gill HS. Additively Produced Ti-6Al-4V Osteosynthesis Devices Meet the Requirements for Tensile Strength and Fatigue. Journal of Manufacturing and Materials Processing. 2025; 9(7):227. https://doi.org/10.3390/jmmp9070227
Chicago/Turabian StyleMacLeod, Alisdair R., Matthew Bishop, Alberto Casonato Longo, Alborz Shokrani, Chris Rhys Bowen, and Harinderjit Singh Gill. 2025. "Additively Produced Ti-6Al-4V Osteosynthesis Devices Meet the Requirements for Tensile Strength and Fatigue" Journal of Manufacturing and Materials Processing 9, no. 7: 227. https://doi.org/10.3390/jmmp9070227
APA StyleMacLeod, A. R., Bishop, M., Longo, A. C., Shokrani, A., Bowen, C. R., & Gill, H. S. (2025). Additively Produced Ti-6Al-4V Osteosynthesis Devices Meet the Requirements for Tensile Strength and Fatigue. Journal of Manufacturing and Materials Processing, 9(7), 227. https://doi.org/10.3390/jmmp9070227











