Comprehensive Prediction Model for Analysis of Rolling Bearing Ring Waviness
Abstract
1. Introduction
2. Materials and Methods
2.1. Bearing Material
2.2. Sample Preparation
2.3. Measurement Methodology
- Lower limit (1 upr): Eliminates shape deviations and centring errors not relevant to waviness analysis
- Upper limit (500 upr): Retains all relevant waviness information while eliminating surface roughness components and measurement noise
- Wavelength range: For RA-608-338 bearings (Ø22 mm), corresponds to 69 μm–0.14 μm wavelengths
- Implementation: Combined Gaussian and Fourier filtering techniques with smooth transient characteristics
- evaluation length (ln) 4.0 mm;
- sampling length (lr) 0.8 mm;
- number of sampling lengths 5;
- tip speed 0.5 mm/s;
- Gaussian filter according to ISO 11562:1996 [35].
- in the axial direction (parallel to the axis of the ring);
- in the circumferential direction (tangential to the orbit);
- in the radial direction (perpendicular to the surface of the orbit).
- surface grinding to achieve a surface roughness Ra < 0.4 μm;
- acetone cleaning to remove any surface contamination;
- clamping in a rigid fixture to ensure perpendicular loading;
- temperature stabilization of 23 ± 2 °C for a minimum of 30 min.
- preload 98.07 N (10 kgf);
- total load 1471 N (150 kgf);
- load time 2–8 s;
- residence time under total load 2–6 s.
2.4. Mathematical Model
2.4.1. Formulation of the Proposed Model
- C denotes the initial amplitude of the oscillations (C values are approximately 0.050).
- D characterizes the rate of exponential decay, specifically the rate at which the amplitude decreases as n increases (it is maintained at approximately 0.050).
- T represents the period of cyclic fluctuations/oscillations, that is, the net frequency with which cyclic changes occur (a value close to 30, which corresponds to the periodic behaviour of the measured process).
- φ represents a phase shift that enables the model to be precisely synchronized with the actual temporal evolution of the oscillations (the value was set to approximately 0.200).
- Initially, the analysis identified that the measured signal comprises two components: trend and periodic fluctuations.
- A power function was employed for trend analysis, facilitating a flexible description of the fundamental development of the values (A · nβ).
- For periodic oscillations, a cosine function augmented with exponential decay was selected, which accurately represents the gradual decrease in amplitude .
- By combining these two components, we obtained the final model, which was subsequently calibrated using experimental data through optimisation methods.
- This complex model is utilized to accurately predict and analyse the dynamics of the measured values, with each component possessing a clearly defined physical interpretation.
2.4.2. Physical Meaning and Interpretation of Parameters
2.4.3. Identification of Parameters
- system stiffness coefficient (k),
- damping coefficient (c),
- geometric nonlinearity parameter (α),
- coefficient of material properties (β),
- process conditions parameter (γ),
- correction factor for dynamic effects (δ).
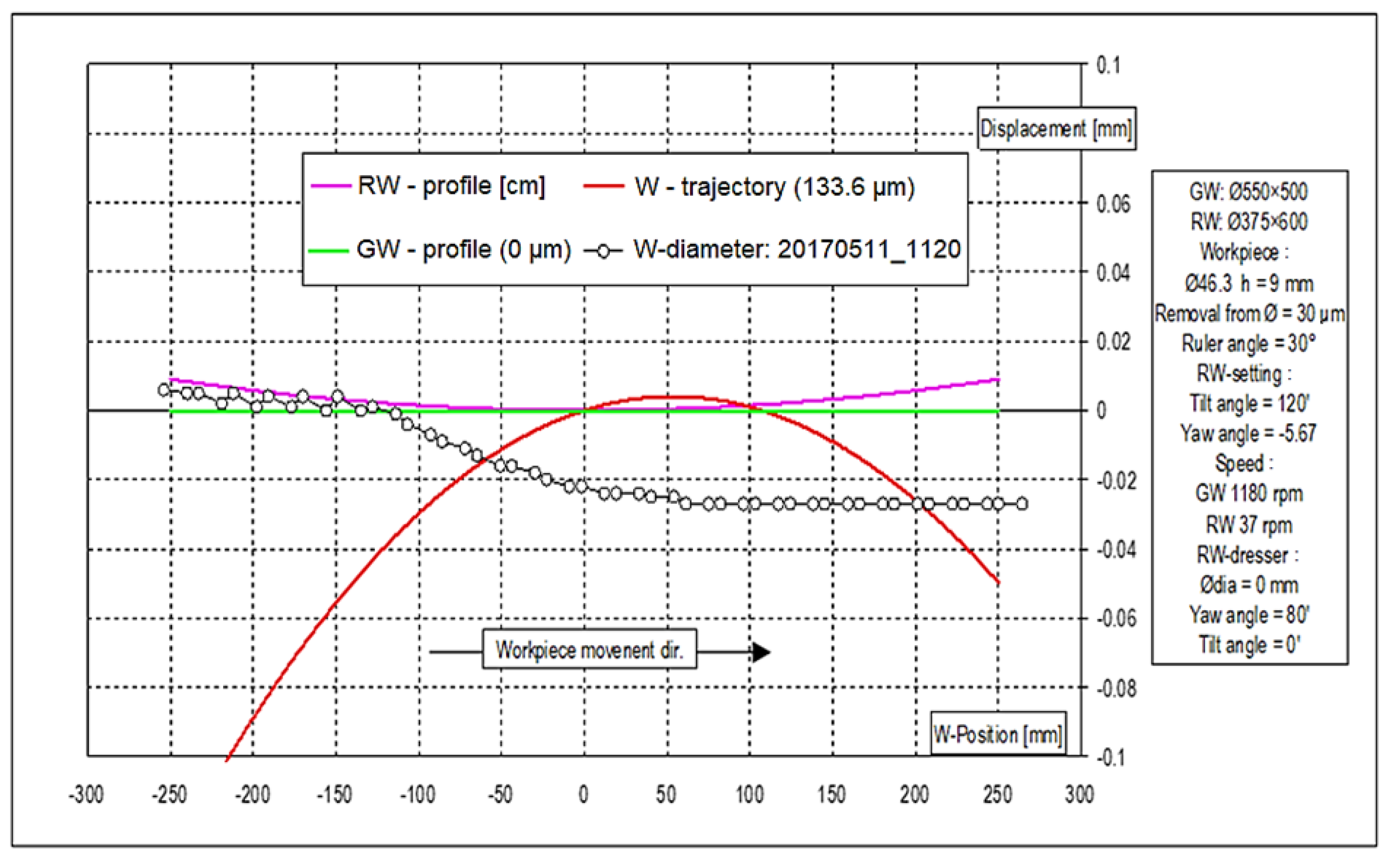
2.4.4. Workpiece Trajectory
- initial phase (position −300 to −150 mm), a gradual increase in deflection up to a maximum of 0.06 mm, corresponds to the startup phase of the grinding process,
- middle phase (position −150 to +150 mm)–relatively stable trajectory with a slight decline–optimal process conditions,
- end phase (position +150 to +300 mm), a gradual decrease in deflection towards zero.
- maximum material removal (0.031 mm),
- distribution of harvesting (initial area: gradual increase in harvesting; middle area: maximum harvesting of material; end area: gradual decrease in harvesting).
- inverse correlation (areas with larger trajectory deviation correspond to smaller material removal);
- procedural stability, which is given by the fact that the stable regions of the trajectory correlate with consistent sampling.
2.4.5. Data Acquisition and Pre-Processing
- moving average: The utilization of a moving average with a predefined window (5 to 10 measurements) facilitated the smoothing of random fluctuations and suppression of high-frequency noise.
- frequency filtering: The application of low-pass filtering, wherein frequency components not pertaining to the main dynamics of the measured process were eliminated, and the filter parameters were optimised based on Fourier analysis of the raw data.
3. Processing of the Proposed Model
3.1. Descriptive Statistical Analysis of Bearing Ring Parameters
3.2. Statistical Summary
- Surface roughness (Ra): 0.787 μm
- Waviness height (Wt): 2.405 μm
- Roundness deviation (RONt): 1119 μm
3.3. Parameter Optimization, Model Calibration, and Evaluation Metrics
- Initialization: Initial parameter values are determined based on previous experimental knowledge and theoretical assumptions.
- Iterative optimization: At each step, the parameters are adjusted according to the gradient of the objective function until the changes cease to be statistically significant (i.e., tolerance is reached).
- Cross-validation. After convergence has been achieved, data partitioning (e.g., 10-fold cross-validation) is performed to verify the generalization capability of the model and avoid overfitting.
- coefficient of determination (R2), which is defined as Equation (3):
- The root-mean-square error (RMSE) is defined by Equation (4):
3.4. Comparison of Models
- Model 1 (trend only) is defined by Equation (5):
- Model 2 (our proposed model), described by Equation (1).
- Model 3 (extended Fourier series):
4. Experimental Results
4.1. Illustration of the Results Obtained
- mean R2: >0.98 (indicating that the model accounts for more than 98% of the variability in the measured values);
- Mean RMSE: These values are substantially lower than those of the alternative models (Models 1 and 3), which demonstrates the superior predictive accuracy of the proposed model.
- Comparison of real and predicted values (Figure 4). The graphical representations illustrate the convergence of the model values (λmodel) towards the real values (λreal) as a function of the measurement index. The plots demonstrate that the deviations are minimal, and that the model accurately replicates the trend and periodic oscillations.
- Logarithmic display (Figure 5). The data were also plotted on a logarithmic scale, which facilitated the effective visualization of differences, particularly when there was a substantial range of values between the initial and final measurements. This approach enhances the clarity of the rings, wherein oscillations decay more rapidly.
4.2. Model Comparison—Experimental Overview
- Model 1 (trend only).
- ○
- Using only the trend component, R2 values of approximately 0.90 were obtained, indicating the inability of the model to capture the periodic fluctuations present in the measured data.
- Model 2 (our proposed model).
- ○
- The integration of trend and periodic components with exponential decay resulted in the model achieving R2 values exceeding 0.98, demonstrating a remarkably low RMSE. The experimental results across all rings consistently corroborated the high accuracy of this model.
- Model 3 (extended Fourier series).
- ○
- Although this model demonstrates a marginally higher R2 value (approximately 0.99), the increased complexity and larger number of parameters present a potential risk of overfitting. The experimental data indicate that the differences in RMSE values between Models 2 and 3 are minimal; however, the interpretation of physical phenomena is more complex in Model 3.
5. Discussion
- high predictive accuracy with statistical robustness substantiated by R2 values > 0.98; and clear physical interpretability of individual parameters, which facilitates practical implementation and model calibration.
- adaptability and integration into real control systems with continuous monitoring of production processes.
5.1. Cost Analysis Related to Bearing Corrugation
- emergency maintenance costs: 3–5 times higher than planned maintenance.
- spare parts costs for emergency replacement: 2–3 times higher than for a planned order (for the bearing manufacturing plant considered from the perspective of the end car manufacturer, not from the perspective of the supplier for the end customer).
5.2. Application of Artificial Intelligence in Bearing Ring Analysis
6. Conclusions
- A reduction in downtime through timely monitoring of abnormal deviations;
- An improvement in product quality due to more precise parameter control;
- The optimization of predictive maintenance, which contributes to energy and time conservation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Palmgren, A. Ball and Roller Bearing Engineering, 3rd ed.; SKF Industries Inc.: Philadelphia, PA, USA, 1959. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Eschmann, P.; Hasbargen, L.; Weigand, K. Ball and Roller Bearings: Theory, Design and Application, 2nd ed.; Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
- Tallian, T.E. Failure Atlas for Hertz Contact Machine Elements, 2nd ed.; ASME Press: New York, NY, USA, 1999. [Google Scholar]
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. Acta Polytech. Mech. Eng. Ser. 1947, 1, 1–52. [Google Scholar] [CrossRef]
- Donaldson, R.R. Simple Method for Separating Spindle Error from Test Ball Roundness Error. CIRP Ann. 1972, 21, 125–126. [Google Scholar]
- Whitehouse, D.J. Surfaces and Their Measurement; Butterworth and Heinemann: Oxford, UK, 2002. [Google Scholar]
- Reason, B.R. Handbook of Surface Metrology; Institute of Physics Publishing: Bristol, UK, 1994. [Google Scholar]
- Butler, C. An investigation into the performance of probes on coordinate measuring machines. Ind. Metrol. 1991, 1, 59–70. [Google Scholar] [CrossRef]
- Evans, C.J.; Hocken, R.J.; Estler, W.T. Self-Calibration: Reversal, Redundancy, Error Separation, and ‘Absolute Testing’. CIRP Ann. 1996, 45, 617–634. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Q.; Wang, B.; Zhang, L.; Yang, H.; Peng, Z. Effect of surface waviness on the static performance of aerostatic journal bearings. Tribol. Int. 2016, 103, 394–405. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Ding, S.; Pang, R. A time-varying friction moment calculation method for an angular contact ball bearing with waviness error. Mech. Mach. Theory 2020, 148, 103799. [Google Scholar] [CrossRef]
- Kania, L. Modelling of rollers in calculation of modified contact stress distribution in a slewing bearing. Mech. Mach. Theory 2013, 68, 29–48. [Google Scholar]
- Sadeghi, F.; Jalalahmadi, B.; Slack, T.S.; Raje, N.; Arakere, N.K. Review of Rolling Contact Fatigue. J. Tribol. 2009, 131, 041403. [Google Scholar] [CrossRef]
- Ioannides, E.; Harris, T.A. Novel fatigue life model for rolling bearings. J. Tribol. 1985, 107, 367–378. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Zhan, Z.; Wu, Q. Robust construction of normalized CNN for online intelligent condition monitoring of rolling bearings considering variable working conditions and sources. Measurement 2021, 174, 108973. [Google Scholar] [CrossRef]
- Yang, Y.J.; Ma, C.; Liu, G.H.; Lu, H.; Dai, L.; Wan, J.L.; Guo, J. Hybrid reliability assessment method based on health index construction and reliability modelling of rolling bearings. Qual. Reliab. Eng. Int. 2024, 40, 4131–4146. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Gupta, P.K.; Dill, J.F.; Bandow, B. Rolling element bearing analysis. Tribol. Trans. 1985, 28, 79–90. [Google Scholar]
- Zmarzły, P. Analysis of Technological Heredity in the Production of Rolling Bearing Rings Made of AISI 52100 Steel Based on Waviness Measurements. Materials 2022, 15, 3959. [Google Scholar] [CrossRef] [PubMed]
- Zmarzły, P. Multi-dimensional mathematical wear models of vibration generated by rolling ball bearings made of AISI 52100 bearing steel. Materials 2020, 13, 5440. [Google Scholar] [CrossRef] [PubMed]
- Šafář, M.; Stejskal, T.; Dovica, M.; Drbúl, M. Optimisation of Steel Bearing Ring Dimensions for Automotive Applications. Appl. Sci. 2021, 11, 2935. [Google Scholar]
- Yin, F.; Yi, Y.; Yang, C.; Cheng, G.J. Nanoengineering steel’s durability: Creating gradient nanostructured spheroidal carbides and lath-shaped nano-martensite via ultrasonic shot peening. Nanoscale 2024, 16, 20570–20588. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, F.; Qian, D.; Yin, F.; Wang, H.; Wang, X.; Hu, S.; Chi, J. Enhanced wear resistance of the ultra-strong ultrasonic shot-peened M50 bearing steel with gradient nanograins. Metals 2022, 12, 424. [Google Scholar] [CrossRef]
- Paladugu, M.; Hyde, R.S. Microstructure deformation and transformation studies of bearing steels subject to rolling contact fatigue. Mater. Charact. 2005, 55, 13–23. [Google Scholar]
- Yu, W.; Harris, T.A.; Lundberg, G. Rolling Bearing Life Prediction, Theory, and Application. Tribol. Trans. 2005, 48, 312–325. [Google Scholar]
- Liu, W.; Zhang, Y.; Feng, Z.J.; Zhao, J.S.; Wang, D. A study on waviness-induced vibration of ball bearings based on signal coherence theory. J. Sound Vib. 2014, 333, 6107–6120. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, A.; Yang, H.; Zhang, T.; Cao, C.; Wu, G. Vibration analysis of a deep groove ball bearing with localized and distributed faults subject to waviness based on an improved model under time-varying velocity conditions. J. Vib. Control 2023, 29, 3259–3274. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q.; Beer, M. Review of vibration-based gear-wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Shestakov, A.L.; Qodirov, I. Correlation-functional method and algorithm for signal processing in bearing fault diagnosis. Meas. Sci. Technol. 2021, 32, 095008. [Google Scholar]
- ISO 492:2014; Rolling Bearings—Radial Bearings—Dimensions and Tolerances. International Organization for Standardization: Geneva, Switzerland, 2014.
- ISO 1132-1:2000; Rolling Bearings—Tolerances—Part 1: Terms and Definitions. International Organization for Standardization: Geneva, Switzerland, 2000.
- ISO 4287:1997; Geometric Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Parameters for Surface Texture. International Organization for Standardization: Geneva, Switzerland, 1997.
- ISO 4288:1996; Geometric Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. International Organization for Standardization: Geneva, Switzerland, 1996.
- ISO 11562:1996; Geometric Product Specifications (GPS)—Surface Texture: Profile Method—Metrological Characteristics of Phase Correct Filters. International Organization for Standardization: Geneva, Switzerland, 1996.
- ASTM E18-20; Standard Test Methods for Rockwell Hardness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- Ljung, L. System Identification: Theory for the User; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Duma, S.; Duma, D.M.; Duma, I.; Buzdugan, D. The Influence of Heat Treatment Applied to 100Cr6 Steel on Microstructure and Hardness. Key Eng. Mater. 2023, 952, 11–16. [Google Scholar] [CrossRef]
- Sri Siva, R.; Mohan Lal, D.; Kesavan Nair, P.; Jaswin, M.A. Influence of cryogenic treatment on the wear characteristics of 100Cr6 bearing steel. Int. J. Miner. Metall. Mater. 2014, 21, 46–51. [Google Scholar] [CrossRef]
- Yu, A.; Ruan, R.; Zhang, X.; He, Y.; Li, K. Reliability analysis of rolling bearings considering failure mode correlations. Qual. Reliab. Eng. Int. 2024, 40, 3079–3095. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of the MDPI and/or editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |

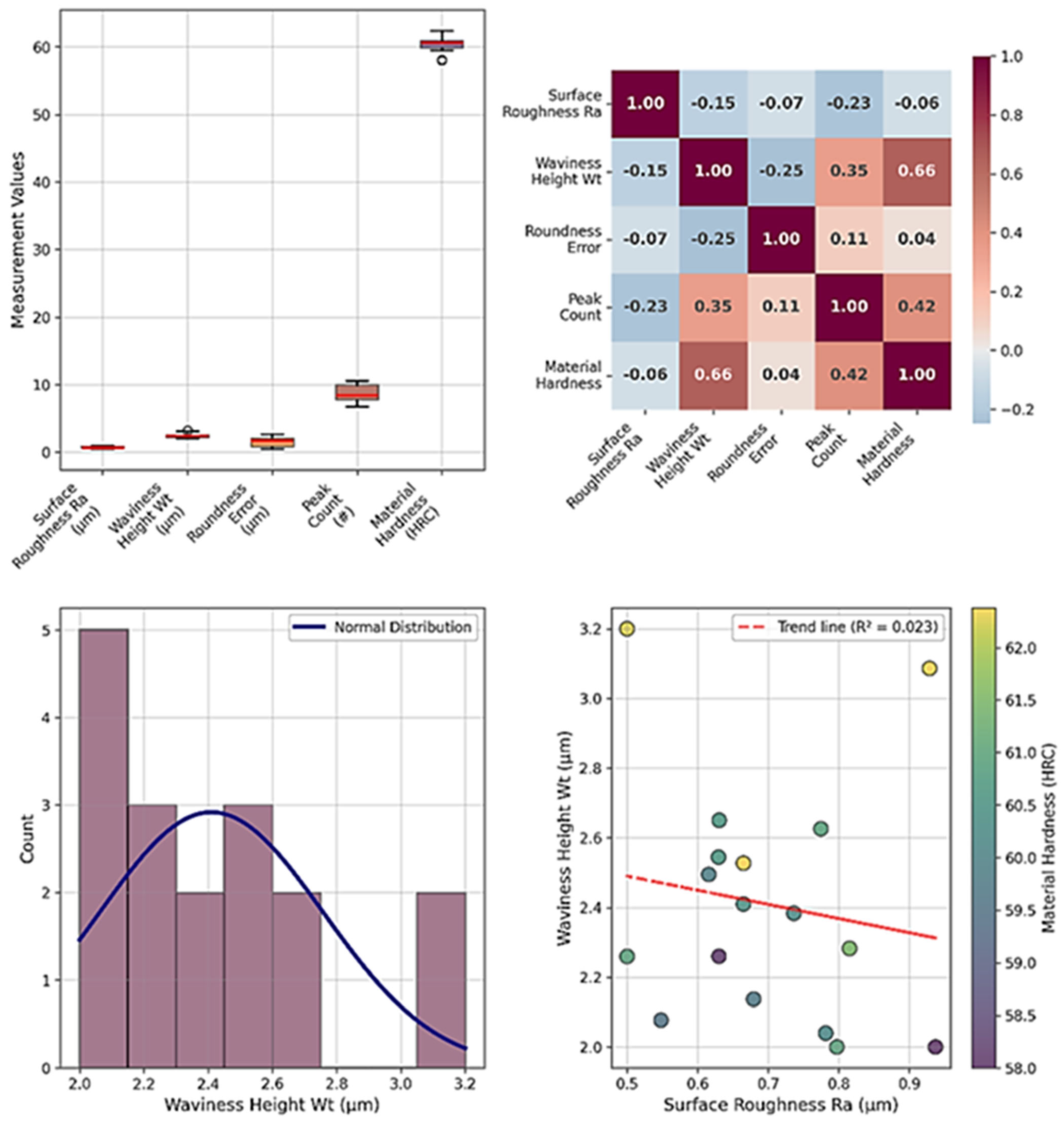


| Statistic | Ring ID | Ra (µm) | Wt (µm) | Roundness Error | Peak Count (µm) | Material Hardness (HRC) |
|---|---|---|---|---|---|---|
| count | 17.0 | 17.0 | 17.0 | 17.0 | 17.0 | 17.0 |
| mean | 9.0 | 0.787 | 2.405 | 1.119 | 7.647 | 61.944 |
| std | 5.05 | 0.146 | 0.365 | 0.235 | 1.32 | 2.256 |
| min | 1.0 | 0.513 | 1.93 | 0.71 | 6.0 | 56.761 |
| 25% | 5.0 | 0.73 | 2.137 | 0.895 | 7.0 | 60.963 |
| 50% | 9.0 | 0.765 | 2.383 | 1.171 | 7.0 | 62.174 |
| 75% | 13.0 | 0.881 | 2.544 | 1.281 | 9.0 | 62.723 |
| max | 17.0 | 1.037 | 3.241 | 1.464 | 10.0 | 65.129 |
| n | Real Values λreal(n) | Limit Values λlimit(n) | Predicted Values λmodel(n) |
|---|---|---|---|
| 1 | 0.098 | 2.90 | 0.095 |
| 2 | 0.094 | 2.79 | 0.092 |
| 3 | 0.090 | 2.70 | 0.089 |
| 4 | 0.087 | 2.62 | 0.086 |
| 5 | 0.085 | 2.55 | 0.083 |
| 6 | 0.082 | 2.48 | 0.080 |
| 7 | 0.080 | 2.42 | 0.078 |
| 8 | 0.078 | 2.36 | 0.076 |
| 9 | 0.076 | 2.31 | 0.073 |
| 10 | 0.074 | 2.26 | 0.071 |
| Ring | A | β | C | D | T | φ |
|---|---|---|---|---|---|---|
| 1 | 0.100 | −0.020 | 0.050 | 0.050 | 30.00 | 0.200 |
| 2 | 0.102 | −0.019 | 0.049 | 0.051 | 30.10 | 0.198 |
| 3 | 0.098 | −0.021 | 0.051 | 0.050 | 29.90 | 0.202 |
| 4 | 0.101 | −0.020 | 0.050 | 0.050 | 30.00 | 0.199 |
| 5 | 0.099 | −0.019 | 0.052 | 0.052 | 30.20 | 0.201 |
| 6 | 0.100 | −0.020 | 0.049 | 0.050 | 29.80 | 0.200 |
| 7 | 0.102 | −0.021 | 0.050 | 0.051 | 30.10 | 0.198 |
| 8 | 0.097 | −0.020 | 0.051 | 0.050 | 30.00 | 0.202 |
| 9 | 0.101 | −0.019 | 0.049 | 0.050 | 29.90 | 0.200 |
| 10 | 0.100 | −0.020 | 0.050 | 0.049 | 30.00 | 0.203 |
| 11 | 0.099 | −0.020 | 0.051 | 0.051 | 30.20 | 0.200 |
| 12 | 0.101 | −0.021 | 0.050 | 0.050 | 30.00 | 0.199 |
| 13 | 0.100 | −0.019 | 0.050 | 0.052 | 30.10 | 0.201 |
| 14 | 0.102 | −0.020 | 0.049 | 0.050 | 30.00 | 0.200 |
| 15 | 0.099 | −0.021 | 0.051 | 0.051 | 29.90 | 0.200 |
| 16 | 0.101 | −0.020 | 0.050 | 0.050 | 30.20 | 0.202 |
| 17 | 0.100 | −0.019 | 0.050 | 0.050 | 30.00 | 0.200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šafář, M.; Dütsch, L.; Harničárová, M.; Valíček, J.; Kušnerová, M.; Tozan, H.; Kopal, I.; Falta, K.; Borzan, C.; Palková, Z. Comprehensive Prediction Model for Analysis of Rolling Bearing Ring Waviness. J. Manuf. Mater. Process. 2025, 9, 220. https://doi.org/10.3390/jmmp9070220
Šafář M, Dütsch L, Harničárová M, Valíček J, Kušnerová M, Tozan H, Kopal I, Falta K, Borzan C, Palková Z. Comprehensive Prediction Model for Analysis of Rolling Bearing Ring Waviness. Journal of Manufacturing and Materials Processing. 2025; 9(7):220. https://doi.org/10.3390/jmmp9070220
Chicago/Turabian StyleŠafář, Marek, Leonard Dütsch, Marta Harničárová, Jan Valíček, Milena Kušnerová, Hakan Tozan, Ivan Kopal, Karel Falta, Cristina Borzan, and Zuzana Palková. 2025. "Comprehensive Prediction Model for Analysis of Rolling Bearing Ring Waviness" Journal of Manufacturing and Materials Processing 9, no. 7: 220. https://doi.org/10.3390/jmmp9070220
APA StyleŠafář, M., Dütsch, L., Harničárová, M., Valíček, J., Kušnerová, M., Tozan, H., Kopal, I., Falta, K., Borzan, C., & Palková, Z. (2025). Comprehensive Prediction Model for Analysis of Rolling Bearing Ring Waviness. Journal of Manufacturing and Materials Processing, 9(7), 220. https://doi.org/10.3390/jmmp9070220












