New Hybrid Method for Buffer Positioning and Production Control Using DDMRP Logic in Smart Manufacturing
Abstract
1. Introduction
- Strategic Inventory Positioning: Identifying critical points within the supply chain for buffer placement, which act as decoupling points to absorb variability and protect material flow.
- Buffer Profiles and Levels: Establishing buffer zones (green, yellow, red) at these critical points, dynamically adjusted based on Lead Times, Demand Variability, and supply reliability.
- Dynamic and Reactive Adjustments: Continuously refining buffer levels in response to changes in demand patterns and supply conditions to optimize inventory levels.
- Demand-Driven Planning: Utilizing actual demand data to drive replenishment decisions, reducing reliance on forecasts, and minimizing the bullwhip effect.
- Visible and Collaborative Execution: Ensuring real-time supply chain visibility and fostering collaboration to promptly address issues and align actions with current market conditions.
2. State of the Art
- Conceptual Studies and Literature Reviews: This group includes seminal works such as the foundational books by [1,7], which established the theoretical underpinnings of DDMRP by integrating concepts from MRP, Kanban, and other planning methods. Literature reviews in this category aim to define the key principles and applications of DDMRP, situating it within the broader landscape of production planning.
- Comparative and Case Studies: Studies in this domain assess DDMRP’s performance relative to traditional PPC systems. These comparisons, often conducted through statistical analyses or simulation models, consistently demonstrate DDMRP’s superiority in terms of service level and operational costs [8,9,10]. For instance, [2] found that DDMRP outperforms other PPCs in regards of bottlenecks, demand variability, and Due Date Tightness.
- Buffer Positioning: Buffer positioning—the first step in DDMRP implementation—involves determining which items in the Bill of Materials should be protected by buffers. This decision is critical, as buffer stocks incur operational costs and should be applied selectively to high-risk items that are vulnerable to demand variability. Research in this area includes optimization-based approaches for strategically positioning buffers. For example, [11] proposed a Genetic Algorithm to optimize buffer placement by balancing operational costs and service levels in a single-stage production setting. Similarly, [12] introduced a mixed-integer programming model for buffer positioning aimed at minimizing buffer levels. However, the first approach provides no performance guarantees, while the second relies on average stock estimates without accounting for actual replenishment triggers.
- Parameterization of DDMRP: Once buffers are positioned, their sizing and replenishment parameters must be determined. These parameters, such as Lead Time Factor and Variability Factor, are often fixed subjectively. [13] suggest using statistical analysis to derive parametrization rules. Some other papers, namely [14], suggest automatic procedures driven by optimization to fix the parameters of DDMRP. In [11], a multi-objective metaheuristic to parameterize DDMRP is proposed. The method determines a comprehensive set of eight parameters while maximizing On Time Demand and minimizing average stock for one production unit. The method combines simulation and optimization [15] to yield solutions rapidly. However, the solutions come with no performance guarantee, which constitutes the major drawback of the method.
3. Problem Statement and Mathematical Modeling of DDMRP
- The system consists of J production stations arranged in a topology with diverging branches, designed to accommodate the processing of multiple product references.
- The processing time pj at each station j is assumed to be constant.
- The primary source of variability is the incoming demand, which directly affects the output stations.
- Each output station is associated with a specific product reference; thus, the model addresses multi-reference Production Planning and Control.
- The production flow is constrained to a directed acyclic structure.
- Only production systems for manufactured products with internal supply chains are considered. This assumption influences the estimation of lead time variations, which will be explicitly modeled in the analysis.
4. Proposed Hybrid Method
4.1. Crossover Operator
4.2. Mutation Operator
4.3. Mutation Probability
4.4. Selection Technique
4.5. Managing MIP Constraints
- Repair-Based Methods: Repair-based methods involve modifying infeasible solutions to satisfy MIP constraints. Techniques such as constraint repair heuristics and projection are commonly employed. For example, infeasible solutions can be adjusted by rounding fractional variables to meet integer constraints or solving a simplified MIP subproblem to project solutions into the feasible region. Studies such [28] highlight repair-based approaches for handling constraints in GAs. While these methods ensure feasibility, they can be computationally expensive, particularly when constraints are complex or highly non-linear.
- Penalty-Based Methods: This approach integrates constraints into the fitness function by adding penalty terms that penalize constraint violations. Penalty coefficients are carefully tuned to balance the exploration of infeasible regions and the emphasis on feasibility. Dynamic penalty strategies, as described by [29], adapt penalty parameters over iterations, increasing the focus on feasibility as the GA converges. This method is simple to implement but requires careful tuning of penalty coefficients, as poor tuning can hinder either exploration or feasibility.
- Feasibility-Based Selection: Feasibility-based selection prioritizes feasible solutions during the selection process without directly repairing or penalizing infeasible solutions. Feasible solutions are ranked higher and infeasible ones are deprioritized, even if their fitness is superior. Alternatively, multi-objective optimization can be employed, treating constraint violations as secondary objectives, as described by [30]. This strategy maintains diversity within the population but may slow convergence since infeasible solutions remain in the pool.
- Direct Encoding of Feasibility: In this method, the GA’s encoding is designed to inherently satisfy MIP constraints. Custom genetic operators ensure that offspring generated during crossover and mutation remain feasible. Works such [31] emphasize the effectiveness of direct encoding for constrained optimization problems. However, this method can limit exploration and is challenging to implement for problems with intricate constraints.
- MIP-Guided Initialization and Repair: MIP solvers can be employed to assist GAs by generating feasible initial solutions or repairing infeasible ones. For example, a solver can be used to refine GA-generated solutions by solving a localized version of the MIP problem. The integration of MIP techniques into GAs has been explored by [32], who demonstrated that MIP solvers can efficiently enforce feasibility while leveraging the exploratory capabilities of GAs. While effective, this approach increases computational overhead due to frequent use of the MIP solver.
- Hybrid Decomposition Strategies: Hybrid decomposition divides the optimization problem into a GA subproblem and a MIP subproblem. The GA explores the broader solution space, while the MIP subproblem ensures feasibility for specific decision variables or constraints.
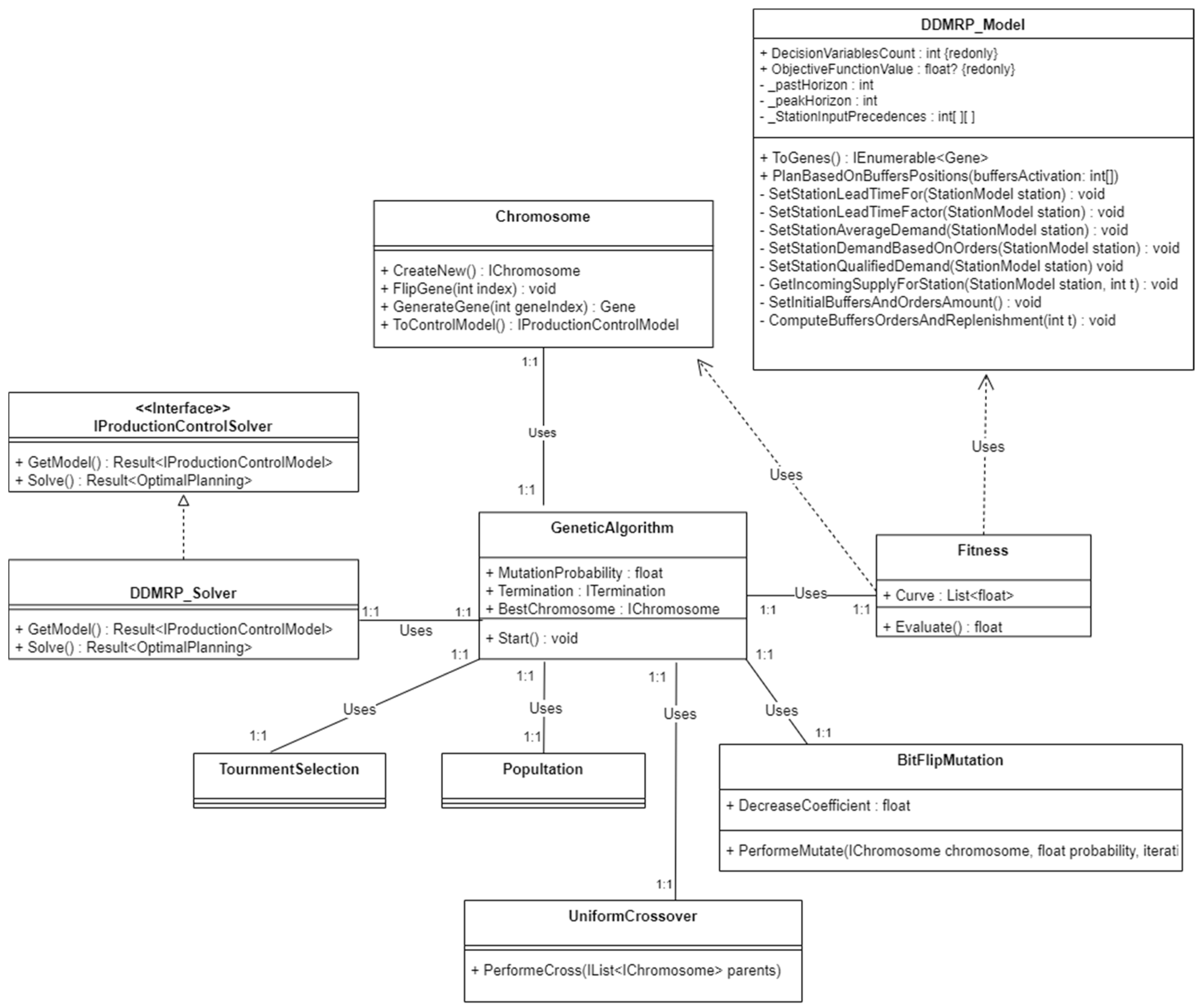
5. Implementation Aspects
- The objective function, defining the optimization goal.
- The constraints, ensuring feasible solutions.
- A collection of Station Models (StationModel), representing individual production stations.
- Dependency constraints between these stations.
- Chromosome and Fitness classes. Fitness class builds an instance of DDMRP_Model based on chromosome genes in order to evaluate the solution fitness when selection is performed.
- Tournament selection, provided by the library, for choosing individuals for reproduction.
- Population management, also based on built-in library classes.
- Built-in uniform crossover operator.
- Built-in Bit-Flip mutation operator.
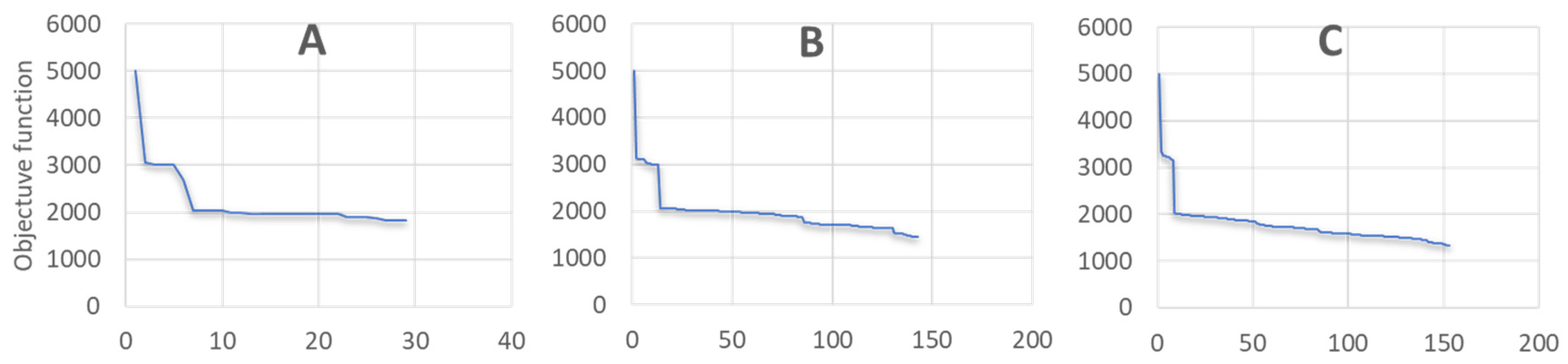
6. Case Study
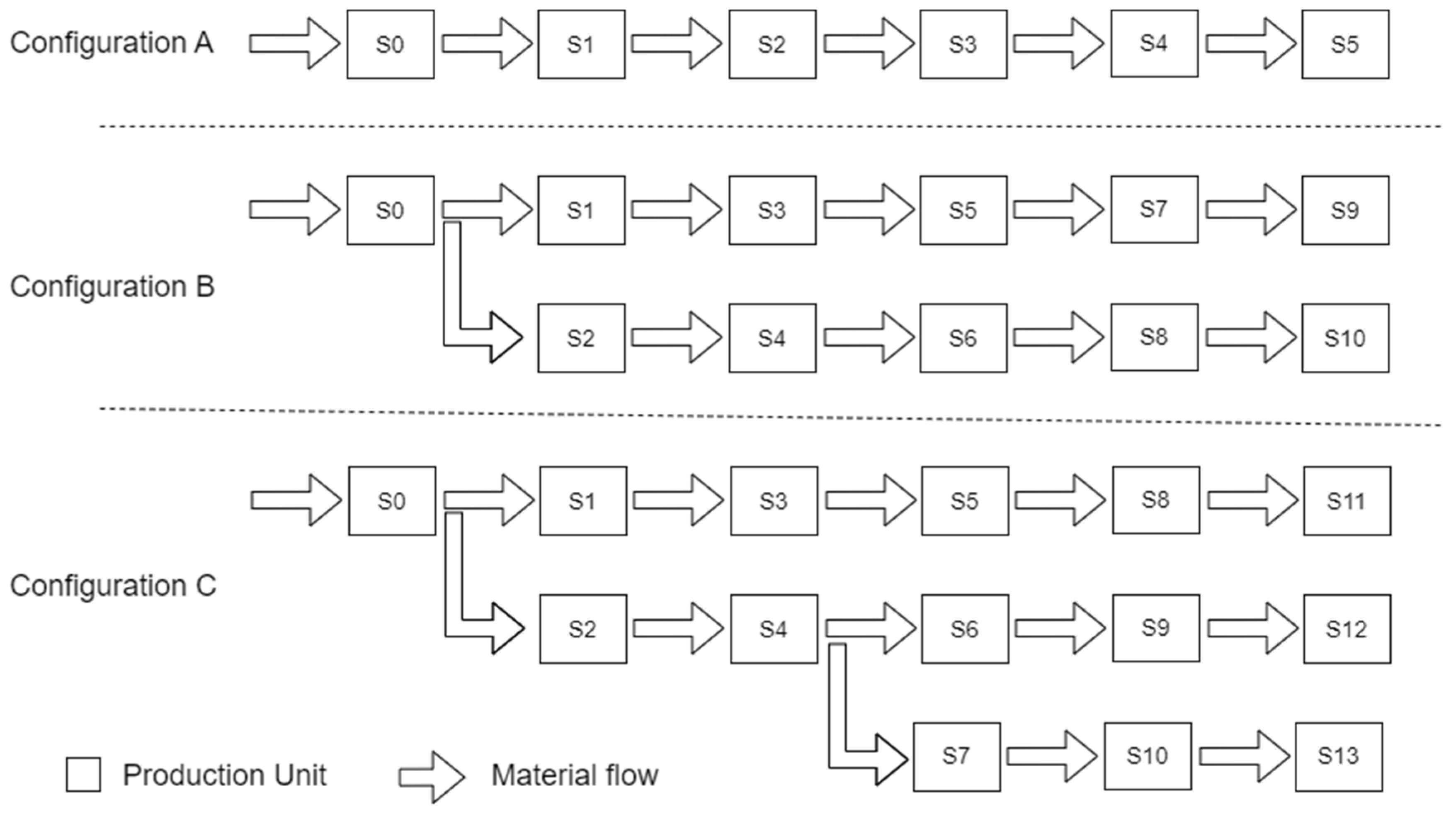
- Configuration A: Simple linear layout composed of six production units. The line is considered balanced, with a uniform processing time of 0.01 at each station. The demand is concentrated at output station S5, with a total demand denoted by DA. The number of possible configurations is .
- Configuration B: Linear layout with a single ramification at station S0, resulting in two branches. The line consists of eleven production units, with output stations located at S9 and S10. The demand is equally distributed between them and is denoted DB = DA/2. The processing time at S0 is 0.01, while all other stations operate at 0.02 to maintain system balance. The number of possible configurations is .
- Configuration C: More complex layout featuring two ramifications, the first at S0 and the second at S4, resulting in three separate material flows. The layout remains balanced, with processing times set to 0.01 at S0, 0.02 at stations S1–S4, and 0.03 at all subsequent stations. The demand at each output station is labeled DC = DA/3. The number of possible configurations is .
7. Conclusions
- Human resources: This includes factors such as workforce skill levels, fatigue, shift schedules, and absenteeism, all of which influence production reliability and performance [37,38,39,40,41]. Moreover, the model introduced in this work can be integrated with simulation techniques to more effectively account for additional sources of variability beyond those related to external demand.
- Machine-related disruptions such as equipment breakdowns, maintenance cycles, or setup delays, which affect lead times and resource availability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Generated Results for Configuration C
| Instant | Net Flow | Buffer | Demand | Qualified Demand | On Order Inventory | Order Amount | Replenishment |
|---|---|---|---|---|---|---|---|
| 0 | −130 | 0 | 52 | 130 | 0 | 0 | |
| 1 | −115 | 0 | 85 | 115 | 0 | 306 | 1 |
| 2 | 214 | 0 | 41 | 92 | 306 | 0 | |
| 3 | 36 | 0 | 150 | 270 | 306 | 155 | 1 |
| 4 | 51 | 156 | 110 | 260 | 155 | 140 | 1 |
| 5 | 221 | 46 | 48 | 120 | 295 | 0 | |
| 6 | 113 | 153 | 72 | 180 | 140 | 78 | 1 |
| 7 | 224 | 221 | 30 | 75 | 78 | 0 | |
| 8 | 169 | 191 | 40 | 100 | 78 | 22 | 1 |
| 9 | 51 | 229 | 80 | 200 | 22 | 140 | 1 |
| 10 | 91 | 149 | 88 | 220 | 162 | 100 | 1 |
| 11 | 188 | 83 | 54 | 135 | 240 | 3 | 1 |
| 12 | 187 | 169 | 34 | 85 | 103 | 4 | 1 |
| 13 | 122 | 235 | 48 | 120 | 7 | 69 | 1 |
| 14 | 78 | 190 | 74 | 185 | 73 | 113 | 1 |
| 15 | 82 | 120 | 88 | 220 | 182 | 109 | 1 |
| 16 | 153 | 101 | 68 | 170 | 222 | 38 | 1 |
| 17 | 158 | 146 | 54 | 135 | 147 | 33 | 1 |
| 18 | 187 | 201 | 34 | 85 | 71 | 4 | 1 |
| 19 | 107 | 205 | 54 | 135 | 37 | 84 | 1 |
| 20 | 197 | 184 | 30 | 75 | 88 | 0 | |
| 21 | 122 | 158 | 48 | 120 | 84 | 69 | 1 |
| 22 | 83 | 194 | 72 | 180 | 69 | 108 | 1 |
| 23 | 79 | 122 | 88 | 220 | 177 | 112 | 1 |
| 24 | 153 | 103 | 68 | 170 | 220 | 38 | 1 |
| 25 | 113 | 143 | 72 | 180 | 150 | 78 | 1 |
| 26 | 224 | 183 | 30 | 75 | 116 | 0 | |
| 27 | 214 | 191 | 22 | 55 | 78 | 0 | |
| 28 | 67 | 247 | 72 | 180 | 0 | 124 | 1 |
| 29 | 224 | 175 | 30 | 75 | 124 | 0 |
| Instant | Net Flow | Buffer | Demand | Qualified Demand | On Order Inventory | Order Amount | Replenishment |
|---|---|---|---|---|---|---|---|
| 0 | −26 | 0 | 0 | 26 | 0 | 0 | |
| 1 | −57 | 0 | 47 | 57 | 0 | 65 | 1 |
| 2 | 1 | 18 | 0 | 17 | 0 | 7 | 1 |
| 3 | −62 | 25 | 47 | 87 | 0 | 70 | 1 |
| 4 | −2 | 48 | 0 | 50 | 0 | 10 | 1 |
| 5 | 34 | 58 | 0 | 24 | 0 | 0 | |
| 6 | 22 | 58 | 0 | 36 | 0 | 0 | |
| 7 | 43 | 58 | 0 | 15 | 0 | 0 | |
| 8 | 38 | 58 | 0 | 20 | 0 | 0 | |
| 9 | 18 | 58 | 0 | 40 | 0 | 0 | |
| 10 | 14 | 58 | 0 | 44 | 0 | 0 | |
| 11 | 31 | 58 | 0 | 27 | 0 | 0 | |
| 12 | 41 | 58 | 0 | 17 | 0 | 0 | |
| 13 | 34 | 58 | 0 | 24 | 0 | 0 | |
| 14 | 21 | 58 | 0 | 37 | 0 | 0 | |
| 15 | 14 | 58 | 0 | 44 | 0 | 0 | |
| 16 | 24 | 58 | 0 | 34 | 0 | 0 | |
| 17 | 31 | 58 | 0 | 27 | 0 | 0 | |
| 18 | 41 | 58 | 0 | 17 | 0 | 0 | |
| 19 | 31 | 58 | 0 | 27 | 0 | 0 | |
| 20 | 43 | 58 | 0 | 15 | 0 | 0 | |
| 21 | 34 | 58 | 0 | 24 | 0 | 0 | |
| 22 | 22 | 58 | 0 | 36 | 0 | 0 | |
| 23 | 14 | 58 | 0 | 44 | 0 | 0 | |
| 24 | 24 | 58 | 0 | 34 | 0 | 0 | |
| 25 | 22 | 58 | 0 | 36 | 0 | 0 | |
| 26 | 43 | 58 | 0 | 15 | 0 | 0 | |
| 27 | 47 | 58 | 0 | 11 | 0 | 0 | |
| 28 | 22 | 58 | 0 | 36 | 0 | 0 | |
| 29 | 43 | 58 | 0 | 15 | 0 | 0 |
References
- Ptak, C.A.; Smith, C.; Orlicky, J.A. Orlicky’s Material Requirements Planning, 3rd ed.; Online-Ausg.; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-0-07-175564-1. [Google Scholar]
- Thürer, M.; Fernandes, N.O.; Stevenson, M. Production Planning and Control in Multi-Stage Assembly Systems: An Assessment of Kanban, MRP, OPT (DBR) and DDMRP by Simulation. Int. J. Prod. Res. 2022, 60, 1036–1050. [Google Scholar] [CrossRef]
- Demand Driven Institute. Demand Driven Case Studies. Available online: https://www.demanddriveninstitute.com/case-studies (accessed on 6 April 2025).
- Ptak, C.; Smith, C. Demand Driven Material Requirements Planning (DDMRP); Industrial Press, Inc.: New York, NY, USA, 2016; ISBN 978-0-8311-9384-3. [Google Scholar]
- Azzamouri, A.; Baptiste, P.; Dessevre, G.; Pellerin, R. Demand Driven Material Requirements Planning (DDMRP): A Systematic Review and Classification. J. Ind. Eng. Manag. 2021, 14, 439. [Google Scholar] [CrossRef]
- Marzougui, M.E.; Messaoudi, N.; Dachry, W.; Sarir, H.; Bensassi, B. Demand Driven MRP: Literature Review and Research Issues. 2020. Available online: https://hal.science/hal-03193163/ (accessed on 29 March 2025).
- Pekarcıkova, M.; Trebuna, P.; Kliment, M.; Trojan, J. Demand Driven Material Requirements Planning. Some Methodical and Practical Comments. Manag. Prod. Eng. Rev. 2019, 10, 50–59. [Google Scholar] [CrossRef]
- Favaretto, D.; Marin, A. An Empirical Comparison Study Between DDMRP and MRP in Material Management. SSRN J. 2018. [Google Scholar] [CrossRef]
- Miclo, R.; Fontanili, F.; Lauras, M.; Lamothe, J.; Milian, B. An Empirical Comparison of MRPII and Demand-Driven MRP. IFAC-Pap. 2016, 49, 1725–1730. [Google Scholar] [CrossRef]
- Shofa, M.J.; Widyarto, W.O. Effective Production Control in an Automotive Industry: MRP vs. Demand-Driven MRP; AIP Publishing: Surakarta, Indonesia, 2017; p. 020004. Available online: https://pubs.aip.org/aip/acp/article/815355 (accessed on 29 March 2025).
- Damand, D.; Lahrichi, Y.; Barth, M. Parameterisation of Demand-Driven Material Requirements Planning: A Multi-Objective Genetic Algorithm. Int. J. Prod. Res. 2023, 61, 5134–5155. [Google Scholar] [CrossRef]
- Achergui, A.; Allaoui, H.; Hsu, T. Optimisation of the Automated Buffer Positioning Model under DDMRP Logic. IFAC-Pap. 2021, 54, 582–588. [Google Scholar] [CrossRef]
- Velasco Acosta, A.P.; Mascle, C.; Baptiste, P. Applicability of Demand-Driven MRP in a Complex Manufacturing Environment. Int. J. Prod. Res. 2020, 58, 4233–4245. [Google Scholar] [CrossRef]
- Lee, C.-J.; Rim, S.-C. A Mathematical Safety Stock Model for DDMRP Inventory Replenishment. Math. Probl. Eng. 2019, 2019, 6496309. [Google Scholar] [CrossRef]
- Trigueiro De Sousa Junior, W.; Barra Montevechi, J.A.; De Carvalho Miranda, R.; Teberga Campos, A. Discrete Simulation-Based Optimization Methods for Industrial Engineering Problems: A Systematic Literature Review. Comput. Ind. Eng. 2019, 128, 526–540. [Google Scholar] [CrossRef]
- El Marzougui, M.; Messaoudi, N.; Dachry, W.; Bensassi, B. Industry 4.0 Technologies on Demand Driven Material Requirement Planning: Theoretical Background and Impacts. In Proceedings of the International Conference on Advanced Intelligent Systems for Sustainable Development; Kacprzyk, J., Ezziyyani, M., Balasy, V.E., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 59–69. [Google Scholar]
- Marzougui, M.E.; Messaoudi, N.; Dachry, W.; Bensassi, B. Integration Model for Demand-Driven Material Requirement Planning and Industry 4.0. SAE Int. J. Mater. Manuf. 2022, 16, 3–14. [Google Scholar] [CrossRef]
- ASCM. Association for Supply Chain Management—ASCM. Available online: https://www.ascm.org/ (accessed on 27 December 2024).
- Llamuca, E.S.; Garcia, C.A.; Naranjo, J.E.; Garcia, M.V. Cyber-Physical Production Systems for Industrial Shop-Floor Integration Based on AMQP; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Haji Mohammad, F.; Benali, M.; Baptiste, P. An Optimization Model for Demand-Driven Distribution Resource Planning DDDRP. J. Ind. Eng. Manag. 2022, 15, 338. [Google Scholar] [CrossRef]
- Reid, D.J. Genetic Algorithms in Constrained Optimization. Math. Comput. Model. 1996, 23, 87–111. [Google Scholar] [CrossRef]
- Zou, Z.; Li, C. Integrated and Events-Oriented Job Shop Scheduling. Int. J. Adv. Manuf. Technol. 2006, 29, 551–556. [Google Scholar] [CrossRef]
- Giacomelli/GeneticSharp. GeneticSharp Is a Fast, Extensible, Multi-Platform and Multithreading C# Genetic Algorithm Library that Simplifies the Development of Applications Using Genetic Algorithms (GAs). Available online: https://github.com/giacomelli/GeneticSharp (accessed on 5 April 2025).
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-58111-0. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms|Wiley; Wiley: Hoboken, NJ, USA, 2001; ISBN 978-0-471-87339-6. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998; ISBN 978-0-262-63185-3. [Google Scholar]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by Localization and Multiobjective Evolutionary Optimization for Flexible Job-Shop Scheduling Problems. IEEE 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Yeniay, Ö. Penalty Function Methods for Constrained Optimization with Genetic Algorithms. Math. Comput. Appl. 2005, 10, 45–56. [Google Scholar] [CrossRef]
- Deb, K. An Efficient Constraint Handling Method for Genetic Algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1999; ISBN 978-0-471-31531-5. [Google Scholar]
- Lu, Y.; Benlic, U.; Wu, Q. A Hybrid Evolutionary Algorithm for the Capacitated Minimum Spanning Tree Problem. Comput. Oper. Res. 2022, 144, 105799. [Google Scholar] [CrossRef]
- Millett, S.; Tune, N. Patterns, Principles, and Practices of Domain-Driven Design; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-71470-6. [Google Scholar]
- UML Class and Object Diagrams Overview—Common Types of UML Structure Diagrams. Available online: https://www.uml-diagrams.org/class-diagrams-overview.html (accessed on 26 June 2025).
- Gewarren Introduction to .NET-.NET. Available online: https://learn.microsoft.com/en-us/dotnet/core/introduction (accessed on 4 April 2025).
- El Mouayni, I. ismail-elmouayni/SmartPPC: SmartPPC a DDMRP based Production Planning and Control Module. Available online: https://github.com/ismail-elmouayni/SmartPPC (accessed on 5 April 2025).
- Dantan, J.-Y.; El Mouayni, I.; Sadeghi, L.; Siadat, A.; Etienne, A. Human Factors Integration in Manufacturing Systems Design Using Function–Behavior–Structure Framework and Behaviour Simulations. CIRP Ann. 2019, 68, 125–128. [Google Scholar] [CrossRef]
- El Mouayni, I.; Etienne, A.; Siadat, A.; Dantan, J.-Y.; Lux, A. A Simulation Based Approach for Enhancing Health Aspects in Production Systems by Integrating Work Margins. IFAC-Pap. 2016, 49, 1697–1702. [Google Scholar] [CrossRef]
- El Mouayni, I.; Etienne, A.; Siadat, A.; Dantan, J.-Y.; Lux, A. AEN-PRO: Agent-Based Simulation Tool for Performance and Working Conditions Assessment in Production Systems Using Workers’ Margins of Manoeuver. IFAC-Pap. 2017, 50, 14236–14241. [Google Scholar] [CrossRef]
- Mouayni, I.E.; Demesure, G.; Haouzi, H.B.-E.; Charpentier, P.; Siadat, A. Jobs Scheduling within Industry 4.0 with Consideration of Worker’s Fatigue and Reliability Using Greedy Randomized Adaptive Search Procedure. IFAC-Pap. 2019, 52, 85–90. [Google Scholar] [CrossRef]
- El Mouayni, I.; Etienne, A.; Lux, A.; Siadat, A.; Dantan, J.-Y. A Simulation-Based Approach for Time Allowances Assessment during Production System Design with Consideration of Worker’s Fatigue, Learning and Reliability. Comput. Ind. Eng. 2020, 139, 105650. [Google Scholar] [CrossRef]
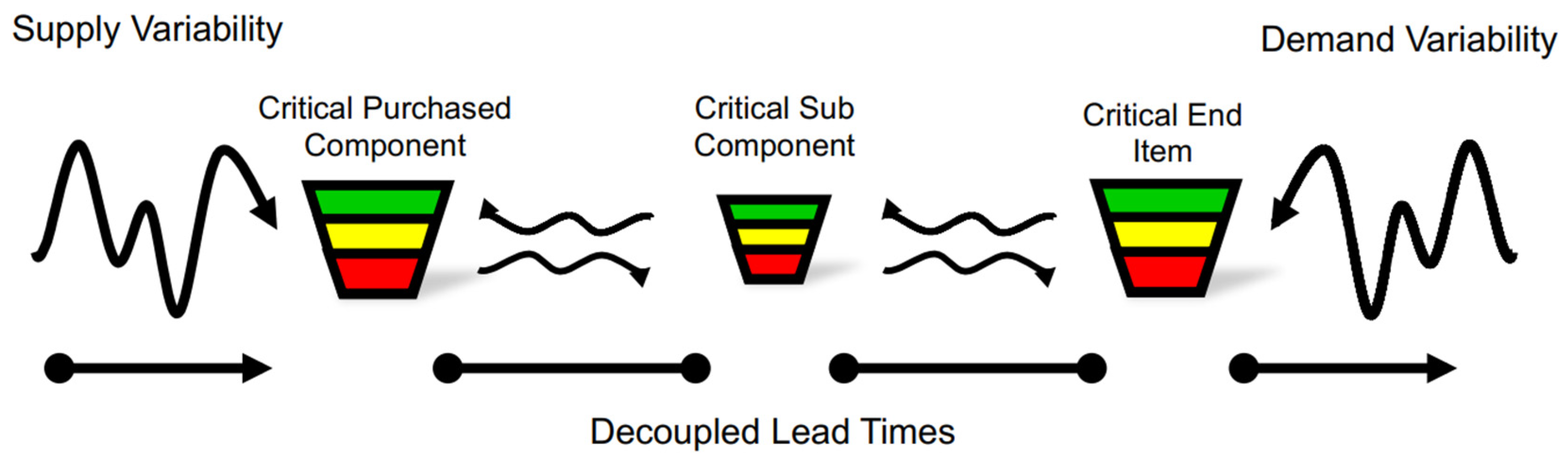
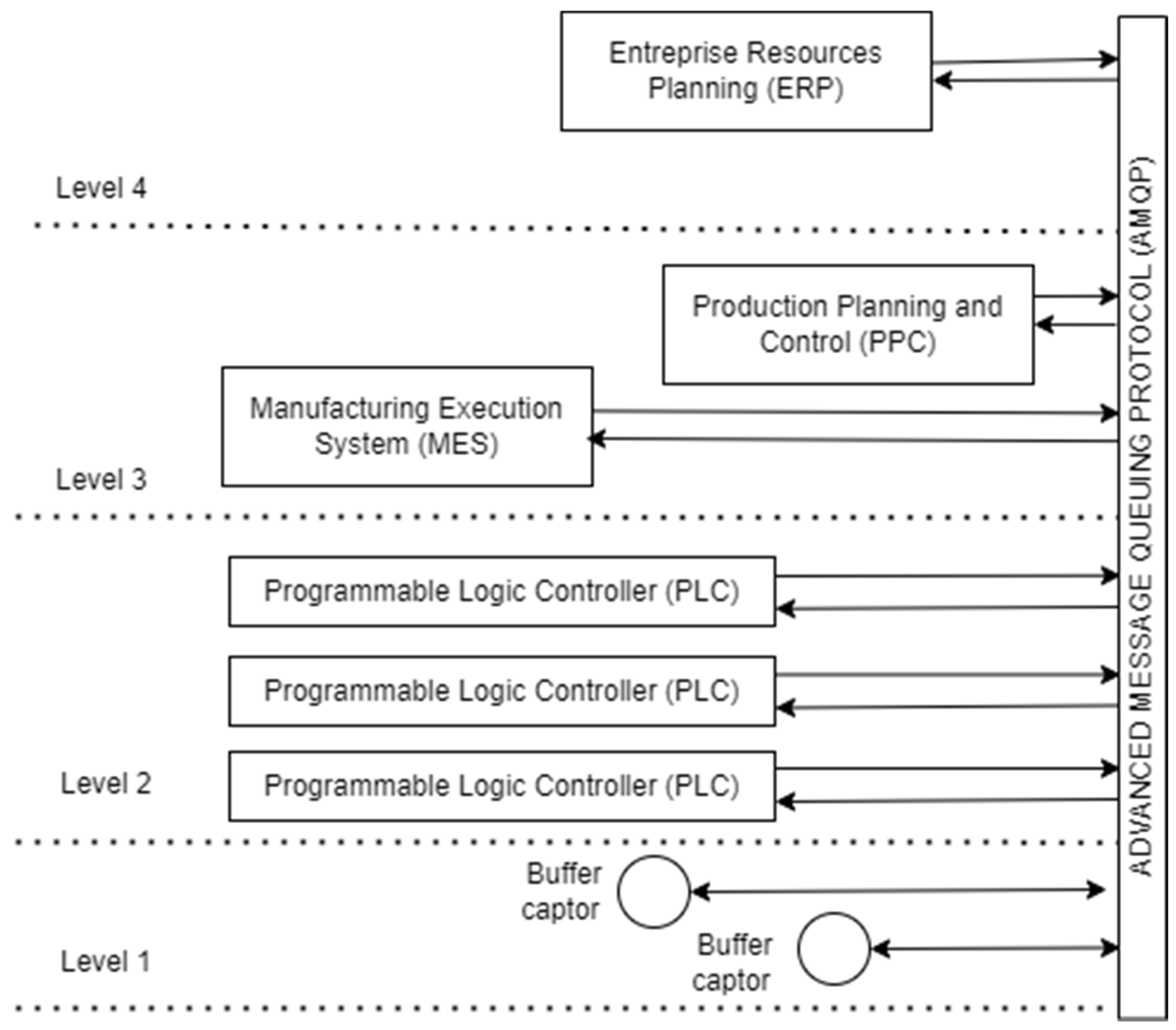
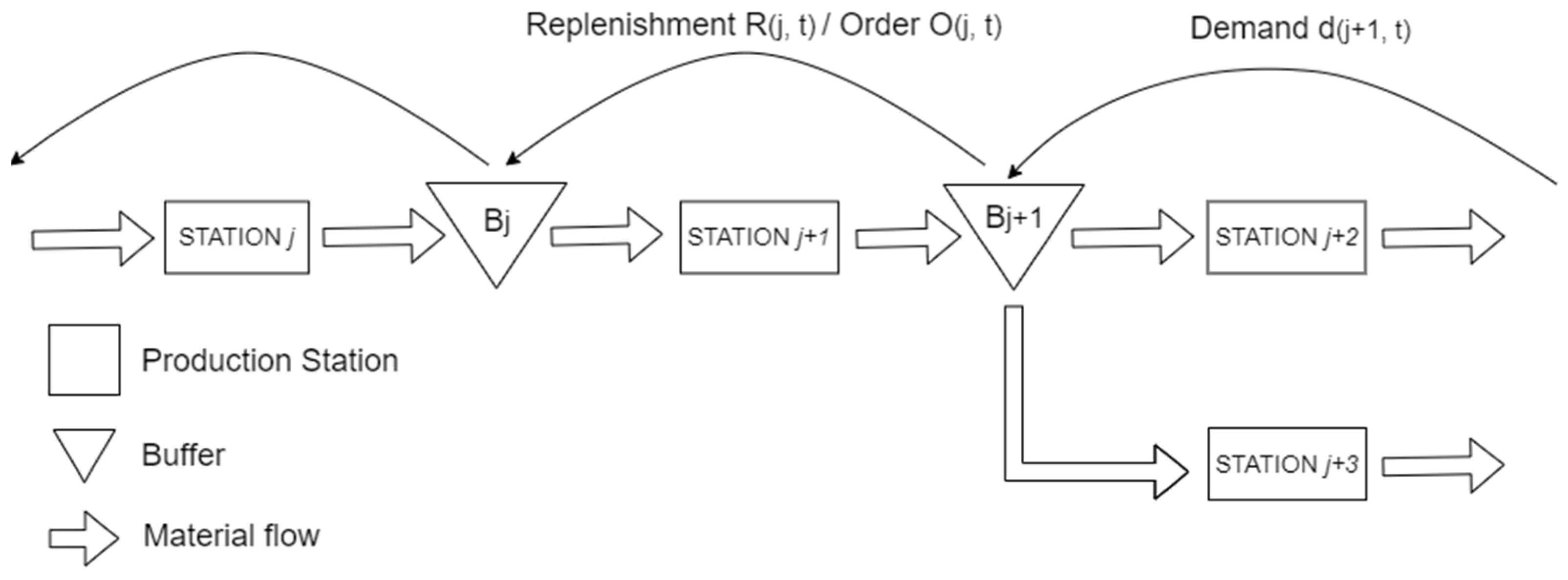
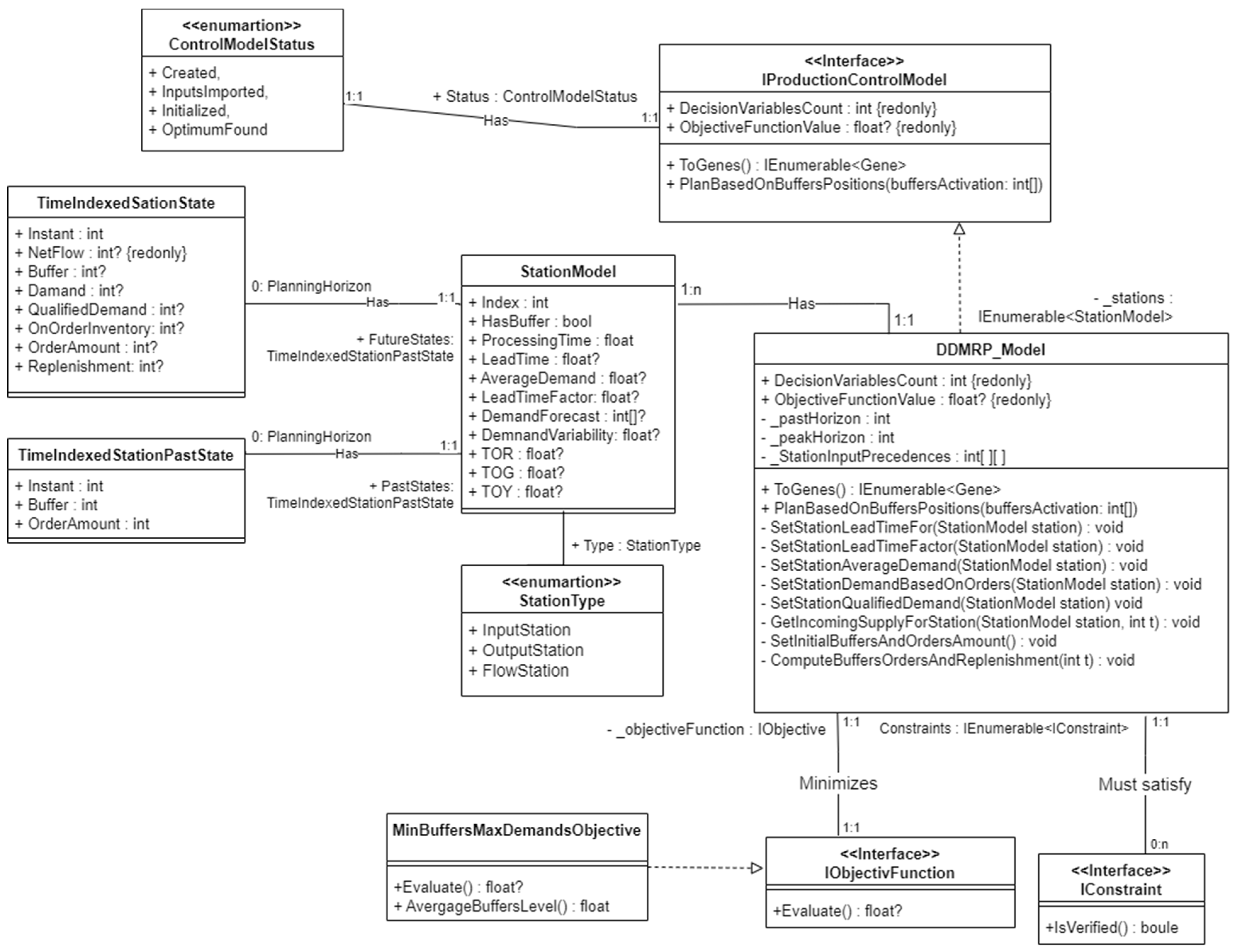

| Lead Time | Lead Time Factor (%) | Decoupled Lead Time (day) |
|---|---|---|
| Long | 20–40 | 10+ |
| Medium | 41–60 | 5–9 |
| Short | 61–100 | 0–4 |
| (a) | |||||||||||||||
| Date | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Demand | 80 | 30 | 50 | 120 | 150 | 70 | 100 | 45 | 60 | 120 | 130 | 80 | 50 | 70 | 106 |
| (b) | |||||||||||||||
| Date | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| Demand | 130 | 100 | 80 | 50 | 80 | 45 | 70 | 106 | 130 | 100 | 106 | 45 | 33 | 106 | 45 |
| Configuration | Optimal Buffer Positionings | Average Buffer Level | Average Unsatisfied Demand |
|---|---|---|---|
| A | 1-1-0-0-0-1 | 442.3 | 13.5 |
| B | 1-1-0-0-0-0-0-0-1-0 | 254.4 | 11.7 |
| C | 1-1-0-1-0-0-0-0-1-0-0-0-0-0 | 194.3 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habbadi, S.; El Mouayni, I.; Herrou, B.; Sekkat, S. New Hybrid Method for Buffer Positioning and Production Control Using DDMRP Logic in Smart Manufacturing. J. Manuf. Mater. Process. 2025, 9, 219. https://doi.org/10.3390/jmmp9070219
Habbadi S, El Mouayni I, Herrou B, Sekkat S. New Hybrid Method for Buffer Positioning and Production Control Using DDMRP Logic in Smart Manufacturing. Journal of Manufacturing and Materials Processing. 2025; 9(7):219. https://doi.org/10.3390/jmmp9070219
Chicago/Turabian StyleHabbadi, Sahar, Ismail El Mouayni, Brahim Herrou, and Souhail Sekkat. 2025. "New Hybrid Method for Buffer Positioning and Production Control Using DDMRP Logic in Smart Manufacturing" Journal of Manufacturing and Materials Processing 9, no. 7: 219. https://doi.org/10.3390/jmmp9070219
APA StyleHabbadi, S., El Mouayni, I., Herrou, B., & Sekkat, S. (2025). New Hybrid Method for Buffer Positioning and Production Control Using DDMRP Logic in Smart Manufacturing. Journal of Manufacturing and Materials Processing, 9(7), 219. https://doi.org/10.3390/jmmp9070219







