Resistance Analysis of a Plastic Container Obtained with Additive Manufacturing Using Finite Elements
Abstract
1. Introduction
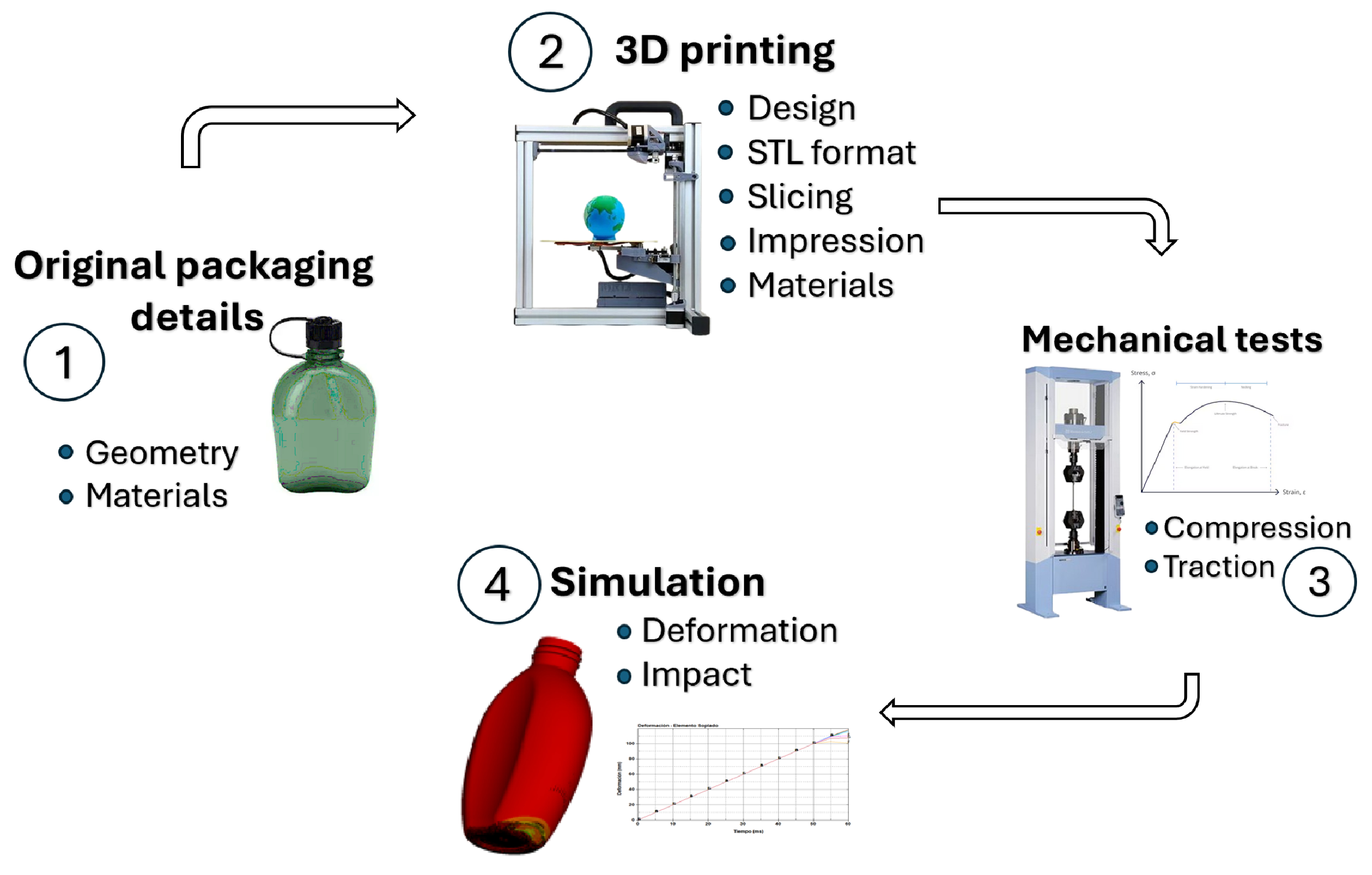
2. Materials and Methods
2.1. Materials
2.2. Method
2.2.1. Three-Dimensional Printing
2.2.2. Stress Analysis of the Printed Material
2.2.3. Compression Analysis of Printed and Original Containers
- Compression resistance;
- Free-fall impact resistance.
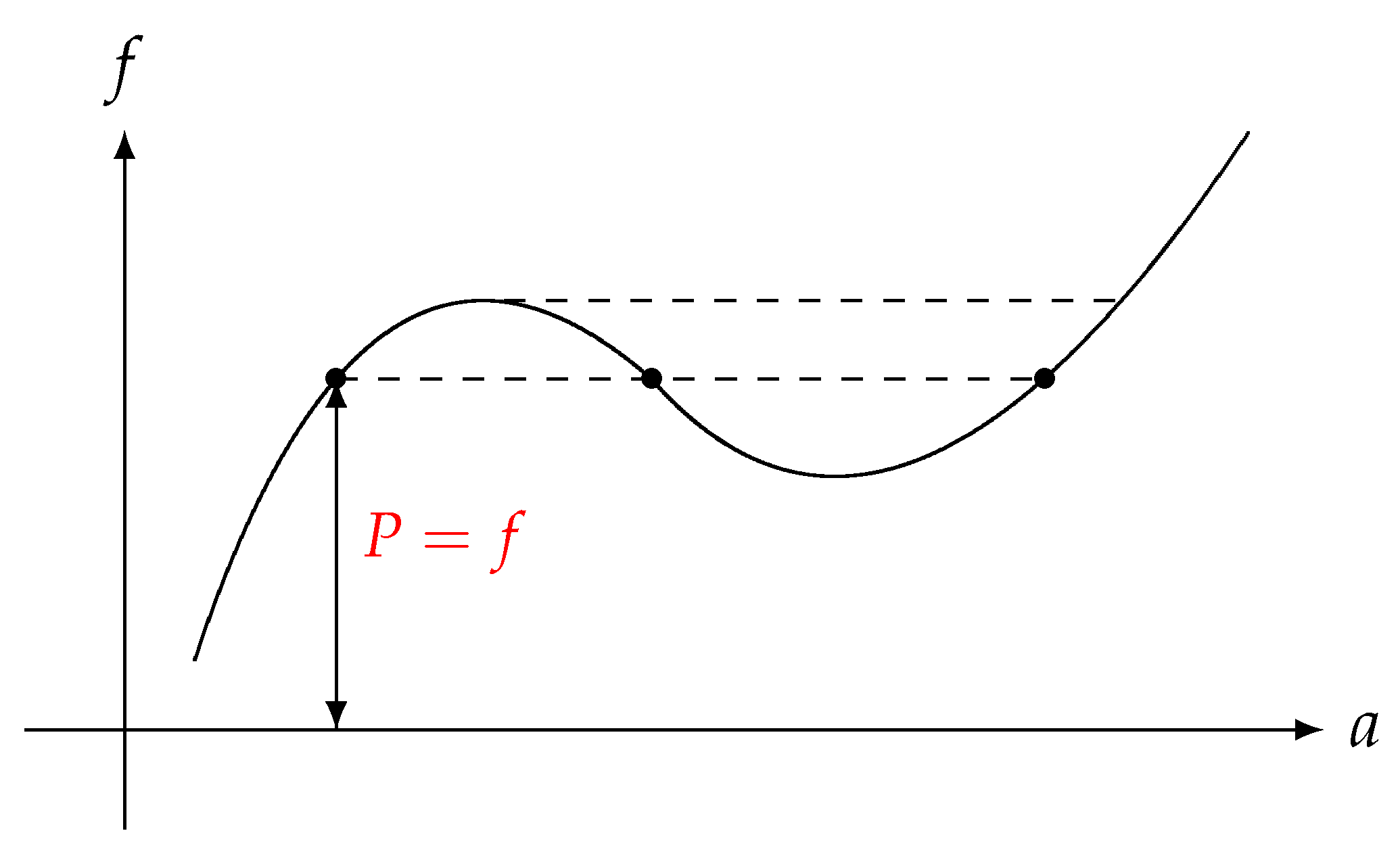
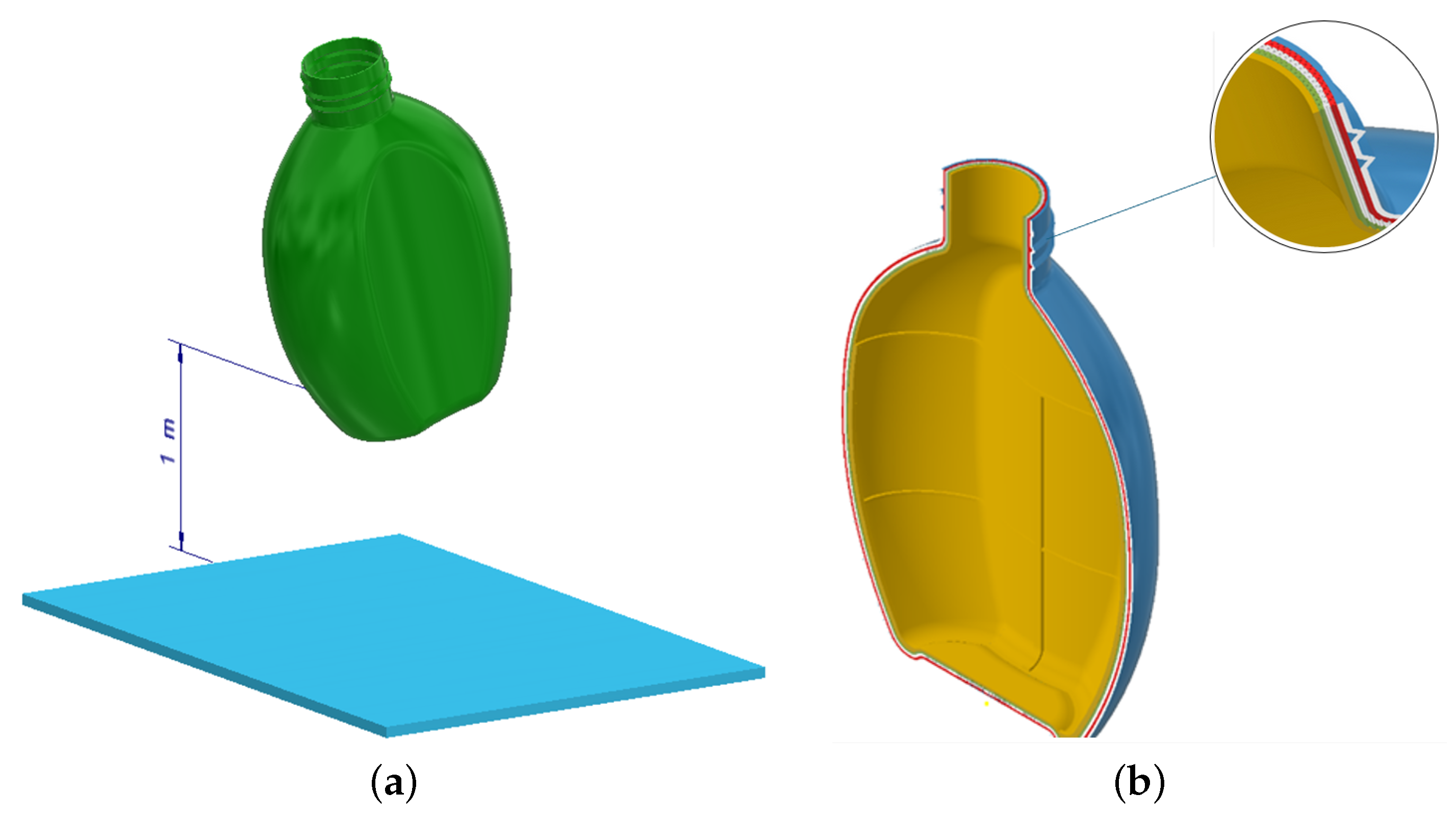
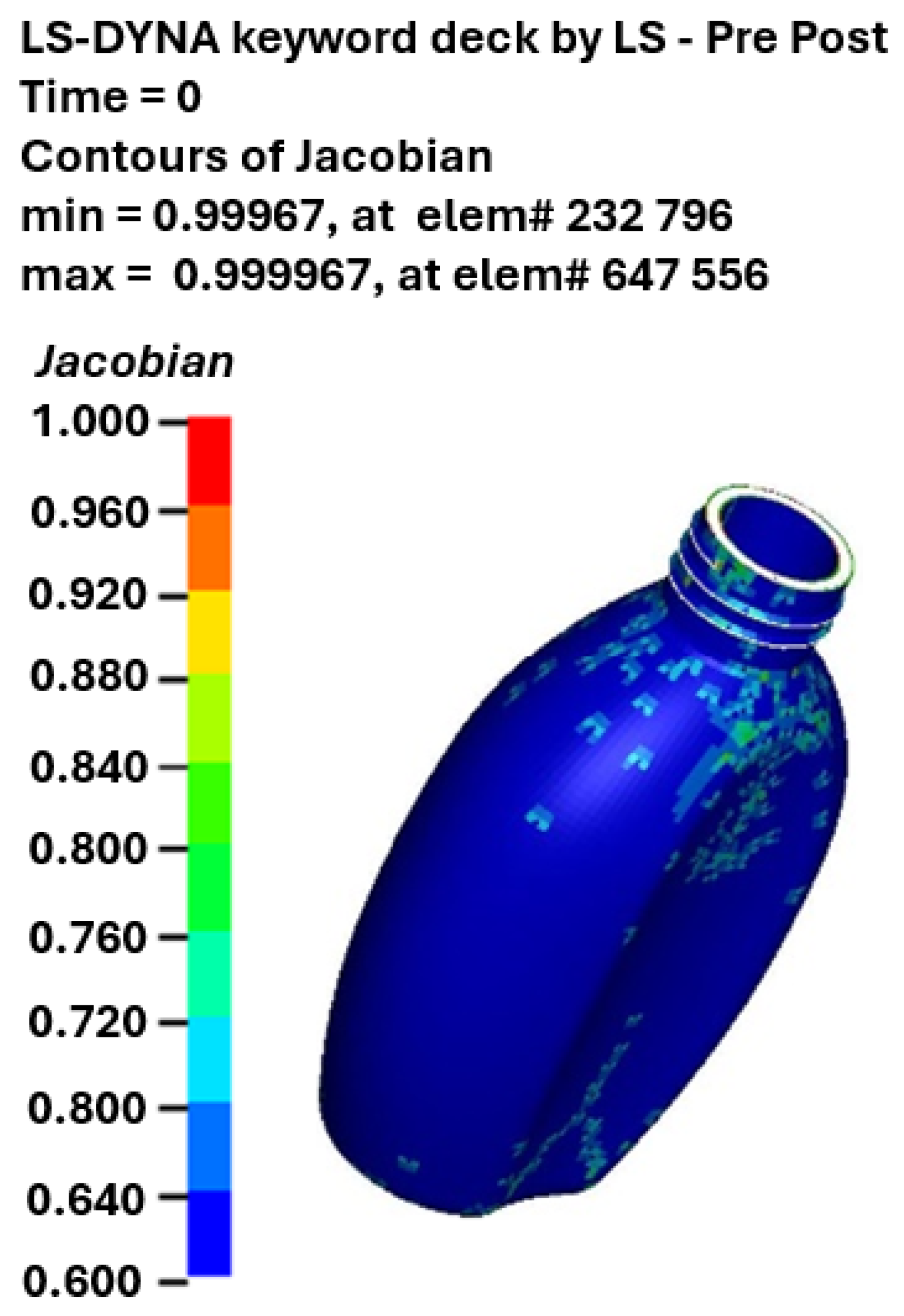
2.3. Finite Element Impact Analysis
- : Nodal or global displacements;
- : Stress (column vector);
- : Domain;
- B: Strain function;
- : Displacement vector;
- : Approximation of ;
- f: Nodal/external element force;
- P: Internal force vector.
3. Results
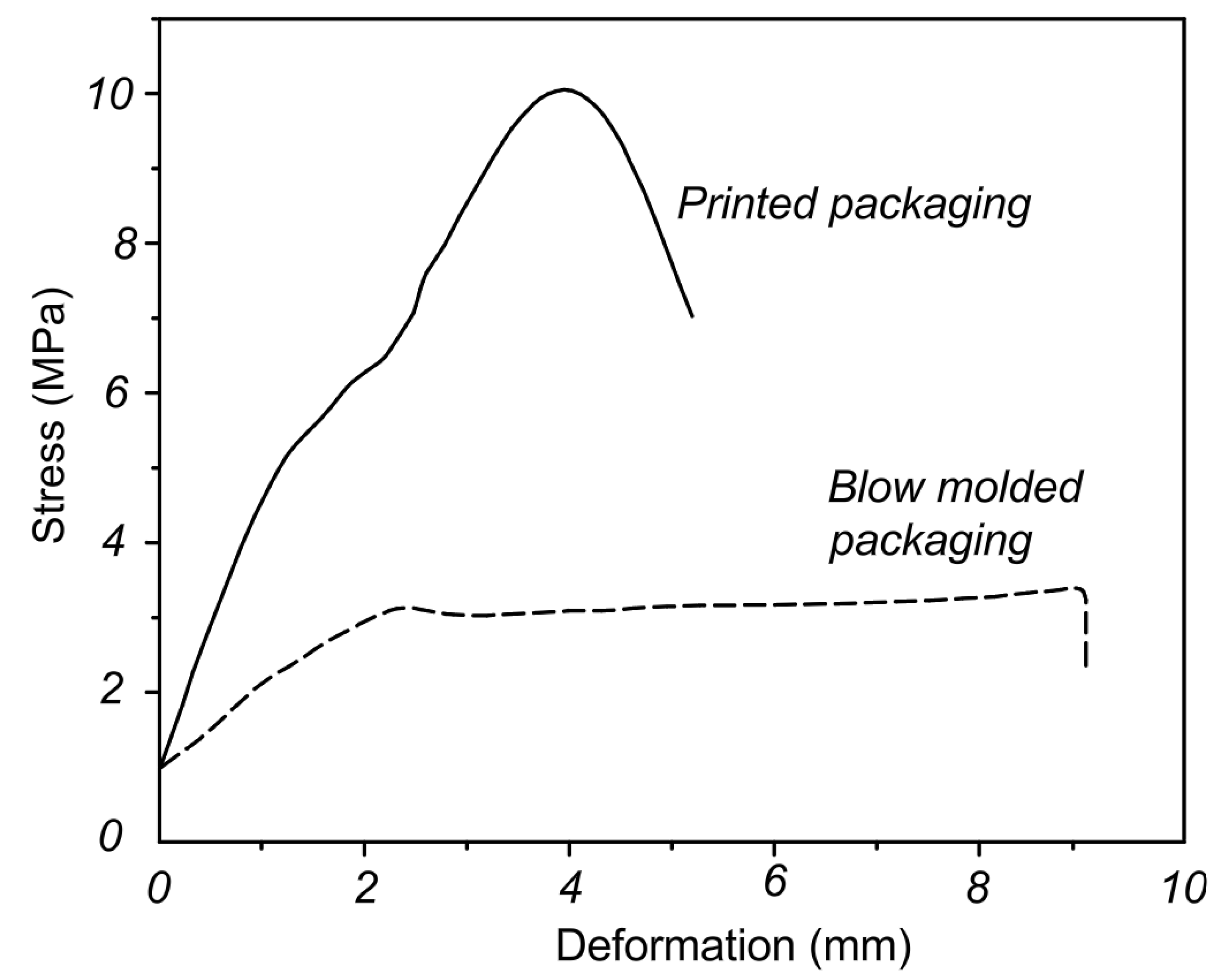
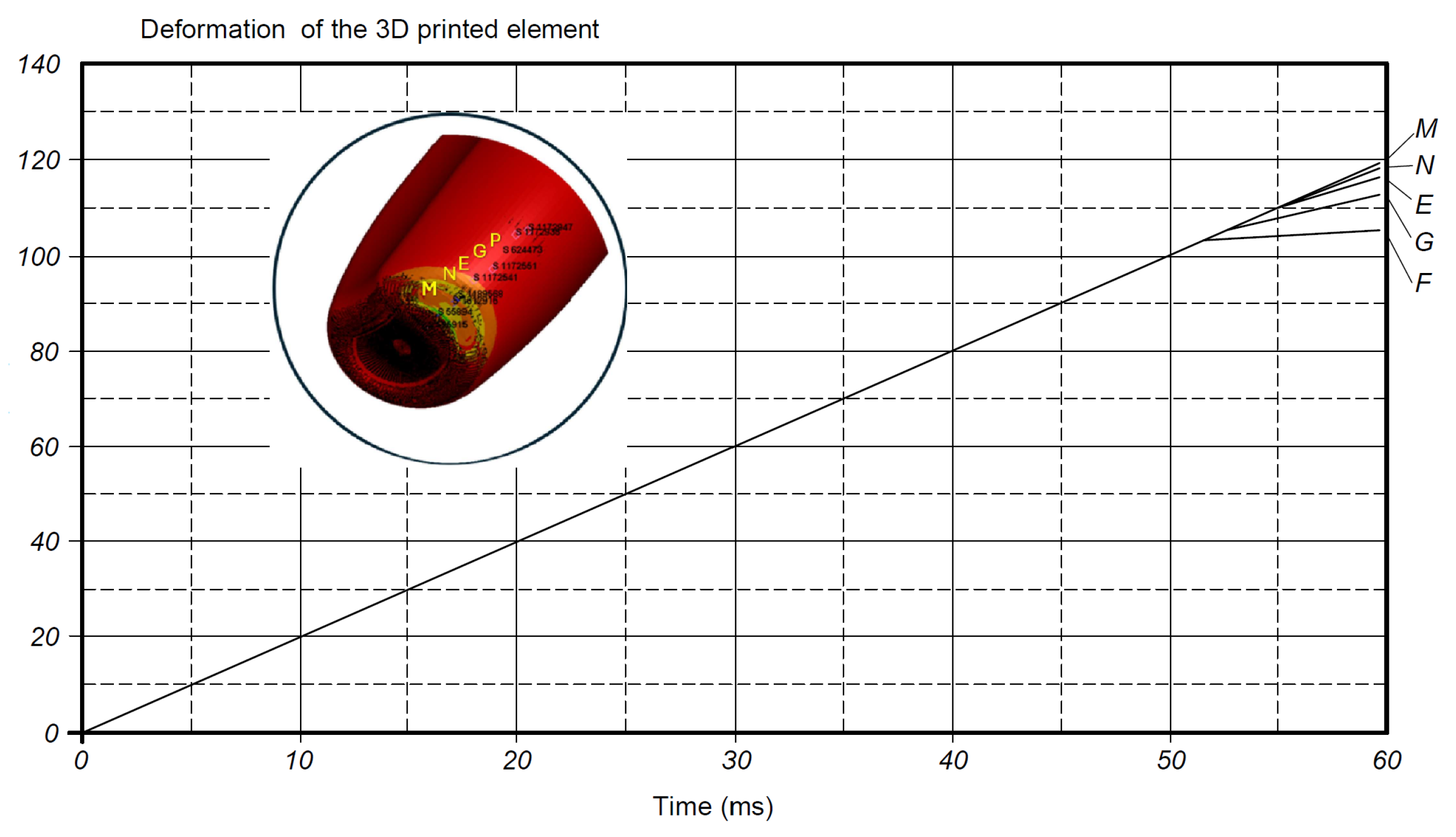
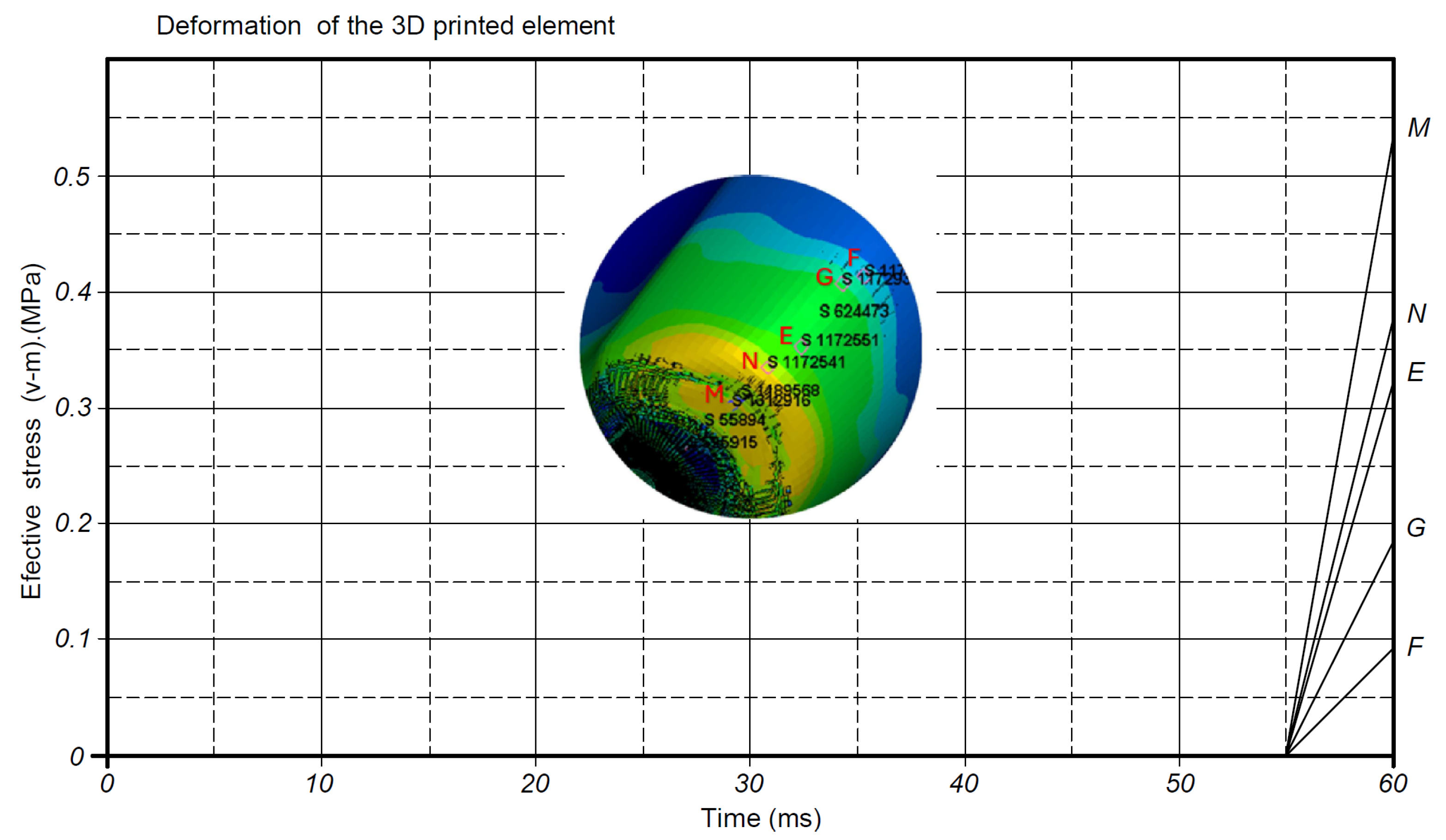
3.1. Evaluation of Tensile Stress of Printed Specimens
3.2. Compression Evaluation
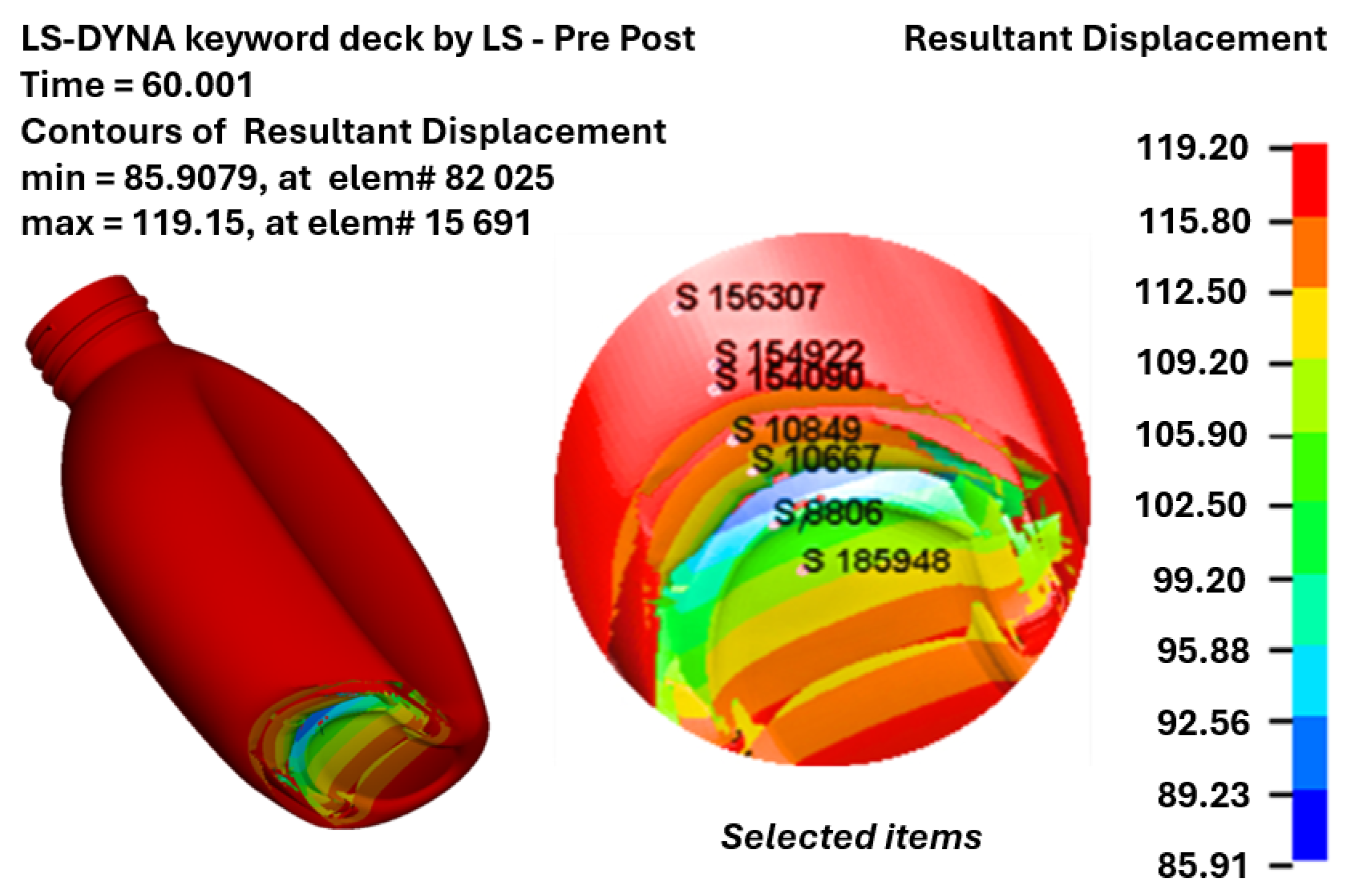
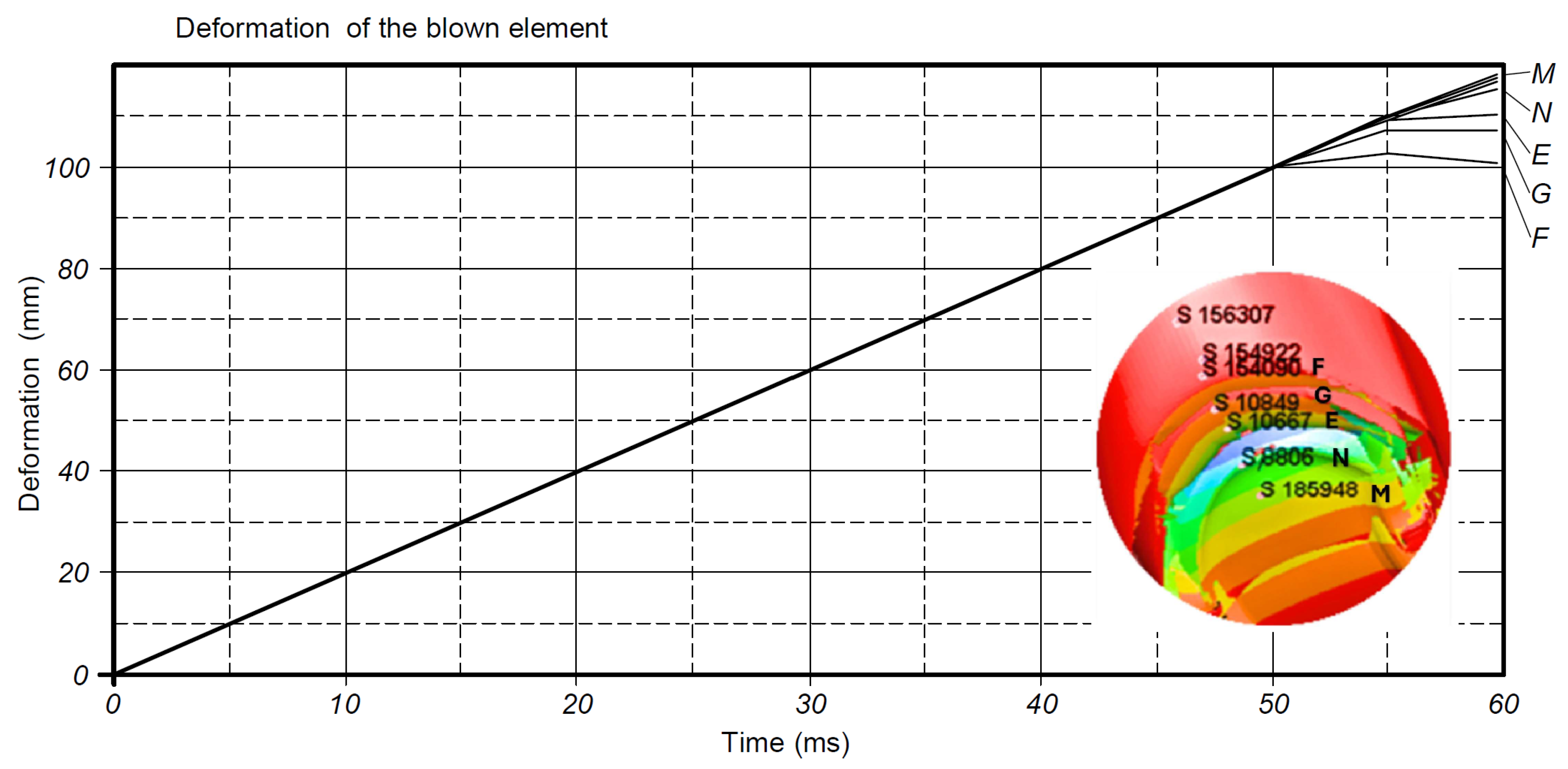
3.3. Impact Resistance Evaluation
4. Discussion
5. Conclusions
- By analyzing the results obtained from the finite element compression and impact resistance tests conducted on two containers manufactured using two different techniques, namely blow molding and 3D printing, it is concluded that the 3D-printed container withstands a load of 10.497 kN—more than double the resistance of the blow-molded container. Furthermore, the additively manufactured container exhibits greater rigidity, evidenced by an approximate deformation of 4 mm caused by the applied force before fracture occurs at the thread base.
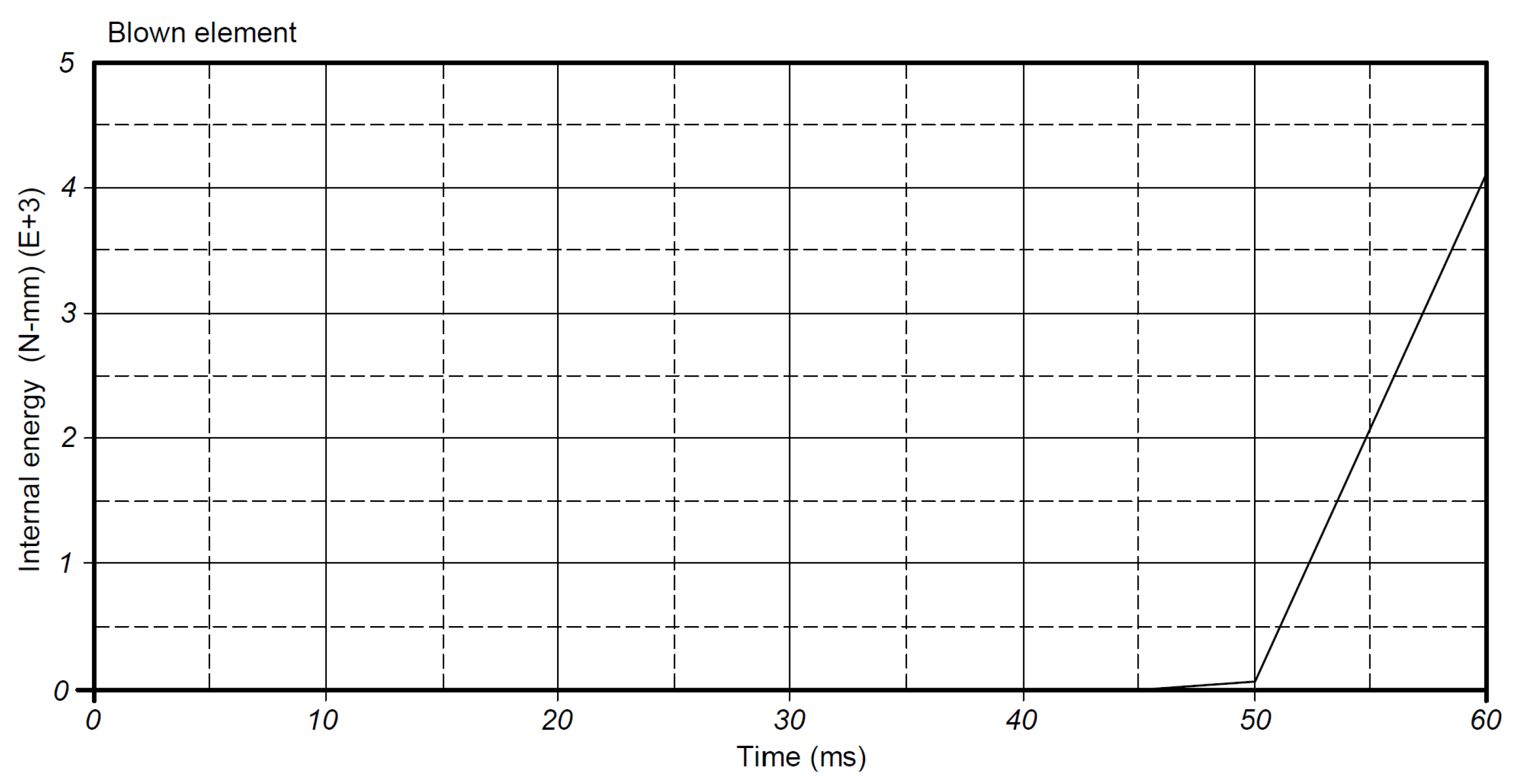
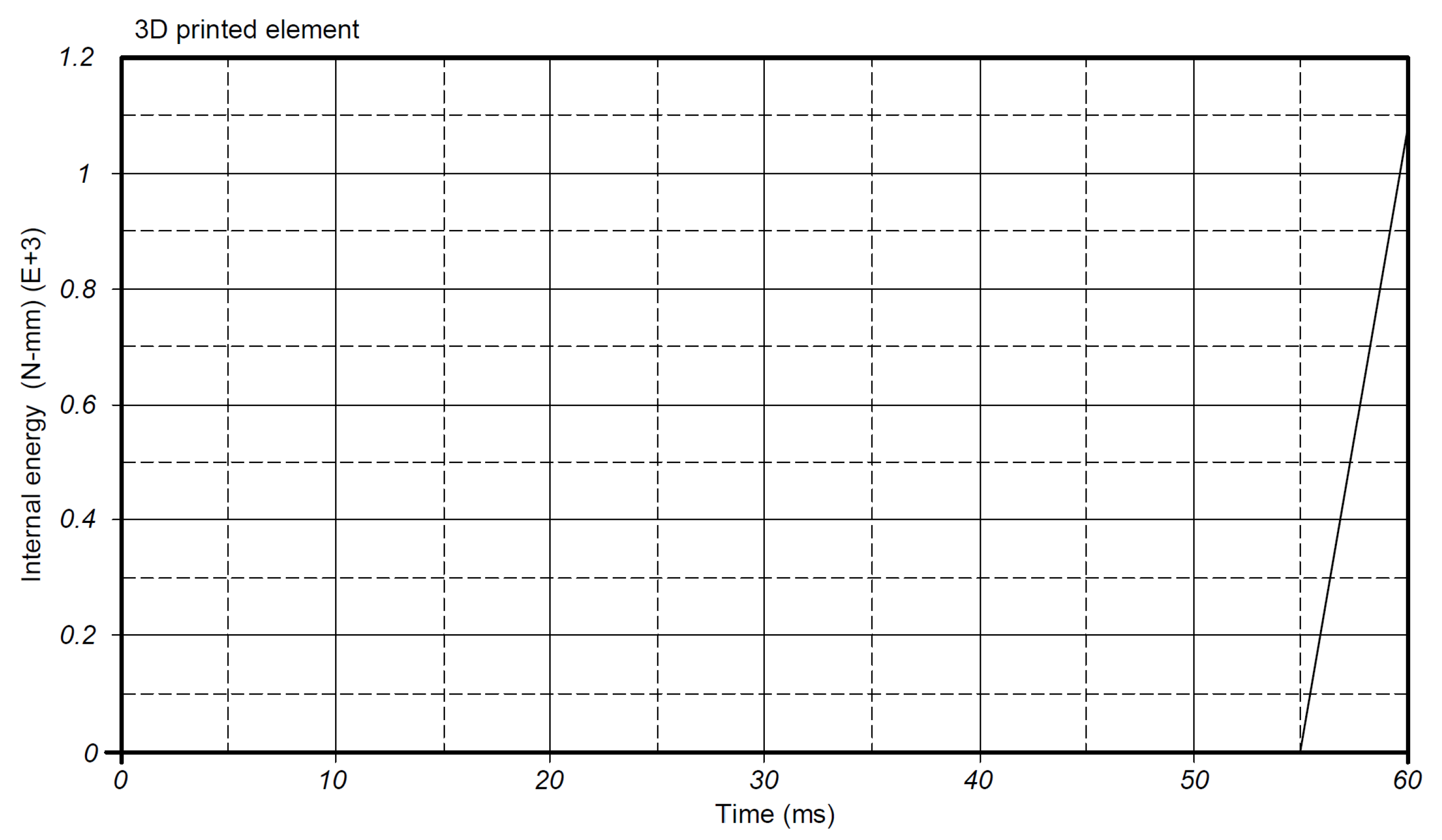
- The impact resistance results obtained from the finite element analysis of the container drop tests indicate minor variations between the two containers: 0.91% in deformation and 2.15% in stress. The 3D-printed object exhibits greater rigidity, as reflected in the deformations and stresses observed. Consequently, the internal energy absorption value of the blow-molded container, at 4 × 103 N·mm, suggests higher elasticity in its structure, leading to greater deformation. It is noted that the finite element analysis did not incorporate more complex loading conditions and failure modes, which could potentially yield a more profound understanding of the structural integrity of the 3D-printed containers.
- Future research directions entail broader comparative analyses of various materials and 3D printing techniques against traditional manufacturing processes, optimizing printing parameters, and subjecting the containers to long-term durability testing under the environmental phenomena to which they are exposed. Consideration should also be given to exploring container design adaptations for specific applications, evaluating how design modifications impact performance and functionality.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Groover, M. Polymers. In Fundamentals of Modern Manufacturing: Materials, Processes, and Systems; John Wiley & Sons Publishing House: Hoboken, NJ, USA, 2010; pp. 185–186. [Google Scholar]
- Marsh, K.; Bugusu, B. Food packaging—Roles, materials, and environmental issues. J. Food Sci. 2007, 72, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Turng, L. Special and emerging injection molding processes. J. Inject. Molding Technol. 2001, 5, 160–179. [Google Scholar]
- Swift, K.; Booker, J. Manufacturig Process Selection, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2003; pp. 175–179. [Google Scholar]
- Altan, T.; Lilly, B.; Yen, Y. Manufacturing of dies and molds. CiRP Ann. 2001, 50, 404–422. [Google Scholar] [CrossRef]
- Hgo, T.; Kashani, A.; Imbalzano, G.; Nguyen, T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2001, 143, 172–196. [Google Scholar]
- Kafle, A.; Luis, E.; Silwal, R.; Pan, H.; Shrestha, P.; Bastola, A. 3D/4D Printing of polymers: Fused deposition modelling (FDM), selective laser sintering (SLS), and stereolithography (SLA). Polymers 2021, 13, 3101. [Google Scholar] [CrossRef] [PubMed]
- Chadha, U.; Aarye, V.; Naman, P.; Tiwari, A.; Shanker, S.; Selvaraj, S. Performance evaluation of 3D printing technologies: A review, recent advances, current challenges, and future directions. Prog. Addit. Manuf. 2022, 7, 853–886. [Google Scholar] [CrossRef]
- Fu, Y.; Downey, A.; Yuan, L.; Pratt, A.; Balogun, Y. In situ monitoring for fused filament fabrication process: A review. Addit. Manuf. 2021, 38, 101749. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.; Wang, C.; Shin, Y.; Zhang, S.; Zavattieri, P. The status, challenges, and future of additive manufacturing in engineering. Comput.-Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Hager, I.; Golonka, A.; Putanowicz, R. 3D printing of buildings and building components as the future of sustainable construction? Procedia Eng. 2016, 151, 292–299. [Google Scholar] [CrossRef]
- Iftekar, S.; Aabid, A.; Amir, A.; Baig, M. Advancements and Limitations in 3D Printing Materials and Technologies: A Critical Review. Polymers 2023, 15, 2519. [Google Scholar] [CrossRef]
- Anketa, J.; Ikshita, C.; Ishika, W.; Ankush, R.; Mir, I. 3D printing—A review of processes, materials and applications in industry 4.0. Sustain. Oper. Comput. 2022, 3, 33–42. [Google Scholar]
- Bouzaglou, O.; Golan, O.; Lachman, N. Process Design and Parameters Interaction in Material Extrusion 3D Printing: A Review. Polymers 2023, 15, 2280. [Google Scholar] [CrossRef] [PubMed]
- Tierra, P.; Arroba, S.; Safla, E.; Jaramillo, J. Simulación matemótica de pruebas de impacto entre diferentes materiales, por medio de software para análisis no lineales. Dominio Cienc. 2020, 6, 1171–1193. [Google Scholar]
- ISO 604:2022; Plastics—Determination of Compressive Properties. International Organization for Standardization (ISO): Geneva, Switzerland, 2022. Available online: https://www.mts.com/la/applications/materials/test-standard/iso/iso-604 (accessed on 5 February 2025).
- ASTM D638-19; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2019. Available online: https://store.accuristech.com/ (accessed on 5 February 2025).
- Almonti, D.; Baiocco, G.; Salvi, D.; Ucciardello, N. Innovative approach for enhancing thermal diffusivity in metal matrix composites using graphene electrodeposition and multi-coating. Int. J. Adv. Manuf. Technol. 2024, 135, 1633–1646. [Google Scholar] [CrossRef]
- Majko, J.; Saga, M.; Vasko, M.; Handrik, M.; Barnik, F.; Dorciak, F. FEM analysis of long-fibre composite structures created by 3D printing. Transp. Res. Procedia 2019, 40, 792–799. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties. International Organization for Standardization (ISO): Geneva, Switzerland, 2012; Available online: https://www.nen.nl/en/nen-en-iso-527-2-2012-en-169105; https://standards.iteh.ai/catalog/standards/cen/f4cb13ef-3b69-40ec-8ff7-4d0f7412fdf1/en-iso-527-2-2012; https://www.une.org/encuentra-tu-norma/busca-tu-norma/norma?c=N0050308; https://www.intertekinform.com/en-au/standards/iso-527-2-2012-580795_saig_iso_iso_1329412/. (accessed on 5 February 2025).
- Zienkiewicz, O.; Taylor, R. El Método de los Elementos Finitos, 4th ed.; McGraw-Hill: Madrid, Spain, 2010; pp. 333–360. [Google Scholar]
- Fadiji, T.; Cotzee, C.; Berry, T.; Ambaw, A.; Opara, U. The efficacy of finite element analysis (FEA) as a design tool for food packaging: A review. Biosyst. Eng. 2018, 174, 20–40. [Google Scholar] [CrossRef]
- Hammou, A.; Duong, P.; Berry, T.; Abbes, B.; Makhlouf, M.; Guo, Y. Finite-element simulation with a homogenization model andexperimental study of free drop tests of corrugated cardboard packaging. Mech. Ind. 2012, 13, 175–184. [Google Scholar] [CrossRef]












| Mechanical Properties | 3D Printing | |
|---|---|---|
| Value | ISO 527 Estandard Test [20] | |
| Tensile modulus of elasticity | 2346.5 MPa | 1 mm/min |
| Tensile yield strength | 49.5 MPa | 50 mm/min |
| Tensile strength at break | 45.6 MPa | 50 mm/min |
| Elongation at break | 5.20% | 50 mm/min |
| Flexural strength | 103.0 MPa | 178 |
| Flexural modulus | 3150.0 MPa | 178 |
| Shrinkage | 2–5% | |
| Description | Value |
|---|---|
| Material | PLA PRO |
| Color | Green |
| Filament diameter | 3 mm |
| Spool | 1 kg |
| Printing speed | 24 mm3/s |
| Nozzle temperature | 215 °C |
| Nozzle diameter | 0.4 mm |
| Nozzle height from base | 0.2 mm |
| Bed temperature | 60 °C |
| Wall thickness | 4 mm |
| Description | Configuration |
|---|---|
| Number of outer walls | 6 |
| Number of inner walls | 6 |
| Infill pattern | Triangular |
| Layer height | 0.15 mm |
| Infill density | 100% |
| Load | Material | Specimen Number | Speed (V) | Initial Length (l0) |
|---|---|---|---|---|
| 20 kN | PLA | 1 | 3 mm/min | 56.32 mm |
| 2 | 3 mm/min | 56.07 mm |
| Load Cell | Working Load | Correction Factor | Disc Diameter | |
|---|---|---|---|---|
| Internal | External | |||
| 200 kN | 20 kN | 1 | 95 mm | 100 mm |
| Container Produced by 3D Printing (PLA) | |
|---|---|
| Density | 7.83 × 10−6 kg/mm3 |
| Young’s modulus | 2346.5 MPa |
| Elastic limit | 49.5 MPa |
| Container produced by blow molding (HDPE) | |
| Density | 9.50 × 10−7 kg/mm3 |
| Young’s modulus | 1200 MPa |
| Elastic limit | 26.0 MPa |
| Container | Load | Container Height | Tread Diameter | ||
|---|---|---|---|---|---|
| Before | After | Before | After | ||
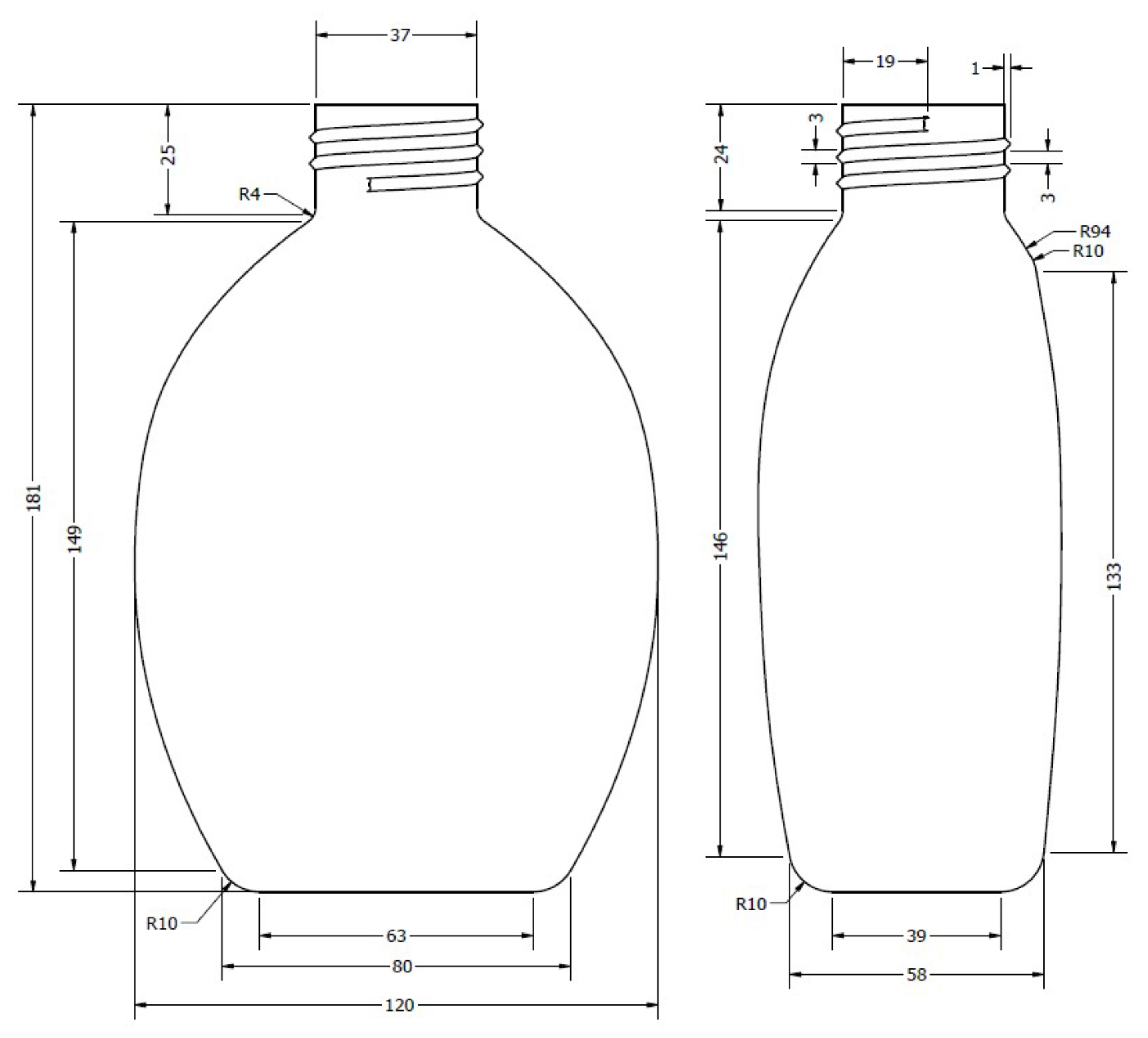
| Printed 1 | 10.497 kN | 181 mm | 175 mm | 37 mm | 37.15 mm |
| Blow molded 2 | 3.449 kN | 182 mm | 178 mm | 36 mm | 36.52 mm |
| Description | CONTAINER | |
|---|---|---|
| Blow-Molded | Printed | |
| Measured Element Deformation (mm) | ≈101–118 | ≈116–120 |
| Maximum Deformation (mm) | 119.2 | 120.3 |
| Measured Stresses (MPa) | ≈0.37–0.57 | ≈0.1–0.54 |
| Maximum Stresses (MPa) | 0.7391 | 0.7554 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-López, L.M.; Maldonado, G.; Paltán-Zhingre, C.; Brito, J.; Loja-Quezada, J.; Amaya-Pinos, M. Resistance Analysis of a Plastic Container Obtained with Additive Manufacturing Using Finite Elements. J. Manuf. Mater. Process. 2025, 9, 204. https://doi.org/10.3390/jmmp9060204
López-López LM, Maldonado G, Paltán-Zhingre C, Brito J, Loja-Quezada J, Amaya-Pinos M. Resistance Analysis of a Plastic Container Obtained with Additive Manufacturing Using Finite Elements. Journal of Manufacturing and Materials Processing. 2025; 9(6):204. https://doi.org/10.3390/jmmp9060204
Chicago/Turabian StyleLópez-López, Luis M., Geovanny Maldonado, Cesar Paltán-Zhingre, Jimmy Brito, Julio Loja-Quezada, and Marco Amaya-Pinos. 2025. "Resistance Analysis of a Plastic Container Obtained with Additive Manufacturing Using Finite Elements" Journal of Manufacturing and Materials Processing 9, no. 6: 204. https://doi.org/10.3390/jmmp9060204
APA StyleLópez-López, L. M., Maldonado, G., Paltán-Zhingre, C., Brito, J., Loja-Quezada, J., & Amaya-Pinos, M. (2025). Resistance Analysis of a Plastic Container Obtained with Additive Manufacturing Using Finite Elements. Journal of Manufacturing and Materials Processing, 9(6), 204. https://doi.org/10.3390/jmmp9060204









