A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures
Abstract
1. Introduction
2. Materials and Methods
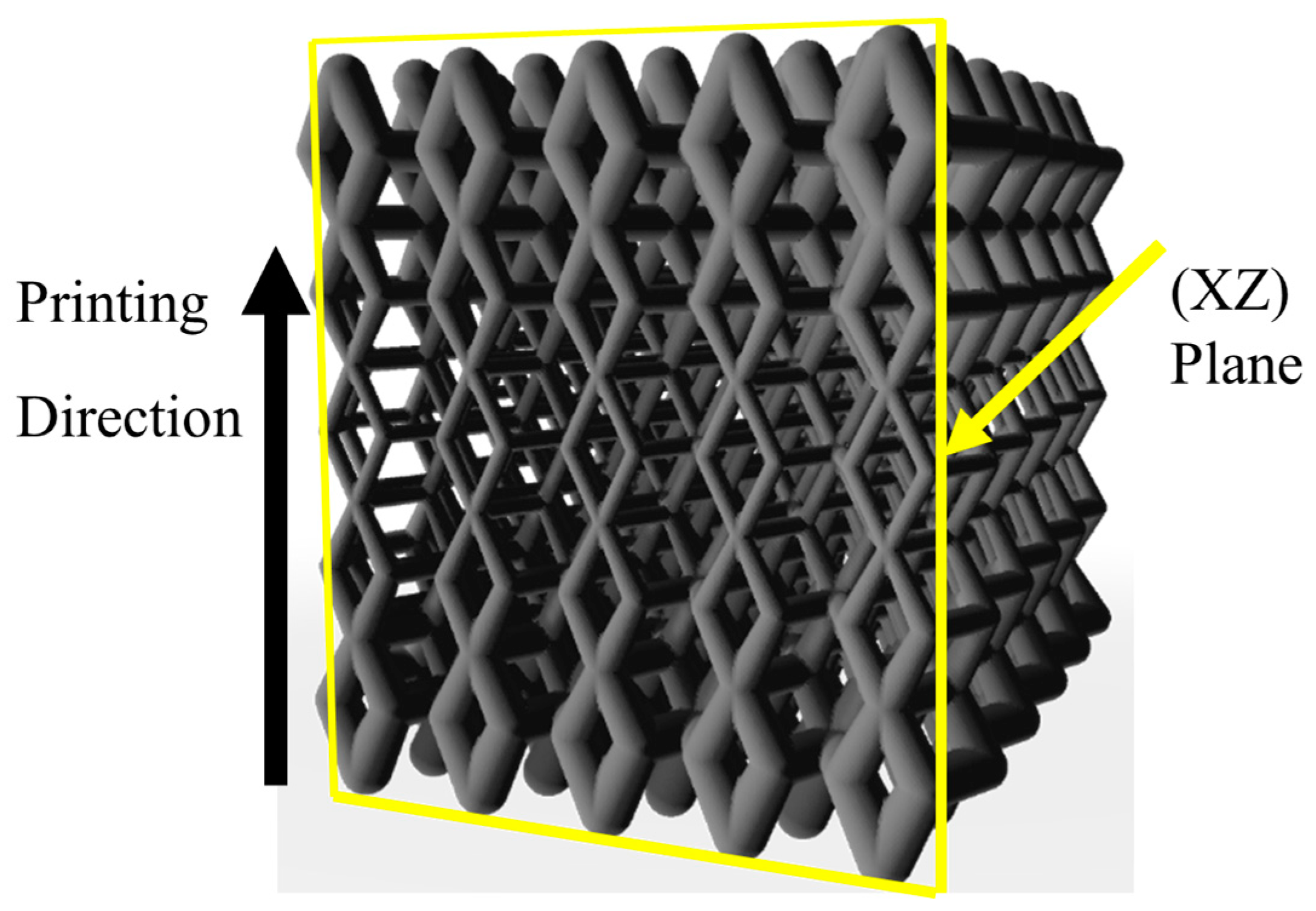
2.1. Parts Design and Manufacturing
2.2. Microstructural Characterization Techniques
2.3. Deformation Analysis
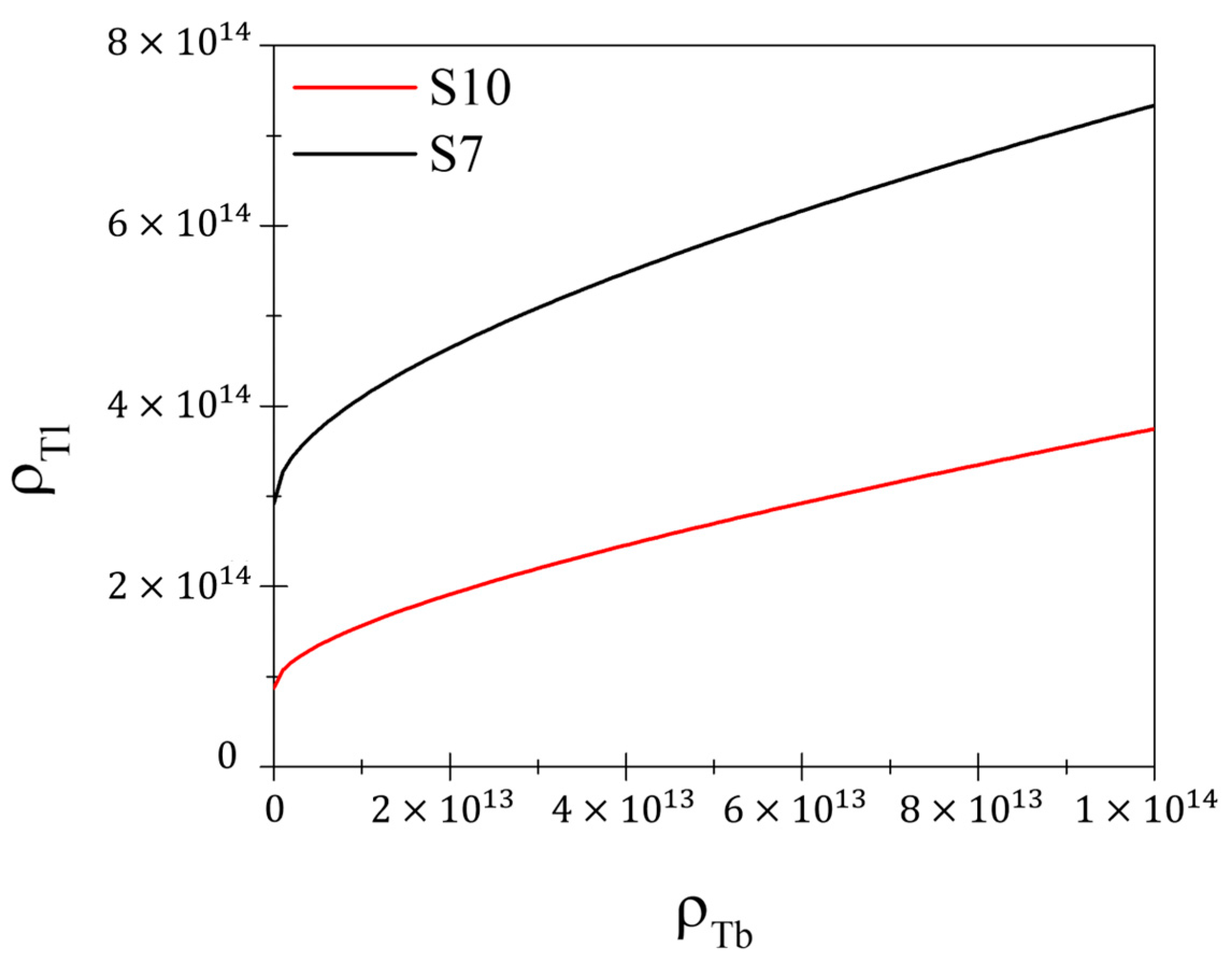
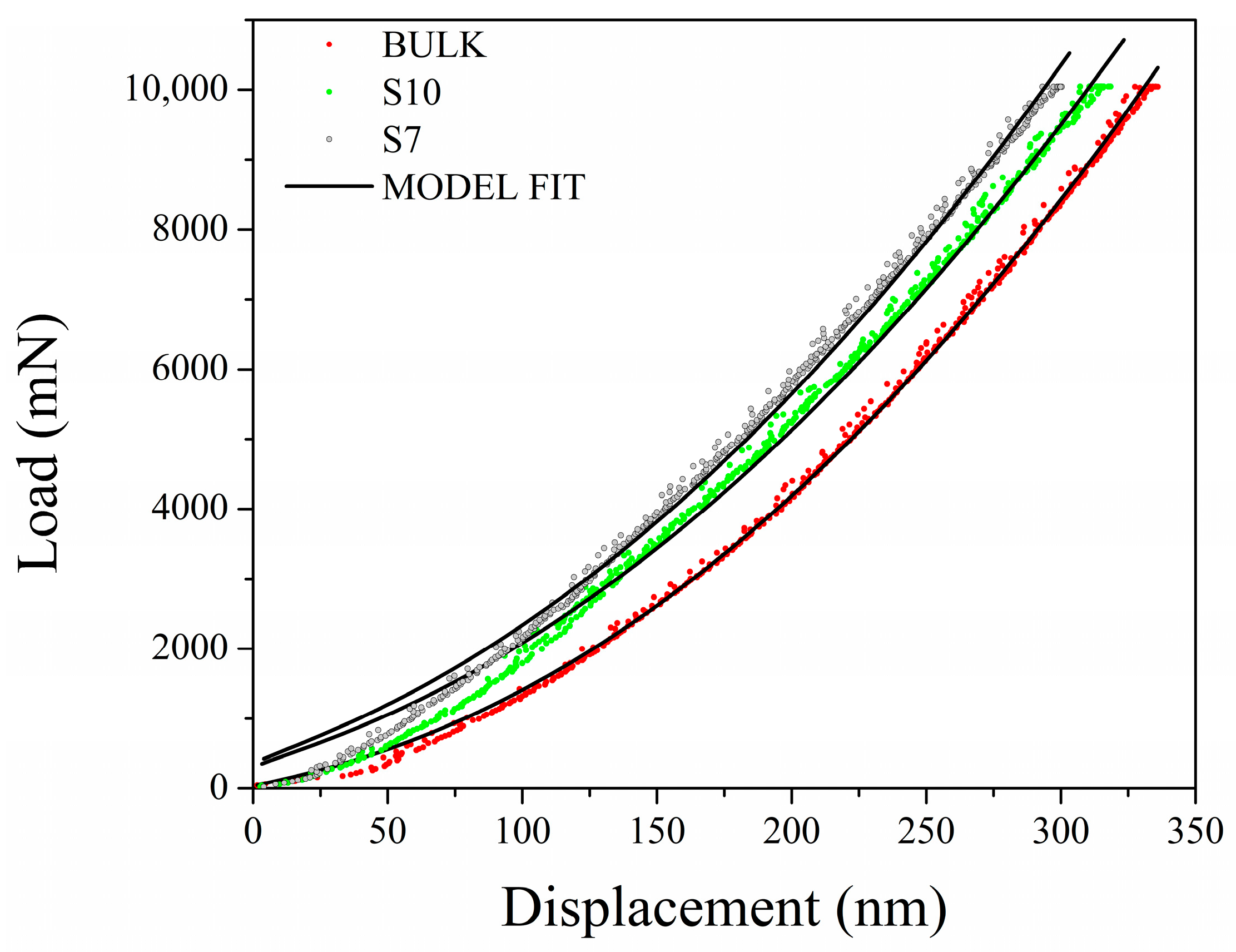
2.4. Dislocation Density by Means of Nanoindentation Approach
2.5. Dislocation Density Using X-Ray Diffraction
3. Results and Discussion
3.1. Microstructural Characterization
3.2. The Mechanical Deformation of the AM Components
3.3. Dislocation Density by Nanoindentation
- (a)
- Thermal gradient and cooling rate: The higher surface-area-to-volume ratio of the S10 structure relative to the bulk component results in faster cooling rates and more pronounced thermal shrinkage, leading to a higher density of dislocations.
- (b)
- Geometric constraints: The interconnected lattice struts in S10 experience greater local mechanical constraints compared to the bulk, amplifying residual stresses and plastic deformation during printing.
3.4. X-Ray Diffraction Results
4. Conclusions
- The as-built microstructure exhibited dendritic structure, and the dendrite sizes were measured as 0.92 µm for the bulk component, 0.65 µm for S10, and 0.47 µm for S7, thus confirming that higher cooling rates in lattice structures led to finer dendrites. Following thermal treatment at 1150 °C for 2 h, complete recrystallization occurred in both the bulk and S10 structures, resulting in the formation of equiaxed grains. However, in the S7 structure, new grain nucleation was observed within the recrystallized structure, likely due to higher stored strain energy from mechanical deformation.
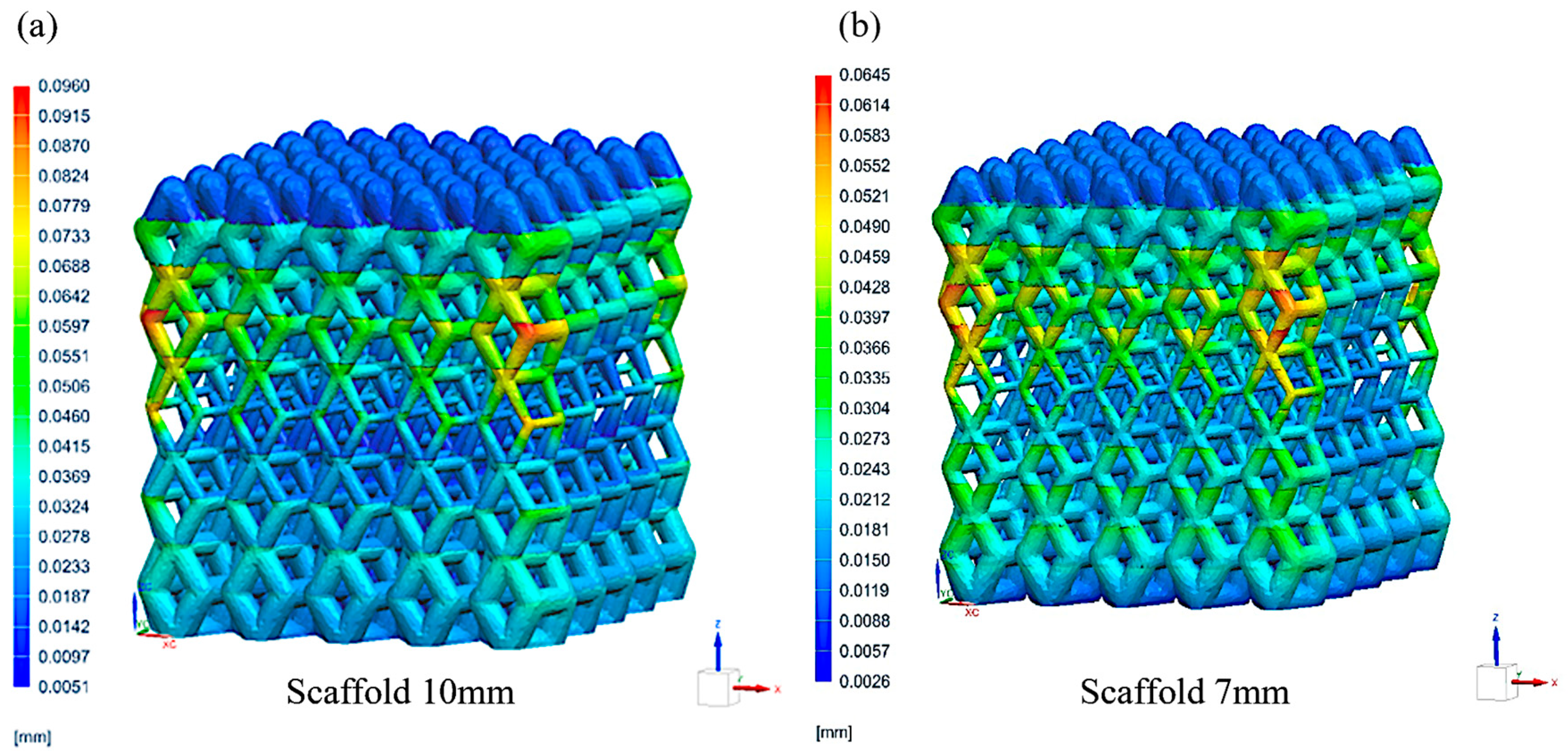
- LPBF-induced thermal stresses result in varying degrees of deformation, as confirmed by both simulation and experimental surface scans. Furthermore, the finer strut size in S7 leads to a more significant shrinkage effect, thereby increasing the mechanical deformation compared to both bulk and S10.
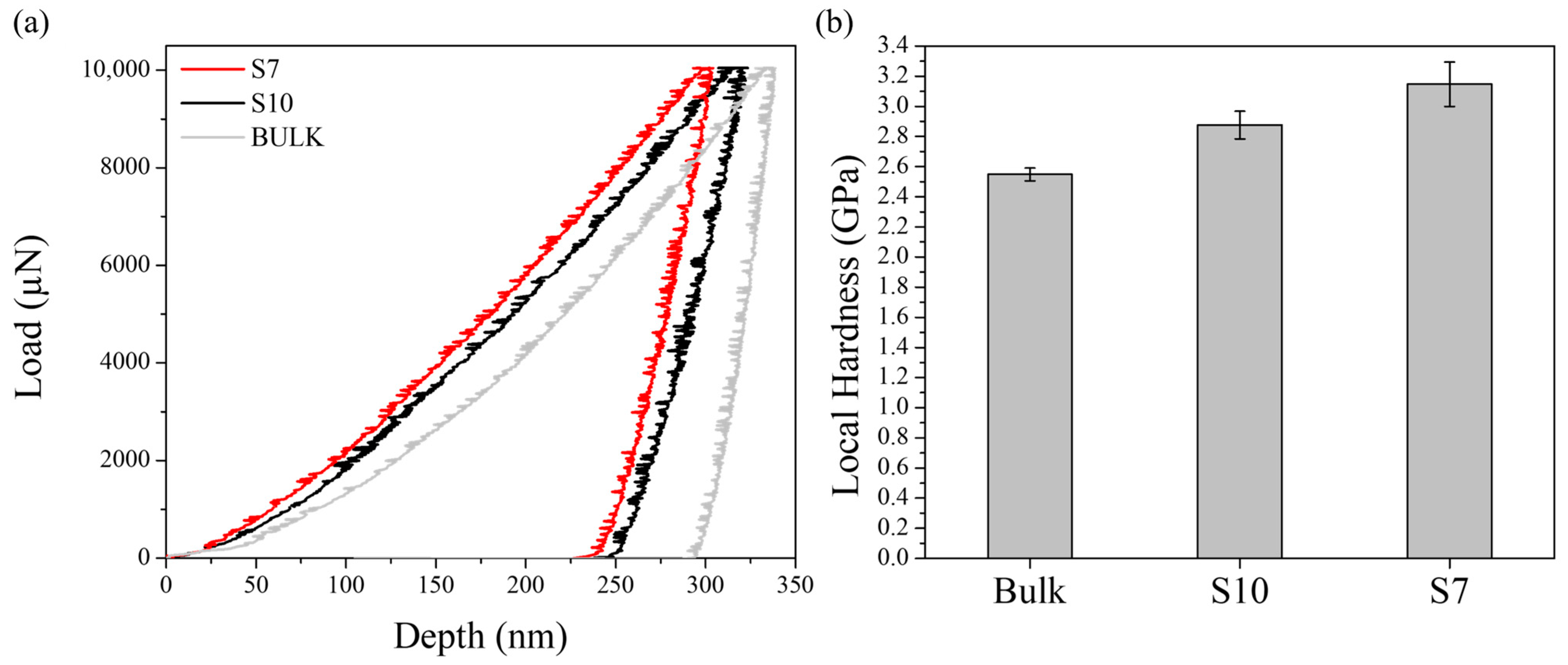
- The investigation revealed a progressive increase in local hardness from the bulk to lattice structures with values of approximately 2.6 GPa for the bulk, 3.2 GPa for S10, and around 3.8 GPa for S7. A correlation was observed between the increase in hardness and the rise in total dislocation density, as determined by nanoindentation and XRD.
- ▪
- Bulk:
- ▪
- S10:
- ▪
- S7:
- The consistency between the XRD and nanoindentation SSD confirms that the dominant contribution to dislocation density in the studied structures arises from stored plastic deformation. However, the trend similarity between the total dislocation density (as determined by nanoindentation) and SSD (as determined by XRD) indicates that GNDs follow a related evolution pattern, influenced by strain gradients imposed by the printing process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GLS | Graded lattice structure |
| AM | Additive manufacturing |
| LPBF | Laser powder bed fusion |
| SEM | Scanning electron microscopy |
| OM | Optical microscopy |
| GND | Geometrically necessary dislocations |
| SSD | Statistically stored dislocations |
References
- Numan, K.; Riccio, A. A systematic review of design for additive manufacturing of aerospace lattice structures: Current trends and future directions. Prog. Aerosp. Sci. 2024, 149, 101021. [Google Scholar] [CrossRef]
- Stephen, D.; Stefanie, F.; Wen Feng, L.; Jun, W. Optimisation of functionally graded lattice structures using isostatic lines. Mater. Des. 2017, 127, 215–223. [Google Scholar] [CrossRef]
- János, P.; Ajit, P. Effect of density and unit cell size grading on the stiffness and energy absorption of short fibre-reinforced functionally graded lattice structures. Addit. Manuf. 2020, 33, 101171. [Google Scholar] [CrossRef]
- Gatto, M.L.; Cerqueni, G.; Groppo, R.; Santecchia, E.; Tognoli, E.; Defanti, S.; Mattioli-Belmonte, M.; Mengucci, P. Improved biomechanical behavior of 316L graded scaffolds for bone tissue regeneration produced by laser powder bed fusion. J. Mech. Behav. Biomed. Mater. 2023, 144, 105989. [Google Scholar] [CrossRef] [PubMed]
- Calignano, F. Design optimization of supports for overhanging structures in aluminum and titanium alloys by selective laser melting. Mater. Des. 2014, 64, 203–213. [Google Scholar] [CrossRef]
- Paul, R.; Anand, S.; Gerner, F. Effect of thermal deformation on part errors in metal powder based additive manufacturing processes. J. Manuf. Sci. Eng. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Xie, D.; Lv, F.; Yang, Y.; Shen, L.; Tian, Z.; Shuai, C.; Chen, B.; Zhao, J. A review on distortion and residual stress in additive manufacturing. Chin. J. Mech. Eng. Addit. Manuf. Front. 2022, 1, 100039. [Google Scholar] [CrossRef]
- Di Pompeo, V.; Santecchia, E.; Santoni, A.; Sleem, K.; Cabibbo, M.; Spigarelli, S. Microstructure and defect analysis of 17-4PH stainless steel fabricated by the Bound Metal Deposition additive manufacturing technology. Crystals 2023, 12, 1312. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and optimization of lattice structures: A review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Liu, L.; Ding, Q.; Zhong, Y.; Zou, J.; Wu, J.; Chiu, Y.L.; Li, J.; Zhang, Z.; Yu, Q.; Shen, Z. Dislocation network in additive manufactured steel breaks strength–ductility trade-off. Mater. Today 2018, 21, 354–361. [Google Scholar] [CrossRef]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2018, 17, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Saeidi, K.; Gao, X.; Zhong, Y.; Shen, Z.J. Hardened austenite steel with columnar sub-grain structure formed by laser melting. Mater. Sci. Eng. 2015, 625, 221–229. [Google Scholar] [CrossRef]
- Gao, S.; Li, Z.; Van Petegem, S.; Ge, J.; Goel, S.; Vas, J.V.; Luzin, V.; Hu, Z.; Seet, H.L.; Sanchez, D.F. Additive manufacturing of alloys with programmable microstructure and properties. Nat. Commun. 2023, 14, 6752. [Google Scholar] [CrossRef]
- Ramirez, D.A.; Murr, L.E.; Martinez, E.; Hernandez, D.H.; Martinez, J.L.; Machado, B.I.; Medina, F.; Frigola, P.; Wicker, R.B. Novel precipitate–microstructural architecture developed in the fabrication of solid copper components by additive manufacturing using electron beam melting. Acta Mater. 2011, 59, 4088–4099. [Google Scholar] [CrossRef]
- Bertsh, K.M.; De Bellefon, G.M.; Kuehl, B.; Thoma, D.J. Origin of dislocation structures in an additively manufactured austenitic stainless steel 316L. Acta Mater. 2020, 199, 19–33. [Google Scholar] [CrossRef]
- Chamma, L.; Pipard, J.M.; Arlazarov, A.; Richeton, T.; Lecomte, J.S.; Berbenni, S. A combined EBSD/nanoindentation study of dislocation density gradients near grain boundaries in a ferritic steel. Mater. Technol. 2022, 110, 203. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Yaghoobi, M. Review of nanoindentation size effect: Experiments and atomistic simulation. Crystals 2017, 7, 321. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Durst, K.; Backes, B.; Franke, O.; Göken, M. Indentation size effect in metallic materials: Modeling strength from pop-in to macroscopic hardness using geometrically necessary dislocations. Acta Mater. 2006, 54, 2547–2555. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 2000. [Google Scholar] [CrossRef]
- Dao, M.; Chollacoop, N.V.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S.J.A. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. A 1934, 145, 362–387. [Google Scholar]
- Barnoush, A. Correlation between dislocation density and nanomechanical response during nanoindentation. Acta Mater. 2012, 60, 1268–1277. [Google Scholar] [CrossRef]
- Gallet, J.; Perez, M.; Guillou, R.; Ernould, C.; Le Bourlot, C.; Langlois, C.; Beausir, B.; Bouzy, E.; Chaise, T.; Cazottes, S. Experimental measurement of dislocation density in metallic materials: A quantitative comparison between measurements techniques (XRD, R-ECCI, HR-EBSD, TEM). Mater. Charact. 2023, 199, 112842. [Google Scholar] [CrossRef]
- Murugesan, S.; Kuppusami, P.; Mohandas, E.; Vijayalakshmi, M. X-ray diffraction Rietveld analysis of cold worked austenitic stainless steel. Mater. Lett. 2012, 67, 173–176. [Google Scholar] [CrossRef]

| Printing Parameter | Range |
|---|---|
| Laser power [W] | 200–270 |
| Scan speed [mm/s] | 400–1000 |
| Hatching distance [mm] | 0.10–0.14 |
| Thickness [mm] | 0.02–0.06 |
| Volumetric energy density [J/mm3] | 48 |
| Factor f | ρGND (m−2) | ρSSD (m−2) | ρTotal (m−2) | |
|---|---|---|---|---|
| Bulk | 2.3 | 4.238 × 1014 ± 1.3765 × 1012 | 2.460 × 1013 ± 4.11096 × 1011 | 4.484 × 1014 |
| S10 | 1.2 | 3.932 × 1015 ± 3.10271 × 1012 | 9.739 × 1013 ± 1.93623 × 1012 | 4.029 × 1015 |
| S7 | 1.02 | 5.799 × 1015 ± 3.74386 × 1012 | 2.308 × 1014 ± 5.59723 × 1012 | 6.029 × 1015 |
| Dislocation Density (m−2) | |
|---|---|
| Bulk | |
| S10 | |
| S7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sleem, K.; Grima, G.; Cabibbo, M. A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures. J. Manuf. Mater. Process. 2025, 9, 59. https://doi.org/10.3390/jmmp9020059
Sleem K, Grima G, Cabibbo M. A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures. Journal of Manufacturing and Materials Processing. 2025; 9(2):59. https://doi.org/10.3390/jmmp9020059
Chicago/Turabian StyleSleem, Kamal, Gabriele Grima, and Marcello Cabibbo. 2025. "A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures" Journal of Manufacturing and Materials Processing 9, no. 2: 59. https://doi.org/10.3390/jmmp9020059
APA StyleSleem, K., Grima, G., & Cabibbo, M. (2025). A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures. Journal of Manufacturing and Materials Processing, 9(2), 59. https://doi.org/10.3390/jmmp9020059








