Fabrication of Al-Cu Alloy via Additive Friction Stir Deposition
Abstract
1. Introduction
2. Materials and Methods
3. Results
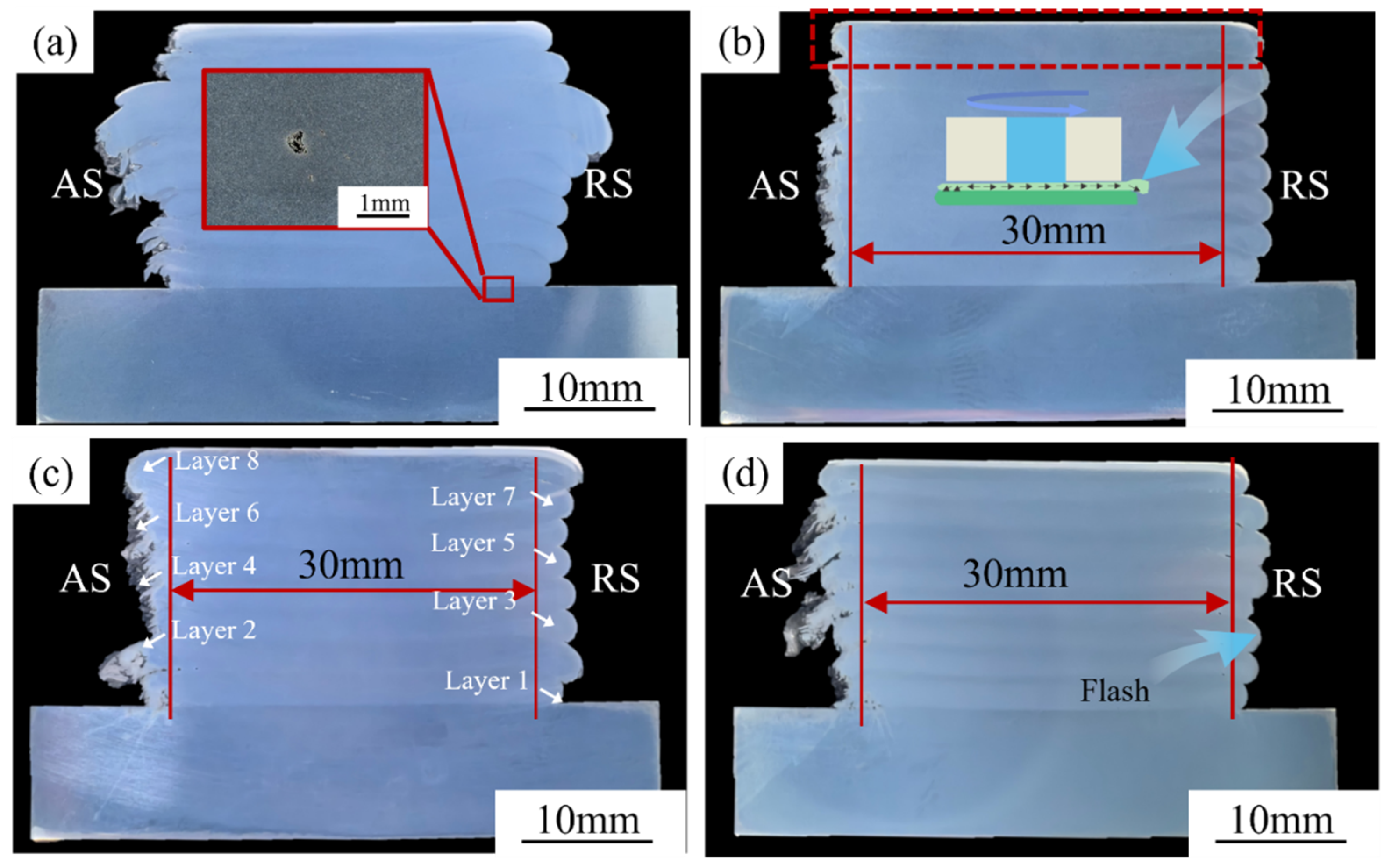
3.1. Effects of Rotational Rate on Macroscopic Morphology
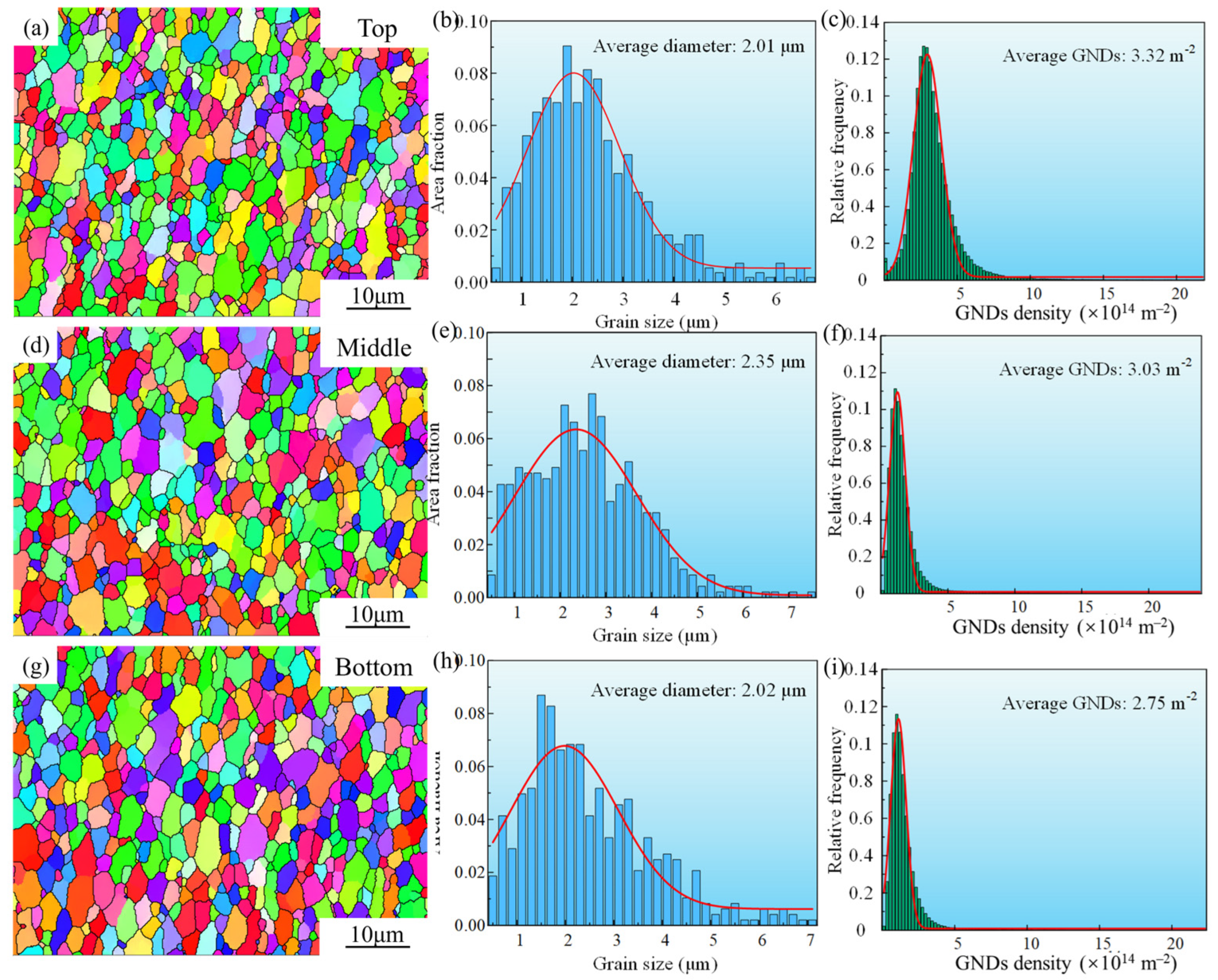
3.2. Effects of Rotational Rate on Microstructures
3.3. Effects of Rotational Rate on Mechanical Properties
4. Discussion
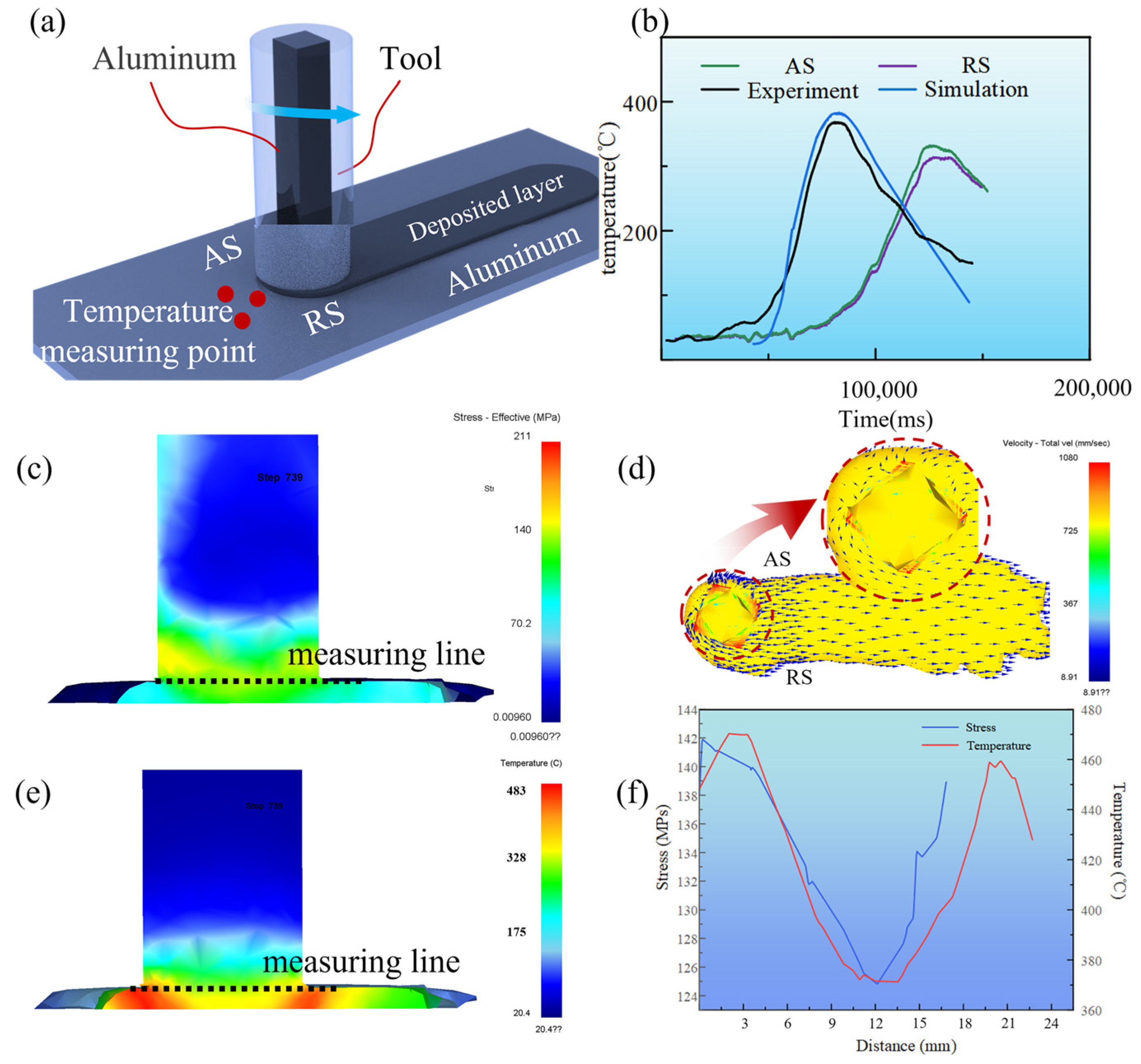
4.1. Numerical Simulation
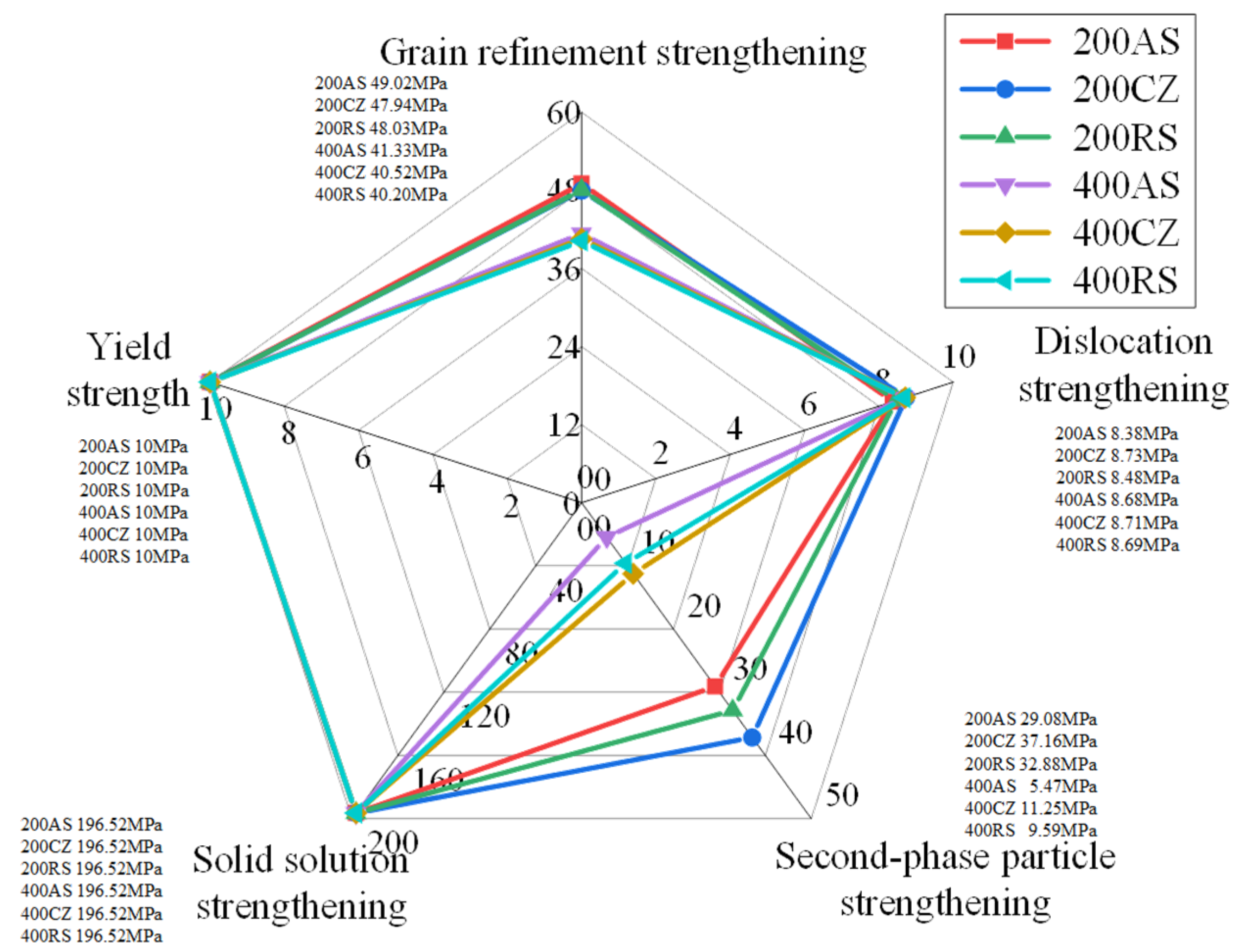
4.2. Assessing the Various Contributions to Strengthening
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shafi, S.M.; Fatima, A.; Hendrickson, N.V. Characterizing Surface Waviness of Aluminum Alloy: An Approach to Minimize Post-Processing in Wire Arc Additive Manufacturing (WAAM) Production. J. Manuf. Mater. Process 2025, 9, 347. [Google Scholar] [CrossRef]
- Barbosa, A.L.; Mariani, F.E.; Pereira, F.M.; Cintho, O.M.; Coelho, R.T.; Gargarella, P.; Zilnyk, K. Directed Energy Deposition-Laser Beam of Semi-Austenitic Precipitation-Hardening Stainless Steel. J. Manuf. Mater. Process 2025, 9, 114. [Google Scholar] [CrossRef]
- Zhang, Z.; Wan, L.; Xie, Y.; Wen, Q.; Mao, D.; Dong, W.; Sun, X.; Tian, H.; Meng, X.; Huang, Y. Achieving high-plasticity pure aluminium from wire-based friction stir additive manufacturing. Mater. Res. Lett. 2024, 166, 936–945. [Google Scholar] [CrossRef]
- Griffiths, R.J.; Perry, M.E.J.; Sietins, J.M.; Zhu, Y.; Hardwick, N.; Cox, C.D.; Rauch, H.A.; Yu, H.Z. A Perspective on Solid-State Additive Manufacturing of Aluminum Matrix Composites Using MELD. J. Mater. Eng. Perform. 2018, 28, 648–656. [Google Scholar] [CrossRef]
- Yoder, J.K.; Hahn, G.D.; Zhao, N.; Brennan, R.E.; Cho, K.; Yu, H.Z. Additive friction stir deposition-enabled upcycling of automotive cast aluminum chips. Addit. Manuf. Lett. 2023, 4, 100108. [Google Scholar] [CrossRef]
- Joey Griffiths, R.; Gotawala, N.; Hahn, G.D.; Garcia, D.; Yu, H.Z. Towards underwater additive manufacturing via additive friction stir deposition. Mater. Des. 2022, 223, 111148. [Google Scholar] [CrossRef]
- Yu, H.Z.; Hahn, G.D. Potential and challenges for large-scale near-net-shaping of 7xxx aerospace grade aluminum via additive friction stir deposition. Mater. Lett. X 2023, 19, 100217. [Google Scholar] [CrossRef]
- Zhu, N.; Avery, D.Z.; Rutherford, B.A.; Phillips, B.J.; Allison, P.G.; Jordon, J.B.; Brewer, L.N. The Effect of Anodization on the Mechanical Properties of AA6061 Produced by Additive Friction Stir-Deposition. Metals 2021, 11, 1773. [Google Scholar] [CrossRef]
- Martin, L.P.; Luccitti, A.; Walluk, M. Evaluation of Additive Friction Stir Deposition of AISI 316L For Repairing Surface Material Loss in AISI 4340. Int. J. Adv. Des. Manuf. Technol. 2022, 121, 2365–2381. [Google Scholar] [CrossRef]
- Robinson, T.W.; Williams, M.B.; Rao, H.M.; Kinser, R.P.; Allison, P.G.; Jordon, J.B. Microstructural and Mechanical Properties of a Solid-State Additive Manufactured Magnesium Alloy. J. Manuf. Sci. Eng. 2022, 144, 061013. [Google Scholar] [CrossRef]
- Phillips, B.J.; Avery, D.Z.; Liu, T.; Rodriguez, O.L.; Mason, C.J.T.; Jordon, J.B.; Brewer, L.N.; Allison, P.G. Microstructure-deformation relationship of additive friction stir-deposition Al–Mg–Si. Materialia 2019, 7, 100387. [Google Scholar] [CrossRef]
- Phillips, B.J.; Williamson, C.J.; Kinser, R.P.; Jordon, J.B.; Doherty, K.J.; Allison, P.G. Microstructural and Mechanical Characterization of Additive Friction Stir-Deposition of Aluminum Alloy 5083 Effect of Lubrication on Material Anisotropy. Materials 2021, 14, 6732. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Zhang, M.; Wang, H.; Gong, W.; Lai, R.; Li, Y.; Teng, J. The corrosion behavior and mechanical properties of 5083 Al-Mg alloy manufactured by additive friction stir deposition. Corros. Sci. 2023, 213, 110972. [Google Scholar] [CrossRef]
- Rivera, O.G.; Allison, P.G.; Brewer, L.N.; Rodriguez, O.L.; Jordon, J.B.; Liu, T.; Whittington, W.; Martens, R.; McClelland, Z.; Mason, C.; et al. Influence of texture and grain refinement on the mechanical behavior of AA2219 fabricated by high shear solid state material deposition. Mater. Sci. Eng. A 2018, 724, 547–558. [Google Scholar] [CrossRef]
- Anderson-Wedge, K.; Avery, D.Z.; Daniewicz, S.R.; Sowards, J.W.; Allison, P.G.; Jordon, J.B.; Amaro, R. Characterization of the fatigue behavior of additive friction stir-deposition AA2219. Int. J. Fatigue 2021, 142, 105951. [Google Scholar] [CrossRef]
- Perry, M.E.J.; Griffiths, R.J.; Garcia, D.; Sietins, J.M.; Zhu, Y.; Yu, H.Z. Morphological and microstructural investigation of the non-planar interface formed in solid-state metal additive manufacturing by additive friction stir deposition. Addit. Manuf. 2020, 35, 101293. [Google Scholar] [CrossRef]
- Aziz, S.B.; Dewan, M.W.; Huggett, D.J.; Wahab, M.A.; Okeil, A.M.; Warren Liao, T. Impact of Friction Stir Welding (FSW) Process Parameters on Thermal Modeling and Heat Generation of Aluminum Alloy Joints. Acta Met. Sin. Engl. Lett. 2016, 29, 869–883. [Google Scholar] [CrossRef]
- Khan, A.S.; Baig, M. Anisotropic responses, constitutive modeling and the effects of strain-rate and temperature on the formability of an aluminum alloy. Int. J. Plast. 2011, 27, 522–538. [Google Scholar] [CrossRef]
- Buffa, G.; Hua, J.; Shivpuri, R.; Fratini, L. A continuum based fem model for friction stir welding—Model development. Mater. Sci. Eng. A 2006, 419, 389–396. [Google Scholar] [CrossRef]
- Williams, M.B.; Robinson, T.W.; Williamson, C.J.; Kinser, R.P.; Ashmore, N.A.; Allison, P.G.; Jordon, J.B. Elucidating the Effect of Additive Friction Stir Deposition on the Resulting Microstructure and Mechanical Properties of Magnesium Alloy WE43. Metals 2021, 11, 1739. [Google Scholar] [CrossRef]
- Tang, W.; Yang, X.; Luo, T.; Wang, R.; Gu, C. Precipitation behavior and strengthening-toughening mechanism of additive friction stir-deposited Al–Mg–Si–Cu alloy. Addit. Manuf. 2023, 76, 103785. [Google Scholar] [CrossRef]
- Garcia, D.; Griffiths, R.J.; Yu, H.Z. Additive Friction Stir Deposition for Fabrication of Silicon Carbide Metal Matrix Composites. In Proceedings of the ASME 2020 15th International Manufacturing Science and Engineering Conference, Cincinnati, OH, USA, 22–26 June 2020; Volume 1, p. 84256. [Google Scholar]
- Salih, O.S.; Ou, H.; Sun, W. Heat generation, plastic deformation and residual stresses in friction stir welding of aluminium alloy. Int. J. Mech. Sci. 2023, 238, 107827. [Google Scholar] [CrossRef]
- Chen, Z.; Ren, J.; Yuan, Z.; Ringer, S.P. Enhanced strength-plasticity combination in an Al–Cu–Mg alloy—Atomic scale microstructure regulation and strengthening mechanisms. Mater. Sci. Eng. A 2020, 787, 139447. [Google Scholar] [CrossRef]








| Cu | Mg | Mn | Fe | Si | Zn | Cr | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| 4.60 | 1.55 | 0.66 | 0.21 | 0.09 | 0.04 | 0.03 | 0.02 | Bal |
| Material | Microhardness (HV) | Ultimate Tensile Strength (MPa) | Elongation (%) |
|---|---|---|---|
| 2024-T4 | 129 | 410 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Q.; Wan, L.; Zhang, Z. Fabrication of Al-Cu Alloy via Additive Friction Stir Deposition. J. Manuf. Mater. Process. 2025, 9, 387. https://doi.org/10.3390/jmmp9120387
Wen Q, Wan L, Zhang Z. Fabrication of Al-Cu Alloy via Additive Friction Stir Deposition. Journal of Manufacturing and Materials Processing. 2025; 9(12):387. https://doi.org/10.3390/jmmp9120387
Chicago/Turabian StyleWen, Qi, Long Wan, and Zeyu Zhang. 2025. "Fabrication of Al-Cu Alloy via Additive Friction Stir Deposition" Journal of Manufacturing and Materials Processing 9, no. 12: 387. https://doi.org/10.3390/jmmp9120387
APA StyleWen, Q., Wan, L., & Zhang, Z. (2025). Fabrication of Al-Cu Alloy via Additive Friction Stir Deposition. Journal of Manufacturing and Materials Processing, 9(12), 387. https://doi.org/10.3390/jmmp9120387






