Bayesian Model Updating for Chatter in Milling
Abstract
1. Introduction
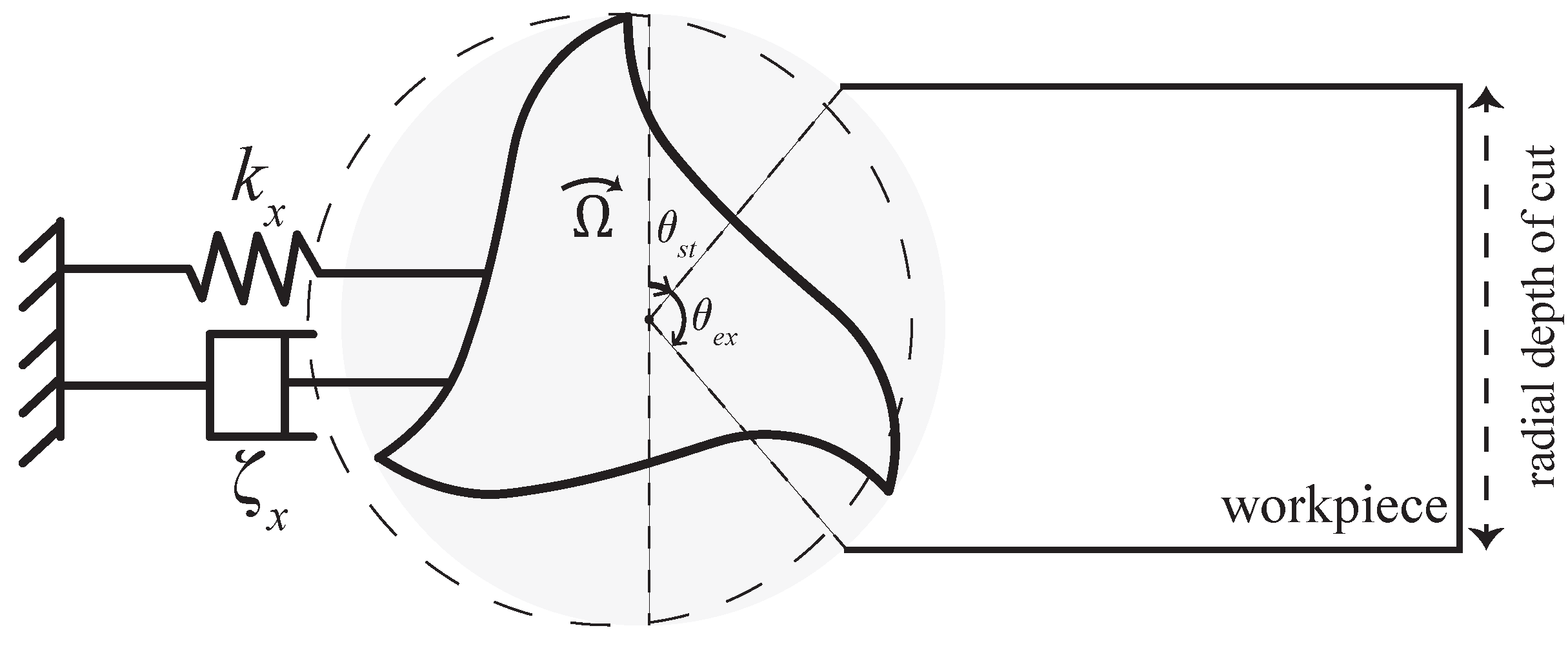
2. Milling Dynamics
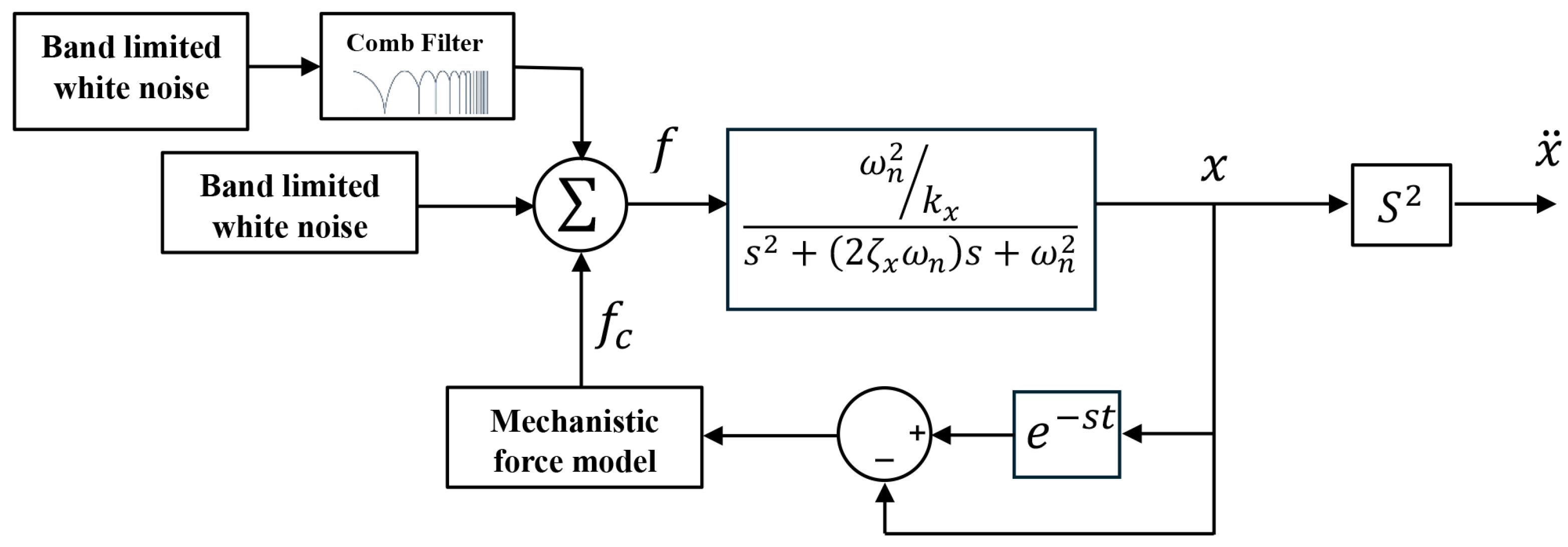
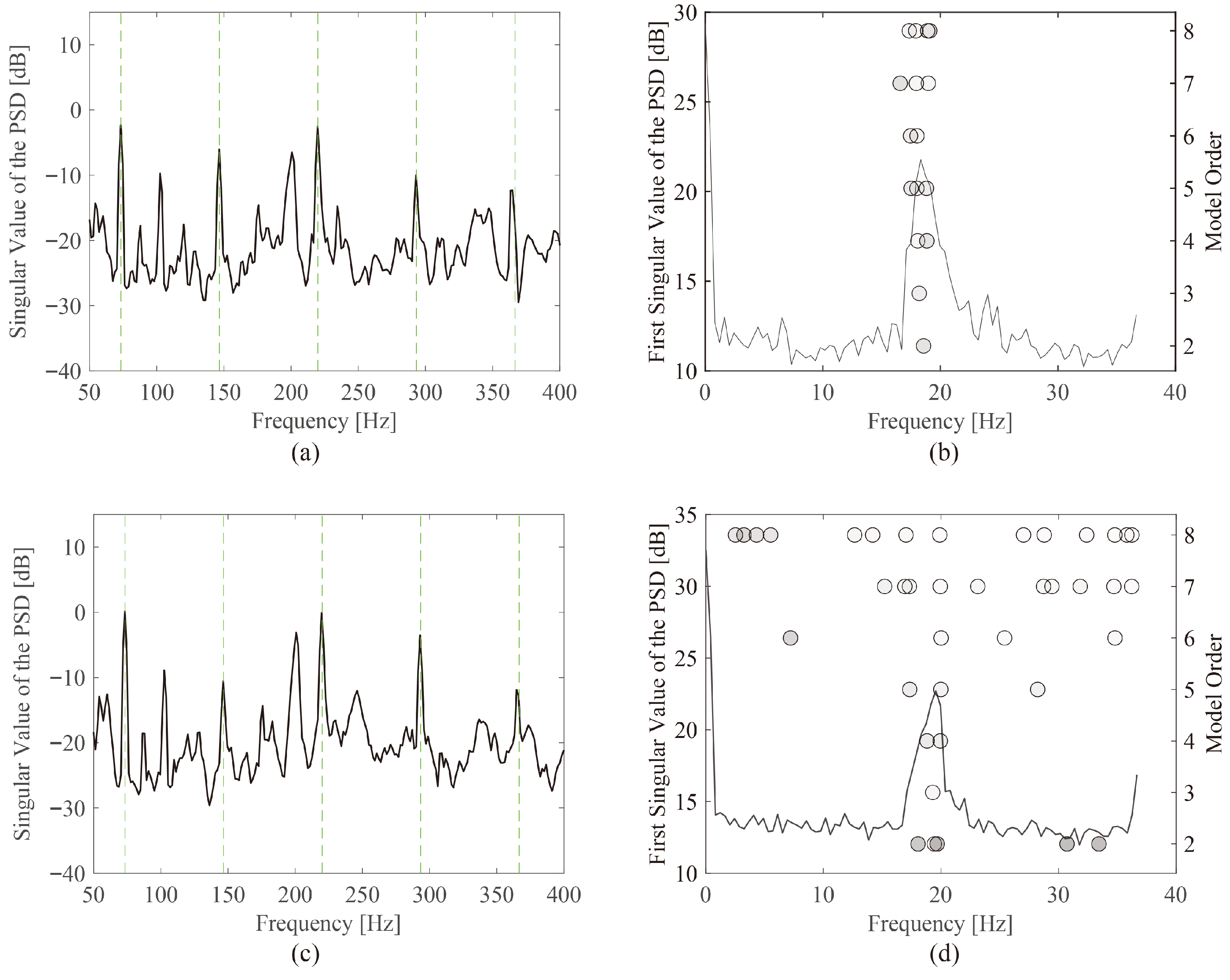
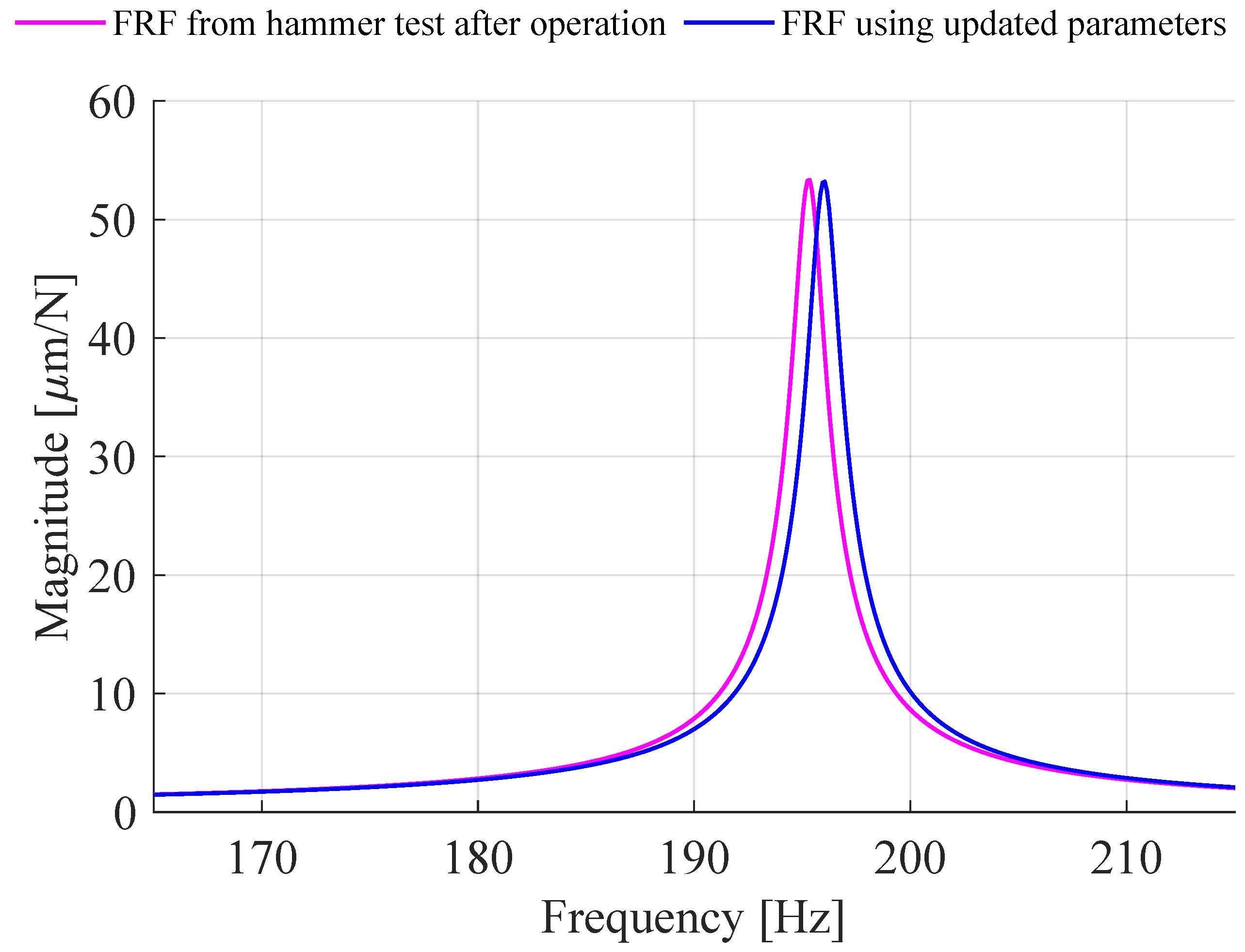
2.1. Operational Modal Analysis
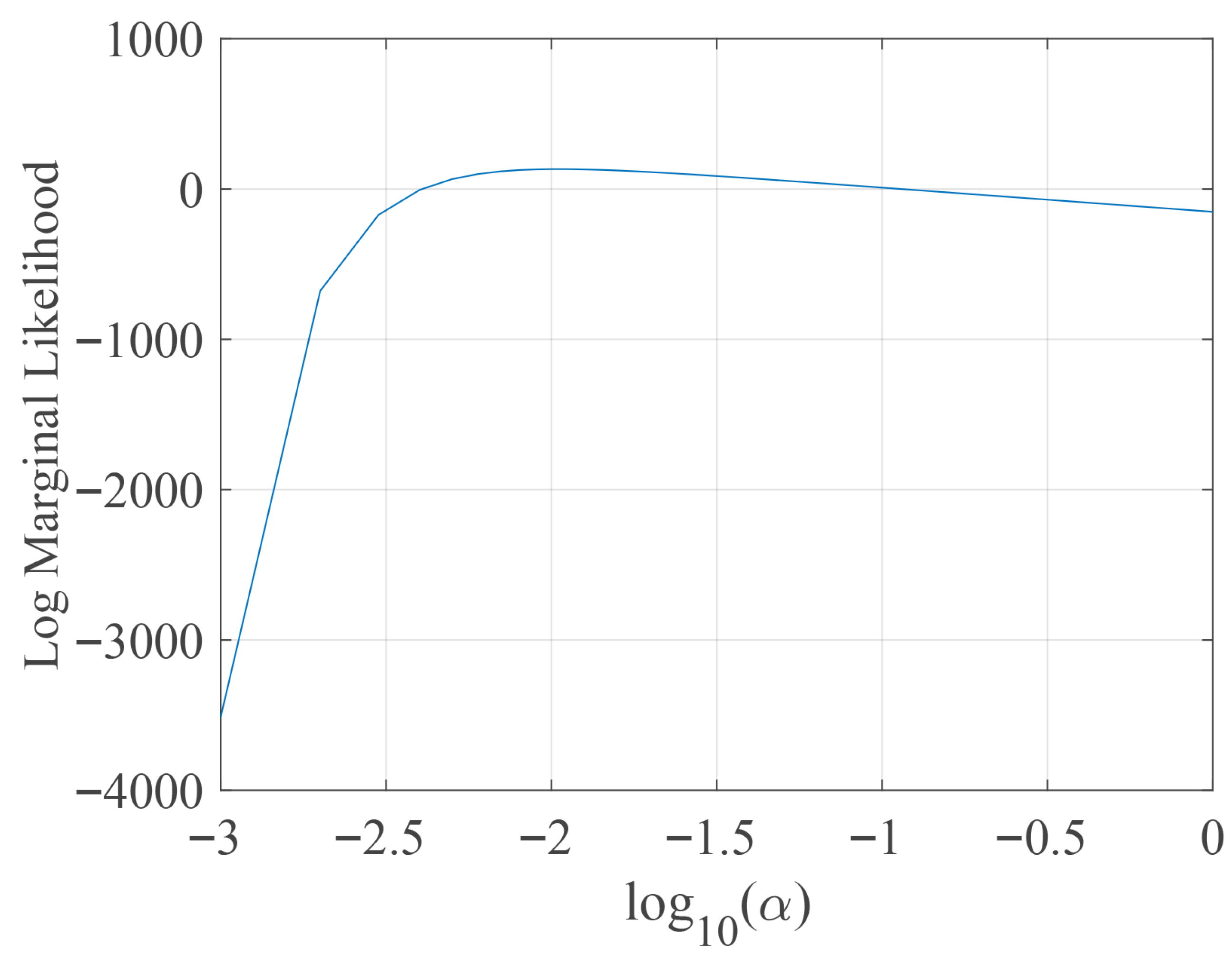
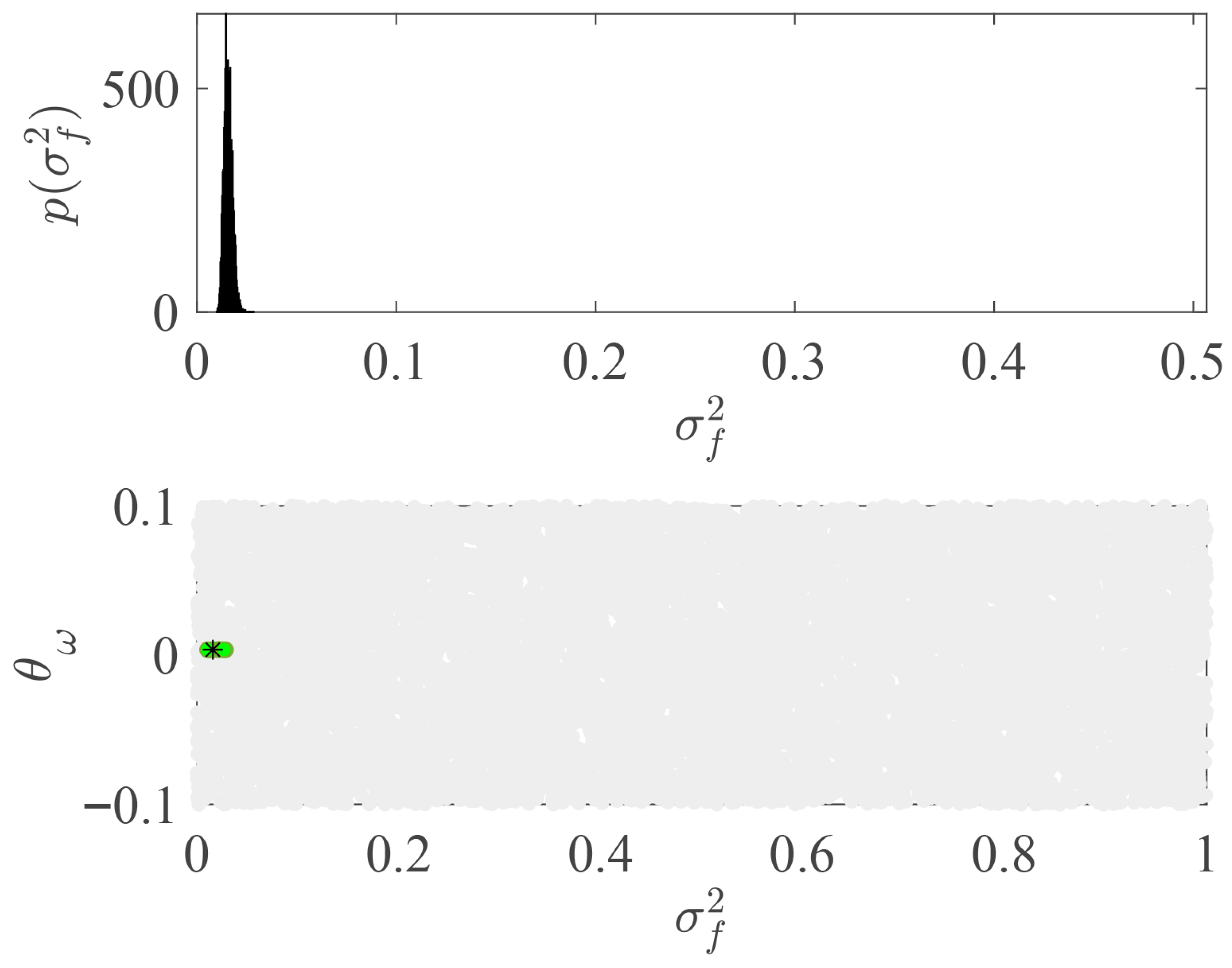
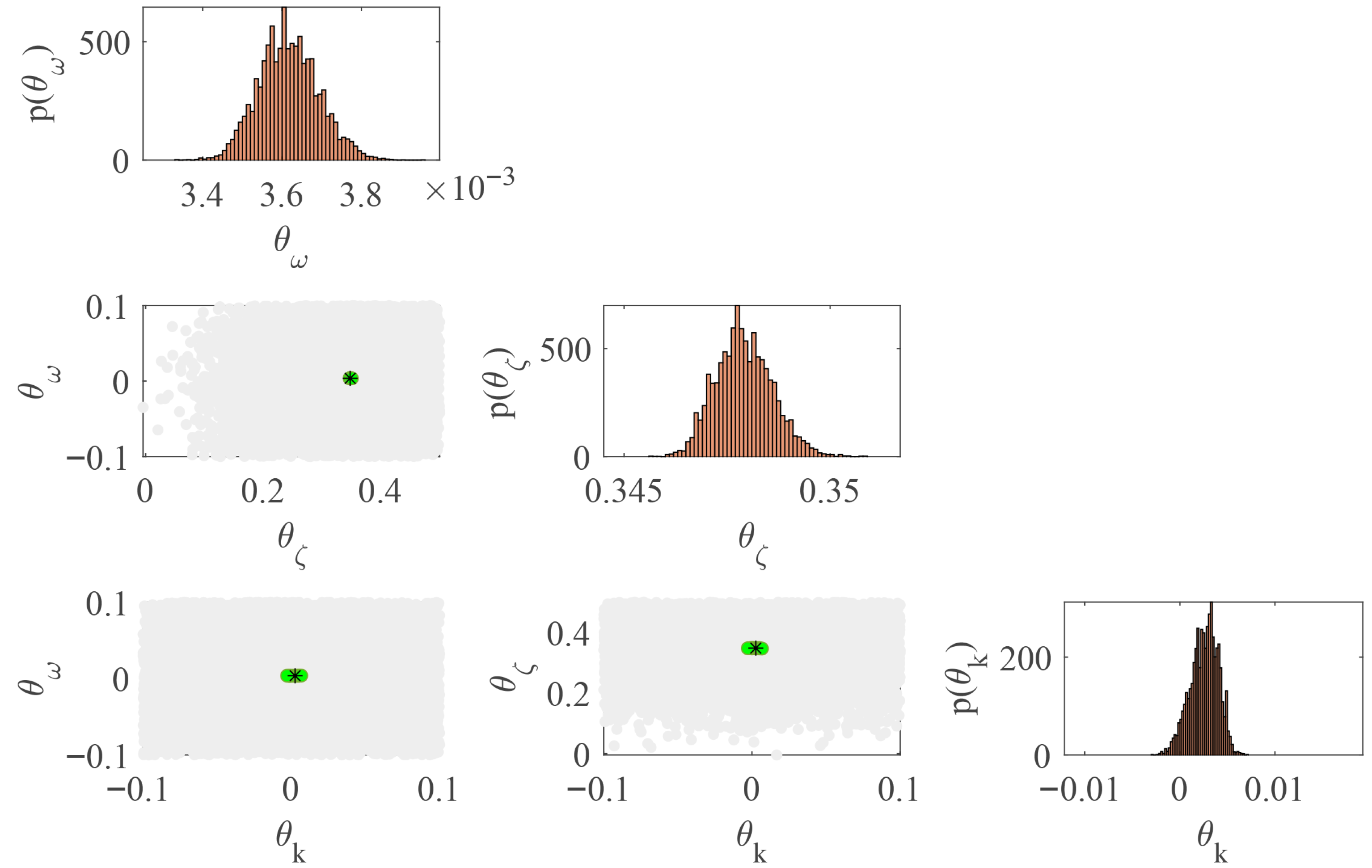
2.2. Model Updating
3. Results and Discussion
3.1. Numerical Simulation
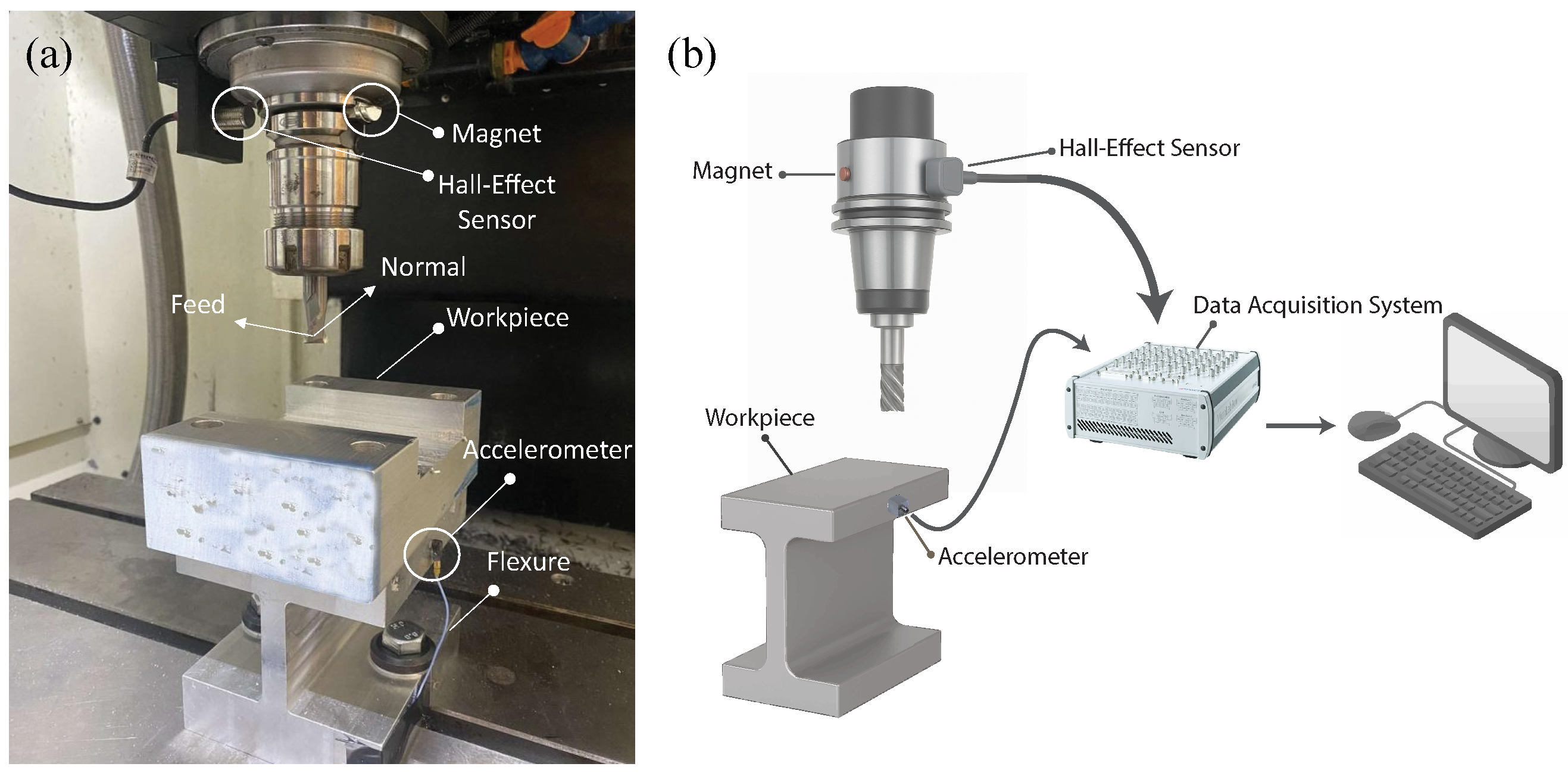
3.2. Experimental Case Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tobias, S.A. Machine Tool Vibration; Blackie and Sons Ltd.: Glasgow, UK, 1965. [Google Scholar]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Altintas, Y.; Stepan, G.; Budak, E.; Schmitz, T.; Kilic, Z.M. Chatter Stability of Machining Operations. J. Manuf. Sci. Eng. 2020, 142, 110801. [Google Scholar] [CrossRef]
- Iglesias, A.; Taner Tunç, L.; Özsahin, O.; Franco, O.; Munoa, J.; Budak, E. Alternative experimental methods for machine tool dynamics identification: A review. Mech. Syst. Signal Process. 2022, 170, 108837. [Google Scholar] [CrossRef]
- Suzuki, N.; Kurata, Y.; Kato, T.; Hino, R.; Shamoto, E. Identification of transfer function by inverse analysis of self-excited chatter vibration in milling operations. Precis. Eng. 2012, 36, 568–575. [Google Scholar] [CrossRef]
- Özşahin, O.; Budak, E.; Özgüven, H. In-process tool point FRF identification under operational conditions using inverse stability solution. Int. J. Mach. Tools Manuf. 2015, 89, 64–73. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. Improved experimental-analytical approach to compute speed-varying tool-tip FRF. Precis. Eng. 2017, 48, 114–122. [Google Scholar] [CrossRef]
- Postel, M.; Özsahin, O.; Altintas, Y. High speed tooltip FRF predictions of arbitrary tool-holder combinations based on operational spindle identification. Int. J. Mach. Tools Manuf. 2018, 129, 48–60. [Google Scholar] [CrossRef]
- Eynian, M. In-process identification of modal parameters using dimensionless relationships in milling chatter. Int. J. Mach. Tools Manuf. 2019, 143, 49–62. [Google Scholar] [CrossRef]
- Karandikar, J.; Traverso, M.; Abbas, A.; Schmitz, T. Bayesian Inference for Milling Stability Using a Random Walk Approach. J. Manuf. Sci. Eng. 2014, 136, 031015. [Google Scholar] [CrossRef]
- Karandikar, J.; Honeycutt, A.; Schmitz, T.; Smith, S. Stability boundary and optimal operating parameter identification in milling using Bayesian learning. J. Manuf. Process. 2020, 56, 1252–1262. [Google Scholar] [CrossRef]
- Rahimi, M.H.; Huynh, H.N.; Altintas, Y. On-line chatter detection in milling with hybrid machine learning and physics-based model. CIRP J. Manuf. Sci. Technol. 2021, 35, 25–40. [Google Scholar] [CrossRef]
- Postel, M.; Bugdayci, B.; Wegener, K. Ensemble transfer learning for refining stability predictions in milling using experimental stability states. Int. J. Adv. Manuf. Technol. 2020, 107, 4123–4139. [Google Scholar] [CrossRef]
- Wiederkehr, P.; Finkeldey, F.; Siebrecht, T. Reduction of experimental efforts for predicting milling stability affected by concept drift using transfer learning on multiple machine tools. CIRP Ann. 2024, 73, 301–304. [Google Scholar] [CrossRef]
- Minis, I.E.; Magrab, E.B.; Pandelidis, I.O. Improved Methods for the Prediction of Chatter in Turning, Part 1: Determination of Structural Response Parameters. J. Eng. Ind. 1990, 112, 12–20. [Google Scholar] [CrossRef]
- Özşahin, O.; Budak, E.; Özgüven, H. Investigating Dynamics of Machine Tool Spindles under Operational Conditions. Adv. Mater. Res. 2011, 223, 610–621. [Google Scholar] [CrossRef]
- Rudel, V.; Kienast, P.; Vinogradov, G.; Ganser, P.; Bergs, T. Cloud-based process design in a digital twin framework with integrated and coupled technology models for blisk milling. Front. Manuf. Technol. 2022, 2, 1021029. [Google Scholar] [CrossRef]
- Brincker, R. Introduction to Operational Modal Analysis; John Wiley & Sons: London, UK, 2015. [Google Scholar]
- Berthold, J.; Kolouch, M.; Regel, J.; Putz, M. Investigation of the Dynamic Behavior of Machine Tools During Cutting by Operational Modal Analysis. MM Sci. J. 2019, 2019, 3078–3085. [Google Scholar] [CrossRef]
- Kim, S.; Ahmadi, K. Estimation of vibration stability in turning using operational modal analysis. Mech. Syst. Signal Process. 2019, 130, 315–332. [Google Scholar] [CrossRef]
- Ebrahimi-Tirtashi, A.; Ahmadi, K. Automated Operational Modal Analysis of Self-Excited Vibrations in Turning. Mech. Syst. Signal Process. 2025, 233, 112705. [Google Scholar] [CrossRef]
- Zorlu, A.; Ahmadi, K.; Ebrahimi-Tirtashi, A. Operational Modal Analysis of Self-Excited Vibrations in Milling Considering Periodic Dynamics. J. Manuf. Sci. Eng. 2025, 147, 021010. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating Models and Their Uncertainties. I: Bayesian Statistical Framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Beck, J.L. Bayesian system identification based on probability logic. Struct. Control Health Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Goller, B.; Beck, J.; Schueller, G. Evidence-based identification of weighting factors in Bayesian model updating using modal data. J. Eng. Mech. 2012, 138, 430–440. [Google Scholar] [CrossRef]
- Ahmadi, K. Bayesian updating of modal parameters for modeling chatter in turning. CIRP J. Manuf. Sci. Technol. 2022, 38, 724–736. [Google Scholar] [CrossRef]
- Insperger, T.; Mann, B.; Stépán, G.; Bayly, P. Stability of up-milling and down-milling, part 1: Alternative analytical methods. Int. J. Mach. Tools Manuf. 2003, 43, 25–34. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Allen, M.S.; Sracic, M.W.; Chauhan, S.; Hansen, M.H. Output-only modal analysis of linear time-periodic systems with application to wind turbine simulation data. Mech. Syst. Signal Process. 2011, 25, 1174–1191. [Google Scholar] [CrossRef]
- Bamieh, B.; Pearson, J.B.; Francis, B.A.; Tannenbaum, A. A lifting technique for linear periodic systems with applications to sampled-data control. Syst. Control. Lett. 1991, 17, 79–88. [Google Scholar] [CrossRef]
- Chib, S.; Jeliazkov, I. Marginal Likelihood From the Metropolis–Hastings Output. J. Am. Stat. Assoc. 2001, 96, 270–281. [Google Scholar] [CrossRef]
- Friel, N.; Pettitt, A.N. Marginal Likelihood Estimation via Power Posteriors. J. R. Stat. Soc. Ser. B Stat. Methodol. 2008, 70, 589–607. [Google Scholar] [CrossRef]
- Betz, W.; Papaioannou, I.; Straub, D. Transitional Markov Chain Monte Carlo: Observations and Improvements. J. Eng. Mech. 2016, 142, 04016016. [Google Scholar] [CrossRef]
- Ching, J.; Chen, Y.C. Transitional Markov Chain Monte Carlo Method for Bayesian Model Updating, Model Class Selection, and Model Averaging. J. Eng. Mech. 2007, 133, 816–832. [Google Scholar] [CrossRef]
- Nobari, A.; Ouyang, H.; Bannister, P. Statistics of complex eigenvalues in friction-induced vibration. J. Sound Vib. 2015, 338, 169–183. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In Summer School on Machine Learning; Notes in Computer Science; Springer: Berlin, Germany, 2003; pp. 63–71. [Google Scholar]
- Insperger, T.; Stépán, G.; Bayly, P.; Mann, B. Multiple chatter frequencies in milling processes. J. Sound Vib. 2003, 262, 333–345. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y.; Armarego, E.J.A. Prediction of Milling Force Coefficients From Orthogonal Cutting Data. J. Manuf. Sci. Eng. 1996, 118, 216–224. [Google Scholar] [CrossRef]







 : Initial SLD using parameters obtained by an impact hammer test before starting the milling operations.
: Initial SLD using parameters obtained by an impact hammer test before starting the milling operations. : Updated SLD using mean of posterior.
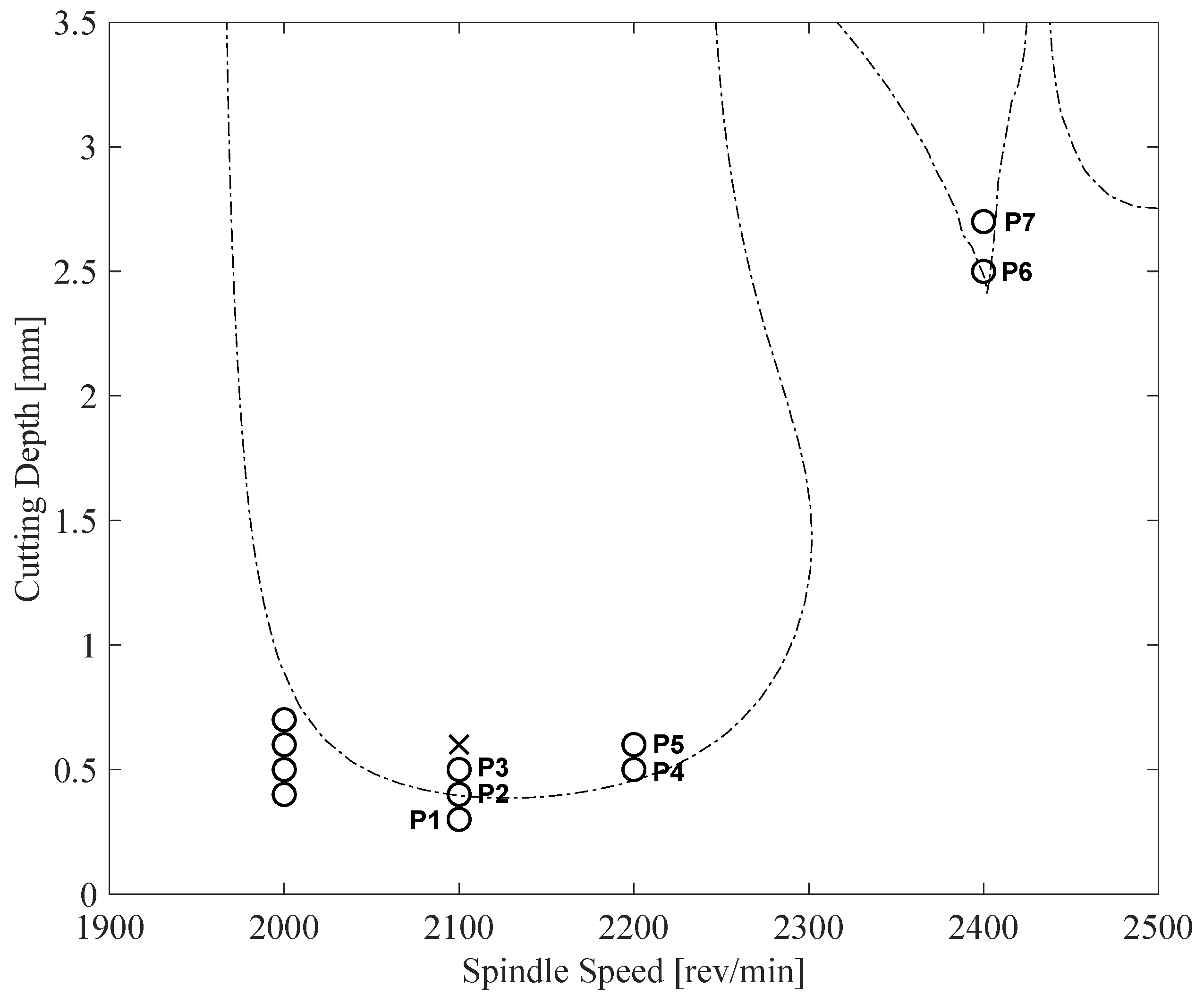
: Updated SLD using mean of posterior.  : SLD using parameters obtained by an impact hammer test after operations [23]. Circles and crosses are experimentally determined stable and unstable points, respectively. P1–P7 are the stable points used in model updating.
: SLD using parameters obtained by an impact hammer test after operations [23]. Circles and crosses are experimentally determined stable and unstable points, respectively. P1–P7 are the stable points used in model updating.
 : Initial SLD using parameters obtained by an impact hammer test before starting the milling operations.
: Initial SLD using parameters obtained by an impact hammer test before starting the milling operations. : Updated SLD using mean of posterior.
: Updated SLD using mean of posterior.  : SLD using parameters obtained by an impact hammer test after operations [23]. Circles and crosses are experimentally determined stable and unstable points, respectively. P1–P7 are the stable points used in model updating.
: SLD using parameters obtained by an impact hammer test after operations [23]. Circles and crosses are experimentally determined stable and unstable points, respectively. P1–P7 are the stable points used in model updating.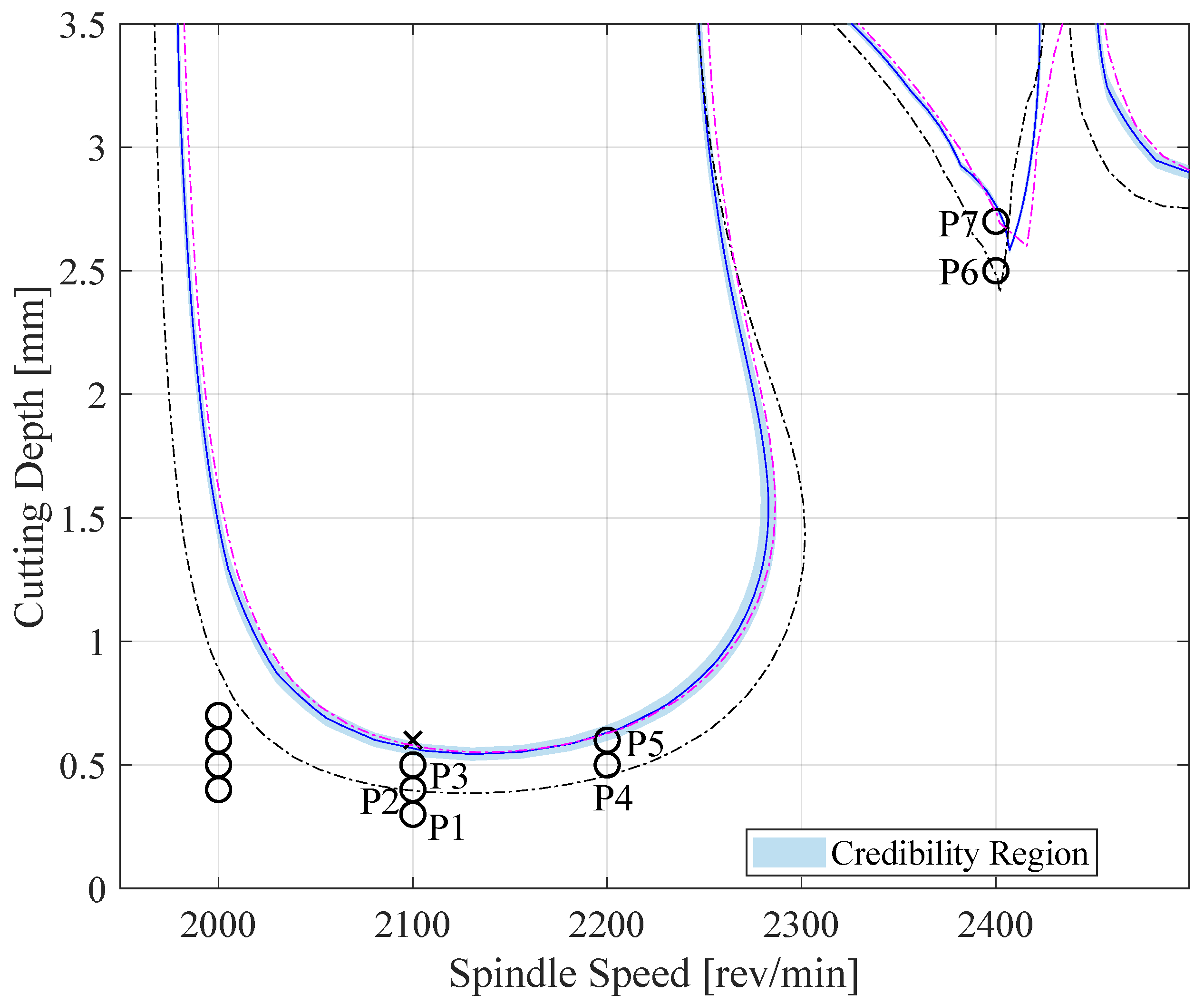
| p | Spindle Speed [RPM] | Cutting Depth [mm] | [Hz] | |
|---|---|---|---|---|
| 1 | 2000 | 0.4 | ||
| 2 | 2000 | 0.5 | ||
| 3 | 2000 | 0.6 | ||
| 4 | 2000 | 0.7 | ||
| 5 | 2000 | 0.8 | ||
| 6 | 2100 | 0.3 | ||
| 7 | 2100 | 0.4 |
| p | Spindle Speed [RPM] | Cutting Depth [mm] | [Hz] | |
|---|---|---|---|---|
| 1 | 2100 | 0.3 | ||
| 2 | 2100 | 0.4 | ||
| 3 | 2100 | 0.5 | ||
| 4 | 2200 | 0.5 | ||
| 5 | 2200 | 0.6 | ||
| 6 | 2400 | 2.5 | ||
| 7 | 2400 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebrahimi-Tirtashi, A.; Ahmadi, K. Bayesian Model Updating for Chatter in Milling. J. Manuf. Mater. Process. 2025, 9, 323. https://doi.org/10.3390/jmmp9100323
Ebrahimi-Tirtashi A, Ahmadi K. Bayesian Model Updating for Chatter in Milling. Journal of Manufacturing and Materials Processing. 2025; 9(10):323. https://doi.org/10.3390/jmmp9100323
Chicago/Turabian StyleEbrahimi-Tirtashi, Ali, and Keivan Ahmadi. 2025. "Bayesian Model Updating for Chatter in Milling" Journal of Manufacturing and Materials Processing 9, no. 10: 323. https://doi.org/10.3390/jmmp9100323
APA StyleEbrahimi-Tirtashi, A., & Ahmadi, K. (2025). Bayesian Model Updating for Chatter in Milling. Journal of Manufacturing and Materials Processing, 9(10), 323. https://doi.org/10.3390/jmmp9100323







