Formability Assessment of Additively Manufactured Materials via Dieless Nakajima Testing
Abstract
1. Introduction
2. Materials and Methods
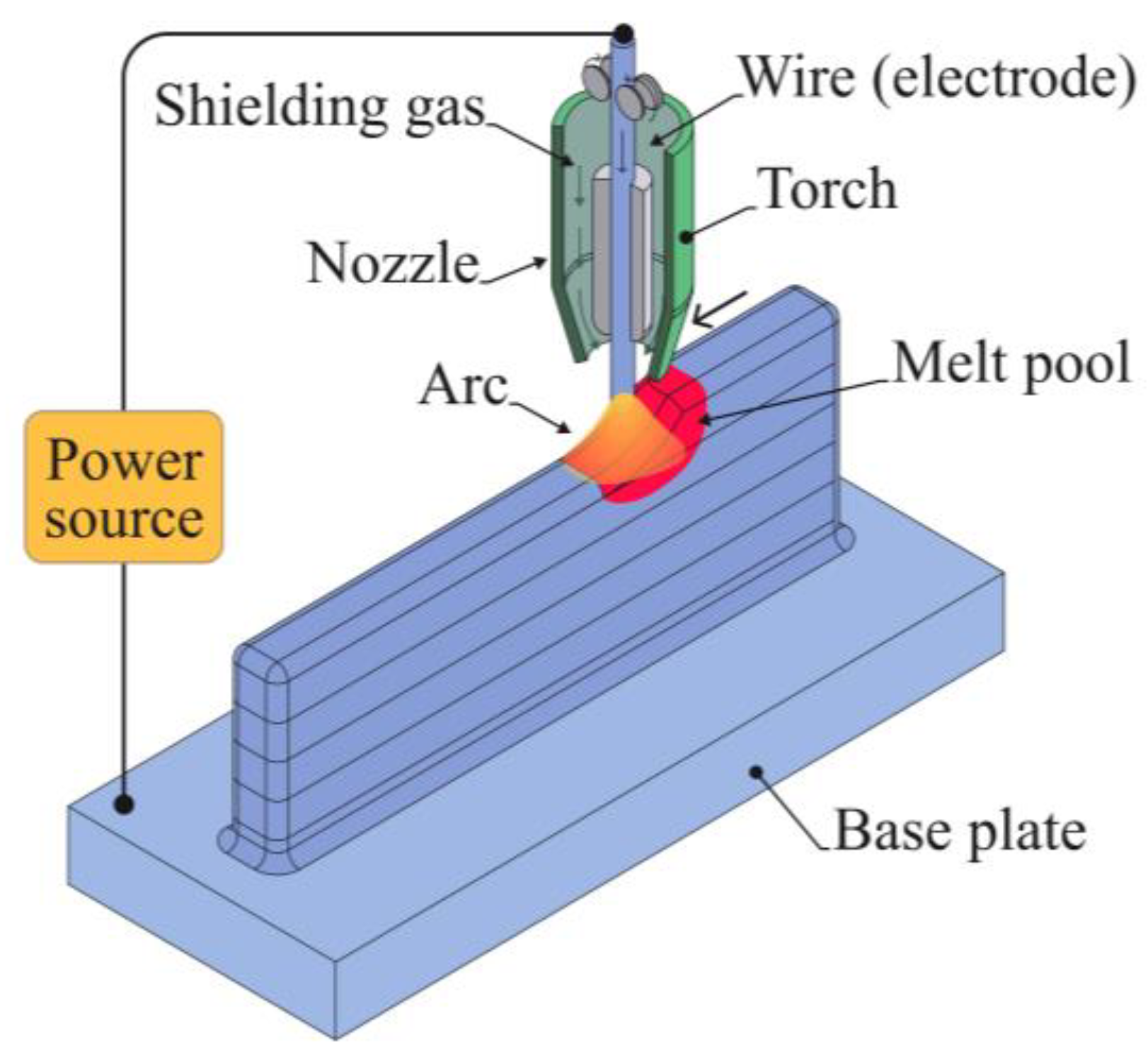
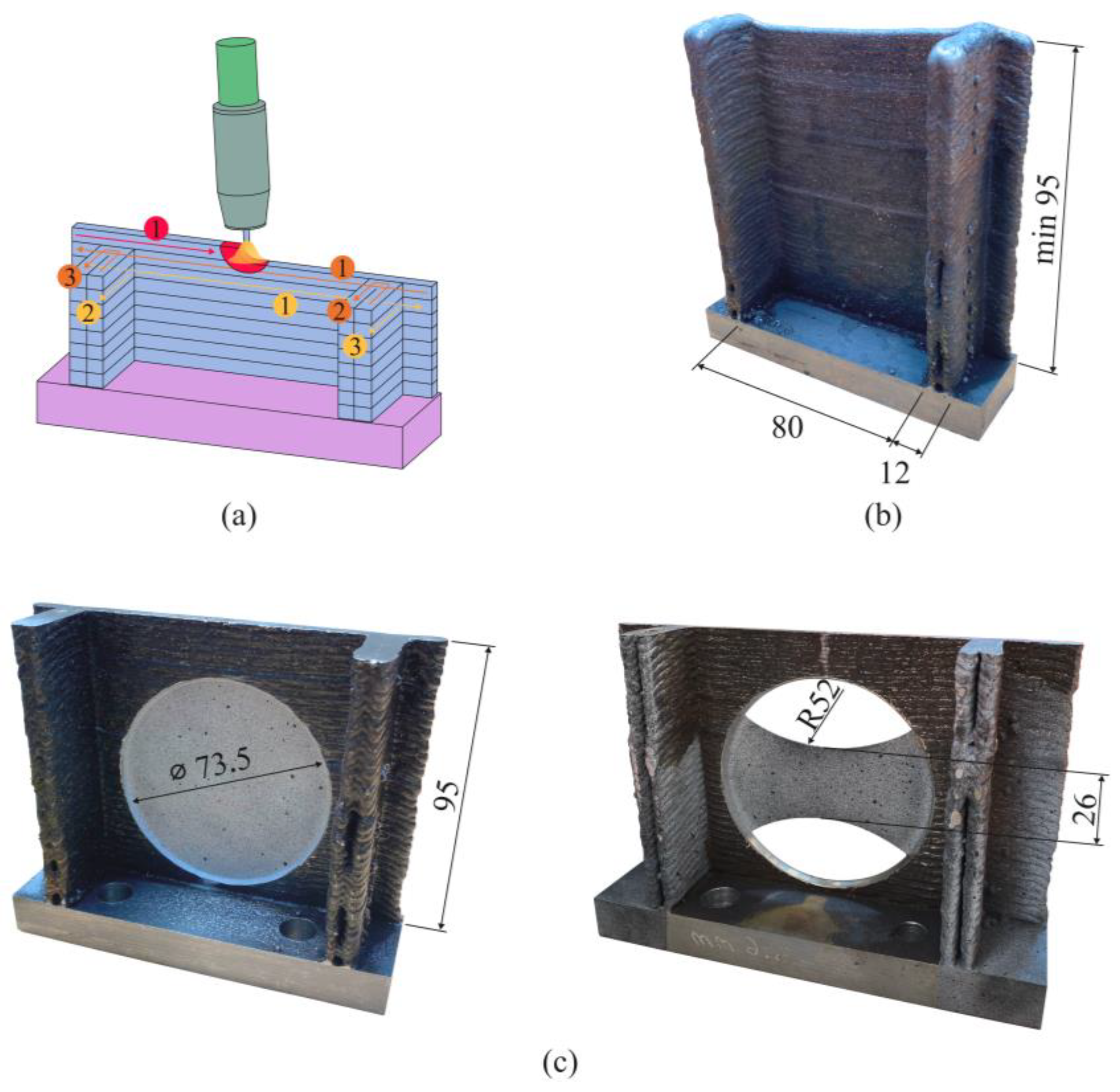
2.1. Material Deposition Using WAAM
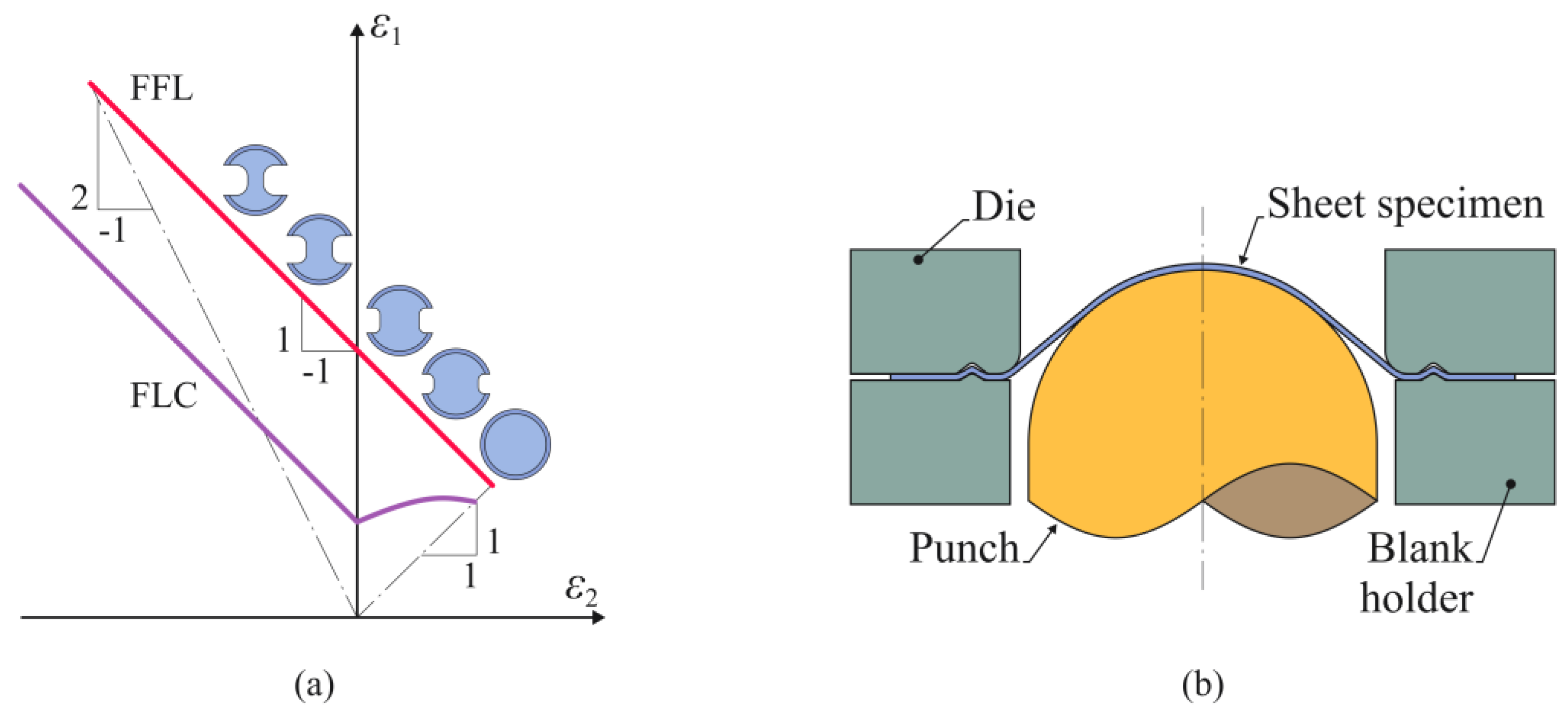
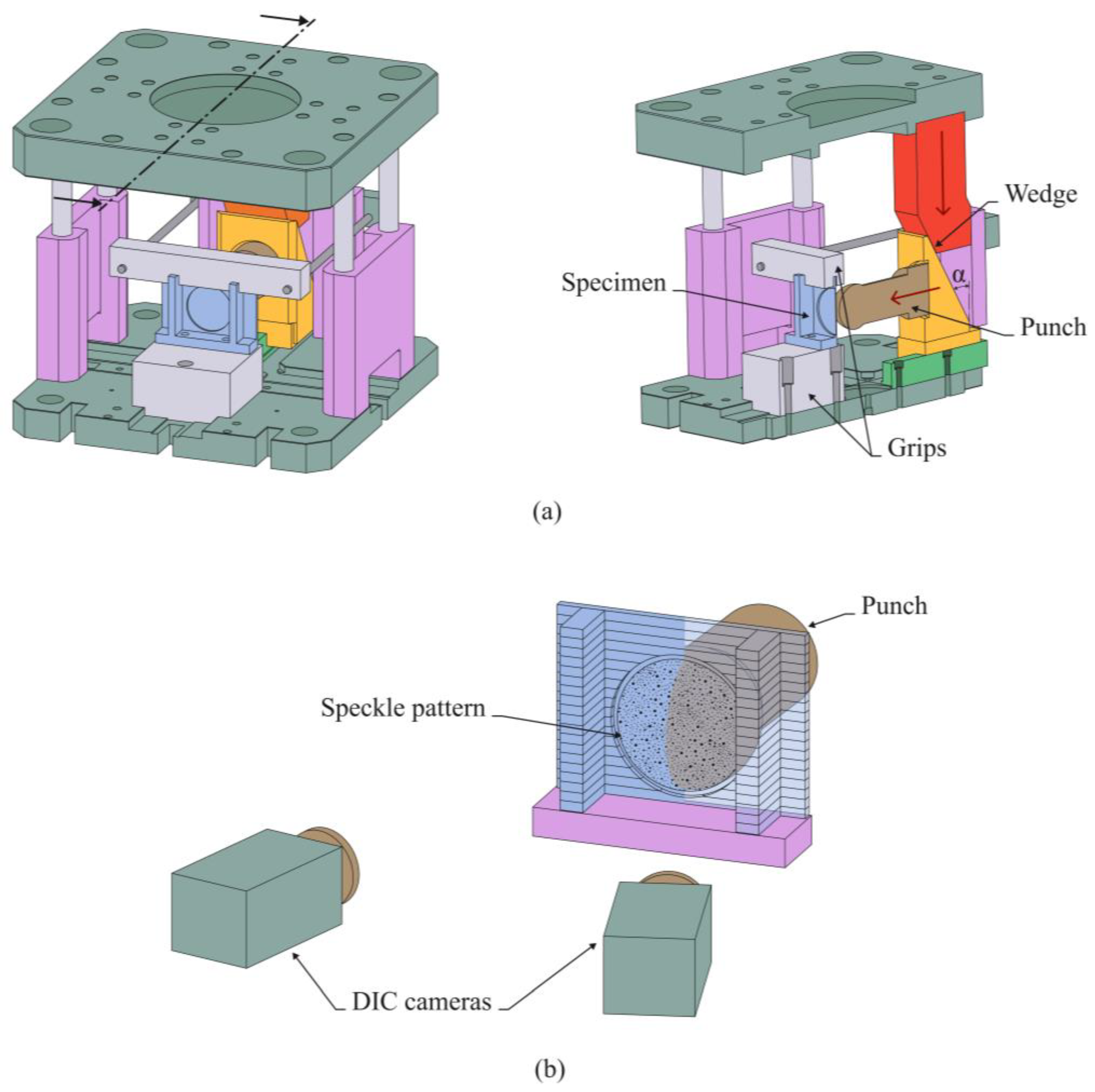
2.2. Dieless Nakajima Test
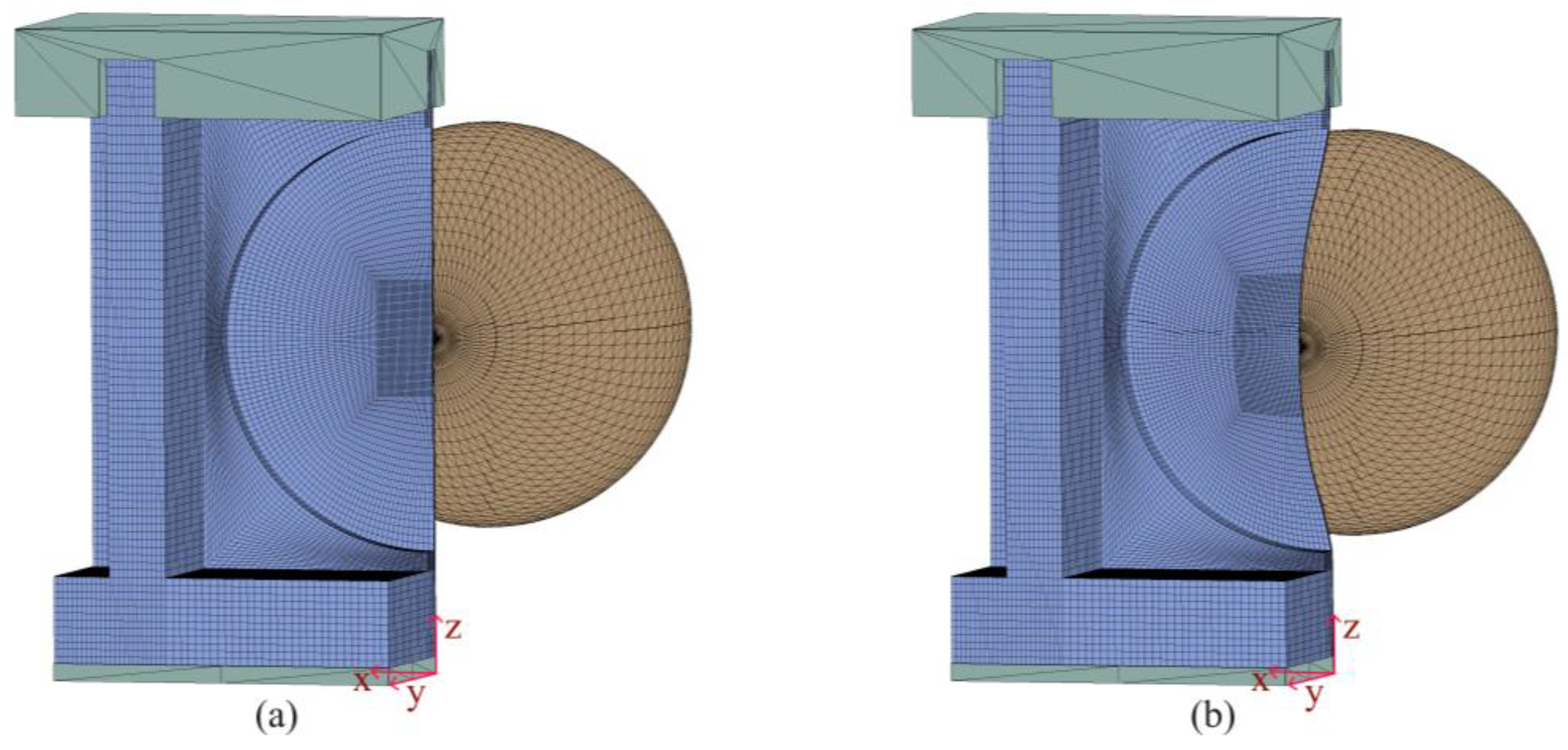
2.3. Numerical Simulation
3. Results and Discussion
3.1. Test Design
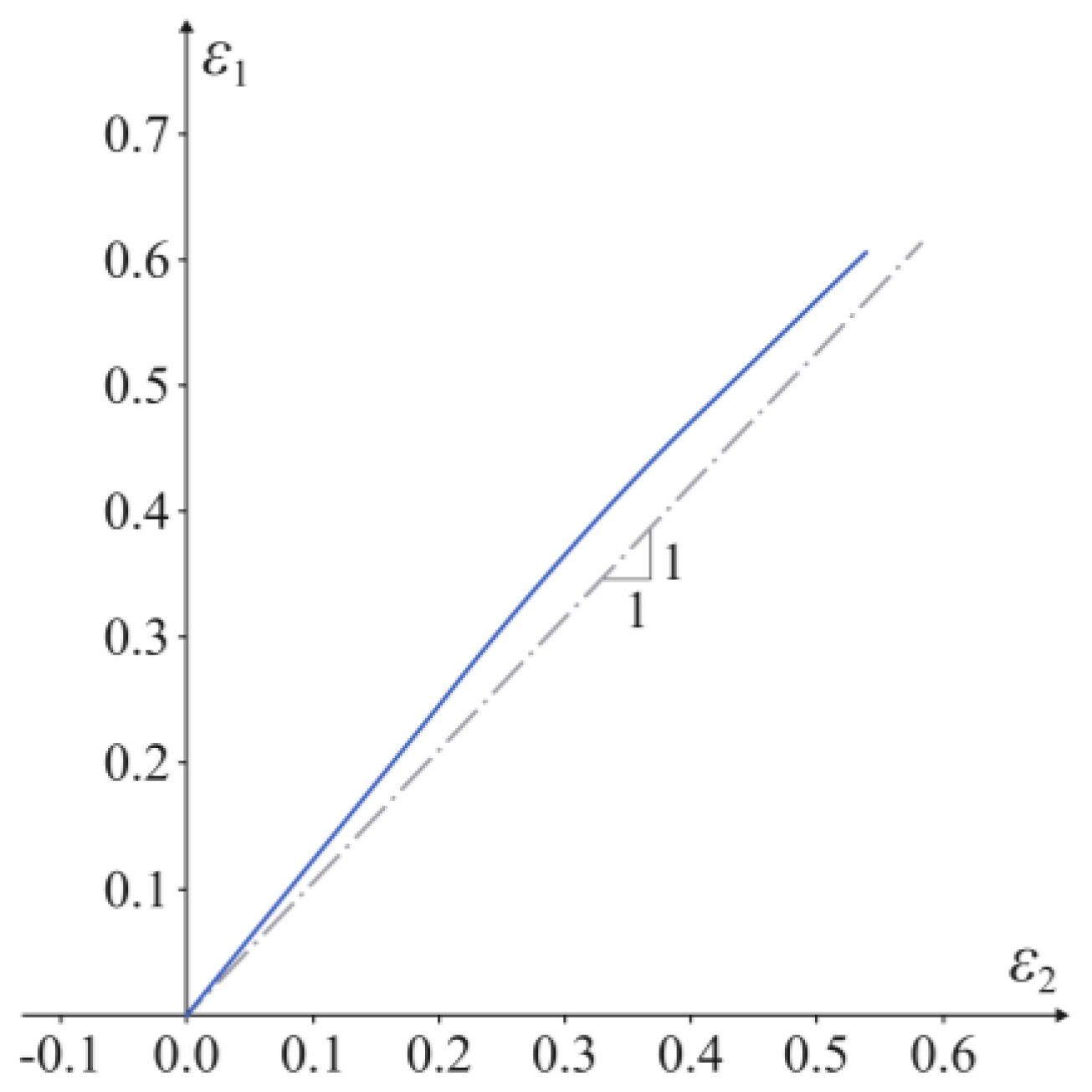
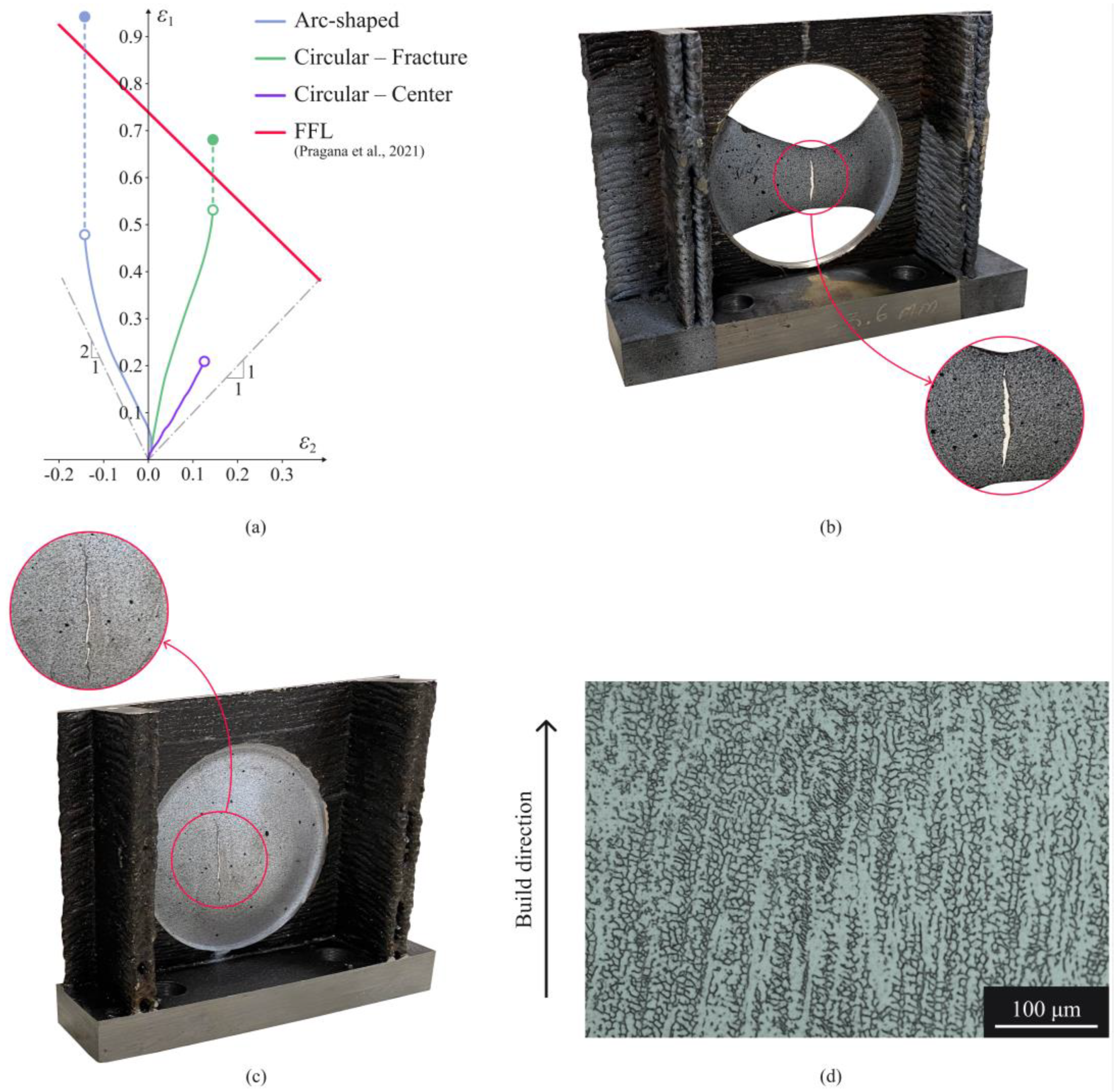
3.2. Experimental Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pragana, J.P.M.; Sampaio, R.F.V.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Hybrid Metal Additive Manufacturing: A State–of–the-Art Review. Adv. Ind. Manuf. Eng. 2021, 2, 100032. [Google Scholar] [CrossRef]
- Bambach, M.; Sviridov, A.; Weisheit, A.; Schleifenbaum, J.H. Case Studies on Local Reinforcement of Sheet Metal Components by Laser Additive Manufacturing. Metals 2017, 7, 113. [Google Scholar] [CrossRef]
- Merklein, M.; Junker, D.; Schaub, A.; Neubauer, F. Hybrid Additive Manufacturing Technologies—An Analysis Regarding Potentials and Applications. Phys. Procedia 2016, 83, 549–559. [Google Scholar] [CrossRef]
- Ambrogio, G.; Gagliardi, F.; Muzzupappa, M.; Filice, L. Additive-incremental forming hybrid manufacturing technique to improve customised part performance. J. Manuf. Process. 2019, 37, 386–391. [Google Scholar] [CrossRef]
- Meiners, F.; Ihne, J.; Jürgens, P.; Hemes, S.; Mathes, M.; Sizova, I.; Bambach, M.; Hama-Saleh, R.; Weisheit, A. New Hybrid Manufacturing Routes Combining Forging and Additive Manufacturing to Efficiently Produce High Performance Components from Ti-6Al-4V. Procedia Manuf. 2020, 47, 261–267. [Google Scholar] [CrossRef]
- Merklein, M.; Schulte, R.; Papke, T. An Innovative Process Combination of Additive Manufacturing and Sheet Bulk Metal Forming for Manufacturing a Functional Hybrid Part. J. Mater. Process. Technol. 2021, 291, 117032. [Google Scholar] [CrossRef]
- López, C.; Elías-Zúñiga, A.; Jiménez, I.; Martínez-Romero, O.; Siller, H.R.; Diabb, J.M. Experimental Determination of Residual Stresses Generated by Single Point Incremental Forming of AlSi10Mg Sheets Produced Using SLM Additive Manufacturing Process. Materials 2018, 11, 2542. [Google Scholar] [CrossRef]
- Hafenecker, J.; Bartels, D.; Kuball, C.-M.; Kreß, M.; Rothfelder, R.; Schmidt, M.; Merklein, M. Hybrid Process Chains Combining Metal Additive Manufacturing and Forming – A Review. CIRP J. Manuf. Sci. Technol. 2023, 46, 98–115. [Google Scholar] [CrossRef]
- Cunningham, C.R.; Flynn, J.M.; Shokrani, A.; Dhokia, V.; Newman, S.T. Invited review article: Strategies and processes for high quality wire arc additive manufacturing. Addit. Manuf. 2018, 22, 672–686. [Google Scholar] [CrossRef]
- Sampaio, R.F.V.; Pragana, J.P.M.; Bragança, I.M.F.; Silva, C.M.A.; Nielsen, C.V.; Martins, P.A.F. Modelling of Wire-Arc Additive Manufacturing—A Review. Adv. Ind. Manuf. Eng. 2023, 6, 100121. [Google Scholar] [CrossRef]
- Bi, X.; Li, R.; Hu, Z.; Gu, J.; Jiao, C. Microstructure and Texture of 2205 Duplex Stainless Steel Additive Parts Fabricated by the Cold Metal Transfer (CMT) Wire and Arc Additive Manufacturing (WAAM). Metals 2022, 12, 1655. [Google Scholar] [CrossRef]
- Zhai, W.; Guo, Y.; Aishwarya; Canturri, C.; Shandro, R.; Zhou, W. Wire arc additive manufacturing of ER70S-6/S355 bimetal component. Mater. Sci. Eng. A 2024, 900, 146498. [Google Scholar] [CrossRef]
- Shah, A.; Aliyev, R.; Zeidler, H.; Krinke, S. A Review of the Recent Developments and Challenges in Wire Arc Additive Manufacturing (WAAM) Process. J. Manuf. Mater. Process. 2023, 7, 97. [Google Scholar] [CrossRef]
- Hönnige, J.R.; Colegrove, P.A.; Ahmad, B.; Fitzpatrick, M.E.; Ganguly, S.; Lee, T.L.; Williams, S.W. Residual Stress and Texture Control in Ti-6Al-4V Wire + Arc Additively Manufactured Intersections by Stress Relief and Rolling. Mater. Des. 2018, 150, 193–205. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H.; Xu, J.; Norrish, J. A Review of the Wire Arc Additive Manufacturing of Metals: Properties, Defects and Quality Improvement. J. Manuf. Process. 2018, 35, 127–139. [Google Scholar] [CrossRef]
- Gornyakov, V.; Sun, Y.; Ding, J.; Williams, S. Modelling and Optimising Hybrid Process of Wire Arc Additive Manufacturing and High-Pressure Rolling. Mater. Des. 2022, 223, 111121. [Google Scholar] [CrossRef]
- Kaščák, L.; Varga, J.; Bidulská, J.; Bidulský, R. Simulation of 316L stainless steel produced the laser powder bed fusion process. Materials 2023, 16, 7653. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K.; Kikuma, T.; Hasuka, K. Study on the Formability of Steel Sheets. Yamata Tech. Rep. 1968, 264, 8517–8530. [Google Scholar]
- Isik, K.; Silva, M.B.; Tekkaya, A.E.; Martins, P.A.F. Formability limits by fracture in sheet metal forming. J. Mater. Process. Technol. 2014, 214, 1557–1565. [Google Scholar] [CrossRef]
- Sampaio, R.F.V.; Pragana, J.P.M.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. A Strain Acceleration Method to Identify the Onset of Diffuse Necking. Adv. Ind. Manuf. Eng. 2024, 9, 100148. [Google Scholar] [CrossRef]
- Pragana, J.P.; Bragança, I.M.; Reis, L.; Silva, C.M.; Martins, P.A. Formability of Wire-Arc Deposited AISI 316L Sheets for Hybrid Additive Manufacturing Applications. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 2839–2850. [Google Scholar] [CrossRef]
- ISO 12004-2; Metallic Materials-Sheet and Strip-Determination of Forming Limit Curves-Part 2. ISO: Geneva, Switzerland, 2008.
- Furushima, T.; Hirose, Y.; Tada, K.; Manabe, K. Development of Compact Marchiniak Testing Apparatus for In-situ Microscopic Observation of Surface Roughening. Procedia Eng. 2017, 207, 1946–1951. [Google Scholar] [CrossRef]
- Sapage, M.S.T.; Pragana, J.P.M.; Sampaio, R.F.V.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Multi-planar injection lap riveting. J. Adv. Join. Process. 2024, 9, 100175. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Martins, P.A.F. Metal Forming, 1st ed.; Elsevier: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C. The determination of friction coefficient in Nakazima test and its application in predicting FLCs with modified M-K model. IOP Conf. Ser. Mater. Sci. Eng. 2020, 967, 012056. [Google Scholar] [CrossRef]
- McClintock, F.A. A Criterion for Ductile Fracture by the Growth of Holes. J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Elmer, J.W.; Allen, S.M.; Eagar, T.W. Microstructural development during solidification of stainless steel alloys. Metall. Trans. A 1989, 20, 2117–2131. [Google Scholar] [CrossRef]
- Laukkanen, A.; Uusikallio, S.; Lindroos, M.; Andersson, T.; Kömi, J.; Porter, D. Micromechanics driven design of ferritic–austenitic duplex stainless steel microstructures for improved cleavage fracture toughness. Eng. Fract. Mech. 2021, 253, 107878. [Google Scholar] [CrossRef]


| Element | Fe | Cr | Ni | Mo | Mn | Si | N | C |
|---|---|---|---|---|---|---|---|---|
| weight% | 65.0 | 18.2 | 12.0 | 2.6 | 1.7 | 0.4 | 0.04 | 0.01 |
| Current [A] | Voltage [V] | Wire Feed Speed [m/min] | Travel Speed [m/min] | Gas Flow Rate [l/min] | Layer Height [mm] |
|---|---|---|---|---|---|
| 100 | 16.5 | 6 | 0.5 | 10 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sampaio, R.F.V.; Rosado, P.M.S.; Pragana, J.P.M.; Bragança, I.M.F.; Silva, C.M.A.; Rosa, L.G.; Martins, P.A.F. Formability Assessment of Additively Manufactured Materials via Dieless Nakajima Testing. J. Manuf. Mater. Process. 2024, 8, 180. https://doi.org/10.3390/jmmp8040180
Sampaio RFV, Rosado PMS, Pragana JPM, Bragança IMF, Silva CMA, Rosa LG, Martins PAF. Formability Assessment of Additively Manufactured Materials via Dieless Nakajima Testing. Journal of Manufacturing and Materials Processing. 2024; 8(4):180. https://doi.org/10.3390/jmmp8040180
Chicago/Turabian StyleSampaio, Rui F. V., Pedro M. S. Rosado, João P. M. Pragana, Ivo M. F. Bragança, Carlos M. A. Silva, Luís G. Rosa, and Paulo A. F. Martins. 2024. "Formability Assessment of Additively Manufactured Materials via Dieless Nakajima Testing" Journal of Manufacturing and Materials Processing 8, no. 4: 180. https://doi.org/10.3390/jmmp8040180
APA StyleSampaio, R. F. V., Rosado, P. M. S., Pragana, J. P. M., Bragança, I. M. F., Silva, C. M. A., Rosa, L. G., & Martins, P. A. F. (2024). Formability Assessment of Additively Manufactured Materials via Dieless Nakajima Testing. Journal of Manufacturing and Materials Processing, 8(4), 180. https://doi.org/10.3390/jmmp8040180












