A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers
Abstract
1. Introduction
- Variable surface finish: arithmetic roughness (Ra) from 0.7 µm to 38 µm for material extrusion printers [8] (depending on the type of measured surface);
- The need for postprocesses to enhance surface topography or to remove the support structures required got the build [2];
- A one or two orders of magnitude higher specific energy consumption than conventional subtractive processes such as machining [9]. The specific energy Cconsumption (SEC) for AM processes ranges from 85 kJ/cm3 for MEX up to 4580 kJ/cm3 for PBF [9], while conventional processes such as milling have a lower SEC of 5 kJ/cm3 to 14 kJ/cm3 [10], depending on the cutting conditions and material milled.
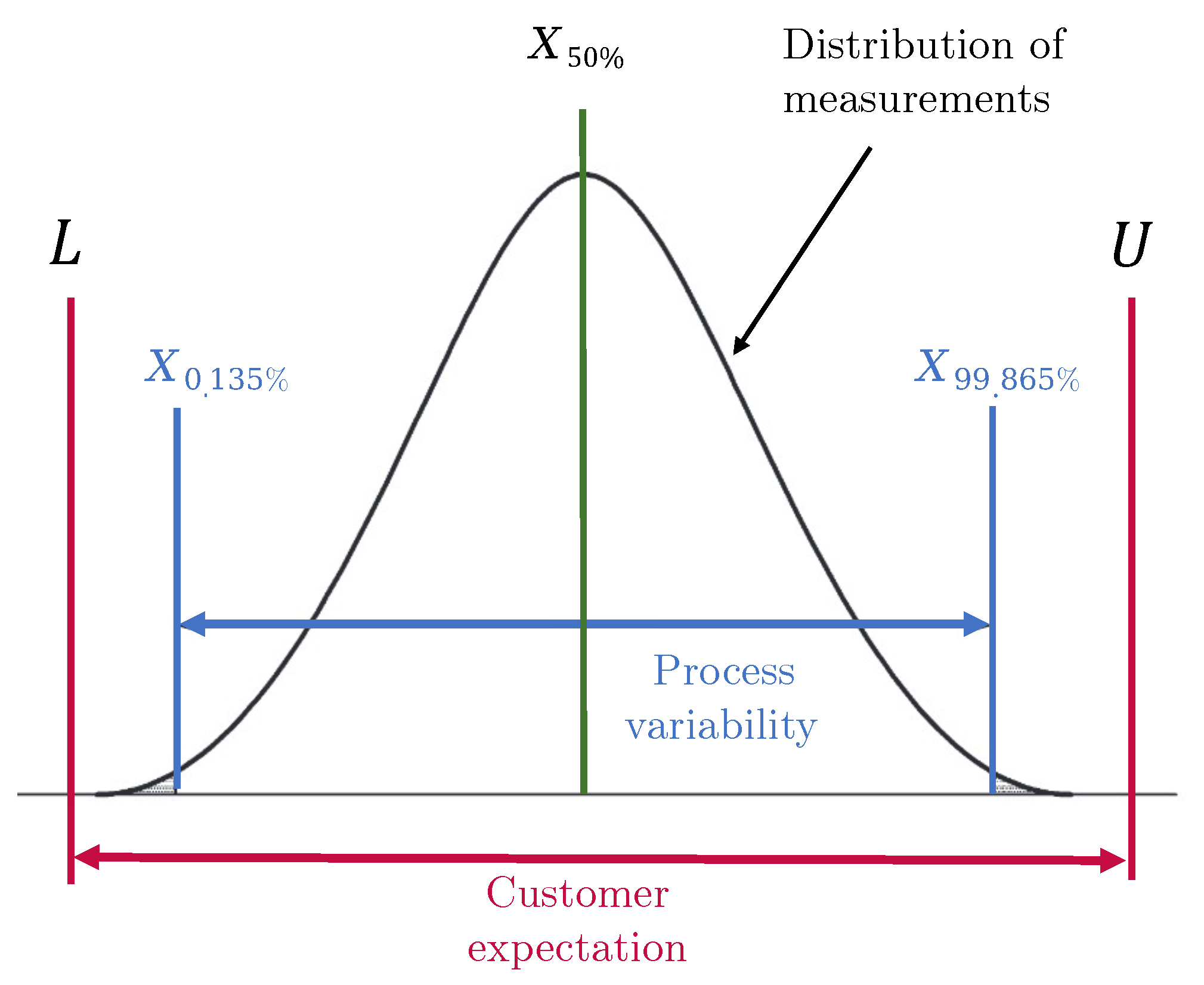
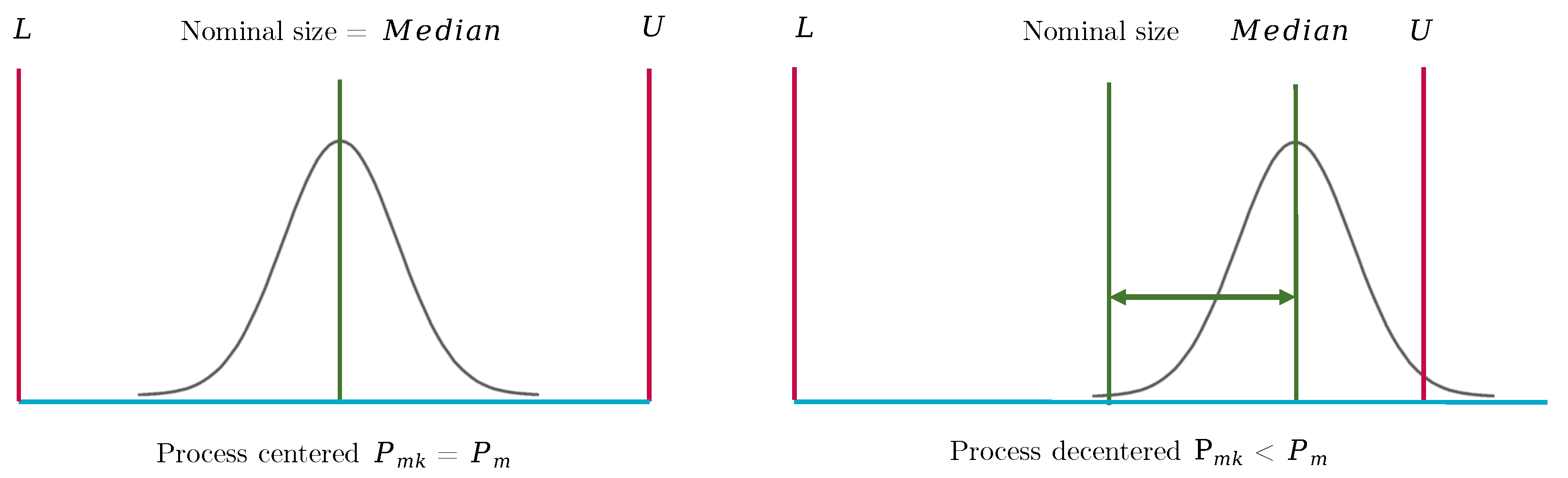
2. ISO 22514 Standard
3. Literature Review on the Capability of AM Printers
- The process and machine they characterize according to ISO 52900 terminology;
- The number of measurements they use to compute the capability indices;
- The link they make (or not) with the existing ISO 22514 standard;
- The type of part design they use;
- The way they measure the produced parts;
- The type of features they assess: dimensional, geometrical, and surface topography;
- The link they make with existing standards already widely used in conventional processes, such as ISO 286-1 and ISO 2768;
- The coverage of the achievable ISO 286-1 dimensional size ranges according to the printer build platform dimensions;
- The way they identify the distribution that best fits the data.
- Considering at least 25 reproductions of each feature;
- Making a link with ISO 22514;
- Using a GBTA with dimensional and geometrical features;
- Measuring the features with an uncertainty four times lower than the value being measured (a CMM, a caliper, a laser scan, or a rugosimeter is suitable according to ISO 52902);
- Making a link with an existing standard to compute the TI (ISO 286-1 and ISO 2768);
- Covering the achievable ISO 286-1 dimensional size ranges according to the printer build platform dimensions;
- Identifying the best distribution fitting the data using statistical tests.
4. GBTA Design
5. Motivation and Objective of the Study
6. Methods
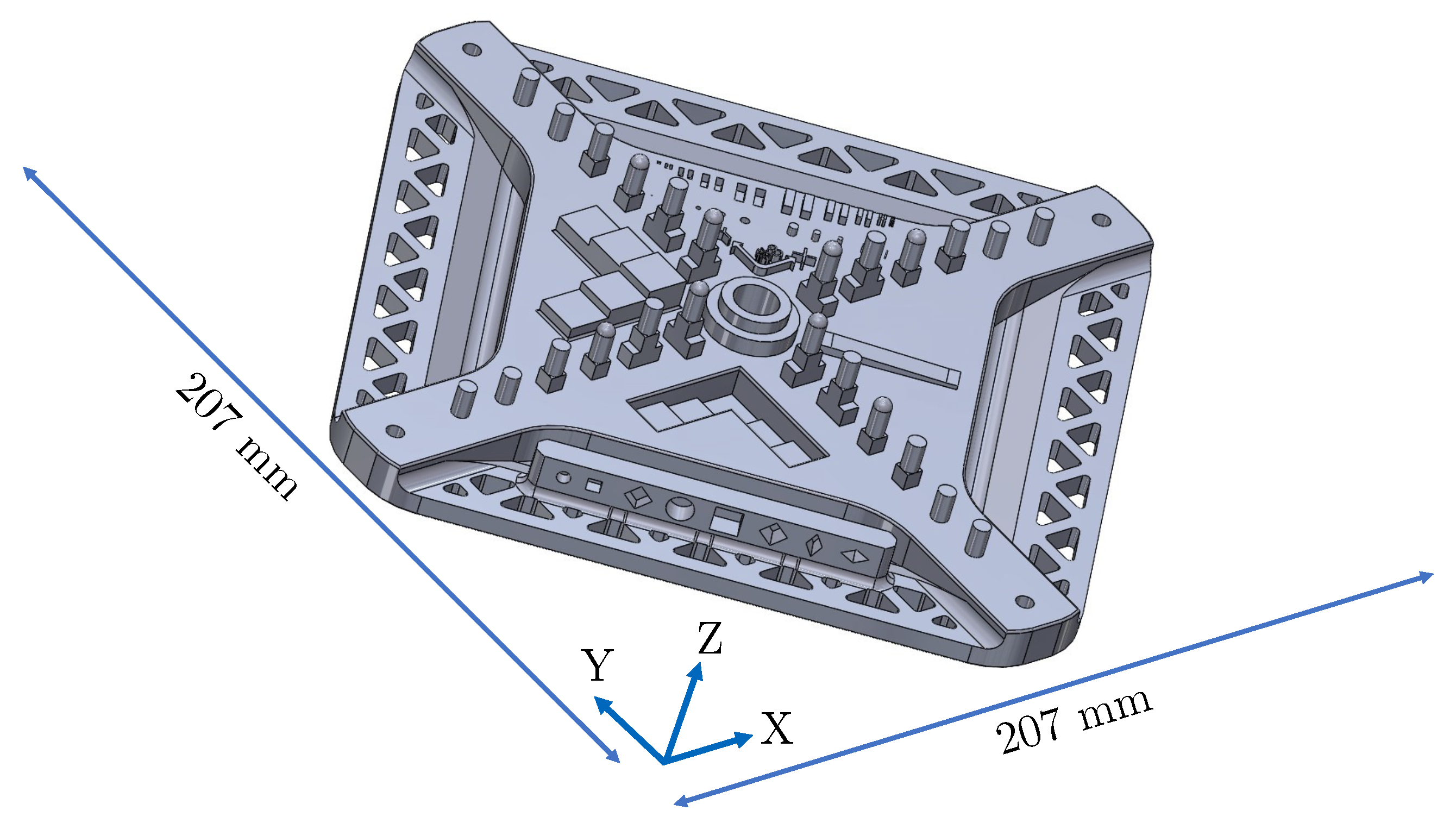
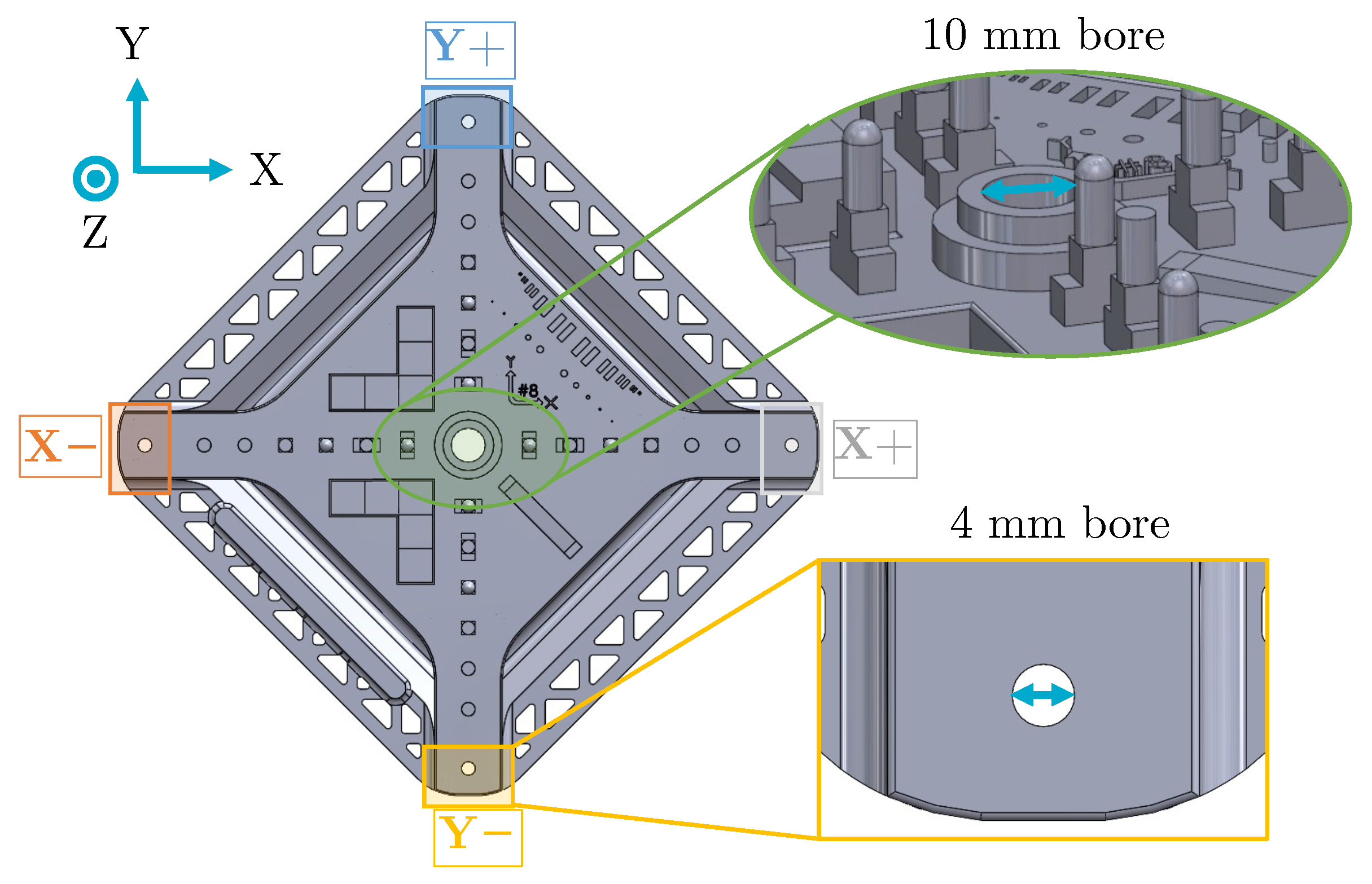
6.1. Tested Machine and Material
6.2. Available Measurements on the GBTA
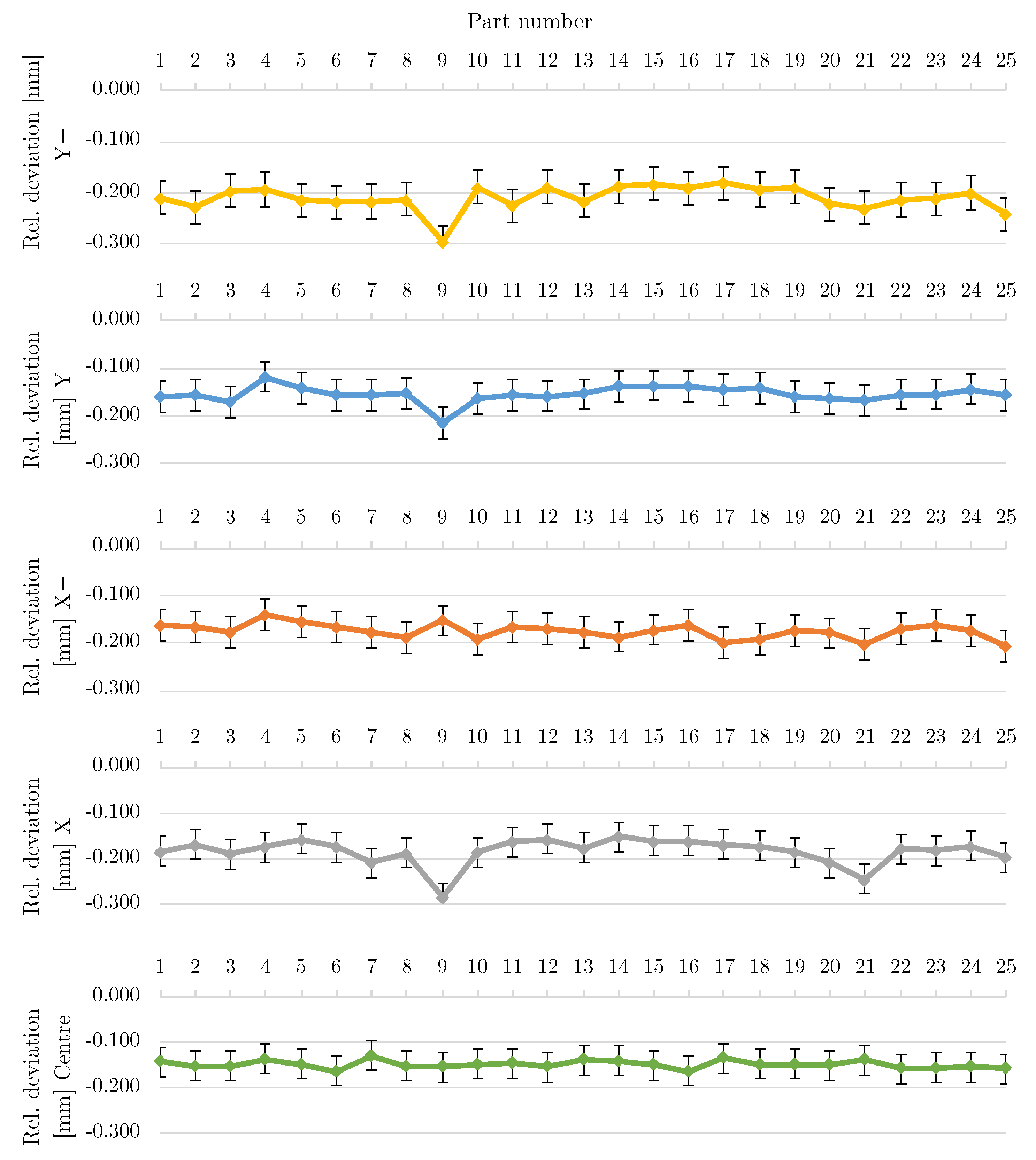
6.3. Measurement of Parts
- 8 points for each cylinder on two different circles;
- 6 points for each plane, except for the smaller ones (top of small cylinders and their parallelepiped base) which were measured by 1 point;
- 39 points for the top surface of the parts;
- 9 points on 3 circles for the hemispheres.
6.4. Data Postprocessing
- Grouping data: First, the dimensional data were grouped according to their size range and their main reference axis (the dimensions between 3 mm and 6 mm for the X axis, for example). Each of the different geometrical data types were also grouped in the same way (the flatness of planes with a normal according to the X axis and exhibiting a main dimension between 18 mm and 30 mm, for example).
- Retrieving the deviation: The deviation from the nominal value was computed () by retrieving the nominal size () from the measured data () as shown in Equation (7). For example, a diameter with a 4 mm nominal value measured at 4.174 mm gave a 0.174 mm deviation.
- Histogram shape check: The shape of the data distribution was then checked by plotting a histogram. This plot allowed the outliers to be detected and manually discarded. The general shape of the histogram also revealed the possible multimodal distribution of the data in some cases. When this happened, a manual separation of the data was performed to identify the different contributions. These datasets were then separately processed for the next operations.
- Distribution fitting: The histogram allowed the general shape of the distribution to be identified. In some cases, the data could not be estimated by a normal distribution. According to the ISO 22514 standard, the data can fit to a normal, log-normal, folded normal, gamma, Rayleigh, or Weibull distribution depending on their nature. Therefore, a fitting of the dataset with these six different statistical distributions was performed. The best fitting distribution was identified using the p-value of a Komolgorov–Smirnov test for each dataset. The distributions were chosen following the highest achieved p-value.
7. Results and Discussion
7.1. Application of the Method to a Dataset
- Grouping data: A total of 600 measurements were available in this group (in blue in the figure), and these encompassed the distances between the planes.
- Retrieving the deviation: The deviations with respect to the nominal value were computed according to Equation (7).
- Histogram shape check: As shown in blue in Figure 4, the histogram does not show outliers and is not multimodal. The measurements, therefore, did not need to be separated.
- Distribution fitting: The six different distributions were tested for the fitting, and the best selected was the Weibull distribution, with a computed p-value from the Komolgorov–Smirnov test reaching 0.998. The resulting distribution is given in orange on the graph and fits the data histogram very well.
- Index computation: The obtained , and percentiles were, respectively, −0.027 mm, 0.058 mm and 0.123 mm. Finally, the tolerance interval achieved by the machine could be computed. No correction was needed for since the number of measurements was above 50. Consequently, a potential tolerance interval of 0.251 mm was obtained for a of 1.67. Using the same target for , the lower (L) and upper (U) bounds of the real tolerance interval could be determined: −0.082 mm and 0.163 mm, respectively. The asymmetry of the real tolerance interval was confirmed with the median value, which was 0.058 mm instead of 0 mm. As depicted in Figure 4, the data slightly shifted to the right on the graph.
7.2. Distribution Identification
7.3. Dimensional Machine Performances Assessment
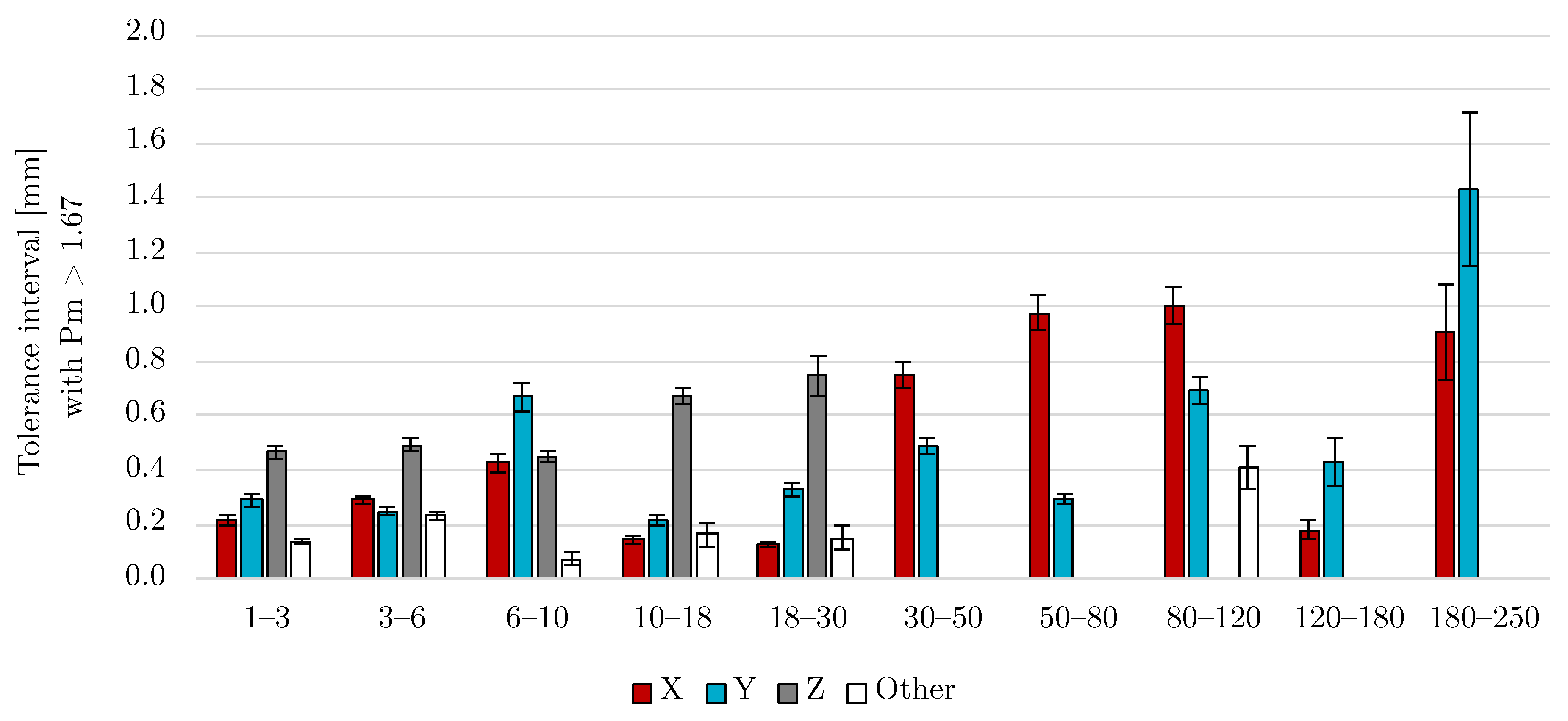
7.3.1. Potential Dimensional Tolerance Intervals
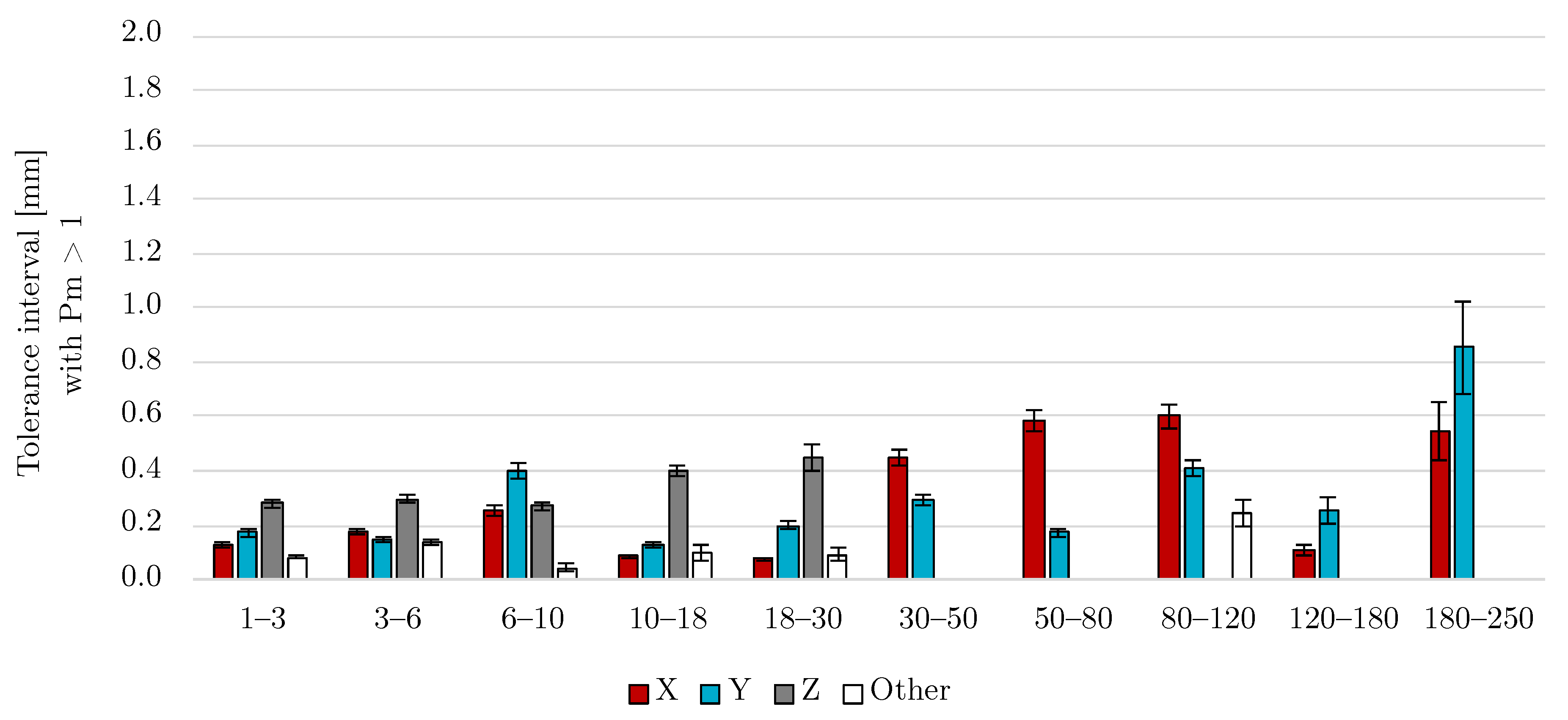
7.3.2. Real Dimensional Tolerance Intervals
7.3.3. Potential Achievable STG of ISO 286-1
7.3.4. Real Achievable STG of ISO 286-1
7.4. Geometrical Machine Performance Assessment
7.4.1. Real Geometrical Tolerance Intervals
7.4.2. Real Achievable Geometrical Tolerances of ISO 2768-2
7.5. Future Challenges and Potential Prospects
- The shrinkage of the part after its cool-down (radius mode);
- The control of the machine movements (ellipse mode);
- The geometrical defects of the machine itself (gap mode).
8. Conclusions
- Most of the dimensional measurements (57.9%) can be described using a normal distribution. The gamma distribution also fitted 24.6% of the measurements, while the log-normal fitted 7%. For the geometrical measurements, 33.3% best fitted a log-normal distribution, while 24.3% and 21.2% best fitted normal and gamma distributions, respectively. This is the first study to investigate the type of distribution that best fits the data.
- The method and GBTA design allowed the ISO 286-1 size ranges from 1 mm to 250 mm for the dimensional measurements to be covered and the dimensional and geometrical machine performance (potential and real) to be assessed. In both cases, the conventional target for and indices of 1.67 (less than one part per million out-of-specification parts with a 95% confidence level) could be challenged. Indeed, depending on the final application of the parts, this index could be lowered to one (2600 rejected parts per million).
- The X and Y axes of the printer performed better than the Z axis, both for the potential and real machine performance. This allowed narrower tolerance intervals for the X and Y axes to be achieved, while ensuring the capable behavior of the printer.
- Both dimensional and geometrical results were sensitive to the design of the measured features as well as the printing conditions (especially layer height, which creates the potential staircase effect). Before foreseeing the fittings using the determined tolerance intervals, the designer should be careful. In some cases, it will be necessary to design a modified version of the GBTA to best take into account the type of geometrical features to be produced.
- Real machine performance should be considered instead of using only the potential . Indeed, as demonstrated, there can be a shift (systematic error) with respect to the middle of the desired tolerance intervals. Software compensation could solve this issue during the design process.
- A total of 27 h was required to print one part. Since 25 were needed, this may hamper the use of this GBTA design for industrial purposes and process monitoring. However, the proposed method is suitable for research and development purposes when assessing a new printer before market launch. Moreover, the method is systematic and provides a framework for assessing the machine performance of material extrusion printers.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ISO/ASTM 52900:2021; Additive Manufacturing General Principles Fundamentals and Vocabulary. ISO: Geneva, Switzerland, 2021.
- Bourell, D.L.; Beaman, J.J.; Wohlers, T. History and Evolution of Additive Manufacturing. In Additive Manufacturing Processes; Bourell, D.L., Frazier, W., Kuhn, H., Seifi, M., Eds.; ASM International: Cleveland, OH, USA, 2020; pp. 11–18. [Google Scholar] [CrossRef]
- Bourell, D.L.; Wohlers, T. Introduction to Additive Manufacturing. In Additive Manufacturing Processes; Bourell, D.L., Frazier, W., Kuhn, H., Seifi, M., Eds.; ASM International: Cleveland, OH, USA, 2020; pp. 3–10. [Google Scholar] [CrossRef]
- Cruz Sanchez, F.A.; Boudaoud, H.; Camargo, M.; Pearce, J.M. Plastic recycling in additive manufacturing: A systematic literature review and opportunities for the circular economy. J. Clean. Prod. 2020, 264, 121602. [Google Scholar] [CrossRef]
- SmarTech Analysis. Ceramics Additive Manufacturing Markets 2017–2028, an Opportunity Analysis and Ten-Year Market Forecast; Technical Report; Research and Markets: Dublin, Ireland, 27 September 2018. [Google Scholar]
- Altıparmak, S.C.; Yardley, V.A.; Shi, Z.; Lin, J. Extrusion-based additive manufacturing technologies: State of the art and future perspectives. J. Manuf. Process. 2022, 83, 607–636. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Golhin, A.P.; Tonello, R.; Frisvad, J.R.; Grammatikos, S.; Strandlie, A. Surface roughness of as-printed polymers: A comprehensive review. Int. J. Adv. Manuf. Technol. 2023, 127, 987–1043. [Google Scholar] [CrossRef]
- Kellens, K.; Mertens, R.; Paraskevas, D.; Dewulf, W.; Duflou, J.R. Environmental Impact of Additive Manufacturing Processes: Does AM Contribute to a More Sustainable Way of Part Manufacturing? Procedia CIRP 2017, 61, 582–587. [Google Scholar] [CrossRef]
- Kara, S.; Li, W. Unit process energy consumption models for material removal processes. CIRP Ann. 2011, 60, 37–40. [Google Scholar] [CrossRef]
- Leach, R.; Bourell, D.; Carmignato, S.; Donmez, A.; Senin, N.; Dewulf, W. Geometrical metrology for metal additive manufacturing. CIRP Ann. 2019, 68, 677–700. [Google Scholar] [CrossRef]
- de Pastre, M.A.; Toguem Tagne, S.C.; Anwer, N. Test artefacts for additive manufacturing: A design methodology review. CIRP J. Manuf. Sci. Technol. 2020, 31, 14–24. [Google Scholar] [CrossRef]
- Beltrán, N.; Álvarez, B.J.; Blanco, D.; Noriega, Á.; Fernández, P. Estimation and Improvement of the Achievable Tolerance Interval in Material Extrusion Additive Manufacturing through a Multi-State Machine Performance Perspective. Appl. Sci. 2021, 11, 5325. [Google Scholar] [CrossRef]
- Flynn, J.M.; Shokrani, A.; Newman, S.T.; Dhokia, V. Hybrid additive and subtractive machine tools - Research and industrial developments. Int. J. Mach. Tools Manuf. 2016, 101, 79–101. [Google Scholar] [CrossRef]
- Dantan, J.Y.; Huang, Z.; Goka, E.; Homri, L.; Etienne, A.; Bonnet, N.; Rivette, M. Geometrical variations management for additive manufactured product. CIRP Ann. 2017, 66, 161–164. [Google Scholar] [CrossRef][Green Version]
- Lussenburg, K.; Sakes, A.; Breedveld, P. Design of non-assembly mechanisms: A state-of-the-art review. Addit. Manuf. 2021, 39, 101846. [Google Scholar] [CrossRef]
- Mavroidis, C.; DeLaurentis, K.J.; Won, J.; Alam, M. Fabrication of Non-Assembly Mechanisms and Robotic Systems Using Rapid Prototyping. J. Mech. Des. 2001, 123, 516–524. [Google Scholar] [CrossRef]
- Minetola, P.; Calignano, F.; Galati, M. Comparing geometric tolerance capabilities of additive manufacturing systems for polymers. Addit. Manuf. 2020, 32, 101103. [Google Scholar] [CrossRef]
- ISO/ASTM 52902:2023; Additive Manufacturing Test Artefacts Geometric Capability Assessment of Additive Manufacturing Systems. ISO: Geneva, Switzerland, 2023.
- Spitaels, L.; Rivière-Lorphèvre, E.; Demarbaix, A.; Ducobu, F. Adaptive benchmarking design for additive manufacturing processes. Meas. Sci. Technol. 2022, 33, 064003. [Google Scholar] [CrossRef]
- Lopes, A.J.; Perez, M.A.; Espalin, D.; Wicker, R.B. Comparison of ranking models to evaluate desktop 3D printers in a growing market. Addit. Manuf. 2020, 35, 101291. [Google Scholar] [CrossRef]
- Vora, H.D.; Sanyal, S. A comprehensive review: Metrology in additive manufacturing and 3D printing technology. Prog. Addit. Manuf. 2020, 5, 319–353. [Google Scholar] [CrossRef]
- Liu, Y.; Pears, N.; Rosin, P.L.; Huber, P. (Eds.) 3D Imaging, Analysis and Applications; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Rivas Santos, V.M.; Thompson, A.; Sims-Waterhouse, D.; Maskery, I.; Woolliams, P.; Leach, R. Design and characterisation of an additive manufacturing benchmarking artefact following a design-for-metrology approach. Addit. Manuf. 2020, 32, 100964. [Google Scholar] [CrossRef]
- ISO 286-1:1988; Geometrical Product Specifications (GPS)—ISO System of Limits and Fits—Part 1: Bases of Tolerances, Deviations and Fits. ISO: Geneva, Switzerland, 1988.
- ISO 2768-2:1989; General Tolerances—Part 2: Geometrical Tolerances for Features without Individual Tolerance Indications. ISO: Geneva, Switzerland, 1989.
- ISO 17296-3:2014; Additive Manufacturing—General Principles—Part 3: Main Characteristics and Corresponding Test Methods. ISO: Geneva, Switzerland, 2014.
- Juran, J.M.; Godfrey, A.B. (Eds.) Juran’s Quality Handbook, 5th ed.; McGraw Hill: New York, NY, USA, 1999. [Google Scholar]
- Kane, V.E. Process Capability Indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Kotz, S.; Johnson, N.L. Process Capability Indices—A Review, 1992–2000. J. Qual. Technol. 2002, 34, 2–19. [Google Scholar] [CrossRef]
- Yum, B.J.; Kim, K.W. A bibliography of the literature on process capability indices: 2000–2009. Qual. Reliab. Eng. Int. 2011, 27, 251–268. [Google Scholar] [CrossRef]
- Yum, B. A bibliography of the literature on process capability indices (PCIs): 2010–2021, Part I: Books, review/overview papers, and univariate PCI-related papers. Qual. Reliab. Eng. Int. 2023, 39, 1413–1438. [Google Scholar] [CrossRef]
- ISO 22514:2016; Statistical Methods in Process Management—Capability and Performance. ISO: Geneva, Switzerland, 2016.
- GmbH, R.B. Booklet No. 9 Machine and Process Capability. In Quality Management in the Bosch Group Technical Statistics, Bosch Group, Stuttgart Germany; Robert Bosch GmbH: Stuttgart, Germany, 2019; Volume 9. [Google Scholar]
- Bissell, A.F. How Reliable is Your Capability Index? Appl. Stat. 1990, 39, 331. [Google Scholar] [CrossRef]
- Chou, Y.M.; Owen, D.B.; Salvador, A.; Borrego, A. Lower Confidence Limits on Process Capability Indices. J. Qual. Technol. 1990, 22, 223–229. [Google Scholar] [CrossRef]
- Montgomery, D. Introduction to Statistical Quality Control, 6th ed.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kampker, A.; Kreiskother, K.; Buning, M.K.; Treichel, P.; Theelen, J. Automotive quality requirements and process capability in the production of electric motors. In Proceedings of the 2017 7th International Electric Drives Production Conference (EDPC), Würzburg, Germany, 5–6 December 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Volvo Group. Supplier Quality Assurance Manual; Volvo Group: Gothenburg, Sweden, 2019. [Google Scholar]
- Safran. S_0002W_QA—Supplier Quality Assurance Requirements; Safran: Paris, France, 2023. [Google Scholar]
- Safran. OP-741-02—Quality Requirements Applicable to Suppliers; Safran: Paris, France, 2020. [Google Scholar]
- Maurer, O.; Herter, F.; Bähre, D. Tolerancing the laser powder bed fusion process based on machine capability measures with the aim of process control. J. Manuf. Process. 2022, 80, 659–665. [Google Scholar] [CrossRef]
- Zongo, F.; Tahan, A.; Aidibe, A.; Brailovski, V. Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion. J. Manuf. Mater. Process. 2018, 2, 56. [Google Scholar] [CrossRef]
- Günay, E.E.; Velineni, A.; Park, K.; Okudan Kremer, G.E. An Investigation on Process Capability Analysis for Fused Filament Fabrication. Int. J. Precis. Eng. Manuf. 2020, 21, 759–774. [Google Scholar] [CrossRef]
- Preißler, M.; Rosenberger, M.; Notni, G. An Investigation for Process Capability in Additive Manufacturing; Universitätsbibliothek Ilmenau: Ilmenau, Germany, 2017. [Google Scholar]
- Singh, R. Process capability study of polyjet printing for plastic components. J. Mech. Sci. Technol. 2011, 25, 1011–1015. [Google Scholar] [CrossRef]
- Siraj, I.; Bharti, P.S. Process capability analysis of a 3D printing process. J. Interdiscip. Math. 2020, 23, 175–189. [Google Scholar] [CrossRef]
- Udroiu, R.; Braga, I.C. System Performance and Process Capability in Additive Manufacturing: Quality Control for Polymer Jetting. Polymers 2020, 12, 1292. [Google Scholar] [CrossRef]
- Yap, Y.L.; Wang, C.; Sing, S.L.; Dikshit, V.; Yeong, W.Y.; Wei, J. Material jetting additive manufacturing: An experimental study using designed metrological benchmarks. Precis. Eng. 2017, 50, 275–285. [Google Scholar] [CrossRef]
- Dolimont, A.; Michotte, S.; Lorphèvre, E.R.; Ducobu, F.; Formanoir, C.D.; Godet, S.; Filippi, E. Characterisation of electron beam melting process on Ti6Al4V in order to guide finishing operation. Int. J. Rapid Manuf. 2015, 5, 320. [Google Scholar] [CrossRef]
- Rebaioli, L.; Fassi, I. A review on benchmark artifacts for evaluating the geometrical performance of additive manufacturing processes. Int. J. Adv. Manuf. Technol. 2017, 93, 2571–2598. [Google Scholar] [CrossRef]
- Bourdet, P. Logiciels des machines à mesurer tridimensionnelles. Techniques de L’ingénieur Mesures Mécaniques et Dimensionnelles Editions T.I. 1999; base documentaire: TIP673WEB. [Google Scholar] [CrossRef]
- McGregor, D.J.; Rylowicz, S.; Brenzel, A.; Baker, D.; Wood, C.; Pick, D.; Deutchman, H.; Shao, C.; Tawfick, S.; King, W.P. Analyzing part accuracy and sources of variability for additively manufactured lattice parts made on multiple printers. Addit. Manuf. 2021, 40, 101924. [Google Scholar] [CrossRef]
- Huang, Q.; Nouri, H.; Xu, K.; Chen, Y.; Sosina, S.; Dasgupta, T. Statistical Predictive Modeling and Compensation of Geometric Deviations of Three-Dimensional Printed Products. J. Manuf. Sci. Eng. 2014, 136, 061008. [Google Scholar] [CrossRef]
- Baturynska, I. Statistical analysis of dimensional accuracy in additive manufacturing considering STL model properties. Int. J. Adv. Manuf. Technol. 2018, 97, 2835–2849. [Google Scholar] [CrossRef]
- Cohen, D.L.; Lipson, H. Geometric feedback control of discrete-deposition SFF systems. Rapid Prototyp. J. 2010, 16, 377–393. [Google Scholar] [CrossRef]
- Dou, C.; Elkins, D.; Kong, Z.J.; Liu, C. Online Monitoring and Control of Polymer Additive Manufacturing Processes. In Additive Manufacturing Design and Applications; Seifi, M., Bourell, D.L., Frazier, W., Kuhn, H., Eds.; ASM International: Cleveland, OH, USA, 2023; pp. 1–13. [Google Scholar] [CrossRef]
- Bernard, A.; Kruth, J.P.; Cao, J.; Lanza, G.; Bruschi, S.; Merklein, M.; Vaneker, T.; Schmidt, M.; Sutherland, J.W.; Donmez, A.; et al. Vision on metal additive manufacturing: Developments, challenges and future trends. CIRP J. Manuf. Sci. Technol. 2023, 47, 18–58. [Google Scholar] [CrossRef]
- Papazetis, G.; Vosniakos, G.C. Feature-based process parameter variation in continuous paths to improve dimensional accuracy in three-dimensional printing via material extrusion. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2241–2250. [Google Scholar] [CrossRef]
- Papazetis, G.; Vosniakos, G.C. Improving deposition quality at higher rates in material extrusion additive manufacturing. Int. J. Adv. Manuf. Technol. 2020, 111, 1221–1235. [Google Scholar] [CrossRef]

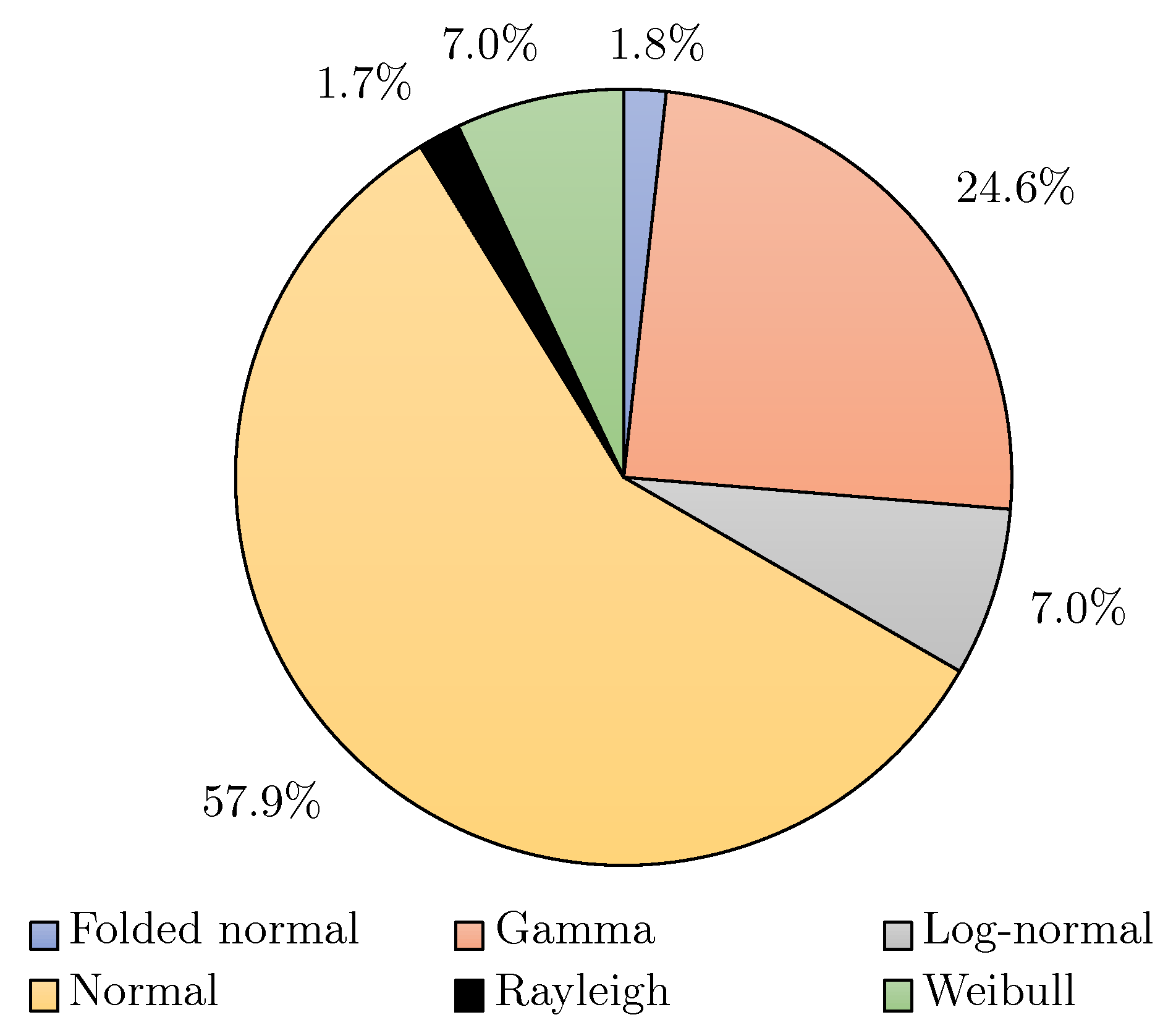
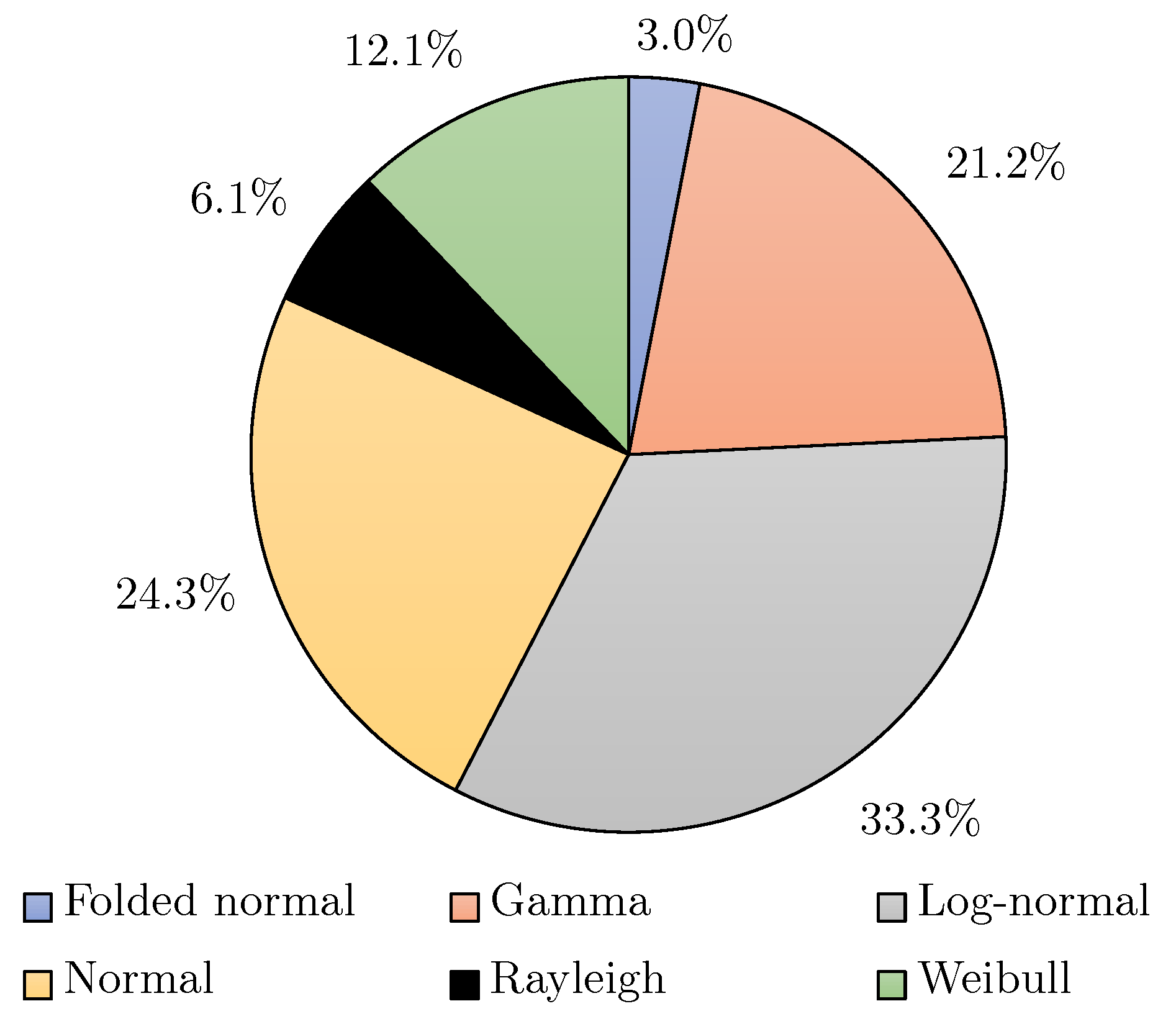

| Out-of-Specification Parts [ppm] | U–L Distance | |
|---|---|---|
| 1 | 2600 | 6 |
| 1.33 | 66 | 8 |
| 1.67 | 0.54 | 10 |
| 2 | 0.002 | 12 |
| Paper | Process | Machine | # Meas. | Use of ISO 22514 | Design of Part | Meas. Means | Type of Features | TI from Standards | Sizes Coverage | Distribution Identification | Complete |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beltran et al. [13] | MEX | BCN3D SIGMA | 52 | YES | Cylinders | CMM | Dim. Geo. | NO | Partial | Assumed as normal | NO |
| Dolimont et al. [50] | PBF | Arcam A2 | from 11 to 20 | NO | Dog bone | CMM | Dim. Surf. Topo. | ISO 8062 ISO 4288 | Partial | Assumed as normal | NO |
| Gunay et al. [44] | MEX | Monoprice Maker Select V2 | 30 | NO | Dog bone | Caliper | Dim. | ISO 286-1 | Partial | Assumed as normal | NO |
| Maurer et al. [42] | PBF | SLM Solutions SLM125 | 40 | NO | Cube and cylinders | Rugo- simeter | Surf. Topo. | NO | Partial | Verified as normal | NO |
| Preißler et al. [45] | MEX | Ultimaker 2+ extended | 25 | NO | Tower with planes | Caliper | Dim. | ISO 2768 | Partial | Assumed as normal | NO |
| Singh et al. [46] | VPP | Stratasys EDEN 260 | 16 | NO | Industrial component | CMM | Dim. | ISO 286-1 | Partial | Assumed as normal | NO |
| Siraj et al. [47] | MEX | Cadx ARYA-PRO | 50 | YES | Dog bone | Caliper | Dim. | NO | Partial | Assumed as normal | NO |
| Udroiu et al. [48] | MJT | Stratasys EDEN 350 | 150 | YES | Industrial component | Caliper | Dim. Geo. | ISO 286-1 ISO 2768 | Partial | Verified as normal | NO |
| Yap et al. [49] | MJT | Objet500 Connex3 PolyJet | undef. | NO | GBTA | CMM | Dim. | NO | Partial | Verified as normal | NO |
| Zongo et al. [43] | PBF | EOS M280 | 147 | YES | Industrial component | Laser scan | Dim. Geo. | ISO 286-1 | Partial | Verified as normal | NO |
| Objectives | MEX | All | min. 25 | YES | GBTA | CMM | Dim. Geo. | ISO 286-1 ISO 2768 | Complete | Verification of the best fitting distribution | / |
| Parameter | Value |
|---|---|
| Nozzle diameter [mm] | 0.4 |
| Layer thickness [mm] | 0.1 |
| Density of infill [%] | 20 |
| Type of infill | Cubic |
| Build platform temperature [°C] | 60 |
| Nozzle temperature [°C] | 220 |
| Size Range [mm] | X | Y | Z | Other |
|---|---|---|---|---|
| 1–3 | 275 | 300 | 550 | 200 |
| 3–6 | 600 | 600 | 800 | 700 |
| 6–10 | 300 | 300 | 850 | 25 |
| 10–18 | 350 | 350 | 825 | 25 |
| 18–30 | 400 | 400 | 200 | 25 |
| 30–50 | 425 | 425 | - | - |
| 50–80 | 425 | 425 | - | - |
| 80–120 | 400 | 400 | - | 50 |
| 120–180 | 50 | 50 | - | - |
| 180–250 | 50 | 50 | - | - |
| Type | Size Range [mm] | X | Y | Z | Other |
|---|---|---|---|---|---|
| Angularity | 18–30 | - | - | - | 50 |
| Coaxiality | 6–10 | - | - | - | 50 |
| Cylindricity | 3–6 | - | - | - | 700 |
| 10–18 | - | - | - | 50 | |
| 18–30 | - | - | - | 25 | |
| Flatness | 6–10 | - | - | 300 | - |
| 18–30 | 100 | 100 | - | - | |
| 50–80 | - | - | 100 | ||
| 180–250 | - | - | 25 | - | |
| Parallelism | 10–18 | - | - | 50 | - |
| 18–30 | 75 | 75 | 50 | - | |
| 80–120 | - | - | - | 50 | |
| 120–180 | 100 | 100 | - | - | |
| 180–250 | - | - | 25 | - | |
| Perpendicularity | 18–30 | - | - | - | 450 |
| 50–80 | - | - | - | 100 | |
| 180–250 | - | - | - | 400 | |
| Form | 3–6 | - | - | - | 200 |
| Straightness | 120–180 | 50 | 50 | - | - |
| X | Y | Z | Other | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sizes [mm] | Cyl. | Planes | Combi. | Cyl. | Planes | Combi. | Planes | Cyl. | Planes |
| 1–3 | 0% | 100% | 0% | 0% | 100% | 0% | 100% | 0% | 0% |
| 3–6 | 0% | 100% | 0% | 0% | 100% | 0% | 100% | 100% | 0% |
| 6–10 | 0% | 83% | 17% | 0% | 83% | 17% | 100% | 100% | 0% |
| 10–18 | 100% | 0% | 0% | 100% | 0% | 0% | 100% | 100% | 0% |
| 18–30 | 75% | 13% | 13% | 75% | 13% | 13% | 100% | 100% | 0% |
| 30–50 | 53% | 24% | 24% | 53% | 24% | 24% | - | - | - |
| 50–80 | 76% | 0% | 24% | 76% | 0% | 24% | - | - | - |
| 80–120 | 25% | 50% | 25% | 25% | 50% | 25% | - | 0% | 100% |
| 120–180 | 100% | 0% | 0% | 100% | 0% | 0% | - | - | - |
| 180–250 | 50% | 50% | 0% | 50% | 50% | 0% | - | - | - |
| X | Y | Z | Other | |||||
|---|---|---|---|---|---|---|---|---|
| Size [mm] | L [mm] | U [mm] | L [mm] | U [mm] | L [mm] | U [mm] | L [mm] | U [mm] |
| 1–3 | −0.112 | 0.100 | −0.142 | 0.148 | −0.233 | 0.233 | −0.055 | 0.082 |
| 3–6 | −0.111 | 0.179 | −0.082 | 0.163 | −0.191 | 0.299 | −0.147 | 0.083 |
| 6–10 | −0.228 | 0.197 | −0.317 | 0.352 | −0.211 | 0.241 | −0.177 | −0.098 |
| 10–18 | −0.096 | 0.050 | −0.138 | 0.080 | −0.095 | 0.577 | −0.039 | 0.138 |
| 18–30 | −0.085 | 0.045 | −0.194 | 0.135 | 0.042 | 0.792 | −0.052 | 0.110 |
| 30–50 | −0.355 | 0.398 | −0.159 | 0.328 | - | - | - | - |
| 50–80 | −0.341 | 0.638 | −0.041 | 0.248 | - | - | - | - |
| 80–120 | −0.734 | 0.270 | −0.357 | 0.332 | - | - | −0.589 | −0.180 |
| 120–180 | −0.048 | 0.130 | −0.120 | 0.310 | - | - | - | - |
| 180–250 | −1.021 | −0.112 | −0.979 | 0.455 | - | - | - | - |
| Size [mm] | X | Y | Z | Other |
|---|---|---|---|---|
| 1–3 | IT 14 | IT 15 | IT 16 | IT 14 |
| 3–6 | IT 14 | IT 14 | IT 16 | IT 14 |
| 6–10 | IT 15 | IT 16 | IT 15 | IT 12 |
| 10–18 | IT 11 | IT 13 | IT 15 | IT 13 |
| 18–30 | IT 12 | IT 13 | IT 15 | IT 13 |
| 30–50 | IT 15 | IT 14 | - | - |
| 50–80 | IT 15 | IT 13 | - | - |
| 80–120 | IT 14 | IT 14 | - | IT 13 |
| 120–180 | IT 11 | IT 13 | - | - |
| 180–250 | IT 14 | IT 15 | - | - |
| X | Y | Z | Other | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size [mm] | Pot. | Real | Diff. | Pot. | Real | Diff. | Pot. | Real | Diff. | Pot. | Real | Diff. |
| 1–3 | IT 14 | IT 14 | 0 | IT 15 | IT 15 | 0 | IT 16 | IT 16 | 0 | IT 14 | IT 14 | 0 |
| 3–6 | IT 14 | IT 15 | 1 | IT 14 | IT 15 | 1 | IT 16 | IT 16 | 0 | IT 14 | IT 14 | 0 |
| 6–10 | IT 15 | IT 15 | 0 | IT 16 | IT 16 | 0 | IT 15 | IT 16 | 1 | IT 12 | IT 15 | 3 |
| 10–18 | IT 11 | IT 12 | 1 | IT 13 | IT 14 | 1 | IT 15 | IT 17 | 2 | IT 13 | IT 14 | 1 |
| 18–30 | IT 12 | IT 13 | 1 | IT 13 | IT 14 | 1 | IT 15 | IT 17 | 2 | IT 13 | IT 13 | 0 |
| 30–50 | IT 15 | IT 15 | 0 | IT 14 | IT 15 | 1 | - | - | - | - | - | - |
| 50–80 | IT 15 | IT 16 | 1 | IT 13 | IT 14 | 1 | - | - | - | - | - | - |
| 80–120 | IT 14 | IT 15 | 1 | IT 14 | IT 15 | 1 | - | - | - | IT 13 | IT 15 | 2 |
| 120–180 | IT 11 | IT 12 | 1 | IT 13 | IT 14 | 1 | - | - | - | - | - | - |
| 180–250 | IT 14 | IT 16 | 2 | IT 15 | IT 16 | 1 | - | - | - | - | - | - |
| = 1.67 | = 1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Type Geo. | Axis | Size [mm] | TI [mm] | LL [mm] | UL [mm] | TI [mm] | LL [mm] | UL [mm] |
| Angularity | Other | 18–30 | 0.137 | 0.110 | 0.164 | 0.086 | 0.066 | 0.098 |
| Coaxiality | Other | 6–10 | 1.833 | 1.471 | 2.194 | 1.143 | 0.881 | 1.314 |
| Cylindricity | Other | 3–6 | 0.144 | 0.136 | 0.152 | 0.088 | 0.082 | 0.091 |
| Other | 10–18 | 0.063 | 0.051 | 0.076 | 0.082 | 0.030 | 0.045 | |
| Other | 18–30 | 0.043 | 0.031 | 0.055 | 0.028 | 0.019 | 0.033 | |
| Flatness | Other | 50–80 | 0.360 | 0.310 | 0.410 | 0.220 | 0.186 | 0.246 |
| X | 18–30 | 0.023 | 0.020 | 0.026 | 0.014 | 0.012 | 0.016 | |
| Y | 18–30 | 0.046 | 0.039 | 0.052 | 0.028 | 0.024 | 0.031 | |
| Z | 6–10 | 0.040 | 0.037 | 0.043 | 0.045 | 0.022 | 0.026 | |
| Z | 180–250 | 0.412 | 0.296 | 0.528 | 0.268 | 0.178 | 0.316 | |
| Parallelism | Other | 80–120 | 0.110 | 0.088 | 0.132 | 0.143 | 0.053 | 0.079 |
| X | 18–30 | 0.115 | 0.096 | 0.133 | 0.153 | 0.058 | 0.080 | |
| X | 120–180 | 0.088 | 0.076 | 0.100 | 0.109 | 0.045 | 0.060 | |
| Y | 18–30 | 0.114 | 0.095 | 0.132 | 0.070 | 0.057 | 0.079 | |
| Y | 120–180 | 0.104 | 0.090 | 0.119 | 0.130 | 0.054 | 0.071 | |
| Z | 10–18 | 0.034 | 0.027 | 0.041 | 0.021 | 0.016 | 0.024 | |
| Z | 18–30 | 0.034 | 0.027 | 0.041 | 0.021 | 0.016 | 0.024 | |
| Z | 180–250 | 0.606 | 0.436 | 0.777 | 0.395 | 0.261 | 0.465 | |
| Perpendicularity | Other | 18–30 | 0.084 | 0.079 | 0.090 | 0.120 | 0.047 | 0.054 |
| Other | 50–80 | 0.069 | 0.059 | 0.079 | 0.091 | 0.036 | 0.047 | |
| Other | 180–250 | 0.122 | 0.113 | 0.130 | 0.154 | 0.068 | 0.078 | |
| Form | Other | 3–6 | 0.288 | 0.260 | 0.316 | 0.176 | 0.156 | 0.189 |
| Straightness | X | 120–180 | 0.065 | 0.052 | 0.078 | 0.042 | 0.031 | 0.047 |
| Y | 120–180 | 0.068 | 0.054 | 0.081 | 0.045 | 0.032 | 0.048 | |
| Type | Size [mm] | X | Y | Z | Other |
|---|---|---|---|---|---|
| Flatness | 1–10 | - | - | L | - |
| 10–30 | H | H | - | - | |
| 30–100 | - | - | - | NC | |
| 100–300 | - | - | L | ||
| Parallelism | 1–10 | - | - | - | - |
| 10–30 | NC | NC | K | - | |
| 30–100 | - | - | - | L | |
| 100–300 | H | K | NC | - | |
| Perpendicularity | 1–100 | - | - | - | H |
| 100–300 | - | - | - | H | |
| Straightness | 100–300 | H | H | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spitaels, L.; Nieto Fuentes, E.; Rivière-Lorphèvre, E.; Arrazola, P.-J.; Ducobu, F. A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers. J. Manuf. Mater. Process. 2024, 8, 36. https://doi.org/10.3390/jmmp8010036
Spitaels L, Nieto Fuentes E, Rivière-Lorphèvre E, Arrazola P-J, Ducobu F. A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers. Journal of Manufacturing and Materials Processing. 2024; 8(1):36. https://doi.org/10.3390/jmmp8010036
Chicago/Turabian StyleSpitaels, Laurent, Endika Nieto Fuentes, Edouard Rivière-Lorphèvre, Pedro-José Arrazola, and François Ducobu. 2024. "A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers" Journal of Manufacturing and Materials Processing 8, no. 1: 36. https://doi.org/10.3390/jmmp8010036
APA StyleSpitaels, L., Nieto Fuentes, E., Rivière-Lorphèvre, E., Arrazola, P.-J., & Ducobu, F. (2024). A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers. Journal of Manufacturing and Materials Processing, 8(1), 36. https://doi.org/10.3390/jmmp8010036








