Modeling the Thermoforming Process of a Complex Geometry Based on a Thermo-Visco-Hyperelastic Model
Abstract
1. Introduction
2. Thermo-Visco-Hyperelastic Material Model
2.1. Hyperelastic Model
- Mooney–Rivlin model [20,21]: this model is highly recommended in previous existing studies for the simulation of material-forming processes. There exist many versions of this model based on the order of level, for instance: two-parameter, three-parameter, etc. The form of the strain energy for the two-parameter model is
2.2. Limitations of Hyperelasticity
3. Experimental and Numerical Tests
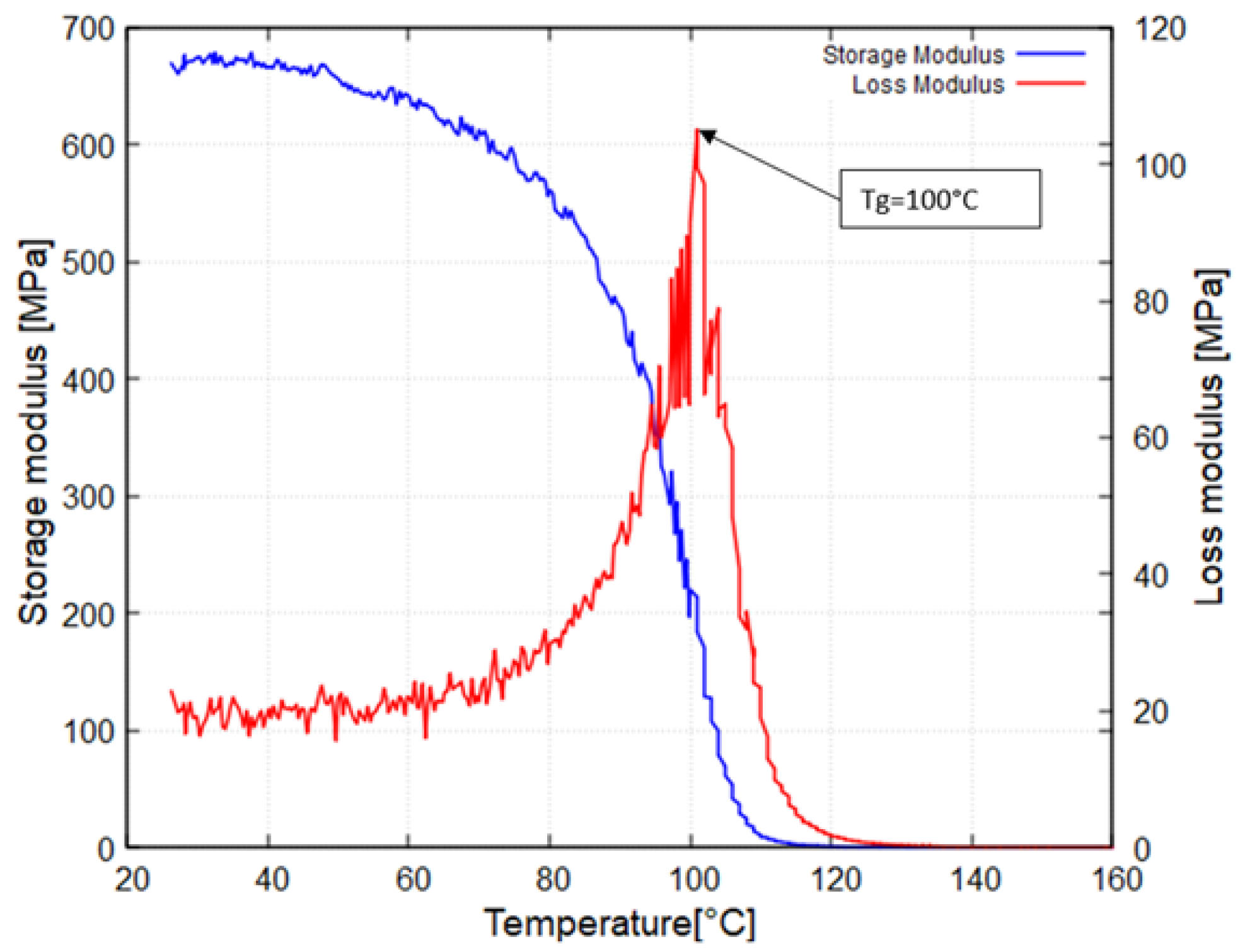
3.1. DMA Tests
- Temperature sweep: A frequency of 1 Hz was used, and a temperature ramp of 1 °C per minute was applied;
- Frequency sweep: Frequencies ranging from 0.1 Hz to 10 Hz were used, with 10 points per decade.
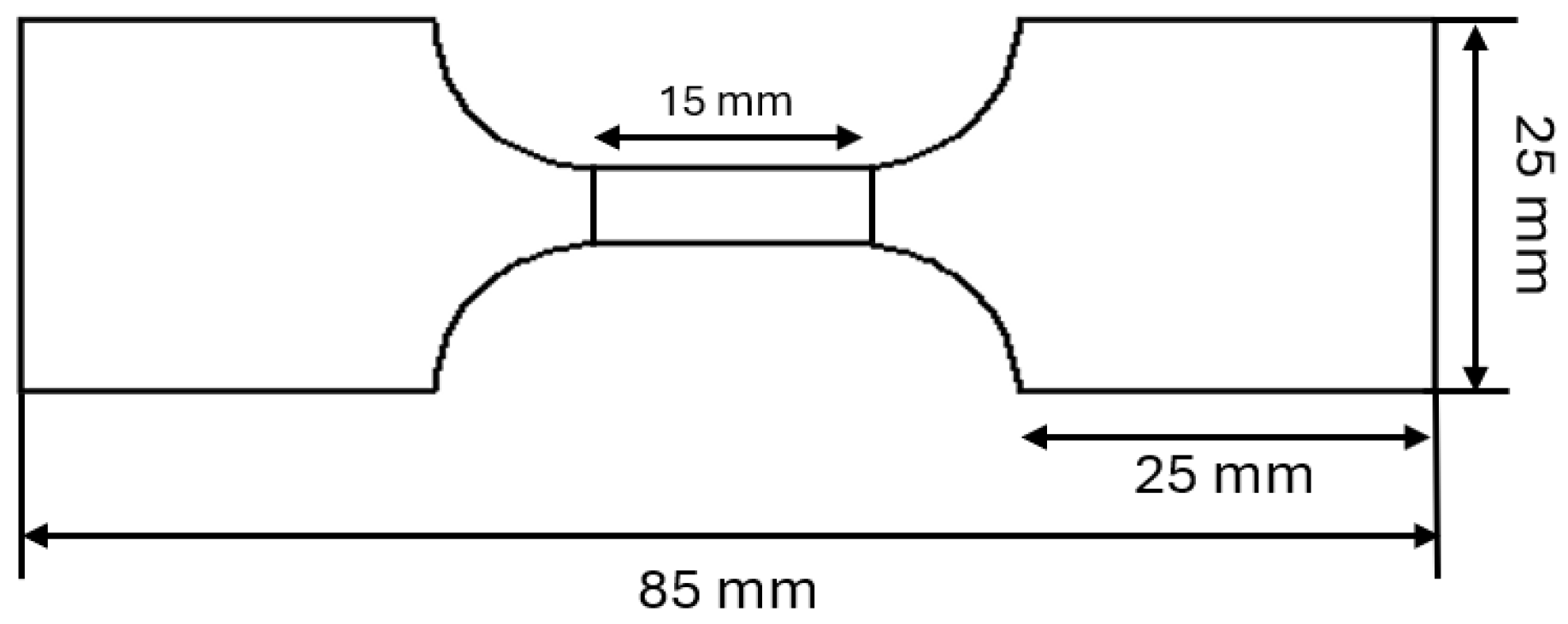
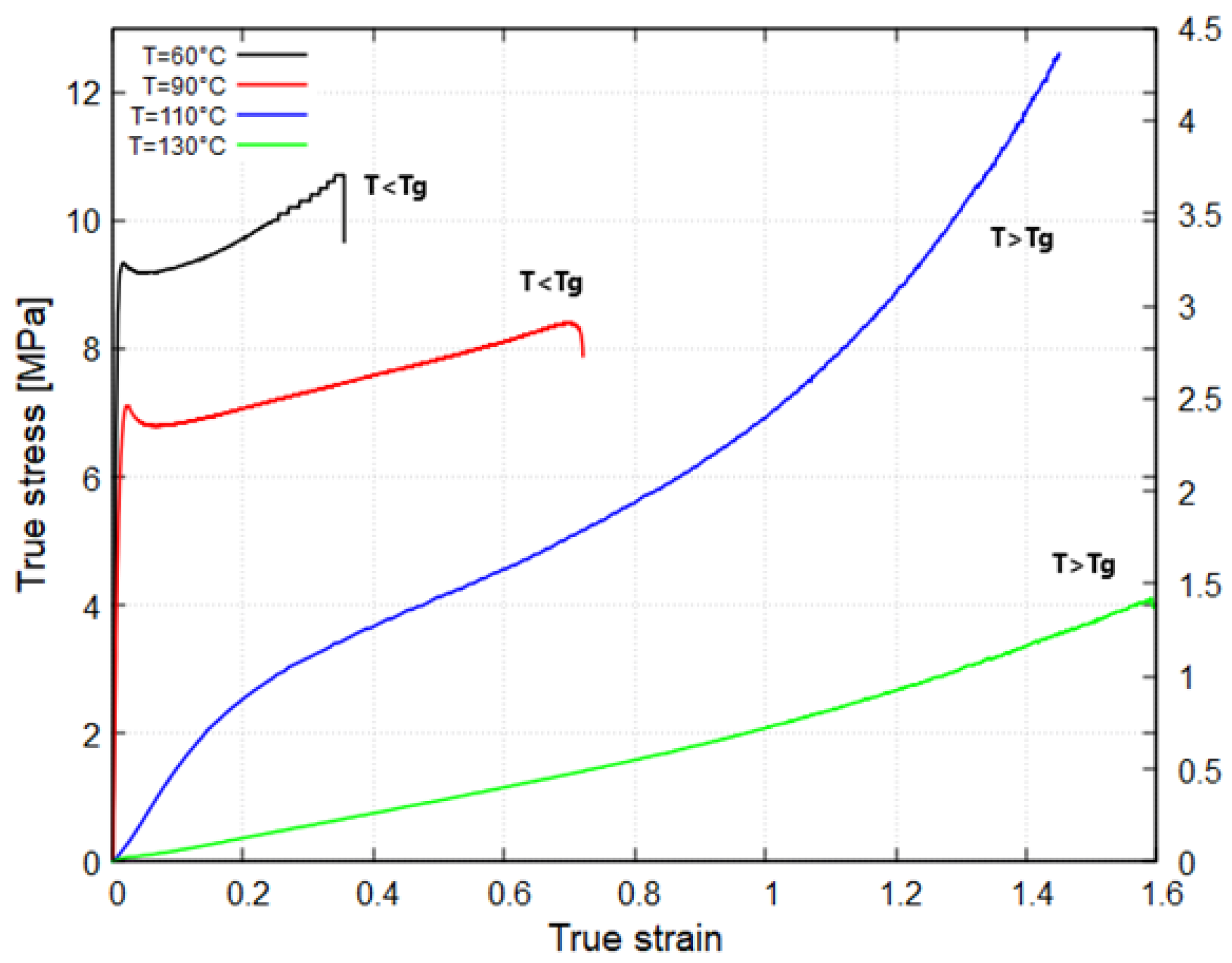
3.2. Tensile Tests
3.3. The Constitutive Model Used in ABAQUS
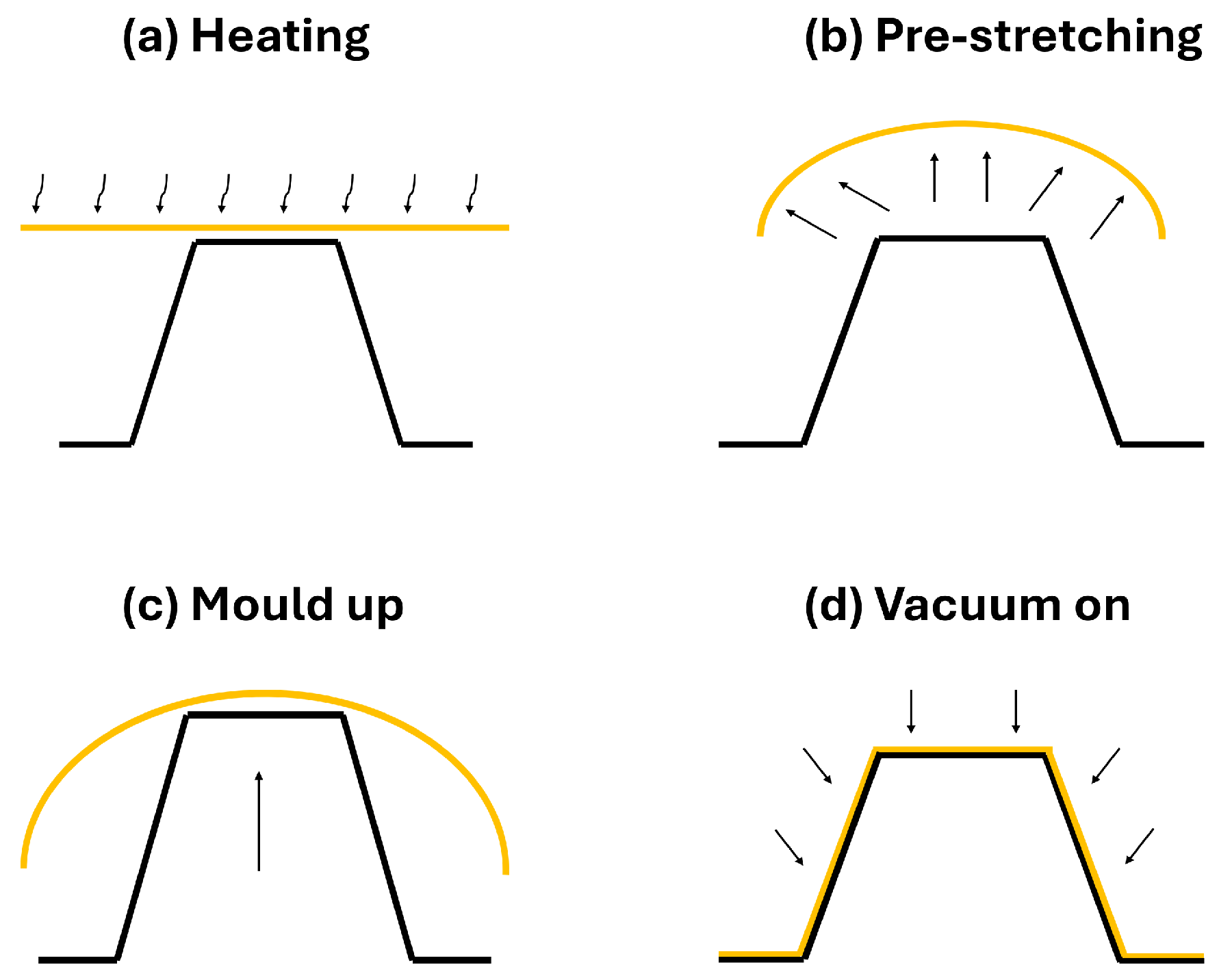
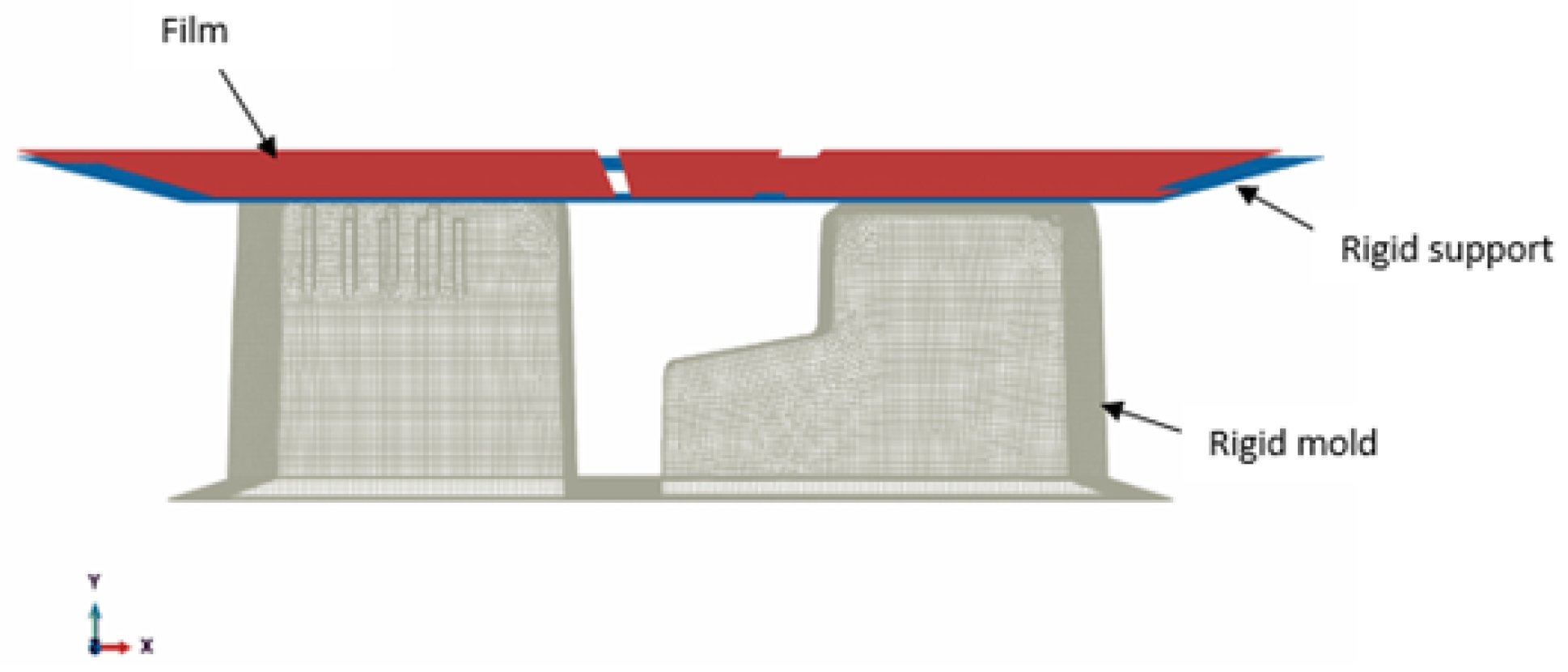
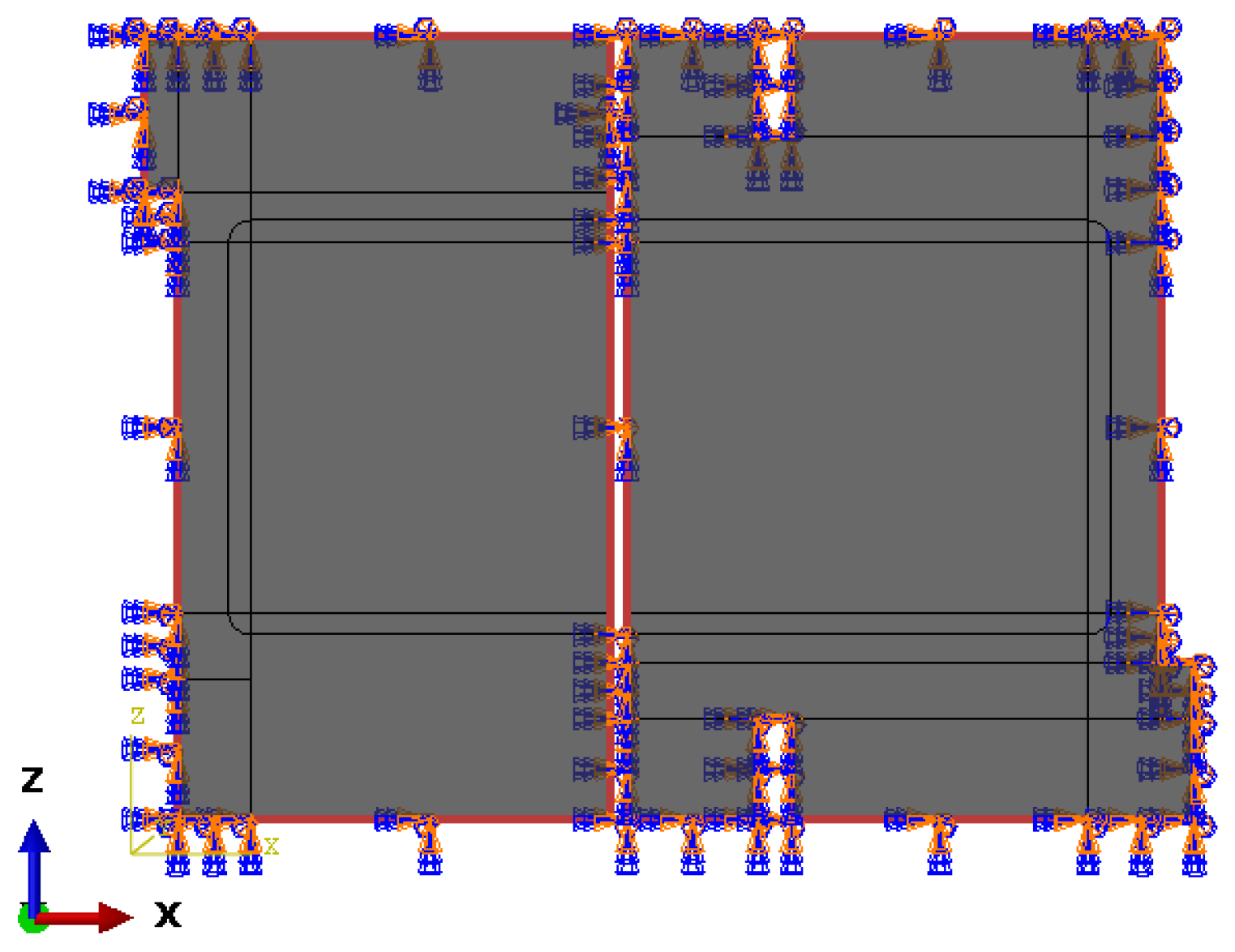
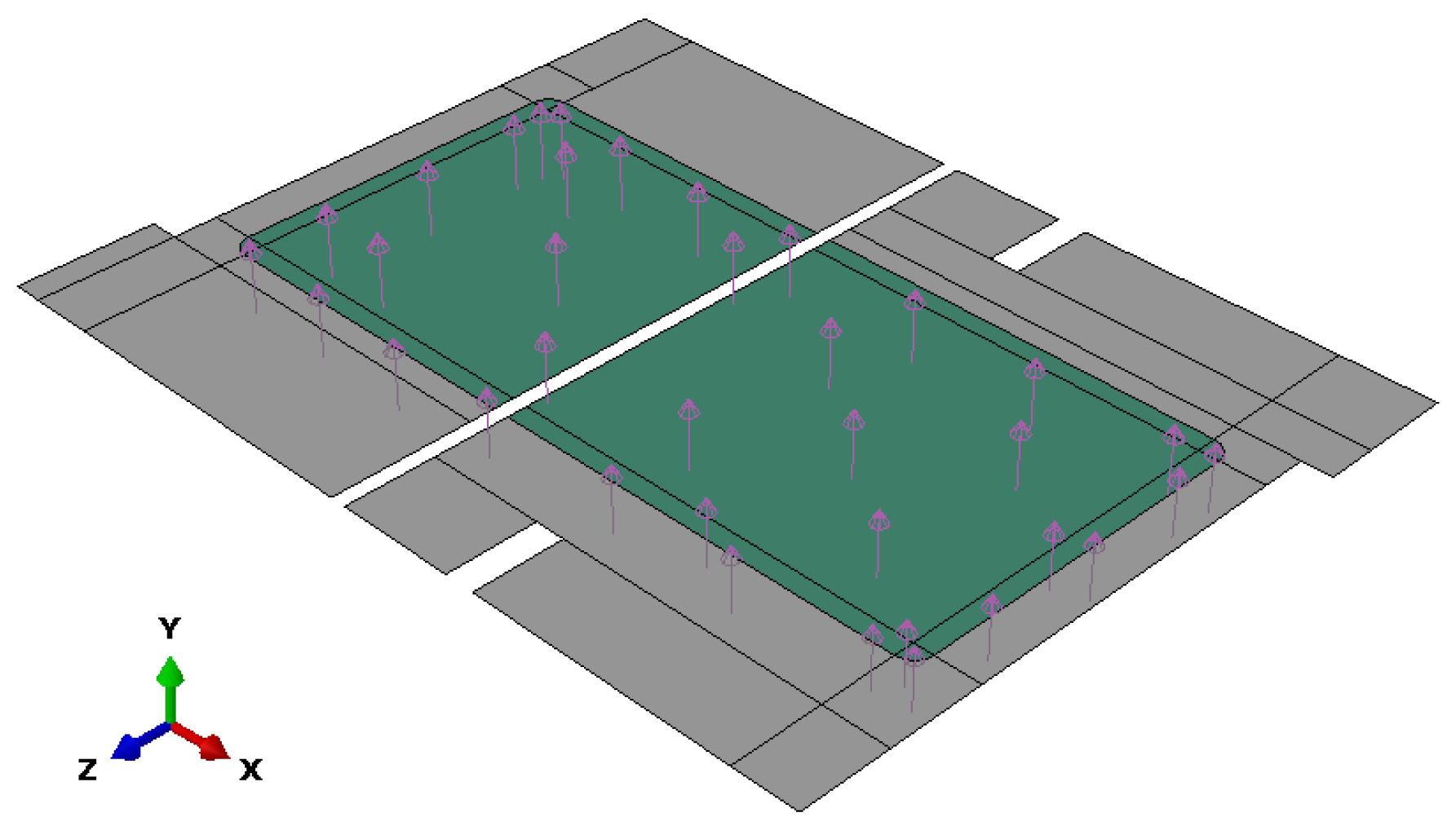
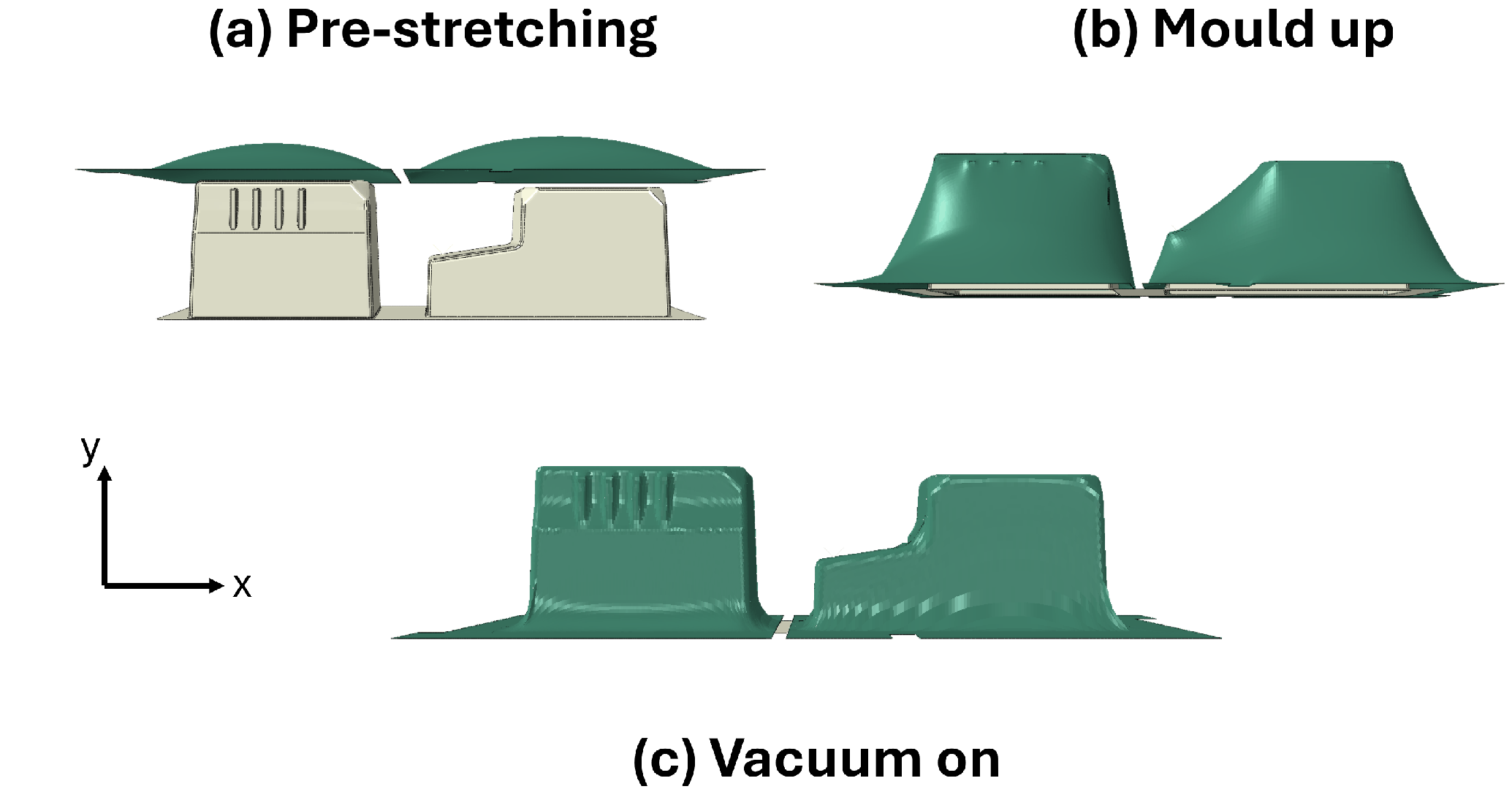
4. Experimental–Numerical Modeling of the Industrial Demonstrator of the Thermoforming Process
5. Results and Discussion
5.1. Baseline Simulation
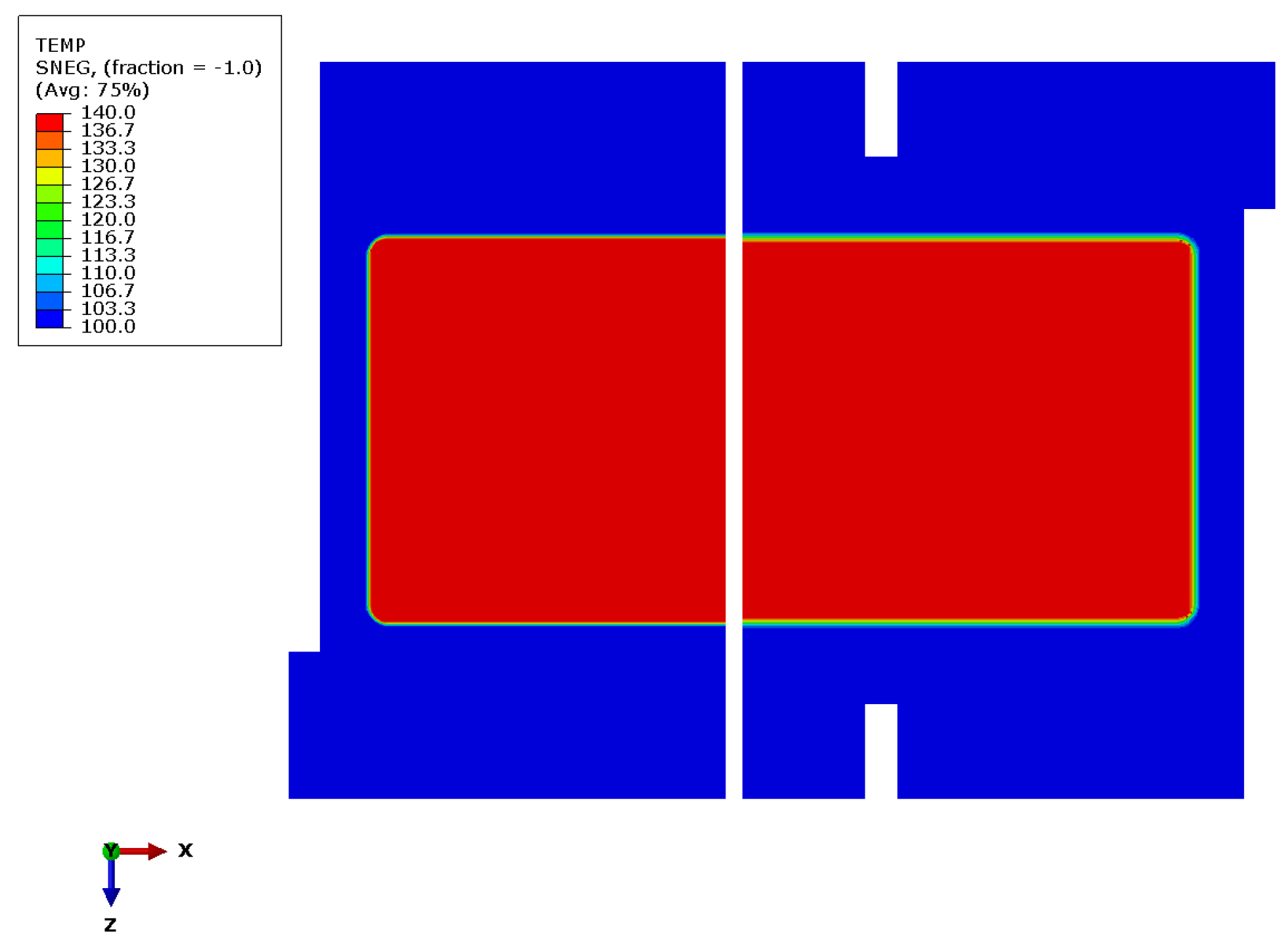
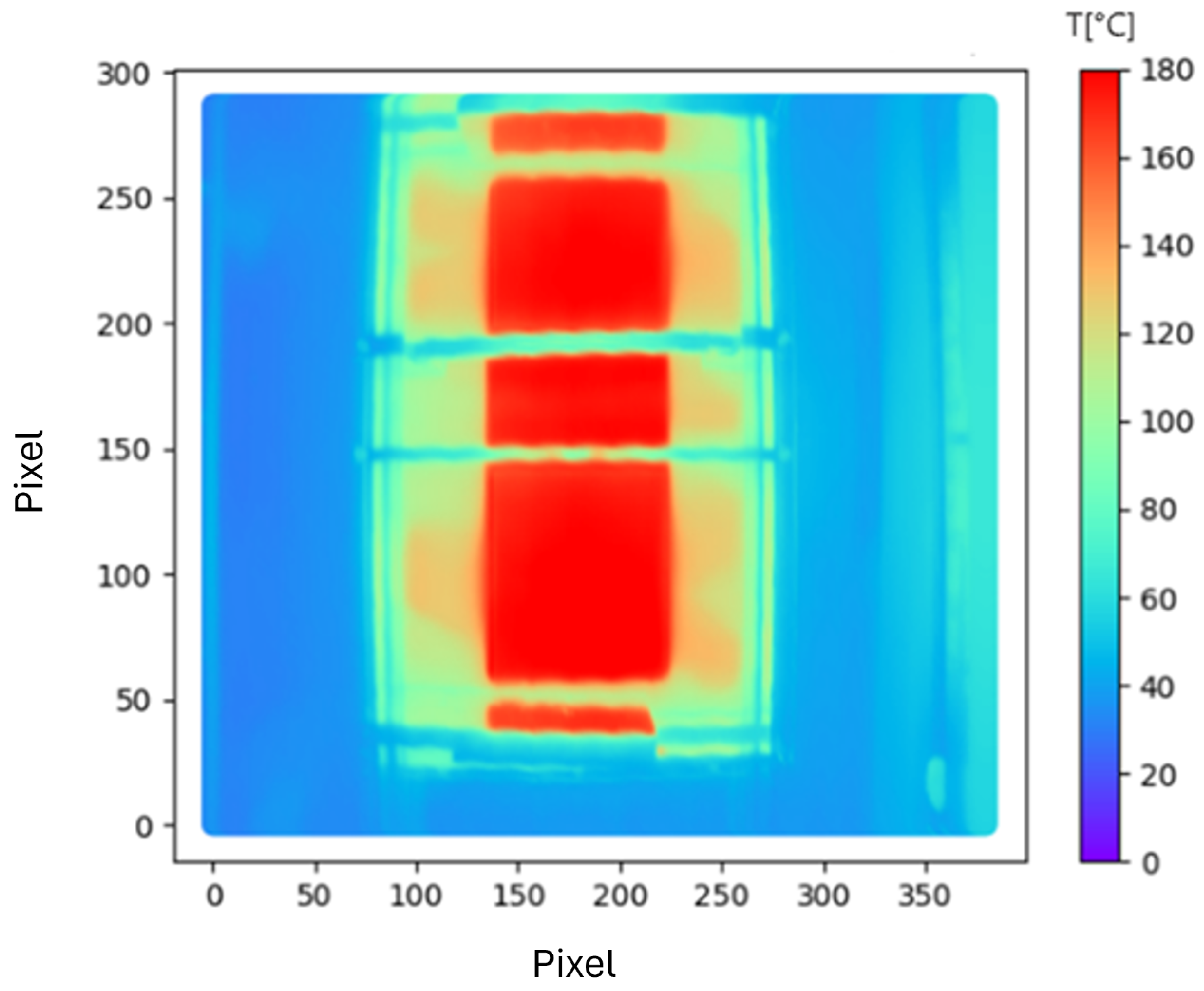
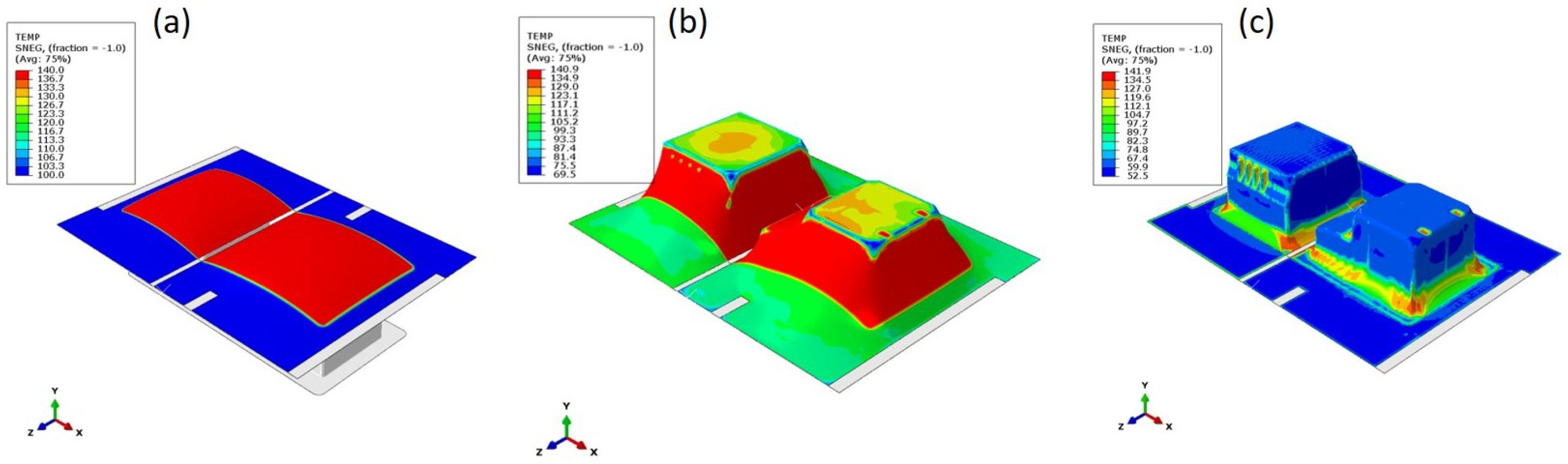
5.2. Temperature Distribution
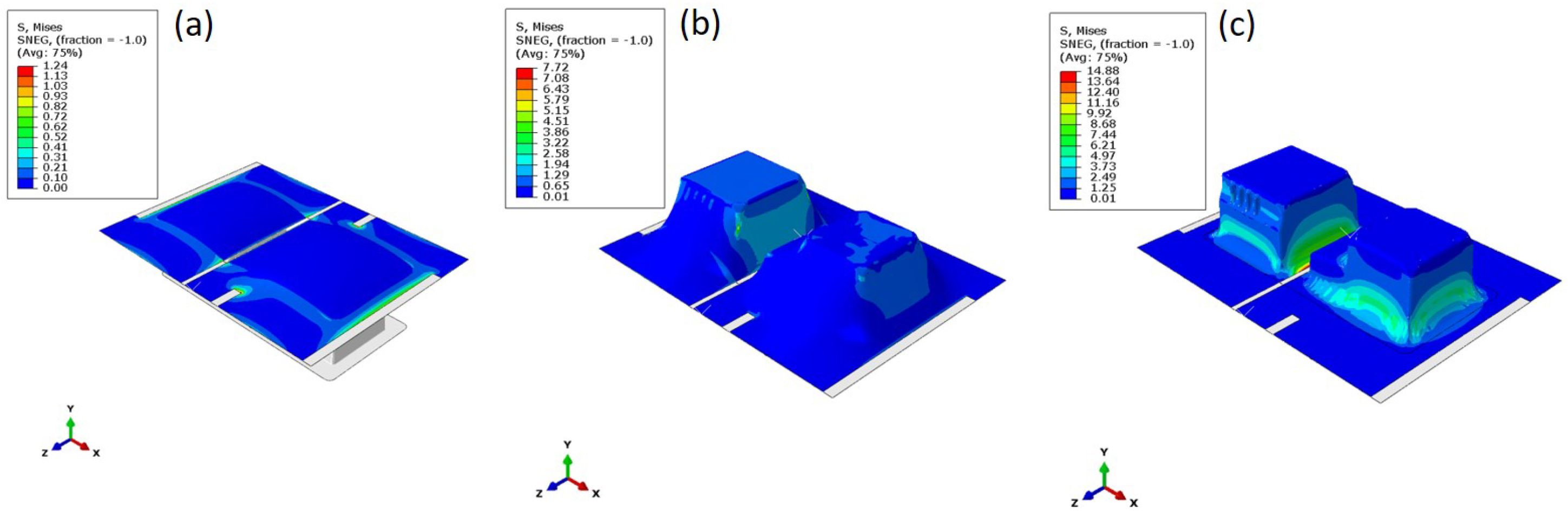
5.3. Stress Distribution
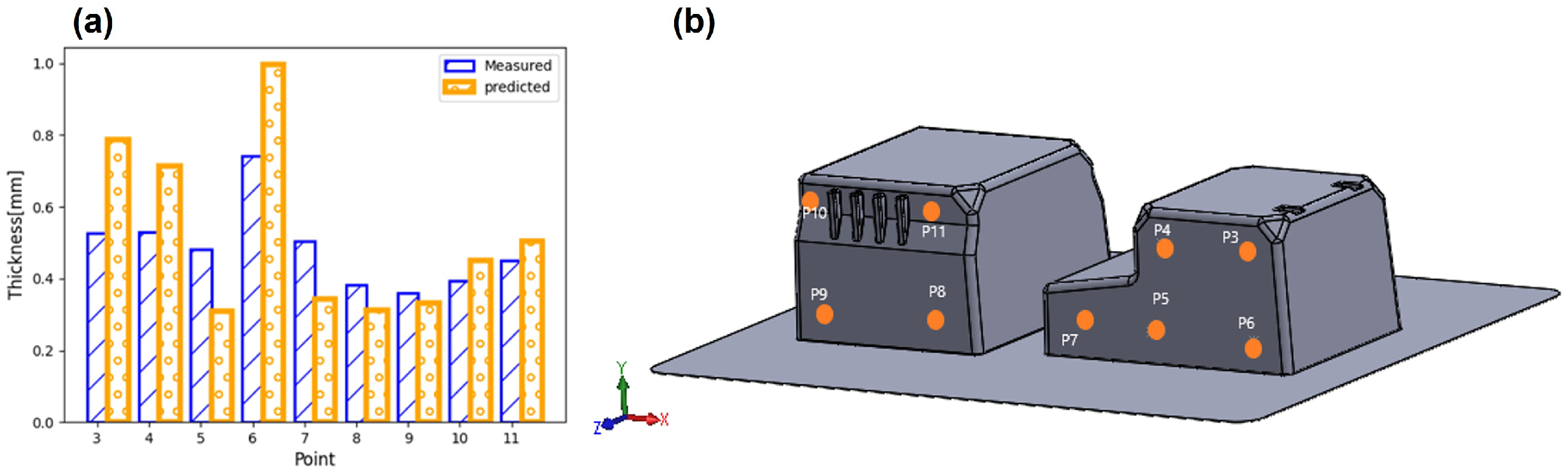
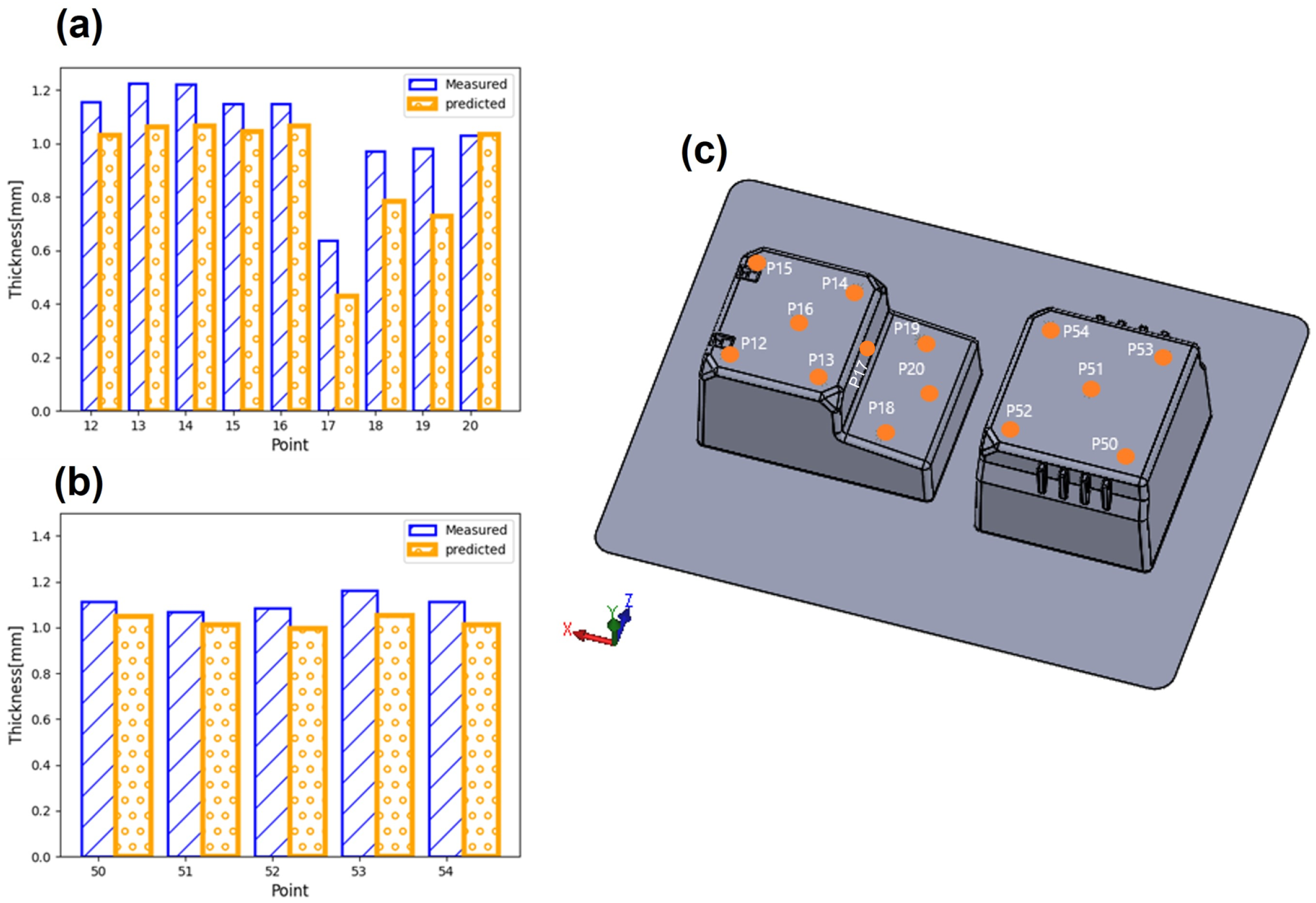
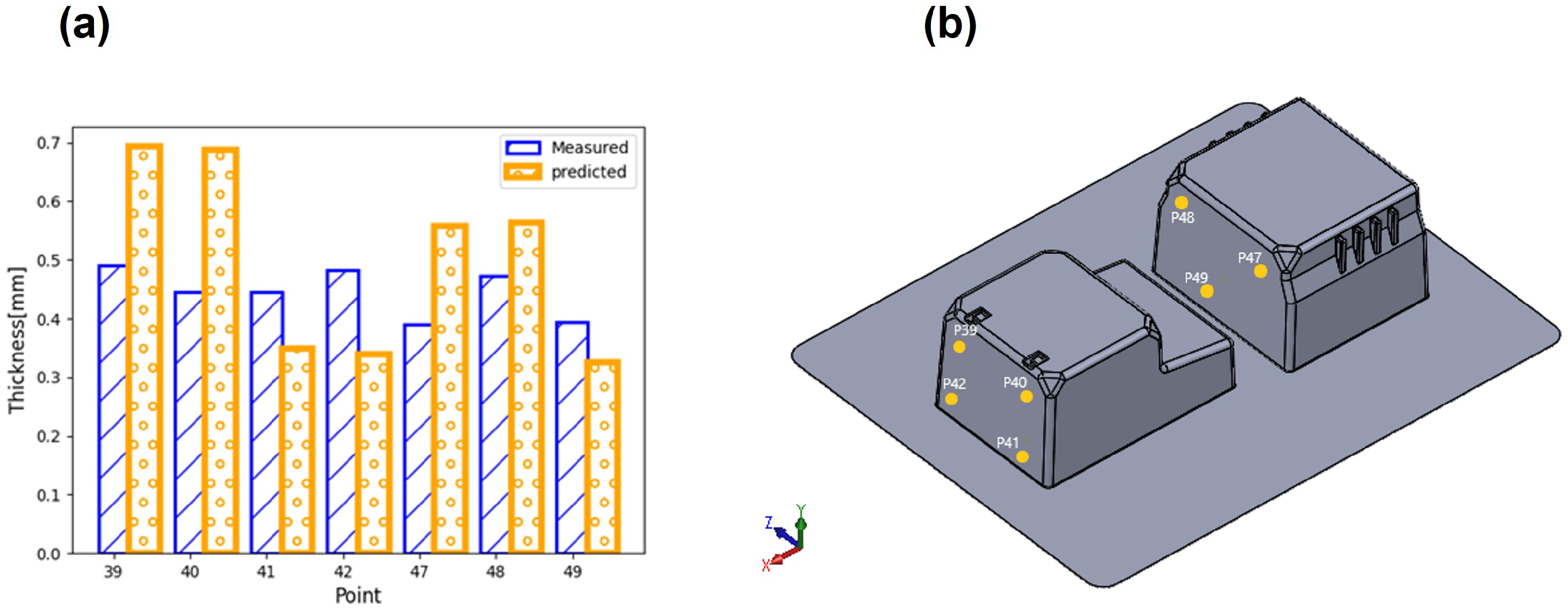
5.4. Thickness Distribution
6. Conclusions
- The type of mesh used in this study does not allow for using automatic selective mesh refinement to improve the deformation of a complex shape.
- The influence of the friction coefficient on the evolution of the thickness was not studied.
- Another important factor that was not studied is the conduction coefficient.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Riley, A. Plastics Manufacturing Processes for Packaging Materials. In Packaging Technology; Elsevier: Amsterdam, The Netherlands, 2012; pp. 310–360. [Google Scholar]
- Cha, J.; Song, H.Y.; Hyun, K.; Go, J.S. Rheological Measurement of the Nonlinear Viscoelasticity of the ABS Polymer and Numerical Simulation of Thermoforming Process. Int. J. Adv. Manuf. Technol. 2020, 107, 2449–2464. [Google Scholar] [CrossRef]
- Bohdan, C. Analysis of plastics packaging domestic market. Polimery 2007, 52, 811–819. [Google Scholar]
- Thermoformage. Plastilex. Available online: http://thermoformage-iledefrance.fr/thermoformage/ (accessed on 28 January 2024).
- Leite, W.D.O.; Campos Rubio, J.C.; Mata Cabrera, F.; Carrasco, A.; Hanafi, I. Vacuum Thermoforming Process: An Approach to Modeling and Optimization Using Artificial Neural Networks. Polymers 2018, 10, 143. [Google Scholar] [CrossRef] [PubMed]
- McCool, R.; Martin, P.J. The Role of Process Parameters in Determining Wall Thickness Distribution in Plug-Assisted Thermoforming. Polym. Eng. Sci. 2010, 50, 1923–1934. [Google Scholar] [CrossRef]
- Collins, P.; Lappin, J.F.; Harkin-Jones, E.M.A.; Martin, P.J. Effects of Material Properties and Contact Conditions in Modelling of Plug Assisted Thermoforming. Plast. Rubber Compos. 2000, 29, 349–359. [Google Scholar] [CrossRef]
- Hosseini, H.; Berdyshev, B.V.; Mehrabani-Zeinabad, A. A Solution for Warpage in Polymeric Products by Plug-Assisted Thermoforming. Eur. Polym. J. 2006, 42, 1836–1843. [Google Scholar] [CrossRef]
- Makradi, A.; Ahzi, S.; Belouettar, S.; Ruch, D. Thermoforming Process of Semicrystalline Polymeric Sheets: Modeling and Finite Element Simulations. Polym. Sci. Ser. 2008, 50, 550–557. [Google Scholar] [CrossRef]
- Atmani, O.; Abbès, B.; Abbès, F.; Li, Y.M.; Batkam, S. Identification of a thermo-elasto-viscoplastic behavior law for the simulation of thermoforming of high impact polystyrene. AIP Conf. Proc. 2018, 1960, 120003. [Google Scholar] [CrossRef]
- Dong, Y.; Lin, R.J.T.; Bhattacharyya, D. Finite Element Simulation on Thermoforming Acrylic Sheets Using Dynamic Explicit Method. Polym. Polym. Compos. 2006, 14, 307–328. [Google Scholar] [CrossRef]
- Takaffoli, M.; Hangalur, G.; Bakker, R.; Chandrashekar, N. Thermo-Visco-Hyperelastic Behavior of Polycarbonate in Forming of a Complex Geometry. J. Manuf. Process. 2020, 57, 105–113. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Atmani, O.; Abbès, B.; Abbès, F.; Lid, Y.M.; Batkam, S. Etude expérimentale et numérique de l’influence de la température et de la vitesse de déformation sur le thermoformage assisté par poinçon du polystyrène. In Proceedings of the 24th French Mechanics Congress, Aachen, Germany, 9–13 September 2019. [Google Scholar]
- Sánchez, E.; Nájera, A.; Sotomayor, O. Numerical Study of the Viscoelastic Mechanical Response of Polystyrene in the Process of Thermoforming through the Generalized Maxwell Model. Mater. Today Proc. 2022, 49, 107–114. [Google Scholar] [CrossRef]
- Erdogan, E.S.; Eksi, O. Prediction of Wall Thickness Distribution in Simple Thermoforming Moulds. J. Mech. Eng. 2014, 60, 195–202. [Google Scholar] [CrossRef]
- Fu, M.W.; Wang, J.L. Size Effects in Multi-Scale Materials Processing and Manufacturing. Int. J. Mach. Tools Manuf. 2021, 167, 103755. [Google Scholar] [CrossRef]
- Tao, F.; Cheng, J.; Qi, Q.; Zhang, M.; Zhang, H.; Sui, F. Digital Twin-Driven Product Design, Manufacturing and Service with Big Data. Int. J. Adv. Manuf. Technol. 2018, 94, 3563–3576. [Google Scholar] [CrossRef]
- Tobajas, R.; Elduque, D.; Javierre, C.; Ibarz, E.; Gracia, L. A Comparative Study of Hyperelastic Constitutive Models for an Automotive Shaft Seal Material. Int. J. Serv. Comput. Oriented Manuf. 2018, 3, 171–189. [Google Scholar] [CrossRef]
- Boukamel, A. Modélisation Mécaniques et Numériques des Matériaux et Structures en éLastomères. HDR Thesis, Universite De La Mediterranee (Aix-Marseille II), Marseille, France, 2010. [Google Scholar]
- Hyperelastic Behavior of Rubberlike Materials. Abaqus Documentation 2017. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch17s01abo16.html (accessed on 28 January 2024).
- Abaqus Documentation, Hyperelastic Material Models in Abaqus. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/key/default.htm?startat=ch20abk03.html (accessed on 28 January 2024).
- Bergström, J. Elasticity/Hyperelasticity. In Mechanics of Solid Polymers; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Time Domain Viscoelasticity. Abaqus Documentation 2017. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch17s07.html (accessed on 28 January 2024).
- Chae, S.-H.; Zhao, J.-H.; Edwards, D.R.; Ho, P.S. Characterization of the Viscoelasticity of Molding Compounds in the Time Domain. J. Electron. Mater. 2010, 39, 419–425. [Google Scholar] [CrossRef]
- Finite-Strain Viscoelasticity. Abaqus Documentation 2017. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/stm/default.htm?startat=ch04s08ath127.html (accessed on 28 January 2024).
- O’Connor, C.P.J.; Menary, G.; Martin, P.J.; McConville, E. Finite Element Analysis of the Thermoforming of Polypropylene. Int. J. Mater. Form. 2008, 1, 779–782. [Google Scholar] [CrossRef]
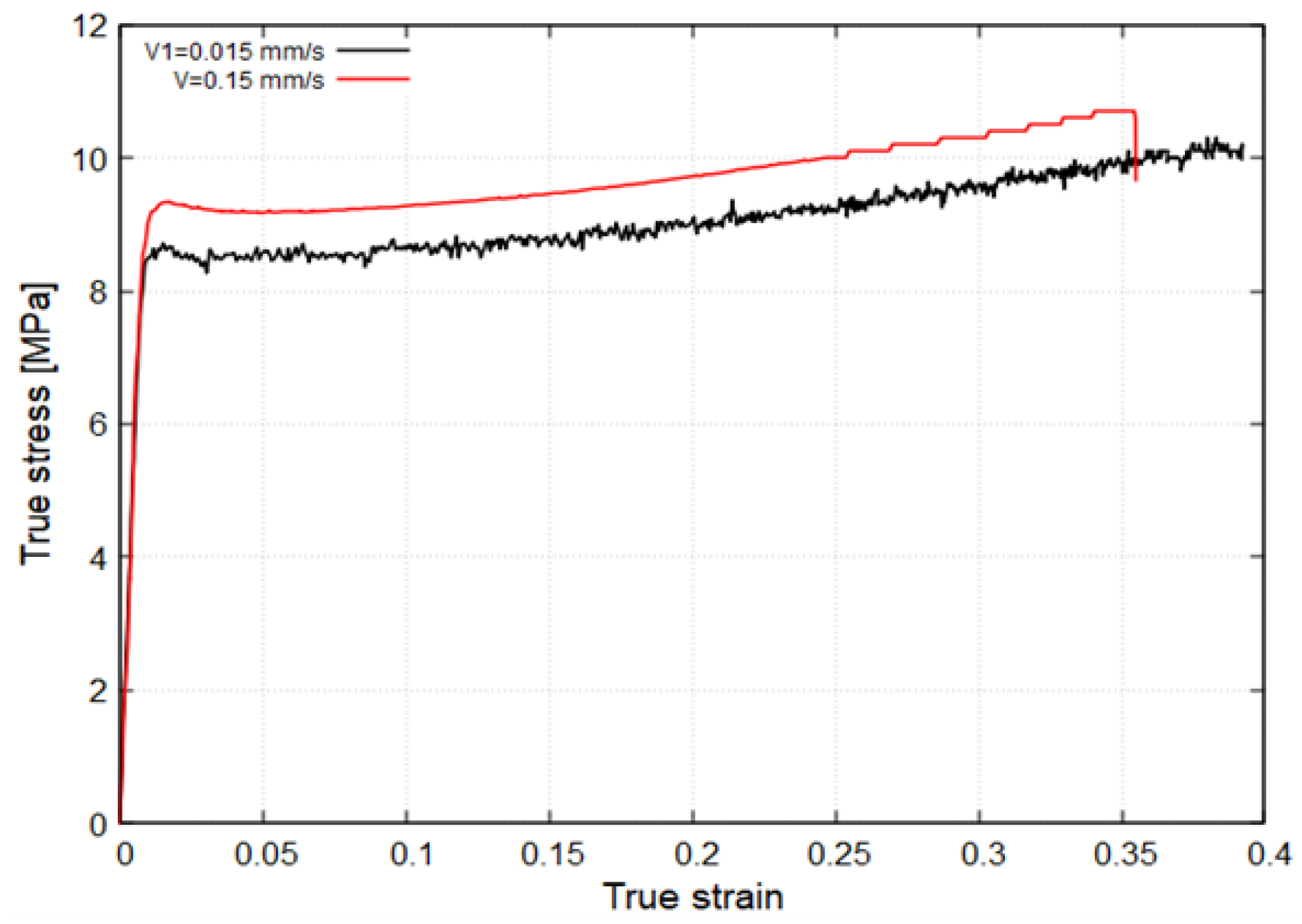
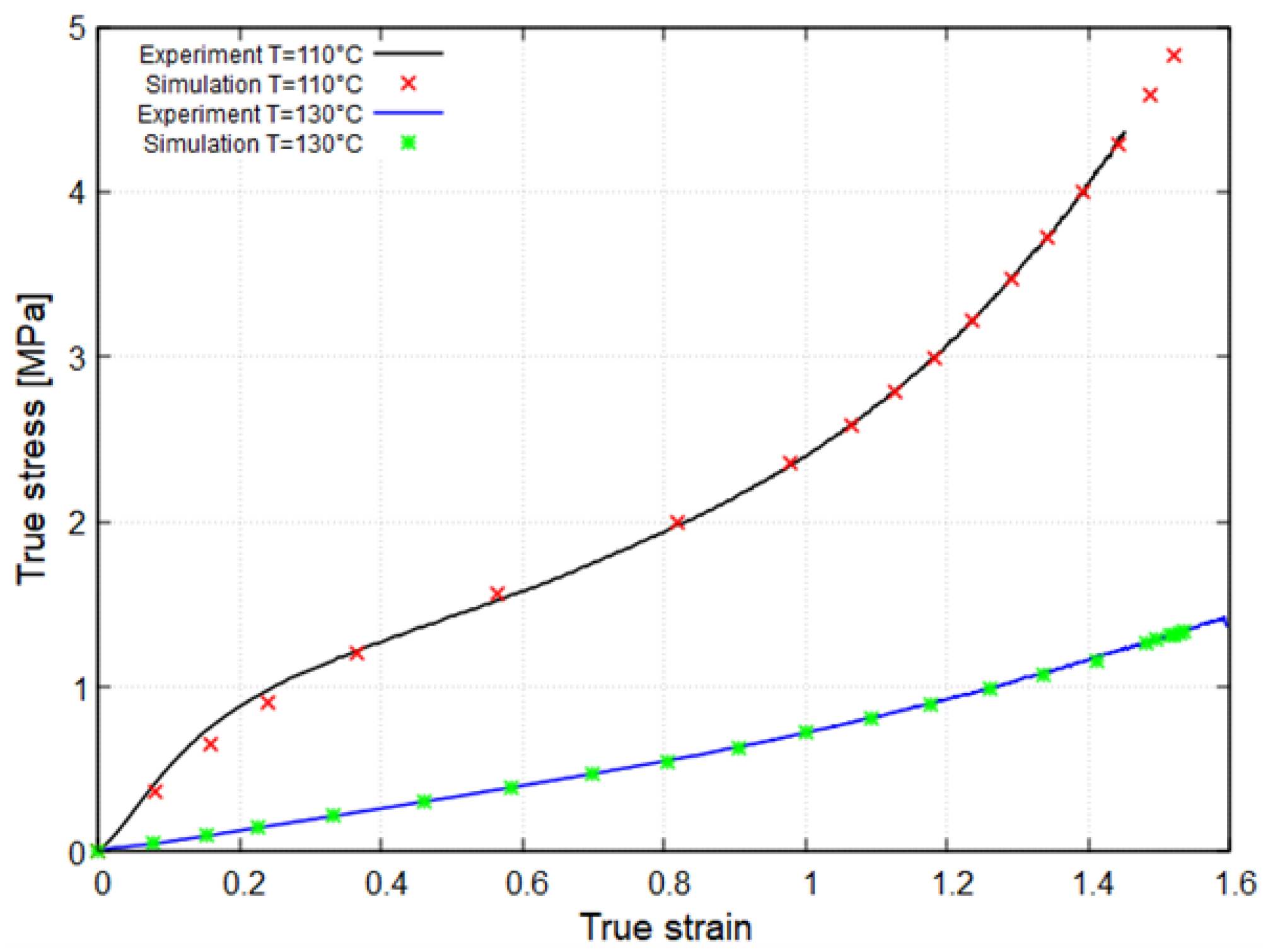
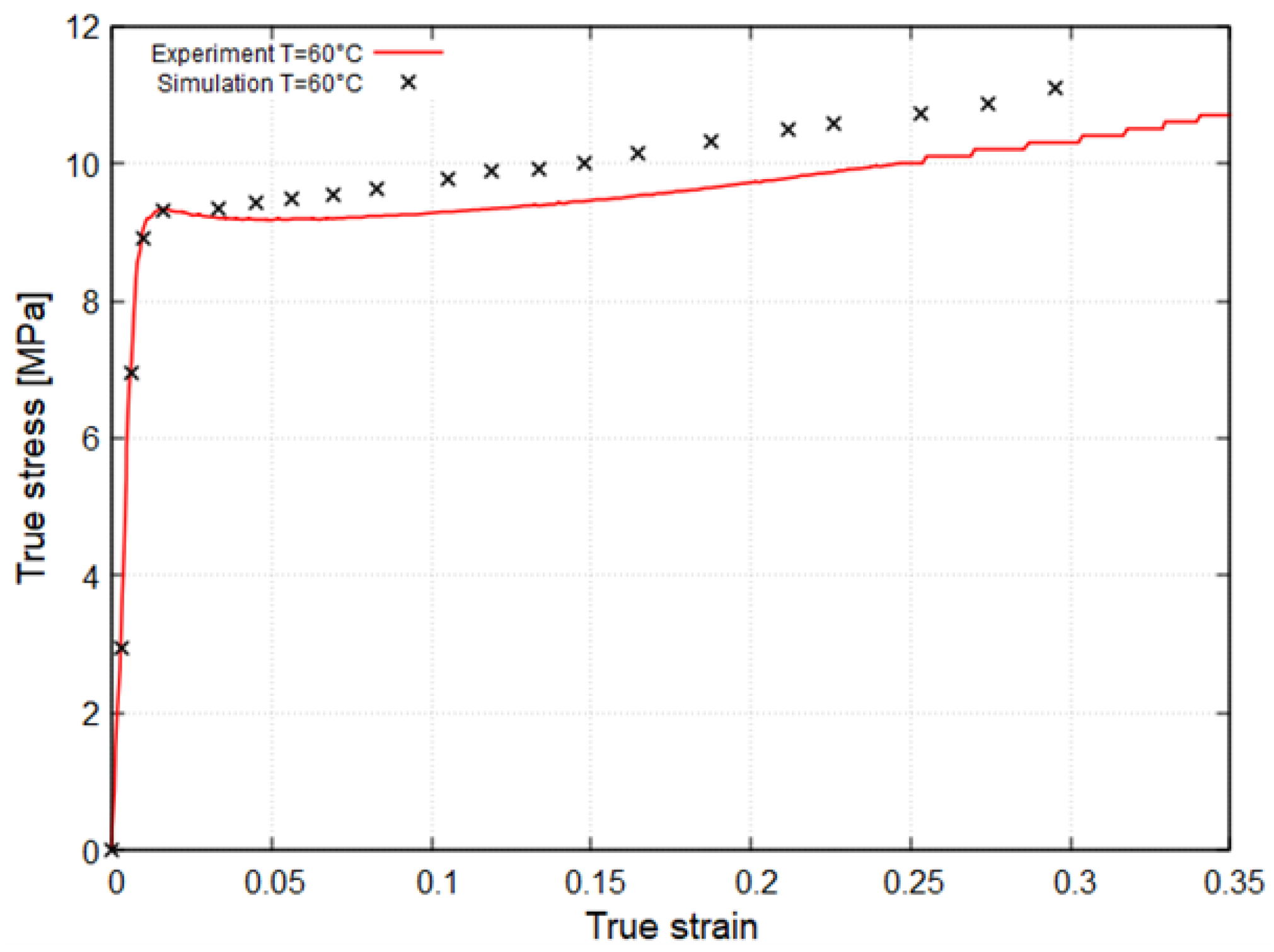

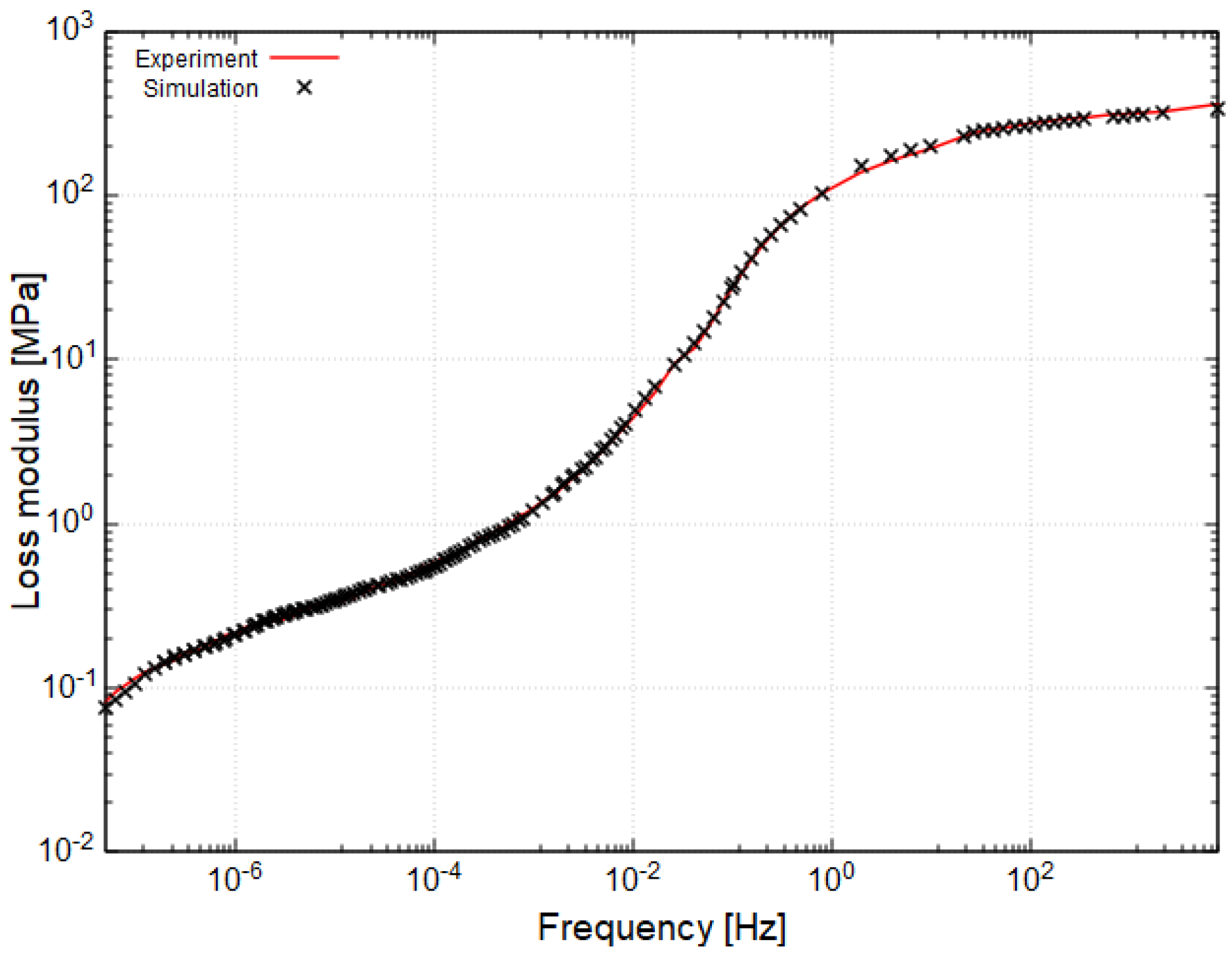

| Temperature [°C] | Test Specimens | Loading Speeds [mm/s] |
|---|---|---|
| 60 | 3 | 0.015–0.15 |
| 90 | 3 | 0.015–0.15 |
| 110 | 3 | 0.15–1.5–15 |
| 120 | 3 | 0.15–1.5–15 |
| 130 | 3 | 0.15–1.5–15 |
| 140 | 3 | 0.15–1.5–15 |
| Temperature [°C] | Input Data | Curve Used |
|---|---|---|
| 60 | Experimental test data | Nominal stress–strain curve |
| 90 | Experimental test data | Nominal stress–strain curve |
| 110 | Experimental test data | Nominal stress–strain curve |
| 120 | Experimental test data | Nominal stress–strain curve |
| 130 | Experimental test data | Nominal stress–strain curve |
| 140 | Experimental test data | Nominal stress–strain curve |
| Term Number | [s] | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | 97 | |
| 6 | 9.9 | |
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
| Step | Pressure [Bar] | Displacement [mm] | Duration [s] |
|---|---|---|---|
| Pre-stretching | 0.01 | - | 0.5 |
| Mould up | - | 102 | 2 |
| Vacuum on | 1 | - | 2 |
| Contact Type | Parts | Properties |
|---|---|---|
| Mechanical contact | Sheet and mold | Hard contact and friction coefficient (f = 0.3) |
| Thermal contact | Sheet and mold | Gap conductance 1 |
| Conductance [] | Clearance [mm] |
|---|---|
| 10 | 0 |
| 5 | 0.005 |
| 2.5 | 0.01 |
| 1.66 | 0.015 |
| 1.25 | 0.02 |
| 1 | 0.025 |
| 0 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragoubi, A.; Ducloud, G.; Agazzi, A.; Dewailly, P.; Le Goff, R. Modeling the Thermoforming Process of a Complex Geometry Based on a Thermo-Visco-Hyperelastic Model. J. Manuf. Mater. Process. 2024, 8, 33. https://doi.org/10.3390/jmmp8010033
Ragoubi A, Ducloud G, Agazzi A, Dewailly P, Le Goff R. Modeling the Thermoforming Process of a Complex Geometry Based on a Thermo-Visco-Hyperelastic Model. Journal of Manufacturing and Materials Processing. 2024; 8(1):33. https://doi.org/10.3390/jmmp8010033
Chicago/Turabian StyleRagoubi, Ameni, Guillaume Ducloud, Alban Agazzi, Patrick Dewailly, and Ronan Le Goff. 2024. "Modeling the Thermoforming Process of a Complex Geometry Based on a Thermo-Visco-Hyperelastic Model" Journal of Manufacturing and Materials Processing 8, no. 1: 33. https://doi.org/10.3390/jmmp8010033
APA StyleRagoubi, A., Ducloud, G., Agazzi, A., Dewailly, P., & Le Goff, R. (2024). Modeling the Thermoforming Process of a Complex Geometry Based on a Thermo-Visco-Hyperelastic Model. Journal of Manufacturing and Materials Processing, 8(1), 33. https://doi.org/10.3390/jmmp8010033







